Vowel constrictions are recoverable from formants

Abstract

The area function of the vocal tract in all of its spatial detail is not directly computable from the speech signal. But is partial, yet phonetically distinctive, information about articulation recoverable from the acoustic signal that arrives at the listener’s ear? The answer to this question is important for phonetics, because various theories of speech perception predict different answers. Some theories assume that recovery of articulatory information must be possible, while others assume that it is impossible. However, neither type of theory provides firm evidence showing that distinctive articulatory information is or is not extractable from the acoustic signal. The present study focuses on vowel gestures and examines whether linguistically significant information, such as the constriction location, constriction degree, and rounding, is contained in the speech signal, and whether such information is recoverable from formant parameters. Perturbation theory and linear prediction were combined, in a manner similar to that in Mokhtari (1998) [Mokhtari, P. (1998). An acoustic-phonetic and articulatory study of speech-speaker dichotomy. Doctoral dissertation, University of New South Wales], to assess the accuracy of recovery of information about vowel constrictions. Distinctive constriction information estimated from the speech signal for ten American English vowels were compared to the constriction information derived from simultaneously collected X-ray microbeam articulatory data for 39 speakers [Westbury (1994). Xray microbeam speech production database user’s handbook. University of Wisconsin, Madison, WI]. The recovery of distinctive articulatory information relies on a novel technique that uses formant frequencies and amplitudes, and does not depend on a principal components analysis of the articulatory data, as do most other inversion techniques. These results provide evidence that distinctive articulatory information for vowels can be recovered from the acoustic signal.

1. Introduction

A central question in phonetics is whether acoustic properties of the speech signal, such as formants, refer directly to linguistic units, or whether they refer to articulatory configurations and actions that themselves have linguistic significance (Fischer-Jørgensen, 1985; Goldstein & Fowler, 2003; Ladefoged, 1976). The answer to this question depends on whether phonetically distinctive articulatory information is accessible from the speech signal. If a listener can extract articulatory constriction parameters from acoustic patterns, e.g., formants or spectral moments, the articulatory pattern may serve the purpose of linguistic contrast. Alternatively, if it is impossible to extract distinctive articulatory information from the speech signal, a perceiver would not be able to depend on that information, and acoustic patterns would have to directly or indirectly signify linguistic categories. The question is central for theories of speech perception. Theories that take the objects of speech perception to be articulatory in nature, such as Motor Theory and Direct Perception (Fowler, 1986; Liberman, 1996; Liberman and Whalen, 2000), have provided evidence that explanation of perceptual patterns necessitates that listeners have access to distinctive articulatory information, but these theories do not point to what aspects of the speech signal actually signify speech gestures. That is, they are not implemented theories that show how the speech signal refers to the articulatory system. Rather experiments supporting these theories show the necessity of referring to articulation, but do not state how this reference is accomplished. On the other hand, other theories of speech perception, e.g., the General Auditory approach (Diehl, Lotto, & Holt, 2004), starting from the impossibility of solving the inverse problem, posit the goals of speech perception to be acoustic/auditory in nature. If it were shown that distinctive articulatory information can be reliably extracted from basic formant parameters, those theories would have to show how articulatory and acoustic information are integrated together, similarly to how audio and visual information are integrated in audio-visual perception (Massaro, 1998).

The question of whether acoustic properties of the speech signal can specify articulatory information is also crucial to theories of the goals of speech production. Theories that posit auditory/acoustic goals (Guenther, Hampson, & Johnson, 1998; Ladefoged, DeClerk, Lindau, & Papcun, 1972) require an inverse model that specifies an articulatory configuration, given an auditory/acoustic one. And theories that posit articulatory goals require a parity between the production and perception systems that assumes that articulatory and acoustic information can specify each other (Goldstein & Fowler, 2003; Liberman & Whalen, 2000). Therefore both types of theories of speech production assume that articulatory information is extractable from an acoustic specification.

Whether distinctive articulatory information is extractable from the acoustic signal is therefore a crucial issue to resolve for further development of basic theories in phonetics. The purpose of this work is to show that, for the particular case of American English vowels, it is possible to extract linguistically significant articulatory information from the speech signal, and, therefore, that it is possible for articulatory patterns to serve the purpose of linguistic contrast. The focus here is not on the general inverse problem of speech, since it is generally agreed that it is not possible to extract the area function in all of its detail from the acoustic signal (Sondhi, 1979), but rather on the extraction of articulatory information that can distinguish phonetic segments from each other in a linguistic system. The distinctive articulatory parameters we focus on are the constriction location, constriction degree, and rounding of the vowel, which have been used to parameterize the area function (Fant, 1960; Stevens & House, 1961) and to contrast vowels (Wood, 1979). We chose the American English vowel system, since it is a relatively dense system (Maddieson, 1984), so if it is possible to recover constriction parameters that distinguish the vowels in this system from each other, the method is likely to work on systems with fewer vowels. We present a novel technique for inversion that uses formant frequencies and amplitudes, and we show that this technique avoids the shortcomings of other methods. The inversion is tested by comparing recovered constriction location (CL), constriction degree (CD), and lip aperture (LA) with measurements of these quantities from simultaneously obtained articulatory data from the X-ray microbeam database (XRMB) for 39 participants and through an indirect comparison with constriction information from area functions measured from MRI data by Story (2005) for the same vowels from 6 speakers of American English.

There is already an extensive modern literature on the inverse problem in speech (Atal, Chang, Mathews, & Tukey, 1978; Ladefoged, Harshman, Goldstein, & Rice, 1978; Hogden, Rubin, McDermott, Katagiri, & Goldstein, 2007; Mokhtari, Kitamura, Takemoto, & Honda, 2007; Yehia, 1997); however the majority of it has been statistical in nature, requiring a principal components analysis or a vector quantization of already existing area functions, and establishing an abstract associative map to acoustic quantities. The technique developed here, on the other hand, makes use of intrinsic physical relations between formant parameters, namely frequencies and amplitudes, and physical parameters of the area function and does not necessitate a principal components analysis or a vector quantization of preexisting data. The reason for focusing on inversion based on physical links is that it is this type of inversion that is most likely to be used by a listener, and is therefore the type that is most phonetically relevant. Inversion based on a statistical analysis of a body of area functions assumes access to such bodies of area functions, which may not be accessible to a listener. Since a goal of this work is to determine the phonetic relevance of the accessibility of articulatory information, the focus is on inversion methods that depend on physical links between formants and constrictions.

2. Inversion based on physical links between acoustics and articulation

The fundamental theorem for recovery of system shape from continuous one-dimensional vibrational systems,¹ as it applies to lossless acoustic vibration in an arbitrarily shaped tube, is that in order to derive the area function uniquely, two sets of resonance frequencies of vibration for the same tube must be known (Borg, 1946). The first set consists of the resonance frequencies of the tube when volume velocity is fixed at zero at one end, while pressure is fixed at zero at the other end (closed-open condition). The second set contains the resonance frequencies of the tube when volume velocity is fixed at zero at both ends (closed–closed condition) or when pressure is zero at both ends (open–open condition). The unique cross-sectional area of an arbitrarily shaped tube undergoing lossless acoustic wave propagation can be determined (up to a scaling constant), if both infinite sets of resonances are known.

If we apply this basic result to speech production by assuming that acoustic wave propagation in the vocal tract is linear, lossless,² one-dimensional, and planar, we arrive at the under-determined nature of the inverse problem: under these highly unrealistic assumptions, all that can be measured from the signal are a few formant frequencies (rarely more than 4) under only one condition, the closed-open condition, and even that assumption is only valid in the few milliseconds of each pitch period when the glottis is closed (which sometimes does not even occur) and ignores radiation of sound at the lips. The inverse problem is said to be ill-posed for the lossless tube, since there is an infinite set of vocal tracts with the same closed-open resonance frequencies, but different closed–closed or open–open resonance frequencies, and also because the length of the vocal tract needs to be known. Thus a formant pattern resulting from a lossless closed-open vocal tract does not uniquely refer to the tract that gave rise to it. This negative result, first put forth by Schroeder (1967), is well known in phonetics (Atal et al., 1978). However, it is important to note that this is not a general result about all vibratory systems. It is a result that assumes a purely lossless model.

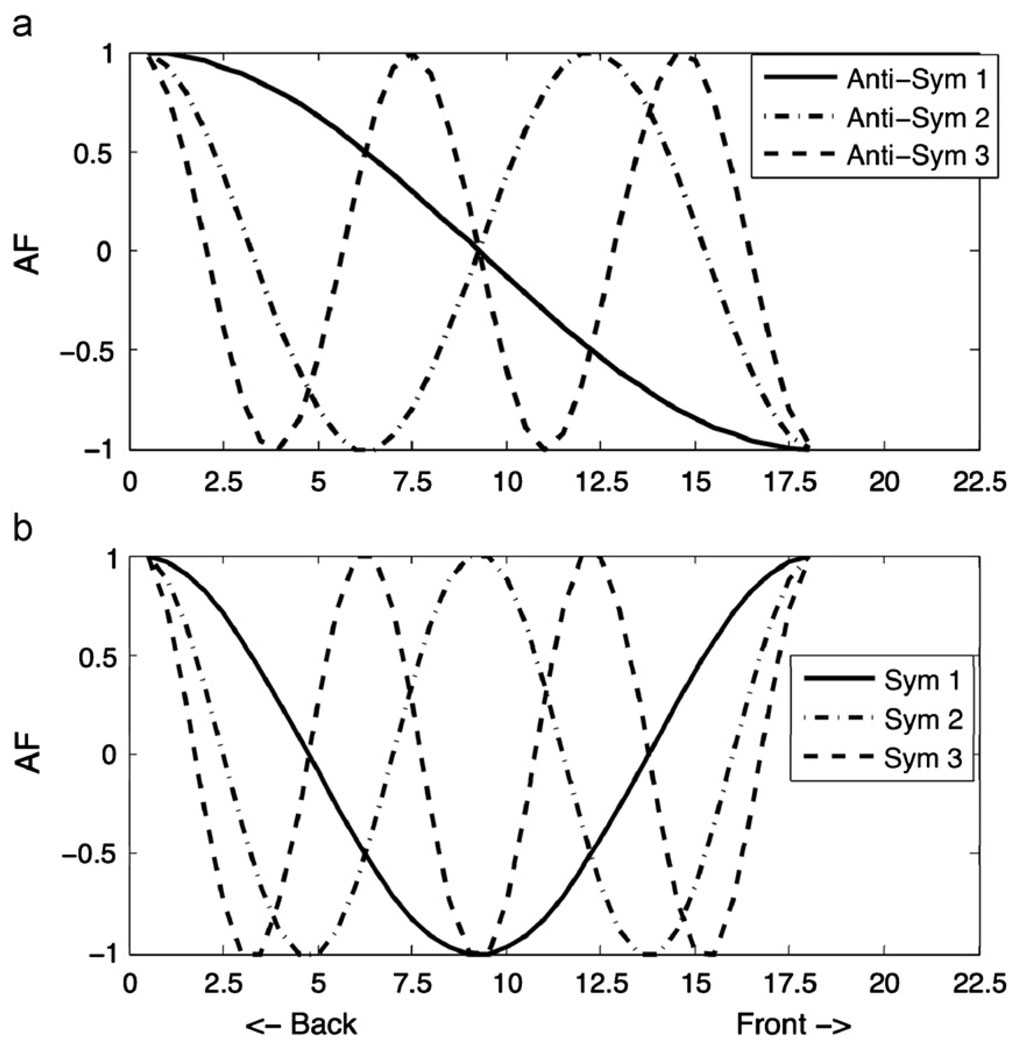
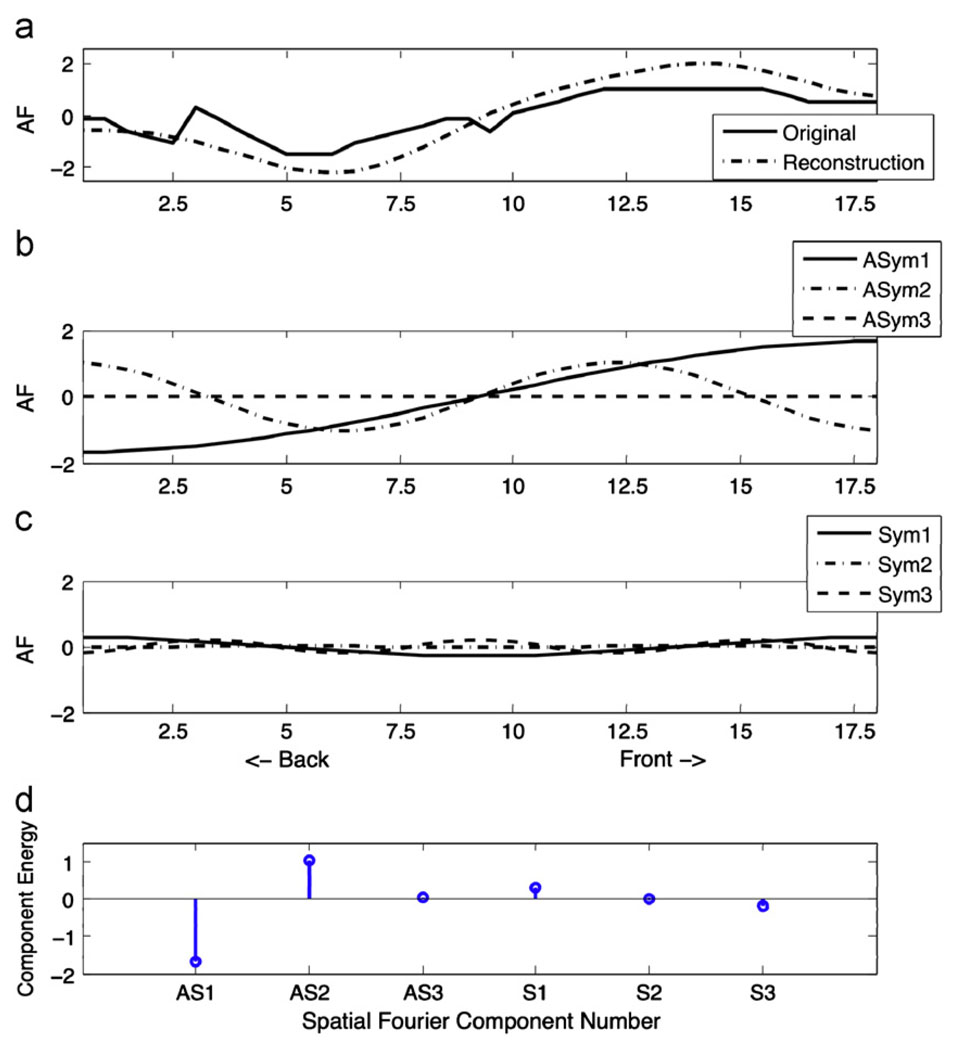
Schroeder (1967) and Mermelstein (1967) also provided an important positive result that is not as well known in phonetics (but see, Broad & Wakita, 1977; Carré & Mrayati, 1995; Mokhtari, 1998; Story, 2007). This result is based on a spatial discrete Fourier transform of the logarithm of the area function. Performing the spatial Fourier transform amounts to finding the similarity between the area function and sinusoids of different spatial frequency, half of which are symmetric around the midpoint of the vocal tract and the other half are anti-symmetric. Fig. 1 shows the first three anti-symmetric sinusoids in the top panel (a) and the first three symmetric sinusoids in the lower panel (b). Fig. 2 shows the area function of the vowel /a/ produced by the Russian speaker of Fant (1960) in the top panel (a), together with a reconstruction of that area function from its lowest three antisymmetric and symmetric spatial frequencies. The second and third panels show the anti-symmetric and symmetric components of that area function. The phonetic interpretation of the spatial Fourier transform of the logarithm of the area function is as follows: if a particular sinusoid is highly similar to an area function, leading to a peak in the spatial spectrum, it means that the area function has a spatial mode of variability similar to that sinusoid. For instance, a high peak for the first anti-symmetric component means that the area function is enlarged in the pharynx and constricted in the oral cavity, whereas a high peak for the first symmetric component means that the vocal tract is constricted in the middle and open at both ends. The spatial spectrum of the logarithm of the area function is shown in the bottom panel, showing a high negative coefficient for the first anti-symmetric component, a high positive coefficient for the second anti-symmetric component, and smaller coefficient for the first symmetric component.

Fig. 1.

Antisymmetric and symmetric basis functions of the discrete Fourier transform.

Fig. 2.

Vowel /a/ area function (top panel) from Fant (1960), with antisymmetric (second panel) and symmetric components (third panel), and reconstruction of the area function from its Fourier components. Bottom panel shows the spatial “spectrum” for /a/.

Schroeder (1967) and Mermelstein (1967)’s main result, based on first-order perturbation theory, is that there is a direct one-to-one linear relation between the coefficients of the Fourier components of the logarithm of the area function and the formant frequencies of the acoustic signal, under two conditions at the ends of the vocal tract. This correspondence was motivated by first-order perturbation theory, and supported by Mermelstein (1967)’s simulations of more general configurations. If the Fourier components are numbered such that the odd numbered ones are anti-symmetric and the even ones are symmetric, the quantitative relation between the spatial anti-symmetric Fourier component coefficients a_2n−1, and the formant frequencies $F_n^{\text{co}}$ for the closed-open condition is

$$a_{2n-1}=-2\frac{F_n^{\text{co}}-f_n^{\text{co}}}{f_n^{\text{co}}},$$

where n = 1, 2, 3,… and $f_n^{\text{co}}$ is nth formant frequency of a neutral tube for a given tube length (e.g., $f_1^{\text{co}}=500,f_2^{\text{co}}=1500,f_3^{\text{co}}=2500$, etc. for a 17.5 cm tube). So if the closed-open formant frequencies are known, along with the corresponding formant frequencies for a neutral tract, the anti-symmetric components of the area function can be constructed. Note that if the formant frequency measured from the signal is higher than the corresponding neutral tract formant frequency, the Fourier component coefficient is negative, whereas if the measured formant frequency is less than the corresponding neutral tract formant frequency, the coefficient is positive. For the area function in Fig. 2, for instance, since the coefficient of the first anti-symmetric component is large and negative, the first formant should be high relative to the neutral configuration, and, since the coefficient of the second anti-symmetric component is large and positive, the second formant should be relatively low, with other formant frequencies close to their neutral value. There is, therefore, a close correspondence between the familiar spectrum derived from the speech waveform, traditionally parameterized with formant frequencies, and the anti-symmetric spatial spectrum of the log area function. It is important that this correspondence is a purely physical relation between formant frequencies and area functions.

Schroeder (1967) and Mermelstein (1967)’s results suggest that partial information about the area function can be obtained from closed-open resonance frequencies alone. Constraints on articulation lead to highly anti-symmetric shapes for area functions of several vowels. Indeed, Mermelstein (1967) was able to perform high quality prediction of the area function changes in natural speech from the formant frequencies alone, while holding the symmetric components of the vocal tract fixed. However, his method was most successful only for vowels like /i/ and /a/, which have a strong anti-symmetric component, but it was not successful for vowels like /u/ with a constriction near the middle of the vocal tract, introducing a strong symmetric component. To directly measure both sets of resonance frequencies for any vowel, speech is measured at the end of a long impedance (Sondhi) tube attached to the mouth (Schroeder, 1967). This technique requires speakers to produce speech without phonating, which is unlikely to accurately reflect natural speech. Schroeder (1967) and Gopinath and Sondhi (1970) used this technique successfully, but for inversion to be useful in natural speech perception, it must be performable on the speech signal as normally produced.

An alternative model (Kelly & Lochbaum, 1962) of the vocal tract is also lossless throughout the tract, but the termination at one end is a resistance, i.e., a frequency-independent loss. This type of model is traditionally termed a Discrete Matched Impedance model (DMI) (Furui, 1989), since a frequency-independent loss at one end of the tube implies that sound waves, when they reach that end, would simply exit without reflecting back into the mouth. So there is no impedance mismatch, i.e., the impedance is matched.

Atal (1970), Atal and Hanauer (1971), and Wakita (1973) showed that if the vocal tract is modeled as DMI, and if radiation and glottal effects on the overall system transfer function can be compensated for, it is possible to invert the speech signal and obtain the shape of the vocal tract.³ They also introduced algorithms for extracting vocal tract shape from the speech signal. Wakita (1973), Markel and Gray (1976), and Harrington and Cassidy (1999) illustrated the working of the vocal tract reconstruction algorithm by deriving reasonable vocal tract shapes for static vowels, vocalic transitions, and consonant–vowel transitions from single participants. However, there has never been an investigation of an entire vowel system for a large number of speakers.

Atal (1970)’s result is based on the following: for a DMI system, both required resonance frequencies (closed-open and closed–closed) are obtainable from the speech signal itself. Atal (1970) and Wakita and Gray (1975) effectively showed that the input impedance of a DMI system is derivable from the transfer function, the frequency-domain representation of speech signal. This is not true for the lossless systems analyzed by Schroeder (1967) and Mermelstein (1967), where the input impedance and transfer function are independent functions. Milenkovic (1984) presented a power balance argument for deriving the simple relation between input impedance and transfer function for DMI systems, and Wakita and Gray (1975) presented an algorithm for deriving the lip input impedance from the speech signal using linear prediction.

However, several researchers have shown that the quality of vocal tract shape reconstruction using these algorithms is sensitive to signal processing issues. The most problematic issues are bandwidth mis-estimation, use of incorrect models to compensate for glottal and radiation spectral effects, and the necessity of assuming vocal tract length. Sondhi (1979) and Strube (1977) showed that it is possible to estimate unlikely vocal tract shapes if the bandwidths are misestimated or if improper preemphasis is applied. Wakita (1977) showed that the algorithms are sensitive to changing the assumed vocal tract length, but that general aspects of the shape, e.g., the location of the major constriction, are not highly sensitive to assumed length. Since it is hard to estimate the parameters of the DMI model and this estimation is prone to signal processing errors, Atal (1970) and Wakita (1973)’s results have not been often cited in phonetics. The other major drawback of this method that has limited its applicability in engineering applications is the low spatial resolution of about 2 cm when the signal is bandlimited to 4 kHz (Strube, 1977). But for the purpose of linguistic phonetics, especially the phonetics of vowels, where constrictions are distributed, this spatial resolution may be sufficient. To recover articulatory information for segments distinguished by smaller distances, e.g., different coronal consonants, it will be necessary to use more elaborate models of the vocal tract.

Rice and Öhman (1976) made an important advance in DMI research. Using a vocal tract model, they showed that individual symmetric components of the area function affect bandwidth pseudo-orthogonally. That is, the first symmetric component increases B1, but changes the other formant locations and bandwidths very little. The second symmetric reduces B2, etc. This is a very important result, since it shows a unique relation between individual bandwidths and the symmetric components of the area function. If bandwidths were measureable, therefore, it is possible to reconstruct the area function from them and the formants, using an algorithm like that used by Schroeder (1967) and Mermelstein (1967), by summing anti-symmetric and symmetric sinusoids weighted by normalized formant frequencies and bandwidths (where the normalization is by the formant frequencies and bandwidths of a neutral tube of a specific length for each subject). Mokhtari (1998) re-discovered the relation between the symmetric components of the area function and individual bandwidths, and used the basic principles of linear prediction to show that variation of each individual bandwidth yields a change in only one symmetric component and very little in others. The results of Rice and Öhman (1976) and Mokhtari (1998) go beyond earlier research in another important way. Instead of relating the speech signal as a whole to the articulatory object it refers to, as Atal (1970) and Wakita (1973) had done, the novel links between bandwidths and the symmetric components of the area function allow us to relate individual components of the signal to individual components of the area function. Indeed it is this decomposition of the relation between acoustics and articulation into individual components that makes these results potentially valuable to phonetics, as will be discussed later.

2.1. Acoustic methods

We believe that the main reason that these results are not routinely used to extract articulatory information from speech signals is that bandwidths are notoriously difficult to estimate. Indeed Bishnu Atal, the pioneer of linear prediction, which is one of the primary methods of formant estimation, has shown that the method often fails in predicting bandwidths (Atal, 1974), since the all-pole spectrum estimated via linear prediction is a good representation of the real spectrum at the peaks of the spectrum, but a poor representation at the troughs. This is of course due to the fact that the all-pole model does not account for the zeros that shape the troughs. Since bandwidths depend on both the location of peaks and troughs, linear prediction yields a poor estimate.

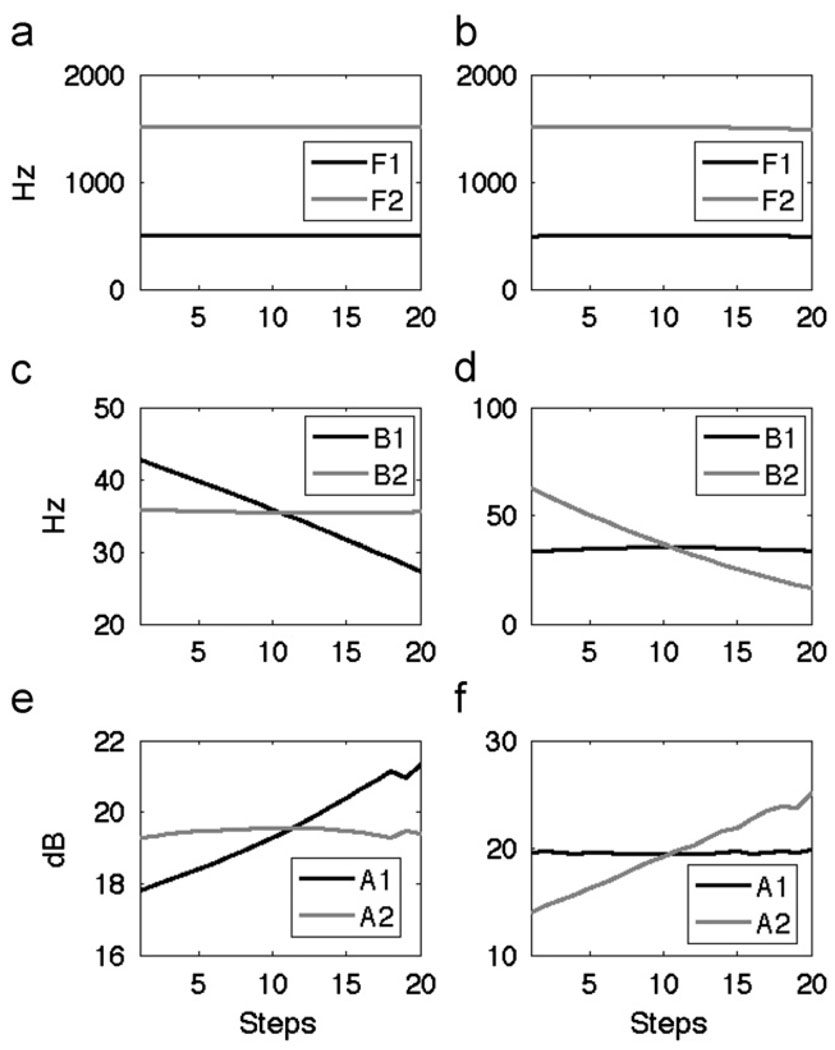
However, formant amplitudes, which are related to band-widths, are measured at the peaks of the LPC spectrum, and may therefore be more reliably measured. The relevance of formant amplitudes is that network theory shows that there are simple relations between bandwidths and spectrum amplitudes for low bandwidth (underdamped) systems. Since reactive (lossless) effects in speech are higher than dissipative effects (Flanagan, 1972), it is reasonable to use the underdamped approximation. If each formant is taken as the output of a second-order system, amplitude and bandwidth are inversely related. This basic relation is superimposed on other sources of variability of formant amplitudes that are result of how close formants are to each other (Fant, 1956). To determine if this simple relation is relevant to distributed models, a simulation was performed to determine the effect of perturbing the symmetric component of the area function on formant frequencies, bandwidths, and amplitudes, similar to the simulations of Rice and Öhman (1976) and Mokhtari (1998). The symmetric perturbations were in the form of the symmetric Fourier components in Fig. 1b. The amplitudes of these symmetric components were varied in small steps, to determine the effect on the formant parameters. In this simulation, the mean area function was 5 cm², and the amplitudes of the maximum perturbations were 3 cm² above and below the average area. There were 20 steps of symmetric perturbation. The simulation consisted of synthesizing area functions by summing sinusoids, transforming the discrete area functions to reflection coefficients, transforming from reflection coefficients to linear prediction coefficients, and finally evaluating the transfer function whose denominator is the linear prediction polynomial at frequencies up to 4 kHz.

The results are shown in Fig. 3. The effects of the first and second symmetric components are shown in the left and right panels, respectively. As expected from the work of Schroeder and Mermelstein, the formant frequencies do not vary markedly due to changes in the symmetric components (Figs. 3a, b). And as expected from the work of Rice and Öhman (1976) and Mokhtari (1998), B1 is affected mostly by the first symmetric component and B2 is affected mostly by the second symmetric component (Fig. 3c,d). As can be seen from Fig. 3e,f, the symmetric components of the area function do have an effect on A1 and A2 (the amplitudes of the first two formants), inversely proportional to the effect on B1 and B2. Moreover, the first symmetric component affects mostly A1, whereas the second component affects mostly A2. We use this inverse relation to approximate the amplitude as a measure of the inverse of the bandwidth in the analysis to follow. It may seem that since amplitudes and bandwidths are inversely related, there is no gain from measuring one, instead of the other. The difference is that amplitudes can be more reliably estimated from an LPC spectrum than are bandwidths, since amplitudes are measured at the peaks of the LPC spectrum, not the troughs, and the former are more reliably estimated in the LPC all-pole spectrum.

Fig. 3.

Effect of perturbing the symmetric components of the vocal tract on Formants (upper row), bandwidths (middle row), and amplitudes (bottom row).

There are several problems with this approach. First, formant amplitude is only approximately related to bandwidth by simple inversion. Second, amplitude is affected by the proximity of formants as was shown by Fant (1956), besides also being affected by the bandwidth through the symmetric component of the area function. In addition, bandwidth and amplitude are affected by losses distributed throughout the vocal tract, where DMI is not a good approximation.

Therefore to quantitatively examine how well the approximate inverse relation between amplitude and bandwidth extends to a vocal tract with losses and with anti-symmetric as well as symmetric perturbations, we performed simulations with Maeda’s digital lossy model (Maeda, 1982). Wall vibration, radiation and friction/heat losses were included.⁴ In the simulations, constriction location was moved along the main axis of the vocal tract (17.5 cm) in 33 steps and constriction degree was varied in three steps from 3 to .8 cm² for a total of 99 configurations. It is to be noted that each configuration contained an anti-symmetric and a symmetric component. The transfer function was calculated for each configuration and the first three formant bandwidths and amplitudes were extracted and correlated with each other. The correlations were as follows: B1 and A1, r = −.774; B2 and A2, r =−.587; and B3 and A3, r = −.376. Therefore for the first two formants of a lossy vocal tract with anti-symmetric and symmetric perturbations there is a high inverse correlation between amplitude and bandwidth, whereas for the third formant, the correlation is weak. We will therefore use the frequencies and amplitudes of only the first two formants.

The algorithm for inversion we use is therefore an extension of the algorithm used by Schroeder (1967) and Mermelstein (1967). In the original algorithm, if we limit the approximation to two formants, the two lowest anti-symmetric and two symmetric Fourier components are weighted by neutral tube normalized closed-open and closed–closed resonance frequencies, respectively. After each of the Fourier components is weighted, the sum of all four functions is computed. And that is the estimate of the area function. In the algorithm used here, the Fourier components differ only in that the symmetric ones are opposite in sign to the ones used for the lossless case, to capture the inverse relation between formants and amplitudes. The closed-open resonance frequencies are approximated by the formant frequencies measured from the speech signal. Another approximation is that instead of trying to measure the length of the vocal tract to determine the neutral tube formants for the normalization step $(a_{2n-1}=-2(F_n^{\text{co}}-f_n^{\text{co}}/f_n^{\text{co}}))$, we instead standardize F1 and F2 for each subject, by calculating for that subject the mean and standard deviation of F1 and F2 across all the vowels for that subject and normalizing F1 and F2, replacing them by their z-scores. And for the closed–closed resonance frequencies, we use the z-scores for A1 and A2, where the z-scores are calculated by subtracting from each amplitude, the mean amplitude for that subject and dividing by the standard deviation within that subject. Therefore instead of relying on information about vocal tract length, we use instead speaker-normalization by standardizing formants within each subject.⁵ F1, F2, A1, and A2 z-scores are then used as the weights for the first two anti-symmetric and symmetric functions (with the latter multiplied by −1 to account for the inverse relation between formant amplitude and bandwidth). The first anti-symmetric component is the cosine function evaluated from 0 to π, while the second anti-symmetric component is the cosine function measured from 0 to 3π. The anti-symmetric components are the sine function evaluated over the same periods. The weighted components are then summed to yield the estimate for the area function.

2.2. Articulatory methods

The goal of this study is to determine whether articulatory information about vowel constrictions is extractable from the acoustic signal. To examine whether this is possible, it is necessary to compare two types of data: measured articulatory data on vowel constrictions and the corresponding acoustically estimated information. The Wisconsin X-ray Microbeam Database (XRMB) (Westbury, 1994) was used, since it contains a fairly good estimate of vocal tract configuration during many tasks by many speakers. The tasks extend in complexity from productions of static vowels to paragraphs produced at natural speaking rates. For this study, the simplest static task was chosen, but as the question of invertibility is extended to dynamic transitions and consonants, it is possible to use more complex tasks, while still using the same speakers. The main advantage for using the Wisconsin database here is to show that constriction location (CL) and constriction degree (CD) are reliably extractable for a large number of speakers. It is still very difficult to acquire and analyze the necessary data from a large number of participants using any of the commonly available techniques, like MRI. The main disadvantages of XRMB for our purpose are that the data are two-dimensional and tracks tongue points only in the oral region (sometimes upper pharyngeal). Therefore the articulatory estimates are also compared to measurements of area functions made by Story (2005). The following subsections will present how CL and CD were estimated from the X-ray pellet data.

2.3. X-ray microbeam speakers and data

39 participants were selected from the database, 17 male and 22 female. Data from more than 50 participants are available in the database, but many of these have missing tongue pellets in one of the tasks chosen from the database. The participants in the study are ones that the articulatory estimation methods used in this study were applicable for. Using the participant numbers from Westbury (1994), the male participants used are: 11,12, 15, 18, 19, 24, 28, 32, 41, 43, 45, 53, 55, 58, 59, 61, and 63 and the female participants are 13, 14, 16, 20, 25, 26, 27, 30, 31, 33, 34, 35, 36, 37, 39, 48, 49, 52, 54, 56, 60, and 62. Speaker characteristics are available in Westbury (1994).

The data analyzed in this study consist of steady state portions of the vowels /i/, /I/, /e/, /ε/, /æ/, /u/, /℧/, /o/, /ɔ/ and /a/. These vowels were chosen because they are a dense set with several vocalic contrasts represented. The database contains tongue, jaw, and lip measures for a large number of American English participants, as well as palate traces and an estimate of the location of the posterior pharyngeal wall. Tongue data consists of the motion of 4 pellets (T1, T2, T3, T4), with the first about 1 cm from the tip and the fourth, usually in the velar-uvular region, but sometimes in the upper pharyngeal region. Task 14 was used, in which participants produced steady state vowels in isolation. Forty millisecond windows were extracted from the middle of each vowel and the articulatory frame in the middle of that window was also extracted.

To obtain constriction location (CL) from the X-ray microbeam data, a cubic spline was passed through the four tongue pellets, then the distance from each point on the tongue was measured from each point on the hard palate. Distance minimization then yields the points on the palate closest to the tongue. The horizontal position of that point on the palate from the occlusal zero is then taken as an estimate of CL. CD was estimated as the highest position of the four pellets. For each participant the CL and CD were converted to z-scores across all of that speaker’s measured tokens.

There are two main sources of error associated with this procedure. First, the tongue is more complexly shaped than a cubic spline interpolating T1–T4, therefore the point on the spline closest to the palate is not necessarily on the tongue. However, a study by Kaburagi and Honda (1994) compared tongue shapes interpolated from points on the tongue tracked by an electromagnetic system to the shape of the tongue simultaneously measured using ultrasound, and found the average error to be approximately a millimeter. Therefore, at least for vowels, the shape of the tongue in the oral region is approximated sufficiently well by cubic spline interpolation between pellets, so that it is possible to use the interpolation as an estimate of the tongue shape. The other main source of error is that for vowels whose constriction is in the pharynx, there will be an error arising from the estimation of CD and CL. For this reason, we have also included an analysis of area function data estimated from MRI scans from 6 American English participants of Story (2005).

Another important aspect of vowel production is lip aperture (LA). The XRMB database contains data for upper lip and lower lip. LA was calculated by subtracting lower lip position from upper lip position.

2.4. Acoustic analysis

The 40 ms at the center of each vowel was extracted. The speech was pre-emphasized and a hamming window was applied. An LPC spectrum (LPC analysis order = 12) was then computed for each vowel from each subject and automatic peak-picking was applied to extract F1, F2, A1, and A2. For each subject, z-scores of each of these quantities were then computed by subtracting the mean quantity for that subject from each measurement of each vowel and dividing by the standard deviation of the quantity within that subject. These numbers were then used as the weights for anti-symmetric and negative symmetric Fourier components, respectively, which were all summed to produce an acoustically estimated area function. CD and CL were then calculated as the degree and area at the point of minimal constriction. As discussed earlier, standardization of the acoustic data is used to make it un-necessary to approximate the length of the vocal tract. This amounts to applying a basic method of speaker-normalization for the data to be comparable across subjects.

2.5. Statistical analysis

To quantitatively analyze how CD, CL, and LA contrasts among the vowels of American English are captured by acoustic reconstruction vs. by the articulatory measurements made across the speakers, the measurements and estimates are all speaker-standardized and replaced by z-scores. One-way analysis of variance is then conducted with the vowels as groups and the dependent measures as CD, CL, or LA z-scores. The quantitative evaluation of how well measurement and estimation reveal the contrasts amongst the vowels is then done through a p-value adjusted post-hoc test and the contrasts are expressed in standard deviations (since z-scores are expressed in standard deviations) as differences in means between the different vowels. The measured and estimated quantities are then compared in how well each of them reveals the contrasts among the American English vowels, which is indicated by whether a particular contrast is registered by the post-hoc analysis as significant or not. We believe that the quantification of vowel contrasts in terms of significant and non-significant differences in means, and quantitatively expressed in standard deviations, is a particularly direct way of quantifying the phonetic differentiation that accompanies linguistics contrast.

3. Results

The aim of this section is to determine if the algorithm used is able to extract the main distinctive features of the vowels of American English. Moreover, we will try to determine the differential contributions of the formant frequencies and the bandwidths/amplitudes.

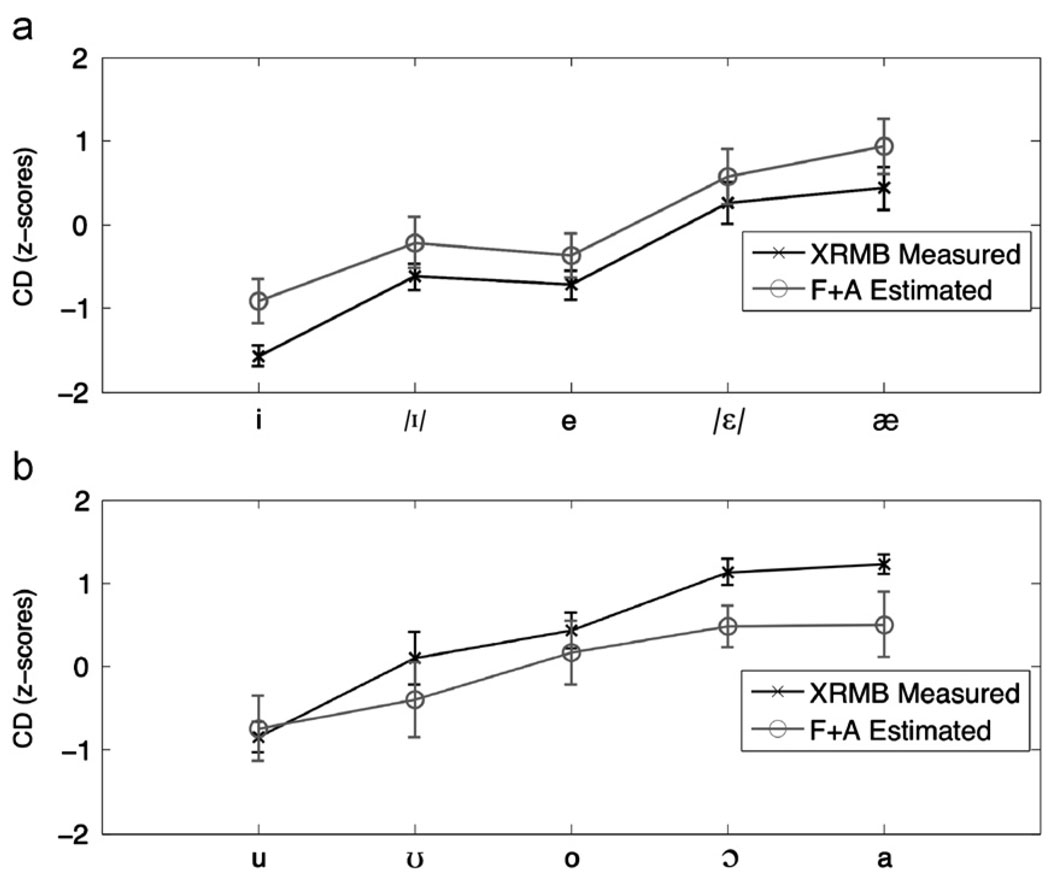
Fig. 4a compares the constriction degrees of the front series of vowels measured from XRMB and estimated from formant frequencies and amplitudes (F+A).⁶ Two sets of acoustic estimates of CD were performed, one with formant frequencies (F1 and F2) and amplitudes (A1 and A2) and the other with formant frequencies only. Male and female data are presented together. The data are presented as z-scores to enable the comparison between the measured and estimated CDs. The measures are presented as means and standard errors. The main features of the measured series are captured by the F+A estimated series as can be seen in Fig. 4. Two ANOVAs were performed, with vowel being the independent variable in both, while the F+A estimated CDs were the dependent variable in one and the CD measured from XRMB data were the dependent variable in the other. Both showed that the data in the groups differed significantly by vowel (p<.001). For the XRMB-measured CDs F(4190)=162.4 and for the F+A estimated CDs F(4190)=34.1. To establish whether the contrasts between the vowels captured in the XRMB are preserved in the F+A estimated CDs, a p-value adjusted post-hoc Tukey HSD test was performed after each ANOVA. Table 1 shows the pairwise difference in means between each of the groups, with the measured value from articulation on the left and the modeled value from acoustics on the right. In the measured data, /i/ is distinct from all the other vowels. The same is true for the F+A estimated data. Indeed, all the other contrasts revealed by pairwise comparison are approximately the same in the measured and F+A estimated sets. Therefore the XRMB-measured CD and the F+A derived CD contrasts agree in how they distinguish American English vowels from each other. Moreover, the formant-only and formant-and-amplitude estimates were almost identical, indicating that the formants alone are sufficient in extracting constriction parameters for the front series.

Fig. 4.

Means and standard errors for constriction degree (CD) for the front series (a) and back series (b) of vowels for 39 speakers of American English, measured from XRMB (black), acoustically reconstructed (dark gray).

Table 1.

Pairwise difference in means of CD for 5 American English front vowels from 39 speakers. In each cell, the left member is the difference measured from XRMB data (XRMB) and the right member is from formant+amplitude reconstruction (F+A). Bold numbers indicate a significant difference (p<.05).

	/I/		/I/		/e/		/ε/		/æ/
	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A
/i/
/I/	−.84	−.65
/e/	−.92	−.47	−.070	.18
/ε/	−1.75	−1.32	−.90	−.67	−.83	−.86
/æ/	−2.09	−1.72	−1.2	−1.16	−1.17	−1.38	−.34	−.44

Fig. 4b shows the CD data for the back series of vowels. Again the overall patterns in both sets are similar and both ANOVAs showed significant differences between the groups (p<.01; measured set F(4, 190)=179.3; estimated set F(4, 190)=22.2). Post-hoc pairwise comparisons were the same in both sets of data except for three pairs: /u/-/℧/, /o/-/ɔ/, and /o/-/a/ as can be seen in Table 2, which shows the pairwise differences in means. Out of the ten pairwise comparisons, the F+A derived CDs differ from the XRMB-derived CDs on three contrasts. Again, the formant-only and formant-and-amplitude estimates perform very similarly, indicating that CD for vowels can be derived from formant frequencies only.

Table 2.

Pairwise difference in means of CD for 5 American English back vowels from 39 speakers. In each cell, the left member is the difference measured from XRMB data (XRMB) and the right member is from formant+amplitude reconstruction (F+A). Bold numbers indicate a significant difference (p<.05). A black box around a pair indicates discrepancy between the articulatory measurement and the acoustic reconstruction.

	/u/		/℧/		/o/		/ɔ/		/a/
	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A
/u/
/℧/	−.91	−.34
/o/	−1.32	−.95	−.40	−.60
/ɔ/	−2.08	−1.22	−1.16	−.90	−.75	−.29
/a/	−2.22	−1.28	−1.31	−.91	−.90	−.30	−.14	−.00

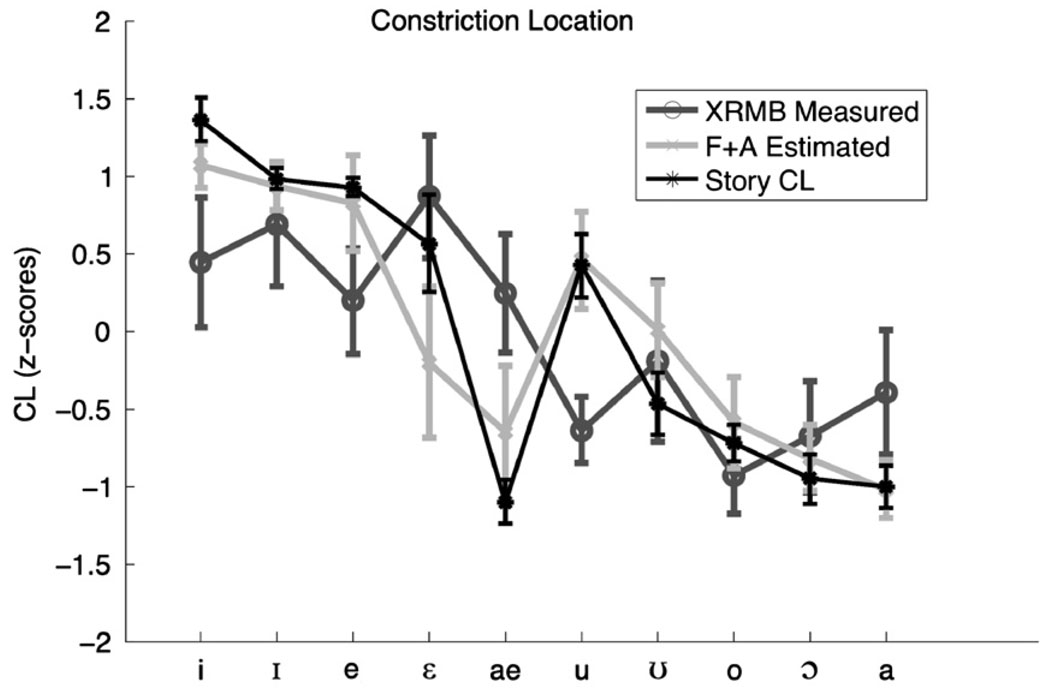
Fig. 5 shows the measured and estimated CL for the front and back series. Acoustic estimates of CL for /i/, /I/, and /e/ are different in z-score magnitude from the XRMB-measured ones, but they agree on the placement of these vowels in the system of American English vowels. For /ε/ and /æ/, however, there is discrepancy. The XRMB-based measurement takes these to be vowels whose major constriction is in the front of the vocal tract, whereas the acoustic reconstruction assigns their constriction location to be in the back. However, this discrepancy is most probably due to the fact that there is no information in the pharyngeal region in the XRMB data. Moreover, these two vowels are low front vowels and may also have a constriction in the pharynx (Wood, 1979). Also superimposed on the figure are CL measurements from the area functions of 6 speakers of American English estimated from MRI by Story (2005),⁷ also expressed in z-scores. Comparison of the articulatory Story CL and F+A acoustic CL estimate in Fig. 5 shows that the two estimates rise and fall together, even though they are from different sets of speakers. This general agreement is an indication of the quality of the acoustic estimate. Crucially, for the vowel /æ/ the F+A derived CD estimates agree with CL estimates from the MRI data in that both are pharyngeal. However, the CL vowel of /ε/ is more advanced than predicted acoustically. This is likely due to the presence of both back and front constrictions as can happen for this vowel, but the acoustic estimate used here is not sensitive enough to approximate the balance between them. The Story data CL estimate also agrees with the F+A estimate, showing that the F+A estimates are able to estimate the presence of a constriction near the middle of the vocal tract. Indeed, the most significant difference between the formant frequencies-only and F+A reconstruction is that for the vowel /u/. The formants-only estimate of /u/ CL is not significantly different from that for /i/, according to a Tukey HSD test, whereas the /u/ CL obtained from formant frequencies and amplitudes is significantly posterior to that for /i/. Table 3 presents the difference in means in standard deviations between the vowel categories for the Story (2005)-derived CL measures and the formant frequencies and amplitudes estimates. Of the 45 contrasts 6 do not agree, however inspection of the z-scores shows that the z-scores are quite similar between the estimates and the measures, therefore the discrepancy is more likely to be due to the different magnitudes of variabilities in the two sets of data, and is not due to essential differences in how each conveys the contrasts between vowels in American English.

Fig. 5.

Mean and standard errors for constriction location (CL) from 3 American English vowels for 39 speakers of American English, measured from XRMB (black cross), acoustically reconstructed (gray circle), and formants-only reconstruction (dashed), and MRI (gray).

Table 3.

Pairwise difference in mean CL estimated acoustically from 39 speakers of American English vs. measured from MRI data from 6 speakers of Story (2005). In each cell, the left member is the difference measured from XRMB data (XRMB) and the right member is from formant+amplitude reconstruction (F+A). Bold numbers indicate a significant difference (p < .05). A black box around a pair indicates discrepancy between the MRI data and the acoustic reconstruction.

	/i/		/I/		/e/		/ε/		/æ/		/u/		/℧/		/ɔ/		/ɔ/
	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A	MRI	F+A
/I/	.38	.14
/e/	.34	24	−.04	.11
/ε/	1.53	1.27	1.15	1.13	1.18	1.02
/æ/	2.32	1.72	1.94	1.58	1.98	1.47	.79	.45
/u/	.65	.61	.28	.47	.31	.36	−.87	−.66	−1.74	−1.1
/℧/	1.29	1.06	.91	.92	.95	.82	−.24	−.21	−1.0	−.66	.64	.45
/o/	1.77	1.65	1.39	1.52	1.43	1.41	.25	.39	−.55	−.06	1.12	1.05	.48	.59
/ɔ/	1.84	1.89	1.46	1.75	1.49	1.64	.31	.62	−.49	.17	1.18	1.28	.54	.83	.06	.23
/a/	2.23	2.09	1.85	1.95	1.89	1.84	.70	.82	−.09	.37	1.57	1.48	.94	1.03	.46	.43	.39	.20

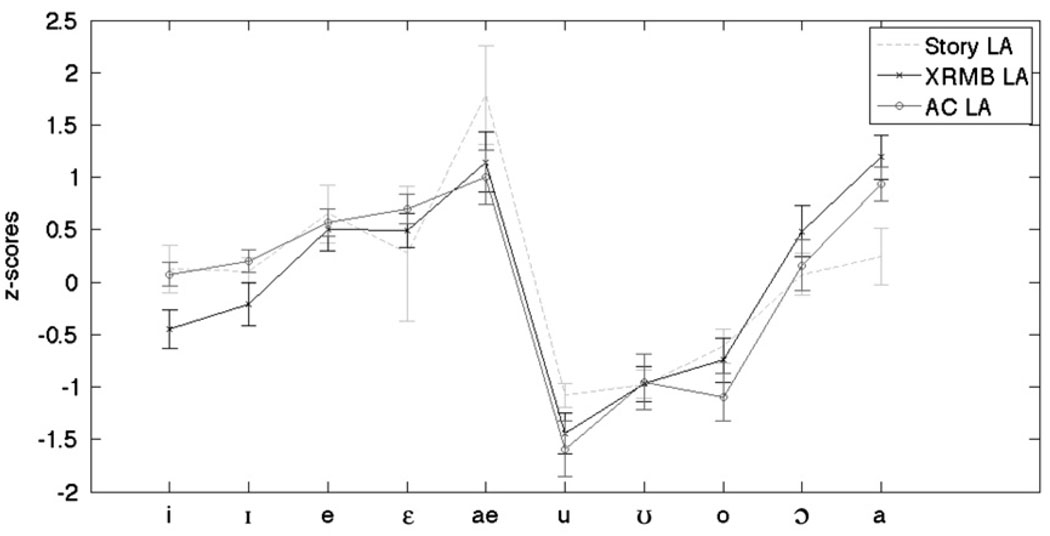
The LA data are shown in Fig. 6. The comparison is between the F+A derived LA (which are the same for the formant frequency only and amplitude and formant frequency data, since the symmetric functions have 0 contribution at the ends of the vocal tract), the XRMB data, and the Story et al. data (calculated simply as the last value in the area function). All the rounded vowels except /ɔ/ have significantly lower LA than the non-rounded vowels for the acoustic estimate and the measurements. The lack of rounding for the vowel /ɔ/ is somewhat unexpected, but the articulatory data also shows that for that vowel, there is no significant rounding. Table 4 presents the difference in means of LA for the American English vowels for the XRMB data (left) and the acoustic reconstruction (right). There is agreement in 40 out of the 45 contrasts. Four out of the 5 discrepancies are over the vowel /ɔ/, which both the articulatory data and the acoustic data estimate to be as unrounded as the front vowels, but they differ in its precise positioning among the vowels leading to the discrepancies. Another discrepancy is for the /ε/-/a/ contrast, however both the measured and estimated LA agree in that both vowels are unrounded as can be seen from the magnitude of the z-scores, which are positive for both.

Fig. 6.

Mean and standard errors for LA from 3 American English vowels for 39 speakers of American English, measured from XRMB (black cross), acoustically reconstructed (gray circle), and MRI (gray).

Table 4.

Pairwise difference in mean LA estimated acoustically from 39 speakers of American English vs. measured from XRMB for same speakers and tokens. In each cell, the left member is the difference measured from XRMB data (XRMB) and the right member is from formant+amplitude reconstruction (F+A). Bold numbers indicate a significant difference (p < .05). A black box around a pair indicates discrepancy between the XRMB data and the acoustic reconstruction.

	/i/		/I/		/e/		/ε/		/æ/		/u/		/℧/		/o/		/ɔ/
	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A	XRMB	F+A
/I/	−.25	−.13
/e/	−.99	−.49	−.75	−.37
/ε/	−.99	−.62	−.74	−.49	.01	−.13
/æ/	−1.66	−.93	−1.41	−.80	−.66	−.43	−.67	−.31
/u/	1.04	1.67	1.28	1.79	2.03	2.16	2.02	2.29	2.69	2.59
/℧/	.55	1.03	.79	1.15	1.54	1.52	1.53	1.65	2.20	1.95	−.49	−.64
/o/	.32	1.18	.56	1.30	1.31	1.67	1.30	1.80	1.97	2.10	−.72	−.49	−.23	.15
/ɔ/	−.98	−.09	−.73	.04	.02	.41	.01	.54	.68	.84	−2.01	−1.75	1.52	−1.11	−1.29	−1.26
/a/	−1.71	−.86	−1.46	−.73	−.72	−.37	−.73	−.24	−.05	.07	−2.75	− −2.53	2.26	−1.89	−2.03	−2.04	−0.74	−0.77

As noted in the discussion of Fig. 5 and Table 2, there are three contrasts in CD for the back series of vowels in which there is discrepancy between the estimated and measured data: /u/-/℧/, /o/-/ɔ/, and /o/-/a/. It should be noted that all these pairs are distinguished in terms of rounding for both the measured and estimated data. Therefore these vowel pairs would be contrasted with each other even based solely on the acoustic data.

4. General discussion

The basic question posed at the beginning of this investigation was whether linguistically significant articulatory configurations can be directly derived from the speech signal. The data presented in the previous section can be taken as a partial answer to this question for the particular case of static vowels. If we apply the DMI approximation to the speech signal and use formant amplitude as the extra information, it is possible to extract information about the place and degree of the primary constriction as well as rounding for most American English vowel contrasts. Specifically, for CD, 20 vocalic contrasts were examined (10 for the front series and 10 for the back series), and only 3 were not adequately modeled by the acoustically derived CDs; however the contrast between these vowel pairs was captured in LA. The total number of contrasts examined were 110 (20CD+45CL+ 45LA), and of those 14 showed discrepancy between articulatory measures and acoustically based articulatory reconstructions, i.e., the contrast accuracy in estimating appropriate articulatory parameters across contrasts is 87%. In addition, the means of CL and LA estimated from the acoustics accord well with the CL and LA measured from area functions of 6 participants in an MRI study.

High agreement between the two sets of articulatory data and the acoustically derived estimates, despite all the approximations involved and the differences in speakers, is evidence that the basic contrasts between American English vowels are captured. The reconstructions were not perfect, however. The CD for the three back vowel contrasts that were not captured and CL for /ε/ need to be further investigated to determine the source of the discrepancy between the articulatory measurements and acoustic estimates.

The second main result concerns the differential contribution of formant frequencies and amplitudes/bandwidths. Formant frequency-only estimates are successful for CD and LA estimation, but bandwidths/amplitudes are necessary for reconstruction of the CL of the vowel /u/, which is highly symmetric at the middle of the vocal tract. The inadequacy of the formant frequency only measure to capture the back constriction for /u/ has been known since Mermelstein (1967). This work shows that measurement of the formant amplitudes from the speech signal is able to capture that back constriction for a large number of speakers. Furthermore, even though the analysis is low in spatial resolution, it is able to capture the contrasts examined, including the fine contrasts between the vowels of a densely populated vowel system like American English.

For these partial results to be meaningful to the larger theoretical questions, of course, they need to be generalized to dynamic vowels and other segments, requiring more complex models of the vocal tract. For each set of segments, the goal of this research program is to explicate the articulatory meaning of the acoustic patterns conventionally used to describe the speech signal, if this is possible.

4.1. Implications for phonetic theories

The results presented here do not imply that it is necessary that listeners do make use of articulatory information. That is, this work does not demonstrate that a General Auditory approach is impossible. Rather it demonstrates that an approach like Direct Perception, or the various theories that require parity between the units of production and acoustics, are not impossible. For theories that assume that the objects of perception are articulatory, the present results imply that these theories are possible, in the sense that there is information about CD, CL, and LA in the speech signal that speakers can access. This articulatory information can then also serve as the referent of phonetic categories, but, again, does not have to. For theories of speech perception that take the referents of phonetic categories to be auditory/acoustic, the implication is not that such theories are not possible, it is that these theories need to discuss how articulatory and acoustic information are integrated in phonetic representation, similar to audio-visual integration.

Beyond the basic question of accessibility of articulatory information, the results also shed light on the basic correspondences between individual articulatory and acoustic parameters. There is a long history of attempts to associate articulatory and acoustic parameters for vowels (Delattre, 1951; Fant, 1980; Joos, 1948; Ladefoged, 1976). One of the implications of this work is that there is a direct relation between formants and the anti-symmetric components of the area function, and between formant amplitudes and the anti-symmetric components. This association provides the acoustic parameters with referents in the articulatory domain, i.e., articulatory meanings.

The one-to-one correspondence between formant frequencies and amplitudes/bandwidths and Fourier components of the area functions argued for here opens up a particular possibility for theories of speech perception that would show commonality between the perception of speech and other auditory phenomena. A body of perception research has developed in the last few decades showing that listeners can identify physical properties of objects in the world from systematic change in the physical properties leading to changes in acoustic properties (e.g., Freed, 1990; Giordano & McAdams, 2006; Jenkins, 1985; Kunkler-Peck & Turvey, 2000; Li, Logan, & Pastore, 1991; Lutfi & Oh, 1997; McAdams, Chaigne, & Roussarie, 2004; Repp, 1987). Several of these works are particularly concerned with how listeners identify the shape of a vibratory object or the physical non-uniformity of a vibratory object from frequency-domain and time-domain parameters of the acoustic signal that the shape or non-uniformity affects (Giordano & McAdams, 2006; Kunkler-Peck & Turvey, 2000; Lutfi & Oh, 1997; McAdams et al., 2004). What is particularly relevant about this work is that it is explicitly about non-arbitrary physical links between physical properties of objects and acoustic parameters, rather than arbitrary links between system and signal parameters established statistically. Therefore these works begin exactly with what the Schroeder and Mermelstein framework, supported and extended in this work, does for speech: identifying one-to-one relations between aspects of the vibratory shape or material non-uniformity and aspects of the sound signal produced when the object is made to sound. The Extended Schroeder and Mermelstein framework identifies a physical link between the formant frequencies and anti-symmetric global shapes of the vocal tract and a physical link between the formant amplitudes and the symmetric global shapes of the vocal tract. One of the main extensions of this work therefore is to investigate whether listeners to speech use the same type of capacity that they exhibit in recognizing physical features of other sounding objects in the world, particularly in whether they actually use F1, F2, A1, and A2 to identify anti-symmetric and symmetric physical perturbations of the vocal tract. If that turns out to be the case, it could be argued that the acoustic parameters are not directly linked to phonetic contrasts, but are mediated by the specific non-uniformity of the area function that they are physically linked to.

5. Conclusion

This work started with the basic question of whether articulatory information is present in the speech signal, and whether it can be extracted. Using a novel method, based on an extension of some classic results in perturbation theory and linear prediction, it was shown that it is possible to recover the basic constriction parameters for static American English vowels. The method needs to be further tested on dynamic speech to prove that it is scalable in general. If it is to be proven that linguistically significant information about articulation is present in the speech signal, the class of segments investigated would also have to be extended to obstruents, liquids, and nasals. This can only occur by using dynamic models, instead of static ones. Also the acoustic models need to be extended to lossy models of the vocal tract with branches. There is evidence in the literature that this is not an impossible task. Lim and Lee (1996) and Schnell and Lacroix (2003) have provided a branched model of the vocal tract with a nasal tube and shown that it is at least possible to estimate articulatory parameters of the model from the speech signal. Frolik and Yagle (1997) have shown that it is possible to invert lossy one-dimensional models by developing asymmetric Levinson–Durbin algorithms.

Further research is necessary to determine if these algorithms are applicable to real speech data. Even for obstruents, there is promising research. Several researchers have investigated how articulatory properties of constrictions can be inferred from the speech signal using models of the noise source mechanism and their interaction with the transfer function (Badin, Mawass, & Castelli, 1995; Krane, 2005; Mcgowan & Howe, 2007; Narayanan & Alwan, 2000; Scully, 1990). This work is likely to inform inversion for stops as well. There is therefore emerging evidence that articulatory information is present in the speech signal for a wide variety of speech segments, and that this information is potentially extractable. Another major extension of this work will be in the direction of links between dynamic articulatory and acoustic parameters, since speech is of course fundamentally dynamic. This line of research has not been at the forefront of development in the phonetic sciences, but it is likely to acquire a central position, since it is about the fundamental relation between acoustic and articulatory phonetics.