Identifying informative subsets of the Gene Ontology with information bottleneck methods

Abstract

Motivation: The Gene Ontology (GO) is a controlled vocabulary designed to represent the biological concepts pertaining to gene products. This study investigates the methods for identifying informative subsets of GO terms in an automatic and objective fashion. This task in turn requires addressing the following issues: how to represent the semantic context of GO terms, what metrics are suitable for measuring the semantic differences between terms, how to identify an informative subset that retains as much as possible of the original semantic information of GO.

Results: We represented the semantic context of a GO term using the word-usage-profile associated with the term, which enables one to measure the semantic differences between terms based on the differences in their semantic contexts. We further employed the information bottleneck methods to automatically identify subsets of GO terms that retain as much as possible of the semantic information in an annotation database. The automatically retrieved informative subsets align well with an expert-picked GO slim subset, cover important concepts and proteins, and enhance literature-based GO annotation.

Availability: http://carcweb.musc.edu/TextminingProjects/

Contact: xinghua@pitt.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Many controlled vocabularies have been developed to define and represent biomedical knowledge in the form of ontology, among which the Unified Medical Language System (UMLS; Lindberg et al., 1993), the Gene Ontology (GO; Ashburner et al., 2000) and the Open Biological Ontology (OBO; Smith et al., 2007) are three well-established biomedical ontologies covering different aspects of biomedical knowledge domains. For example, UMLS is a collection of controlled vocabularies representing broad biomedical knowledge; OBO consists of a collection of ontologies representing a variety of biology concepts; and GO is a controlled vocabulary representing molecular biology aspects of genes and proteins. Designed to provide comprehensive representations of the knowledge in their corresponding domains, the sizes of these controlled vocabularies are often overwhelmingly large, and many terms (concepts) defined in the vocabularies are seldom used in the real world of annotation or indexing. Therefore, there are needs to identify subsets of the controlled vocabularies to represent knowledge in a concise manner. Recognizing such needs, the GO Consortium provides several subsets of GO terms, referred to as GO slims (http://www.geneontology.org/GO.slims.shtml). These terms are manually picked by domain experts to cover the major concepts of specific domains, with a trade-off between specificity of the concepts and the size of the ontology that is deemed acceptable to the experts. However, it is of both theoretical and practical interests to develop methods that can automatically identify informative subsets of GO terms to represent the major semantic concepts in an objective manner and to meet different needs of different domains. As a concrete example, we have developed a method (Richards et al., 2010) for assessing the functional coherence of a gene set by constructing a graph with GO terms and genes as nodes, and a part of evaluation is to visualize such graphs enabling users to capture the major theme of the functions and their relations to the genes. However, such a graph usually has a large number of specific terms making it difficult for users to identify the main concepts associated with the genes.

Recently, the Database for Annotation, Visualization and Integrated Discovery (DAVID) tool box (Huang et al., 2007, 2009) provides tools to identify representative GO terms based on the genes associated with them. Similarly, Du et al. (2009) reported clustering disease ontology (DO) concepts using gene–DO associations as features. In this study, instead of using gene-centered approaches, we address the task of automatically identifying subsets of GO within the framework of semantic representation and information theory—identifying subsets of GO terms that retain as much as possible of the original semantic information contained in an annotation database. In order to achieve the goal, some fundamental issues related to the semantic information of GO terms need to be addressed: (i) how to represent the semantic context of a GO term; (ii) how to measure the difference in semantic context (a.k.a. semantic distance) between a pair of GO terms; and (iii) how to identify an informative subset of GO that retains as much as possible of the semantic information within an annotation database.

Measuring semantic distances between GO terms has attracted much attention (Lord et al., 2003; Schlicker et al., 2006; Sheehan et al., 2008; Tao et al., 2007; Wang et al., 2007) in the bioinformatics field. In particular, a quantity referred to as information content (IC) (Jiang and Conrath, 1998; Lin, 1998; Lord et al., 2003; Resnik, 1995) has been widely used as a measure to assess the amount of information that a GO term contains, and the difference in the IC between a pair of terms is used to measure their ‘semantic distance’. From the information theory point of view, IC measures the amount of uncertainty associated with observing a term. As such, it does not represent the ‘semantic context’, and therefore a difference in ICs does not necessarily reflect the ‘semantic difference’ between two terms per se.

On the other hand, the definitions of GO terms are usually parsimonious and render insufficient information for assessing the relationships and semantic distances among the terms, as illustrated by the following examples. In the GO, the semantic meaning of a GO term is reflected by its synonym (a human understandable name) and its definition. For example, the synonym and definition for the term GO:0050794 are, respectively, ‘Regulation of cellular physiological process’ and ‘Any process that modulates the frequency, rate or extent of a cellular process, any of those that are carried out at the cellular level, but are not necessarily restricted to a single cell’. Let us further consider one of its child terms, GO:0007165, whose synonym and definition are, respectively, ‘Signal transduction’ and ‘The cascade of processes by which a signal interacts with a receptor, causing a change in the level or activity of a second messenger or other downstream target, and ultimately effecting a change in the functioning of the cell’. Although the two terms have a parent–child relationship, they share very few biological words in their synonyms and definitions, and the organization of the terms in the GO hierarchy is guided by additional information/knowledge that is not explicitly reflected in the definitions. As a result, unless a reader is equipped with sufficient biological knowledge, it would be difficult to discern and quantify the relationship of the two terms solely based on their definitions.

In this study, we propose to represent the semantic context of GO terms using the word-usage profiles derived from the biomedical literature associated with the GO terms. This representation enables us to measure differences in the semantic context between terms through quantifying the differences in their word-usage profile. This framework further allows us to use information bottleneck (IB) methods (Slonim and Tishby, 2000; Tishby et al., 1999) to identify subsets of GO terms, striving to retain the information with respect to the word-usage profiles of GO terms. Here, we demonstrate that: (i) our approach to representing semantic context and semantic distances is intuitive and consistent; (ii) automatically identified informative GO subsets align well with the expert-picked GO slim set and cover broad concepts and proteins; and (iii) automatic annotation with the informative subsets achieves better accuracy.

2 METHODS

2.1 Preprocessing data and building the GO graph

The gene–GO association files of mouse, human, yeast and Uniprot were downloaded from the web site of the GO Annotation (GOA) project of the European Bioinformatics Institute (Camon et al., 2004). Entries containing the triplet of a gene product id, a GO term and a PubMed identification number (PMID) were extracted and used as the evidence of an association between GO terms and PMIDs. In this study, we only retain the GO terms belonging to the Biological Process branch of GO. A total of 33 479 MEDLINE entries corresponding to the PMIDs associated with these terms were downloaded from the National Center for Biotechnology Information (NCBI). In the corpus preprocessing, common words were first removed from the corpus according to a standard English ‘stop words’ list; the words in the corpus were then stemmed using the Porter stemmer algorithm (Porter, 1980); and then the words with fewer than five occurrences in the corpus were discarded. As a result, the final vocabulary of the corpus had 37 782 unique tokens, and we denoted it with V.

We constructed a graph representation of GO using a Python software package (Muller et al., 2009). In a GO graph, each node represents a GO term, and each directed edge corresponds to the IS_A relationship between a parent–child GO term pair. Since we are interested in semantic relationships, only IS_A relationships were considered in the GO graph. We propagated protein ids (referred to as proteinIDs) associated with each GO node to their ancestors in a bottom-up fashion. After propagation, each GO node was further associated with a set of protein ids referred to as proteinAllIDs, consisting of the union of its own proteinIDs and its children's proteinAllIDs. A set of PMIDs, referred to as nodeUniqPMIDs, was associated with each GO node, and they were further propagated to their ancestor nodes, as with protein id propagation. At this stage, a new PMID set, referred to as nodeTotalPMIDs, was created at each node, which is the union of its own nodeUniqPMIDs and its children's nodeTotalPMIDs sets. To reflect the semantic context of the literature associated with a GO term, a word-vector was constructed for each GO node by collecting the words from PubMed records (titles and abstracts) based on the nodeTotalPMIDs. An element in the word-vector represents the count of the times that a word is observed in the PubMed records associated with the GO term. Each word-vector was further normalized to represent the word (multinomial) probability distribution.

2.2 Semantic distances

2.2.1 Semantic distance based on IC

We followed the previous reported method (Lin, 1998; Lord et al., 2003; Resnik, 1995) to calculate the IC of a term t as follows,

(1)

where P(a_t) is the number of annotation instances by term t divided by the number of total annotation instances in an annotation collection. Then the semantic distance between the term and its parent p is determined as

(2)

2.2.2 Distance measures for word-usage profile

There are many measures that can be used to assess the differences among word-usage profiles. In this study, we investigated the following measures in the framework of IB: Kullback–Leibler (KL) divergence, D_KL; L1 distance, D_L1; and Euclidean distance, D_Eu (El-Yaniv et al., 1997; Lin, 1991; Slonim and Tishby, 2000). The definitions of the measures are as follows:

(3)

(4)

(5)

In the definitions, 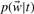denotes the distribution of words associated with a GO term t, which can be calculated by dividing the number of times a word w occurs in the documents associated with the term t with the total number of words in the documents associated with term t. Theoretically speaking, L1 and Eu are real distance measures in that they satisfy the triangle inequality, while KL is not a metric distance in that it does not satisfy the requirements of symmetry and triangle inequality.

2.3 IB methods

The IB methods (Slonim and Tishby, 2000; Tishby et al., 1999) provide a general framework to identify the information structures contained by one set of variables with respect to another set of variables based on information theory. In our case, we defined a vector of variables, T, to represent the GO terms and a vector of variables, W, to denote the words observed in the annotation corpus. We then represented observed GO annotations and their associated words using a |T| × |W| matrix, such that the semantic context of a term was represented by a row of words reflecting the word-use profile of the literatures associated with the terms. The overall information that the GO terms have with respect to the words can be determined using mutual information as follows:

(6)

The task is to identify a new compact presentation of GO terms 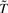such that the original mutual information I(T; W) is preserved as much as possible by 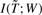. One way to produce the new representation 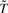is to iteratively group the members of the original T by merging the terms into clusters and to use the clusters as the new representation of GO, while constraining the process to retain as much information as possible. This can be readily achieved using the agglomerative IB algorithm (Slonim and Tishby, 2000; Tishby et al., 1999). For each step, the algorithm selects the pair of clusters that results in the minimal loss in information after merging. The information loss 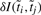of merging two terms/clusters 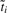and 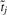is determined as follows:

(7)

where

(8)

(9)

(10)

(11)

In the equations, 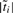is the number of terms within the cluster 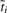. The clustering procedure will eventually result in a graph in which that GO terms sharing similar word-usage-profiles will be preferentially grouped. Two observations are noteworthy: (i) the information loss of a merge is a weighted Jenson–Shanon (JS) divergence consisting of two components: the losses resulted from removing nodes i and j. Thus, the loss is decomposable; (ii) the JS distance, D_JS in Equation (9) is one of many possible measures that can be used to measure the difference in two distributions, and other word-use-profile-based distance measures discussed in the previous subsection can also be used in place of D_JS as in the IB framework.

2.4 GO graph compression

While the agglomerative IB clustering is capable of producing de novo clusters as informative representations of GO terms, it is more sensible to identify such clusters that comply with the current organization of GO terms. To this end, we extended the IB methods so that clustering (collapsing) of GO terms obeys the predefined GO graph structure. This approach transforms the task of identifying an informative subset of GO terms to a graph compression (trimming) task, instead of attempting to identify informative clusters ab initio. Taking advantage of the observation that information loss from merging a pair of GO terms is decomposable, we developed a greedy algorithm to sequentially remove the leaf terms that resulted in the least information loss, see Algorithm S1 in Supplementary Materials. Let t_i denote a leaf node, t_p stand for its parent node, 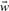represent the word vector associated with the term and |t_i| denote the number of the descendant nodes of t_i. We determined the information loss of removing a leaf node as follows:

(12)

where

(13)

(14)

(15)

In addition to the above weighted JS, we also used the weighted L1 distance (WL1) to measure information loss as follows:

(16)

2.5 Graph-based multi-label classification

The graph-based multi-label classification system with support vector machine (SVM; Vapnik, 1998) as base classifiers was utilized to perform graph-based multi-label classification (Jin et al., 2008). In brief, a protein annotated with a GO term is also considered to be annotated by ancestors of the term because of the hierarchical organization of GO; thus, the protein annotation is a multiple-labeling task. The system performs localized classification in a top-down manner, referred to as TP-SVM. When given a PubMed record related to a protein, the TP-SVM outputs a graph consisting of predicted positive GO terms as candidate annotations for the protein. In this study, the classification performance on the trimmed GO graph was evaluated in the same manner as described in Jin et al. (2008).

3 RESULTS AND DISCUSSION

3.1 Semantic context of GO terms

The task of identifying an informative subset of GO terms requires us to quantify the amount of information retained by the subset as guidance to search for informative terms. In other words, we need to measure the differences in the semantic context to reflect the amount of loss in semantic information during the process. We reason that the semantic context of a GO term can be more effectively represented by the word-usage-profile associated with it because, as the semantic symbols of human languages, a word-usage-profile of a term reflects the context in which the concept is being discussed. By collecting all the words used to discuss a concept and its descendents, the word-usage-profile of a term can overcome the difficulty resulting from the parsimony of GO definitions, and the large number of available annotation instances may provide a potentially more accurate representation of context than a single definition. Under such a setting, the semantic distances between a pair of terms can be readily represented by the differences in the word-usage-profiles.

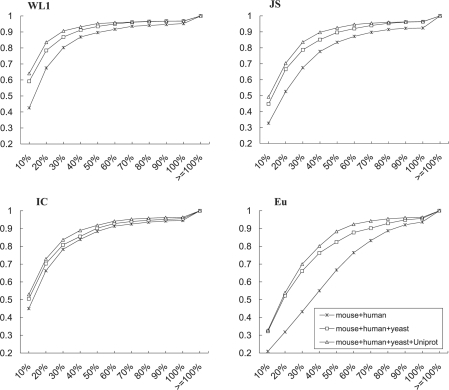
We investigated and compared different measures of semantic distances, namely the IC-based semantic distance and three different word-usage-profile distances: (i) the WL1 distance; (ii) the JS divergence (El-Yaniv et al., 1997; Lin, 1991; Slonim and Tishby, 2000); and (iii) the Euclidean distance. Ideally, a semantic distance between a pair of GO terms should remain constant as long as the semantic meanings of the terms are unchanged. However, measures based on annotation instances, including those studied in this article, will change as the annotation instances change. Under such a circumstance, a good measure should become stable as the number of annotation instances increases. To investigate the stability of the semantic distances, we first identified a subset of common GO terms that have been used to annotate genes from multiple species. The GO subset constitutes a subgraph of 1355 GO nodes (terms) and 2170 edges. We then monitored the impact of adding more annotation instances on the semantic distances of the edges, by evaluating the percent of changes in the edge distances after progressively adding annotation instances from mouse, human, yeast and the combined multiple-species Uniprot dataset. The results are shown in Figure 1.

Fig. 1.

Edge distance change summary. The figure shows the cumulative distributions of number of edges grouped according to their percent changes after sequentially adding annotation instances of mouse, human, yeast and Uniprot. X-axis represents the percent changes of edge distances in the GO graph; Y-axis represents the cumulative density of edges with different degree of changes in length.

The panels in Figure 1 show the cumulative distributions of the number of edges binned according to their percent changes in the edge distances after sequentially adding annotation instances. The results from the figure can be interpreted as follows. When more annotation instances are added to the GO, all annotation-instance-based semantic measures tend to be more stable (i.e. edges show progressively smaller percent changes after addition annotations). Semantic distances measured with the IB-based methods showed better convergence (i.e. more edges with small percent changes). For example, when adding annotation instances from Uniprot, >60% of edges measured with WL1 showed < 10% change in distances.

Although all annotation-based measures show a tendency to converge, the underlying mechanisms are different. For the measures based on word-usage-profiles, the stabilization of semantic distances is due to the convergence of the word-usage-profiles; for IC-based measures, the stabilization of edge distances is likely due to the relatively small change in the probabilities of observing terms as total annotations increase and the shrinking effect of the logarithm. It should also be noted that, due to the differences in their scales and the non-metric nature of the above measures, it is difficult and meaningless to directly compare the changes in the numeric values of different measures.

3.2 Identifying informative GO subsets

The capability of representing the semantic context of GO terms with word-usage-profiles and measuring their differences enables us to quantify the amount of information retained (or lost) during the process of selecting informative GO terms. This information can be used to guide the compression of the GO graph. The intuition of our method is as follows: when a leaf GO term is removed from the GO graph, its semantic context information is lost, but its parent term retains some of the leaf term's information because of their IS_A relationship. The amount of information loss should be proportional to the differences in the semantic context between the pruned term and its parent(s), and such differences can be readily measured according to IB methods based on the divergence of the word distributions associated with the terms (Slonim et al., 2002, 2005).

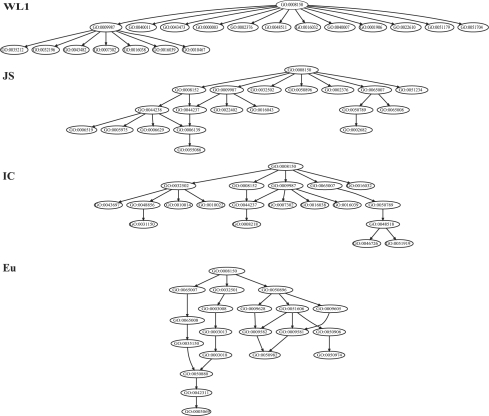
With the algorithm defined in Algorithm S1 in Supplementary Materials, we compressed the GO graph of the Biological Process using the annotation data from all species. We used the potential information loss, calculated with the IB-based semantic measures (JS and WL1), as the edge weight to prune this GO graph. As comparisons, we also used the IC and Eu to calculate edge weights in the algorithm although these two measures do not necessarily reflect the semantic loss. For the purpose of visualizing the characteristics and differences among these measures, we compressed GO graph to produce two sets of subgraphs: one group consisting of subgraphs with a total of 20 nodes (shown in Fig. 2) and the other consisting of the subgraphs with a total of 20 leaves (shown in Supplementary Fig. S1.2). We investigated the characteristics of the graphs in the following aspects.

Fig. 2.

Compressed GO subgraphs. The graph of Biological Process subontology is compressed under different setting of edge distance measures, as indicated next to the graphs. A large version of the figure is shown in Supplementary Figure S1.1, and the names of GO terms are listed in Supplementary Table S2.

An ideal compression of a GO graph should lead to a subgraph whose leaf GO terms cover major biological aspects of the GO graph without much semantic overlap. One possible way to quantify such a characteristic is to calculate the ratio of the number of leaf nodes over the total number of nodes in the compressed graph, referred to as R_lt; the higher the ratio, the more diverse the concepts covered because of less overlap among the concepts. We calculated the ratios for the subgraphs obtained using different edge length measures and ranked the subgraphs according to their R_lts. Figure 2 (subgraphs with a total of 20 nodes) shows that different semantic distance measures produced subgraphs with distinct patterns; their R_lts are as follows, WL1: 0.9; JS: 0.60; IC: 0.55; and Eu: 0.15, and the R_lts for subgraphs with 20 leaves are WL1: 0.91; JS: 0.67; IC: 0.57; and Eu: 0.14. The subgraphs obtained based on the IB framework with WL1 and JS measures show higher R_lts, and their leaves cover a broader range of concepts. On the other hand, the concepts from the subgraphs obtained using the IC-based edge distance and Euclidean distance show increasingly higher degrees of overlap. It should be noted that, when the total size of a subgraph is fixed, the broadness of the coverage and the specificity of the concepts trade-off with each other. The graphs returned by different measures span a broad spectrum, with WL1 covering broad but general concepts and Eu containing a narrow range of more specific concept. Based on these observations, WL1 and JS measures performed better than IC and Eu measures in terms of meeting the goal of retaining as much semantic information of the GO graph as possible with a relatively small number of GO terms.

Another aspect of assessing the utility of the subgraphs returned by different measures is to evaluate how many proteins are covered by the leaf (specific) terms of subgraphs. Ideally, a good informative subset of GO terms should cover a broad range of concepts and as many proteins in the original annotation database as possible. We counted the number of proteins covered by each of the leaf terms of the GO subgraph, shown as the number in parenthesis within each node in Supplementary Figure S1.2. The total numbers of proteins covered by the leaves of the subgraphs based on different measures are as follows: WL1: 13 042; JS: 62 132; IC: 19; and Eu: 188.

The results clearly indicate that IC-based semantic measure is not suitable for identifying an informative subset under this setting. Instead of measuring the difference in semantic context, the IC-based measure assesses in essence the difference in protein counts; as such a longer edge is usually the one with many proteins associated at the parent end but very few proteins at the child end. This leads to the phenomenon that the leaf nodes of the subgraph derived with this measure are the ones with the least number of protein annotation instances. On the other hand, IB-based compression retains leaf nodes covering diverse concepts, thus potentially covering more proteins. Based on the results, we believe that the subgraph returned by a JS-based measure is the most suitable informative subset due to its balanced breadth and depth and the larger number of proteins covered by its leaves.

3.3 Aligning informative subsets with GO slim

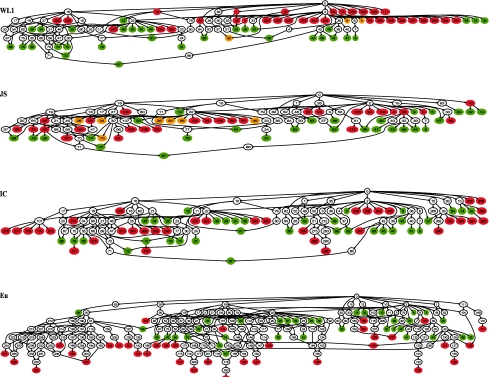
The capability of identifying subgraphs in an automatic and objective manner would enable one to identify potential ‘slim’ GO sets for different research domains, according to different criteria and to meet different needs. It would be of interest to see how well the automatically identified subsets agree with manually picked GO slim terms, which arguably can be treated as the ‘gold standards’ of informative subsets. We downloaded the yeast GO slim terms (http://www.geneontology.org/GO.slims.shtml) and extracted all terms from the Biological Process namespace (a total of 35), which were used to reconstruct the GO subgraph with these terms as leaves. Then we used the graph compression algorithm to identify subgraphs that had exactly 35 leaves from the yeast GO graph with the four measures. In order to make a comparison, the subgraphs returned by the compression algorithm were further merged with the yeast GO slim subgraph, as shown in Figure 3. The names of the GO terms in the figure are listed in Supplementary Table S3.

Fig. 3.

Alignments of GO slim and compressed subgraphs. The compressed subgraphs using different semantic measures were merged with the subgraph constructed with yeast GO slim terms as leaves. Green nodes are GO slim leaf terms; red nodes are leaves of compressed graphs; deep yellow nodes are shared by GO slim and the compressed subgraph; uncolored nodes are non-leaves. The high-resolution versions of the figure are shown in Supplementary Figures S2 and S3.

We evaluated the ‘goodness’ of the informative subsets by measuring how close the leaf terms of the automatically identified subsets are located to those in the GO slim subset on the merged graph. We cast the evaluation as a match assignment problem (Kuhn, 1955, 1956; Munkres, 1957). The task is to find an optimal pairwise match between the entities from two sets so that the total cost of the matches is minimized. In our case, we sought to find a one-to-one match between 35 leaf terms in the informative GO subsets and those in the GO slim subset so that the overall distance between the two sets is minimal, where the distance of a matching pair was measured by the number of edges in the shortest path between them. We first used Dijkstra's algorithm to find the shortest paths between all leaf pairs and applied Munkres algorithm (Munkres, 1957) and then find the optimal matches through these shortest paths. The total numbers of edges after matching were as follows, WL1: 103; JS: 87; IC: 124; and Eu: 187 (see Supplementary Table S4.1–S4.4 for details). The results indicate that the informative subset returned by the IB method based on JS divergence was most closely aligned with the manually picked GO slim subset. In particular, 7 out of 35 of GO terms from the subset directly intersected with the GO slim subset, while none of those from IC- and Eu-based subgraphs did.

In addition to assessing alignment of the informative GO subsets with the human-chosen GO slim subset, we also evaluated how many proteins from the database could be covered (annotated) by the informative subsets. As stated before, an ideal subset of informative GO terms should not only cover a broad range of biological concepts but also annotate as many different proteins as possible. We have evaluated the total number of different proteins covered by the leaf terms (the union of all leaves' proteinAllIDs) in each compressed GO subgraph, and the results were as follows: WL1: 2297; JS: 4597; IC: 72; and Eu: 52. Compared with 3952 proteins covered by the GO slim subset, the results indicate that the GO compression with the IB method based on WL1 and JS measures was comparable with the manual GO compression in terms of the number of annotated proteins. We further evaluated the number of the different intersected proteins covered by the JS- and WL1-derived leaf subsets and the GO slim leaf subset, and the counts were: JS-vs-GOSlim: 3665 and WL1-vs-GOSlim: 1856. In summary, we believe that the informative subset of GO terms identified using the JS-based measures is the most suitable informative subset, due to its closest relationship to the manually picked GO slim terms and its broader coverage of proteins.

3.4 Automatic protein annotation with informative GO subsets

The main purpose of GO is to annotate gene products in a unified and computable format. One main thrust in bioinformatics is to automatically annotate proteins based on the literatures associated with genes. Often, this task is cast as a text categorization problem in which, upon given a text related to a gene, a computational agent predicts what GO annotation can be assigned to the gene (Camon et al., 2005; Cohen and Hersh, 2006; Cohen and Hunter, 2008). As reported in our previous study (Jin et al., 2008), out of 5797 observed GO terms associated with documents in the GO annotation database, >80% of them had fewer than 10 training documents, which poses severe challenges to contemporary text classification algorithms. One practical approach is to train text classifiers with fewer but more informative classes. The graph compression approach developed in this study enables us to choose the subset of GO terms in an automatic and objective manner. This allows users to select not only the level of specificity but also the classification accuracy of an informative subset to meet their annotation needs.

We tested our graph-based multi-label classification algorithm (TP-SVM) on the progressively compressed GO graphs to investigate the impact of compression with different semantic measures on classification accuracy. In order to verify that the enhanced classification accuracy was not simply due to reduced number of classes, we also trim graph by randomly selecting a leaf node, referred to as RandomTrim, in contrast to selectively trimming nodes according to certain criteria by our compression approach. In another experiment, we tested a method that naively attempts to retain orthogonal nodes during trimming, in which all pairwise dot-products (a measure of similarity) between the word vectors of leaf nodes were calculated at each step, and the leaf with the highest total similarity with all other nodes, a.k.a. least orthogonal to others, was selectively trimmed, referred to as DotProdTrim (see Algorithm S2 in Supplementary Materials for details).

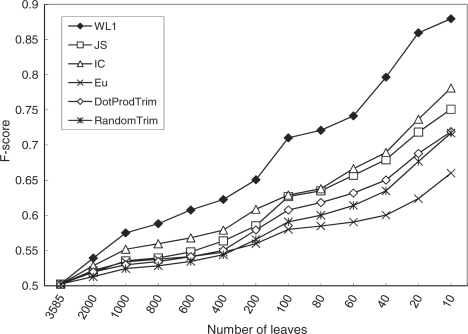
We compressed the GO graph to different sizes using different measures or methods, which then were used as the class hierarchy to train TP-SVM. Figure 4 shows the F-scores (a metric reflecting overall accuracy of an agent) of the classifiers trained with the GO of different sizes. In this figure, each point represents the F-score of a classifier trained on a graph with a specific number of leaf nodes, e.g. the graph compressed using the WL1 measure with 100 leaves.

Fig. 4.

Impact of GO compression on TP-SVM performance. The figure shows how TP-SVM performance (F-score) changes with respect to the number of leaves (X-axis) in the progressively compressed GO graph. The plots for recall and precision of the classifiers are shown in Figure S4.

The figure shows that as the size of GO graphs becomes smaller, the overall classification accuracy increases and that the classification accuracies based on the graphs produced by IB methods are better than the others. These overall trends can be explained as follows. First, it is understandable in that the GO nodes in the smaller hierarchy tend to have more training documents associated due to the propagation of training documents. Second, the possible explanation for superior performance of graph from IB methods is that our compression algorithm tends to retain leaves (classes) that are differentiable. As such, it is not surprising that the classifier performed best when trained with the subgraphs derived with the WL1 measure because, as shown in Figure 2, the classes in such subgraphs are mostly orthogonal to each other. In comparison, the methods of simply reducing the size of class hierarchy or naively attempting to retain the orthogonality of leaves do not necessarily improve classification accuracy as much as the principled IB methods. The recall and precision of the algorithm with the GO of different sizes are shown in Supplementary Figure S4.

We further evaluated the TD-SVM performance on the GO slim and the compressed GO graphs of the same number of leaves with yeast-specific PubMed records, and the results are shown in Supplementary Figure S5. The results show that the classifiers trained with subgraphs derived with WL1 and JS measures perform better than those based on yeast GO slim, and the latter outperform those trained with the subgraph derived with Eu. The results indicate that information theory based WL1 and JS methods are capable of retaining GO terms reflecting distinct concepts that are more differentiable than those manually picked GO-slim terms, and that simple trimming based on Eu measure does not capture the same information.

4 CONCLUSION

Combining word-usage-profiles with IB methods provides a means to identify within the complexity of GO informative subsets for specific purposes.

Funding: National Institutes of Health (grants R01LM009153, R01LM010144 and P20RR017677 to X.L., partially).

Conflict of Interest: none declared.