Reliability and bifurcation in neurons driven by multiple sinusoids

Abstract

The brain produces dynamical rhythms at many frequencies that shift in amplitude and phase. To understand the functional consequences of mixtures of oscillations at the single cell level, we recorded the spike trains from single rat cortical neurons in vitro in response to two mixed sine wave currents. The reliability of spike timing was measured as a function of the relative power, phase and frequencies of the sine wave mixture. Peaks in the reliability were observed at a preferred phase difference, frequency and relative power. These results have a natural interpretation in terms of spike train attractors and bifurcations.

1. Introduction

The responses of individual neurons depend on the ongoing background activity that varies with the behavioral state of an animal. The electroencephalogram (EEG) contains multiple rhythms that reflect spatially and temporally coherent neural activity [1]. Slow oscillations with strong delta rhythms (0.5–2 Hz) are found in slow wave sleep, oscillations dominated by theta oscillations (4–12 Hz) are related to cognitive processing and cortico-hippocampal interactions, and gamma oscillations (30–80 Hz) are found in the cortex and other brain structures under attentive behavioral conditions [1,3]. Power in the gamma and theta bands is modulated by attention [3]. For example, the responses recorded from a macaque V4 neuron to the same stimulus were compared with two conditions, with attention inside or outside the neuron’s receptive field. As attention shifted to the receptive fields of a cluster of neurons, these became more synchronized at high frequencies (30–70 Hz) and less so at low frequencies (0–10 Hz) [3]. In a human visual selective attention task, stimulus presentation induced phase resetting of different frequency components in the EEG [5].

The reason why the brain exhibits these dynamical rhythms is unknown, but recent experiments suggest that rapidly changing correlations may reflect internal events and regulate the flow of neural information, rather than its meaning [7]. The reliability of cortical neurons depends in part on the frequency content of their input [4,9] and pyramidal cells and interneurons are reliable in different frequency ranges when injected with pure sinusoidal currents of varying frequency [2]. The goal is to measure spike time reliability when neurons are stimulated by synaptic inputs containing the types of correlated and synchronous inputs that are observed in vivo. Here we report that reliability is greatly affected by the choice of the relative power, phase and frequencies of two mixed pure sine waves injected into pyramidal cells in vitro.

2. Methods

Experimental protocols were approved by the Salk Institute Animal Care and Use Committee and they conform to USDA regulations and NIH guidelines for humane care and use of laboratory animals. Regularly spiking layer five pyramidal neurons in 350 μm-thick coronal slices of rat pre-limbic and/or infra-limbic cortex were injected with 20 different stimulus waveforms, over multiple trials. Each stimulus waveform was a sum of two sinusoids:

$$I(t)=I_0+I_{1}sin(2\pi f_{1}t+2\pi \mathrm{\Delta }\phi )+I_{2}sin(2\pi f_{2}t).$$ (1)

The relative phase (Δφ), the relative frequency (f₂) and the relative power (I₁ and I₂) were varied (see Fig. 1). Whole-cell patch-clamp recordings using glass electrodes (4–10 MΩ) were performed under visual control at room temperature. Data were acquired in current clamp mode using an Axoclamp 2A amplifier (Axon Instruments, Foster City, CA). Data acquisition and current injection used standard computer protocols [2]. Programs were written in Labview 6.1 (National Instrument, Austin, TX), and data were acquired with a PCI-16-E1 data acquisition board (National Instrument, Austin, TX). Data acquisition rate was 10 kHz. Data were analyzed oPine using MAT-LAB (The Mathworks, Natick, MA).

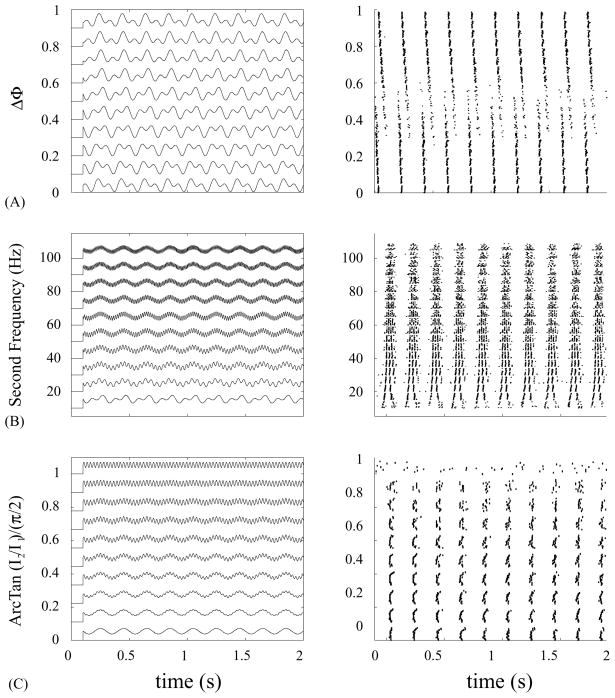
Fig. 1.

Sample current stimuli and corresponding cell responses. (A) Variation in relative phase of two sine waves at 5 and 10 Hz. (B) Variation in the frequency of the second sine wave with a 5 Hz frequency for the first sine wave. (C) Variation in relative power between two sine waves at θ (5 Hz) and γ (35 Hz). Larger values correspond to more power in the γ sine wave. Left panels show 10 examples of the 20 stimulus waveforms used, the right panels show corresponding sample rastergrams obtained in response to the injection. Each response (A–C) was obtained from a different layer 5 pyramidal cell.

3. Results

3.1. Experiment 1

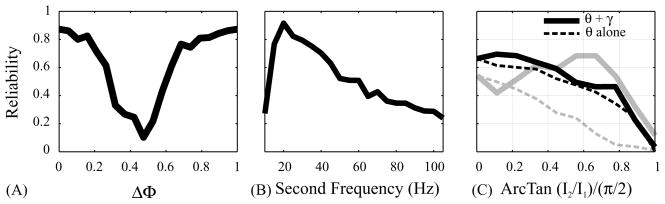
Cells were injected with a constant (100 pA) depolarizing current superimposed on the sum of two sinusoids of equal amplitude (50 pA each) with 20 different phase offsets (ranging from Δφ = 0.0 to 0.95) and fixed frequencies of 5 and 10 Hz, respectively. Fig. 1A shows a few of the injected waveforms and a typical cell’s response. For Δφ =0, the cell exhibited a 1:1 firing pattern locked to the periodic stimulus, firing regularly at the fundamental frequency of the stimulus (5 Hz). As the phase offset Δφ increased, the cell fired earlier and earlier in the stimulus cycle. For Δφ = 0.30, the cell exhibited a new firing pattern with times interspersed between the existing one. As Δφ varied from 0.30 to 0.55 the two sets of firing times shifted gradually while the fraction of trials with spikes lying in one versus the other shifted smoothly as well. At Δφ = 0.55, the new pattern dominated, and for larger phase offsets the first pattern no longer occurred. As the phase offset continued to increase the spike times continued to shift until Δφ = 0.95 where they nearly coincided with the spike times in the original pattern at Δφ = 0.0. The reliability of the cell’s response, calculated on a 5 ms time scale using a correlation-based reliability measure [8], showed a pronounced dip at Δφ = 0.45 (Fig. 2A).

Fig. 2.

Effects of parameter changes on reliability: (A) variation in relative phase of two sine waves at 5 and 10 Hz; (B) variation in the frequency of the second sine wave (the frequency of the first sine wave was 5 Hz); (C) variation in relative power between two sine waves at θ (5 Hz) and γ (35 Hz). Larger values correspond to more power in the γ sine wave. Solid curves represent reliability for θ and γ mixture, dashed curves represent the reliability for θ alone, with the same power as for the mixture. Two cells are shown (dark and grey curves).

In an integrate-and-fire model neuron driven by the same stimulus, the spike times also varied smoothly until a critical value of the phase offset at which a spike time bifurcation occurred; that is, at the critical value of the phase offset, a small change in this parameter caused a discontinuous change in the resultant pattern of spike times (data not shown). The reliability is expected to show a minimum in the neighborhood of such a bifurcation point, where two alternative spike response patterns coexist. Because of the intrinsic noise of the recorded neuron from stochastic ion channel fluctuations and other noise sources transitions between the two coexisting patterns occur over a range of parameters near the critical parameter value.

3.2. Experiment 2

Cells were injected with a constant (100 pA) depolarizing current superimposed on the sum of two sinusoids of equal amplitudes (50 pA each) and fixed phase offset (Δφ = 0.5), at two different frequencies: f₁ = 5 Hz and f₂ varied from 10 to 105 Hz in steps of 5 Hz. Fig. 1B shows some of the injected waveforms and a typical cell response. For f₂ = 10, 15, 20 Hz most cells fired two spikes on each f₁-cycle. For 25 ≤ f₂ ≤ 40 Hz the cell reliably fired triplet bursts, and for higher values of f₂ it fired irregularly, with clusters of spikes occurring at the frequency f₁. The reliability had a maximum at f₂ = 20 Hz (Fig. 2B).

3.3. Experiment 3

Cells were injected with a constant (100 pA) depolarizing current superimposed on the sum of two sinusoids of frequencies f₁ = 5 Hz (θ) and f₂ = 35 Hz (γ). The relative amplitude of the two components was varied to keep the total stimulus constant, I₁ =I cos(η) and I₂ =I sin(η), with I =100 pA. η =ArcTan(I₂/I₁) took 20 evenly spaced values from 0 to π/2. Fig. 1C shows 10 of the injected waveforms and the response from one cell. The response to this stimulus varied from cell to cell. For the cell shown here, a single spike occurred in each θ-cycle. Once the γ power I₂ exceeded the θ power I₁, the cell fired in one of two alternative γ cycles on each θ cycle, decreasing reliability.

Fig. 2C shows the reliability (on the 5 ms time scale) of the cell in Fig. 1C (black line) as well as a second cell (gray line). For comparison, the cells were also injected with θ frequency alone at varying values of I₁, with I₂ = 0 (dotted lines). Both cells steadily decreased in reliability as I₁ decreased, for I₂ = 0. The first cell (black line) had peak reliability for mixtures of θ and γ, with θ predominating. The second cell (gray line) decreased in reliability upon shift of power from θ to γ, and then showed a peak in reliability for a mixture of θ and γ with γ predominating.

4. Discussion

Cortical activity often contains multiple distinct frequency bands, whose relative phase [5] and power [3] change dynamically with behavioral state. To understand the effects of varying phase- and power-relationships between different frequency components on neuronal response, we studied the behavior of in vitro neurons driven by periodic stimuli containing multiple superposed frequency components. Our results show that when multiple input frequencies are present, the reliability and precision of the neuronal response is sensitive not only to the frequencies (Fig. 2B) but also to their relative phases (Fig. 2A) and power (Fig. 2C). In an earlier study, the addition of a γ-range frequency to a θ-range rhythm increased spike time precision [6].

Reliability is important for understanding neural coding. The precision of a neural response governs the amount of information about the stimulus that can be communicated and influences the flow of information in the network containing the neuron. Just as reliable timing is necessary for neural codes using the detailed temporal structure of spike-trains, unreliable timing erases information about the stimulus. The ability to modulate reliability by moving in and out of resonance with a given frequency component may be an important means of regulating correlation and gating information flow in cortical networks [7].

Depending on the relative phase relationships of different frequency components, a pyramidal cell can support either a precise spike-time code or a rate code in which spike-times show great variability but spike rate is conserved. This transition in behavior may be understood as a bifurcation between dynamical attractors that occur as the phase-offset varies. The precision and reliability of neural spike-timing depends on the interplay of synaptic input and the internal dynamics of a given neuron. When two dynamical attractors or spike patterns are close enough in phase space that intrinsic neuronal noise can induce transitions between them, then the timing of individual spikes becomes unpredictable. Thus, bifurcations are a general mechanism for controlling neural reliability and information flow.

Biographies

Peter J. Thomas received his Ph.D. in Mathematics from the University of Chicago in 2000, under Jack Cowan. He is currently a Research Associate in the Computational Neurobiology Laboratory at the Salk Institute. His research includes single-neuron dynamics, signal transduction in biochemical networks, pattern formation in cortical maps, and mathematical biology.

Paul Tiesinga studied Theoretical Physics at Utrecht University in the Netherlands. His PhD thesis there was on the dynamics of Josephson-junction arrays. As a postdoctoral fellow at Northeastern University he worked on biophysically realistic modeling of thalamus and hippocampus. While at the Salk Institute in La Jolla as a postdoctoral Sloan fellow he studied the role of synchronized oscillations in cortical information processing. Presently he is an assistant professor in the Department of Physics & Astronomy at the University of North Carolina at Chapel Hill.

Jean-Marc Fellous did his undergraduate studies in Marseille, France. Graduate studies included a Master’s degree in artificial intelligence (Paris VI University, France), and a PhD in Computer Science with an emphasis on brain theory and neural networks at the University of Southern California, Los Angeles. Postdoctoral studies included slice neurophysiology and neural modeling in the laboratories of John Lisman (Brandeis University) and Terrence Sejnowski (Salk Institute). Jean-Marc Fellous is currently a Howard Hughes Institute Research Associate in Prof. Sejnowski’s laboratory. His interests include the computational roles of neuromodulation and rhythmogenesis.

Terrence Sejnowski is an Investigator with Howard Hughes Medical Institute and a Professor at the Salk Institute for Biological Studies where the directs the Computational Neurobiology Laboratory. He is also Professor of Biology at the University of California, San Diego, where he is Director of the Institute for Neural Computation. Dr. Sejnowski received a B.S. in physics from the Case-Western Reserve University, a M.A. in physics from Princeton University, and a Ph.D. in physics from Princeton University in 1978. In 1988, Dr. Sejnowski founded Neural Computation, published by the MIT press. The long-range goal of Dr. Sejnowski’s research is to build linking principles from brain to behavior using computational models.