Variations in the Nanomechanical Properties of Virulent and Avirulent Listeria monocytogenes

Abstract

Atomic force microscopy (AFM) was used to quantify both the nanomechanical properties of pathogenic (ATCC 51776 & EGDe) and non-pathogenic (ATCC 15313 & HCC25) Listeria monocytogenes strains and the conformational properties of their surface biopolymers. The nanomechanical properties of the various L. monocytogenes strains were quantified in terms of Young’s moduli of cells. To estimate Young’s moduli, the classic Hertz model of contact mechanics and a modified version of it that takes into account substrate effects were used to fit the AFM nanoindentation-force measurements collected while pushing onto the bacterial surface biopolymer brush. When compared, the classic Hertz model always predicted higher Young’s moduli values of bacterial cell elasticity compared to the modified Hertz model. On average, the modified Hertz model showed that virulent strains are approximately twice as rigid (88.1 ± 14.5 KPa) as the avirulent strains (47.3 ± 7.6 kPa). To quantify the conformational properties of L. monocytogenes’ strains surface biopolymers, two models were used. First, the entropic-based, statistical mechanical, random walk formulation, the wormlike chain (WLC) model was used to estimate the elastic properties of the bacterial surface molecules. The WLC model results indicated that the virulent strains are characterized by a more flexible surface biopolymers as indicated by shorter persistence lengths (L_p = 0.21 ± 0.08 nm) compared to the avirulent strains (L_p = 0.24 ± 0.14 nm). Second, a steric model developed to describe the repulsive forces measured between the AFM tip and bacterial surface biopolymers indicated that the virulent strains are characterized by crowded and longer biopolymer brushes compared to those of the avirulent strains. Finally, scaling relationships developed for grafted polyelectrolyte brushes indicated L. monocytogenes strains’ biopolymer brushes are charged. Collectively, our data indicate that the conformational properties of the bacterial surface biopolymers and their surface densities play an important role in controlling the overall bacterial cell elasticity.

Introduction

Listeria monocytogenes are Gram-positive food-borne bacteria responsible for an array of infectious diseases including fatal listeriosis ^{1, 2}. L. monocytogenes are motile via flagella below 30 °C, but at temperatures above 30 °C such as those in vivo, they lose their motility and their mechanical properties adapt to their intracellular life functions ^3–5. The overall mechanical properties of L. monocytogenes are largely affected by their cell wall composition ⁶. The cell wall of L. monocytogenes is composed of 20% lipids, 40% common amino acids, 6% amino sugars, 29% neutral sugars, and 5% phosphate. All percentages are on the basis of dry cell mass ^{7, 8}.

The role of bacterial cell wall composition and molecules in controlling the biological ⁹ and chemical ¹⁰ properties of L. monocytogenes has been well documented in the literature. However, the role of bacterial cell wall molecules in controlling the mechanical properties of virulent and avirulent L. monocytogenes is still lacking. The mechanical properties of Gram-positive bacterial cells are generally affected by the osmotic pressure of the cell ^{11, 12}, the rigidity of cellular membrane ^13–15, and the biopolymer composition of bacterial surface ^16–18. The contribution of each of the above three factors to the overall cell mechanical properties will largely depend on the environmental conditions in which bacteria reside ^{19, 20}.

The overall nanomechanical properties of bacterial cells can be quantified using atomic force microscopy (AFM) nanoindentation measurements. The use of AFM as a powerful tool to probe elastic properties of Gram-negative bacterial cells such as Escherichia coli JM109 and Shewanella putrefaciens is well documented in the literature ^20–26. However, the use of AFM to probe the elasticity of Gram-positive bacterial cells has been rarely reported. A demonstration of the use of AFM to probe the elasticity of Gram-positive bacterial cells reported on Staphylococcus aureus before and after treatment with chitooligosaccharide in air ²⁷. The nanoindentation results revealed a reduction in cell wall stiffness after chitooligosaccharide treatment. Similarly, AFM was used to probe the elasticity of Lactobacillus rhamnosus strains in PBS buffer ²⁸. The results of the later study showed that the CMPG5413 mutant impaired in adherence, biofilm formation, and polysaccharide production was approximately twice as rigid as the LGG wild-type strain.

In addition to quantifying the overall elastic modulus of the bacterial cell, the elastic properties of bacterial surface biopolymers can be quantified using entropic-based statistical mechanical random walk formulation models of chain elasticity ²⁹. The two most commonly models used to describe biopolymer chain elasticity are the freely jointed chain (FJC) and the wormlike chain (WLC) models ^{30, 31}. While both models can predict entropic biopolymer elasticity, the FJC model is preferred for studying polysaccharides’ elasticities and the WLC model is preferred for studying the elasticities of stiffer biopolymers such as proteins and DNA ^{29, 32–34}. However, irrespective of the model used to quantify biopolymer elasticity, both models predict similar biopolymer elasticities. The Kuhn length estimated by the FJC is usually twice that of the persistence length estimated for the same chain using the WLC ²⁹. In this study, since more than half of the cell wall of virulent L. monocytogenes is composed of proteins ⁸ and since the peptidoglycans layer on L. monocytogenes is considered to be composed of stiff molecules, the WLC was chosen to be used in the current study ³⁵.

Finally, the conformational properties of the bacterial surface biopolymer brush can be quantified using a model developed to describe steric interactions measured between the AFM tip and a high-density polymer surface ^{36, 37}. When fit to the approach distance-force data, the model can be used to estimate the bacterial surface biopolymer brush thickness and the grafting density of the bacterial surface biopolymers.

In this study, we are interested in quantifying the elastic properties of virulent and avirulent L. monocytogenes model strains. In addition, we are interested in investigating the crucial role played by bacterial surface biopolymers in bacterial elasticity. Understanding the elasticity of bacterial cells is challenging due to the heterogeneity and complexity of the bacterial cell wall composition. Motivated by this challenge, we will combine existing models of cellular elasticity with insights from single molecule biophysics to shed the light in a comprehensive manner on Gram-positive bacterial cell elasticity.

Materials and Methods

Bacterial Cultures

Four Listeria monocytogenes strains that vary in their virulence were used in our experiments (Table 1). All strains used were obtained from Dr. Mark Lawrence at the Department of Basic Sciences at Mississippi State University, MS except for the ATCC 51776 which was purchased from the American Type Culture Collection (ATCC, Manassas, VA) ³⁸. All cells were grown at 30 °C and 150 rpm in brain heart infusion (BHI) broth adjusted to a pH value of 6.0 using 2N HCl solution for 12 hours to activate the cells ³⁹. After activation of cells, 1% of culture was transferred into triplicate of 20 ml of BHI broth and grown at the same conditions above and harvested when they reached the late exponential phase of growth.

Table 1.

A summary of the types, sources, serovars, and nanomechanical properties of the L. monocytogenes strains used in the current study. The data analyzed for each strain represent those of 15 cells taken from three different cultures.

Model	Strain	15313$	HCC25$	EGDe&	51776&
	Source	Rabbit	Catfish kidney	Guinea pig	Cheese
	Serovar	1	4	½a	4b
	Radius (nm)	724 ± 144	694 ± 85	768 ± 124	714 ± 96
	Height£ (nm)	388 ± 33	346 ± 43	371 ± 88	378 ± 52
Steric Model (Equation 8)	L (nm)	141 ± 9	134 ± 19	175 ± 45	178 ± 37
	Γ× 10−16(m−2)	1.86 ± 0.14	1.32 ± 0.24	2.26 ± 0.49	2.71 ± 0.23
	r2	0.96 ± 0.03	0.90 ± 0.05	0.96 ± 0.04	0.99 ± 0.01
Height of Internal Cell Structure (T, nm)*		247	212	196	200
Classic Hertz Model (Equation 3)	E (KPa)	52.6 ± 6.6	52.2 ± 10.2	82.1 ± 9.9	113 ± 23
	r2	0.95 ± 0.02	0.99 ± 0.01	0.99 ± 0.01	0.96 ± 0.03
Modified Hertz Model (Equations 4 and 5)	E (KPa)	47.1 ± 5.9	47.4 ± 9.3	75.1 ± 9.0	101 ± 20
	r2	0.96 ± 0.02	0.99 ± 0.00	0.99 ± 0.01	0.96 ± 0.03
WLC Model (Equation 7) # of Chains Fit to WLC	Lp (nm)	0.24 ± 0.13	0.24 ± 0.16	0.22 ± 0.10	0.20 ± 0.05
	Lc (nm)	505.0 ± 223.8	451.9 ± 186.1	614.2 ± 313.6	623.9 ± 264.4
	n	196	325	190	106
	r2	0.73 ± 0.11	0.70 ± 0.13	0.75 ± 0.14	0.69 ± 0.13

^*The difference between the cell height estimated from tapping mode images (H) minus the bush thickness (L) estimated using the steric model (Equation 8).

^$Avirulent strain.

^&Virulent strain

Immobilization of L. monocytogenes for AFM Measurements

Prior to AFM measurements, bacterial cells grown until late exponential phase of growth and centrifuged twice at 5100 rpm for 10 minutes were attached to gelatin-coated mica disks ⁴⁰. Briefly, a mica disk (Ted Pella, Inc.) was cleaved five times on both sides to obtain fresh surfaces and then gelatin-coated by dipping into a gelatin solution prepared by dissolving 0.5 g of gelatin (Sigma G6144) in 100 ml ultra-pure deionized water at 60°C and then cooled to 40°C. The gelatin-coated mica disks were allowed to air-dry overnight by standing on edge on a paper towel. After drying, a 20 μl aliquot of bacterial suspension was pipetted onto the gelatin-coated disk and allowed to stand for 10 minutes for the attachment to occur between the bacteria and the gelatin at room temperature. The disks were then rinsed gently with DI water and used directly.

Atomic Force Microscopy

All AFM experiments were performed with a PicoForce scanning probe microscope with Nanoscope IIIa controller and extender module (Veeco Inc., Santa Barbara, CA). Silicon nitride cantilevers (DNP-S, Veeco Inc., Santa Barbara, CA) were used in all experiments. The force constant of each cantilever was determined at the beginning of each experiment from the power spectral density of the thermal noise fluctuations in DI water ⁴¹. On average, the spring constant was found to be 0.07 ± 0.01 N/m (n = 6). Prior to force measurements, L. monocytogenes were imaged in TappingMode^™ under DI water. Real-time images were used to locate the cells, ensure the cells population homogeneity, and correct morphology. We have chosen to perform our measurements under water since we are interested in quantifying how L. monocytogenes mechanical properties vary in vitro. Water is the main solvent used in the food processing industries and the main solvent used in preparing foods ⁴², both of which are considered as two common processes during which L. monocytogenes strains contaminate food. Contamination of food is considered as the first step towards L. monocytogenes infections ⁴³.

AFM Force Measurements

For all strains investigated, fifteen cells from three different cultures were examined. For each bacterial cell, force measurements were performed on fifteen locations selected using the point and shoot feature of the AFM software to cover all bacterial cell surface. In general, AFM measures forces between bacterial surface biopolymers and the AFM cantilever in a cycle that consists of an approach curve recorded upon the probe approaching the surface (Figure 1A, raw data) and a retraction curve recorded upon the probe is moving away from the surface (Figure 1D, converted data). Approach and retraction curves were measured at a rate of 580 nm/sec to minimize the hydrodynamic drag forces ⁴⁴ and a resolution of 4096 points. When analyzed, the approach curves were averaged because of the minimal variation observed between individual curves. Retraction curves however, were considered individually due to observed heterogeneity in the measured forces.

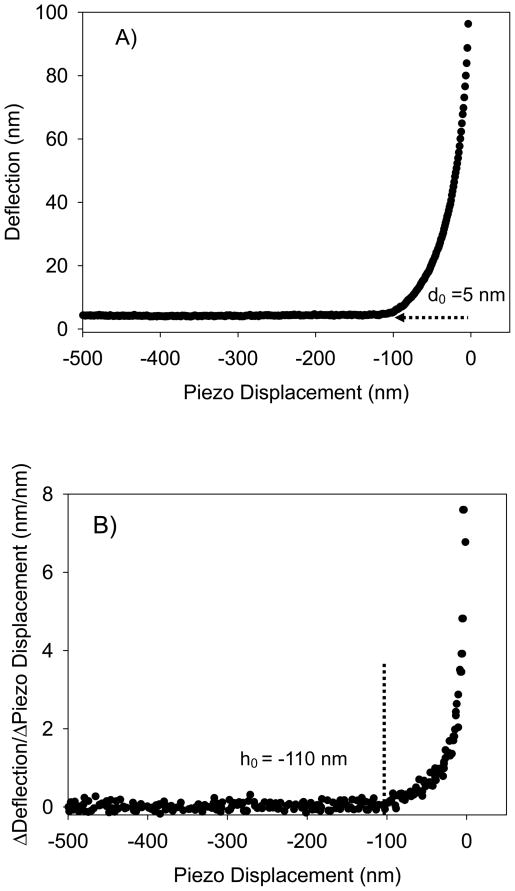
Figure 1.

A) A typical approach curve measured between the AFM tip and the bacterial surface biopolymer brush of ATCC 51776. The curve is shown as raw data in terms of the relationship between piezo displacement (h) and cantilever deflection (d). The d₀ value represents the deflection offset that was subtracted from all deflection data prior to conversion of the raw deflection data to force data. B) This curve represents the change in slope of the curve in Figure 1A as a function of piezo displacement. Note that the contact point between the tip and the bacterial surface biopolymer brush was taken as the initial value at which the slope of this curve changed from zero (h₀ = −110 nm). C) The force-indentation file that results from the treatments done in Figures 1A and 1B as described in the methods section. This curve is an example of curves fitted to the classic and modified Hertz models. D) A typical AFM retraction curve measured between L. monocytogenes ATCC 51776 surface biopolymers and silicon nitride. The solid gray line represents the zero force baseline. Finally, the dotted grey lines that show up on the retraction curve represent the portions of the retraction curves being stretched.

AFM approach raw piezo position-deflection data files (example in Figure 1A) were converted to force-indentation files (example in Figure 1C) as described previously ^{20, 21}. It is worth mentioning though that the contact point between the tip and the bacterial surface biopolymers (h₀) was defined following the approach taken by Mahaffy et al. as the point at which the force curve initially changed its slope (Figure 1B) ⁴⁵. The deflection offset (d₀) and the piezo displacement offset (h₀) were subtracted from deflection and piezo displacement values (Figure 1A), respectively. To create a force–indentation curve (Figure 1C), the compliance of the sample is taken into account. On a stiff sample, the slope of the compliance region of the force–indentation curve is expected to be 1, but this slope is <1 for soft biological samples. The indentation depth is the difference between the separation distance that would be obtained (between the tip and the sample) on a hard surface compared to the separation distance obtained for a soft sample, and is defined by:

$$\delta =(h-h\text{o})-(d-d\text{o})$$ (1)

Cantilever deflection is converted to force (F) using Hooke’s law, with the knowledge of the spring constant of the cantilever, K_c, as

$$F=K_{\text{c}}(d-d\text{o})$$ (2)

Precise determination of the contact point (h₀) between an AFM tip and a soft biological surface such as the bacterial biopolymer brush has been a proven to be a challenging task for all researchers working with soft samples. This is mainly because the contact point will be largely affected by the force applied by the cantilever on the surface being studied, the heterogeneity in the mechanical properties of the surface indented, and the nature of interactions between the tip and the surface of interest. The later is mainly problematic if strong attractive forces were observed upon approach between the tip and the sample. In our case, the bacterial surfaces studied (data not shown) and the AFM tips used are negatively charged leading to a net of repulsive forces between the tip and the bacterial surfaces ⁴⁶. The repulsive forces are mainly the result of electro-steric forces with a minimal contribution from Derjaguin-Landau-Verwey-Overbeek (DLVO) interactions ⁴⁷. The nature of the forces leading to repulsive forces upon approach is not a factor in determining the contact point. The magnitude of the repulsive forces are important however, and taken into account in our methodology for determining the contact point. Finally, to address the first two effects on the contact point, we applied approximately constant loads to our bacterial surfaces across all indentation measurements. To describe heterogeneity effects, we have indented the bacterial surface on fifteen locations that cover the entire bacterial surface.

Thickness of Thin Gelatin Film

To measure the thickness of the gelatin film coating the mica surface, gelatin films were carefully scored with a razor blade tip, removing only the gelatin film. The gelatin film thickness was determined from cross-sectional analysis of AFM height images taken at the boundary between the scratched and non-scratched regions as the difference in heights between that of the gelatin layer and that of the reference mica surface. The average height of the gelatin film was found to be 47.2 ± 5.7 nm (n=2).

Elasticity of Bacterial Cells

Quantitative information on bacterial elasticity can be obtained from modeling the measured force-indentation data (Figure 1C) using both the classic Hertz (Equation 3, Figure 3A) and the modified Hertz (Equation 4–6, Figure 3B) models of contact mechanics ^{20, 48}. According to the classic Hertz model, the indentation force (F) applied by a non- deformable sphere indenter (the AFM silicon nitride tip) required to indent a distance (δ) into an infinitely deformable elastic half space (the bacterial surface) is given by:

$$F=\frac{4}{3}\frac{E}{(1-{\nu }^2)}{R}^{1/2}{\delta }^{3/2}$$ (3)

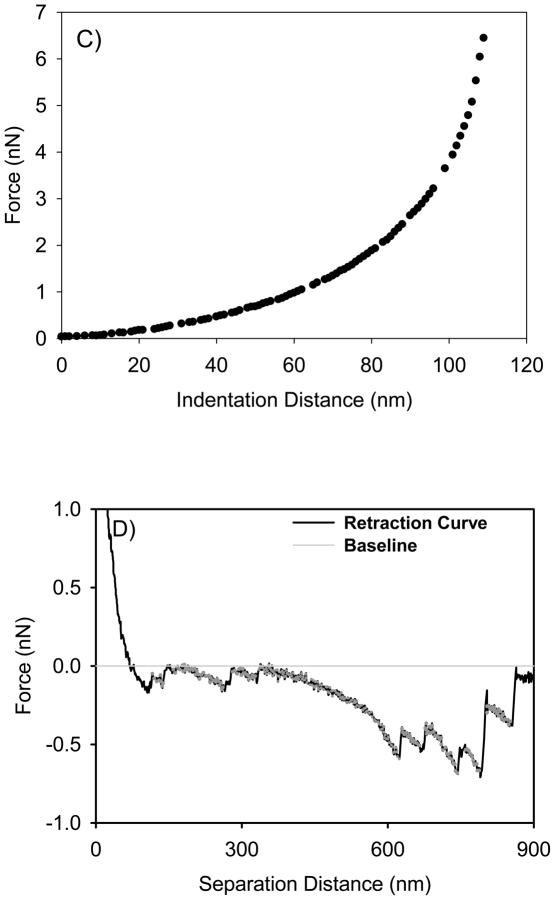
where E is the Young’s modulus of bacterium, R is the radius of the spherical indenter taken as 40 nm (the average of manufacturer reported range of values for tip radius), and ν is the Poisson ratio of the bacterium ²¹ or gelatin film ⁴⁹ taken as 0.5. Young’s modulus of the bacterium is the only fitting parameter in Equation 3. In comparison, the modified Hertz model adds a modification to the classic Hertz model described by Equation 3 such that the indentation force (F) applied by a non-deformable sphere indenter (the AFM silicon nitride tip) required to indent a distance (δ) into a deformable elastic half space (the bacterial surface) of a finite thickness is given by ⁴⁸:

$$F=\frac{4}{3}\frac{E}{(1-{\nu }^2)}{R}^{1/2}{\delta }^{3/2}\times \left[1-\frac{2{\alpha }_0}{\pi }\chi +\frac{4{\alpha }_0}{{\pi }^2}{\chi }^2-\frac{8}{{\pi }^3}\left({\alpha }_0^3+\frac{4{\pi }^2}{15}{\beta }_0\right){\chi }^3+\frac{16{\alpha }_0}{{\pi }^4}\left({\alpha }_0^3+\frac{3{\pi }^2}{5}{\beta }_0\right){\chi }^4\right]$$ (4)

where $\chi =\sqrt{R\delta }/H$, H is the thickness of the bacterial cell, and the constants α₀ and β₀ are functions of the sample Poisson ratio (v) and depend on whether or not the sample indented was bonded to the substrate beneath it or not. When the sample is not bonded to the surface, α₀ and β₀ are given by ⁴⁸:

$${\alpha }_0=-0.347\frac{3-2\nu }{1-\nu },{\beta }_0=0.056\frac{5-2\nu }{1-\nu }$$ (5)

and when the sample is bonded to the substrate, they are given by :

$$\begin{array}{l}{\alpha }_0=-\frac{1.2876-1.4678\nu +1.3442{\nu }^2}{1-\nu },\\ {\beta }_0=\frac{0.6387-1.0277\nu +1.5164{\nu }^2}{1-\nu }\end{array}$$ (6)

Figure 3.

Schematics of the indentation experiments using A) classic Hertz model and B) modified Hertz model. In the schematics, F is the applied indentation force, δ is the bacterial cell indentation distance resulting upon applying the indentation force, and R is the radius of the indenter (AFM tip). Note that the size of the indenter and the thickness of the bacteria and substrate are drawn not to scale for clarity purposes.

Note that both the classic and modified Hertz models are only valid for elastic surfaces in contact and do not take into account tip-surface adhesion. Therefore, since all approach curves measured in the current study between the AFM tip and the bacterial surface biopolymer brush displayed only repulsive interactions, the Hertz models could be applied with no problems.

Elasticity of Bacterial Surface Biopolymers

At zero force, polymer chains exist in coiled state to maximize their conformational freedom (entropy). Extension of a relaxed chain generates an opposing force that reduces the chain entropy ²⁹. This entropic elasticity of bacterial surface biopolymers can be described using statistical thermodynamic polymer elasticity models such as the Wormlike Chain (WLC) ⁵⁰. According to WLC, the polymer chain is an intermediate between a rigid rod and a flexible coil and considered to be continuously curved in random directions. The WLC model takes into account the local stiffness of the chain in terms of the persistence length (L_P) and the long-range flexibility (see inset in Figure 6A for description). The force (F_chain) required to stretch a WLC chain to a length D is given by ³⁰:

$$F_{\mathit{chain}}=\frac{-k_{B}T}{L_p}\left[\frac{D}{L_c}+\frac{1}{4{\left(1-\frac{D}{L_c}\right)}^2}-\frac{1}{4}\right]$$ (7)

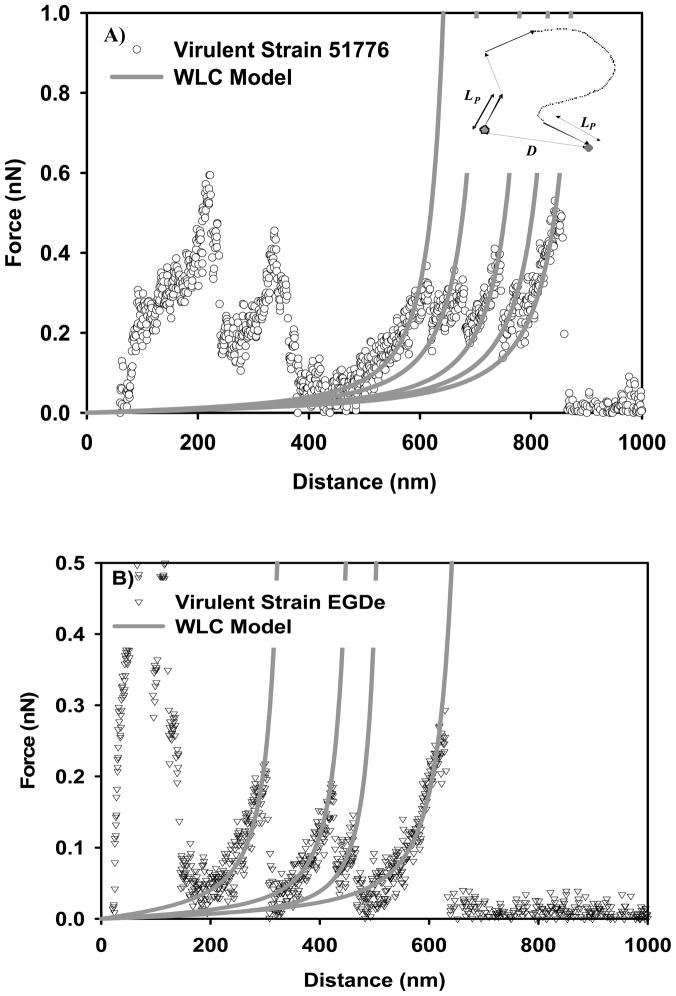
Figure 6.

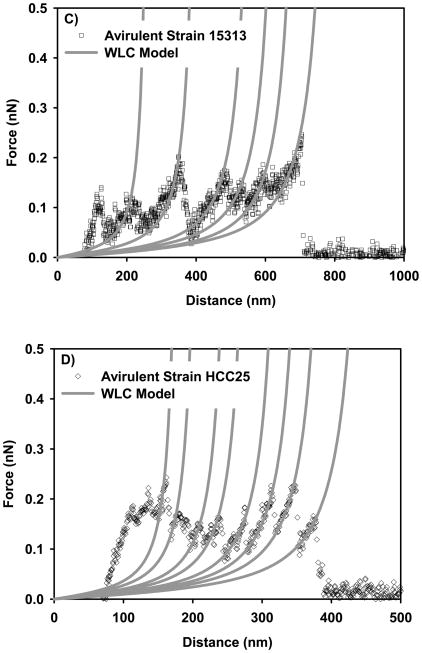
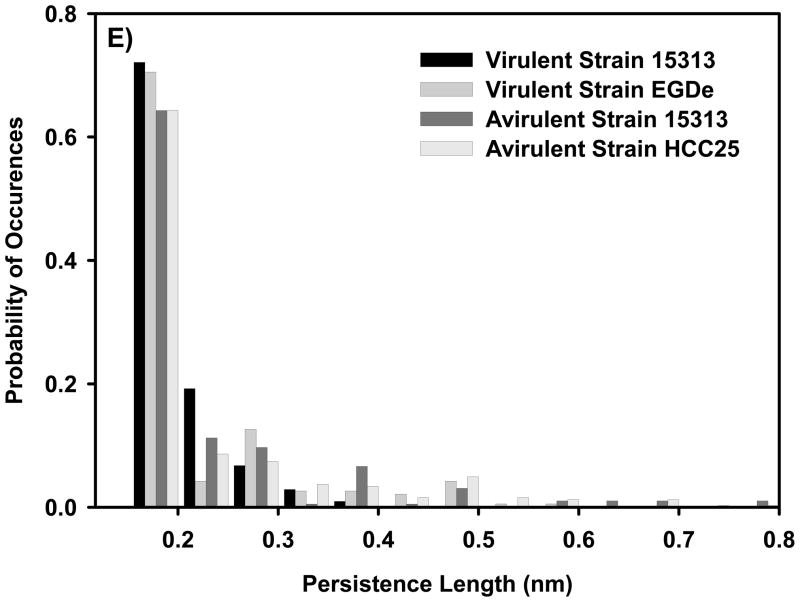
Examples on the ability of WLC model to fit the force-distance profiles representing the stretching of the bacterial surface biopolymers of: A) virulent strain 51776, B) virulent strain EGDe, C) avirulent strain 15313, and D) avirulent strain HCC25. Each solid line represents the fitting results of the WLC model to a stretching event of a bacterial surface biopolymer or a part of it and is characterized by its own values of persistence and contour lengths. Circles represent the experimental data. The inset on part A shows a schematic of a WLC chain. E) Probability histogram that shows the distribution of persistence length values estimated using WLC model for all strains investigated.

Where k_B is the Boltzmann constant, T is absolute temperature, L_c is the biopolymer contour length taken as the total length of the polymer chain. The WLC model is usually applied to a portion of the retraction data (grey dotted lines in Figure 1D) ³⁰. These portions represent the force required to stretch a biopolymer chain to a distance D. In fitting the force-extension data, L_p values were limited to those larger than 0.154 nm (C-C bond length).

Determination of Biopolymer Brush Layer Thickness and Grafting Density

A model developed for grafted polymers at relatively high surface coverage was used to model steric interactions between the AFM tip and L. monocytogenes surface biopolymers. The force per unit area between two surfaces, F_St, only one of which is coated with polymer, has been modeled following the work of Alexander ⁵¹ and de Gennes ⁵². This model was modified by Butt et al.⁵³ to describe the forces between a spherical AFM tip and a flat surface by integrating the force per unit area over the tip surface, to produce the interaction force:

$$F_{St}=50K_B\mathit{RTL}{\mathrm{\Gamma }}^{3/2}\mathit{Exp}(-2\pi h/L)$$ (8)

Where k_B is Boltzmann constant, T is temperature, R is the tip radius taken as reported by the manufacturer (40 nm), Γ is the grafted polymer density in the brush layer (m⁻²) and reflects how much of the surface is covered by polymers, h is the distance between the two surfaces, and L is the equilibrium height of the polymer brush layer ⁴⁷.

Scaling Relationships for Grafted Polyelectrolyte Brushes

The steric model described above was developed for uncharged polymer brushes ⁴⁷. However, bacterial biopolymer brushes such as those on L. monocytogenes are frequently charged (data not shown) and can be modeled as grafted polyelectrolyte brushes. For uncharged polymer brushes, scaling theories developed based on self consistent field theory predict that the brush layer height (L) is proportional to Γ^{1/3 51}. The behavior of charged polymer brushes deviates substantially from this relationship, especially at low ionic strengths such as those investigated here in water. To account for the behavior of charged polymer brushes, electrostatic blob models were developed ⁵⁴. Blob models account for excluded volume effects resulting from chain expansions due to interactions between the charged chains (electrostatic, van der Waals, and steric), and some blob models can also be made to account for the elasticity of the biopolymers. For polyelectrolytes, the brush layer thickness was related to the excluded volume (ν), the contour length of the polymer brush (L_c), the grafting density of the polymer brush (Γ), and the Kuhn segment length (L_k) through the relation L ~ Lc(νΓ/L_k)^1/3. The contour length is in turn related to the brush height. For the purpose of applying the grafted polyelectrolyte scaling relationship to the biopolymers of L. monocytogenes, we assumed that the polymer contour length would be related to the brush height, and the relationship L_c = 1.25L was used. We could not use the L_c values estimated from application of the WLC model to the AFM data because these “contour lengths” (L_c values) represent the contour length of some region of the polymer chain that was stretched ⁴⁷. The AFM tip may have come into contact with the polymer chain anywhere along its length (i.e., not necessarily at the end), and these contour length values will most likely represent the lengths of shorter sections of the chains, rather than the whole chain molecules. The arbitrary factor that we assumed (1.25) does not affect the observed relationships between contour length, polyelectrolyte grafting density and Kuhn length ⁴⁷.

The excluded volume interaction parameter accounts for chain interactions. A version of the Daoud-Cotton model that was corrected for polymers attached to a spherical surface was used to calculate the excluded volume parameter (ν) ^{55, 56}

$${(\frac{L}{a_B}+1)}^{\frac{5}{3}}=1+\frac{{kL}_c}{a_B}{(\frac{\mathrm{\Gamma }}{L_k})}^{\frac{1}{3}}{\nu }^{\frac{1}{3}}$$ (9)

where k is a constant whose value is close to unity and a_B is the bacterial strain radius estimated from 15 AFM images of bacterial individual cells taken under tapping mode in water. Values of L_k were considered as twice those of L_P values obtained from the application of the WLC model to the AFM retraction curves ²⁹, where an average L_P value was found for each strain. L and Γ were obtained from applying the steric model (eq 8) to AFM approach curves.

Statistical Description of AFM Data

The non-parametric group comparisons Mann-Whitney Rank Sum Test available in Sigma Stat 2.03 (Jandel Scientific) was applied to the measured data to determine if statistical variations were present between the two strains tested. Pair-wise multiple comparison procedure (The Tukey test) was sued to compare a certain parameter across all strains tested. The classic and modified Hertz, WLC, and steric models abilities to fit the experimental data were judged based on the estimated values of r² (the coefficient of determination, often used to judge the adequacy of a regression model) using the TableCurve fitting program (Windows, version 1.11, Jandel Scientific).

Results and Discussion

Thickness and Grafting Density of Bacterial Surface Biopolymer Brush

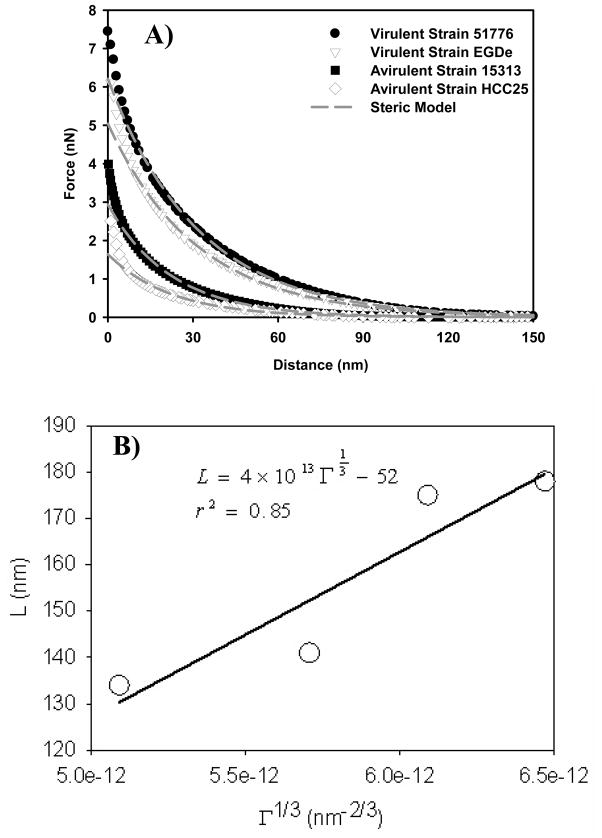
The presence of bacterial surface biopolymers caused electro-steric repulsions between the bacterium and the AFM tip. These forces were modeled using Equation 8 (Figure 2A) to estimate the bacterial surface biopolymer brush thickness and grafting density (Table 1). The height of the bacterial surface biopolymer brush was longer for the virulent strains (176.5 ± 40.6 nm) compared to the avirulent strains (137.2 ± 14.4 nm). Pair-wise multiple comparison procedure (Tukey test) indicated that the variations in the bacterial surface biopolymer brush thicknesses are statistically significant among strains that belong to different virulence categories (P< 0.05) and not-statistically different among strains that belong to the same virulence category.

Figure 2.

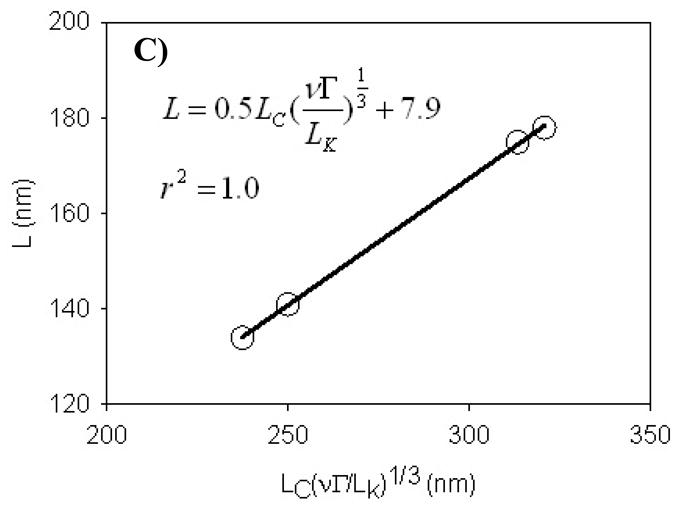
A) Force-distance curves measured on virulent and avirulent strains of L. monocytogenes. Each curve is the average of 225 individual curves measured on fifteen individual cells taken from three different cultures. The solid black lines are the steric model (eq 8) fits to the force-distance data. B) The scaling relationship for uncharged grafted polyelectrolyte brush. C) The scaling relationship for charged grafted polyelectrolyte brush. Symbols in B and C are experimental values (or calculated values based on experimental data) for all four strains tested and the line is the best line fit to the data. The excluded volume (ν) values were estimated using eq 9 for all strains, values of Γ were obtained from the steric model (eq 8) fit to the approach curves data in Figure 2A collected for the four strains, L_c values were 1.25 of the brush heights, and the Kuhn length segment values (L_K) were obtained from the application of the wormlike chain (WLC) model to the AFM retraction data.

Similarly, the grafting density of the bacterial surface biopolymer brush was larger on the virulent strains (2.49 × 10¹⁶ ± 0.36 × 10¹⁶ biopolymers/m²) compared to the avirulent strains (1.59 × 10¹⁶ ± 0.19 × 10¹⁶ biopolymers/m²) (Table 1). Pair-wise multiple comparison procedure (Tukey test) indicated that the variations in the bacterial surface biopolymer grafting densities are statistically significant among strains that belong to different virulence categories (P< 0.05) and not-statistically different among strains that belong to the same virulence category. Larger grafting densities of virulent cells agree well with genetic studies that indicate that virulent L. monocytogenes strains have more proteinacious surfaces compared to avirulent L. monocytogenes strains ^57–61.

Our results of the bacterial surface biopolymer brush thickness and grafting densities agree well with previous studies in the literature. Grafting densities resulted from fitting the steric model to the approach curves collected on Acidithiobacillus ferrooxidans were estimated to be between 3.4×10¹⁶ and 7.1×10¹⁶ moleules/m^{2 37}. Previously, we have showed that the brush thickness and grafting density of surface molecules of E. coli JM109 ⁴⁶ and Pseudomonas putida KT2442⁴⁷ in water were 242 nm and 3.5×10¹⁵ moleules/m² and 440 nm and 1.6×10¹⁵ moleules/m², respectively.

Qualitatively, the steric model results are in good agreement with the cell heights obtained from tapping mode imaging results (Table 1). If one compares the two types of measurements, it is interesting to find that the height of the internal structural components of the cell taken as the difference between the height estimated from the tapping mode images minus the polymer brush thickness estimated from the steric model is relatively independent of the strain type (Table 1). However, the biopolymer brush layer thickness is a function of the L. monocytogenes strain type.

Scaling Relations for Grafted Polyelectrolyte Polymer Brushes

The steric model discussed above assumes the polymer brush modeled to be neutral ⁴⁷ which is not the case for most bacterial surfaces ⁶². For neutral polymer brushes on a solid surface, short-range intermolecular repulsion causes the chains to partially stretch in the direction normal to the grafting surface ⁵¹. Polyelectrolyte polymer brushes such as those on the bacterial surface also stretch in the direction normal to the grafting surface, but the stretching is caused primarily by electrostatic interactions in the layer instead of short-range repulsion between individual units of the molecule⁵⁴. To investigate whether the charge of the L. monocytogenes polymer brushes play an important role in their conformation, we applied both scaling relationships developed for charged and uncharged brushes to our experimental data (Figures 2B and 2C). For uncharged polymer brushes, scaling relationships predict that the polymer brush layer height can be correlated with Γ1/3 ⁵¹. Figure 2B shows that the scaling relationship developed for the uncharged polymer brushes was quite satisfactory for our data (r² = 0.85). For charged polymer brushes, scaling relationships correlate the polymer brush height with L_c(Γν)^1/3L_k^−1/3. The polyelectrolyte model accounts for excluded volume interactions between adjacent “blobs” of the polymer chain and also accounts for the elastic properties of the polymers. Figure 2C shows that the scaling relationship developed for grafted polyelectrolyte brushes is in excellent agreement with our data (r² = 1.0). The validity of the polyelectrolyte scaling relationship confirms that the biopolymer brush layer on the surface of L. monocytogenes is charged. Our results here agree well with our previous study on Pseudomonas putida KT2442 which reported that the surface of P. putida KT2442 is charged as the scaling relationships developed for the grafted polyelectrolyte brushes fits the experimental data very well ⁴⁷.

Elasticity of Thin Gelatin Film

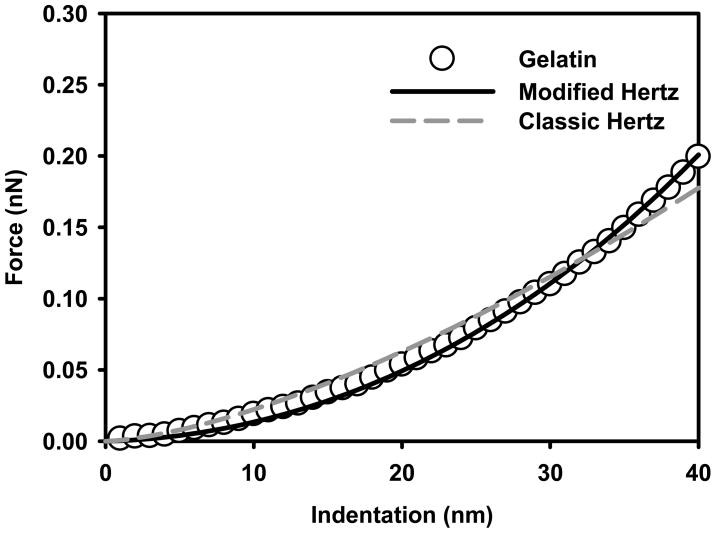
Prior to indentation measurements, L. monocytogenes cells were immobilized by adsorption on thin gelatin films. As a control, the elasticities of these thin gelatin films in water were determined using both the classic (Equation 3, Figure 3A) and modified Hertz (Equations 4 and 5, Figure 3B) models ⁴⁸ (Figure 4). Our results indicate that the Young’s modulus value obtained using the classic Hertz model (64.4 ± 6.5 kPa, n = 225, r² = 0.98 ± 0.01) was three times that estimated using the modified Hertz model (21.9 ± 2.2 kPa, n = 225, r² = 0.99 ± 0.00) (results are statistically different, P<0.05, Mann-Whitney Rank Sum Test). The higher Young’s modulus value obtained using the classic Hertz model is not real and reflects mainly the contribution of the rigid mica (E = 137 GPa) to the gelatin film elasticity. Mica is the substrate lying below the thin gelatin film. However, when the thickness of the gelatin film was taken into account, the modified Hertz model predicted much lower elasticity values that agree well with values reported in the literature for relatively thick gelatin films (> 1μm) ⁴⁹. This comparison indicates that modified Hertz model is more appropriately suited to study the elasticity of soft samples that have a thickness lower than 1 μm compared to the classic Hertz model.

Figure 4.

Force-indentation curves measured on the thin gelatin film. Circles plotted curve represents the average of 255 individual curves measured on fifteen different spots taken from three different locations on the gelatin film. The solid and dashed lines are the classic and modified Hertz models fits to the force-indentation data.

Elasticity of Virulent and Avirulent L. monocytogenes Cells

The elasticities of virulent and avirulent L. monocytogenes cells were determined from the indentation-force data using both the classic and modified Hertz models (Table 1). When the classic Hertz model was used to fit the indentation-force data measured on cells in water (Figure 5), virulent strains were found to be more rigid (97.6 ± 16.5 kPa, n = 450, r² = 0.97 ± 0.02) compared to avirulent strains (52.4 ± 8.4 kPa, n = 450, r² = 0.98 ± 0.02). Pair-wise multiple comparison procedure (Tukey test) indicated that the variations in the Young’s moduli values are statistically significant among strains that belong to different virulence categories (P< 0.05) and not-statistically different among strains that belong to the same virulence category.

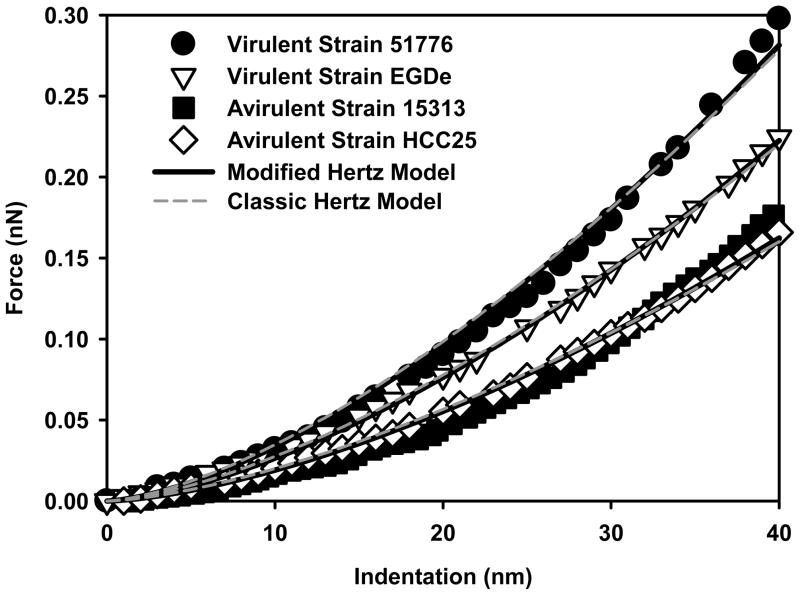
Figure 5.

Force-indentation curves measured on virulent and avirulent strains of L. monocytogenes. Each curve is the average of 225 individual curves measured on fifteen individual cells taken from three different cultures. The solid black lines are the modified Hertz model fits to the force-indentation data while the dashed grey lines are the classic Hertz model fits to the data.

To apply the modified Hertz model to the indentation-force data, the heights of the bacterial cells need to be accounted for. To estimate each bacterial strain height, we used AFM tapping mode to capture images of fifteen randomly selected cells of each of the virulent and avirulent strains of L. monocytogenes. The images were analyzed for their height using the cross-sectional offline feature available in the AFM software. Our results showed that virulent and avirulent L. monocytogenes strains have comparable heights (375 ± 70 nm, 367 ± 38 nm, n = 30, respectively, Table 1) (results are not statistically different, (P = 0.081>0.05, Mann-Whitney Rank Sum Test). When the modified Hertz model was used to fit the indentation-force data measured on cells in water (Equations 4 and 5, Figure 5), virulent strains were found to be more rigid (88.1 ± 14.5 kPa, n = 450, r² = 0.98 ± 0.02) compared to avirulent strains (47.3 ± 7.6 kPa, n = 450, r² = 0.98 ± 0.01). Pair-wise multiple comparison procedure (Tukey test) indicated that the variations in the Young’s moduli values are statistically significant among strains that belong to different virulence categories (P< 0.05) and not-statistically different among strains that belong to the same virulence category.

When the results of the classic and modified Hertz models were compared, the modified Hertz model always estimated relatively smaller Young’s moduli values compared to those obtained by the classic Hertz model. The slight differences in the values of Young’s moduli estimated using both models on three out of the four strains studied were not great enough to exclude the possibility that such differences are the result of random sample variability (results are not statistically different, P = 0.097, Mann-Whitney Rank Sum Test). Differences in the Young’s moduli values estimated for the avirulent ATCC 15313 strain using both models were statistically significant (P = 0.016, Mann-Whitney Rank Sum Test). The smaller Young’s moduli values obtained using the modified Hertz model are mainly the result of taking into account the bacterial cell thickness and thus minimizing the stiffening effect that can be observed in the classic Hertz model due to the underlying mica substrate. However, differences in Young’s moduli values of bacterial cells estimated using both two models were not as profound as differences in the Young’s moduli values of the gelatin film estimated using both models (Figures 4 and 5). This can be attributed to the combined effect of the relatively thick bacterial cell that makes it less affected by the substrates below and to the cushioning effect of the relatively thin gelatin film that separates bacterial cells from the rigid mica.

The relatively small standard deviation values associated with the estimated Young’s moduli values are a strong indicator of the reproducibility of the indentation measurements and evidence on the consistency of Young’s moduli values among cells cultivated from independent cell cultures. In addition, such small standard deviations indicate that the investigated sample size was statistically sufficient to represent the Young’s modulus of the bacterial surface. When compared, Young’s moduli values estimated for virulent strains spanned a larger range compared to those estimated for the avirulent strains. This larger range is expected due to the more heterogeneous proteinacious surface of virulent strains compared to avirulent strains as indicated by genetic studies ⁵⁷.

When the steric repulsions measured between the AFM tip and the L. monocytogenes cell surface biopolymers were modeled using the steric model developed for grafted polymers at relatively high surface coverage ⁴⁷, brush thicknesses of L. monocytogenes virulent and avirulent strains were found to be less than 200 nm (Figure 2, Table 1). In our experiments, applied forces to indent the bacterial cell wall were only sufficient to indent distances less than a 150 nm (smaller than brush thickness estimated by the steric model) (Figures 2 and 5). This indicates that indentation forces applied were used mainly to compress of the outer biopolymers’ brush of the cell wall. However, this does not mean that the role of membrane rigidity or cell turgor pressure is ignored in the estimated Young’s modulus values. We can think of the turgor pressure and the cytoskeleton elements lying beneath the membrane’ surface as additional substrate layers that can result in stiffening effects similar to those contributed by gelatin and mica.

The results of the current study showed that virulent strains (ATCC 51776 and EGDe) were approximately twice as rigid as the avirulent strains (ATCC 15313 and HCC25). Our results correlate well with current knowledge of the surface structure of virulent and avirulent strains of L. monocytogenes in general. Genetic studies performed on L. monocytogenes strains indicate that virulent strains are characterized by a more proteinacious surface in comparison to avirulent strains ^58–61. The higher stiffness observed for the virulent L. monocytogenes strains compared to the avirulent strains agrees well with our steric model results. The steric model indicated that the virulent L. monocytogenes strains were characterized by approximately 60% higher grafting densities compared to the avirulent strains, leading to stiffer surfaces. Note that the thicknesses of internal structures of the avirulent strains are slightly longer than those of the virulent strains. At a constant indentation distance, this would mean that the estimated Young’s moduli for virulent strains will be potentially subjected more to the stiffening effects of the internal cellular structures compared to the Young’s moduli estimated for the avirulent strains.

Previously, we have shown that the adhesion of L. monocytogenes bacterial biopolymer brush to silicon nitride AFM tips is positively correlated with L. monocytogenes strain virulence ⁶³. Extra stiffness for virulent L. monocytogenes strains compared to avirulent strains could therefore be implicitly correlated with the increased adhesion capabilities of the AFM tip to the virulent bacterial biopolymer brush compared to the biopolymers of the avirulent brush.

Variations in the composition of the bacterial surface biopolymers can be a key factor in determining the mechanical properties of bacterial cells. Previously, AFM force measurements performed on pathogenic E. coli strain (EAEC 042pet) and disperin knockout mutant of the same E. coli strain (EAEC 042aap) indicated that the wild-type strain has a more rigid surface compared to the mutant that lacks disperin ²². The Young’s moduli values of the L. monocytogenes strains obtained in the current study compare well with previously reported Young’s moduli values obtained for other bacterial strains using the classic Hertz model ^{20, 26, 28}. For example, Young’s moduli of Shewanella putrefaciens CIP 8040 measured in 0.1 M KNO₃ solution at two pH values (4 and 10) using a silicon nitride cantilever as an indenter were found to be 210 and 37 kPa, respectively ²⁶. Compared to the above study which was performed in 0.1 M KNO₃, our study was performed under water. As the ionic strength of the media increases, bacterial surface biopolymers were shown to collapse on the bacterial surface leading to a stiffer overall bacterial surface compared to a softer swollen bacterial surface expected in water (lower ionic strength) ⁴⁷. Another example is given by the study on probiotic bacterium Lactobacillus rhamnosus strain GG (LGG) and its derived mutant (strain CMPG5413). Young’s moduli of the wild and mutant strains were measured in PBS buffer (pH 7.4) using oxide-sharpened micro-fabricated silicon nitride cantilever. The mutant strain (184 ± 40 kPa) appeared to be two times softer compared to the wild strain (300 ± 63 kPa). The authors suggested that different surface compositions resulted in the varied nanomechanical properties ²⁸.

Elasticity of Bacterial Surface Biopolymers

The WLC model of polymer elasticity was used to quantify the conformational properties of bacterial surface biopolymers (Equation 7). Figures 6A through 6D show representative examples of how the WLC model was used to fit the force (F) needed to stretch a biopolymer chain to a certain distance (D) on the investigated virulent and avirulent strains of L. monocytogenes. It has to be noted here that the WLC model was only applied to 45% and 51% of the retraction data measured on the virulent and avirulent strains respectively. This is mainly because the WLC chain model is only applicable to stretching single molecule chains. The slightly higher chance for pulling single biopolymer chains on the avirulent strains compared to the virulent strain could be explained by the fact that their surfaces are less crowded by biopolymers as observed from the steric model fits (Table 1). Based on our steric model grafting densities’ results and by assuming that the whole AFM tip surface (sphere) is in contact with the bacterial biopolymer brush, we can estimate that ~ 321 and 501 molecules of the bacterial surface biopolymers will be in contact with the AFM tip at one point of time for the avirulent and virulent strains, respectively. However, this scenario is not always the case. As the cantilever retracts away from the bacterial surface biopolymer brush, biopolymers fall from the cantilever and single molecules can be stretched by the cantilever occasionally. Peaks that represent pulling of more than one molecule were determined as peaks with large force magnitudes and thus were excluded from the WLC analysis. Stretching single molecules usually requires forces on the order of few hundred pN ^{32, 34}. If larger forces were observed, it is usually a strong indication that more than one chain was pulled by the AFM cantilever. The likelihood of pulling only single molecules would have been increased if the cantilever was tagged with a specific protein. However, in that case, we would be only probing the role of that specific protein on bacterial cell elasticity. Using bare silicon nitride cantilevers to stretch bacterial surface biopolymers increases the likelihood of pulling different molecules on the bacterial surface and thus more representative of the role of bacterial cell wall molecules on bacterial cell elasticity.

In addition, the WLC model might fail to fit the data if the biopolymer chain was stretched beyond its contour length. Note that the WLC model (Equation 7) has a singularity at D = L_c. Other statistical thermodynamic models of polymer elasticity such as extensible wormlike chain (WLC⁺) can be used in such cases ²⁹. Fitting the retraction data with the WLC⁺ model may could have resulted in more data fits, however, WLC⁺ requires much more extensive data analysis as it requires the use of numerical techniques to extract fitting parameters from the data²⁹. The ability of the WLC model to fit approximately half the data does not imply that model is inapplicable to our data. It is however implying that only a subset of the data satisfies the model requirements and that subset fit the model very well.

The persistence lengths of biopolymer chains taken from 15 cells of each strain estimated using the WLC model ranged from 0.16 nm to 0.60 nm (mean 0.21 ± 0.08 nm, n = 296) for virulent strains and between 0.16 nm to 0.95 nm (mean 0.24 ± 0.14 nm, n =521) for avirulent strains (Figure 6E). On average, the persistence length estimated for the virulent strains was lower than that estimated for the avirulent strains, indicating the presence of more flexible chains on the surfaces of virulent strains (the differences in the median values among the treatment groups are greater than would be expected by chance; there is a statistically significant difference (P = 0.028), Kruskal-Wallis One Way Analysis of Variance on Ranks). The range of persistence lengths measured on all investigated L. monocytogenes strains indicates the heterogeneity of the biopolymers composing the bacterial surface ³¹.

The contour lengths ranged between 128 nm and 1810 nm (mean 617.7 ± 296.0 nm) for virulent strains and between 85 nm and 1280 nm (mean 471.9 ± 200.3 nm) for avirulent strains. The contour lengths estimated for the virulent strains were on average longer than those estimated for the avirulent strains. Pair-wise multiple comparison procedure (Dunn’s method) indicated that the contour lengths of surface biopolymers are statistically different among strains that belong to different levels of virulence (P< 0.001) and are not statistically different among strains that belong to the same virulence category. Our contour length estimates are in good agreement with our longer brush thicknesses obtained using the steric model for the virulent strains compared to the avirulent strains (Table 1). Although contour lengths can be used as an indication on how far biopolymers extend from the bacterial surface, their estimated values are greatly affected by the distance at which the cantilever contacted the biopolymer chain ^{30, 64}.

Figure 6E shows that almost 71% and 64% of the biopolymer chains composing the virulent and avirulent strains’ surfaces were extremely flexible as they could be fitted with a persistence length between 0.16 nm and 0.21 nm, which is slightly higher than the C-C bond length (0.154 nm). Although all strains shared the presence of flexible polymers on their surface, 30 % of the biopolymer chains of the avirulent L. monocytogenes strains were stiff and had persistence lengths longer than 0.4 nm compared to only 11% of the biopolymer chains of virulent L. monocytogenes strains.

The estimated persistence lengths of the surface biopolymers of L. monocytogenes are similar to values observed for other bacterial surface biopolymers in the literature. For example, we have shown previously that the persistence length of the surface biopolymers of Pseudomonas putida KT2442 in water spanned a range of 0.154 nm to 0.28 nm indicating that bacterial surface polymers are very flexible ^{30, 31}. In another study, when the WLC was used to quantify the elasticities of the surface biopolymers of the yeast strain Sacchrmoyces cerevisiae stretched using a lectin-modified tip, a range of persistence length values (0.03 to 0.56 nm) were necessary to fit the retraction data with rupture lengths that are less than a 400 nm. The authors suggested that the range of persistence lengths observed is indicative of the fact that both oligosaccharides and polypeptide chains of the manno-proteins were stretched on S. cerevisiae. Note that in this study, unrealistic persistence length values were necessary to fit some of the data²⁸. In a third study, the WLC model was applied to the AFM force-distance stretching profiles measured for Escherichia coli surface biopolymers. The authors combined the AFM sawteeth signature force profiles observed in the retraction data and the WLC theoretical predictions of chain elasticity to predict the presence of two unique proteins on the bacterial surface ⁶⁵.

In biopolymers with known structure, composition, and contour length, all the force-extension data can be normalized by the contour length of the biopolymer ⁵⁰. In the current study, the retraction data measured on both virulent and avirulent cells could not be normalized by the estimated contour lengths. Our inability to normalize the retraction data by a fixed contour length value indicates that the AFM cantilever stretched a wide array of bacterial surface biopolymers and was not limited to a specific biopolymer type on the bacterial surface.

Implications for L. monocytogenes Nanomechanical Properties

Our results indicated that the virulent L. monocytogenes strains exhibited a more rigid surface at cellular level compared to the avirulent strains as indicated by the higher Young’s moduli values estimated using the classic and modified Hertz models. At the molecular level however, the virulent strains exhibited more flexible surface biopolymers compared to the avirulent strains. Finally, when repulsive steric forces measured between the AFM tip and the bacterial surface biopolymers of L. monocytogenes were modeled (Equation 8), biopolymer brushes of virulent strains were longer and more crowded with surface molecules compared to those of avirulent strains’. Applying scaling relations developed for grafted polyelectrolytes to our experimental data implied that the biopolymer brushes of L. monocytogenes strains investigated are charged. Collectively, our observations indicate that the conformational properties of the bacterial surface biopolymers and their surface densities and charge play an important role in controlling the overall bacterial cell elasticity. In addition, our data is suggestive of the presence of possible differences in the nanomechanical properties of virulent and avirulent strains of L. monocytogenes.