Abstract
To examine the impact of the complex radial organization of the rat outer medulla (OM) on the distribution of nitric oxide (NO), superoxide (O2−) and total peroxynitrite (ONOO), we developed a mathematical model that simulates the transport of those species in a cross section of the rat OM. To simulate the preferential interactions among tubules and vessels that arise from their relative radial positions in the OM, we adopted the region-based approach developed by Layton and Layton (Am J Physiol Renal Physiol 289: F1346–F1366, 2005). In that approach, the structural organization of the OM is represented by means of four concentric regions centered on a vascular bundle. The model predicts the concentrations of NO, O2−, and ONOO in the tubular and vascular lumen, epithelial and endothelial cells, red blood cells (RBCs), and interstitial fluid. Model results suggest that the large gradients in Po2 from the core of the vascular bundle toward its periphery, which stem from the segregation of O2-supplying descending vasa recta (DVR) within the vascular bundles, in turn generate steep radial NO and O2− concentration gradients, since the synthesis of both solutes is O2 dependent. Without the rate-limiting effects of O2, NO concentration would be lowest in the vascular bundle core, that is, the region with the highest density of RBCs, which act as a sink for NO. Our results also suggest that, under basal conditions, the difference in NO concentrations between DVR that reach into the inner medulla and those that turn within the OM should lead to differences in vasodilation and preferentially increase blood flow to the inner medulla.
Keywords: mathematical model, rat kidney, generation rates, peroxynitrite, thick ascending limb sodium transport
blocking the synthesis of nitric oxide (NO) in the renal medulla leads to a reduction in blood flow, salt retention, and hypertension (12, 36, 40). NO and its scavenger superoxide (O2−) both modulate renal medullary vascular and tubular function, albeit in opposite ways. Whereas NO inhibits tubular sodium reabsorption and increases medullary blood flow by promoting the vasodilation of descending vasa recta (DVR), O2− enhances medullary thick ascending limb (mTAL) Na+ reabsorption (19) and acts to reduce medullary blood flow by mechanisms that have yet to be fully elucidated (17). The product of the NO-O2− reaction, ONOO−, is thought to inhibit Na+ reabsorption (19). In vitro experiments suggest that the interactions between O2− and NO ultimately determine the effectiveness of tubulovascular cross talk (39). The overall objective of this study was to investigate the impact of the radial organization of the outer medulla (OM) of the rat kidney on the interactions between NO and O2−. In the current study, we examined the effects of low medullary Po2 on the distribution of NO, O2−, and total peroxynitrite (the sum of ONOO− and ONOOH, denoted ONOO). In a companion study (15), we considered the effects of kinetic and transport rates on the concentration profiles of these species, and the importance of tubulovascular cross talk and of NO-O2− interactions in vivo.
Anatomic studies have revealed that the medullary organization of tubules and vessels is highly structured in a number of mammals (29), including rats and mice (28, 30). DVR and ascending vasa recta (AVR) form tightly packed vascular bundles that appear to dominate the histotopography of the OM, especially in the inner stripe. Throughout the OM, collecting ducts (CDs) are found distant from vascular bundles, whereas the loops of Henle are positioned nearer the bundles. Modeling studies have shown that the structural organization results in preferential interactions among tubules and vasa recta (33, 49). In an earlier modeling study, we examined the impact of the structural organization of the rat OM on O2 distribution (5). We found that the segregation of DVR, the main supply of O2, at the center and immediate periphery of the vascular bundles gives rise to large radial differences in Po2.
In the current study, we developed a mathematical model that simulates the generation, transport, and consumption of NO, O2−, and ONOO in cross sections of the rat OM. We had previously built a model of NO transport in a cross section of the rat OM (53). That model, which we refer to as the ZE model, also accounted for the radial organization of the rat OM, by explicitly representing all tubules and vessels associated with a vascular bundle, and by assigning each tubule and vas rectum a distinct position in the model cross section. (A total of 154 tubules and 230 vasa recta were individually represented in the ZE model.) In contrast, the present model, which accounts for the preferential interactions among tubules and vessels using the region-based approach developed by Layton and Layton (33), represents only one model tubule or vessel for each class of tubules or vessels. The radial position of the tubules and vessels is specified by assigning them to one of the four concentric regions; the portion of each concentric region that is exterior to both tubules and vasa recta represents interstitial cells, merged capillary plasma, and interstitial space. Since the representation of the position of individual structures is less detailed using the region-based approach, the present model requires substantially less computational time than the ZE model. This has allowed us to introduce more complexity in other ways. First, in the present model, the concentrations of O2− and ONOO are explicitly calculated, whereas O2− levels were arbitrarily fixed in the ZE model. Second, the present model accounts for the effects of medullary hypoxia, which were neglected in the ZE model. Third, in contrast to the present model, the ZE model did not incorporate the OM capillary plexus. As described below, the addition of each of these new features has a significant impact on the predicted NO, O2−, and ONOO concentration profiles.
MODEL DESCRIPTION
In this section, we describe a base-case model configuration, model equations, and a set of base-case model parameters, including physical dimensions and transport parameters. In addition, we briefly describe the numerical methodology used to obtain model solutions. Acronyms and symbols are given in the glossary.
Configuration and Radial Organization
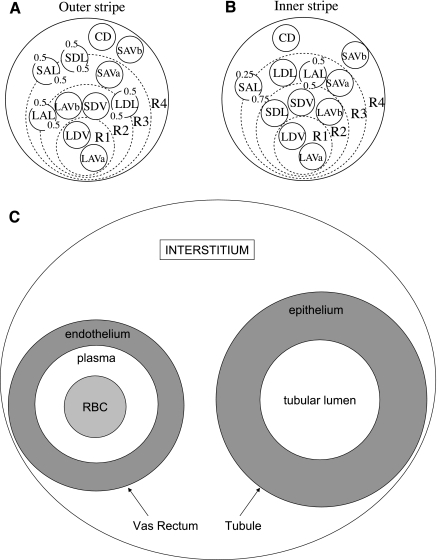
We seek to investigate the effects of the radial organization of the rat OM, and the resulting preferential interactions among tubules and vessels, on the distribution of NO and O2−. To achieve that goal, we use the region-based approach developed by Layton and Layton (33). In the region-based formulation, the structural organization of the OM is represented by means of four concentric regions centered on a vascular bundle: an innermost region containing the central vascular bundle (R1), where all the long DVR (i.e., DVR that reach into the inner medulla) and one-third of the long AVR (i.e., AVR that reach into the inner medulla) are sequestered; a peripheral region of the vascular bundle (R2), where the short DVR (i.e., DVR that turn within the OM) and the remaining long AVR reside; a region neighboring the vascular bundle (R3), which contains most thick ascending limbs, both long and short, and some short AVR; and the region most distant from the vascular bundle (R4), where collecting ducts (CDs) and the remaining short AVR are located. Descending limbs that reach into the inner medulla are situated in R2 and R3 in the outer stripe (OS) and move toward the CDs in the inner stripe (IS). Conversely, the short descending limbs (i.e., those that turn within the OM) straddle R3 and R4 in the OS and move toward the bundle periphery (R2) in the IS.
We consider the cross sections at two axial positions of the OM: one at the mid-OS (0.3 mm from the corticomedullary boundary in a typical rat OM that is 2.1 mm long) and another at the mid-IS (1.35 mm from the corticomedullary boundary). These two positions are chosen because the radial positions of some of the tubules and vessels differ substantially in the OS and in the IS (see above). Also, in a model of O2 transport in the OM (5), the Po2 in the IS was predicted to be substantially lower than in the OS, so a comparison of the model predictions for the two cross sections should illustrate the effects of O2 availability on the distribution of NO and O2−. The radial organization of tubules and vasa recta with respect to vascular bundles is represented by specifying the fractions of the tubules and vasa recta assigned to each concentric region at each medullary level. Figure 1 shows the relative positions of tubules and vessels in a cross section through the OS (Fig. 1A) and through the IS (Fig. 1B).
Fig. 1.
Model representation of tubules, vasa recta, and regions in the rat outer medulla (OM). Displayed in A and B are the cross sections of the outer stripe (OS) and inner stripe (IS), respectively. The different compartments that are distinguished in each vas rectum and each tubule are shown in C. In the model formulation, the 4 regions (R1–R4) have coincident centers; the display here is intended to minimize the figure area. LDV, long descending vasa recta; SDV, short descending vasa recta; LAVa and LVAb, 2 populations of long ascending vasa recta; SAVa and SAVb, 2 populations of short ascending vasa recta; LDL, long descending limb of Henle's loop; SDL, short descending limb; LAL, long ascending limb; SAL, short ascending limb; CD, collecting duct. The decimals represent the relative weight of interaction between a type of vessel or tubule and a given region (i.e., the parameter κi, R in Eq. 7).
To simulate the distribution of NO, O2−, and ONOO in a cross section of the OM, we distinguish the concentrations of those species in different “compartments.” NO and O2− are generated within vascular endothelia and tubular epithelia but not within the lumen, and the rates of NO consumption in red blood cells (RBCs) and plasma differ by orders of magnitude (see below). Hence, to accurately represent the generation and consumption of NO and O2−, we distinguish between the lumen and the surrounding epithelium in each tubule, and between the RBC compartment, the plasma compartment, and the surrounding endothelium in each vas rectum, as illustrated in Fig. 1C. The interstitia of each of the four concentric regions also constitute separate compartments. The capillaries that traverse radially across the OM cross sections are also represented. Given that the properties (e.g., dimensions and permeabilities) of the medullary capillary network have not been well documented, capillary plasma is assumed to be well mixed with the local interstitium. In this model, the capillaries thus consist of two compartments, which exchange directly with each other: the capillary RBCs and the surrounding capillary endothelium. The solute concentrations and reaction rates associated with the capillary RBC cytosol and the capillary endothelium in a given region (R1–R4) represent radial averages in that region.
Solutes Represented in the Model
The model is formulated for three solutes, NO, O2−, and ONOO; the latter represents the total amount of peroxynitrite (ONOO− + ONOOH). Hemoglobin concentrations in RBCs, and Po2 in the lumen, RBC, and interstitial fluid are set a priori, based on the predictions of an O2 model (4). That O2 model does not represent the endothelium and epithelium explicitly; thus, in the current study, the Po2 values in the endothelial and epithelial compartments are taken as the average between interstitial and luminal Po2. The present model predicts the concentrations of NO, O2−, and ONOO (as well as the associated fluxes) in the tubular and vascular lumen, epithelial and endothelial cells, RBCs, and interstitial fluid (i.e., a total of 40 compartments).
Conservation Equations
Solute concentrations are determined by solving conservation equations in each compartment. At steady state, the conservation of solute k (k = NO, O2−, or ONOO) in a given vascular endothelium or tubular epithelium (denoted “cell”) is given by
| (1) |
where Ψki is the volumetric rate of net production (i.e., generation minus consumption) of solute k in compartment i, Ai is the cross-sectional area of compartment i, Jklumen, cell is the flux of solute k from the vascular or tubular lumen into the surrounding cellular layer, and Jkcell, R is the flux of solute k from the cellular layer into the surrounding interstitium of region R. The latter may be zero if the tubule or vessel does not reside in R. For example, for the short descending limb, JSDLcell,R4 is non-zero in the OS, where the limb straddles R3 and R4, but is null in the IS, where the limb straddles R2 and R3, but not R4 (see Fig. 1).
Conservation of solute k within the tubular lumen is expressed as
| (2) |
In the above equation, axial advective flux is neglected because its magnitude is believed to be sufficiently small compared with the synthesis rate or the transmembrane flux (52). In vasa recta lumen, we distinguish between the RBC compartment (denoted “RBC”) and the outer, plasma layer (denoted “pl”). Conservation of solute k within these two compartments is written as
| (3a) |
| (3b) |
Conservation of solute k within the capillary RBC cytosol (denoted “cap RBC”) and the surrounding endothelium (denoted “cap endo”) is expressed as
| (4a) |
| (4b) |
Axial advective flux is also neglected in these equations, as in Eq. 2. Following the approach of Layton and Layton (33), solute conservation in the interstitium of each concentric region is expressed as
| (5) |
The first term represents the net production of solute k within the interstitium of region R; AintR is the area occupied by interstitium in region R (R = R1, R2, R3, and R4). The second term, JktotR, is the total flux of solute k into region R from tubules, vasa recta, capillaries, and adjoining regions. The third term represents the capillary source term, where SDV denotes short DVR, CkSDV is the concentration of solute k in SDV, and QSDV, R is the rate of blood flow from SDV into region R. Although water fluxes are not explicitly computed in this model, they are incorporated as parameters, using values predicted by a previous model (4), so that the roles of AVR and capillary sinks in the conservation of solutes can be represented. In a given region, the sum of the capillary source flows and water fluxes emanating from tubules and vessels equals the total fluid reabsorbed into that region; at steady state, there is no fluid accumulation, that is, the fluid reabsorbed is drained away in its entirety, via entry into AVR and capillary transport into surrounding regions. The fourth term in Eq. 5 represents the solute that is carried away by the AVR located in region R; QAVR, R is the fluid flow entering the AVR in R. The last term represents the solute that is carried by capillary flow into an adjoining region R′; QR, R′ is the fluid flow from region R into region R′.
Flux Calculations
Across most barriers, water and solutes do not share the same pathway, so that the solute flux is driven only by diffusion [exceptions include NO fluxes across aquaporin-1 (AQP1) water channels in DVR endothelium and descending limb epithelium, as noted below]. In this case, the transmural flux (in mol·s−1·m−1) of solute k (k = NO, O2−, or ONOO) from compartment i into compartment j, taken positive into compartment j, can be written as
| (6) |
For a tubule, i = lumen and j = epithelium; for a vessel, i = plasma and j = endothelium, or i = RBC and j = plasma; for capillaries, i = RBC cytosol and j = endothelium. In Eq. 6, Ri, j is the radius at the i-j interface, Pki, j is the permeability of the i-j interface to solute k, and Cki and Ckj are the concentrations of solute k in compartments i and j. Some vessels and tubules straddle several regions (Fig. 1), so the transmural flux of solute k from the vascular endothelium or tubular epithelium into a surrounding region R is calculated as (33)
| (7) |
where Rcell, R is the outer radius of the cellular layer, and κcell, R is the fraction of the vascular endothelium or tubular epithelium in contact with region R, such that . For example, for the long ascending limb in the OS, κcell, R1 = 0, κcell, R2 = 0.5, κcell ,R3 = 0.5, and κcell ,R4 = 0.
Across AVR fenestrations, water is reabsorbed directly from the interstitium into the AVR lumen, and solutes are carried along. The convective-diffusive flux of solute k (k = NO, O2−, or ONOO) across the fenestrations, from the AVR lumen (“lum”) into the interstitium of the surrounding region R (“R”), is expressed as
| (8) |
where Jvfen denotes the volume flux (in m2/s) across the fenestrations, Pekfen is the Péclet number for solute k associated with the fenestration flow, and Rlum is the AVR internal diameter. The permeability of the fenestrations to solute k (Pkfen) is calculated as the ratio of the diffusivity of solute k in water to the AVR wall thickness, times the fractional area occupied by the fenestrations (0.057).
As described below, AQP1 water channels are permeable to NO (21, 22). Hence, NO convection must also be considered across RBCs, DVR, and descending limbs, all of which express AQP1. Since water and NO share the same pathway across descending limbs and DVR, the flux of NO between descending limb compartments i and j (i = lumen and j = epithelium), and between DVR compartments i and j (i = plasma and j = endothelium, or i = RBC and j = plasma), is expressed as
| (9) |
where Jvi, j denotes the volume flux (in m2/s) between i and j, and PeNOi, j is the Péclet number associated with compartments i and j. JNOi, j is taken positive into compartment j. Similarly, the flux of NO from the descending limb epithelium or the DVR endothelium (denoted i) into region R is calculated as
| (10) |
The total flux of solute k (k = NO, O2−, or ONOO) into region R is then given by (33)
| (11) |
The first term on the right-hand side represents the sum of solute fluxes from tubular epithelia, vascular endothelia, and capillary endothelia (indexed by i) into R. The term Jki, R denotes the flux of solute k of one model tubule or vessel i, taken positive into the region. To account for the fluxes of all tubules and vessels associated with the model vascular bundle, each flux term is scaled by the number of vessels or tubules of type i per vascular bundle, denoted ni. The second term represents the diffusive solute flux into R from adjacent regions R′; RR, R′ is the radius at the interface between regions R and R′, and PkR, R′ denotes the effective permeability to solute k of the boundary separating regions R and R′. This effective permeability takes into account the diffusion resistance that represents the effects of macromolecules and interstitial cells in the interstitium, and the effect of tortuosity on the diffusion path length around tubules and vessels (see below).
Vascular, Tubular, and Interregion Permeabilities
Estimates of the RBC membrane permeability to NO (PNORBC) vary over a wide range, from 400 to 450 μm/s (16, 47), to 45,000 or 64,000 μm/s (25, 35). In this study, the plasma and RBC compartments are taken to be well mixed. To account for the diffusive resistance within these layers, the base-case value of PNORBC is set to 1,000 μm/s (0.1 cm/s), that is, in the lower range.
Herrera and colleagues (21, 22) recently found that AQP1 water channels transport NO and thereby regulate endothelium-dependent vasorelaxation. Given that DVR, RBCs, proximal tubules, and thin descending limbs all express AQP1, AQP1-mediated NO transport may significantly affect NO levels throughout the medulla. In Chinese ovary K1 cells stably transfected with an AQP1 expression vector, Herrera et al. (22) observed a linear relationship between the water permeability (Pf, in μm/s) and the NO permeability (PNO, in fluorescence units per time)
| (12) |
We use this relationship to estimate the NO permeability of the endothelial or epithelial layer surrounding the lumen in vessel or tubule i (Pi,NOcell), given the RBC permeability to NO
| (13) |
where Pi, fcell is the water permeability of the endothelium or epithelium. In the vessels and tubules i that do not express AQP1 (i.e., AVR, ascending limbs, and CDs) Pi, fcell is taken as zero in Eq. 13.
In the current model, the cellular layers are modeled as compartments, not as single barriers. To estimate the NO permeability at the interface between the cellular layer of vessel or tubule i and the surrounding interstitium (denoted Pi, NOcell-int), and the NO permeability at the interface between the lumen of tubule i (or the plasma of vessel i) and the surrounding cell layer (denoted Pi, NOlumen-cell), we apply the concept of resistances in series, which gives the relationship Pi, NOcell-int = Pi, NOlumen-cell = 2Pi, NOcell. Thus, given the transmembrane NO permeability Pi, NOcell (from Eq. 13), we can estimate Pi, NOcell-int and Pi, NOlumen-cell. In a given vessel i, the NO permeability at the plasma-RBC interface (denoted Pi, NORBC-pl) is given by PNORBC.
In the absence of data for the tubular and vascular permeability to O2−, the latter is estimated based upon the O2− diffusivity across membranes (). The O2− permeability at the interface between the cellular layer of vessel or tubule i and the surrounding interstitium (denoted ) and that at the interface between the lumen of tubule i (or the plasma of vessel i) and the surrounding cell layer (denoted ) are calculated as
| (14) |
where Lcell is the thickness of the epithelial or endothelial layer. Similarly, the O2− permeability at the RBC-plasma interface is determined as where LRBC is the thickness of the RBC compartment. We use an identical approach to determine the permeabilities to ONOO. The diffusivity of O2− and ONOO at 37°C in dilute solution has been reported as 2,800 and 2,600 μm2/s, respectively (3). We assume that, as is the case for NO (14), their diffusivity across membranes is five times smaller.
Following the approach developed by Layton and Layton (33), the effective permeability to solute k of the boundary separating regions R and R′ is estimated as
| (15) |
where AF, R, R′ is the fraction of the R-R′ interface available for interstitial diffusion, Dk is the diffusivity of solute k in dilute solution, and dR, R′ is the distance between the midpoints of regions R and R′. The parameter Ω is a diffusion resistance which represents the hindering effects of macromolecules and cells in the interstitium; as described above, it is taken as 5 (14); τ represents the effect of tortuosity on the diffusion path length around tubules and vessels and is taken as π/2 (33). The diffusivity of NO in dilute solution is taken as 3,300 μm2/s (37).
NO Generation Rates
The net production rate of solute k in compartment i (Ψki, Eq. 1) is the difference between its generation rate in i (denoted Gki) and its consumption rate in i. The rate of synthesis of NO and O2− in the vascular endothelium and tubular epithelium depends on O2 availability. The O2 dependence of the NO generation rate is modeled using a Michaelis-Menten relationship (1)
| (16) |
where the Michaelis-Menten constant KO2NO is the Po2 at half the maximum rate of NO production in cell layer i, itself denoted by GNO, maxi. Reported values for neuronal nitric oxide synthase (nNOS) and endothelial NOS (eNOS) KO2NO vary over a wide range (2), from 7.7 to 88 μM (∼5–60 mmHg), with one estimate as high as 400 μM. In our model, the base-case value of KO2NO is taken as 38 mmHg (50).
The rate of synthesis of NO does not appear to be well characterized. Chen and Popel (9, 10) modeled the biochemical pathways of nNOS (NOS1) and eNOS (NOS3) to estimate NO production in the microvasculature. They predicted that the steady-state NO generation rate in arterioles is in the range of 0.005–0.1 μM/s for eNOS, and 1 μM/s for nNOS. However, using these values, predicted NO concentrations (CNO) in the vicinity of the arteriolar wall were orders of magnitude lower than perivascular NO measurements. Experimental values of GNO from in vitro studies (reviewed in Ref. 9) range from 0.035 to 12 μM/s, depending on shear stress. In the kidney, Wu et al. (51) measured the production of l-citrulline from microdissected segments in the rat kidney and estimated the NO generation rates from vasa recta, OM thin limbs, mTALs, and OM collecting ducts as 3.2, 0.6, 0.5, and 0.3 fmol·mm−1·h−1, respectively, which is equivalent to 15.3, 2.46, 0.197, and 0.083 nM/s, respectively, based upon the cellular layer thicknesses assumed herein. In a previous study of NO transport in vasa recta, we found it necessary to multiply these estimates by a factor of ∼1,000 to match experimental determinations of interstitial CNO (54). Similarly, other mathematical models of NO transport have assumed NO generation rates on the order of 100 μM/s (1, 48). In the current study, GNO,max is taken as 76.6, 12.3, 0.985, and 0.415 μM/s in the cellular layers surrounding vasa recta, thin limbs, mTALs, and OMCDs, respectively, that is, 5,000 times the values obtained from the in vitro experiments of Wu et al. (51). This choice is investigated and discussed in the companion study (15).
The ability of erythrocytes to release NO under hypoxic conditions has given rise to two hypotheses, according to which SNOHb or RBC nitrite constitutes a pool of bioavailable NO (13, 42). Following the approach of Chen et al. (6, 8), the volumetric generation rate of NO via the SNOHb and nitrite pathways is calculated as, respectively
| (17) |
| (18) |
where Hb denotes deoxyhemoglobin. The form under which the NO thereby formed is exported out of the RBC cytosol remains uncertain. If it were released into the RBC cytosol, it would immediately react with hemoglobin and would not have any vasodilatory effect. Thus Chen and colleagues (6, 8) postulated that the RBC membrane possesses a mechanism that facilitates the export of NO out of the cell, or that another NO-related species is the immediate product of these two reactions, and they modeled the SNOHb- and nitrite-mediated NO release rate as a surface reaction at the RBC-plasma interface. Given our compartmental approach, we assume instead that the amount of NO thereby generated is released uniformly throughout the adjacent plasma layer. Hence, the volumetric NO generation rate in the plasma compartment is given by
| (19) |
NO Consumption Rates
As in our previous model of NO transport (54), the NO consumption reactions considered here are the autoxidation of NO (rate v1), the scavenging of NO by O2− (rate v2), the irreversible reaction of NO with oxyhemoglobin (HbO2) to form methemoglobin (rate v3), and the reversible reaction of NO with deoxyhemoglobin (Hb) to form HbNO (rate v4)
| (20) |
| (21) |
| (22) |
| (23) |
In Eqs. 20–23, the superscripts i denoting the compartment in which the reaction is occurring have been omitted for simplicity. The net production rate of NO in compartment i is then equal to
| (24) |
The vasodilating effects of NO stem from its activation of soluble guanylate cyclase (sGC) within the pericytes encircling DVR endothelia. The pericytes are not represented explicitly in this model, but the reaction of NO with sGC is slow (k ∼ 0.01 s−1; see Ref. 1) compared with the reactions considered above (e.g., kNO-SupCO2− > 0.1 s−1 in endothelia) and can therefore be neglected.
O2− Generation Rates
Li et al. (34) measured the production of O2− in glomeruli and renal tubular segments; under well-oxygenated conditions (95% O2), the rates for the mTAL, the medullary CD, the thin limb of Henle's loop, and the glomerulus were ∼800, 400, 500, and 500 fluorescence units/mm2, respectively. In the absence of data for vasa recta, we assume that the O2− production rate in medullary vessels is similar to that in glomeruli. Given the lumen diameter and the thickness of the surrounding cellular layer, the rates per square millimeter are converted to volumetric rates, respectively yielding 0.071, 0.041, 0.342, and 0.473 fluorescence units/mm3 for the mTAL, the CD, the thin limb, and vasa recta. The vasa recta-to-mTAL ratio of O2− synthesis is therefore taken as 0.473/0.071, the vasa recta-to-CD ratio as 0.473/0.041, and the vasa recta-to-thin limb ratio as 0.473/0.342. When Po2 is plentiful, the rate of O2− production in vasa recta endothelium is assumed to be equal to the measured rate of O2− production in aortic endothelial cells, that is, 0.7 μM/s (43).Thus, under well-oxygenated conditions, the volumetric rate of O2− generation (denoted ) is taken as 0.106, 0.061, and 0.508 μM/s in the epithelium of mTALs, OMCDs, and thin limbs, respectively.
The effects of low medullary Po2 on the O2− generation rate remain to be fully understood. Chen et al. (11) observed that NADPH-dependent O2− production in kidney homogenates was reduced by 60–90% as Po2 was decreased from 76 to 2 mmHg. The Po2 value at which NADPH-dependent O2− production was halved in normotensive rats was estimated as 15.4 mmHg. On the other hand, Li et al. (34) found that exposure of cortical thick ascending limbs to low Po2 (5–10 mmHg) significantly raised O2− production, by 35 and 65%, respectively (relative to well-oxygenated conditions), in the absence and presence of NADH. Whereas NAD(P)H oxidase is the major source of O2− under physiological conditions, other O2− synthesis pathways include xanthine oxidase, mitochondrial respiratory chain enzymes, and NOS. Hypoxia-induced stimulation of O2− production has been reported in other tissues. In the left ventricular myocardium, intermittent hypoxia was found to increase NADPH-dependent O2− production (38), while hypoxia increased xanthine oxidase activity in pulmonary artery endothelial cells (26, 46). Thus different sources of O2− may contribute to the increase in GO2− under low-Po2 conditions in certain cell types. Given these conflicting findings and the absence of cell-specific data in the renal medulla, we consider three different scenarios.
Case A.
Under low-Po2 conditions, the rate of O2− synthesis (denoted in the endothelium or epithelium of vessel or tubule i) is assumed to be rate limited by oxygen availability. The O2 dependence of the O2− generation rate is modeled using a Michaelis-Menten relationship (1)
| (25a) |
where KO2O2− is taken as 15.4 mmHg, based upon the data of Chen et al. (11).
Case B.
We assume that the rate of O2− synthesis remains independent of Po2
| (25b) |
Case C.
O2− production under low-Po2 conditions is taken to be 50% higher than under well-oxygenated conditions
| (25c) |
That is, under physiological (i.e., hypoxic) conditions in the medulla, the volumetric rate of O2− production is taken as 1.05, 0.159, 0.092, and 0.762 μM/s in vasa recta, mTALs, OMCDs, and thin limbs, respectively.
O2− Consumption Rates
The O2− consumption reactions considered here are the scavenging reactions with NO (rate v2) and with superoxide dismutase, or SOD (rate v5). Both occur in every compartment, and the volumetric rate of the latter reaction is calculated as
| (26) |
Thus the net production rate of O2− in compartment i is given by
| (27) |
ONOO Generation and Consumption Rates
ONOO is formed by the reaction between NO and O2−. ONOO− and ONOOH (i.e., peroxynitrous acid) form an acid/base pair, and the fraction of total peroxynitrite that is present in ionic form can be calculated as (3)
| (28) |
The pK for ONOO ionization is taken as 6.8 (1, 3). As reviewed by Ferrer-Sueta and Radi (18), under physiological conditions the most rapid scavengers of ONOO− and ONOOH are CO2, peroxiredoxins, and heme proteins. In the current model, we account for the reaction of peroxynitrite with CO2 (rate v6), with HbO2 in RBCs (rate v7), with peroxiredoxin 2 (Prx2) in RBCs (rate v8), as well as the spontaneous decay of peroxynitrous acid to nitrate (rate v9). Those reaction rates are calculated as
| (29) |
| (30) |
| (31) |
| (32) |
where CONOO denotes the total concentration of peroxynitrite (ONOO− and ONOOH). The net production rate of peroxynitrite in compartment i is calculated as
| (33) |
Additional Model Inputs
Water fluxes and the concentrations of the solutes that react with the model species NO, O2−, and ONOO (i.e., O2, CO2, Hb, HbO2, Prx2, SOD) are assumed known a priori. Values for Po2, Hb, and HbO2 concentrations, as well as transmural water fluxes (Jv, Eqs. 8–11) and interstitial flows (QSDV, QAVR, R, and QR, R′ in Eq. 5) at a given medullary depth are taken from our recent model of O2 transport in the rat OM (4). The Po2, Hb, and HbO2 concentrations in the capillary RBC cytosol compartment associated with a given region are taken to be the averages of the corresponding concentrations in the capillary RBC fluid of that region. Concentration values are obtained for the mid-OS and for the mid-IS. At the mid-OS, the flow of water into AVR (i.e., the parameter QAVR, R in Eq. 5) is calculated as 4.5 × 10−7 cm2·s−1·bundle−1 in R1, 2.8 × 10−7 in R2, 3.4 × 10−5 in R3, and 3.0 × 10−5 in R4. The interregion flow of water (i.e., the parameter QR, R′ in Eq. 5) is calculated as 2.4 × 10−8 cm2·s−1·bundle−1 (R1 to R2), 5.4 × 10−6 (R2 to R3), and 8.4 × 10−6 (R3 to R4). At the mid-IS, QAVR, R is determined as 1.1 × 10−6 cm2·s−1·bundle−1 in R1, 1.5 × 10−6 in R2, 2.3 × 10−5 in R3, and 6.5 × 10−6 in R4, whereas QR, R′ is determined as 5.6 × 10−8 cm2·s−1·bundle−1 (R1 to R2), 2.9 × 10−5 (R2 to R3), and 5.7 × 10−6 (R3 to R4).
The total concentration of heme species (Hb + HbO2) also comes from our recent O2 model (4); at the mid-OS and mid-IS, it ranges between 20 and 27 mM , depending on the vessel, except in the short AVR at the mid-IS, where it is ∼34 mM. The concentration of HbNO is taken as 1 μM, an estimate in the midrange of reported values (24, 31); results were found to be insensitive to that parameter (not shown). The structural organization of the medulla is thought to result in radial pH and CO2 concentration gradients (32). The pH is taken as 7.4 in R1 and R2, and as 7.2 in R3 and R4; the Pco2 is taken as 40 mmHg (i.e., 1.2 mM) in R1 and R2 and 50 mmHg (i.e., 1.5 mM) in R3 and R4.
To compute solute fluxes across capillaries, the circumference of the capillary compartments is needed. The circumference of the capillary RBC cytosol compartment for a given region is computed as the product of the circumference of the capillary RBC tube (predicted by the model in Ref. 4) and the capillary path length within that region, then multiplied by the rate at which the short DVR turn at the appropriate medullary level (mid-OS or mid-IS). To compute net generation rates, the surface area of the capillary compartments is needed. The surface area of the capillary RBC cytosol compartment is given by the product of the capillary RBC tube cross-sectional surface area and the capillary path length within that region, then multiplied by the rate at which the short DVR turn at that medullary level (mid-OS or mid-IS). The thickness of the capillary endothelium is taken to be equal to that of the vasa recta endothelium (1 μm).
Parameters related to the physical properties and dimensions of vessels, tubules, and interstitial regions are derived from the region-based model of Layton and Layton (33) and are given in Tables 1 (vessels and tubules) and 2 (interstitial regions and capillaries). Reaction and diffusion rates are summarized in Table 3, volumetric generation rates and cross-sectional areas are given in Table 4, and permeabilities are shown in Table 5.
Table 1.
Vessel and tubule dimensions and number
| Vessel or Tubule | *Inner Diameter, μm | Endothelial/Epithelial Layer Thickness, μm | No./Vascular Bundle | *Permeability to Water, μm/s |
|---|---|---|---|---|
| Long descending vasa recta | 11.0 | 1.0 | 12 | 1,257 |
| Short descending vasa recta | 11.0 | 1.0 | Mid-OS: 43.4 | 1,257 |
| Mid-IS: 21.4 | ||||
| Long ascending vasa recta | 27.0/15.3 | 1.0 | 50 (17 in R1, 33 in R2) | † |
| Short ascending vasa recta | 27.0/15.3 | 1.0 | Mid-OS: 288 (216 in R3, 72 in R4) | † |
| Mid-IS:142 (106.5 in R3, 35.5 in R4) | ||||
| Long descending limbs | 80.0/8.6 | 1.1 | 23.7 | 3,570/2,295 |
| Short descending limbs | 20.0/18.3 | 1.1 | 47.3 | 3,570/3,257 |
| Long ascending limbs | 20.0 | 8.0 | 23.7 | 0 |
| Short ascending limbs | 20.4/13.2 | 8.0 | 47.3 | 0 |
| Collecting ducts | 30.5/24.7 | 9.0 | 11.5 | 463 |
Diameters, numbers, and permeabilities are taken from Ref. 33, and thicknesses from Ref. 5. The large diameter of the long descending limbs in the outer stripe (OS) represents the tortuosity of the proximal straight tubules.
When 2 values are given, the first one corresponds to the mid-OS, the second to the mid-inner stripe (mid-IS). Otherwise, diameters are taken to remain constant along the corticomedullary axis
Ascending vasa recta (AVR) water permeability is not given because AVR water fluxes are computed based on fluid accumulation into a region (R1–R4).
Table 2.
Region parameters
| R1 | R2 | R3 | R4 | |
|---|---|---|---|---|
| Radii, μm | 38.0/42.4 | 202/121 | 313/191 | 352/226 |
| Interstitial areas, ×10−6 cm2 | 2.38/2.26 | 71.9/16.2 | 128.4/137 | 61.7/91.6 |
| Fractional area available for diffusion, AF, R, R+1 | 0.0524/0.0398 | 0.0702/0.120 | 0.0878/0.199 | |
| Perimeter of capillary RBC cytosol compartment, μm | 0.073/1.10 | 32.2/191 | 32.4/253 | 3.78/42.1 |
| Area of capillary RBC cytosol compartment, ×10−6 cm2 | 0.0054/0.0794 | 2.38/12.9 | 2.40/17.0 | 0.279/2.83 |
| Perimeter of capillary endothelial compartment, μm | 0.078/1.17 | 34.4/206 | 34.6/272 | 4.04/45.3 |
| Area of capillary endothelial compartment, ×10−6 cm2 | 0.0008/0.0114 | 0.333/1.98 | 0.335/2.62 | 0.0390/0.437 |
The first value corresponds to the mid-OS, and the second to the mid-IS.
Table 3.
Reaction and diffusion parameters
| Parameter Definition | Parameter Value |
|---|---|
| NO-O2 reaction rate constant, kO2, M−2•s−1 | 6.3 × 106 |
| NO-O2− reaction rate constant, kNO-Sup, M−1•s−1 | 6.7 × 109 |
| NO-HbO2 reaction rate constant, koxy, M−1•s−1 | 2.5 × 107 |
| NO-Hb reaction rate constants, kdeoxy, M−1•s−1 and krev, s−1 | 2.5 × 107 and 10−4 |
| O2−-SOD reaction rate constant, kSOD, M−1•s−1 | 1.6 × 109 |
| ONOO-CO2 reaction rate constant, kCO2, M−1•s−1 | 5.9 × 104 |
| ONOO-HbO2 reaction rate constant, kheme, M−1•s−1 | 2.0 × 104 |
| ONOO-Prx2 reaction rate constant, kPrx2, M−1•s−1 | 1.7 × 107 |
| ONOO decay rate constant, kdecay, s−1 | 4.5 |
| Nitrite-mediated NO release constant, knitrite, M−1•s−1 | 4.4 |
| SNOHb-mediated NO release constant, kSNOHb, s−1 | 2.9 × 10−3 |
| SOD concentration, μM | 1 |
| RBC concentration of Prx2, CPrx2RBC, μM | 240 |
| RBC concentration of nitrite, CnitriteRBC, μM | 0.288 |
| RBC concentration of SNOHb, CSNOHbRBC, μM | 1.33 |
| NO diffusivity in dilute solution, DNO, μm2•s−1 | 3,300 |
| O2− diffusivity in dilute solution, DO2−, μm2•s−1 | 2,800 |
| ONOO diffusivity in dilute solution, DONOO, μm2•s−1 | 2,600 |
NO, nitric oxide; HbO2, oxyhemoglobin; O2−, superoxide; ONOO, peroxynitrite; Prx2, peroxiredoxin 2.
Table 4.
Endothelial and epithelial solute generation rates
| Descending Vasa Recta | Ascending Vasa Recta | Descending Limbs | Ascending Limbs | Collecting Ducts | |
|---|---|---|---|---|---|
| Maximal NO generation rate, GNO, max, μM•s−1 | 76.6 | 76.6 | 12.3 | 0.985 | 0.415 |
| O2− generation rate at high Po2, GO2−highPO2, μM•s−1 | 0.700 | 0.700 | 0.508 | 0.106 | 0.061 |
| *Area of vascular endothelium/tubular epithelium, ×10−6 cm2/vessel or tubule | All DVR: 0.377 | All AVR: 0.881/0.513 | LDL: 2.80/0.681SDL: 0.729/0.671 | LAL: 7.04SAL: 7.14/5.34 | CD: 11.17/9.52 |
| *Area of plasma/tubular lumen, ×10−6 cm2/vessel or tubule | LDV: 0.513/0.523SDV: 0.513/0.551 | LAVa: 4.34/1.42LAVb: 4.22/1.44 | LDL: 50.27/2.72 | LAL: 3.14 | CD: 7.32/4.78 |
| SDL: 3.14/2.64 | SAL: 3.27/1.38 | ||||
| SAVa: 4.13/1.46 | |||||
| SAVb: 2.30/0.945 | |||||
| Area of RBC compartment, ×10−6 cm2/vessel | LDV: 0.437/0.428 | LAVa: 1.41/0.424 | N.A. | N.A. | N.A. |
| SDV: 0.437/0.399 | LAVb: 1.52/0.406 | ||||
| SAVa: 1.61/0.387 | |||||
| SAVb: 3.45/0.848 |
DVR, descending vasa recta; LDV and SDV, long and short descending vasa recta, respectively; LAVa and LAVb and SAVa and SAVb, two populations of LAV and SAV, respectively; LDL and SDL, long and short descending limb of Henle's loop, respectively; LAL and SAL, long and short ascending limb of Henle's loop, respectively; CD, collecting ducts; N.A. not applicable.
When 2 values are given, the first corresponds to the mid-OS, the second to the mid-IS.
Table 5.
Vessel and Tubule Permeability to NO, O2−, and ONOO
| Vessel or Tubule | *NO Permeability, cm/s | *O2− Permeability, cm/s | *ONOO Permeability, cm/s |
|---|---|---|---|
| Long descending vasa recta | 1.00 | 5.60 × 10−2 | 5.20 × 10−2 |
| Short descending vasa recta | 1.00 | 5.60 × 10−2 | 5.20 × 10−2 |
| Long ascending vasa recta | 2.44 × 10−2 | 5.60 × 10−2 | 5.20 × 10−2 |
| Short ascending vasa recta | 2.44 × 10−2 | 5.60 × 10−2 | 5.20 × 10−2 |
| Long descending limbs | 2.77/1.79† | 5.09 × 10−2 | 4.72 × 10−2 |
| Short descending limbs | 2.77/2.53† | 5.09 × 10−2 | 4.72 × 10−2 |
| Long ascending limbs | 2.44 × 10−2 | 7.00 × 10−3 | 6.50 × 10−3 |
| Short ascending limbs | 2.44 × 10−2 | 7.00 × 10−3 | 6.50 × 10−3 |
| Collecting ducts | 2.44 × 10−2 | 6.22 × 10−3 | 5.78 × 10−3 |
Permeabilities are given for the cell-interstitial and lumen-cell interfaces, which are taken to be equal.
The permeability of descending limbs varies between the mid-OS (first value) and the mid-IS (second value) because aquaporin-1 (AQP1) expression also varies.
Numerical Method
The present model yields NO, O2−, and ONOO fluxes and concentrations in each of the 40 compartments considered herein. These fluxes and concentrations are determined by simultaneously solving conservation equations in each compartment. The model equations are solved by means of Newton's method. Calculations are performed using a Fortran program which is executed in double precision on a computer equipped with an Intel Core2 Duo 2.4-GHz processor with 2-GB of RAM.
RESULTS
Using the model configuration and parameter set, the model equations were solved to obtain NO, O2−, and ONOO concentrations in each compartment, as well as the solute fluxes between adjacent compartments (note that transmembrane fluxes can be related to, or inferred from, the difference in concentrations between two adjacent compartments). Simulations were performed for the mid-OS and mid-IS, and trends were generally found to be the same at these two axial positions. Hence, when mid-OS and mid-IS results do not differ substantially, only the latter are described. To assess the effect of low Po2 on the distribution of NO, O2−, and ONOO, we first simulated a case in which the OM is assumed to be well oxygenated. Those results were then compared with the base case which incorporates the effects of low Po2 in the regions away from the vascular bundles, a result of the radial organization of tubules and vessels in the OM.
Concentration Profiles Under Well-Oxygenated Conditions
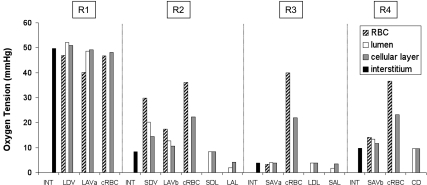
The synthesis of both NO and O2− is O2 dependent. Given that Po2 is low in the OM, the production of NO is likely to be severely limited by the availability of oxygen. As described in our previous study (5), the segregation of O2-rich long DVR within the core of the vascular bundle limits O2 reabsorption from these vessels, preserves O2 delivery to the inner medulla, and creates large radial Po2 gradients between regions. Region R1, which represents the bundle core, is well oxygenated, but in the surrounding regions, interstitial Po2 is predicted to be much lower, as illustrated in Fig. 2. At the mid-OS, interstitial Po2 is calculated as 56.3, 17.5, 9.7, and 9.0 mmHg, respectively, in R1, R2, R3, and R4; at the mid-IS, it is calculated as 49.7, 8.4, 3.9, and 9.7 mmHg, respectively. (At the mid-IS, interstitial Po2 is lowest in R3, in part because of its largest population of mTAL, whose metabolic needs are high due to active NaCl reabsorption; see Fig. 1.)
Fig. 2.
Oxygen tension (Po2) profiles at the mid-IS in the interstitium, vasa recta, capillaries, and tubules in each region. Each tubule or vas rectum is assigned to the region with which it is in contact for 50% or more in the IS. In vasa recta, Po2 values in red blood cells (RBCs), plasma, and endothelium are displayed separately. In capillaries (denoted “cRBC”), Po2 values in the RBC cytosol and surrounding endothelium are also distinguished. Similarly, in tubules, Po2 values in lumen and epithelium are shown separately. The term “cellular layer” denotes the endothelium in vasa recta and capillaries, and the epithelium in tubules. Data are taken from Ref. 4.
To understand how low medullary Po2 affects NO, O2−, and ONOO concentration profiles, in the first set of simulations we assumed that the generation rate of NO and O2− is independent of Po2. This would be the case if Po2 were very high and not rate limiting. In other words, the value of KO2NO in the NO generation rate was set to zero (Eq. 16), and the O2− generation rate was fixed at .
NO.
In the OM, NO is generated within vascular endothelia and tubular epithelia. A fraction of that NO then diffuses from those cell layers toward the interstitium, and another fraction diffuses toward the vascular or tubular lumen. As water is reabsorbed from descending vessels and limbs into the interstitium and subsequently removed by AVR, a negligible portion of NO in the interstitium is also driven by convection into AVR. In every compartment, a small amount of NO reacts with O2− and O2. Within RBCs, a much larger amount reacts with Hb; the rate of NO consumption by Hb (v3, v4) is ∼103 times faster than that by O2− (v2), and ∼108 times faster than that by O2 (v1).
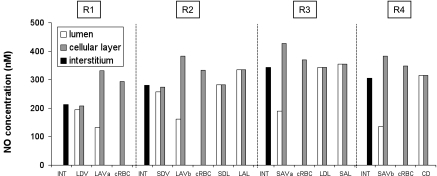
As displayed in Fig. 3, predicted CNO values at the mid-IS are relatively homogeneous within each region, with the exception of AVR and capillaries. As shown in Eq. 1, the net amount of NO generated within the vascular endothelium or the tubular epithelium is equal to the volumetric rate of net NO production times the cross-sectional area of the cellular layer; the latter is proportional to the lumen diameter, assuming that the cell layer thickness is fixed. The volumetric rate of NO production is the highest in vasa recta (Table 4); in addition, the diameter of AVR is 50–150% larger than that of DVR (Table 1). Given this and the fact that the NO permeability of AVR, which do not express AQP1, is significantly smaller than that of DVR (Table 5), the model predicts that CNO are maximal in AVR endothelia.
Fig. 3.
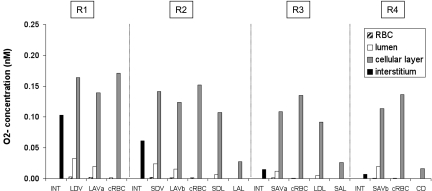
Nitric oxide (NO) concentrations (CNO) at the mid-IS in the interstitium, vasa recta, capillaries, and tubules in each region under well-oxygenated conditions. RBC CNO is <1 nM and is not shown.
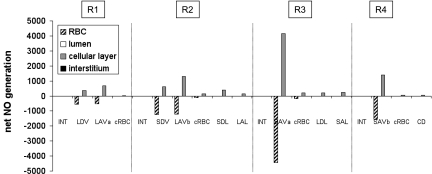
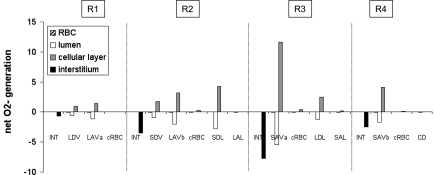
Interstitial CNO is predicted to increase by ∼20% (mid-OS) and 45% (mid-IS) from the core of the vascular region, which contains mostly long vasa recta, toward the outermost regions, where tubules are concentrated. The R1-to-R4 CNO gradient arises because the RBCs within vasa recta form a sink that depletes a large fraction of the endothelium-generated NO; thus the net amount of NO produced within vasa recta (i.e., in RBC + plasma + endothelium) is significantly lower than that within adjoining tubules, even though the volumetric NO production rate is significantly higher in vascular endothelia than in tubular epithelia (Fig. 4).
Fig. 4.
Net generation (production minus consumption) rate of NO (×10−3 nmol·cm−1·s−1) at the mid-IS in the interstitium, vasa recta, capillaries, and tubules under well-oxygenated conditions. The rates for a given type of tubule or vessel take into account the number of such tubules or vessels.
The scavenging of NO by Hb is so rapid that CNO are two to three orders of magnitude lower in RBCs than in other compartments, and CNO are lower in plasma relative to endothelium (Fig. 3). In contrast, the lumen-to-epithelial CNO gradient is negligible in tubules. This is because NO scavenging by O2− in the tubular lumen is much slower compared with the scavenging of NO by Hb in vessels. Hence, endothelium-to-plasma and plasma-to-RBC NO fluxes (∼10−2 nmol·cm−1·s−1) are several orders of magnitude higher than epithelium-to-lumen NO fluxes (∼10−6 nmol·cm−1·s−1).
Our previous model of NO transport (53) did not incorporate the effects of Po2 on NO generation and implicitly assumed that KO2NO equals zero. Thus its results can be compared with those of the present model for the well-oxygenated case. However, it should be noted that the NO generation rate of vasa recta was taken as 22.1 μM/s in the ZE model, whereas it was increased to 76.6 μM/s in the current model so as to yield base-case interstitial CNO values on the order of 100 nM. The ZE model focused on the CNO difference between long DVR, which are destined to the inner medulla, and the short DVR, which perfuse the interbundle region of the OM; that difference is expected to modulate blood flow distribution in the medulla, as described below. The ZE model predicted that at the mid-IS the average CNO is ∼10% higher in short DVR than in long DVR under well-oxygenated conditions; in the present model, CNO is ∼30% higher in short-DVR endothelia (∼270 mM) than in long-DVR endothelia (∼210 nM) under these conditions. The discrepancy likely stems from the fact that the NO generation rate of descending limbs (which are closer to short DVR) relative to that of vasa recta is taken to be higher in the present model, because we assumed different descending limb dimensions than in the ZE modeling study.
O2−.
O2− is also generated within vascular endothelia and tubular epithelia in the OM. Since the rate of O2− synthesis in vasa recta is taken to be 100-fold slower than that of NO synthesis, O2− concentrations (CO2−) are predicted to be in the 1–200 pM range, about three orders of magnitude lower than CNO (Fig. 5). O2− reacts with SOD and NO in all compartments, and the former reaction is significantly faster than the latter (v5 is 1–2 orders of magnitude greater than v2).
Fig. 5.
Superoxide (O2−) concentrations (CO2−) at the mid-IS in the interstitium, vasa recta, capillaries, and tubules in each region under well-oxygenated conditions.
In contrast with CNO, CO2− do not increase from the vascular bundle core outward. This is because the RBCs do not constitute a sink for O2−: the dominant O2− scavenger is SOD, which is taken to be present in the same concentration everywhere (i.e., in all cells, plasma, and tubular fluid). Thus, contrary to NO, the net generation rate of O2− (i.e., production minus consumption) is positive in all vessels and tubules, as shown in Fig. 6. Given that the volumetric generation rate of O2− is highest in vasa recta and descending limbs (Table 4), CO2− varies in proportion with the fractional area occupied by vasa recta and descending limbs within each region. At the mid-OS, this fractional area is 43.0% in R1, 6.4% in R2, 13.4% in R3, and 9.9% in R4; interstitial CO2− decreases and increases accordingly (results not shown). At the mid-IS, the relative area occupied by vasa recta and descending limbs is 23.4% in R1, 14.1% in R2, 10.3% in R3, and 4.0% in R4; thus interstitial CO2− decreases monotonically from R1 to R4 (Fig. 5).
Fig. 6.
Net generation (production minus consumption) rate of O2− (×10−3 nmol·cm−1·s−1) at the mid-IS in the interstitium, vasa recta, capillaries, and tubules under well-oxygenated conditions.
Even though the O2− volumetric generation rate is significantly larger in endothelia than in epithelia (Table 4), more O2− is generated in a given ascending limb than in an ascending vas rectum (34); note that the former is much wider than the latter (Table 1). This difference in surface area also means, however, that more O2− is consumed (mainly by SOD) in ascending limbs than in AVR. Hence, both the net generation rate and the concentration of O2− are lower in ascending limbs than in AVR (Figs. 5–6). The effect of surface area is such that, more generally, CO2− values are the highest in the endothelia of vasa recta and capillaries in each region. Within vessels, O2− concentration decreases from endothelium to the RBC, because O2− generated in the endothelium must first diffuse into the plasma and then into the RBCs. At the mid-IS, CO2− decreases by a factor of 5–10 from endothelium to plasma, and by a factor of 10–20 from plasma to RBC. The decrease in CO2− is sharper in AVR at the mid-OS, because these vessels are much wider at that level (27.0 μm in diameter) than at the mid-IS (13.5 μm in diameter). It is noteworthy that a larger endothelium or epithelium gives rise to a higher O2− generation rate as well as a larger area for diffusion out of the cellular layer. Our simulation results suggest that in general, these two competing factors result in higher O2− concentration in larger endothelium or epithelium. In the tubules, which are generally wider than the vasa recta, the epithelium-to-lumen CO2− ratio is higher, ranging from 15 to 200. Luminal CO2− is lowest in CDs, which have a large diameter (30.5 μm at the mid-OS, 24.7 μm at the mid-IS) and produce little O2−. Long descending limbs are larger (their diameter is taken to vary from 80.0 to 18.6 μm), but they produce significantly more O2− (Table 4).
ONOO.
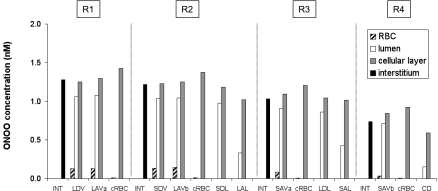
ONOO is formed by the reaction between NO and O2−. As shown in Fig. 7, ONOO concentrations (CONOO) are predicted to be in the 0.01–2 nM range. Within each region, they are highest in vascular endothelia and tubular epithelia, that is, the compartments where NO and O2− are produced and where these species are the most abundant. The most potent ONOO scavengers, Prx2 and HbO2, are in the RBCs. Thus ONOO concentrations decrease significantly more from plasma to RBC than from endothelium to plasma. Prx2 and HbO2 are absent from tubules; the ONOO concentration gradient from epithelium to tubular lumen is therefore comparable to that from endothelium to plasma, albeit larger, because most tubules are wider than vessels.
Fig. 7.
Peroxynitrite (ONOO) concentrations (CONOO) at the mid-IS in the interstitium, vasa recta, capillaries, and tubules in each region under well-oxygenated conditions.
As described above, CNO increases from the vascular bundle core toward the outer regions, at both the mid-OS and the mid-IS. In contrast, at the mid-OS, interstitial CO2− drops sharply between R1 and R2 and then varies little between R2, R3, and R4. At that level, the product of CNO and CO2− is the lowest in R2, and therefore so is CONOO (results not shown). At the mid-IS, the product of CNO and CO2− decreases monotonically from R1 to R4, and therefore so does CONOO (Fig. 7).
Base-Case Concentration Profiles
To study the effects of low Po2 on the distribution of NO, O2−, and ONOO in the OM, we accounted for the effects of medullary hypoxia on the NO and O2− generation rates. In these simulations, the Po2 value at which NO synthesis is reduced two-fold (KO2NO, see Eq. 16) was taken as 38 mmHg (50), i.e., a midrange value. Given the conflicting findings regarding the effects of hypoxia on O2− synthesis, as described in detail above in model description, we examined several scenarios: the O2− generation rate was taken to either decrease with decreasing Po2 (case A), to remain independent of Po2 (case B), or to increase with decreasing Po2 (case C).
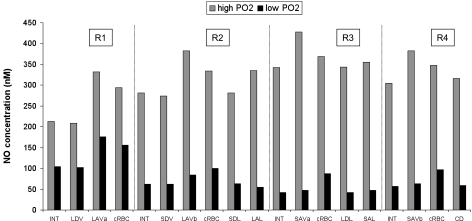
NO concentrations.
As described in the companion study (15), under physiological conditions O2− has a small impact on NO bioavailability. Hence, predicted NO concentrations differ by <2% in cases A, B, and C, and results are shown for case B.
In the core of the vascular bundle, Po2 hovers around 50 mmHg (Fig. 2), but at the bundle periphery, interstitial Po2 is predicted to be lower than 18 mmHg at the mid-OS, and 10 mmHg at the mid-IS. Thus the extent to which the generation rate of NO is reduced by limited O2 availability is much greater in the outer regions (R2–R4) than in R1. As a consequence, base-case NO concentrations are predicted to be maximal in R1, in contrast to the trends obtained under well-oxygenated conditions. At the mid-IS, CNO is reduced by a factor of ∼2 in R1, and 5–8 to in R3-R4, relative to the well-oxygenated case (Fig. 8). Interstitial CNO range from 104 nM in R1 (vs. 213 with KO2NO) to 42 nM in R3 (vs. 343 with KO2NO). The highest NO concentrations (∼180 nM) are still found in the endothelium of the widest, and least-permeable, vessels in the vascular bundle, that is, the long ascending vasa recta in R1 (Fig. 8). NO fluxes are largest at the endothelium-plasma and plasma-RBC interfaces of DVR and AVR in R1.
Fig. 8.
Effect of low medullary Po2 on CNO at the mid-IS in interstitium, vasa recta, capillaries, and tubules. In this figure and Figs. 9 and 10, concentrations in vessels and tubules are those of the endothelium/epithelium. In addition, the “high Po2” case corresponds to well-oxygenated conditions (KO2NO = 0), whereas “low Po2” refers to the base case (KO2NO = 38 mmHg). Results for cases A, B, and C cannot be distinguished.
O2− concentrations.
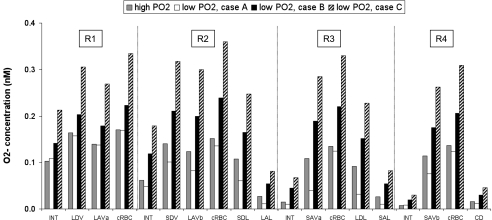
Hypoxia reduces the rate of O2− consumption by decreasing the generation rate (and thus the concentration) of one of its scavengers, NO. If we assume that low medullary Po2 also reduces the rate of O2− synthesis (case A), then which of these competing effects prevails depends on the region. In the vascular bundle core they almost balance each other, so that in R1, basal CO2− are close to the values predicted for the well-oxygenated case (Fig. 9). In R2 and R3, where O2 is the scarcest, the reduction in O2− synthesis predominates, and basal CO2− are significantly lower than in the well-oxygenated case. For instance, at the mid-IS, interstitial CO2− is 26 and 46% lower in R2 and R3, respectively (relative to the well-oxygenated case). In R4, where Po2 is slightly higher than in R2 and R3 at the mid-IS, the reduction in vascular and tubular O2− synthesis is not as significant as in the latter regions, but CO2− is generally lower than in the well-oxygenated case.
Fig. 9.
Effect of low medullary Po2 on O2− concentration (CO2−) at the mid-IS in interstitium, vasa recta, capillaries, and tubules. Medullary hypoxia is assumed to either reduce (case A), have no impact on (case B), or enhance (case C) O2− synthesis.
Assuming that O2− synthesis is independent of O2 levels (case B), low medullary Po2 only affects the consumption of O2− by NO and leads to a CO2− increase throughout the medulla, as shown in Fig. 9. This increase is even greater in case C, which assumes that hypoxia stimulates O2− synthesis. Under these conditions, low medullary Po2 raises O2− levels under the combined effect of higher production and lower consumption. At the mid-IS, O2− concentrations are two- to fivefold greater than under well-oxygenated conditions. The increase is more pronounced in the peripheral regions (R2–R4) where the Po2-induced inhibition of NO synthesis is more significant, and where O2− scavenging by NO therefore decreases more (Fig. 9). As in the well-oxygenated case, interstitial CO2− is the highest in R1, where the fractional area occupied by vasa recta is the highest.
Predicted O2− concentrations range from 0.1 to 170 pM in case A, from 0.3 to 240 pM in case B, and from 0.5 to 360 pM in case C. In all cases, O2− fluxes are largest across AVR endothelia.
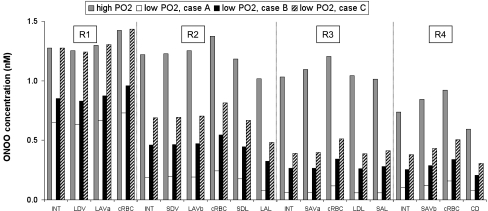
ONOO concentrations.
The rate of ONOO synthesis is proportional to the NO and O2− concentration product (Eq. 21) and therefore varies accordingly. For instance, at the mid-IS, the product of CNO and CO2− in the endothelium of the long DVR located in R1 is 34.2 in the well-oxygenated case, and 16.2 in case A (that is, 2.1 times lower). The DVR endothelial concentration of ONOO in those vessels follows the same trend: it is 1.25 nM in the well-oxygenated case, and 0.63 nM in case A (that is, 2.0 times lower).
ONOO concentrations are the lowest in case A because the latter assumes that generation rates of both NO and O2− are reduced by hypoxia. In case A, CONOO is about 2-fold lower in R1 and 7- to 20-fold lower in R2–R4, relative to the well-oxygenated case (Fig. 10). Predicted ONOO concentrations then range from 1 to 730 pM. In case B, CO2− and therefore CONOO are higher than in case A; the latter varies between 2 and 960 pM.
Fig. 10.
Effect of low medullary Po2 on ONOO concentrations at the mid-IS in interstitium, vasa recta, capillaries, and tubules. Medullary hypoxia is assumed to either reduce (case A), have no impact on (case B), or enhance (case C) O2− synthesis.
In case C, as described above, medullary hypoxia reduces CNO and increases CO2− by a factor of ∼2 in the vascular bundle core. Thus ONOO concentrations in R1 are not much different than in the well-oxygenated case. In the peripheral regions, however, CONOO remains significantly lower than in the well-oxygenated case, since the hypoxia-induced decrease in CNO is much greater than the hypoxia-induced increase in CO2− in those regions. Hence, CONOO is about twofold lower in R2–R4, relative to the well-oxygenated case (Fig. 10). Predicted ONOO concentrations then range from 3 pM to 1.4 nM. In all cases, ONOO fluxes are largest at the endothelium-to-plasma interface in long ascending vasa recta in R1.
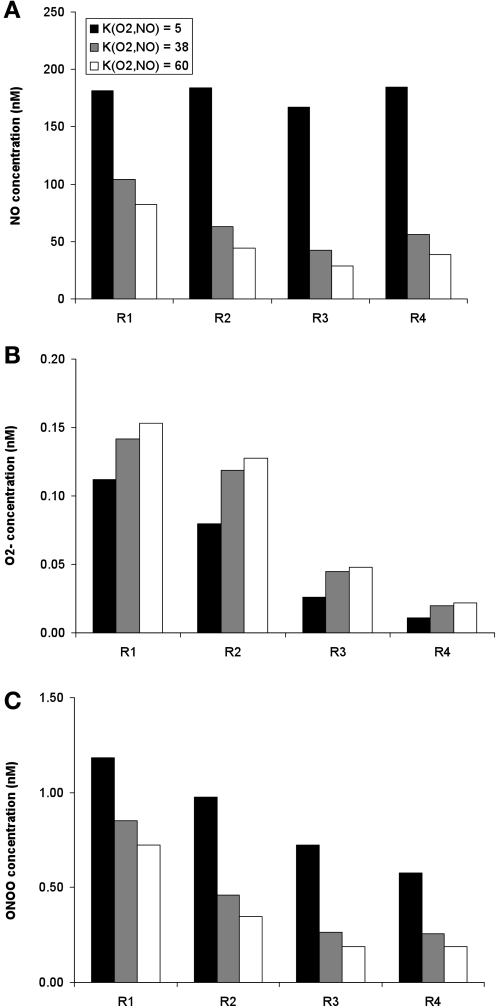
Effects of KO2NO Variations
Given that the range of reported KO2NO values is wide (see above), we then examined the effect of varying the latter parameter in a set of parameter studies. To facilitate result interpretation, the O2− generation rate was kept constant in those studies; i.e., it was fixed as in case B.
Assuming a lower bound value of 5 mmHg for KO2NO, the rate-limiting effects of O2 on the NO generation rate are less considerable than in the base case, but they are significant nonetheless, as illustrated in Fig. 11A. Since the O2-mediated decrease in GNO is smaller when KO2NO is taken as 5 mmHg than in the base case, NO concentrations are conversely higher. Relative to the base case, the predicted CNO is about twofold higher in R1, and three- to fourfold higher in R2–R4. At the mid-IS, interstitial, endothelial, and epithelial CNO are remarkably homogeneous across all regions, ranging from 167 to 184 nM (Fig. 11A).
Fig. 11.
Effect of variations in the Po2 value at which maximal NO synthesis is half inhibited (denoted KO2NO) on interstitial CNO (A), CO2− (B), and CONOO (C) at the mid-IS. Results are shown for 3 values of KO2NO: 5, 38 (base case), and 60 mmHg. The rate of O2− synthesis is kept fixed as in case B.
Conversely, if KO2NO is taken as 60 mmHg, i.e., an upper range value (2), GNO drops even further than in the base case and CNO are significantly reduced. In every compartment except for AVR and capillary endothelium, they are predicted to remain below 90 nM at the mid-OS, and 82 nM at the mid-IS. In the interstitium, CNO ranges from 29 to 82 nM at the mid-IS (Fig. 11A).
Since KO2NO has a large impact on medullary CNO, it also has a significant effect on O2− consumption, and therefore on CO2−. If KO2NO is lowered to 5 mmHg, CNO rises relative to the base case (where KO2NO = 38 mmHg), thereby increasing O2− scavenging by NO, and reducing CO2−. Given that Po2 is less rate limiting in the vascular bundle, concentration variations are also smaller in that region. Relative to the base case, CO2− is ∼20–30% lower in R1, and 30–50% lower in R2–R4. Conversely, if KO2NO is taken as 60 mmHg, CO2− increases by ∼10% relative to the base case (Fig. 11B).
The lower KO2NO, the higher CNO, and the higher the rate of ONOO formation. Thus CONOO increases significantly as KO2NO is decreased. If KO2NO is taken as 5 mmHg, CONOO is 40% higher in R1, and 110–180% higher in R2–R4, relative to the base. The peak interstitial CONOO is then 1.18 nM, vs. 0.85 nM in the base case. If KO2NO is increased to 60 mmHg instead, CONOO is reduced by ∼15% in R1, and ∼30% in R2–R4, relative to the base case. The peak interstitial CONOO is then 0.72 nM (Fig. 11C).
DISCUSSION
We have developed a mathematical model of a cross section of the rat OM to simulate the interactions between NO and O2−. The model accounts for the relative positions of the tubules and vessels in the OM by representing four concentric regions, centered on a vascular bundle (Fig. 1). The model also takes into account medullary O2 distribution and radial convection by incorporating Po2 and volume flux data from a three-dimensional model of oxygen transport in the rat OM that we developed previously (4, 5).
In the current study, we examined the impact of the three-dimensional architecture of the rat OM on the distribution of NO, O2−, and ONOO. The companion study (15) focuses on the importance of tubulovascular cross talk and the interactions between NO and O2−. The radial organization of the rat OM around vascular bundles has two implications for NO, O2−, and ONOO. First, the sequestration of O2-rich DVR within the vascular bundles results in large radial Po2 gradients from the vascular bundle core (R1) toward the outer regions (R2–R4) (5). Those Po2 gradients, taken in isolation, mean that the generation of NO is slower away from the bundles. Second, the vascular bundles have the highest density of RBCs, which carry the most potent NO scavenger, namely Hb.
Our present results suggest that the first of these two competing effects predominates: the steep radial Po2 gradients generate similar radial NO and ONOO concentration gradients. As displayed in Fig. 8, the base-case concentration of NO is predicted to be the highest in the bundle core, where O2 is relatively plentiful, and where generation rates are therefore significantly larger than at the bundle periphery. If the synthesis of NO were not limited by O2 availability, CNO would be the lowest in R1, owing to the high density of vasa recta in that region combined with the very fast rate of NO consumption by Hb and HbO2 in RBCs (Fig. 8). In contrast, interstitial CO2− is highest in R1 under all conditions, because the volumetric rate of O2− generation is the largest in vasa recta, the density of which is maximal in R1, while there are no O2− potent scavengers in RBCs (Fig. 9). Thus ONOO would be more homogeneously distributed across the four regions in the absence of O2 rate-limiting effects (Fig. 10).
Comparison With a Previous Modeling Study
Our previous model of cross-sectional NO transport, referred to as the ZE model (53), did not include the effects of medullary hypoxia on NO generation rates. Thus it predicted that the average interstitial CNO is highest in R2, where the density of descending limbs, which represent the most significant epithelial source of NO, is the highest. However, the current study suggests that the O2 dependence of NO and O2− synthesis has a large impact on medullary concentration profiles, and that it leads to a sharp CNO decrease between the vascular bundle core (R1) and the peripheral regions (R2–R4), as described above.
In addition, the ZE model did not explicitly consider the generation, transport, and consumption of CO2− and CONOO. Instead, the concentration of CO2− was fixed at 0.25 nM in the interstitium, 0.10 nM in endothelium, and 0.05 in plasma. The basal CO2− values predicted by the current model are lower in the interstitium (ranging from 0.01 to 0.21 nM) but comparable in plasma. As such, the ZE model may have overestimated the effect of a 10-fold increase in O2− levels on NO, as discussed in the companion study (15).
Finally, the ZE model did not incorporate radial convection. We examined the impact of radial convection in the current model by setting all the transmembrane water fluxes to zero: the effect on the predicted concentration profiles is negligible (<0.1%), because Péclet numbers (i.e., the ratio of convective-to-diffusive fluxes; Eq. 10) are lower than 10−2 everywhere.
Comparison with Experimental Findings
Measurements of physiological CNO in the OM range from 100 (56) to 800 nM (44, 45). In this study, we chose the base-case NO generation rate so that theoretical NO concentrations would be comparable to the lower bound measurements, as discussed in more detail in the companion study (15). Thus, in the base case, interstitial CNO are predicted to range from 63 to 112 nM at the mid-OS, and from 42 to 104 nM at the mid-IS (Fig. 8).
To the best of our knowledge, there have been no direct measurements of O2− and ONOO concentrations in the renal medulla. Under physiological (i.e., low Po2) conditions, our model yields medullary CO2− on the order of 10–200 pM in the interstitium and ∼1–10 pM within RBCs. Buerk et al. (1) developed a model of NO and O2− transport in and around a small arteriole. They assumed a lower NO generation rate than the one used here, and their model yields lower CNO (∼20 nM in the perivascular tissue surrounding the small arteriole), and therefore slightly higher CO2− (100–250 pM in tissue), than the ones predicted in this study. Our CO2− estimates are also comparable to, if slightly higher than, the 10–50 pM range estimated by Ferrer-Sueta and Sadi (18) in their review of the chemical biology of ONOO.
Our model predicts that interstitial concentrations of total ONOO (ONOO− and ONOOH) at the mid-IS range from ∼0.05 to 1 nM under physiological conditions. Within RBCs, the predicted CONOO varies between 5 and 30 pM in the AVR located in the outermost regions, and between 20 and 130 pM in the vascular bundle vessels. These values are consistent with the range predicted by Ferrer-Sueta and Sadi (18), who suggested that CONOO should not exceed 2–3 nM under basal conditions, and could plummet to <25 pM in erythrocytes.
Effects of NO on Medullary Blood Flow Distribution
DVR are surrounded by pericytes, smooth muscle cells that impart contractile properties to these vessels. Solute concentrations in pericytes, which are not explicitly considered in this study, should be close to those in the endothelium. In the current base case, the predicted endothelial CNO is 72% higher in long DVR than in short DVR at the mid-OS (110 vs. 64 nM), and 66% higher at the mid-IS (103 vs. 62 nM). Long DVR are located at the center of the vascular bundle and are destined to the inner medulla, whereas short DVR peel off from the bundle periphery and supply the OM. Given the vasodilatory properties of NO, the long DVR-to-short DVR pericyte CNO ratio is expected to modulate the distribution of medullary blood flow between the inner medulla and OM (41). As we described previously (53), the experimental results of Zhang et al. (55) and Kakoki et al. (27) suggest that CNO variations on the order of 10 nM may affect blood flow. Our results therefore suggest that the difference in endothelial CNO between long DVR and short DVR preferentially increases blood flow to the inner medulla under basal conditions.
It should be noted that our previous modeling study had predicted higher NO concentrations in short DVR than in long DVR, but that model had assumed fixed, O2-independent NO generation rates (53). Under similar conditions (i.e., when O2 is plentiful), the current model also predicts that CNO is higher in short DVR than in long DVR (Fig. 3).
Model Limitations
The model presented here only represents a slice of the rat OM and does not describe countercurrent flows along the corticomedullary axis. It is limited to the transport of NO, O2−, and ONOO and cannot predict the effects of these radicals on NaCl reabsorption across the mTAL and OM concentrating capability, and on blood flow. The transmembrane O2− fluxes do not take into account the electrical charge of the species. In addition, because only steady-state solutions were sought, the model does not capture the effects of transient events. At each systole, vascular endothelial cells release a puff of NO (20). The impact of these puffs beyond local areas in the endothelial cell cytoplasm remains unclear. As NO diffuses from multiple cells into the interstitium, the integrated effects of many different cells will be superimposed on the rhythmic release of NO from the endothelium. The NO puffs may not generate a standing wave unless they are synchronized. In short, it is possible that medullary CNO gradients vary with the cardiac cycle, but there are not enough data as yet to investigate this issue.
Nevertheless, the model constitutes a convenient tool to examine the impact of kinetic and transport parameters on the distribution of NO, O2−, and ONOO in the OM. In addition, it explicitly accounts for the endothelial and epithelial layers, whereas three-dimensional models of water and solute transport in the medulla represent vascular and capillary walls as a single barrier. Since NO and O2− are generated within vascular endothelia and tubular epithelia, explicit consideration of these cellular layers yields more accurate results.
The current study shows how the large radial Po2 gradients in the rat OM, which arise from the specific three-dimensional architecture of the rat OM, affect the distribution of NO, O2−, and ONOO. The reciprocal effects of NO on medullary Po2 may be significant as well. As a vasodilator, NO acts to increase local blood flow and O2 supply. NO also reduces tubular O2 demand by inhibiting active NaCl reabsorption across mTALs (23). Moreover, NO inhibits mitochondrial O2 utilization by competing with O2 for binding to mitochondrial cytochrome c oxidase. Since the CNO at which tissue O2 consumption is inhibited by half (IC50) is on the order of 10–100 nM, and since perivascular NO concentrations are generally higher than IC50 values, cellular respiration is likely to be significantly inhibited under physiological conditions (7). As noted above, O2− exerts opposite effects: it enhances mTAL Na+ reabsorption and acts to reduce medullary blood flow. There is also evidence that ONOO− inhibits mTAL Na+ reabsorption (19), and it may therefore modulate O2 consumption. A full three-dimensional model of transport in the renal medulla would be necessary to investigate those issues.
In summary, our model of NO, O2−, and ONOO transport in the rat OM suggests that the large Po2 gradients from the bundle core toward the outer regions, which stem from the specific three-dimensional organization of tubules and vessels in the OM, in turn generate steep radial CNO gradients, since NO synthesis is O2 dependent. The resulting difference in endothelial CNO between long DVR and short DVR is likely to increase blood flow to the inner medulla, to the detriment of the OM, under basal conditions.
GRANTS
This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK053775 to A. Edwards.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
ACKNOWLEDGMENTS
The authors thank Dr. Jing Chen for providing water flow and Po2 data.
Footnotes
- Ai
- Cross-sectional area of compartment i
- AF, R, R′
- Fraction of the R-R′ interface available for interstitial diffusion
- AVR
- Ascending vasa recta
- CNO, CO2−, CONOO
- Concentration of NO, O2−, and ONOO
- Cki
- Concentration of solute k in compartment i
- Dk
- Diffusivity of solute k in dilute solution
- dR, R′
- Distance between the midpoints of regions R and R′
- DVR
- Descending vasa recta
- fion
- Fraction of total peroxynitrite that is present in ionic form
- GNO, GO2−
- Volumetric rate of NO and O2− generation
- GNO, max
- Maximal volumetric rate of NO generation
- IS
- Inner stripe
- Jki, j
- Flux of solute k from compartment i to compartment j
- JktotR
- Total flux of solute k into region R
- Jvi, k
- Flux of volume from compartment i to compartment j
- KO2NO
- Oxygen tension at half the maximal rate of NO generation
- OM
- Outer medulla
- OS
- Outer stripe
- Po2
- Oxygen tension
- Pki, j
- Permeability of the i-j interface to solute k
- PkR, R′
- Permeability to solute k of the boundary separating regions R and R′
- PNORBC
- Red blood cell permeability to NO
- PeNOi, j
- Péclet number associated with compartments i and j
- QAVR, R
- Fluid flow entering the AVR in region R
- QSDV, R
- Capillary flow into region R
- QR, R′
- Fluid flow from region R into region R′
- Ri ,j
- Radius at the i-j interface
- RR, R′
- Radius at the interface between regions R and R′
- RBC
- Red blood cell
- R1, R2, R3, R4
- Concentric regions 1–4
- v
- Volumetric reaction rate
- ΓNOSNOHb
- Volumetric generation rate of NO via the SNOHb pathway
- ΓNOnitrite
- Volumetric generation rate of NO via the nitrite pathway
- κcell, R
- Fraction of vascular endothelium or tubular epithelium in contact with region R
- Ω
- Diffusion resistance in interstitium
- Ψki
- Net generation rate of solute k in compartment i
- τ
- Tortuosity factor in interstitium
REFERENCES
- 1.Buerk D, Lamkin-Kennard K, Jaron D. Modeling the influence of superoxide dismutase on superoxide and nitric oxide interactions, including reversible inhibition of oxygen consumption. Free Radic Biol Med 34: 1488–1503, 2003 [DOI] [PubMed] [Google Scholar]
- 2.Buerk DG. Can we model nitric oxide biotransport? A survey of mathematical models for a simple diatomic molecule with surprisingly complex biological activities. Annu Rev Biomed Eng 3: 109–143, 2001 [DOI] [PubMed] [Google Scholar]
- 3.Chen B, Deen WM. Analysis of the effects of cell spacing and liquid depth on nitric oxide and its oxidation products in cell cultures. Chem Res Toxicol 14: 135–147, 2001 [DOI] [PubMed] [Google Scholar]
- 4.Chen J, Edwards A, Layton AT. Effects of pH and medullary blood flow on oxygen transport and sodium reabsorption in the rat outer medulla. Am J Physiol Renal Physiol, In Press [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen J, Layton AT, Edwards A. A mathematical model of oxygen transport in the rat outer medulla. I. Model formulation and baseline results. Am J Physiol Renal Physiol 297: F517–F536, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen K, Piknova B, Pittman RN, Schechter AN, Popel AS. Nitric oxide from nitrite reduction by hemoglobin in the plasma and erythrocytes. Nitric Oxide 18: 47–60, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen K, Pittman RN, Popel AS. Nitric oxide in the vasculature: where does it come from and where does it go? A quantitative perspective. Antioxid Redox Signal 10: 1185–1198, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen K, Pittman RN, Popel AS. Vascular smooth muscle NO exposure from intraerythrocytic SNOHb: a mathematical model. Antioxid Redox Signal 9: 1097–1110, 2007 [DOI] [PubMed] [Google Scholar]
- 9.Chen K, Popel AS. Theoretical analysis of biochemical pathways of nitric oxide release from vascular endothelial cells. Free Radic Biol Med 41: 668–680, 2006 [DOI] [PubMed] [Google Scholar]
- 10.Chen K, Popel AS. Vascular and perivascular nitric oxide release and transport: biochemical pathways of neuronal nitric oxide synthase (NOS1) and endothelial nitric oxide synthase (NOS3). Free Radic Biol Med 42: 811–822, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen Y, Gill PS, Welch WJ. Oxygen availability limits renal NADPH-dependent superoxide production. Am J Physiol Renal Physiol 289: F749–F753, 2005 [DOI] [PubMed] [Google Scholar]
- 12.Chin SY, Wang CT, Majid DSA, Navar LG. Renoprotective effects of nitric oxide in angiotensin II-induced hypertension in the rat. Am J Physiol Renal Physiol 274: F876–F882, 1998 [DOI] [PubMed] [Google Scholar]
- 13.Crawford JH, Isbell TS, Huang Z, Shiva S, Chacko BK, Schechter AN, Darley-Usmar VM, Kerby JD, Lang JD, Jr, Kraus D, Ho C, Gladwin MT, Patel RP. Hypoxia, red blood cells, and nitrite regulate NO-dependent hypoxic vasodilation. Blood 107: 566–574, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Denicola A, Souza JM, Radi R, Lissi E. Nitric oxide diffusion in membranes determined by fluorescence quenching. Arch Biochem Biophys 328: 208–212, 1996. [DOI] [PubMed] [Google Scholar]
- 15.Edwards A, Layton AT. Nitric oxide and superoxide transport in a cross section of the rat outer medulla. II. Reciprocal interactions and tubulovascular cross talk. Am J Physiol Renal Physiol. (doi:10.1152/ajprenal.00681.2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.El-Farra NH, Christofides PD, Liao JC. Analysis of nitric oxide consumption by erythrocytes in blood vessels using a distributed multicellular model. Ann Biomed Eng 31: 294–309, 2003 [DOI] [PubMed] [Google Scholar]
- 17.Evans R, Fitzgerald S. Nitric oxide and superoxide in the renal medulla: a delicate balancing act. Curr Opin Nephrol Hypertens 14: 9–15, 2005 [DOI] [PubMed] [Google Scholar]
- 18.Ferrer-Sueta G, Radi R. Chemical biology of peroxynitrite: kinetics, diffusion, and radicals. ACS Chem Biol 4: 161–177, 2009 [DOI] [PubMed] [Google Scholar]
- 19.Garvin J, Ortiz P. The role of reactive oxygen species in the regulation of tubular function. Acta Physiol Scand 179: 225–232, 2003 [DOI] [PubMed] [Google Scholar]
- 20.Gross SS. Vascular biology: targeted delivery of nitric oxide. Nature 409: 577–578, 2001 [DOI] [PubMed] [Google Scholar]
- 21.Herrera M, Garvin JL. Novel role of AQP-1 in NO-dependent vasorelaxation. Am J Physiol Renal Physiol 292: F1443–F1451, 2007 [DOI] [PubMed] [Google Scholar]
- 22.Herrera M, Hong NJ, Garvin JL. Aquaporin-1 transports NO across cell membranes. Hypertension 48: 157–164, 2006 [DOI] [PubMed] [Google Scholar]
- 23.Herrera M, Ortiz PA, Garvin JL. Regulation of thick ascending limb transport: role of nitric oxide. Am J Physiol Renal Physiol 290: F1279–F1284, 2006 [DOI] [PubMed] [Google Scholar]
- 24.Hobbs AJ, Gladwin MT, Patel RP, Williams DLH, Butler AR. Haemoglobin: NO transporter, NO inactivator, or NOne of the above? Trends Pharmacol Sci 23: 406–411, 2002 [DOI] [PubMed] [Google Scholar]
- 25.Huang KT, Huang Z, Kim-Shapiro DB. Nitric oxide red blood cell membrane permeability at high and low oxygen tension. Nitric Oxide 16: 209–216, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jankov RP, Kantores C, Pan J, Belik J. Contribution of xanthine oxidase-derived superoxide to chronic hypoxic pulmonary hypertension in neonatal rats. Am J Physiol Lung Cell Mol Physiol 294: L233–L245, 2008 [DOI] [PubMed] [Google Scholar]
- 27.Kakoki M, Zou AP, Mattson DL. The influence of nitric oxide synthase 1 on blood flow and interstitial nitric oxide in the kidney. Am J Physiol Regul Integr Comp Physiol 281: R91–R97, 2001 [DOI] [PubMed] [Google Scholar]
- 28.Kriz W. Der architektonische and funktionelle Aufbau der Ratttenniere. Z Zellforsch 82: 495–535, 1967 [PubMed] [Google Scholar]
- 29.Kriz W. Structural organization of the renal medulla: comparative and functional aspects. Am J Physiol Regul Integr Comp Physiol 241: R3–R16, 1981 [DOI] [PubMed] [Google Scholar]
- 30.Kriz W, Schnermann J, Koepsell H. The position of short and long loops of Henle in the rat kidney. Z Anat Entwickl-Gesch 138: 301–319, 1972 [DOI] [PubMed] [Google Scholar]
- 31.Kumura E, Yoshimine T, Takaoka M, Hayakawa T, Shiga T, Kosaka H. Hypothermia suppresses nitric oxide elevation during reperfusion after focal cerebral ischemia in rats. Neuroscience Lett 220: 45–48, 1996 [DOI] [PubMed] [Google Scholar]
- 32.Kuramochi G, Kersting U, Silbernagl S, Dantzler WH. Changes in the countercurrent system in the renal papilla: diuresis increases pH and HCO3− gradients between collecting duct and vasa recta. Pflügers Arch 432: 1062–1068, 1996 [DOI] [PubMed] [Google Scholar]
- 33.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol 289: F1346–F1366, 2005 [DOI] [PubMed] [Google Scholar]
- 34.Li N, Yi FX, Spurrier JL, Bobrowitz CA, Zou AP. Production of superoxide through NADH oxidase in thick ascending limb of Henle's loop in rat kidney. Am J Physiol Renal Physiol 282: F1111–F1119, 2002 [DOI] [PubMed] [Google Scholar]
- 35.Liu X, Yan Q, Baskerville KL, Zweier JL. Estimation of nitric oxide concentration in blood for different rates of generation. J Biol Chem 282: 8831–8836, 2007 [DOI] [PubMed] [Google Scholar]
- 36.Majid DS, Williams A, Navar LG. Inhibition of nitric oxide synthesis attenuates pressure-induced natriuretic responses in anesthetized dogs. Am J Physiol Renal Fluid Electrolyte Physiol 264: F79–F87, 1993 [DOI] [PubMed] [Google Scholar]
- 37.Malinski T, Taha Z, Grunfeld S, Patton S, Kapturczak M, Tomboulian P. Diffusion of nitric oxide in the aorta wall monitored in situ by porphyrinic microsensors. Biochem Biophys Res Commun 193: 1076–1082, 1993 [DOI] [PubMed] [Google Scholar]
- 38.Matsumoto C, Hayashi T, Kitada K, Yamashita C, Miyamura M, Mori T, Ukimura A, Ohkita M, Jin D, Takai S, Miyazaki M, Okada Y, Kitaura Y, Matsumura Y. Chymase plays an important role in left ventricular remodeling induced by intermittent hypoxia in mice. Hypertension 54: 164–171, 2009 [DOI] [PubMed] [Google Scholar]
- 39.Mori T, Cowley AW., Jr Angiotensin II-NAD(P)H oxidase-stimulated superoxide modifies tubulovascular nitric oxide cross-talk in renal outer medulla. Hypertension 42: 588–593, 2003 [DOI] [PubMed] [Google Scholar]
- 40.Nakanishi K, Mattson DL, Cowley AW., Jr Role of renal medullary blood flow in the development of l-NAME hypertension in rats. Am J Physiol Regul Integr Comp Physiol 268: R317–R323, 1995 [DOI] [PubMed] [Google Scholar]
- 41.Pallone TL, Zhang Z, Rhinehart K. Physiology of the renal medullary microcirculation. Am J Physiol Renal Physiol 284: F253–F266, 2003 [DOI] [PubMed] [Google Scholar]
- 42.Pawloski JR, Hess DT, Stamler JS. Export by red blood cells of nitric oxide bioactivity. Nature 409: 622–626, 2001 [DOI] [PubMed] [Google Scholar]
- 43.Quijano C, Romero N, Radi R. Tyrosine nitration by superoxide and nitric oxide fluxes in biological systems: modeling the impact of superoxide dismutase and nitric oxide diffusion. Free Radic Biol Med 39: 728–741, 2005 [DOI] [PubMed] [Google Scholar]
- 44.Salom MG, Arregui B, Carbonell LF, Ruiz F, Gonzalez-Mora JL, Fenoy FJ. Renal ischemia induces an increase in nitric oxide levels from tissue stores. Am J Physiol Regul Integr Comp Physiol 289: R1459–R1466, 2005 [DOI] [PubMed] [Google Scholar]
- 45.Salom MG, Nieto Ceron S, Rodriguez F, Lopez B, Hernandez I, Gil Martinez J, Martinez Losa A, Fenoy FJ. Heme oxygenase-1 induction improves ischemic renal failure: role of nitric oxide and peroxynitrite. Am J Physiol Heart Circ Physiol 293: H3542–H3549, 2007 [DOI] [PubMed] [Google Scholar]
- 46.Terada LS, Guidot DM, Leff JA, Willingham IR, Hanley ME, Piermattei D, Repine JE. Hypoxia injures endothelial cells by increasing endogenous xanthine oxidase activity. Proc Natl Acad Sci USA 89: 3362–3366, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Vaughn MW, Huang KT, Kuo L, Liao JC. Erythrocyte consumption of nitric oxide: competition experiment and model analysis. Nitric Oxide 5: 18–31, 2001 [DOI] [PubMed] [Google Scholar]
- 48.Vaughn MW, Kuo L, Liao JC. Estimation of nitric oxide production and reaction rates. Am J Physiol Heart Circ Physiol 274: H2163–H2176, 1998 [DOI] [PubMed] [Google Scholar]
- 49.Wexler A, Kalaba R, Marsh D. Three-dimensional anatomy and renal concentrating mechanism. Am J Physiol Renal Fluid Electrolyte Physiol 260: F369–F383, 1991 [DOI] [PubMed] [Google Scholar]
- 50.Whorton AR, Simonds DB, Piantadosi CA. Regulation of nitric oxide synthesis by oxygen in vascular endothelial cells. Am J Physiol Lung Cell Mol Physiol 272: L1161–L1166, 1997 [DOI] [PubMed] [Google Scholar]
- 51.Wu F, Park F, Cowley AW, Jr, Mattson DL. Quantification of nitric oxide synthase activity in microdissected segments of the rat kidney. Am J Physiol Renal Physiol 276: F874–F881, 1999 [DOI] [PubMed] [Google Scholar]
- 52.Zhang W, Edwards A. Mathematical model of nitric oxide convection and diffusion in a renal medullary vas rectum. J Math Biol 53: 385–420, 2006 [DOI] [PubMed] [Google Scholar]
- 53.Zhang W, Edwards A. A model of nitric oxide tubulovascular cross talk in a renal outer medullary cross section. Am J Physiol Renal Physiol 292: F711–F722, 2007 [DOI] [PubMed] [Google Scholar]
- 54.Zhang W, Pibulsonggram T, Edwards A. Determinants of basal nitric oxide concentration in the renal medullary microcirculation. Am J Physiol Renal Physiol 287: F1189–F1203, 2004 [DOI] [PubMed] [Google Scholar]
- 55.Zhang Z, Rhinehart K, Solis G, Pittner J, Lee-Kwon W, Welch WJ, Wilcox CS, Pallone TL. Chronic ANG II infusion increases NO generation by rat descending vasa recta. Am J Physiol Heart Circ Physiol 288: H29–H36, 2005 [DOI] [PubMed] [Google Scholar]
- 56.Zou AP, Wu F, Cowley AW., Jr Protective effect of angiotensin II-induced increase in nitric oxide in the renal medullary circulation. Hypertension 31: 271–276, 1998 [DOI] [PubMed] [Google Scholar]