Interplay between Secondary and Tertiary Structure Formation in Protein Folding Cooperativity

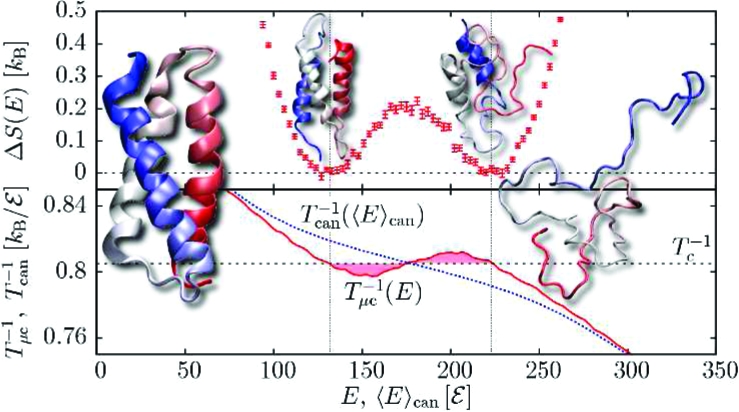
Abstract

Protein folding cooperativity is defined by the nature of the finite-size thermodynamic transition exhibited upon folding: two-state transitions show a free-energy barrier between the folded and unfolded ensembles, while downhill folding is barrierless. A microcanonical analysis, where the energy is the natural variable, has proved to be better suited than its canonical counterpart to unambiguously characterize the nature of the transition. Replica-exchange molecular dynamics simulations of a high-resolution coarse-grained model allow for the accurate evaluation of the density of states in order to extract precise thermodynamic information and measure its impact on structural features. The method has been applied to three helical peptides: a short helix shows sharp features of a two-state folder, while a longer helix and a three-helix bundle exhibit downhill and two-state transitions, respectively. Extending the results of lattice simulations and theoretical models, we have found that it is the interplay between secondary structure and the loss of non-native tertiary contacts that determines the nature of the transition.

The folding cooperativity of proteins is characterized by the relative population of intermediate states at the transition temperature: while two-state transitions exhibit two energetic peaks characterizing the folded and unfolded ensembles, downhill folders show a unimodal distribution of energetic states without any barrier.^1,2 This aspect of finite-size thermodynamic transitions can provide insight into the folding mechanism, but energetic populations can be difficult to measure. Therefore, protein folding cooperativity is often probed using the calorimetric criterion,(3) which quantifies the sharpness of the specific heat curve. From a computer simulation point of view, however, evaluating the probability density p(E) remains an appealing idea, as it would provide an unambiguous description of the thermodynamic transition. Although this is currently untractable atomistically because of sampling limitations, high-resolution coarse-grained models offer an alternative approach.(4) While cutting down significantly on computational time, they can retain much chemical detail, and some are even able to model the folding of simple peptides with no prior knowledge of the native state. In this communication, we study the link between thermodynamics and structure for helical peptides using such a coarse-grained model,(5) details of which can be found in the Supporting Information.

To characterize the thermodynamics of finite-size systems, it has been shown that a microcanonical analysis based on the entropy S(E) is often more informative than a canonical analysis.^6,7 Microcanonically, S(E) = k_B ln Ω(E), where Ω(E) is the density of states. One remarkable feature of such a description is its ability to unambiguously distinguish between discontinuous (i.e., two-state) and continuous (i.e., downhill) transitions. Indeed, two-state transitions exhibit a depletion of intermediate energetic states that leads to local convexity in the entropy. This can best be observed by defining the quantity ΔS(E) = ℋ(E) − S(E), where the first term is the (double-)tangent to S(E) in the transition region.⁸⁻¹⁰ The method relies on accurate measurements of the density of states, which were calculated here using the weighted histogram analysis method.(11) All of the order parameters were analyzed as a function of energy.

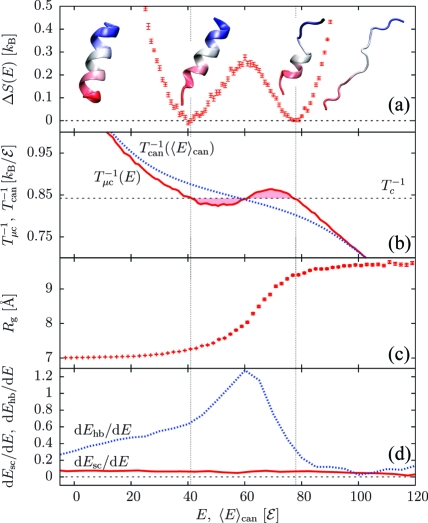
We first examined a short α-helix having the sequence (AAQAA)₃.(12) The density of states reveals a discontinuous transition between the folded and unfolded ensembles with nonzero latent heat ΔQ (Figure 1a; representative conformations at different energies are shown). Phase coexistence is associated with a back-bending(6) of the microcanonical inverse temperature T_μc⁻¹ = ∂S/∂E, while the corresponding canonical relation T⁻¹(⟨E⟩_can), where ⟨E⟩_can is the average energy, is monotonic (Figure 1b). The radius of gyration (R_g) quickly changes inside the coexistence region (Figure 1c), indicating that most of the structural rearrangements happen within this energy interval. We will assume the hydrogen-bond and side-chain energies E_hb and E_sc to be suitable proxies of secondary structure and tertiary contacts, repectively. It proves instructive to look at their energetic rates, dE_hb/dE and dE_sc/dE (Figure 1d): even though dE_sc/dE stays virtually flat over the energy range considered, the sharp peak in dE_hb/dE indicates that most of the secondary structure forms within the coexistence region.

Figure 1.

Results for (AAQAA)₃. (a) ΔS(E); error bars reflect the variance of the data points (1σ interval). (b) Inverse temperatures from canonical [T_can⁻¹(⟨E⟩_can), blue] and microcanonical [T_μc(E) = ∂S/∂E, red] analyses, where ⟨E⟩_can is the canonical average energy. (c) Radius of gyration R_g(E) with the error of the mean. (d) Rates of H-bond and side-chain energies dE_hb/dE and dE_sc/dE. Vertical lines delimit the transition region, whose width corresponds to the microcanonical latent heat ΔQ.

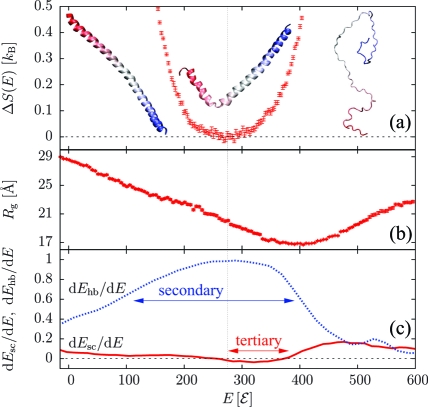
Elongating the sequence to (AAQAA)₁₅ led to a qualitative change in the folding mechanism. The ground state again forms a single α-helix, but the transition is now continuous: as shown in Figure 2a and Figure S2 in the Supporting Information, there is a single transition point, and the latent heat is zero. The radius of gyration (Figure 2b) features a sharp minimum above the transition point, indicative of chain collapse into “maximally compact non-native states”.(13) Upon a further decrease in the energy, the chain reorganizes from such non-native states into the helical state. In doing so, the rate of tertiary contact formation dE_sc/dE dips below zero (Figure 2c), so there is an energetic penalty associated with tertiary rearrangements. Hydrogen-bond formation occurs over a large energetic interval, as indicated by the broad maximum in dE_hb/dE. The absence of any two-state signal is consistent with theoretical models of the helix−coil transition:(14) the energetic cost of breaking a hydrogen bond is outweighed by the conformational entropy gained. Further analysis indicates two helices on average at the transition point.

Figure 2.

Results for (AAQAA)₁₅. (a) ΔS(E). (b) Radius of gyration R_g(E). (c) Rates of H-bond and side-chain energies dE_hb/dE and dE_sc/dE. Horizontal arrows indicate where most of the secondary structure forms and where non-native tertiary contacts dissolve. The vertical line marks the transition point.

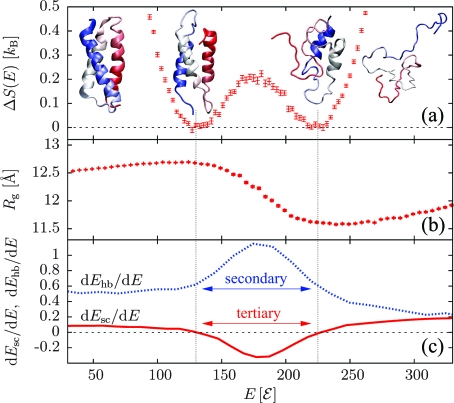
While of similar length, the 73 amino acid de novo three-helix bundle α3D (PDB entry 2A3D)(15) does show a discontinuous transition (Figure 3a). Representative conformations sampled in the two coexisting ensembles stand as good proxies of the ground and unfolded states, unlike the case of the downhill-folding transition of (AAQAA)₁₅. The radius of gyration again shows a minimum above the transition (Figure 3b), and folding once more starts from maximally compact non-native states. Notably, secondary structure formation and the loss of non-native tertiary contacts (Figure 3c) are sharp and predominantly localized within the coexistence region. The three helices form inside the same energetic interval because of the interhelical cooperativity imprinted in the sequence.(16) Chain compaction is due to strong side chain−side chain interactions.

Figure 3.

Results for the three-helix bundle α3D. (a) ΔS(E). (b) Radius of gyration R_g(E). (c) Rates of H-bond and side-chain energies dE_hb/dE and  dE_sc/dE.

Overall, we can correlate thermodynamic features with structural information from the three peptides studied here. While (AAQAA)₃ is too short for tertiary interactions to play any role, the transitions associated with (AAQAA)₁₅ and the bundle α3D are both associated with tertiary rearrangements. These two examples suggest that independent of its nature, the folding transition is driven by the loss of non-native tertiary contacts (i.e., the region where dE_sc/dE < 0), which is reminiscent of the heteropolymer collapse model.(13) On the other hand, secondary structure formation shows very different signals: (AAQAA)₃ and α3D exhibit sharp peaks, whereas (AAQAA)₁₅ displays a broad maximum. As shown in Figure 2c, secondary structure formation in a downhill-folding peptide occurs over a much broader interval than for the loss of non-native tertiary contacts, whereas these two quantities are contained within the same narrow interval for a two-state peptide (Figure 3c). Cooperative secondary and tertiary structure formation has been proposed as a mechanism for two-state folding on the basis of lattice simulations(17) and theoretical models.(16) Beyond this, our results also highlight the interplay between secondary structure formation and the loss of non-native tertiary contacts. Our conclusions about the thermodynamics of the short, long, and bundled helixes are compatible with the calorimetric criterion; we find δ = 0.78,  0.52,  and 0.78, respectively, for the calorimetric ratio.(3) It should be noted that Ghosh and Dill(16) predicted δ = 0.72 for the similar bundle α3C. However, the main strength of a microcanonical analysis stems from its access to fine aspects of thermodynamic information that are otherwise difficult to obtain either canonically or from experiments. It thus stands as a complementary tool for gaining further insight.

Supporting Information Available

Peptide model and simulation and analysis methods. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States