Skip to main content
PMC home page
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences logoLink to Philosophical transactions. Series A, Mathematical, physical, and engineering sciences
. 2010 May 13;368(1918):2221–2236. doi: 10.1098/rsta.2010.0038

Phase-resolved analysis of the susceptibility of pinned spiral waves to far-field pacing in a two-dimensional model of excitable media

Philip Bittihn 1,2,*, Amgad Squires 2,5, Gisa Luther 2, Eberhard Bodenschatz 2, Valentin Krinsky 2,6, Ulrich Parlitz 1, Stefan Luther 2,3,4
PMCID: PMC2944386  PMID: 20368243

Abstract

Life-threatening cardiac arrhythmias are associated with the existence of stable and unstable spiral waves. Termination of such complex spatio-temporal patterns by local control is substantially limited by anchoring of spiral waves at natural heterogeneities. Far-field pacing (FFP) is a new local control strategy that has been shown to be capable of unpinning waves from obstacles. In this article, we investigate in detail the FFP unpinning mechanism for a single rotating wave pinned to a heterogeneity. We identify qualitatively different phase regimes of the rotating wave showing that the concept of vulnerability is important but not sufficient to explain the failure of unpinning in all cases. Specifically, we find that a reduced excitation threshold can lead to the failure of unpinning, even inside the vulnerable window. The critical value of the excitation threshold (below which no unpinning is possible) decreases for higher electric field strengths and larger obstacles. In contrast, for a high excitation threshold, the success of unpinning is determined solely by vulnerability, allowing for a convenient estimation of the unpinning success rate. In some cases, we also observe phase resetting in discontinuous phase intervals of the spiral wave. This effect is important for the application of multiple stimuli in experiments.

Keywords: excitable media, cardiac dynamics, spiral waves, virtual electrodes, chaos control,  arrhythmia

1. Introduction

Cardiac tissue is a biological excitable medium. Generic activation patterns, such as plane waves, spiral waves and spiral defect chaos, which are known from many different excitable media also occur in the heart. Plane waves are associated with normal activity, when excitation waves generated by specific pacemaker cells travel through the myocardium resulting in coordinated contraction. During tachycardias, reentrant waves (spiral or scroll waves) produce increased heart rate. Effects such as spiral-wave breakup can ultimately lead to a complex dynamical state, which is composed of many unstable spirals and represents lethal ventricular fibrillation (Cherry & Fenton 2008; Otani et al. 2008). One method of terminating this irregular activity is defibrillation: by a high-energy electric current, the whole medium is excited at once, setting every single cell to its refractory period and thus ending any activity. Because of the adverse side effects of defibrillation (such as cardiac lesions that imply a higher probability of future arrhythmias), there is a search for methods which require less energy. This article examines a control method known as far-field pacing (FFP), which exploits natural heterogeneities in the tissue and has been discussed in a number of studies (Takagi et al. 2004; Pumir et al. 2007). Experimentally, the tissue is subjected to a weak-pulsed electric field. Although the method is very promising in providing an alternative approach to even terminate fast arrhythmias and fibrillation (Fenton et al. 2009), the mechanisms are still not well understood. However, such understanding is essential in order to successfully and reliably apply FFP in an experimental (or even clinical) situation. This conceptual numerical study sheds some new light on the preconditions for the success and failure of one specific mechanism of FFP control known as unpinning, which is a specific form of interaction between a single spiral wave and a heterogeneity in the tissue. The aim is to open a way towards clarifying the potential mechanisms (and limitations) underlying the complex interaction of waves during FFP.

Both anti-tachycardia pacing (ATP) and FFP are based on the idea that the local initiation of additional waves could also be an effective means to control wave dynamics. The energy required by such approaches is much smaller than for defibrillation because only the local excitation threshold has to be overcome. However, ATP requires the implantation of an additional pacing electrode. Emission of pacing waves from this electrode with a frequency higher than the frequency of arrhythmia should cause any free spiral to drift out of the medium (Krinsky & Agladze 1983) and thus end the irregular activity. Some implantable defibrillators use ATP as an alternative control strategy before delivering a defibrillating shock as a last resort (Exner 2005). The disadvantage of this method is the fixed location of the pacing electrode. If spirals are pinned to obstacles (such as blood vessels or scars), the pacing electrode will generally emit waves far away from the pinning location, which, in most cases, results in no unpinning (and subsequently neither drift nor termination). If the spiral core is larger than the obstacle, unpinning by ATP from a distance is possible. This effect is studied in detail in the work of Pumir et al. (2010). Other cases of success rely on a specific kind of velocity restitution that is not present in the model used in this article (Isomura et al. 2008). The limitations of ATP can be overcome by FFP (Bittihn et al. 2008) because it is able to initiate a pacing wave from the boundary of the obstacle, to which the spiral is pinned. Pacing from a location near the spiral core has been shown to make unpinning possible (Krinsky et al. 1995; Huyet et al. 1998). As the location of a physically implanted electrode is fixed, ATP generally cannot unpin spirals.

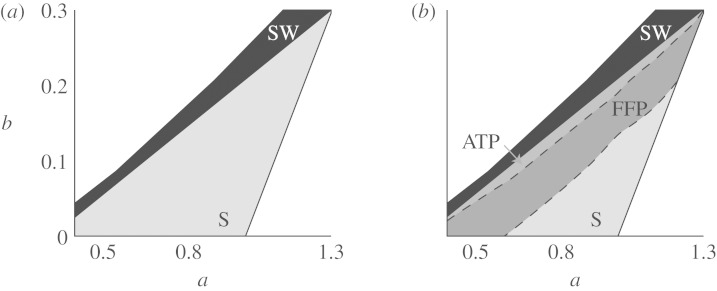
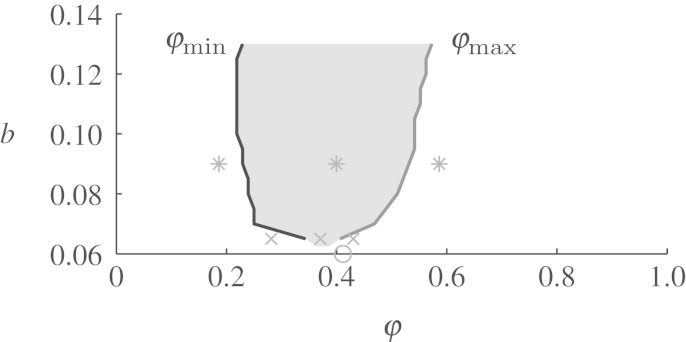
In contrast, FFP locations are those same obstacles to which spirals can also potentially pin: by the application of an electric field to a whole piece of tissue, depolarizations and hyperpolarizations (Weidmann zones) are created at abrupt conductancy changes (as occur at obstacles such as blood vessels and scars). If the depolarization exceeds the excitation threshold, a wave is created at the boundary of the obstacle. In this way, obstacles can be used as virtual electrodes (Sepulveda et al. 1989; Sobie et al. 1997; Fast et al. 1998; Fishler 1998; Woods et al. 2006). Figure 1 shows one of the mechanisms of detaching a spiral wave from an obstacle using FFP. Unpinning by means of virtual electrodes has already been the subject of a number of numerical and experimental studies (Ripplinger et al. 2006; Pumir et al. 2007), also showing the possibility of failure of the FFP mechanism (Pumir & Krinsky 1999; Takagi et al. 2004) and comparing its performance with the performance of ATP in a generic model of an excitable medium (Bittihn et al. 2008). The main result of the last publication is shown in figure 2. The details of the numerical simulations performed to obtain this figure can be found in Bittihn et al. (2008). The figure shows that, for a specific obstacle radius, FFP can be successful in a much larger parameter region of the Barkley model (§3) than ATP. This plot raises the following question: why is FFP only successful for increased excitation threshold (parameter b in the model) and not in the whole parameter region S? The aim of the following analysis is to look more closely at the specific conditions that have to be fulfilled for FFP unpinning to be successful. For computational simplicity, we will restrict this analysis to the line a=0.8 in the parameter space of the Barkley model.

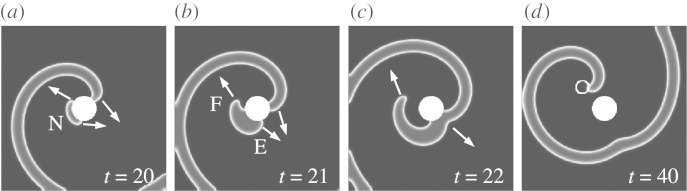
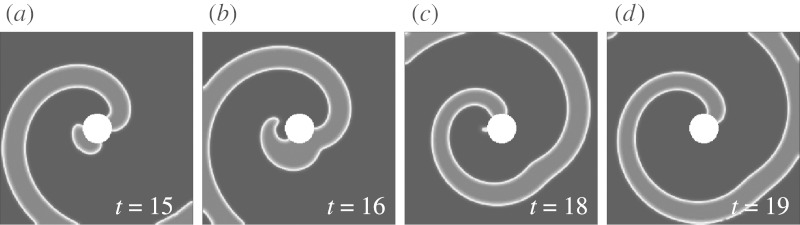
Figure 1.

Figure 1.

Open in a new tab

Successful unpinning by FFP. (a) At t=20 (just after the pulse), the new wave N has been nucleated. (b) At t=21, end F has disconnected from the obstacle because its propagation along the boundary of the obstacle is inhibited by the refractory tail of the spiral wave. (c) End E forms a pinned wave and collides with the original spiral (t=22). (d) The result (t=40) is a free spiral, formed by the free end F. The new spiral core is indicated by a circular white line. (Adapted from Bittihn et al. 2008.)

Figure 2.

Figure 2.

Open in a new tab

Performance of FFP. In the S region (grey), the medium exhibits excitable dynamics and supports spiral waves. (a) In the shrinking wave (SW) region (black), broken plane waves do not form spirals but shrink (called subexcitable in the work of Alonso et al. (2003)). The right and top white domains represent non-excitable dynamics: bistability and no waves, respectively. (b) The ATP domain represents the model parameters for which ATP can potentially unpin spiral waves from an obstacle of size R=3. The FFP domain (which includes the ATP region) marks the parameter combinations for which unpinning by FFP is successful, if the pulse is delivered at the right time. FFP is successful in a much larger region than ATP. An increased excitation threshold (parameter b) facilitates unpinning. (Adapted from Bittihn et al. 2008.)

2. Vulnerable window and unpinning window

It is commonly thought that the success or failure of FFP is determined by a well-known phenomenon called vulnerability (Mines 1914; Wiggers & Wégria 1940). Indeed, we can explain the success of the unpinning mechanism sketched in figure 1 by looking first at a one-dimensional cable.

An excitation placed at any position in a quiescent cable creates two waves travelling in opposite directions. The situation is different if we place the stimulus in the refractory tail of a travelling wavefront. Immediately after the wave has passed the stimulus site, no wave at all will be initiated because the medium is still too refractory. However, there is a time window (called the vulnerable window) in which the stimulus creates only one wave because the medium is capable of producing an action potential, but the wave that would normally travel behind the original wave is inhibited by the refractory tail. If the cable has periodic boundary conditions, the two waves (the original wave and the single newly created wave) annihilate each other. A systematic numerical and analytical characterization of the vulnerable window in different models of excitable media has been performed by Starmer et al. (1993).

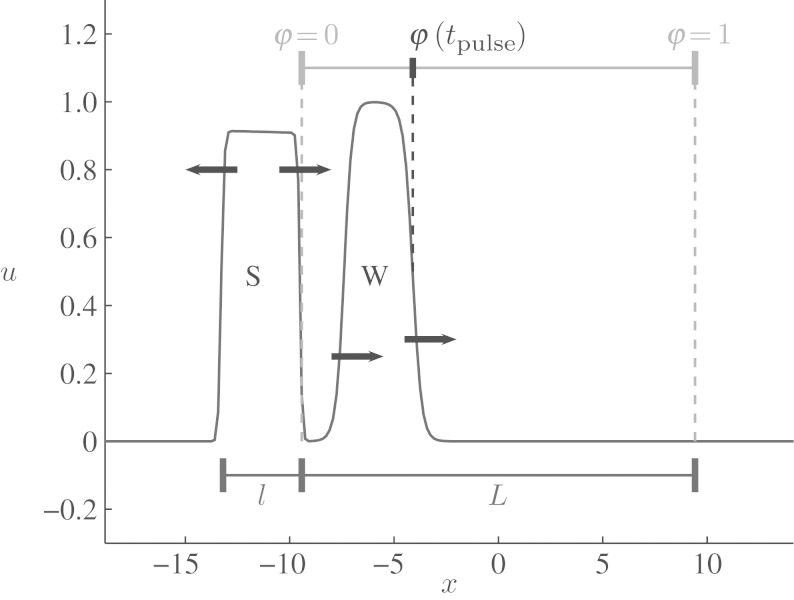
The vulnerable window is located at the transition from the refractory period to the state of excitability. In the situation described above (a travelling wave in a one-dimensional cable of length L), we can define a phase φ∈[0,1] for every position of the travelling wavefront. We define φ=0 to be the position where the stimulus will be applied. The result of this stimulus will depend on its spatial extent l and the phase of the travelling wave in the cable (Starmer et al. 1993). We define

2. 2.1

as the normalized stimulus width, where L is the length of the cable. Figure 3 illustrates the spatial parameters and the definition of the phase as they were implemented in the simulation (see §3 for details). In this scenario, the vulnerable window is the phase interval 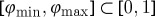Inline graphic, such that a stimulus creates only one wave, if 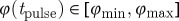Inline graphic. When the phase of the travelling wave at the time of the pulse φ(tpulse)∈[0,1] is unknown, the width of this window ρvw=φmax−φmin is also the probability that the stimulus is inside the vulnerable window. With the vulnerable window 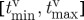Inline graphic in time, the success rate can also be calculated as

2. 2.2

where T is the time for one travelling wave to travel the length L of the cable. The three cases (pulses (i) before, (ii) during and (iii) after the vulnerable window) are shown in figure 4.

Figure 3.

Figure 3.

Open in a new tab

Definition of phase and stimulus application in the one-dimensional cable. A section of length L in the cable (spatial coordinate x) corresponds to phases φ∈[0,1]. The values of the fast variable u are shown at time t=tpulse, when the stimulus S of width l has just been delivered at phase φ=0. The travelling wavefront W (by definition located at phase φ(tpulse)) is propagating to the right.

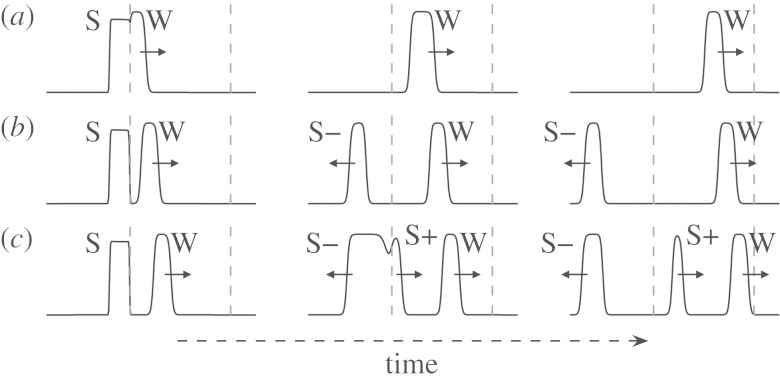
Figure 4.

Figure 4.

Open in a new tab

Example dynamics inside and outside the vulnerable window. (a)–(c) show different pulse phases φ(tpulse). As in figure 3, the grey dashed lines mark the test section of length L in the cable. (a) φ(tpulse)<φmin: the stimulus S is completely in the refractory period of the travelling wavefront W and thus is not able to initiate a wave. (b) φmin<φ(tpulse)<φmax: the pulse S is within the vulnerable window. One direction of propagation is blocked and only one wave S− is created by the stimulus. (c) φ(tpulse)>φmax: the medium is excitable again, which leads to the creation of two waves S− and S+ by the stimulus S.

This is a simple analogue for the situation along the boundary of the obstacle shown in figure 1, taken as a one-dimensional cable: the wave created by the far-field pulse is inside the vulnerable window, because only one end E of the new wave can travel along the boundary, whereas the other end F is blocked on this one-dimensional path. Krinsky et al. (1995) showed that a stimulus placed in the vulnerable area of a spiral creates a semicircular wave with two spiral defects. One vortex created by the new wave E is pinned to the obstacle, whereas the other vortex at end F has to detach from the boundary. As in the one-dimensional case, the two waves on the boundary of the obstacle (‘in the cable’) then annihilate each other. But the vortex created by the free end F remains at a distance. Thus, the original spiral has effectively been unpinned by the far-field pulse.

For a given model and fixed field strength of the electric-field pulse, the success of FFP critically depends on the timing of the pulse. More specifically, if we look at an isolated spiral rotating around an obstacle, this spiral exhibits exactly periodic dynamics, so that we can map every possible position of the spiral to a phase φ∈[0,1]. For simplicity, we define φ=0 to be the point on the obstacle boundary where a far-field pulse initiates a new wave. The unpinning window is defined as the largest continuous interval 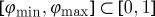Inline graphic, such that a far-field pulse produces successful unpinning if φ(tpulse)∈[φmin,φmax]. We call ρuw=φmax−φmin the normalized unpinning window width (not to be confused with the vulnerable window width ρvw). If [φmin,φmax] is the only phase interval producing successful unpinning, ρuw is also a success rate, i.e. the probability that a pulse at an arbitrary time is successful in unpinning the wave from the obstacle. With the largest success interval in time 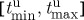Inline graphic, the normalized unpinning window width can also be calculated as

2. 2.3

where T is the spiral rotation period. In figure 2, the FFP region covers those parameters where ρuw>0 for a rectangular far-field pulse of field strength E=7 unit u amplitude/unit length applied for 0.1 time units at an obstacle of radius R=3.

Because of the similar definitions of (2.2) and (2.3) and their close relationship through the FFP unpinning mechanism, one might be tempted to identify the two success rates ρvw and ρuw with each other. Pumir & Krinsky (1999) mention the vulnerable window as a fundamental mechanism similar to unpinning. However, they observe that a too small distance of the spiral tip from the obstacle after wave detachment can cause unpinning to fail. Takagi et al. (2004) state that the vulnerable window sets the limits for the unpinning mechanism considered here without relating both windows directly. Furthermore, in both studies, only models with fixed parameters are considered. This study aims at generalizing these results and clarifying the limitations of this specific unpinning mechanism by looking at the relation of the unpinning window and the vulnerable window. As we will show, the position and the extension of the unpinning window within the vulnerable window can be qualitatively different for varying model parameters.

3. Simulations

All the simulations in this article are carried out using the Barkley model (Barkley et al. 1990) with the reaction–diffusion equations,

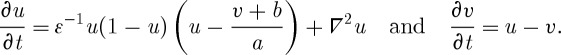3. 3.1

The model consists of a fast activator u, a slow inhibitory variable v and three parameters ε (determining the time scale of the fast variable), a and b. All simulations were carried out with a constant spatial resolution of Δx=1/6 and a simple Euler time step of Δt=1/400. ε is fixed to 0.02. For our purposes, using a simple generic model of excitable media has several advantages compared with more detailed cardiac (or even ionic) models: the two parameters a and b determine the excitation threshold (b/a) and the action potential duration (a function of a). Thus, by exploring the parameter space of the model, effects can be related to generic properties of any excitable medium in contrast to model-specific parameters in a large parameter space. Additionally, computational simplicity facilitates the investigation in this paper because it requires numerically intensive calculations.

FFP simulations were performed exactly as described in Bittihn et al. (2008). Similar simulations were carried out for the vulnerable window in a one-dimensional cable, sufficiently larger than the length L described in §2 to avoid boundary effects. To connect these simulations to the specific geometric arrangement used for the FFP simulations, we chose L=2πR, where R=3 is the radius of the obstacle used to calculate figure 2. From one end of the cable, a travelling wave was started in order to determine the time T for the wave to travel a section of length L (in the middle of the cable, far away from any boundaries). A stimulus was placed at the beginning of this section a time span T·n/N after the travelling wave had entered it, where n=0,1,…,N−1 (i.e. N simulations were performed). This was done by setting the values of u to 0.9 in an interval of length l=δ·L, where δ is the normalized stimulus width as defined in §2 (see figure 3). From these simulations, the normalized vulnerable window width or vulnerable window success rate ρvw can be determined to an accuracy of ±1/N with N=128 in our case.1

4. Results

(a). Outside the unpinning window

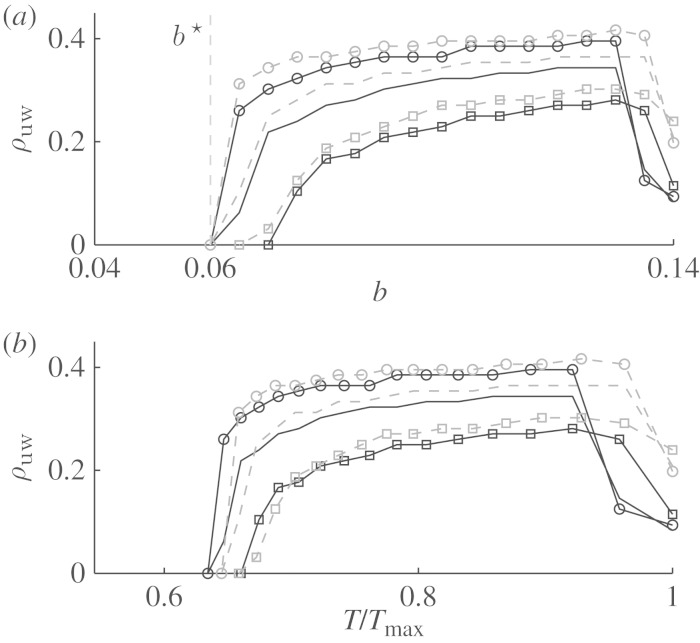
Figure 5 shows the normalized unpinning window width ρuw along a line of constant a=0.8. As one might expect, ρuw is generally larger for higher field strengths at a constant obstacle size. One reason for this could be the increased size of the area depolarized by the far-field pulse. The range of the model parameter b, in which unpinning is possible (i.e. where ρuw>0) increases with increasing field strength and obstacle size. In the one-dimensional analogy, this can also be explained by an increased depolarized area at the boundary of the obstacle, which corresponds to an increased stimulus width (compare to §4b). For stronger electric fields and larger obstacles, there seems to be a saturation: the datasets for (R,E)=(3,7),(3,14),(4.5,7) and (4.5,14) show a transition to ρuw=0 between b=0.065 and b=0.06.

Figure 5.

Figure 5.

Open in a new tab

Parameter dependence of unpinning window width. (a) For a=0.8, the normalized unpinning window width ρuw is plotted against the model parameter b (in steps of Δb=0.005). The lines represent ρuw for different obstacle radii and electric-field strengths. Error bars are not shown, as (owing to the algorithm) accuracy is constantly ±1/96 T. For R=3 and E=7 at b=0.06:=b★ this means that ρuw<T/96. (b) The same data, but plotted against the spiral rotation period T, normalized by the maximum rotation period Tmax at b=0.14. For each configuration (R,E), there is a critical spiral rotation frequency, above which unpinning by FFP is not possible. Empty square on a solid line, R=3, E=4; solid line, R=3, E=7; empty circle on a solid line, R=3, E=14; empty square on a dashed line, R=4.5, E=4; dashed line, R=4.5, E=7; empty circle on a dashed line, R=4.5, E=14.

Figure 6 shows one of the datasets (for R=3 and E=7) in more detail, also resolving the position of the unpinning window in phase for each value of b. The lines of φmin and φmax approach each other as 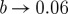Inline graphic from above, which explains why 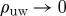Inline graphic. From this plot, we can determine the phases at which to deliver a pulse if we want to analyse the unpinning window and its boundaries in more detail.

Figure 6.

Figure 6.

Open in a new tab

Unpinning window in detail for a=0.8. For the same parameters as in figure 5, the minimum and maximum phase at which unpinning is possible are shown. Consequently, in the shaded region between the two lines, unpinning by FFP is possible. The markers show the parameters used to produce the snapshots in figures 7 (asterisk), 8 (cross) and 9 (empty circle).

Figure 7 shows a series of snapshots taken from FFP simulations at a=0.8 and b=0.09, i.e. parameters at which a large unpinning window exists. Figure 7a–c shows the effect of a pulse before, during and after the unpinning window (compare to asterisks in figure 6). As can be seen from the snapshots, the finite boundaries of the unpinning window can be fully explained by the one-dimensional vulnerable window mechanism introduced in §2: in figure 7a, the pulse is delivered before the vulnerable window (defined in the cable that represents the boundary of the obstacle), i.e. in the refractory tail of the wave. The pulse does not initiate a wave. In figure 7b, the propagation of the newly initiated wave is prohibited in one direction by the refractory tail of the spiral, meaning that the pulse was inside the vulnerable window. In figure 7c, the new wave travels along the boundary of the obstacle in both directions, leading to unsuccessful unpinning, and indicating that the pulse was delivered outside the vulnerable window.

Figure 7.

Figure 7.

Open in a new tab

Inside and outside the unpinning window (a=0.8 and b=0.09). Pulse times for (a)–(c) are indicated by asterisks in figure 6. (a) Early pulse. The area depolarized by the electric field is still too refractory. No wave is initiated. (b) Pulse within the unpinning window. Unpinning mechanism according to figure 1. (c) Late pulse. Both ends of the newly initiated wave can travel along the boundary of the obstacle. Because of the annihilation of one end with the original spiral, the result is a topologically unchanged situation.

To date, there is still no contradiction if we identify the vulnerable window ρvw with the unpinning window ρuw. The importance of the second dimension is revealed if we look at lower values of the model parameter b, when ρuw approaches zero. Figure 8a–c shows pulse times before, during and after the unpinning window as in figure 7, but for b=0.065. The corresponding phases, at which the pulses are delivered, are indicated by crosses in figure 6. Clearly, figure 8b shows the case of successful unpinning because the pulse phase is inside the unpinning window, which, as we have seen, implies (at least for this unpinning mechanism) that it also lies inside the vulnerable window. Already from these snapshots, it can be seen that the unpinning window is about to vanish if b is further reduced because the distance of the detached spiral from the obstacle is just large enough to prevent it from reattaching. That this effect takes place at a certain distance from the obstacle boundary (i.e. in the ‘second dimension’) is already a hint that it cannot be covered by the one-dimensional vulnerable window mechanism. This can be clearly seen from figure 8a,c. Both before and after the unpinning window, the pulse is still delivered in the vulnerable window, as in both cases a new wave can be initiated that is blocked in one direction (compare to figure 7a,c, where one pulse is delivered in the refractory tail and the other is not blocked along the boundary). The reason why the pulses fail to unpin the spiral is not that they miss the vulnerable window, but rather that the initiated wave uses the additional degrees of freedom in the second dimension to make a detour and finally connect to the obstacle boundary, which has, by then, recovered its excitability.

Figure 8.

Figure 8.

Open in a new tab

Inside and outside the unpinning window (a=0.8 and b=0.065). Pulse times for (a–c) are indicated by crosses in figure 6. (a,c) Both early and late pulses create a wave that briefly detaches from the obstacle and then reattaches. (b) The pulse within the unpinning window is able to create a free end slightly further away from the obstacle as in (a) or (c), which leads to successful unpinning. The small distance between the unpinned spiral and the obstacle for this lower value of b already indicates that the unpinning window will completely vanish for even lower b.

Having seen this mechanism, it is not surprising that, even for b=0.06, where the unpinning window is already zero, pulses can still detach spiral waves temporarily from the obstacle by being placed inside the vulnerable window, as shown in figure 9.

Figure 9.

Figure 9.

Open in a new tab

Temporary wave detachment (a=0.8 and b=0.06). According to figure 5 (with R=3 and E=7), there is (to accuracy ±T/96) no unpinning window for these parameters. But there are pulse times for which one end of the FFP wave temporarily detaches from the obstacle. One of these cases is shown here. Its timing is indicated by a circle in figure 6. The time evolution looks similar to figure 8a,c. Apparently, these cases have converged and eliminated the unpinning window in between.

(b). Comparison with the vulnerable window

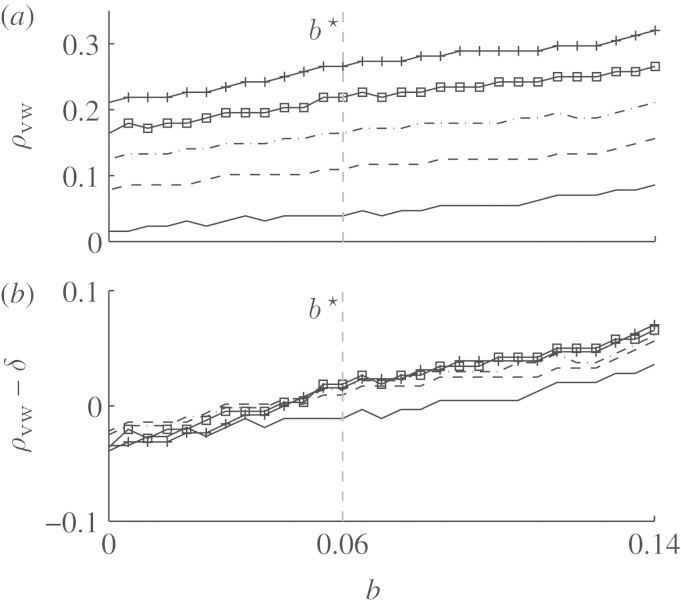
The above analysis suggests that the vulnerable window itself is not sufficient to predict the size of the unpinning window for specific values of the excitation threshold b. Although the unpinning window always lies within the vulnerable window, the vanishing unpinning window as shown above cannot be explained by a shrinking vulnerable window. To confirm this result directly, we determined the normalized vulnerable window width ρvw for the same model parameters as in figure 5 using the algorithm described in §3. The results for different normalized stimulus widths δ can be seen in figure 10. The value b★ below which no unpinning window ρuw>0 at all was observed (see figure 5) is marked by vertical dashed lines in figures 5 and 10. For none of the different stimulus widths does ρvw show any extraordinary behaviour at b=b★. ρvw displays an almost linear behaviour over the whole range of the parameter b shown in figure 10. Additionally, we have seen in §4a that, in the two-dimensional setting, the vulnerable window does not vanish at the same value of b as the unpinning window, which rules out an insufficient stimulus width as a reason for the sharp transitions to ρuw=0 in figure 5. Of course, the model parameter b does not only influence the FFP mechanism by changing the vulnerable window width ρvw, but may also alter the depolarization dynamics induced by the electric field. Therefore, there is a possibility that the effective depolarization area (as opposed to the stimulus width along the boundary of the obstacle) created by the electric field is reduced by decreasing b, resulting in the observed effects of reattachment within the vulnerable window. However, the saturation of the limiting value of b in figure 5 for higher field strengths (and thus a larger depolarization area) suggests that the reason for the failure of unpinning below b★ is an even more fundamental limitation.

Figure 10.

Figure 10.

Open in a new tab

Vulnerable window width for a=0.8 (numerical step Δb=0.005). (a) For the values of b inside the region S (compare to figure 5), the normalized vulnerable window width ρvw is plotted for five different stimulus widths δ. (b) The same data as in (a). Here, ρvw−δ is plotted instead of ρvw. The results for different δ are very similar, with increased deviation only for the smallest value δ=0.05. The almost identical curves in (b) can be explained by the linear dependence of the ρvw found analytically by Starmer et al. (1993). Plus symbols on a solid line, δ=0.25; empty squares on a solid line, δ=0.2; dot-dashed line, δ=0.15; dashed line, δ=0.1; solid line, δ=0.05.

From these results, we can conclude that the reduced one-dimensional view generally taken to analyse the interaction of waves at obstacle boundaries lacks the ability to explain a very robust mechanism which leads to unpinning failure, even in this simple model of an excitable medium. In this study, there has been no systematic analysis of FFP parameters showing the universality of the limiting value b★. However, the sharp transitions to ρuw=0 shown in figure 5 and the comparison with the vulnerable window yield the conjecture that this limitation is due to the spiral’s spatial structure and the two-dimensional spatial extent of the induced depolarizations and not only to the part of the wave travelling along the boundary of the obstacle.

(c). Consequences for the application of multiple far-field pacing stimuli

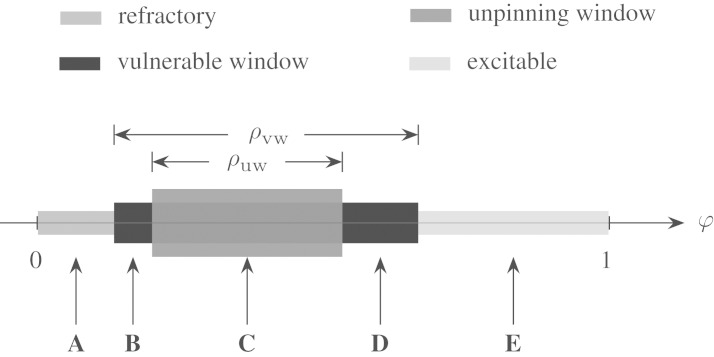
From the above analysis, we can deduce the qualitative structure of the spiral’s reaction to an FFP pulse applied at an arbitrary phase φ. As we have seen, the vulnerable window and the unpinning window are two different concepts that are nevertheless connected by the fact that successful unpinning according to the mechanism in figure 1 is only possible inside the vulnerable window. Considering also the refractory period before and the excitable time after the vulnerable window, the complete qualitative picture can be described as in figure 11. A pulse delivered at phase A is in the refractory period and does not initiate a wave. The existing spiral is not influenced. Pulses B and D are in the vulnerable window but not in the unpinning window. This leads to temporary detachment of the wave, but results in no unpinning and (after some further wave interaction) an unchanged topological situation of one spiral pinned to the obstacle. In these cases, however, the pulse has an effect: with the pulse, a new spiral with phase φ≈0 is initiated (see the definition of φ in §2). Apart from a delay caused by the temporary detachment and possibly a reduced propagation velocity, this spiral then evolves into the remaining spiral at the obstacle. Thus, neglecting the transient state of multiple spirals at the obstacle, the phase of the spiral is effectively reset to φ≈0 at the time of the pulse. The most surprising thing about this is the fact that such a region can exist between the refractory period and the unpinning window. Phase resetting also occurs with pulse E, only without the temporary detachment of the wave.

Figure 11.

Figure 11.

Open in a new tab

Schematic view of the unpinning window. The unpinning window is contained in the vulnerable window but does not necessarily span its whole width. A–E mark different FFP pulse times. A leads to no phase resetting, whereas B, D and E cause the phase to reset. C corresponds to successful unpinning.

The kind of phase resetting found here is different from other studies such as Gray & Chattipakorn (2005). In their study, a spatially distributed phase θ(x) was defined throughout the domain and its shift, induced by global defibrillating shocks, was investigated. Type 0 resetting was able to alter the phase distribution around phase singularities in such a way that the spiral wave is destroyed (i.e. topological charge conservation is violated). In contrast, we have only defined the phase φ for ‘macroscopic’ spiral waves as a position around an obstacle. It is possible to condense information in this way because FFP only creates spiral waves that are captured by this global definition.2

The mechanism of phase resetting must be taken into account when considering pulse trains instead of single stimuli. As mentioned in §2, ρuw can be thought of as a success rate for hitting the unpinning window with a randomly timed pulse (as would be done in experiments where only the frequency, and not the phase, of the spiral is known). By choosing a suitable inter-pulse interval Tpacing (different from the spiral period Tspiral), one would try to distribute the pulses over the spiral phase and thus increase the success rate. With every pulse, the stimulus moves with respect to the spiral phase by Δφ=(Tpacing−Tspiral)/Tspiral. However, we have seen that φ does not necessarily evolve uniformly during the application of unsuccessful pulses. Rather, these pulses are potentially able to create a scenario of defined phase, namely φ≈0. In this way, an unsuccessful pulse, by resetting the phase, may imply the failure of the following stimulus.

Seen from a different angle, phase resetting may present an advantageous opportunity: in contrast to the usual experimental situation where at most the spiral frequency (most prominent frequency of the arrhythmia) is known, but not the phase, this mechanism could open a way to set the phase to a defined value as a basis for a more sophisticated, now phase-resolved, pacing algorithm. However, as seen in figure 11, the intervals in which phase resetting takes place can be fragmented across the possible stimulus phases, if the unpinning window does not span the whole vulnerable window.

5. Conclusion

We have demonstrated that, in the Barkley model, the vanishing unpinning window effect is a fundamental limitation of FFP. A comparison with the well-known vulnerable window reveals that this is a genuinely two-dimensional effect. We have found that spiral waves detach from the obstacle when the stimulus is inside the vulnerable window, but that they can reattach after a short time if the stimulus is outside the unpinning window. The one-dimensional view that is generally taken cannot account for the interaction of the detached vortex with the refractory tail of the spiral wave. The exact mechanism that determines the distance of detached waves from the obstacle boundary after an FFP stimulus still has to be understood. It may be that the model parameters alter the spatial structure (curvature, propagation velocity) of the spiral as well as the spatio-temporal dynamics of the depolarization induced by the FFP pulse such as to prevent the detached wave from moving far enough away from the obstacle. However, the confinement of the unpinning window to a phase interval smaller than the vulnerable window is not present for all parameters. For high excitation thresholds, the unpinning window spans the whole vulnerable window and thus the one-dimensional analogy is perfectly able to predict the size of the unpinning window. Interestingly, the behaviour at both ends of the unpinning window may be affected by the additional distance restriction (of the spiral tip from the obstacle) on the unpinning window, leading to scattered phase intervals in which phase resetting takes place.

Not unexpectedly, we found that higher field strengths and larger obstacles extend the range of excitability thresholds b in which unpinning is possible and widen the unpinning window ρuw.

The relationship of the unpinning window to the vulnerable window and the surrounding refractory and excitable periods on the obstacle’s boundary has been clarified, including possible consequences for controlling the phase of the spiral. Even in this simple model, the time intervals at which phase resetting takes place are not necessarily continuous. Further research is needed in order to deal with the positive and negative effects of phase resetting.

Acknowledgements

P.B. is grateful for support by the International Max Planck Research School for Physics of Biological and Complex Systems. A.S. acknowledges funding from the National Institutes of Health. U.P. acknowledges financial support from the Max Planck Society (research contract ‘Analyse biophysikalischer Daten’). S.L. and E.B. acknowledge support from the BMBF (FKZ 01EZ0905/6).

1

The simulations for determining the unpinning window were similar to those described here for the vulnerable window. For these simulations, the number of unpinning trials (thus determining the accuracy of ρuw) was N=96. Details can be found in the previous study (Bittihn et al. 2008).

2

In a way, this is also an effect of the low-energy approach via FFP: a defibrillating shock, because of its high energy, can change topology in the system so strongly that even phase singularities are destroyed, whereas a more subtle (sufficiently weak) FFP stimulus has to obey topological charge conservation and can only create two new defects with opposite charge.

One contribution of 10 to a Theme Issue ‘Experiments in complex and excitable dynamical systems’.

References

  1. Alonso S., Sagués F., Mikhailov A. S. Taming Winfree turbulence of scroll waves in excitable media. Science. 2003;299:1722–1725. doi: 10.1126/science.1080207. ( ) [DOI] [PubMed] [Google Scholar]
  2. Barkley D., Kness M., Tuckerman L. S. Spiral-wave dynamics in a simple model of excitable media: the transition from simple to compound rotation. Phys. Rev. A. 1990;42:2489–2492. doi: 10.1103/PhysRevA.42.2489. ( ) [DOI] [PubMed] [Google Scholar]
  3. Bittihn Ph., Luther G., Bodenschatz E., Krinsky V., Parlitz U., Luther S. Far field pacing supersedes anti-tachycardia pacing in a generic model of excitable media. New J. Phys. 2008;10:103012. doi: 10.1088/1367-2630/10/10/103012. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cherry E. M., Fenton F. H. Visualization of spiral and scroll waves in simulated and experimental cardiac tissue. New J. Phys. 2008;10:125016. doi: 10.1088/1367-2630/10/12/125016. ( ) [DOI] [Google Scholar]
  5. Exner D. V. Is antitachycardia pacing a safe and efficacious alternative to shocks for fast ventricular tachyarrhythmia treatment? Nature Cl. Pract. Card. Med. 2005;2:68–69. doi: 10.1038/ncpcardio0116. ( ) [DOI] [PubMed] [Google Scholar]
  6. Fast V. G., Rohr S., Gillis A. M., Kléber A. G. Activation of cardiac tissue by extracellular electrical shocks. Circ. Res. 1998;82:375–385. doi: 10.1161/01.res.82.3.375. [DOI] [PubMed] [Google Scholar]
  7. Fenton F. H., Luther S., Cherry E. M., Otani N. F., Krinsky V., Pumir A., Bodenschatz E., Gilmour R. F., Jr Termination of atrial fibrillation using pulsed low-energy far-field stimulation. Circulation. 2009;120:467–476. doi: 10.1161/CIRCULATIONAHA.108.825091. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fishler M. G. Syncytial heterogeneity as a mechanism underlying cardiac far-field stimulation during defibrillation-level shocks. J. Cardiovasc. Electrophysiol. 1998;9:384–394. doi: 10.1111/j.1540-8167.1998.tb00926.x. ( ) [DOI] [PubMed] [Google Scholar]
  9. Gray R. A., Chattipakorn N.2005Termination of spiral waves during cardiac fibrillation via shock-induced phase resetting Proc. Natl Acad. Sci. USA 1024672–4677( 10.1073/pnas.0407860102) [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Huyet G., Dupont C., Corriol T., Krinsky V. Unpinning of a vortex in a chemical excitable medium. Int. J. Bifurc. Chaos. 1998;8:1315–1323. doi: 10.1142/S0218127498001017. ( ) [DOI] [Google Scholar]
  11. Isomura A., Hoerning M., Agladze K., Yoshikawa K. Eliminating spiral waves pinned to an anatomical obstacle in cardiac myocytes by high-frequency stimuli. Phys. Rev. E. 2008;78:066216. doi: 10.1103/PhysRevE.78.066216. ( ) [DOI] [PubMed] [Google Scholar]
  12. Krinsky V. I., Agladze K. I. Interaction of rotating waves in an active chemical medium. Physica D. 1983;8:50–56. doi: 10.1016/0167-2789(83)90310-X. ( ) [DOI] [Google Scholar]
  13. Krinsky V., Plaza F., Voignier V. Quenching a rotating vortex in an excitable medium. Phys. Rev. E. 1995;52:2458–2462. doi: 10.1103/PhysRevE.52.2458. ( ) [DOI] [PubMed] [Google Scholar]
  14. Mines G. R. On circulating excitations in heart muscle and their possible relation to tachycardia and fibrillation. Trans. Roy. Soc. Can. 1914;8:43–52. [Google Scholar]
  15. Otani N. F., Mo A., Mannava S., Fenton F. H., Cherry E. M., Luther S., Gilmour R. F., Jr Characterization of multiple spiral wave dynamics as a stochastic predator–prey system. Phys. Rev. E. 2008;78:021913. doi: 10.1103/PhysRevE.78.021913. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pumir A., Krinsky V. Unpinning of a rotating wave in cardiac muscle by an electric field. J. Theor. Biol. 1999;199:311–319. doi: 10.1006/jtbi.1999.0957. ( ) [DOI] [PubMed] [Google Scholar]
  17. Pumir A., Nikolski V., Hörning M., Isomura A., Agladze K., Yoshikawa K., Gilmour R., Bodenschatz E., Krinsky V. Wave emission from heterogeneities opens a way to controlling chaos in the heart. Phys. Rev. Lett. 2007;99:208101. doi: 10.1103/PhysRevLett.99.208101. ( ) [DOI] [PubMed] [Google Scholar]
  18. Pumir A., Sinha S., Sridhar S., Argentina M., Hörning M., Filippi S., Cherubini Ch., Luther S., Krinsky V. Wave-train-induced termination of weakly anchored vortices in excitable media. Phys. Rev. E. 2010;81:010901. doi: 10.1103/PhysRevE.81.010901. ( ) [DOI] [PubMed] [Google Scholar]
  19. Ripplinger C. M., Krinsky V. I., Nikolski V. P., Efimov I. R. Mechanisms of unpinning and termination of ventricular tachycardia. Am. J. Physiol. Heart Circ. Physiol. 2006;291:H184–H192. doi: 10.1152/ajpheart.01300.2005. ( ) [DOI] [PubMed] [Google Scholar]
  20. Sepulveda N. G., Roth B. J., Wikswo J. P., Jr Current injection into a two-dimensional anisotropic bidomain. Biophys. J. 1989;55:987–999. doi: 10.1016/S0006-3495(89)82897-8. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Sobie E. A., Susil R. C., Tung L. A generalized activating function for predicting virtual electrodes in cardiac tissue. Biophys. J. 1997;73:1410–1423. doi: 10.1016/S0006-3495(97)78173-6. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Starmer C. F., Biktashev V. N., Romashko D. N., Stepanov M. R., Makarova O. N., Krinsky V. I. Vulnerability in an excitable medium: analytical and numerical studies of initiating unidirectional propagation. Biophys. J. 1993;65:1775–1787. doi: 10.1016/S0006-3495(93)81233-5. ( ) [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Takagi S., Pumir A., Pazó D., Efimov I., Nikolski V., Krinsky V. A physical approach to remove anatomical reentries: a bidomain study. J. Theor. Biol. 2004;230:489–497. doi: 10.1016/j.jtbi.2004.01.016. ( ) [DOI] [PubMed] [Google Scholar]
  24. Wiggers C. J., Wégria R. Ventricular fibrillation due to single localized induction and condenser shocks applied during the vulnerable phase of ventricular systole. Am. J. Physiol. 1940;128:500–505. [Google Scholar]
  25. Woods M. C., Sidorov V. Y., Holcomb M. R., Langrill Beaudoin D., Roth B. J., Wikswo J. P. Virtual electrode effects around an artificial heterogeneity during field stimulation of cardiac tissue. Heart Rhythm. 2006;3:751–752. doi: 10.1016/j.hrthm.2005.11.003. ( ) [DOI] [PubMed] [Google Scholar]

Articles from Philosophical transactions. Series A, Mathematical, physical, and engineering sciences are provided here courtesy of The Royal Society

RESOURCES