General Requirement for Harvesting Antennae at Ca²⁺ and H⁺ Channels and Transporters

Abstract

The production and dissipation of energy in cells is intimately linked to the movement of small molecules in and out of enzymes, channels, and transporters. An analytical model of diffusion was described previously, which was used to estimate local effects of these proteins acting as molecular sources. The present article describes a simple but more general model, which can be used to estimate the local impact of proteins acting as molecular sinks. The results show that the enzymes, transporters, and channels, whose substrates are present at relatively high concentrations like ATP, Na⁺, glucose, lactate, and pyruvate, do not operate fast enough to deplete their vicinity to a meaningful extent, supporting the notion that for these molecules the cytosol is a well-mixed compartment. One specific consequence of this analysis is that the well-documented cross-talk existing between the Na⁺/K⁺ ATPase and the glycolytic machinery should not be explained by putative changes in local ATP concentration. In contrast, Ca2⁺ and H⁺ transporters like the Na⁺/Ca2⁺ exchanger NCX and the Na⁺/H⁺ exchanger NHE, show experimental rates of transport that are two to three orders of magnitude faster than the rates at which the aqueous phase may possibly feed their binding sites. This paradoxical result implies that Ca2⁺ and H⁺ transporters do not extract their substrates directly from the bulk cytosol, but from an intermediate “harvesting” compartment located between the aqueous phase and the transport site.

Introduction

The flux of energy in a cell is closely associated with the cycling of molecules between subcellular compartments. One example is the stoichiometric relationship between the cycling of H⁺ across the inner mitochondrial membrane and the synthesis of ATP. Another example is the close relationship between the cycling of Na⁺ across the plasma membrane and the glycolytic machinery in astrocytes, which couples neuronal activity and local energy production in a phenomenon termed the Astrocyte-to-Neuron Lactate Shuttle (ANLS; Pellerin and Magistretti, 1994). Whereas the most recent formulation of the ANLS hypothesis does not require a strict relationship between Na⁺ cycling and glucose consumption (Pellerin et al., 2007), such fixed stoichiometry was proposed in a more quantitative model, which assumes that the Na⁺/K⁺ ATPase, the pump that extrudes Na⁺ out of the cell, is fed by glycolytic ATP and not by mitochondrial ATP (Hyder et al., 2006). However, as discussed below, it is not obvious how such exclusivity may be achieved. In a previous article, we presented a model based on Brownian diffusion which allowed quantitative analysis of the solvent region immediately adjacent to molecular sources, such as enzymes, pumps, transporters, and channels (Barros and Martínez, 2007). An outcome of that analysis was that these proteins are only capable of building up significant local domains if they have high turnover numbers and their products are present at low concentrations, which is often the case for Ca²⁺ and H⁺. When molecules are present at higher concentrations, the mixing effect of diffusion impedes the building up of significant local domains, even in the close vicinity of fast ion channels. Thus, for ATP, glucose, lactate, pyruvate, Na⁺, K⁺, and any other molecules present at bulk concentrations over the micromolar range, the cytosol was shown to behave as a well-mixed compartment.

Enzymes, pumps, transporters, and channels are also sinks, which will lower the local concentration of their substrates, perhaps affecting the activity of other proteins located nearby. With the aim of quantifying such depleted domains, we sought to extend the model presented earlier. In this paper, a more general model is presented that allows the mapping of both sources and sinks. For the Na⁺/K⁺ ATPase pump the rate of ATP extraction was found to be negligible compared to the rate of ATP delivery by diffusion from the bulk cytosol, resulting in failure of the pump to affect local ATP concentration. This result casts a doubt on the notion that the pump is preferentially fed by glycolysis and prompts the search for alternative mechanisms for the observed control of glycolysis by the sodium pump. A surprising outcome of the study is that for transporters and enzymes that take Ca²⁺ and H⁺, the observed turnover rates are much higher than the rates at which simple diffusion may replenish their vicinity, implying that these proteins do not extract the molecules directly from the aqueous phase. Possible mechanisms explaining the high turnover number observed for these proteins are discussed.

Theory

We consider a model where the molecules are assumed to diffuse following Brownian motion. In this way, the concentration u(r,t), at the point r, in a time t, is given by the standard diffusion equation

$$D{\nabla }^{2}u(r,t)=\frac{\partial u(r,t)}{\partial t},$$ (1)

where D is the diffusion coefficient. We are interested in the steady-state regime, where concentration does not change over time. In this case, the concentration is fixed by the Laplace equation

∇²u(r) = 0.

Now we consider a region bounded by two spherical surfaces having radius of a and b, with a < b (Figure 1A). We study two cases. In the first, named I, the surface of the inner sphere, with radius a, is the source of molecules that are evacuated through the surface of the outer sphere of radius b. Thus there is an outgoing flux. This case was previously analyzed in Barros and Martínez (2007) and here it is revisited. In the second case, named II, the inner surface corresponds to a sink, where the molecules coming from the outer surface are evacuated. This situation corresponds to an ingoing flux.

Figure 1.

A general diffusional model applicable to molecular sources and sinks. (A) Diffusion occurs in the steady-state between two concentric spheres, an inner sphere of radius a and an outer sphere of radius b. (B) Case I. The inner sphere acts as a source, determining a higher concentration of molecules locally. (C) Case II. The inner sphere acts as a sink, determining a lower concentration of molecules locally. Concentrations were calculated using Eq. 8, cases I and II, with a = 0.5 nm, b = 10 μm, D = 13 μm²/s, u = 6022 molecules/μm³ (10 μM), and q = 400 s⁻¹. The arrows indicate the direction of flux.

Assuming that the concentration is isotropic and hence depending only on the radial distance r ∈ [a,b], we write the Laplace equation using spherical coordinates

$$\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{du(r)}{dr}\right)=0.$$ (2)

This equation is easily solved, yielding

$$u(r)=C_1+\frac{C_2}{r}$$ (3)

as its general solution, where C₁ and C₂ are integration constants.

Since r²du/dr is a constant for this class of solutions, then flux of molecules is conserved and is proportional to −C₂. This result is a consequence of the isotropy of the model and it is not dependent on the boundary conditions imposed at a and b.

The integration constants C₁ and C₂ will be related to two observable quantities, flux and average concentration. With q as flux, the number of molecules per unit of time crossing a surface of radius r is

$$q=4\pi D{r}^2\left|\frac{du}{dr}\right|.$$ (4)

Thus, from Eqs 3 and 4 we obtain that

$$\left|C_2\right|=\frac{q}{4\pi D}.$$ (5)

In case I, the concentration u is a decreasing function of r, and C₂ must be a positive number, so C₂ = q/(4πD). On the other hand, for case II, C₂ = −q/(4πD) is a negative number since u is a increasing function of r.

An observable quantity is the average concentration. Its value is given by

$$\overline{u}=\frac{4\pi }{V}{\displaystyle \underset{a}{\overset{b}{\int }}u(r)r^{2}dr},$$ (6)

where V = 4π(b³ − a³)/3 is the volume enclosed between the two spheres. Replacing Eq. 3 into Eq. 6 gives

$$\overline{u}=C_1+\frac{3(a+b)}{2(a^2+ab+b^2)}{C}_2.$$ (7)

Expressions 5 and 7 allow us to set the integration constants C₁ and C₂ as functions of the observable data a, b, q, $\overline{u}$. Thus, we can write the concentration curve for each case

$$u(r)=\{\begin{array}{l}\overline{u}+\frac{q}{4\pi D}\left(\frac{1}{r}-\frac{3(a+b)}{2(a^2+ab+b^2)}\right)\text{\hspace{1em}case\hspace{0.17em}I},\\ \overline{u}-\frac{q}{4\pi D}\left(\frac{1}{r}-\frac{3(a+b)}{2(a^2+ab+b^2)}\right)\text{\hspace{1em}case\hspace{0.17em}II}.\end{array}$$ (8)

As expected, each concentration curve can be obtained from the other by interchanging a ↔ b and q ↔ −q. It is worth noticing that the concentration curves do not depend on the specific boundary conditions at either surface. Once the geometry is fixed (a and b), the concentration is defined by measurable quantities q, $\overline{u}$, and D. Examples of cases I and II for a specific set of parameters are illustrated in Figures 1B,C.

For clarity, each case will be discussed separately in the rest of this paper.

Case I: outgoing flux

In order to illustrate the strength of a domain it is useful to determine the ratio between the concentration at the source, u(a) and the average concentration $\overline{u}$ in the cell. We termed this ratio, Amplitude

$$\text{Amplitude}=\frac{u(a)}{\overline{u}}=1+\frac{2b^2-ab-a^2}{8\pi (a^2+ab+b^2)}\frac{q}{a\overline{u}D}.$$ (9)

Note that if b ≫ a,

$$\text{Amplitude}\sim 1+\frac{q}{4\pi a\overline{u}D}.$$ (10)

To quantify the size of a domain we define the parameter Extension as the distance from the source at which the concentration is twice the average

$$\text{Extension}=b{\left[\frac{4\pi Db\overline{u}}{q}+\frac{3b(a+b)}{2(b^2+ab+a^2)}\right]}^{-1}-a.$$ (11)

If b ≫ a,

$$\text{Extension}\sim b{\left[\frac{4\pi Db\overline{u}}{q}+\frac{3}{2}\right]}^{-1}-a.$$ (12)

The expressions for the Amplitude and Extension, given by Eqs 9 and 11, respectively, coincide exactly with those contained in Barros and Martínez (2007).

Case II: ingoing flux

In this case the sink is located at r = a and the Amplitude is giving by

$$\text{Amplitude}=\frac{u(a)}{\overline{u}}=1-\frac{2b^2-ab-a^2}{8\pi (a^2+ab+b^2)}\frac{q}{a\overline{u}D}.$$ (13)

Note that if b ≫ a,

$$\text{Amplitude}\sim 1-\frac{q}{4\pi a\overline{u}D}.$$ (14)

The Extension is now defined as the distance from the sink at which concentration is half of the average in the bounded region. Then,

$$\text{Extension}=b{\left[\frac{2\pi Db\overline{u}}{q}+\frac{3b(a+b)}{2(b^2+ab+a^2)}\right]}^{-1}-a.$$ (15)

If b ≫ a,

$$\text{Extension}\sim b{\left[\frac{2\pi Db\overline{u}}{q}+\frac{3}{2}\right]}^{-1}-a.$$ (16)

Results

The previous model considered steady-state Brownian diffusion between a small spherical source and a larger concentric sink representing the plasma membrane, at which efflux was assumed to be directly proportional to concentration (Barros and Martínez, 2007). Since then, we have realized that the boundary conditions built into the model were redundant, because flux and average concentration are sufficient to determine the concentration profile. Accordingly, the revised model is more economical, making no assumptions as to the laws governing flux at either boundary (see Theory), which allows using it to describe systems in which flux is centrifugal (from a central source) and also systems in which flux is centripetal (toward a central sink). Previously, two parameters were introduced to describe local domains around a central source: Amplitude, which is the ratio between the concentration of product in the immediate vicinity of the source and the average concentration of the cell, and Extension, defined as the distance from the source at which concentration is twice the average concentration. For a sink, the parameter Amplitude remains as previously defined, but the parameter Extension is now defined as the distance from the sink at which concentration is half of the average concentration in the compartment.

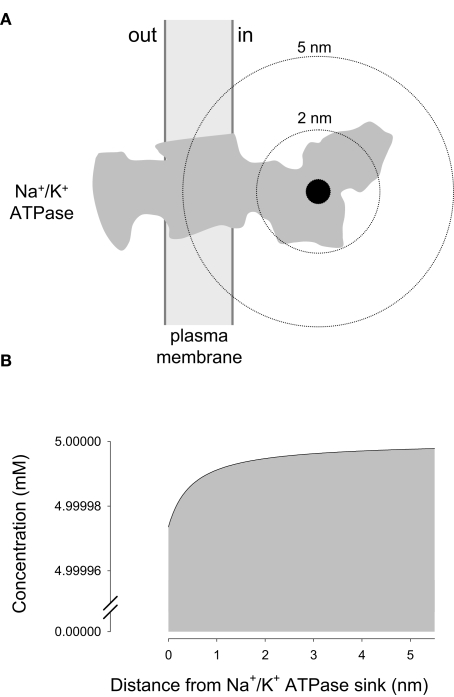
For an inner source, the equations and therefore the results obtained with the new model were identical to those reported earlier and will not be discussed further. For an inner sink, the focus of the current investigation, the model was first applied to the Na⁺/K⁺ ATPase pump, a major ATP sink that has been proposed to control glycolysis by modifying local ATP levels. However, the diffusional model showed that the impact of the sodium pump on local ATP concentration is negligible (Figure 2). The calculated Amplitude of the “depleted” ATP domain around the sodium pump was 0.999995, meaning that at its binding site, the concentration of ATP is 4.999975 mM, a mere 25 nM lower than in the bulk cytosol. We reckon that no enzyme may possibly distinguish between 4.999975 and 5 mM, so whatever mechanism is involved in the cross-talk between the sodium pump and the glycolytic machinery, it is unlikely to involve local ATP. Another way to visualize this is to compare the actual rate of ATP extraction by the pump (48 s⁻¹) with the maximum rate of bulk ATP delivery to the pump (9 × 10⁶ s⁻¹), calculated by forcing the sink concentration at 0 (Table 1). Similar results were obtained for glucose, pyruvate, and lactate, which are present in the cytosol at high concentrations and are taken up by slow enzymes and transporters (Table 1). These results support the view that for these compounds, the aqueous phase of the cytosol of compact cells is a well-mixed compartment devoid of significant concentration gradients.

Figure 2.

Negligible local ATP depletion caused by the Na⁺/K⁺ ATPase. (A) A sink with a radius of 0.5 nm is shown in black, overimposed on the gray silhouette of the Na⁺/K⁺ ATPase, adapted from Morth et al. (2007). (B) ATP concentrations in the immediate vicinity of the Na⁺/K⁺ ATPase were calculated using Eq. 8, case II, with the following values: a = 0.5 nm, b = 10 μm, D = 500 μm²/s, u = 5 mM, and q = 48 s⁻¹.

Table 1.

Characteristics of concentration domains at some molecular sinks.

Molecule		Diffusion coefficient (D; μm2 s−11)		Average concentration (u; mM)NB		Sink		Observed turnover number (q; s−11)		Amplitude		Maximum supply capacity (s−11)
ATP		500 (de Graaf et al., 2000)		5		Na+/K+ ATPase		48 (Lupfert et al., 2001)		0.9999		9.0 × 106
Glucose		500 (Vega et al., 2003)		1		GLUT1		187 (Barros et al., 2007)		0.9999		1.8 × 106
Pyruvate		120 (Pfeuffer et al., 2000)		0.1		LDH		269*		0.9941		4.5 × 104
Lactate		120 (Pfeuffer et al., 2000)		1.25		LDH		269*		0.9995		5.6 × 105
		120 (Pfeuffer et al., 2000)		1.25		MCT		85 (Ovens et al., 2010)		0.9998		5.6 × 105
Na+		1160 (Goodman et al., 2005)		10		Na+/K+ ATPase		144 (Lupfert et al., 2001)		0.9999		4.3 × 107
Ca2+		13 (Allbritton et al., 1992)		10−4		NCX		5000 (Shigekawa and Iwamoto, 2001)		<0		4.9
		13 (Allbritton et al., 1992)		10−4		PMCA		149*		<0		4.9
H+		37.8 (Vaughan-Jones et al., 2002)		4 × 10−5		NHE		2000 (Dixon et al., 1987)		<0		5.7
		37.8 (Vaughan-Jones et al., 2002)		4 × 10−5		MCT		85 (Ovens et al., 2010)		<0		5.7
		37.8 (Vaughan-Jones et al., 2002)		4 × 10−5		PMCA		298*		<0		5.7
		37.8 (Vaughan-Jones et al., 2002)		4 × 10−6		cytochrome oxidase		500*		<0		0.5

Domains were estimated assuming a sink radius a of 0.5 nm and a cell radius b of 10 μm, with the source located at the cell surface. NB, for simplicity concentration (u) is given in millimolar but note that unit consistency requires u to be entered in the equations as molecules/μm³ (and distances in micrometers). Na⁺/K⁺ ATPase (EC 3.6.3.9); GLUT1, glucose transporter isoform 1; LDH, lactate dehydrogenase (EC 1.1.1.27); MCT, proton-coupled monocarboxylate transporter; NCX, Na⁺/Ca²⁺ exchanger; PMCA, plasma membrane Ca²⁺ ATPase (EC 3.6.3.8); cytochrome oxidase (EC 1.9.3.1). Maximum supply capacities were estimated with Eq. 8, case II, by setting sink concentration equal to 0.

*BRENDA database, University of Cologne, Germany. The highest turnover numbers for mammalian enzymes are given.

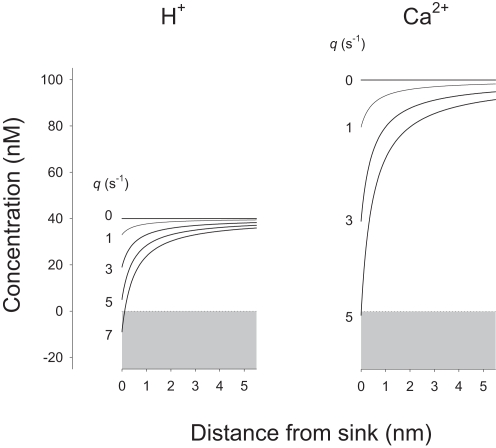
For substrates present at much lower concentration such as Ca²⁺ and H⁺, which in addition present lower diffusion coefficients, uptake by enzymes and transporters resulted in substantial local depletion. Figure 3 shows that for these ions, small fluxes in the order of few s⁻¹ produced a strong effect. The cytosolic diffusion coefficient for H⁺ is higher than that for Ca²⁺ by a factor of 3 but the H⁺ concentration is lower by a factor of 2.5, resulting in a similar behavior for both ions. By solving Eq. 8, case II for a sink concentration of 0, i.e., affording the maximum possible gradient between bulk and sink, the maximum rate of supply from bulk cytosol to H⁺ and Ca²⁺ sinks was estimated to be 5.7 and 4.9 s⁻¹, respectively. However, these values are much lower than the turnover rates measured for many transporters and enzymes, which are 149 s⁻¹ for the plasma membrane Ca²⁺ ATPase, 85 s⁻¹ for the monocarboxylate transporter MCT, 2000 s⁻¹ for the Na⁺/H⁺ exchanger NHE, and 5000 s⁻¹ for the Na⁺/Ca²⁺ exchanger NCX (Table 1). Reflecting the paradox, the calculated Amplitude values for Ca²⁺ and H⁺ at the cytosolic mouth of their transporters were all found to be negative (Table 1), showing that the observed turnover rate may only be sustained by a negative concentration at the sink, a physical impossibility. In summary, the model demonstrates that these transporters extract molecules from the cytosol at rates well above the capacity for simple diffusion to replenish their immediate vicinity.

Figure 3.

H⁺ and Ca²⁺ sinks can only sustain very small fluxes. H⁺ and Ca²⁺ concentrations in the immediate vicinity of their sinks were calculated at increasing fluxes (q values from 0 to 7 s⁻¹), using Eq. 8, case II, and the following values: a = 0.5 nm, b = 10 μm, D = 37.8 μm²/s (H⁺), and 13 μm²/s (Ca²⁺), u = 40 nM (H⁺, pH 7.4), and 100 nM (Ca²⁺). Note that negative concentrations would be required at the H⁺ and Ca²⁺ sinks to sustain fluxes greater than 6 and 5 s⁻¹.

As stated by Eq. 14, only four parameters affect the Amplitude of the local concentration domain: flux, diffusion coefficient, size of the sink, and average concentration. The values of flux and diffusion coefficient are well established and allow little room for speculation. A larger sink would increase the area available for capture and thus decrease the steepness of the concentration gradient required to drive a given flux. Up to this point, we have considered a sink of 1 nm diameter, a presumably reasonable estimate given that within this volume several H⁺ or Ca²⁺ molecules can fit comfortably, even with their solvation layer. The size of the binding vestibules in transporters is typically in the range of 1–2 nm so it seems unlikely that a significant error would be introduced here. But even if the domains are recalculated with a larger, much less likely sink of 4 nm diameter, the value of Amplitude would still be negative (e.g., −86 for the NHE). Expressing this in terms of the maximum flux calculated at zero concentration, a H⁺ sink of 4 nm diameter may only drive up to 22 s⁻¹, well short of the 2000 s⁻¹ reported for the NHE (Table 1).

Local production by molecular sources may increase H⁺ and Ca²⁺, so that the discrepancy between observed flux and modeled flux may in principle be due to transporters not extracting their substrates from the bulk cytosol but from local cytosolic domains produced by a neighboring source. However, this explanation does not seem likely, as we can calculate from Eq. 8 that sustaining the 5000 s⁻¹ reported for NCX would require a local Ca²⁺ concentration of at least 1 mM. A Ca²⁺ channel may produce such a strong domain (Eq. 10), but only while open, and Ca²⁺ is of course efficiently extruded by the NCX after channels have closed and local Ca²⁺ is down to the micromolar level. At 10 μM, the maximum rate of Ca²⁺ extrusion can be calculated at 490 s⁻¹, which is less than 10% of the observed rate for NCX. At 200 nM, a concentration at which extrusion is catalyzed by the plasma membrane Ca²⁺ pump, the maximum rate of calcium delivery to the pump is 9 s⁻¹, short of the reported turnover number of 149 s⁻¹. A similar conclusion may be reached for H⁺ handling. For example, maintaining a turnover rate of NHE at 2000 s⁻¹ would require a local pH lower than 5, which is beyond the capabilities of the fastest H⁺-producing transporters and enzymes. These results show that the high rates observed for Ca²⁺ and H⁺ extrusion can not be solely explained by the participation of local sources.

The above analysis has assumed a spherical geometry, which allows to derive and to solve simple equations for diffusion and fits well to soluble enzymes. For membrane proteins, the presence of membrane invaginations and small processes introduces a degree of uncertainty about local geometry. However, it can be shown that this is not a significant factor. For example, an alternative geometry for a membrane protein may be a hemisphere, where the protein “sees” the cytosol via a solid angle of 2π instead of 4π. Therefore to sustain a given flux, a hemisphere needs to double the gradient at all points and also the difference between 1 and the Amplitude. As a result, the Amplitude of the ATP gradient at the sodium pump would decrease slightly from 0.999995 to 0.999990, whereas the maximum theoretical fluxes at Ca²⁺ and H⁺ sinks would be halved, e.g., from 6 to 3 s⁻¹.

Discussion

Our previous study showed how the steady-state production of molecules by small sources such as enzymes, transporters, and channels determines in some cases the creation of strong local concentration domains and in other cases does not. The aim of the present work was to investigate the mirror problem of how removal of molecules by these proteins may lead to local depletion of substrates. This is a relevant problem for neuroenergetics, for many of the proteins involved in energy transduction are often kept in close proximity to other proteins by lipid microdomains or by protein–protein interactions and may be affected by local concentration changes. To be able to simulate local effects of molecular sinks, the previous model was developed into a general analytical tool that is easily accessible to non-mathematicians. Using it, we hope that biochemists and cell physiologists will be able to predict whether their proteins of interest are or are not able to generate local concentration domains and whether harvesting antennae are to be searched for in their vicinity.

Slow molecular sinks can not generate concentration domains for abundant molecules like ATP

The application of the model to several examples of transporters and channels that move abundant molecules like ATP, glucose and lactate, showed that these proteins can not deplete their vicinity to a meaningful extent, complementing the previous observation that they can not generate enriched domains either. This means that the cytosol of a compact cell will not sustain concentration gradients for these substances, not even transient ones, and that the observed modulatory effect of enzymes and transport proteins that handle abundant molecules is not to be explained by hypothetic substrate or product domains. A recent study has used Brownian Dynamics to propose “channeling by proximity” between a molecular source and a neighboring sink (Bauler et al., 2010), an analysis that is fully consistent with our model for molecules whose bulk concentration is very low, i.e., in the nanomolar range or lower. But at micromolar concentrations or higher, the impact of local sources becomes irrelevant because there are so many more molecules that arrive from the bulk. In view of our previous work (Barros and Martínez, 2007), it has been argued that metabolite microdomains may still exist if local diffusion were much slower than expected (Saks et al., 2008), but for this to happen, local diffusion coefficients around each source and sink would have to be four to six orders of magnitude lower than actually measured in the bulk cytosol, and there is no theory on how this may occur.

In this article, the case of the Na⁺/K⁺ ATPase pump was analyzed in more detail because of previous evidence of a functional link between the pump and glycolysis, e.g., inhibition of the pump with ouabain or stimulation with intracellular Na⁺ resulting in corresponding changes in glycolytic rate. Classical test-tube biochemistry had shown that several glycolytic enzymes are modulated by ATP and there is evidence in erythrocytes that glycolytic enzymes are located in close proximity to the plasma membrane, near the Na⁺/K⁺ ATPase (Campanella et al., 2005), so it has been assumed that local ATP depletion by the pump may be the mechanism whereby glycolysis is modulated. Extrapolated to astrocytes, this assumption was pivotal for one of the models of metabolic coupling in the brain (Hyder et al., 2006). However, the current analysis has concluded that the Na⁺/K⁺ ATPase may hardly affect local ATP, leaving open the question of the mechanism linking the pump and glycolysis. One theoretical possibility, which we do not favor, is that the sodium pump is not fed by bulk ATP but from a preferential source. In an extreme form, metabolic channeling, one or both ATP-producing enzymes of the glycolytic pathway, phosphoglycerate kinase and pyruvate kinase, would pass ATP directly to the pump in a way that remains hidden from the solvent and equally critically, in a way that the abundant bulk ATP does not have access to the ATP binding site of the pump. Metabolic channeling is a controversial issue but has been demonstrated for selected examples like bacterial tryptophan synthase, where an indole molecule is passed between two adjacent proteins through an intermolecular hydrophobic tunnel (Miles, 2001). A less extreme scenario is that the pump extracts its ATP from another compartment and not directly from the bulk cytosol. For instance in ghost erythrocytes, the sodium pump has been proposed to be fed by a membrane-associated ATP pool that is in turn replenished by pyruvate kinase (Hoffman et al., 2009). However, the crystal structure of the pump shows the ATP binding site as located far away from the plasma membrane (see Figure 2). Both metabolic channeling and strict reliance on a membrane ATP pool seem unlikely to us because a complex sieve mechanism would have to be in place to stop bulk ATP from reaching the pump while allowing entry of Na⁺, exit of K⁺ and exit of inorganic phosphate, which is not a substrate for the glycolytic enzymes that produce ATP. Such sieve mechanism would have to be restricted to some cell types because in neurons, kidney cells and other oxidative cells where the sodium pump uses over 50% of the ATP, glycolysis generates less than 10% (Erecinska and Dagani, 1990). In these oxidative cells most ATP used by the pump is generated in mitochondria, which are not near the plasma membrane, meaning that ATP must necessarily go through the bulk cytosol before reaching the putative membrane pool. ATP hydrolysis produces ADP, which may be converted to AMP by adenylate kinase. Both AMP and ADP are present at much lower concentrations than ATP and therefore their production by the pump is expected to have a larger impact on local concentrations, but still, this is not sufficient to generate a domain. Considering a bulk ADP concentration of 1 μM, a D value of 500 μm² s⁻¹ and a source radius of 0.5 nm, the Amplitude of the ADP domain at the sodium pump calculated with Eq. 9 is only 1.02, and without a local ADP domain there will be no AMP domain either. In the absence of ATP, ADP and AMP nanodomains, the possibility remains that regulation of glycolysis may be a global phenomenon, a notion consistent with the observation that sodium pump-mediated activation of astrocytic glycolysis that occur during glutamate-driven Na⁺ uptake is accompanied by a global decrease in ATP concentration, estimated from free magnesium measurements (Magistretti and Chatton, 2005). Alternatively, the effect of the sodium pump over glycolysis may not be mediated by adenine nucleotides. The sodium pump forms part of a large macromolecular complex and its activity can affect the function of other membrane and cytosolic proteins through protein–protein interaction, a notable example of which is the astrocytic Na⁺-glutamate cotransporter (Rose et al., 2009). Some of these interactions lead to activation of calcium signaling and phosphorylation cascades that may eventually affect the metabolic machinery (Xie and Askari, 2002; Lingrel, 2010).

Diffusion from the bulk cytosol fails to account for the rates measured at h+ and ca2+ sinks

Having discarded all four parameters, flux, diffusion coefficient, size of sink, and average concentration, as likely explanations to account for the discrepancy between local diffusion and the observed high rates of Ca²⁺ and H⁺ extrusion, it can be concluded that these transporters do not extract their substrates directly from the aqueous phase. This means that another kinetic compartment needs to be located between the aqueous phase and the binding site of the transporters, a compartment that has to be able to exchange with the aqueous phase through a surface much larger than that of the binding site and be able to exchange with the transport site at rates higher than those expected from simple diffusion. Previously, the concept of a “proton-harvesting antenna” was advanced to explain the high turnover rate of mitochondrial cytochrome oxidase (Adelroth and Brzezinski, 2004; Branden et al., 2006). The term antenna, i.e., a device that increases the area of harvesting, seems appropriate to term the kinetic compartment predicted by the present analysis to exist at the binding site of Ca²⁺ and H⁺ transporters (Figure 4). Using the current model it can be appreciated that cytochrome oxidase represents an extreme example of limited substrate supply, for the maximum delivery rate calculated by assuming a mitochondrial pH of 8.4 and a diffusion coefficient similar to that in the cytosol, is only 0.5 s⁻¹, whereas the measured rate is 1000-fold higher! (Table 1). Antennae do not only allow faster extrusion but also faster uptake, minimizing the build up of substrate in the aqueous phase immediately adjacent to a source. Moreover, an antenna may allow molecules to circulate between source and sink with minimal effect on the bulk concentration (Heberle et al., 1994; Branden et al., 2006).

Figure 4.

Harvesting antennae can explain high rates of H⁺ and Ca²⁺ extrusion. The standard model of transport assumes that molecules reach their binding sites by random diffusion through the aqueous phase. However, because of the low prevailing concentrations of H⁺ and Ca²⁺, the probability of this occurring is too small to sustain the observed rates of translocation. A harvesting antenna increases the binding probability, allowing the aqueous phase to feed the transporter at high rates.

Possible candidates for harvesting antennae are the Ca²⁺ and H⁺ binding sites present in membrane proteins and lipids, particularly at the inward-facing side of the plasma membrane. To contribute to an antenna, these sites would have to be in sufficient proximity to the transport site helping to bridge the electrostatic gap between the transport site and the rest of the antenna. Thus, the transport sites would exchange ions with the antenna, which in turn would harvest their replacement from the aqueous phase due to its large area of exchange. Distribution of ions within the antenna at rates much higher than that of simple diffusion is thought to be mediated by electrostatic repulsion due to overlapping coulomb cages, analogous of the way in which motion is transmitted in the Newton's cradle and require typical distances of <1 nm between binding sites within the antenna. A specific molecular candidate to participate in one antenna has been suggested by a recent study of MCT1 expressed in frog oocytes, which found that the rate of H⁺ permeation through the transporter is greatly dependent on the presence of carbonic anhydrase, an abundant enzyme that is found in close proximity to the plasma membrane. The key observation of the oocyte study was that the effect of carbonic anhydrase on MCT turnover is unrelated to its enzyme activity but was critically dependent on its capacity to bind H⁺ (Becker and Deitmer, 2008). Carbonic anhydrase was therefore proposed to be part of the H⁺ harvesting antennae of the MCT.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.