External Urethral Sphincter Motoneuron Properties in Adult Female Rats Studied In Vitro

Abstract

The external urethral sphincter (EUS) muscle plays a crucial role in lower urinary tract function: its activation helps maintain continence, whereas its relaxation contributes to micturition. To determine how the intrinsic properties of its motoneurons contribute to its physiological function, we have obtained intracellular current-clamp recordings from 49 EUS motoneurons in acutely isolated spinal cord slices from adult female rats. In all, 45% of EUS motoneurons fired spontaneously and steadily (average rate = 12–27 pulses/s). EUS motoneurons were highly excitable, having lower rheobase, higher input resistance, and smaller threshold depolarization than those of rat hindlimb motoneurons recorded in vitro. Correlations between these properties and afterhyperpolarization half-decay time are consistent with EUS motoneurons having characteristics of both fast and slow motor unit types. EUS motoneurons with a slow-like spectrum of properties exhibited spontaneous firing more often than those with fast-like characteristics. During triangular current ramp-induced repetitive firing, recruitment typically occurred at lower current levels than those at derecruitment, although the opposite pattern occurred in 10% of EUS motoneurons. This percentage was likely underestimated due to firing rate adaptation. These findings are consistent with the presence of a basal level of persistent inward current (PIC) in at least some EUS motoneurons. The low EUS motoneuron current and voltage thresholds make them readily recruitable, rendering them well suited to their physiological role in continence. The expression of firing behaviors consistent with PIC activation in this highly reduced preparation raises the possibility that in the intact animal, PICs contribute to urinary function not only through neuromodulator-dependent but also through neuromodulator-independent mechanisms.

INTRODUCTION

The external urethral sphincter (EUS) muscle performs the critical function of restricting urinary flow through the urethra during continence and permitting flow during micturition. Much prior research has focused on how the brain controls spinal cord networks that operate this muscle and coordinate its function with the other muscles important in bladder control and on how peripheral input contributes to the control of lower urinary tract function (de Groat 2006).

A full understanding of how descending and sensory inputs contribute to control of urethral function requires knowledge of how the EUS motoneuron integrates and transforms supraspinal motor commands, sensory inputs, and spinal interneuronal activity into sphincter muscle activity. The intrinsic properties of EUS motoneurons are similar in many ways to the much more extensively studied hindlimb motoneurons, but with specific differences that are consistent with their physiological function (Hochman et al. 1991; Sasaki 1991). EUS motoneurons are more readily excited by current injection than are hindlimb motoneurons. This probably supports their role of providing tonic activation of the EUS muscle during continence. Recently, EUS motoneurons have been found to exhibit self-sustained repetitive firing that can be terminated by hyperpolarizing synaptic input, which is consistent with the activation of persistent inward currents (PICs) (Paroschy and Shefchyk 2000). These conductance mechanisms are crucial for expression of normal repetitive firing behavior in hindlimb motoneurons (Heckmann et al. 2005). Their presence in EUS motoneurons suggests their participation in maintaining continence (Paroschy and Shefchyk 2000; Shefchyk 2006).

The aforementioned studies of EUS motoneuron properties have all been performed in cats. An increasing number of studies of lower urinary tract function are being performed in rats, both with and without spinal cord injury. The pattern of EUS muscle activation during micturition differs between cats (and humans) and rats (de Groat et al. 2001; Kruse and de Groat 1993; Maggi et al. 1986). Because current knowledge of the intrinsic properties of EUS motoneurons is limited to cats (Hochman et al. 1991; Sasaki 1991), identification of EUS motoneuron properties in rats will be important for interpretation of the results of studies of urinary function in this species. This information will become increasingly important as the use of rats in experimental models of spinal cord injury increases.

To address the lack of electrophysiological information about rat EUS motoneurons, we have used intracellular recording to study the intrinsic properties of EUS motoneurons in spinal slices prepared from adult rats. This work takes advantage of a new spinal cord slice preparation that allows study of viable spinal motoneurons from adult rats (Carp et al. 2008b). Because supraspinal and segmental inputs to motoneurons in this preparation are largely removed, the EUS motoneurons can be studied in relative isolation from synaptic and neuromodulatory influences. Portions of this work were reported previously (Carp et al. 2007, 2008a).

METHODS

Spinal slice preparation

All animal procedures were in accord with the Guide for the Care and Use of Laboratory Animals of the Institute of Laboratory Animal Resources, Commission on Life Sciences, National Research Council (National Academy Press, Washington, DC, 1996), and Department of Health, Education, and Welfare Publication No. 0309-05377-3, Guide for the Care and Use of Laboratory Animals, and were approved by the Wadsworth Center IACUC.

Spinal slices were prepared from 26 female rats (Sprague–Dawley, 146–275 g, 7–14 wk) using the method of Carp et al. (2008b). Briefly, rats were anesthetized with a ketamine–xylazine mixture (80 and 10 mg/kg, administered intraperitoneally, respectively) and placed in a prone position to permit a dorsal laminectomy. After rotating the rats to a supine position, they were perfused through the heart for 1 min with 100 ml of 2–4°C artificial cerebrospinal fluid (aCSF) in which NaCl had been replaced with sucrose (sucrose-aCSF) that contained (in mM): sucrose, 212.5; KCl, 3.5; NaHCO₃, 26; MgSO₄, 1.3; KH₂PO₄, 1.2; MgCl₂, 2.0; CaCl₂, 1.2; and glucose, 10 (298 mOsm). Rats received 100% oxygen by mask throughout the laminectomy and up until the start of the perfusion.

After a dorsal laminectomy, the spinal cord was excised and transferred to a dissection dish filled with 2–4°C sucrose-aCSF. The dura was removed and the spinal roots were trimmed short. The spinal cord was embedded in low-gelling-temperature agarose, glued to the platform of a vibrating microtome (Vibroslice, Campden), and cut into 380- to 450-μm-thick (typically 400 μm) transverse sections in 2–4°C sucrose-aCSF. Immediately after cutting, each slice was incubated for 60 s in polyethylene glycol (PEG, 30% wt/vol in distilled water; Sigma) and was then rinsed for 1 min in normal aCSF at 34–36°C twice immediately prior to a 1-h incubation at 34–36°C in normal aCSF, which consisted of (in mM): NaCl, 125; KCl, 3.5; NaHCO₃, 26; MgSO₄, 1.3; KH₂PO₄, 1.2; CaCl₂, 2.4; and glucose, 10 (294 mOsm). The slices were then transferred to holding chambers with mesh floors with normal aCSF at 29–31°C and remained there until used for recordings. All solutions (except PEG) were bubbled with 95% O₂-5% CO₂.

Motoneuron recording and data analysis

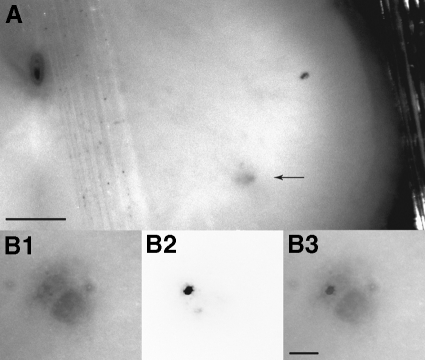
Intracellular current-clamp recordings were made with sharp electrodes in transverse slices of lumbar spinal cord from these adult rats. Only cells with action potential amplitudes ≥60 mV were included in the data pool. In three cells, stimulation of their ventral root stub elicited antidromic action potentials, thus positively identifying these cells as motoneurons. Although ventral root stimulation was not performed routinely, the other recorded cells were almost certainly motoneurons because they were located in lateral gray matter where motoneurons are expected to be found and because their input resistances were all lower than the values expected for spinal interneurons capable of repetitive firing (Theiss and Heckman 2005). Furthermore, recordings were restricted to the three to four slices that exhibited characteristic regions in the lateral gray matter of the ventral horn that appear darker than the adjacent gray matter under oblique illumination (arrows in Fig. 1A). In female rats, these areas contain primarily (if not exclusively) the cell bodies of EUS motoneurons and their dendritic bundles (McKenna and Nadelhaft 1986; Schroder 1980). We confirmed this localization by injecting choleratoxin conjugated to fluorescein isothiocyanate (FITC) into the EUS muscle to retrogradely label EUS motoneurons in three rats. All retrogradely labeled motoneurons were in the dorsolateral nucleus (e.g., Fig. 1, B1–B3). No labeled EUS motoneurons were found outside of the dorsolateral cell group, nor have any motoneurons innervating hindlimb muscles been reported to be in this region (Carp et al. 2008b; Nicolopoulos-Stournaras and Iles 1983; Swett et al. 1986).

Fig. 1.

Transverse 400-μm-thick slices (presumably at L5–L6) from unfixed spinal cord of a 12-wk-old female rat. A: image captured using a combination of trans- and oblique illumination to maximize contrast between the dorsolateral cell group (arrow) that contains the external urethral sphincter (EUS) motoneurons (McKenna and Nadelhaft 1986; Schroder 1980) and the rest of the ventral gray matter. The vertically oriented line adjacent to the central canal in the top left corner is an elastic band that secures the slice. Scale bar: 250 μm. B: high-magnification image from another slice showing the dorsolateral cell group (B1), a motoneuron retrogradely labeled by transurethral injection of choleratoxin conjugated to Alexa 594 (B2, in which the image intensity has been inverted), and the images in B1 and B2 superimposed (B3). Scale bar: 50 μm.

Each slice to be studied was transferred to the recording chamber, held on a mesh platform by harp-shaped silver wires with elastic threads, and superfused with normal aCSF at 3 ml/min at 29–31°C. Intracellular impalements were made with 10–20 MΩ rapidly tapering electrodes filled with 3 M potassium acetate and 0.01 M KCl. Data were recorded (Dagan 8700), low-pass filtered at 3–10 kHz, sampled at 6–20 kHz, and stored using WinWCP (Strathclyde Electrophysiology Software), and were analyzed using custom software.

Input resistance and membrane time constant were determined from responses to hyperpolarizing 40-ms current pulses. Input resistance was calculated from the slope of the relationship between current pulse amplitude (six different levels) and the maximum voltage deflection. The depolarizing sag in membrane potential that occurred during hyperpolarizing pulses was quantified as the difference in amplitude between the maximum hyperpolarizing membrane potential deflection and that during the last 5 ms of the current pulse, expressed as a percentage of the maximum response. Time constant was calculated by curve fitting the response to the largest hyperpolarizing current pulse (−0.9 nA).

Action potentials were elicited by short (0.6- to 1.0-ms) depolarizing current pulses and/or by antidromic activation. Action potential amplitude was calculated as the difference between the peak of the action potential and the average resting potential during the 5 ms prior to stimulation. Afterhyperpolarization (AHP) duration, amplitude, and half-decay time (i.e., time from AHP maximum amplitude until recovery to half-maximal amplitude) were determined from action potentials elicited by the short current pulses.

To assess excitability during elicitation of individual action potentials, 40-ms depolarizing current pulses were used to determine rheobase (i.e., current at which probability of eliciting a single action potential is 50%). The difference in amplitude between action potentials elicited by these long pulses and short depolarizing pulses described earlier determined the depolarization threshold (i.e., the depolarization from resting potential needed to reach the voltage threshold for action potential initiation; Carp 1992; Gustafsson and Pinter 1984b). Voltage threshold was calculated as the sum of the depolarization threshold and the resting membrane potential.

Slow triangular current ramps provide information about the initiation (recruitment) and termination (derecruitment) of repetitive firing and the relationship between injected current and firing rate (i.e., the frequency–current [F–I] relationship). During the ramps, current increased at a constant rate (0.2–2.0 nA/s) for 5 s and then decreased at the identical but oppositely signed rate for another 5 s. The triangular ramps were superimposed on a rectangular current offset starting 100 ms before and ending 100 ms after the current ramps. The net current produced by summation of the triangular ramp current and the rectangular current pulse determined the duration and magnitude of firing. Excitability during current ramps was assessed by the instantaneous firing rates and currents at recruitment and derecruitment and by the slope of the F–I relationship on the ascending limb of the ramp calculated between 10 and 90% of the time from firing onset to maximum current (ramp F–I slope).

Because PICs activate slowly on depolarization (between tens and hundreds of milliseconds), their influence on repetitive firing is expected to increase gradually during the ascending ramp. The contribution of PIC activation to repetitive firing behavior during ramps was assessed by determining the instantaneous firing rates and currents at recruitment and derecruitment and then calculating their difference [i.e., derecruitment current or firing rate minus recruitment current or firing rate (ΔI or ΔF, respectively)]. Negative values of ΔI and ΔF indicate PIC activation by the end of repetitive firing that was more pronounced than that occurring at the onset of firing (Heckmann et al. 2005). Average ΔI values more negative than twice the current noise (defined as the SD of the baseline current; ∼0.01 nA) below the baseline current level identified cells with firing behavior consistent with PIC expression.

Bennett et al. (2001) reported that repetitive firing behavior is sensitive to the magnitude of the current injected. The relationship between ΔI and injected current magnitude is described in the following text (see Long current ramps in results). For summary data presented in the tables, we focused quantitative analyses of responses to ramps on the four trials with the lowest current amplitudes tested in each motoneuron, to minimize the influence of differences in the magnitude of injected current ramps.

Repetitive firing was also characterized using 4-s rectangular current pulses. The reduction in firing rate that occurred during the constant-current pulses (i.e., rate adaptation) was quantified as the average firing rate during the final second of the 4-s pulse expressed as a percentage of the instantaneous rate calculated for the second interspike interval (ISI) after current onset.

EUS motoneuron labeling

Three additional female Sprague–Dawley rats received transurethral injections of cholera toxin subunit-B conjugated to FITC or Alexa 594 (2 μg/μl solution in sterile saline; Invitrogen) to retrogradely label the EUS motoneuron pool. Under isoflurane anesthesia, the urethra was catheterized with PE-50 tubing. The EUS muscle was injected (four to six sites, 0.5–1.0 μl per site) by inserting a 31-gauge needle attached to a 10-μl syringe into the urethra, using the catheter as a guide, and then angling the needle laterally at about 45° and inserting it into the EUS muscle. Each site was injected slowly and the needle was kept in place for ≥1 min after each injection and then the catheter was slowly withdrawn. Four or 10 days after injection, spinal slices were prepared as described earlier and imaged with a compound upright microscope.

Statistics

Statistical analyses of continuous variables between EUS and other motoneurons used the Student's t-test. Relationships between continuous variables were assessed by linear regression. Dependencies of motoneuron properties on animal age were assessed by linear regression of continuous variables (averaged for each animal) on age. Comparisons involving numbers of motoneurons expressing different behaviors (e.g., spontaneous firing vs. quiescent) were made using chi-square tests.

No Bonferroni corrections were made for performing multiple statistical tests because of the extensive covariation among the factors tested (e.g., see relationships between AHP half-decay time and input resistance, threshold depolarization, and rheobase in Fig. 8). This would result in an overly conservative P value criterion for significance due to violation of the assumption that the tests performed are independent (Souba and Wilmore 2001).

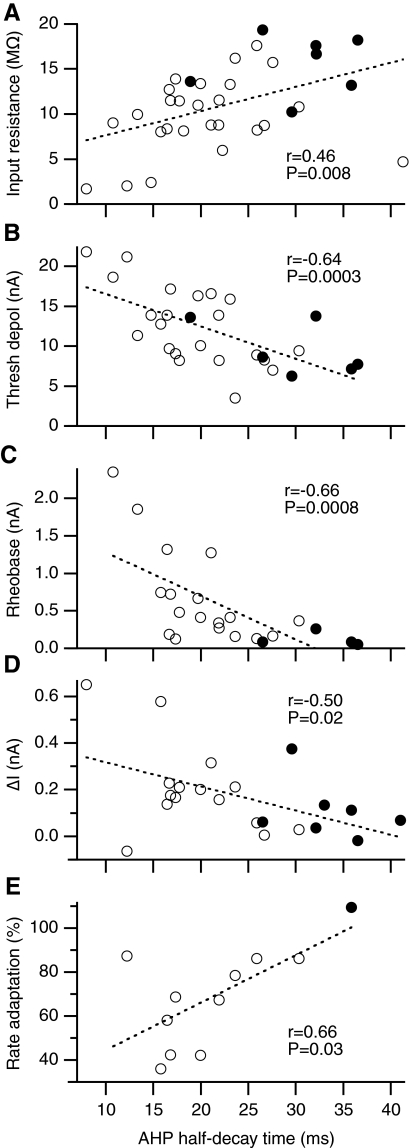
Fig. 8.

Relationships between AHP half-decay time and (A) input resistance, (B) threshold depolarization, (C) rheobase (i.e., the amplitude of a 40-ms current pulse that elicits an action potential 50% of the time), (D) ΔI (i.e., ramp derecruitment current minus recruitment current), and (E) firing rate adaptation (average firing rate during the last second of a 4-s current pulse expressed as a percentage of the instantaneous firing rate of the second ISI). Statistically significant linear relationships exist between AHP half-decay time and each of the 5 variables (dashed lines show the best-fit line by linear regression).

RESULTS

Motoneuron data pool

We recorded from 49 putative motoneurons with action potential amplitudes ≥60 mV in slices from 26 rats (median of two motoneurons/rat). Of these, 22 (45%) spontaneously fired trains of action potentials. The repetitive firing always began as soon as the cell was impaled. Played through an audio monitor, the recorded signal was unlike the “death wail” characteristic of a poor impalement, but rather had the characteristics of stable repetitive firing during prolonged constant-current injection. Firing rates changed gradually over time in some cells, although not in a consistent direction. Figure 2A illustrates typical behavior in a motoneuron firing steadily (about 20 pulses per second [pps] in this example). For all 16 cells in which this spontaneous activity was recorded (observed, but not recorded in the 6 other cells), the average firing rate ± SD was 20.2 ± 3.2 pps (range = 12.0–26.5 pps). In all cells, repetitive firing could be reduced or suppressed by hyperpolarizing current injection (illustrated for one cell in Fig. 2B). No evidence of rhythmic oscillation of membrane potential was observed in any of the spontaneously active motoneurons when silenced by hyperpolarizing current injection (e.g., see membrane potential during most negative current step in Fig. 2B). Repetitive firing emerged again in all cells after abrupt removal of injected current (Fig. 2C). In 9 of these cells, long hyperpolarizing current injections (0.5–2 min) and gradual reduction in current injection magnitude quelled resumption of spontaneous firing, allowing characterization of intrinsic motoneuron properties in response to brief (≤40 ms) rectangular current pulses (as performed in quiescent cells; see methods). These properties were not assessed in the spontaneously firing cells that could not be silenced in this way.

Fig. 2.

Examples of recordings from one motoneuron that exhibited spontaneous repetitive firing immediately on impalement and throughout the recording. Membrane potential (top panels) and instantaneous firing rate in pulses/s (pps) (middle panels) are shown with (B) and without (A, C) current injections (bottom panels). A: the motoneuron fires with a stable mean rate (recording made about 4 min after impalement). B: the motoneuron continues firing at the same rate (recording made ∼1.5 min after end of recording in A). During a series of manually adjusted hyperpolarizing current steps, the spontaneous firing rate slows and the motoneuron finally derecruits. No ongoing postsynaptic potentials were detected in the subthreshold resting potential (see membrane potential in rightmost current step). C: immediately after returning the current to zero, the motoneuron resumes spontaneous firing (recording made about 30 s after discontinuing hyperpolarizing current used in B).

Long depolarizing current injections intended to elicit repetitive firing were typically evaluated after performing short current-pulse protocols and thus due to attrition, were able to be evaluated in only 33 of the 49 motoneurons. Of these 33 motoneurons, repetitive firing was sustained throughout 10-s triangular ramp current injection in 29 motoneurons; 4 cells could not sustain repetitive firing throughout current injection. Responses to 4-s rectangular pulses (which were performed after current ramp data were collected) were assessed in only 13 motoneurons, of which 11 motoneurons exhibited sustained repetitive firing throughout the current pulse.

To summarize the disposition of the 49 recorded motoneurons: 27 were quiescent and 22 fired spontaneously; repetitive firing was evaluated during long current ramps in 29 motoneurons and during long current pulses in 11 motoneurons; short-current pulse protocols (i.e., for measuring input resistance, AHP properties, and current and voltage thresholds) were assessed in 36 motoneurons (i.e., 27 quiescent motoneurons plus 9 initially spontaneous motoneurons that were silenced by hyperpolarizing current).

Short current pulses

Rat EUS motoneurons respond to current injection in a way qualitatively similar to hindlimb motoneurons in rats, but exhibit a consistent pattern of quantitative differences (Beaumont and Gardiner 2003; Beaumont et al. 2004; Button et al. 2006; Carp et al. 2008b). Table 1 summarizes the properties of EUS motoneurons recorded in vitro and compares them to those of rat hindlimb motoneurons recorded under similar conditions¹ (data from Carp et al. 2008b and unpublished data). EUS motoneurons appear to be more excitable than hindlimb motoneurons, in that EUS motoneurons require significantly less current to elicit single action potentials (i.e., rheobase) and require significantly less depolarization to elicit an action potential from rest (threshold depolarization in Table 1) than do hindlimb motoneurons. In addition, resting membrane potentials of EUS motoneurons are significantly more depolarized than those of hindlimb motoneurons.

Table 1.

EUS and hindlimb motoneuron properties from adult rats in vitro

Property	All EUS	Hindlimb	Quiescent EUS	Spontaneous EUS
Action potential amplitude, mV	74.2 ± 7.2**	77.9 ± 9.0	74.9 ± 1.4	71.5 ± 2.7
Resting potential, mV	−55.0 ± 8.0***	−66.0 ± 12.0	−56.0 ± 2.0	−53.0 ± 2.0
Input resistance, MΩ	11.1 ± 4.6***	5.1 ± 3.4	9.9 ± 0.8	15.6 ± 1.2††
Sag, %	4.0 ± 5.9	3.2 ± 4.4	4.8 ± 1.2	0.7 ± 0.5††
Time constant, ms	4.9 ± 1.5**	3.6 ± 2.3	4.7 ± 0.3	5.8 ± 0.7
AHP amplitude, mV	−6.7 ± 3.3***	−3.0 ± 2.0	−6.1 ± 0.6	−8.9 ± 1.3
AHP half-decay time, ms	24.3 ± 10.1**	17.3 ± 7.0	20.4 ± 1.4	34.4 ± 3.2†††
Number of motoneurons	32–36	32–38	25–27	7–10
Depolarization threshold, mV	11.9 ± 4.6***	17.4 ± 7.4	12.5 ± 1.0	9.5 ± 1.4
Firing threshold, mV	−45.0 ± 7.0	−50.0 ± 12.0	−45.0 ± 2.0	−46.0 ± 2.0
Rheobase, nA	0.6 ± 0.6***	4.3 ± 3.0	0.7 ± 0.1	0.1 ± 0.0††
Number of motoneurons	23–28	32–33	19–22	4–6
Recruitment current, nA	0.8 ± 3.1***	6.6 ± 4.3	2.2 ± 1.0	−0.8 ± 0.2††
Derecruitment current, nA	0.9 ± 3.1***	6.7 ± 4.6	2.4 ± 1.0	−0.7 ± 0.2††
ΔI, nA	0.2 ± 0.2	0.1 ± 0.5	0.2 ± 0.1	0.1 ± 0.0
Recruitment rate, pps	9.3 ± 3.4***	15.5 ± 7.4	11.1 ± 1.0	7.4 ± 0.3††
Derecruitment rate, pps	9.9 ± 3.6*	13.2 ± 6.6	12.1 ± 0.9	7.5 ± 0.5†††
ΔF, pps	0.5 ± 1.8***	−2.5 ± 3.2	1.0 ± 0.6	0.1 ± 0.3
Ramp F–I slope, pps/nA	6.4 ± 3.9	8.8 ± 7.3	7.7 ± 1.2	4.8 ± 0.6†
Number of motoneurons	29	23–25	15	14

Values are means ± SD for motoneurons innervating the external urethral sphincter (All EUS; present study) or hindlimb (Carp et al. 2008 and unpublished data) muscles recorded in vitro. Values are means ± SE for EUS motorneurons that never fired spontaneously (Quiescent EUS) and those that fired spontaneously upon impalement (Spontaneous EUS). Action potential amplitude, peak minus resting potential for action potentials elicited by 0.6-ms duration current pulses; sag, % decrease in slope of current–voltage relationship (i.e., input resistance) calculated for final 10 ms of 40-ms hyperpolarizing current pulses with respect to the slope calculated using the peak hyperpolarization; rheobase, current threshold for action potential initiation during 40-ms depolarizing pulse; ramp recruitment rate, average instantaneous firing rate from the first two interspike intervals during the ascending limb of current ramp; ramp derecruitment rate, average instantaneous firing rate from the last two interspike intervals during the descending limb of current ramp; ramp F–I slope, slope of frequency–current relationship on ascending limb of current ramp.

^* P < 0.05,

^** P < 0.01, and

^*** P < 0.001, EUS different from hindlimb motoneurons;

^† P < 0.05,

^†† P < 0.01,

^††† P < 0.001, spontaneous EUS motoneurons from quiescent EUS motoneurons.

Regression analysis suggests that the differences in excitability between EUS and hindlimb motoneurons depend on multiple factors (Table 2). Single-factor linear regressions show that a significant percentage of the variation in rheobase can be accounted for individually by motoneuron identity, resting membrane potential (RMP in Table 2), or the inverse of input resistance (i.e., input conductance, which would be predicted by Ohm's Law to be directly related to rheobase). Regression of rheobase on resting potential and motoneuron identity jointly (two-factor analysis) shows that these two variables together account for little more of the variance in rheobase (∼46%) than does motoneuron identity alone (∼41%). In the two-factor analysis, almost half of the variation in rheobase is uniquely attributable to motoneuron identity (∼20%), suggesting that there is an intrinsic difference in rheobase between EUS and hindlimb motoneurons that is independent of variation in resting potential. The remaining variation in rheobase is accounted for by variation in resting potential that is unique to this independent variable or that covaries with motoneuron identity. Inclusion of the inverse of input resistance as a third factor in the regression analysis removes this unique dependence of rheobase on motoneuron identity without affecting its modest dependence on resting potential and reveals its large dependence on input conductance alone and on covariant aspects of the three factors. This suggests that the difference in rheobase between EUS and hindlimb motoneurons is attributable to differences between these two pools of motoneurons in both input conductance and (to a lesser extent) resting potential.

Table 2.

Regression analyses of excitability in EUS and hindlimb motoneurons

		Percentage of Dependent Variable Variance Accounted for by Independent Variable(s)
Test Design	Independent Variables That Account for Variance in Dependent Variable	Rheobase	Depolarization Threshold	Recruitment Current	Derecruitment Current
One-factor	Motoneuron	40.9***	13.6**	39.0***	36.4***
	RMP	26.1***	21.7***	29.4***	27.6***
	l/Input resistance	58.9***	6.2	65.7***	63.7***
Two-factor	All factors	45.6***	25.3***	40.1***	37.2***
	Motoneuron (unique)	19.5***	3.4	10.7**	9.6*
	RMP (unique)	4.7*	11.6**	9.6*	9.3*
	Motoneuron and RMP (common)	21.4	10.3	19.8	18.3
Three-factor	All factors	66.7***	25.3**	73.7***	70.3***
	Motoneuron (unique)	0.7	2.9	1.3	0.9
	RMP (unique)	4.4*	10.6**	4.3*	4.0*
	l/Input resistance (unique)	21.0***	0.0	34.9***	34.8***
	Motoneuron, RMP, and l/Input resistance (common)	40.5	11.7	33.2	33.6

Regressions of rheobase (current threshold for action potential initiation during 40-ms depolarizing pulse), depolarization threshold (voltage excursion from resting potential to reach the action potential threshold), and input resistance on motoneuron identity [Motoneuron; EUS (present study) vs. hindlimb (>Carp et al. 2008 and unpublished data], resting membrane potential (RMP), and/or the inverse of input resistance determine the variance in the dependent variables, accounted for by the independent variables. For multiple regressions (i.e., two- and three-factor designs), the percentage of variance in the dependent variable accounted for is shown for the entire model (All), for the unique contribution of each independent variable individually (Motoneuron, RMP, or 1/Input resistance only), and for the covariation among independent variable contributions (Common; calculated as the difference between the variance accounted for by the entire model and the sum of the unique contributions of the independent variables individually).

^* P < 0.05,

^** P < 0.01, and

^*** P < 0.001, variance accounted for by variable(s) significantly different from zero.

Table 2 also shows that depolarization threshold is dependent on motoneuron identity and resting potential, but not on the inverse of input resistance using single-factor regressions. Multiple regression of threshold depolarization on resting potential and motoneuron identity (two-factor) or on resting potential, motoneuron identity, and the inverse of input resistance (three-factor) show that motoneuron identity does not account for a significant amount of the variation in depolarization threshold in a way that is independent of resting potential. This suggests that there is no intrinsic difference in threshold depolarization between the two groups of motoneurons.

Long current pulses and rate adaptation

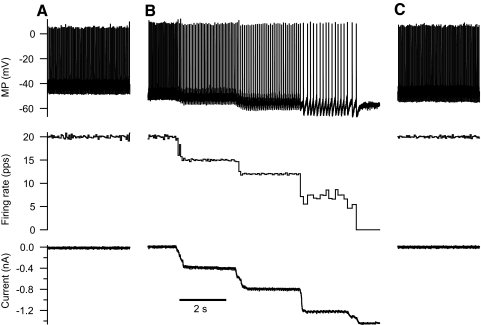
In the 11 of the 13 EUS motoneurons tested that fired repetitively throughout 4-s rectangular depolarizing current pulses, instantaneous firing rate decreased rapidly during the first few action potentials and then continued to decrease more gradually over several seconds (Fig. 3, A–C), i.e., firing rate adaptation, as described for hindlimb motoneurons (Kernell 1965; Kernell and Monster 1982). The degree of firing rate adaptation varied with the amplitude of the current pulse. Figure 3 illustrates for one motoneuron that firing rate decreased more rapidly with a higher current amplitude and approached a lower fractional steady-state firing rate after several seconds (traces labeled 1) than did the response to a lower current amplitude (traces labeled 2). Figure 3D shows the firing rate adaptation that occurred in the last second of the current pulse (expressed as a percentage of the instantaneous frequency of the second ISI (% firing rate adaptation) as a function of the current amplitude for all 11 motoneurons. The steady-state firing rate decreased significantly with increasing current (P < 0.0001 by within-cell regression analysis; n = 10 for this analysis because one motoneuron was tested with only a single current amplitude). The within-cell best-fit lines all have negative slopes (indicated by the dotted lines associated with the different symbols for each motoneuron). The average slope of the relationship between the % firing rate adaption and current pulse amplitude was −5.2 (±2.8 SE) %/nA.

Fig. 3.

Rate adaptation in external urethral sphincter (EUS) motoneurons. A: for one EUS motoneuron, rectangular current pulse injections (C) elicit repetitive firing (A). Firing rate (B) decreases rapidly initially and then continues to decrease more slowly over the course of the 4-s current pulse. The larger and smaller currents and their responses are identified as traces 1 and 2, respectively, in A–C. The firing rate associated with the first interspike interval (ISI) induced by the larger current is 150 pps, but is truncated in the figure. B: the average firing rate during the last 1 s of the 4-s current pulse [expressed as a percentage of the instantaneous firing rate of the second ISI (% firing rate adaptation) decreases with increasing current above the firing threshold (firing current, defined as current pulse amplitude − recruitment current)], indicating that rate adaptation increases with the level of excitation. Data from individual motoneurons are shown using the same symbol. The dotted lines are the best-fit lines determined from the within-cell regression of firing rate adaptation on current pulse amplitude − recruitment current.

Long current ramps

The repetitive firing properties of EUS motoneurons were assessed in response to injection of 10-s triangular current ramps in 29 of the 49 cells. Application of depolarizing ramps of different sizes during hyperpolarizing or depolarizing current offsets (median of 12 trials per cell) allowed evaluation of repetitive firing in motoneurons under a variety of conditions in motoneurons in different states of excitability [i.e., quiescent and spontaneous (both currently active and silenced)].

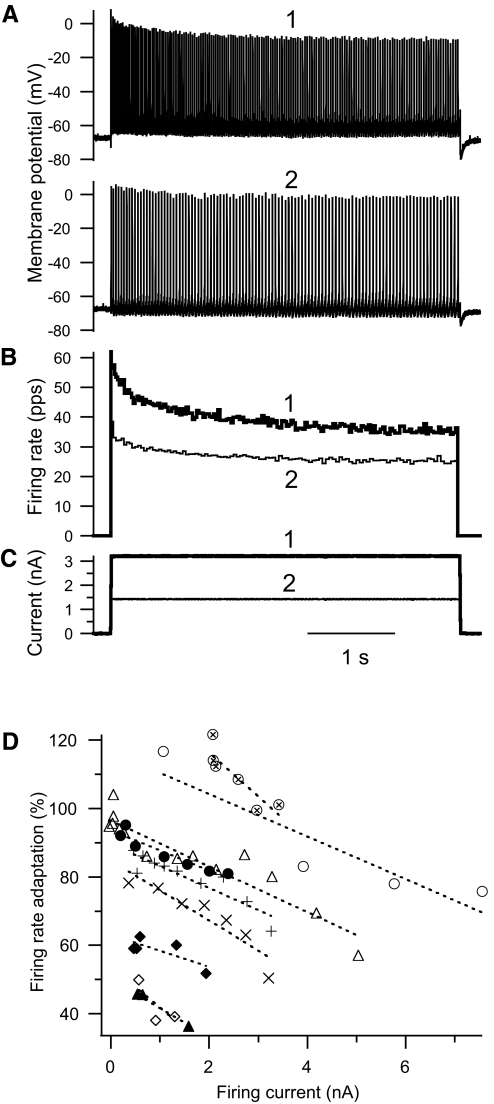
Current ramps elicited responses in EUS motoneurons qualitatively similar to those recorded from hindlimb motoneurons in vitro (Carp et al. 2008b) and in vivo (Button et al. 2006). Recruited during the ascending current ramp, EUS motoneurons fired repetitively until they were derecruited during the descending current ramp, as illustrated by examples in Fig. 4. Firing behavior during the ramps was dependent on both the base-to-peak amplitude of the ramp and the rectangular current pulse amplitude on which the ramp was superimposed (offset). Within-cell regressions of variables used to characterize firing behavior during ramps on ramp amplitude and offset showed significant relationships (Table 3). Variables that described the current threshold and firing rates associated with recruitment and derecruitment generally showed statistically significant direct dependencies on ramp amplitude and offset, but the amount of variance accounted for by ramp amplitude and/or offset that was independent of interanimal differences was modest. Ramp shape parameters did account for a substantial amount of variation in ΔI, a variable that assesses the potential contribution of PIC activation to repetitive firing, as indicated by the difference between recruitment and derecruitment currents. Negative values of ΔI are consistent with activation of a PIC that helps sustain repetitive firing even when the current injected during the descending leg of the ramp falls below that at which the motoneuron initially recruited (Bennett et al. 2001; Button et al. 2006; Heckmann et al. 2005). In EUS motoneurons, ΔI values were typically positive (i.e., motoneurons recruited at lower currents than those at which they derecruited; see ΔI values in bottom panels of Fig. 4). The examples in Fig. 4 illustrate the results of the regression analysis summarized in Table 3, in that ΔI is positively correlated with ramp amplitude [right-hand panel, in which the ramp with the higher amplitude (trace 1) was associated with a more positive ΔI than that associated with the lower amplitude (trace 2)]. There was no relationship between ΔI and ramp offset overall (main effect of offset not significant; Table 3). The significant dependence of ΔI on the interaction of ramp offset and amplitude suggests that ΔI did vary with ramp offset in a way that depended on the current ramp amplitude.

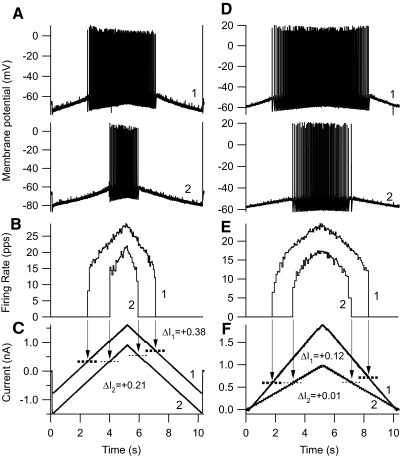
Fig. 4.

Repetitive firing elicited by current injections in 2 different EUS motoneurons. Pairs (traces 1 and 2) of 10-s triangular (5 s up, 5 s down) ramp current injections (C, F), membrane potential responses (A, D), and instantaneous firing rates (B, E; in pps) are shown as a function of time. Downward arrows point from the times of recruitment and derecruitment in the firing rate traces to dashed horizontal lines that intersect the current traces at the recruitment and derecruitment current levels. The pairs of current injections have (A) the same ramp amplitude, but different offsets, and (B) different ramp amplitudes, but the same offset (zero in this case). For all ramps, the currents at recruitment are lower than the currents at derecruitment [i.e., derecruitment minus recruitment current (ΔI) is positive]. In both motoneurons, the current ramp with the more positive peak (trace 1) elicits the response producing the more positive ΔI value.

Table 3.

Dependence of firing behavior during triangular ramps on ramp characteristics

	Average Slope of Regression Line		Percentage Variance Accounted for by Independent Variables
Dependent Variable	Amplitude, nA	Offset, nA	Amplitude	Offset	Amplitude × Offset	Pooled
Recruitment current, nA	0.075	0.21	0.5***	0.2***	0.1***	0.8
Derecruitment current, nA	0.21	0.24	0.1***	0.2***	0.1***	0.4
ΔI, nA	0.13	0.00	28.7***	0.0	2.1***	30.8
Recruitment rate, pps	0.87	0.41	8.4***	1.1**	0.3	9.8
Derecruitment rate, pps	0.53	−0.16	3.0***	0.1*	0.4*	3.5
ΔF, pps	−0.25	−0.20	1.6*	1.3	0.1	3.0

Within-cell regressions of variables characterizing firing behavior during triangular current ramps (Dependent variables) on the following independent variables: base-to-peak amplitude of the ramp (Amplitude), rectangular current pulse on which the ramp is superimposed (Offset), the interaction of amplitude and offset (Amplitude × Offset), and cell. The percentages of the total variance of the dependent variables that was uniquely accounted for by the regressions are shown for Amplitude, Offset, their interaction, and for all three factors summed (Pooled). ΔI, decrecruitment − recruitment current; ΔF, decrecruitment − recruitment rate; pps, pulses per second.

^* P < 0.05,

^** P < 0.01, and

^*** P < 0.001, variance accounted for by variable(s) significantly different from zero.

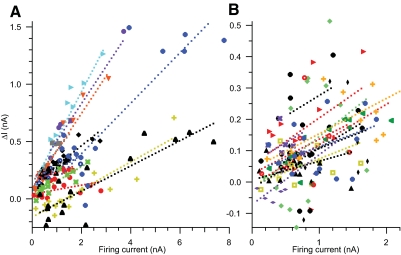
Illustration of the dependence of ΔI on both ramp amplitude and offset in a two-dimensional plot is not feasible, but combining the two aspects of ramp shape into a single variable makes this problem more tractable. ΔI is linearly dependent on the sum of ramp amplitude and offset (i.e., the absolute current level at the peak of the ramp), having 22.8% of variance in ΔI accounted for uniquely by ramp peak current (P < 0.0001 by within-cell regression analysis). Even more variance in ΔI can be accounted for by regression of ΔI on ramp peak current minus the ramp recruitment current (defined here as firing current because it reflects only the portion of the ramp current that actually elicits firing), having 28.4% of variance in ΔI accounted for uniquely by firing current (P < 0.0001 by within-cell regression analysis). For the purpose of illustration, Fig. 5 shows the relationship between ΔI and firing current for all ramps tested in all motoneurons. Data from each motoneuron are shown using the same colored symbol, along with the best-fit lines in the matching color for each motoneuron based on the regression of ΔI on firing current, motoneuron, and the interaction of peak ramp current and motoneuron (whole model r² = 0.81, P < 0.0001). Regression lines had positive slopes for all motoneurons [average regression line slope = 0.15 (±0.08 SD) nA/nA].

Fig. 5.

Values of ramp derecruitment current minus recruitment current (ΔI) are shown for each ramp trial from 29 EUS motoneurons as a function of the firing current (i.e., peak ramp current minus ramp recruitment current; see text for rationale for use of this variable). To reduce the overlap of symbols, data from motoneurons in which the range of peak currents tested exceeded 2 nA are shown in A and those <2 nA are shown in B. Data from each motoneuron have the same colored symbol. The best-fit lines (dotted lines with the same color as that of their motoneuron data symbol) were determined by within-cell regression of ΔI on the peak ramp current, cell, and the interaction of peak ramp current and cell (see text for details of statistical analysis). The statistical model predicts that the relationship between ΔI and peak ramp current has a positive slope in all cells. Note that the axis scales in the 2 panels are drawn such that a line with a given slope will form the same angles with the axes in both plots. The majority of trials have positive values of ΔI, but 10 of 29 (34%) of motoneurons have at least one negative ΔI value (a hallmark of persistent inward current [PIC] expression).

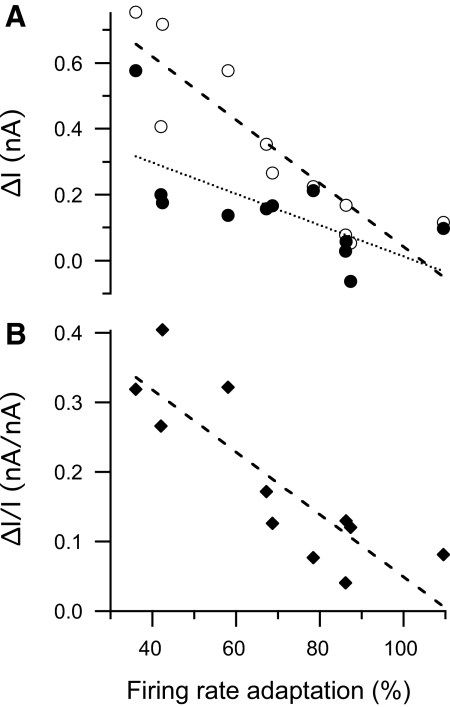
That the majority of current ramps elicited responses with positive ΔI values that became even more positive with increasing current amplitude (Fig. 5) suggests the development of processes during the ramp that decrease motoneuron excitability, not unlike the firing rate adaptation that occurs during current pulses. These processes appear to be linked, in that the slope of the relationship between the degree of firing rate adaptation varies significantly with ΔI recorded from the same motoneurons (open circles in Fig. 6A; r² = 0.47, P = 0.02 by linear regression). This relationship is not driven simply by differences in the average ramp current used to elicit the responses because the degree of firing rate adaptation is also significantly related to the slope of the relationship between ΔI and the ramp peak current for individual motoneurons from the regression analysis described earlier (and illustrated in Fig. 5) (Fig. 6B; r² = 0.80, P = 0.0002 by linear regression). The relationship between firing rate adaptation and ΔI raises the possibility that PIC expression may be obscured by processes associated with current magnitude-dependent firing rate adaptation. When ΔI is calculated from trials with the four lowest firing current amplitudes, the relationship is still significant, but weaker (r² = 0.46, P = 0.02 by linear regression). This is consistent with the previous assumption that ΔI is influenced not only by PIC expression, but also by the mechanisms underlying firing rate adaptation (Bennett et al. 2001). It also suggests that the influence of rate adaptation on ΔI is reduced, but not fully removed, by limiting the quantitative analysis of ramp current trials to those with the lowest amplitudes.

Fig. 6.

A: relationship between firing rate adaptation (average firing rate during the last second of a 4-s rectangular current pulse expressed as a percentage of the instantaneous firing rate based on the second ISI after current onset) and ΔI (derecruitment current minus recruitment current). Data are by-motoneuron averages calculated from all trials (open circles) and from the 4 trials with the lowest firing currents (peak ramp current − ramp recruitment current; filled circles). ΔI calculated from all trials varies inversely with firing rate adaptation [r² = 0.79, P = 0.0003 by linear regression (dashed line)]. ΔI calculated from the 4 low-current trials varies inversely, but less strongly with firing rate adaptation (r² = 0.46, P = 0.02 by linear regression; dashed line). B: relationship between firing rate adaptation and the slope of the relationship between ΔI and firing current (ΔI/I). ΔI/I varies inversely with firing rate adaptation (r² = 0.73, P = 0.0008 by linear regression; dotted line).

Because ΔI and other ramp-related variables are also sensitive to current amplitude and/or offset (Table 3), we have focused quantitative analysis of these variables on the four trials from each cell elicited by the lowest values of firing current (Table 1). As with short current pulses, ramp currents more readily excited EUS motoneurons than hindlimb motoneurons. EUS motoneurons required significantly less current to initiate (recruitment current) or terminate (derecruitment current) repetitive discharge during triangular current ramp injection than did hindlimb motoneurons recorded under similar conditions in vitro (Table 1). As with rheobase, the differences in recruitment and derecruitment currents between EUS and hindlimb motoneurons were still evident after accounting for the contribution of differences in resting potential to excitability (Table 2, two-factor analysis). In addition, inclusion of the inverse of input resistance in the statistical model largely removed the differences in recruitment and derecruitment currents between the two groups of motoneurons (i.e., compare the % variance accounted for that is unique to Motoneuron between the two-factor and three-factor analyses). These findings are consistent with input resistance being an important determinant of the difference in excitability between EUS and hindlimb motoneurons.

Table 1 also shows that EUS motoneurons have mean ΔI values that are slightly positive. However, not all cells exhibited this firing behavior: 3 of 29 EUS motoneurons had mean ΔI values that were negative, with 47–53% of the individual trials (13–17 total trials/cell) having negative ΔI values. This suggests that basal PIC expression is present in a limited number of EUS motoneurons in this reduced preparation. Average ΔI values are statistically comparable in isolated hindlimb motoneurons, but the latter have negative average ΔF values that are significantly lower than those in EUS motoneurons, which is consistent with hindlimb motoneurons expressing more gradually activating currents that support lower firing rates than EUS motoneurons.

Distributions of EUS motoneuron properties

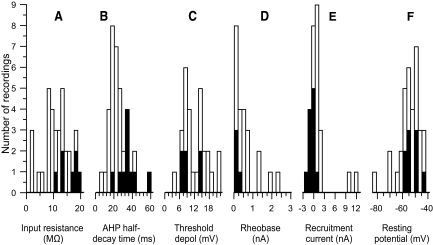
Figure 7 shows the distributions of values of input resistance (Fig. 7A), AHP half-decay time (Fig. 7B), and threshold depolarization for EUS motoneurons (Fig. 7C). The range of values (calculated as the ratio of the 95th to the 5th percentiles of the distribution) for input resistance was 9.6- and 7.3-fold for EUS and hindlimb motoneurons, respectively, for AHP half-decay time was 4.2-fold for both EUS and hindlimb motoneurons, and for threshold depolarization was 4.6- and 4.3-fold for EUS and hindlimb motoneurons, respectively. Thus the differences in the mean values of these variables (Table 1, and see preceding text) are unlikely to be due to the EUS motoneuron pool, having a restricted range of values with respect to that of hindlimb motoneurons.

Fig. 7.

Distributions of: (A) input resistance, (B) afterhyperpolarization (AHP) half-decay time, (C) threshold depolarization (i.e., depolarization from the resting level required to reach the voltage threshold for action potential initiation), (D) rheobase (i.e., the amplitude of a 40-ms current pulse that elicits an action potential 50% of the time), (E) recruitment current (i.e., the current at which the motoneuron is recruited by the ascending limb of a triangular current pulse), and (F) resting potential. Black bars show the motoneurons that exhibited spontaneous repetitive firing at any point during their recording session; white bars show the quiescent motoneurons. The sum of the black and white bars shows the total number of cells in each range of values. Rheobase was not measured in cells that were actively in the process of firing spontaneously. Thus there are no values below zero. In these cells, current ramps were applied superimposed on rectangular hyperpolarizing current pulses so that recruitment and derecruitment could be assessed during ramp current application (e.g., see Fig. 4C). Thus recruitment current values extend below zero, giving a more complete picture of the distribution of current threshold values in EUS motoneurons than does the rheobase distribution.

Rheobase values (Fig. 7D) were small, but positive. Because rheobase was not determined in spontaneously firing cells in which prolonged hyperpolarizing current injection did not suppress firing after termination of the current pulse (11 of 22 spontaneously firing cells), this distribution is skewed, in that it lacks the expected negative rheobase values. Thus the true mean rheobase value is almost certainly lower than the value reported in Table 1. Along with quiescent motoneurons, the 11 motoneurons with ongoing activity were studied using triangular current ramps (the ongoing spontaneous firing was temporarily suppressed using a hyperpolarizing current bias) and thus the recruitment current distribution for ramps is more representative of the full range of excitability of the EUS motoneuron pool (Fig. 7E) than is the rheobase distribution (Fig. 7D). Indeed, the missing negative rheobase values are likely to be even lower than the ramp recruitment current values because the rectangular current pulse used to assess rheobase would not be subject to the same degree of accommodation expected to occur with the slowly rising triangular current ramps.

Comparison of motoneuron properties in spontaneous and quiescent motoneurons

In the histograms of Fig. 7, black bars identify data from motoneurons that initially displayed spontaneous repetitive firing and white bars identify quiescent cells. Spontaneous motoneurons tended to have among the highest input resistances (Fig. 7A), longest AHP decay times (Fig. 7B), and lowest rheobases (Fig. 7D) and ramp recruitment currents (Fig. 7E) of all EUS motoneurons. Table 1 compares the properties of spontaneous motoneurons (including those with ongoing firing and those temporarily silenced) with those of quiescent motoneurons (i.e., those that never exhibited spontaneous firing). Compared with quiescent motoneurons, spontaneous motoneurons had significantly higher input resistance, less sag, longer AHP half-decay time, lower rheobase, and lower recruitment and derecruitment currents and firing rates (P < 0.01 for all by t-test). In hindlimb motoneurons, this spectrum of properties is typically associated with motoneurons that preferentially innervate slow-twitch (S), but not fast-twitch (F), muscle. To the extent that comparable motor unit types are expressed in EUS motoneurons, the observed features are consistent with the spontaneous motoneurons being more S-like than quiescent motoneurons.

Measurements of current threshold (i.e., rheobase, recruitment current, and derecruitment current) vary with resting potential (Table 2). Figure 7F shows the distribution of resting potentials from quiescent (white bars) and spontaneous (black bars) motoneurons. There was no significant difference in resting potential between these groups of motoneurons (Table 1). Similarly, there was no difference in threshold depolarization (which is correlated with resting potential) between quiescent and spontaneous motoneurons (Fig. 7C, Table 1).

Relationships among EUS motoneuron properties

In hindlimb motoneurons, the duration of the AHP following an action potential and several other properties are differentially distributed among motoneurons that innervate different muscle types (Burke 1981). In both rats and cats, variables that describe the duration of the AHP distinguish between F and S motor units (Burke et al. 1973; Gardiner 1993; Zengel et al. 1985). In EUS motoneurons, regression analysis indicates that AHP half-decay time varied systematically with input resistance, threshold depolarization, rheobase, ΔI, and firing rate adaptation (Fig. 8, A–E, respectively; statistical analysis in Table 4). Motoneurons with short AHP half-decay times tended to have low-input resistances, high-threshold depolarizations, and high rheobases, whereas those with long AHP half-decay times tended to have high-input resistances, low-threshold depolarizations, and low rheobases. Recruitment and derecruitment current thresholds for firing during triangular ramps exhibited similar relationships with AHP half-decay time (Table 4).

Table 4.

Regression analyses of EUS motoneuron properties on afterhyperpolarization (AHP) half-decay time and resting membrane potential (RMP)

		Percentage of Dependent Variable Variance Accounted for by Independent Variable(s)
Test Design	Independent Variables That Account for Variance in Dependent Variable	Input Resistance	Depolarization Threshold	Rheobase	ΔI	Recruitment Current	Derecruitment Current
One-factor	AHP half-decay time	20.8**	40.6***	43.5***	21.8*	45.6***	47.2***
	RMP	12.7*	28.7**	35.4**	2.1	61.8***	60.2***
Two-factor	All factors	22.2*	45.9**	65.0***	22.8*	77.0***	77.0***
	AHP half-decay time (unique)	9.9	17.3*	29.7**	21.4*	16.8**	18.6**
	RMP (unique)	2.8	9.0	22.8**	0.3	33.6***	31.6***
	AHP half-decay time and RMP (common)	9.5	19.6	12.5	1.1	26.6	26.8

Regressions of input resistance, depolarization threshold (voltage excursion from RMP to reach the action potential threshold), rheobase (current threshold for action potential initiation during 40-ms depolarizing pulse), ΔI (ramp decrecruitment − recruitment current), ramp recruitment current, and ramp derecuitment current on AHP half-decay time and/or RMP determine the variance they account for in the dependent variables. The two-factor analyses show the percentage of the dependent variable variance accounted for by the variation in: all factors together (All factors), the unique contribution of each independent variable (unique), and the variance that is common among independent variable (common; calculated as the difference between the variance accounted for by the entire model and the sum of the unique contributions of the independent variables individually).

^* P < 0.05,

^** P < 0.01, and

^*** P < 0.001, variance accounted for by variable(s) significantly different from zero.

All of the properties described in Table 4 show significant linear relationships with AHP half-decay time (see One-factor analyses for resting potential), which also varies with resting potential (r² = 0.21, P = 0.01 by linear regression), raising the possibility that the systematic variation in motoneuron properties shown in Fig. 8 could have been due to variation in resting potential (e.g., due to differences in impalement quality). Multiple regression analyses that include both AHP half-decay time and resting potential indicate that AHP half-decay time accounts for a significant percentage of the variance in rheobase, depolarization threshold, recruitment current, and derecruitment current in a way that is independent of variation in resting potential [see AHP half-decay time (unique) in Table 4]. Input resistance tended to vary uniquely with AHP half-decay time, but this effect was not statistically significant (P = 0.07).

Input resistance did not vary systematically with time constant (r = 0.00, P = 0.98 for linear regression). This relationship is also not evident in rat hindlimb motoneurons recorded in vitro (r = 0.23, P = 0.22; data from Carp et al. 2008b), but is evident in cat motoneurons recorded in vivo (Hochman et al. 1991), suggesting that in rats, factors other than membrane resistivity account for more of the variation in input resistance values.

Dependence of motoneuron properties on age

In general, EUS motoneuron properties did not vary with body weight or age. Neither variable accounted for a significant amount of variation in any of the motoneuron properties (P > 0.1 for all by linear regression), except for ramp recruitment and derecruitment current (slope = −0.48 and −0.46 nA/wk, r² = 0.30 and 0.26, and P = 0.02 and 0.04, respectively, for linear regression on age of average value of recruitment and derecruitment current, respectively). These relationships were driven by two cells with very large current thresholds (∼10 and 12 nA) that came from two different animals of about 8 wk of age. All other values of current threshold from the 5 cells from three younger animals (between 0.1 and 0.6 nA) fell within the range of values seen in the 28 cells from 12 older animals (between −2.1 and 2.2 nA). Thus there did not appear to be a consistent age-dependent bias in the data. Whatever age dependence did exist did not appear to interfere with comparisons of the EUS data with those from hindlimb motoneurons. For example, EUS motoneurons had significantly lower recruitment and derecruitment currents than those of hindlimb motoneurons, even when age was included as a covariate in the analysis (P < 0.006 for both current variables by ANCOVA).

DISCUSSION

Role of EUS motoneuron properties in excitability in rats and other species

This study provides the first description of the intrinsic properties of EUS motoneurons in the rat. The data show that rat EUS motoneurons are more excitable than are rat hindlimb motoneurons studied either in vitro or in vivo. Their resting potentials are more depolarized and their input resistances are higher, giving them a low threshold for action potential initiation in response to current injection. The breadth of the range of input resistance values found in rat EUS motoneurons was comparable to that of rat hindlimb motoneurons, suggesting an overall shift in this property rather than a compression of its range.

The high excitability of EUS motoneurons in vitro is most clearly illustrated by the observation that 45% of them were spontaneously active. Impalement-related damage was ruled out as the primary basis of this spontaneous activity because 1) firing was stable and long-lasting; 2) single motor unit firing rates (average rate = 24 pps) recorded in vivo under ketamine anesthesia (Kerns et al. 2000) were comparable to those recorded here; and 3) similar impalements in hindlimb motoneurons never yielded stable spontaneous activity (Carp et al. 2008b). Furthermore, if the difference between the spontaneous and quiescent cells were just that the former had a consistently larger impalement-induced leak conductance, then we would expect that resting potential would be more depolarized and input resistance would be lower in the spontaneous cells; in fact, we observed that input resistance was >55% higher in spontaneous cells without a significant difference in resting potential (Table 1). Given these findings, it seems unlikely that impalement-induced injury is the sole (or even primary) mechanism underlying spontaneous firing in some, but not other cells.

Rat EUS motoneuron properties are qualitatively similar to those of cat EUS motoneurons (Hochman et al. 1991; Sasaki 1991). Both have low rheobases, high-input resistances, and long AHP durations compared with those properties in hindlimb motoneurons. These findings are consistent with EUS motoneurons being smaller on average than hindlimb motoneurons (Chen and Wolpaw 1994; Collins Jr et al. 1992; McKenna and Nadelhaft 1986). Cat and rat EUS motoneurons do differ in that the significant relationship between input resistance and time constant that is evident in cats (Hochman et al. 1991) is absent in rats. According to a simple passive neuronal model (Gustafsson and Pinter 1984a), input resistance is expected to be related to membrane time constant and somatodendritic shape-related factors. Assuming that variation in time constant largely reflects variation in specific membrane resistivity (and not specific membrane capacitance), then specific membrane resistivity appears to make a relatively greater contribution to the range of input resistance values in cats than in rats. Shape-related factors (e.g., motoneuron size and/or geometry) would presumably make a relatively larger contribution to the range of input resistance values in rats than in cats. These size-related factors are likely to account for the input resistance-dependent difference in excitability between rat EUS and hindlimb motoneurons (Table 2).

One caveat that needs to be kept in mind while considering the mechanism underlying the high excitability of EUS motoneurons is that the present sample comes from female rats, whereas the previous in vitro study of rat hindlimb motoneurons was from male rats. Female rats were chosen for the present study because the dorsolateral nucleus contains only EUS motoneurons in females, whereas in males it also contains ischiocavernosus motoneurons (McKenna and Nadelhaft 1986; Schroder 1980). Although data on male–female size differences in spinal motoneurons are conflicting (Chen and Wolpaw 1994; Collins Jr et al. 1992; McKenna and Nadelhaft 1986), it is possible that gender-dependent size (or other) differences between EUS and hindlimb motoneurons contribute to differences in their current sensitivity.

Do EUS motoneurons have properties that vary with muscle type?

For many muscles in different species of animals, the intrinsic properties of their motoneurons vary with the contractile properties of the muscle fibers that they innervate (Burke 1981; Kernell et al. 1999). Although the contractile properties of rat EUS muscle units have not been characterized, it seems likely that the relationships between rat EUS motoneurons and muscle are qualitatively similar to those seen in other motor units. Histochemical evidence indicates that rat EUS muscle contains both F and S myosin isoforms (Praud et al. 2003). In addition, EUS motoneurons exhibit a spectrum of properties that is consistent with the existence of F and S motor units. In hindlimb motoneurons, several motoneuron properties vary systematically with motor unit type. In particular, the time course of the AHP is correlated with twitch contraction time, which contributes to the match between motoneuron firing rate and the speed of muscle contraction (Kernell et al. 1999). Variables describing the AHP time course correlate with several other motoneuron properties (see Gardiner 1993 for rat data and Zengel et al. 1975 for cat data). These relationships describe the spectrum of properties that contribute to the distribution of motoneuron excitabilities that help to determine their recruitment order.

Our data are consistent with EUS motoneurons having a comparable organization of motoneuron properties and excitabilities, in that 1) the data exhibit a wide range of values comparable to the ranges seen for hindlimb motoneurons (i.e., the values do not appear to be limited to ranges exhibited by F or S motor units alone); 2) relationships similar to those seen in hindlimb motoneurons exist among the properties of EUS motoneurons [e.g., compare the relationship between rheobase and AHP half-decay time in the present rat EUS motoneurons (Fig. 8C) and in rat gastrocnemius motoneurons (see Figs. 8 and 9 in Gardiner 1993)]; 3) the most readily recruitable motoneurons (as indicated by their spontaneous firing or by their low rheobase and ramp recruitment currents) are typically the cells with the longest AHP half-decay times (i.e., the variable that distinguishes F and S hindlimb motor units in rat gastrocnemius muscle; Gardiner 1993); and 4) the distributions of AHP half-decay time in EUS and gastrocnemius motoneurons have qualitatively similar shapes [i.e., unimodal (or at least not overtly bimodal) distributions with a long tail skewed to higher values]. Thus it seems likely that the EUS motor pool contains both F and S motor units and that their motoneurons exhibit properties consistent with the type of muscle fiber that they innervate.

The presence of EUS motoneurons having characteristics consistent with S motoneurons would appear to contradict muscle histochemical analysis indicating that rat EUS muscles contain predominantly the F myosin isoform (Praud et al. 2003). A similar discrepancy has been noted between motoneuron type and muscle type in the cat EUS, in which a large proportion of cat EUS motoneurons displayed properties consistent with S motor units (Hochman et al. 1991) but had muscle contractile properties more consistent with F motor units (Bowen et al. 1976). Hochman et al. (1991) proposed that F motoneurons innervate many more muscle fibers than do S motoneurons, resulting in a large pool of low-force S motoneurons and a small number of high-force F motoneurons.

In theory, differences in distributions of EUS and hindlimb motor unit type could also contribute to the observed difference in excitability if there were proportionally more high excitability S than F motoneurons in the EUS than in the hindlimb motoneuron pool. This seems unlikely, given that EUS muscle contains predominantly F myosin isoforms (Praud et al. 2003). Furthermore, motoneuron excitability (as indicated by lower rheobase, higher input resistance, and lower threshold depolarization) was still significantly higher in EUS motoneurons than that in hindlimb motoneurons, even after accounting for motor unit type by including AHP half-decay time as a covariate in the analysis (P < 0.01 for variance in rheobase, input resistance, and threshold depolarization uniquely accounted for by motoneuron identity by ANCOVA). Thus the differences between EUS and hindlimb motoneurons reflect (at least in part) intrinsic differences in excitability between these motoneuron pools that are independent of motor unit type-dependent distributions.

Expression of PICs in EUS motoneurons

Somatic motoneurons express PICs, which produce potent self-sustaining membrane depolarization; are essential for normal repetitive firing behavior; amplify currents induced by synaptic inputs; and determine the shape of the relationship between injected current and firing rate under the appropriate neuromodulatory influences (Heckmann et al. 2005; Rekling et al. 2000). EUS motoneurons also express PICs and appear to have comparable neuromodulatory influences (Burgard et al. 2008; Paroschy and Shefchyk 2000; Rajaofetra et al. 1992; Thor et al. 1993; Ye et al. 2009). In vivo studies of lower urinary tract function show that drugs that interact with these neuromodulatory influences alter EUS activity (Danuser and Thor 1996; de Groat et al. 1990; Mbaki and Ramage 2008; Thor and Katofiasc 1995; Thor et al. 2002). These observations are consistent with PICs having a role in EUS motoneuron firing behavior during urinary function.

In the absence of neuromodulatory input, basal PIC expression is modest (Heckmann et al. 2005; Rekling et al. 2000). The present data are largely in agreement with this, in that consistent evidence for PIC expression was found in very few EUS motoneurons. PIC expression was expected to be minimal at most in this in vitro preparation, in which descending monoaminergic and segmental neuromodulatory inputs have been removed (or greatly reduced) by transverse sectioning. Despite the apparent isolation of these motoneurons, we did observe firing behavior that was consistent with modest PIC expression in some EUS motoneurons, in that 1) average ΔI values were negative in 10% of EUS motoneurons; and 2) during low-amplitude current ramps, rate acceleration (i.e., % rate adaptation >100%, suggesting PIC activation) was observed instead of the expected rate deceleration (i.e., % rate adaptation <100%) at low current pulse amplitudes in 3 of the 11 cells studied (Fig. 3D). In addition, values of ΔI are likely to be underestimated due to interaction with slowly activating currents that decrease excitability (i.e., the apparent influence of current amplitude-dependent rate adaptation is not fully removed by limiting the trials to those with the smallest peak ramp amplitudes, as illustrated in Fig. 6). Such an interaction between PICs and rate adaptation could also account for the infrequent occurrence (7–27% of ramps) of negative ΔI values in seven other EUS motoneurons (see Fig. 5). These findings are consistent with basal PIC expression (albeit modest) in at least some EUS motoneurons in this preparation. This PIC expression is unlikely to be due to neuromodulatory input from ongoing interneuronal activity in the slice because no sign of ongoing synaptic activity was ever detected in the subthreshold membrane potential. This modest PIC expression is more likely due to spontaneous release of neuromodulators from severed nerve terminals and/or to constitutively active neuromodulator receptors on EUS motoneurons (Harvey et al. 2006; Murray et al. 2010).

PICs are preferentially expressed in the low-threshold motoneurons that express the least amount of firing rate adaptation (Button et al. 2006, 2007; Kernell and Monster 1982). The relationship between the current pulse dependence of firing rate adaptation and the current ramp size dependence of ΔI (Fig. 6) suggests that these phenomena share common mechanisms. The mechanism of firing rate adaptation is as yet unknown, but is likely to involve a gradual decrease in inward current (e.g., increased inactivation of transient or persistent sodium channels) and/or increase in outward current (e.g., increased calcium-dependent potassium current that contributes to the AHP) (Brownstone 2006; Miles et al. 2005; Powers et al. 1999; Schwindt and Crill 1982). PICs mediated by sodium ions exhibit preferential inactivation in high-rheobase motoneurons (Lee and Heckman 2001). A greater degree of sodium-mediated PIC inactivation in F motoneurons has been suggested to underlie the weaker bistability (a PIC-dependent firing behavior) and greater firing rate adaptation than that observed in S motoneurons (Button et al. 2007). This mechanism could also explain our findings of preferential expression of firing rate adaptation and positive ΔI in low excitability (i.e., quiescent) EUS motoneurons with short AHP half-decay times (Fig. 8 D and E).

Relationship between EUS motoneuron properties and motor function

The properties of hindlimb motoneurons are matched to those of the muscle fibers they innervate (Kernell et al. 1999). F and S motor units differ in their peak force production, speed of contraction, and sensitivity to fatigue, rendering each of them more suited to different functions. The predominant function of the EUS muscle is to contribute to continence by contracting, and thus occluding, the urethra (de Groat 2006). The present data are consistent with previous suggestions (Brading 1999; Shefchyk 2006) that S motor units are ideally suited to sustained activation, in that their motoneurons are the most readily recruited among EUS units and can fire repetitively for long periods of time. In addition, spontaneously active EUS motoneurons exhibit little rate adaptation (see Comparison of motoneuron properties in spontaneous and quiescent motoneurons). PICs in S motoneurons would promote stable repetitive discharge, especially in the presence of facilitatory neuromodulatory influences. Presumably, the muscle fibers innervated by S motoneurons are highly fatigue-resistant and their slow contraction times would not be detrimental to this sustained function.

In many species, EUS activity increases during the early stages of bladder filling in a way that is dependent on both descending and segmental inputs (Garry et al. 1959; Kruse and de Groat 1993; Mackel 1979; Pikov et al. 1998; Shimoda et al. 1992). For example, tonic EUS activity increases during bladder filling in a manner that helps maintain continence (i.e., guarding reflex; Cruz and Downie 2005; Kruse et al. 1993). The ease with which EUS motoneuron firing rate can be modulated by current injection indicates that these motoneurons are well suited to this integrative function. Filling-induced bladder distention would require increased firing rate and/or recruitment of additional motor units. Large and/or rapid increases in intraabdominal pressure might recruit large (presumed F) motor units as well (Brading 1999; Praud et al. 2003).

During micturition, any PICs that were active would presumably need to be deactivated by inhibitory input (Hounsgaard et al. 1984) to allow EUS relaxation, either tonically (as in humans) or phasically (as in rats) (Kruse et al. 1990; Maggi et al. 1986; Praud et al. 2003; Streng et al. 2004). Given the role of abnormally enhanced neuromodulator-independent PICs in skeletal muscle spasticity after spinal cord injury (Li and Bennett 2003; Li et al. 2004; Murray et al. 2010), it is plausible that alterations in basal PIC expression in EUS motoneurons could contribute to abnormalities of urinary function after spinal cord injury, such as bladder-sphincter dyssynergia.

Conclusions

The data presented here demonstrate that the EUS motoneuron pool in the rat is highly excitable (compared with other lumbar motoneurons) when studied in a largely synaptically isolated preparation in vitro in the absence of anesthetics. This high level of excitability is likely to reflect a combination of morphological factors as well as passive and active membrane properties. Like motoneurons innervating skeletal muscle, EUS motoneurons exhibit a spectrum of intrinsic properties that is consistent with the existence of F and S motor units. In addition, the expression of firing behaviors consistent with PIC activation in at least some motoneurons in this highly reduced preparation suggests that neuromodulator-independent PICs (like neuromodulator-dependent PICs) play a role in EUS motoneuron firing behavior in intact animals.

GRANTS

This work was supported by National Institutes of Health Grants NS-22189 to J. R. Wolpaw and HD-36020 to X. Y. Chen.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).