Characteristics and Organization of Discharge Properties in Rat Hindlimb Motoneurons

Abstract

The discharge properties of hindlimb motoneurons in ketamine–xylazine anesthetized rats were measured to assess contributions of persistent intrinsic currents to these characteristics and to determine their distribution in motoneuron pools. Most motoneurons (30/37) responded to ramp current injections with adapting patterns of discharge and the frequency–current (f–I) relations of nearly all motoneurons included a steep subprimary range of discharge. Despite the prevalence of adapting f–I relations, responses included indications that persistent inward currents (PICs) were activated, including increased membrane noise and prepotentials before discharge, as well as counterclockwise hysteresis and secondary ranges in f–I relations. Examination of spike thresholds and afterhyperpolarization (AHP) trajectories during repetitive discharge revealed systematic changes in threshold and trajectory within the subprimary, primary, and secondary f–I ranges. These changes in the primary and secondary ranges were qualitatively similar to those described previously for cat motoneurons. Within the subprimary range, AHP trajectories often included shallow approaches to threshold following recruitment and slope of the AHP ramp consistently increased until the subprimary range was reached. We suggest that PICs activated near recruitment contributed to these slope changes and formation of the subprimary range. Discharge characteristics were strongly correlated with motoneuron size, using input conductance as an indicator of size. Discharge adaptation, recruitment current, and frequency increased with input conductance, whereas both subprimary and primary f–I gains decreased. These results are discussed with respect to potential mechanisms and their functional implications.

INTRODUCTION

The intrinsic discharge properties of motoneurons are critical determinants of the motoneuron and muscle activity generated in response to synaptic inputs. Commonly investigated and assessed according to their frequency–current (f–I) relations (Granit et al. 1963; Kernell 1965a), several intrinsic properties influence motoneuron discharge characteristics. A primary factor is the magnitude and time course of the conductance that produces the medium-duration afterhyperpolarization (mAHP) (Kernell 1965b; Manuel et al. 2006; Viana et al. 1993). In addition, persistent inward currents (PICs), which amplify synaptic inputs and appear critical for normal motoneuron function (Heckman et al. 2005), contribute significantly to motoneuron discharge characteristics (Lee and Heckman 1998a; Li et al. 2004; Schwindt and Crill 1982).

PICs are mediated by persistent Na⁺ and Ca²⁺ L-type (Ca_V1.3) currents (Li and Bennett 2003), with N- and P-type Ca²⁺ channels contributing in some motoneurons (Powers and Binder 2003). Persistent Na⁺ currents are activated below the threshold for discharge and are critical to the ability of motoneurons to sustain discharge. The activation of Ca²⁺ PICs coincides with the increased gain observed in the secondary range of the f–I relationship (Schwindt and Crill 1982) and with the acceleration of discharge that can occur during ramp current injection (Lee and Heckman 1998b; Li et al. 2004). L-type Ca²⁺ PICs are also activated below or at threshold in many motoneurons in states of increased PIC expression (Lee and Heckman 1998b; Li et al. 2004), helping to initiate and sustain discharge. Moreover, by amplifying synaptic inputs, PICs can significantly increase the gain of motoneurons (Lee et al. 2003).

The depolarizing actions of PICs are opposed by the calcium-dependent potassium currents that produce the mAHP and also by other outward currents (Li and Bennett 2007; Powers and Binder 2003). Outward currents acting in concert with PICs influence the discharge properties of motoneurons (Lee and Heckman 1999; Schwindt and Crill 1982), particularly at greater levels of activity of the motoneuron. Voltage-clamp recordings from motoneurons show that the contribution of outward currents may be particularly important at the larger depolarizations expected at higher rates of discharge (Lee and Heckman 1998a; Li and Bennett 2007; Powers and Binder 2003). Moreover, outward currents likely contribute to systematic variation in rhythmic discharge patterns of motoneurons with input conductance (Lee and Heckman 1999).

The intrinsic properties of motoneurons are subject to several sources of neuromodulation (Rekling et al. 2000) and PIC expression is dependent on monoamines (Hounsgaard and Kiehn 1989; Hounsgaard et al. 1988; Lee and Heckman 2000; Li et al. 2007). Changes in the intrinsic properties of motoneurons could contribute to abnormal manifestations of motor control. For example, although acutely depressed following spinal cord transection, PIC activation increases in the chronic spinal animal (Li and Bennett 2003) and possibly contributes to the development of spasticity (Bennett et al. 2004). Considering the importance of PICs to motoneuron function and their lability in different modulatory states and following injury, we were particularly interested in examining activation of PICs and their contribution to motoneuron discharge characteristics for subsequent comparison with motoneuron responses following injury. Indirect evidence of PIC activation can be seen in counterclockwise f–I relations, in which discharge rates are greater during falling than during rising currents, and in recruitment currents that are greater than the currents needed to sustain discharge (Bennett et al. 2001; Button et al. 2006; Hounsgaard et al. 1988; Lee and Heckman 1998b). However, less information is available for direct comparison of discharge characteristics and PIC activation during membrane depolarization. Much of this information has been obtained for turtle or cat motoneurons or rat sacrocaudal (tail) motoneurons. Several studies have been performed on the discharge properties of rat hindlimb motoneurons to assess normal function or changes following spinal injury, hindlimb disuse, or hindlimb exercise (Beaumont et al. 2004, 2008; Button et al. 2006, 2008; Cormery et al. 2005), but direct measurements of PIC activation have not been made in rat hindlimb motoneurons.

A primary goal of this study was to determine discharge characteristics and interspike membrane potential trajectories during discharge of rat hindlimb motoneurons, to assess probable contributions of persistent inward and outward currents to their discharge. Second, we characterized discharge properties of these motoneurons over a wide physiological range, in which contributions of both PICs and outward currents to discharge responses would likely be evident. Finally, noting that discharge characteristics of cat motoneurons associated with PIC activation are correlated with input conductance (Lee and Heckman 1998a,b), we asked whether the discharge characteristics of rat hindlimb motoneurons are organized by size, as assessed by input conductance. We found that the discharge properties of rat hindlimb motoneurons include a high-gain region just above recruitment current, with characteristics consistent with features of motor-unit activity. Our results show that these discharge properties are organized according to motoneuron size and suggest that these properties depend on a balance of intrinsic inward and outward currents. The contributions by both persistent inward and outward currents to discharge characteristics are supported by determinations of persistent currents from voltage-clamp measurements reported in the companion article (Hamm et al. 2010). A preliminary and partial account of this work was previously presented (Turkin et al. 2009).

METHODS

The experiments were conducted on adult Long–Evans rats (350–500 g). All experimental procedures were reviewed and approved by the Institutional Animal Care and Use Committee at St. Joseph's Hospital and complied with principles from the Guide for the Care and Use of Laboratory Animals.

The rat was sedated in a chamber using an isoflurane and oxygen mix. Ketamine–xylazine anesthesia was given intramuscularly (90:10 mg/kg) or intravenously (iv; 9:1 mg·kg⁻¹·h⁻¹). Atropine (100 μg/kg) was given subcutaneously. A tracheotomy was performed and the rat was ventilated with a 1:2 oxygen–air mix. End-tidal carbon dioxide was measured and maintained between 3.6 and 4.0% by adjustments to rate and tidal volume. Heart rate and blood oxygen saturation were also monitored. The carotid artery was cannulated to measure blood pressure and the jugular vein was cannulated with a double-lumen catheter to administer an iv infusion of ketamine–xylazine cocktail (9 mg·kg⁻¹·h⁻¹ of ketamine and 1 mg·kg⁻¹·h⁻¹ of xylazine in lactated Ringer's solution with 4% Ficol and 10% dextrose), adjusted as needed to maintain an appropriate depth of anesthesia sufficient to block whisker tremor, corneal reflexes, and maintain stable heart rate. Norepinephrine (0.2% in physiological saline) was given as needed to maintain blood pressure >80 mmHg (typically 4 μg·kg⁻¹·h⁻¹). Core body (rectal) temperature was monitored and maintained at 37°C with a servo-controlled heating pad.

Following removal of paravertebral muscles, the lumbar spinal column was stabilized with parallel steel rods and clamps and a laminectomy was performed to expose the spinal cord area between the T12 and L4 vertebrae. The hindlimb was dissected to isolate the following hindlimb nerves: common peroneal (CP, superficial peroneal and deep peroneal branches); gastrocnemius-soleus (GS); and the distal part of the tibial nerve (Tib), including branches to plantaris, flexor hallucis longus, tibialis posterior, and flexor digitorum longus. The exposed nerves were cut and placed on bipolar silver-wire electrodes for stimulation; the exposed hindlimb tissue and spinal cord were covered with warm mineral oil. A silver-wire electrode was used to gently deflect dorsal roots to expose the dorsolateral surface of the spinal cord for microelectrode tracks and to record cord dorsum volleys.

Electrophysiological recordings

With the start of recording, pancuronium bromide (1 mg·kg⁻¹·h⁻¹) was administered iv to prevent muscle contraction. The paralysis was allowed to lapse after each administration to assess the depth of anesthesia. To reduce respiration-related movement, a left-side pneumothorax was performed. Sharp glass microelectrodes (1.5 mm) filled with 2 M potassium citrate were used for intracellular recording. Electrodes were pulled from 1.5-mm-diameter borosilicate glass, cleaned in several changes of reverse-osmosis purified boiling water, using a Flaming/Brown-type puller (Model P-97; Sutter Instrument, Novato, CA). Electrodes gradually tapered, with shaft lengths of about 7 mm and diameters of about 20 μm at 1 mm from the tip. Small openings were torn in the pia mater with Dumont #5 forceps and a broken electrode to facilitate electrode entry to the spinal cord. Electrode tracks were run using a custom-made spinal stereotaxic arc and piezoelectric microdrive system, usually using 6-μm steps. Electrodes were cleared frequently by passage of constant or oscillatory current and settling time during discontinuous current clamp following capacitance compensation was checked usually once or twice before cell penetration. Electrodes with unsatisfactory current-passage characteristics were promptly discarded. Motoneurons were identified by antidromic invasion in response to muscle nerve stimulation. Motoneurons were accepted for recording with spike amplitudes of ≥60 mV. (One motoneuron subsequently found in analysis to have a 59-mV spike amplitude was also accepted for analysis.) Intracellular recordings were made using an Axoclamp 2A amplifier and a custom-made sample-and-hold amplifier.

Averages (16 samples) were made of the antidromic and orthodromic action potentials, the latter produced in response to injection of 0.5-ms depolarizing current pulses. Ia excitatory postsynaptic potential (EPSP) amplitude was determined by homonymous muscle–nerve stimulation <1.8-fold threshold for a detectable cord dorsum volley; stimulation strength was adjusted to attain maximum EPSP amplitude. Input conductance was determined by injecting a series of hyperpolarizing and depolarizing 50-ms current pulses (usually 1 and 2 nA, average of eight). Rheobase current was determined as the intensity of 50-ms current pulses that produced spikes in approximately half the trials.

The discharge of motoneurons was recorded in response to injection of triangular ramp currents using the discontinuous-current-clamp mode of the Axoclamp amplifier, which was also used to determine input conductance. Sampling frequencies were 8–10 kHz. The monitor output of the amplifier was inspected throughout current injection to assess the completeness of electrode recovery following each current pulse. Current ramps were symmetrical, lasting 5 s on the ascending ramp and 5 s on the descent. Intervals of >10 s, usually ≥20 s, separated trials to avoid facilitation of PICs. Motoneurons were tested with current ramps of two or more amplitudes, usually with one or more repetitions at each amplitude. We usually started with a ramp current 1.5- to 2-fold rheobase, applying larger current amplitudes in subsequent trials. In cells with acceptable electrode performance and continued stable recording conditions, voltage-clamp recordings were made following the determination of discharge properties to obtain current–voltage (I–V) relations and measure net PICs. Results of the latter analyses are presented in the companion article (Hamm et al. 2010).

At the end of all intracellular measurements, the microelectrode was withdrawn from the motoneuron and the extracellular potential was measured as a reference for determination of membrane potentials. Low-gain and high-gain intracellular records, injected current, and cord dorsum signals were low-pass filtered (4.8 kHz) and digitized at rates of 10 kHz (input conductance, rheobase), 20.8 kHz (ramp current injection), and 25 kHz (all other records) and stored for subsequent analysis.

Analysis procedures

Analysis was conducted using standard functions and custom-written scripts and functions in Matlab. Some statistical procedures (Student's t-test, correlations) were performed with Statistica. Averages were computed with Matlab routines after inspection of individual samples. Input conductance was determined by the regression slope of at least three, usually four measurements of current and membrane potential change from averaged responses. Measurements of the potential change were made at the peak of the voltage response for input conductance and also at the end of the current pulse to evaluate hyperpolarization-activated cationic (I_h) current-related sag. Sag ratio was computed as the quotient of the I–V slope (from regression curves) at pulse end and at the peak of the voltage response; values of sag ratio increased from 1 with the prominence of the sag response. EPSP averages were measured for latency from cord-dorsum potential (to confirm monosynaptic latencies) and maximum amplitude. The AHP average following orthodromic spikes was used to determine AHP amplitude and half-decay time (time between AHP minimum and return of membrane potential halfway to prespike baseline). Conduction velocity was calculated from conduction distances for each nerve from the muscle–nerve electrode cathode to a reference site on the spinal cord, adjusted for distance of the electrode track from this site, and the conduction time, adjusted by 0.1 ms for utilization time.

Discharge rates during current injection were determined as instantaneous frequencies (1/interspike interval [ISI]) and these values and average currents injected during each ISI were used to construct f–I diagrams. f–I gains were computed from the slopes of regression lines fit to each range in the f–I diagrams (see results). The onset and end of discharge were sometimes associated with a few intervals of low-frequency irregular discharge; recruitment and derecruitment currents and frequencies were determined as frequencies became more regular and were clearly produced by the injected current rather than background activity. Leak conductances were computed in selected trials for each motoneuron from regression slopes fit to the linear portions of ascending and descending ramps. Voltage-activated depolarizations were evident in many motoneurons before and after discharge. The potential for their activation was estimated by the divergence of the membrane potential trajectory from this regression line and their amplitude was measured as the difference between their peak before (or after) discharge and the extrapolated regression line for leak conductance at that current.

In selected records for each motoneuron, measurements were made of spike threshold, mean membrane potential between spikes, and AHP minimum. We also determined spike duration at half-amplitude and the maximum rates of spike depolarization and repolarization. Spike threshold was determined as the potential at which dV_m/dt exceeded 10 mV/ms (Brownstone et al. 1992; Sekerli et al. 2004). Derivatives of the membrane potential V_m were computed at each time point t(i) by [V_m(i − 2) − 8V_m(i − 1) + 8V_m(i + 1) − V_m(i + 2)]/12[t(i + 1) − t(i − 1)], derived from a Taylor series approximation (Sekerli et al. 2004). Inspection of phase planes (dV_m/dt vs. V_m) in several motoneurons supported this method of threshold determination, as indicated by a rapid increase in dV_m/dt as the derivative exceeded 10 mV/ms. Mean membrane potential was computed as the mean of the interspike potential trajectory from the end of the preceding spike (dV_m/dt < −10 mV/ms) to threshold of the next spike. AHP minimum was the minimum potential during each trajectory, excluding the fast AHP at the start of the trajectory. Some interspike trajectories were also selected for determination of slope of the AHP “ramp” that followed the AHP “scoop” (Schwindt and Calvin 1972) and preceded the flattened portion of the interspike trajectory (see results), if present. This slope was determined by regression applied to a section of each trajectory selected by the analyst. Ramp slopes of other trajectories in the selected trial were determined by an automated Matlab routine, with sections chosen for regression based on the manual selections by interpolation.

Determinations of instantaneous frequencies, mean currents, spike thresholds, and trajectory potentials were made using automated Matlab routines. Results of these analyses were routinely inspected and spot checked for accuracy.

RESULTS

Intracellular recordings were obtained from 37 motoneurons, including 15 tibial motoneurons, 14 GS motoneurons, and 5 CP motoneurons in 15 successful experiments. Three motoneurons were unidentified; these were ventral to the GS motoneuron pool and were likely hamstring motoneurons (Nicolopoulos-Stournaras and Iles 1983). The properties of this sample of motoneurons are summarized in Table 1. The means and ranges of most properties were in general agreement with those found in previous studies (Bakels and Kernell 1993a,b; Beaumont et al. 2004; Button et al. 2006, 2007; Cormery et al. 2005; Gardiner 1993). However, only one motoneuron had an AHP half-decay time >20 ms, suggesting that nearly all motoneurons innervated fast-twitch muscle units (Gardiner 1993). In addition to the measurements summarized in Table 1, we also measured the amplitudes of action potentials just after the start of discharge during ramp current injection (from preramp potential to spike peak). These amplitudes, 74.6 ± 7.5 with a range of 53 to 88 mV, were similar to those found for the antidromic action potentials at the start of recording.

Table 1.

Properties of rat hindlimb motoneurons

Property	Value	Range
Resting potential, mV	−63.74 ± 6.80	−78.50 to −52.6
AP amplitude, mV	72.91 ± 6.76	58.30–91.68
Conduction velocity, m/s (n = 32)	51.11 ± 7.10	37.86–80.82
AHP amplitude, mV (n = 36)	1.78 ± 0.65	0.74–3.86
AHP half-decay time, ms (n = 36)	12.61 ± 2.33	7.50–21.1
Ia EPSP amplitude (GS), mV (n = 14)	2.36 ± 1.38	0.54–5.05
Ia EPSP amplitude (Tib, CP), mV (n = 20)	3.97 ± 2.62	0.99–11.53
Rheobase, nA	8.35 ± 4.36	1.00–18.00
Input conductance, μS	0.51 ± 0.14	0.17–0.81
Initial discharge frequency, Hz	24.61 ± 8.63	10.27–46.38
Final discharge frequency, Hz	22.27 ± 10.95	9.94–58.38
Recruitment current (Ir), nA	9.54 ± 5.63	1.60–22.04
Derecruitment current (Id), nA	12.93 ± 8.84	0.00–32.48
ΔI (Id − Ir), nA	3.49 ± 4.00	−1.94 to 14.8

Values are means ± SD, n = 37 unless indicated otherwise.

The f–I relation of most rat hindlimb motoneurons is adapting and includes a subprimary range

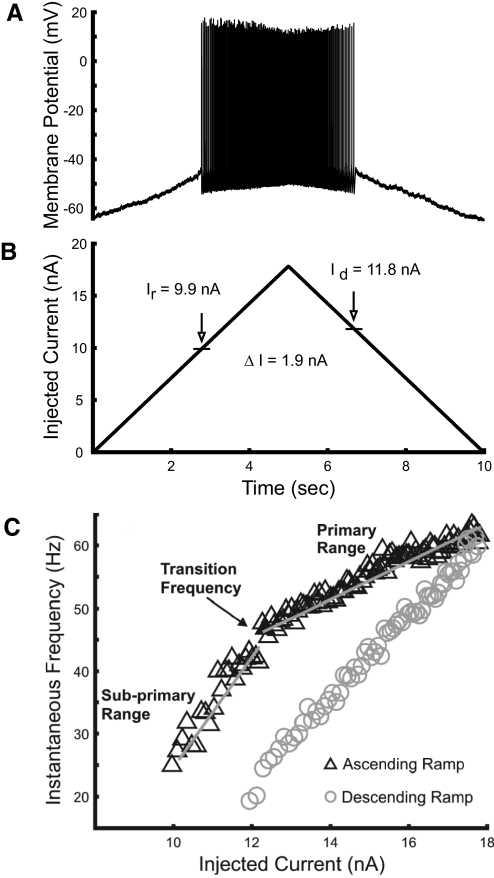
Discharge properties of lumbar motoneurons were investigated in response to ramp current injection. Figure 1A shows an example of the repetitive discharge in response to the current ramp. This motoneuron had a resting membrane potential of −63 mV and began repetitive firing when the membrane potential depolarized to −46 mV at a current of 9.9 nA. Discharge stopped on the descending ramp when the membrane potential reached −44 mV at 11.8 nA. The difference between the currents at which the cell was recruited and derecruited (ΔI; Fig. 1B) has been used as an indirect indication of the presence and amplitude of PICs, since their activation supports motoneuron discharge at currents less than the amount required for recruitment (Bennett et al. 2001; Button et al. 2006). The positive value of ΔI in this example (derecruitment current > recruitment current) provides no evidence of PIC activation. Positive values of ΔI were found in most cells (n = 34) with the ramp amplitudes that were applied.

Fig. 1.

Motoneuron (MN) response to ramp current injection. A: an example of an adaptive pattern of MN discharge, typical of most recordings, in which discharge starts at a smaller current than the current at which discharge stops. B: a 10-s ramp current with 18-nA amplitude was injected via glass microelectrode into the soma of the MN. The vertical arrows show the level of current at recruitment I_r and derecruitment I_d. C: frequency–current (f–I) relations for this MN, showing subprimary and primary gains and the transition frequency at their boundary during the ascending current ramp. Discharge during the ascending current ramp is indicated by black triangles, on the descending ramp by gray circles. The gray lines show regression lines fit to each range during the ascending ramp to determine f–I gains.

Nearly all cells (34 of 37) showed an initial steep slope, or gain, in the ascending limb of the f–I relation (Fig. 1C). We refer to this region as the subprimary range, following description of a subprimary range in mouse motoneurons (Manuel et al. 2009). The subprimary range of mouse motoneurons started with frequencies as low as 2–3 Hz and was very irregular, preventing meaningful estimation of the f–I gain in this range. The subprimary range that we observed in our experiments differed in some respects. Although discharge tended to be more irregular than that in the primary range, discharge was sufficiently regular to reliably estimate f–I gains, as evident in Fig. 1C. We were unable to evaluate subprimary f–I gain in only three cells. Two of these had atypically variable initial discharge and one cell responded with only a couple of spikes at low frequency before discharge in the primary range started. Further comparisons with the subprimary range in mouse motoneurons are provided in the following text.

Discharge usually started at frequencies >10–12 Hz, although occasional intervals at lower frequencies were observed in some cells. The f–I gains within the subprimary range varied from 4.6 to 38.7 Hz/nA (mean of 14.8 ± 7.1). Discharge frequency rose quickly with current after recruitment, achieving rates at the start of the primary f–I range that varied systematically with motoneuron properties (see following text). Typically, the boundary between the subprimary and primary ranges, which we call the transition frequency, was distinct. The primary f–I gain was smaller, ranging from 0.6 to 14.7 Hz/nA (mean of 4.7 ± 3.3). Discharge rates typically reached 50–80 Hz in the primary range (although currents were not always increased sufficiently to exceed the primary range or produce spike failure, so maximum primary-range discharge rates were not available for some cells).

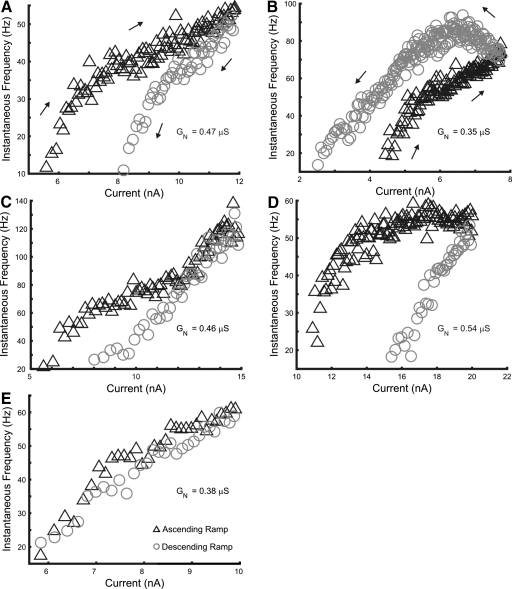
Discharge rates during descending ramp declined smoothly in most motoneurons, but four cells had two distinct ranges with different f–I gains and a distinct transition frequency between them, similar in character to the ascending ramp response. An example of such an f–I profile is shown in Fig. 2A.

Fig. 2.

Examples of f–I relations in rat hindlimb motoneurons. A: an adapting discharge pattern with clockwise hysteresis. The presence of subprimary ranges in both the ascending and descending current ramps was exceptional. B: a discharge pattern with late acceleration and counterclockwise hysteresis, indicating persistent inward current (PIC) activation. C: an adapting pattern of discharge with secondary-range acceleration during the latter part of the ascending ramp. D: an adapting pattern of discharge with a slight deceleration during the late ascending ramp. E: an example of a type 1 (linear) f–I response. The input conductance (G_N) for each motoneuron is indicated in the panel showing its f–I relation. Symbols are the same as those used in Fig. 1.

Previous studies have described four types of f–I relations for rat motoneurons; these relations differ with the presence or absence of adaptation and PIC activation (Bennett et al. 2001; Button et al. 2006). The first, linear type (type 1), in which discharge frequency on the ascending ramp overlaps that on the descending ramp, shows no signs of adaptation or PIC activation. Type 2 is an adapting pattern in which firing stops at a higher current on the descending ramp than that on the recruitment current, producing a clockwise f–I relation. In contrast, type 3 and type 4 responses both exhibit signs of PIC activation, with ΔI <0. Type 3 responses are linear, with continued discharge during the descending ramp to currents below the recruitment current, indicative of PIC activation before recruitment. Type 4 responses include an acceleration of discharge during the ramp, consistent with PIC activation following recruitment, producing counterclockwise hysteresis in the f–I relation.

We found three of these four types of f–I relations in our study, although some differences in these patterns were observed compared with those in previous studies. Examples are shown in Fig. 2. Most motoneurons (30 of 37) had a clearly adapting pattern of discharge with clockwise hysteresis and a positive ΔI, as shown in Figs. 1C and 2, A, C, and D. The f–I relations of these cells resembled type 2 responses, but they usually included an initial subprimary range with increased gain.

Four cells of the remaining seven cells had f–I relations similar to type 1, showing little sign of either adaptation or PIC activation. These cells had recruitment currents that approximately matched the derecruitment current; an example is shown in Fig. 2E. The other three cells had counterclockwise f–I relations and negative ΔI values, corresponding to type 4 responses as illustrated in Fig. 2B. Two of these cells stopped discharge at positive currents as in Fig. 2B, whereas one exhibited self-sustained firing, continuing to discharge at the end of the current ramp (see Fig. 8). These f–I characteristics provide clear evidence of PIC activation in these motoneurons. We did not observe any motoneurons with type 3 f–I responses.

Fig. 8.

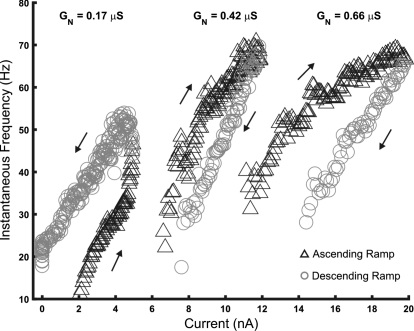
f–I relations for 3 MNs of different input conductance. Input conductance (G_N), used as a measure of cell size, is indicated near the f–I relation for each MN. Increasing input conductance was associated with adapting patterns of discharge and less sensitivity to injected current; cells with small input conductance were more sensitive and more likely to have a counterclockwise f–I pattern.

More complex responses were observed in some motoneurons as the amplitude of the injected current increased. In 6 of the 30 cells with type 2 responses, we observed acceleration in discharge rate in the latter half of the ascending current ramp consistent with a secondary range, as shown in Fig. 2C. This acceleration lasted until the end of ascending phase in some cells, with rate declining on the descending ramp as in the example shown in Fig. 2C. In some cases the discharge acceleration was interrupted by accommodation and falling discharge (see Fig. 7B). Including cells with type 4 responses, 9 of the 37 motoneurons had f–I relations consistent with a secondary range and PIC activation above threshold. Another 14 of the 37 cells showed a plateau or even deceleration in the discharge rate with larger currents during the ascending ramp (Fig. 2D), indicating that additional adaptation and/or accommodation occurred with increasing current injection in these motoneurons. Motoneurons with a discharge plateau or deceleration at larger currents had larger values of input conductance than those with acceleration and a secondary range (G_N = 0.60 ± 0.09 vs. 0.39 ± 0.11, respectively; t = 4.79, P < 0.001).

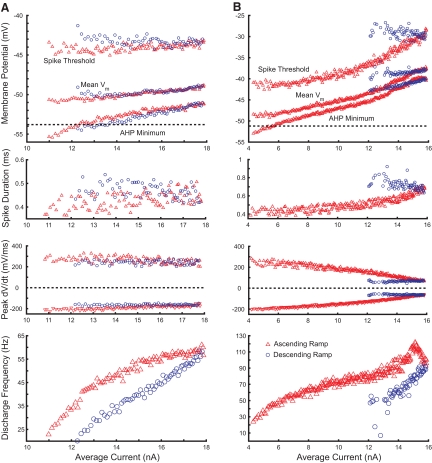
Fig. 7.

Changes in spike threshold, average membrane potential, and AHP minima with injected current and discharge frequency. A: interspike membrane potentials for MN with adapting discharge pattern. B: membrane potentials for MN with secondary-range acceleration and accommodation. Top panels show spike threshold, mean membrane potential between spikes, and minimum membrane potential during medium-duration afterhyperpolarization (mAHP; excluding fast AHP); panels in 2nd row show spike durations at half-amplitude; maximum rates of spike depolarization (positive values) and repolarization (negative values) are illustrated in 3rd-row panels; bottom panels show corresponding f–I relations. Red triangles indicate data from ascending current ramp, blue circles from descending current ramp. Dashed horizontal lines in top panels indicate membrane potential at which predischarge depolarization diverges from voltage projected from leak conductance (see Fig. 4).

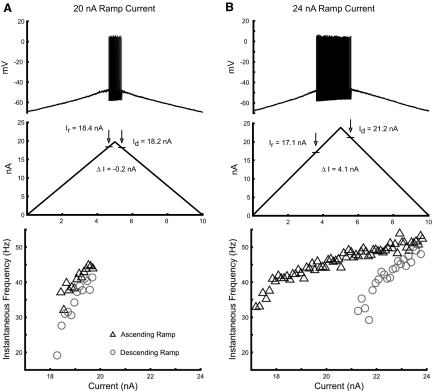
The presence of a subprimary range and the large proportion of motoneurons with adapting f–I relations distinguish our results from those of earlier studies (Bennett et al. 2001; Button et al. 2006; Li et al. 2004). We suspected that this difference could be produced in part by the increased levels of current injected relative to that needed for recruitment. Figure 3 illustrates the responses in one motoneuron in which the amplitude of the current ramp was set just positive to the recruitment current. The test was then repeated using a larger current ramp. With application of a 20-nA ramp (Fig. 3A), the current level needed for recruitment was just exceeded; discharge was relatively brief and continued during the descending ramp to currents less than the recruitment current, yielding what appears to be a type 3 f–I response and a small negative ΔI. However, application of the larger current ramp produced longer-lasting, more vigorous discharge and conversion of the f–I relation to an adapting type 2 response with a positive ΔI (Fig. 3B). The same responses were obtained in repetitions of the two current amplitudes. Although anecdotal, this example suggests that the difference between studies lies partially in the different ranges of current used. Additionally, it stresses the need to verify that type 3 responses are linear over a range of currents, consistent with PIC activation below spike threshold (Li et al. 2004).

Fig. 3.

Dependence of f–I relation characteristics on ramp current amplitude. A: the discharge pattern of a gastrocnemius-soleus (GS) motoneuron in response to a level of injected current that just exceeded threshold. Under these conditions, the MN displays an apparent type 3 response with a small negative ΔI (the difference between the currents at derecruitment and recruitment). B: the f–I relation for the same GS motoneuron in response to a higher level of injected current. Symbols and abbreviations are the same as those used in Fig. 1.

Discharge properties of rat hindlimb motoneurons have characteristics consistent with PIC activation

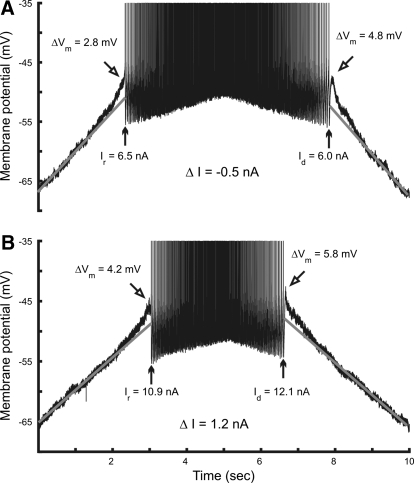
Despite the prevalence of motoneurons with an adapting pattern of discharge, plateaus and other evidence of PIC activation were observed in many of these cells. The membrane potential during the ascending current ramp often depolarized more than the value expected from the projected leak conductance and the level of noise in the membrane potential increased before discharge (Figs. 1, 3, 4, and 5). Figure 4 shows profiles of discharge for two different hindlimb motoneurons, one in which the f–I relation indicated PIC activation and one in which the f–I relation did not. The motoneuron represented in Fig. 4A had a negative ΔI and counterclockwise hysteresis. The cell whose response is shown in Fig. 4B had a typical adapting discharge with positive ΔI and clockwise hysteresis. Despite the different f–I profiles, the membrane potentials of both motoneurons depolarized in a similar manner above the level expected from the projected leak conductance. The amplitude of this additional depolarization before and after discharge is indicated by ΔV_m in Fig. 4. These depolarizations were observed in 26 of 37 discharging motoneurons before and after discharge, consistent with voltage-dependent activation of PICs. Average values for these potentials were 2.62 (±0.97) mV (ascending ramp) and 2.37 (±2.16) mV (descending ramp). The mean membrane potential for activation of these depolarizations was −52.7 (±6.5) mV, well below the mean spike threshold of −44.3 (±6) mV.

Fig. 4.

Evidence of PIC activation in motoneurons with different types of f–I relations. A: discharge of a motoneuron with counterclockwise hysteresis and negative ΔI. B: discharge of MN with clockwise hysteresis and positive ΔI. Vertical arrows indicate the current at recruitment (I_r) and derecruitment (I_d). Angled arrows indicate the maximum depolarization (ΔV_m) above the potential expected from the projected leak conductance (shown by gray regression lines) before and after discharge.

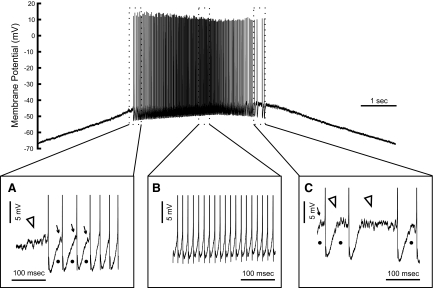
Fig. 5.

Voltage-activated high-frequency fluctuations appear in some motoneurons before, during, and after MN discharge. The top of the figure shows the MN response to a current ramp; the panels below show truncated and expanded sections of this record at the start (A), peak (B), and end (C) of discharge. A: high-frequency fluctuations in membrane potential start shortly before discharge (open arrowhead) and similar transient potentials can be seen (arrows) in flattened regions between spikes (indicated by dots), which vanish after several interspike intervals (ISIs). B: oscillations and flattened trajectories are absent during most of the response. C: high-frequency fluctuations (open arrowheads) and flattened interspike trajectories (dots) reappear at the end of discharge.

In several cases we observed long-lasting plateaus either preceding (one cell) or following discharge (four cells). In each of these cases, spike failure or a substantial decrease in spike amplitude was observed during injection of large currents (twice rheobase or more). In the one motoneuron in which a plateau preceded discharge, the plateau developed over several trials.

We also observed voltage-dependent noise at depolarized membrane potentials, usually positive to −55 mV. This noise started and ended approximately at the same membrane potential. At these depolarized potentials, some cells (9) demonstrated more regular, voltage-dependent high-frequency oscillations. The frequency of these oscillations in different cells varied between 70 and 170 Hz. Inspection of interspike trajectories sometimes revealed the presence of these oscillations, especially when discharge was irregular, i.e., at the beginning and/or end of discharge (Fig. 5, A and C). At higher rates of discharge, these oscillations were absent (Fig. 5B). In most repetitively discharging cells (25 of 37), the interspike trajectory flattened toward the end of the ISI at low frequencies, at both the start and the end of discharge (Figs. 5 and 6). The combination of noise and oscillations, probably produced by low-threshold PICs, and flattened trajectories likely contributes to low-frequency and irregular discharge (Li et al. 2004; Manuel et al. 2009).

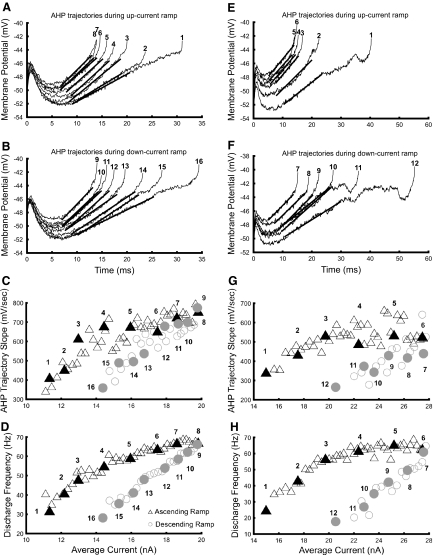
Fig. 6.

Changes in afterhyperpolarization (AHP) trajectories during MN discharge. Panels in the left and right columns show responses from different MNs. A and E: AHP trajectories between spikes during the ascending current ramp. B and F: trajectories during the descending current ramp. C and G: slopes of the ramp component of AHP trajectories. Slopes were determined from regression lines fit to each ramp, shown by thick black lines superimposed on trajectories shown in pairs A and E and B and F. D and H: f–I relations. Black triangles and gray circles indicate responses during the ascending and descending current ramps, respectively. Numbered, filled symbols indicate ISIs whose trajectories are shown in A and E and B and F. Only one of every 3 intervals is shown in C, D, G, and H for clarity.

Manuel et al. (2009) noted the contribution of similar oscillations and flattened interspike trajectories to discharge variability and the subprimary range in mouse spinal motoneurons. We compared the current ranges in which oscillations and flattened trajectories occurred to the subprimary range to determine whether these phenomena were sufficient to explain the subprimary range in rat hindlimb motoneurons. The range of currents and frequencies in which flattened trajectories occurred did not correspond completely with the subprimary range. In most cells with flattened trajectories (15 of 25), flattened interspike regions were observed following only the first three or four spikes, well before the end of the subprimary range; in other cells (10 of 25) flattened trajectories could be observed throughout the subprimary range. Considering also the cells in which flattened trajectories were not observed, these characteristics appear insufficient to produce the subprimary range in rat motoneurons.

Changes in AHP trajectories correspond to different f–I relation ranges

As noted in the introduction, the AHP is a primary determinant of f–I gain. We examined AHP trajectories to compare their values, shape, and time course in the subprimary and primary ranges of the f–I relation. AHP trajectories consisted of a “scoop and ramp” as described for cat motoneurons (Schwindt and Calvin 1972). The depth and width of the early portion of the AHP (the “scoop”) decreased in the subprimary and primary ranges of discharge as the ISI shortened with increasing current. Within the primary range, the slope of the subsequent AHP trajectory (the “ramp”) was nearly constant, such that depolarization and shortening of the scoop accounted for changes in ISI and frequency, as described by Schwindt and Calvin (1972). However, AHP trajectories within the subprimary range often included flattened regions preceding subsequent spikes, as noted earlier; these shortened and usually vanished before the end of the subprimary range. Also within the subprimary range, ramp slope increased from a minimum at the lowest rates of discharge to the value achieved in the primary range at the transition frequency.

These characteristics are illustrated in Fig. 6, which shows AHP trajectories for two motoneurons with typical adapting patterns of discharge. One motoneuron lacked flattened interspike trajectories during the ascending current ramp (panels in left column of Fig. 6), whereas the AHP trajectories of the other motoneuron were more typical. Each trajectory shown in these figures can be identified in the plots of ramp slope and f–I relation as a filled symbol with corresponding number. Trajectories 1 and 2 are positioned in the subprimary range and trajectory 3 approximately marks the transition frequency in each set of plots. The correspondence between the subprimary range and the region in which ramp slope increases with current and frequency can be seen by comparing the f–I relations in Fig. 6, D and H with the AHP trajectory ramp slopes in Fig. 6, C and G, respectively. This correspondence was a consistent finding.

Some MNs (9 of 37) displayed a secondary range, with acceleration of discharge rate in the latter portion of the ascending current ramp. In these cells the acceleration in discharge rate could be very strong, quickly reaching rates >100 Hz in some cases. As observed in cat motoneurons (Schwindt and Calvin 1972), within this range the scoop of the AHP trajectories was altered, becoming inverted and shortening further as the intervals between spikes shortened (not shown).

Comparisons of the variation with current and frequency of AHP minimum, mean membrane potential between spikes, and spike threshold did not reveal substantial differences between the subprimary and primary ranges (Fig. 7). Figure 7A shows a motoneuron with an adapting pattern of discharge. AHP minimum, mean membrane potential, and spike threshold all depolarized with increasing current, but changes in these potentials were modest through the subprimary and primary ranges and were less than described previously for cat motoneurons (Schwindt and Crill 1982). Changes in spike threshold were often in the range of 1–2 mV within the primary range. Spike threshold tended to be somewhat more positive on the down-ramp, although this difference was usually small, as shown here. Comparing the subprimary and primary ranges, greater variability in spike threshold was often observed within the subprimary range on the ascending current ramp and threshold was often constant or even decreased slightly with increasing current within this range (24 of 37 cells), compared with consistent increases with current in the primary range.

An example of a motoneuron with larger changes in spike threshold and the other potentials is shown in Fig. 7B. Although changes in these potentials were larger, the pattern of changes is similar to the example in Fig. 7A. The f–I relation of this motoneuron also includes the start of secondary range discharge at about 14 nA, although the acceleration in discharge was interrupted by accommodation. Spike generation failed on the descending current ramp in this motoneuron, leaving a plateau potential. The region of spike rate acceleration and following accommodation is marked by increasing spike threshold depolarization, as well as depolarization of mean membrane potential and AHP minimum with initiation of the plateau potential. The extent of spike threshold depolarization during secondary range firing varied with the increase in discharge rate, with increases of roughly 5 mV in some cells with large increases in discharge rate.

Figure 7, A and B also shows the membrane potentials at which the predischarge depolarization diverged from the linear trajectory expected from leak conductance. In most cells AHP minima were hyperpolarized relative to this level at the start of discharge. The AHP minima depolarized with increasing current and frequency, approximating the potential for activation of these prepotentials near the end of the subprimary range; the mean difference between AHP minima at the end of the subprimary range and prepotential activation was <0.1 mV. Within the subprimary range, interspike trajectories usually passed through the membrane potentials for prepotential activation, exceeding this threshold in the primary range.

We also examined changes in spike duration and maximum rates of spike depolarization and repolarization during discharge, as shown in the middle two panels of Fig. 7. Each of these variables changes progressively throughout discharge, with larger changes in the cell with accommodation. The average spike duration at the start of discharge was 0.41 ± 0.04 ms, increasing to 0.55 ± 0.09 ms at discharge termination. As was the case for membrane potentials, these variations occurred smoothly through the subprimary and primary ranges. These were consistent findings in all discharging motoneurons. Across the population of cells the increase in spike duration was correlated with the decreases in rates of both spike depolarization (r = 0.54, P < 0.001) and repolarization (r = 0.82, P < 0.001). Changes in these variables are consistent with some fast Na⁺ inactivation that may have contributed to changes in threshold and slowing rates of discharge.

In summary, variations in AHP trajectories and spike thresholds corresponded to different regions of the f–I relation. Spike thresholds varied through the primary range and particularly in the secondary range, as described previously for cat motoneurons. We also observed progressive increases in spike duration and decreases in rates of spike depolarization and repolarization. Changes correlated to the f–I relation included a progressive increase in AHP ramp slope throughout the subprimary range and the AHP trajectories in this range crossed potentials at which signs of PIC activation occurred. These latter changes suggest contributions of the first PICs activated to f–I gain in the subprimary range.

Discharge properties of rat hindlimb motoneurons are correlated with input conductance

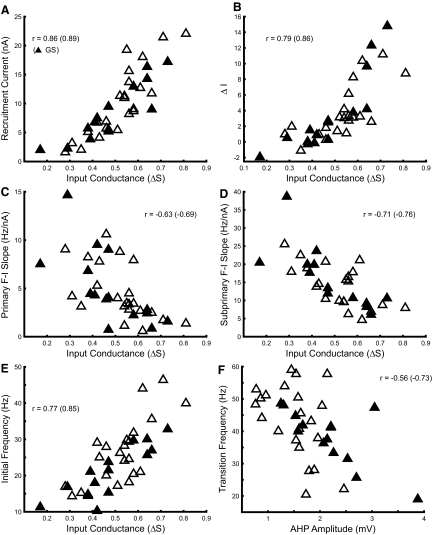
The tendency of rat hindlimb motoneurons to accelerate or decelerate at larger amplitudes of injected current depends on their input conductance, as noted earlier. We found that several discharge characteristics of rat hindlimb motoneurons were strongly associated with input conductance, which we used in this study as a measure of motoneuron size. Figure 8 illustrates f–I relations for three motoneurons of different input conductance. Current at recruitment and initial discharge rate were smallest in the motoneuron with the smallest input conductance (G_N = 0.17 μS), which responded to ramp current amplitudes of 1–5 nA. PIC activation was also evident in this motoneuron, as indicated by the counterclockwise hysteresis and self-sustained discharge following the end of current injection. This motoneuron's response was similar to that of the fully bistable cells described by Lee and Heckman (1998b); discharge was stopped after several seconds of self-sustained firing by injection of a hyperpolarizing current pulse. The second motoneuron of intermediate size (G_N = 0.42 μS) required currents of 6–11 nA for discharge. This motoneuron had an adapting pattern of discharge with a small positive value of ΔI. The largest motoneuron (G_N = 0.66 μS) required a current of 12–20 nA for discharge and displayed more discharge adaptation and a larger, more positive value of ΔI. The differences in recruitment current and discharge rate at recruitment were expected and these associations with motoneuron size are well known. However, it is also apparent from this figure that f–I gains of both the subprimary and primary ranges varied with input conductance, as well as ΔI. On the whole, larger values of input conductance were associated with adapting patterns of discharge and less sensitivity to injected current, whereas evidence of PIC expression in f–I relations was strongest in motoneurons with lower input conductance.

The associations between input conductance and discharge characteristics are shown for the entire sample of motoneurons in Fig. 9. Symbols representing GS motoneurons are filled to distinguish them from unidentified motoneurons or those that innervated the tibial or common peroneal nerves, since these latter groups are more functionally heterogeneous. Moreover, we sought to ensure that any associations observed were not produced or obscured by differences in organization between motoneuron pools (Bakels and Kernell 1993a). The expected ordering of recruitment current by size is shown in Fig. 9A. The relation between rheobase and input conductance is essentially the same (not shown). The tendency of discharge rate to adapt during ramp current injection was also directly correlated with input conductance (Fig. 9B). Accordingly ΔI increased with motoneuron size and negative values indicating that discharge continued at currents below the recruitment current were found only in smaller motoneurons. (The value of ΔI in the one cell with self-sustained discharge was truncated at −1.9 nA, i.e., the additive inverse of recruitment current. However, this bias would not significantly affect the overall correlation evident in Fig. 9B.)

Fig. 9.

Associations of MN discharge properties with input conductance. Several discharge properties were correlated with input conductance. A: recruitment current. B: ΔI, the difference between the currents at derecruitment and recruitment. C: f–I gain in the primary range. D: f–I gain in the subprimary range. E: discharge frequency at recruitment. F: transition frequency (Fig. 1) was best correlated with AHP amplitude. Filled symbols represent values for GS motoneurons. Correlation coefficients are shown in each panel; value in parentheses is correlation coefficient for GS population. All correlation coefficients were significant (P < 0.01).

A consistent feature in our results was the presence of a subprimary range in the f–I relation of rat hindlimb motoneurons. Unexpectedly, we found that f–I gains in both subprimary and primary ranges were inversely correlated with input conductance (Fig. 9, C and D). The largest f–I gains were found in low-conductance motoneurons and gains decreased as input conductance increased. Consequently, increases in discharge rate in rat hindlimb motoneurons following recruitment require progressively more current in larger, later recruited cells.

The initial discharge frequency at the start of discharge increased with input conductance (Fig. 9E), consistent with previous findings that minimum discharge rates or rates at recruitment vary with size and motor unit properties (Button et al. 2006; Kernell 1979). The discharge frequency at the border between the subprimary and primary ranges, the transition frequency, was also correlated with input conductance (not shown), but this correlation was weaker than that presented earlier (r = 0.45, P < 0.01) and depended heavily on the cell with the smallest input conductance and longest AHP half-decay time whose f–I relation is shown in Fig. 8 (r = 0.34, P = 0.051 without this cell). A stronger correlation was found between transition frequency and AHP amplitude, which was not correlated with input conductance (r = −0.14, P = 0.41). As shown in Fig. 9F, transition frequencies varied over a substantial range, from roughly 20 to 60 Hz, 10 to 25 Hz higher than the discharge frequency at recruitment in most cases, with a mean increase of 17.4 Hz. Transition frequency was inversely correlated with AHP amplitude, decreasing as AHP amplitude increased. An inverse correlation was also observed between transition frequency and AHP half-decay time, although as in the association of transition frequency with input conductance, this correlation was weaker (r = −0.37, P = 0.026; not shown) and depended on the cell with the largest AHP half-decay time (r = −0.20, P = 0.26 without this cell).

All correlations shown in Fig. 9 were significant in GS motoneurons as well as the entire sample of motoneurons and tended to be somewhat stronger in the GS pool. All associations shown were also significant in the sample when GS motoneurons were excluded and when the cell with smallest input conductance and longest AHP half-decay time was excluded. These correlations were not the result of variation in cell condition; input conductance was uncorrelated with either antidromic spike amplitude (r = −0.001, P = 0.996) or resting membrane potential (r = −0.02, P = 0.88).

The I_h current produces a resonance in cat motoneurons (Manuel et al. 2007; cf. Maltenfort and Hamm 2004). Activation of fast PICs in resonant motoneurons enhances their responsiveness to the dynamic components of excitatory synaptic inputs, but facilitates plateau activation and amplification of synaptic inputs in nonresonant motoneurons (Manuel et al. 2007). We examined sag ratio, a measure of I_h current, in relation to input conductance. Sag ratio was directly correlated with input conductance in the entire set of motoneurons (r = 0.54, P < 0.001) and a similar tendency was observed in GS motoneurons (r = 0.53, P = 0.054). We also examined the size dependence of homonymous Ia EPSP amplitudes in GS motoneurons. EPSP amplitudes tended to be inversely correlated with input conductance (r = −0.48, P = 0.083), although this tendency was not observed in the heterogeneous mix of non-GS motoneurons. These results suggest a greater dynamic responsiveness of larger rat hindlimb motoneurons to excitatory synaptic inputs with fast PIC activation, whereas amplification of larger, static EPSP components would be favored in smaller motoneurons.

DISCUSSION

This study demonstrates that discharge properties of rat hindlimb motoneurons are strongly associated with input conductance, suggesting that discharge properties of these motoneurons vary systematically with their size. A prominent feature of these discharge properties is a steep subprimary range preceding the primary range. We also found evidence of PIC activation, but often in the presence of adapting patterns of motoneuron discharge. In addition, we found associations between the features of AHP trajectories, ranges of the f–I relations, and indicators of PIC activation. These results are consistent with determination of discharge properties by the combined actions of PICs, gradual inactivation of fast Na⁺ currents, and outward currents. In the following discussion we consider factors and mechanisms that might contribute to these properties and their functional implications.

Subprimary range in rat hindlimb motoneurons

The form of the f–I relationship in the vicinity of recruitment current is variable in different species and conditions. A “subprimary range” of the type presented here has not been described previously in studies of cat motoneurons, which inform much of our understanding of motoneuron discharge characteristics and the initial nonlinear portion of the f–I relation in different motoneurons may consist of nothing more than a slight undershoot. However, several investigators have reported f–I relations with features similar to those of the subprimary range reported here. The characteristics of a subprimary range recently found in mouse motoneurons (Manuel et al. 2009) have already been described. Also, it should be noted that discharge characteristics consistent with a subprimary range were reported previously for rat jaw-elevator motoneurons. Moore and Appenteng (1990), using injected current ramps, also found steep increases in discharge rate following recruitment before transition to a region of smaller gain. This subprimary range was insensitive to the rate of current injection. Similar bilinear f–I relations have been reported in other neuron types as well, e.g., neurons in cat sensorimotor cortex (Stafstrom et al. 1984). Thus a subprimary range may contribute to discharge characteristics in various species and neuron types.

Mean f–I gains in the subprimary range (14.8) and their variation are very similar to those reported by Button and colleagues (15.3 and 17.8 slow and fast motoneurons) who also used ramp currents to assess discharge properties of rat hindlimb motoneurons (Button et al. 2006). Button et al. did not report separate subprimary and primary ranges, but the current amplitudes appear to have been limited and insufficient to enter the primary range. By comparison, several studies that used long current pulses rather than ramps reported f–I gains (∼6–7) (Beaumont et al. 2004, 2008; Button et al. 2006, 2008) comparable with those found in our primary range (4.8), suggesting that the primary ranges obtained by these different methods provide similar assessments of motoneuron responsiveness. Although the subprimary range is evident in f–I diagrams of mouse motoneurons constructed from pulse responses (Manuel et al. 2009), it appears to be absent or difficult to detect in similarly constructed f–I diagrams of rat motoneurons, a difference perhaps attributable to different properties of adaptation.

The functional implications of larger gains in the f–I relation following recruitment can be assessed by considering the discharge rates produced during normal activities and the rates required for force production in hindlimb motor units. During unrestrained locomotion, discharge rates of 20–30 Hz are typically observed in slow-twitch motor units, whereas fast-twitch units discharge at frequencies ranging from 60 to as high as 100 Hz (Gorassini et al. 2000; Hennig and Lomo 1985). Functionally isolated rat medial gastrocnemius motor units produce 60% of their force at rates of about 15 to 60 Hz, depending on contraction speed (Mrówczynski et al. 2006). The rates needed for this level of force production correspond well with transition frequencies at the end of the subprimary range (Fig. 9F). With the larger f–I gains in the subprimary range, relatively little current would be required to attain this level of activity, placing units at a suitable operating point for effective grading of force by rate modulation and achieving the rates of discharge required for locomotion through the combination of additional synaptic current and PIC activation.

Rate limiting is a prominent feature of rate modulation of human motor units during contractions of increasing force (Binder et al. 1996; Monster and Chan 1977), not readily explained by traditional intrinsic properties of motoneurons and the organization of their synaptic inputs (Heckman and Binder 1993). A tertiary firing range with full PIC activation (Elbasiouny et al. 2006; Li et al. 2004) and the initiation of PIC activation near the threshold for discharge in conditions that favor PIC activation (Lee and Heckman 1998b; Li et al. 2004) suggest the possibility that rate limitation corresponds to this tertiary range discharge (Heckman et al. 2008). However, entry into the primary range following subprimary range discharge should be considered as an alternative explanation for rate-limiting discharge patterns. Particularly at low forces, a subprimary–primary range pattern of activation would achieve efficient modulation of motor-unit force while reserving secondary range modulation for more intense efforts, as suggested by some studies of motor-unit activity (Kanosue et al. 1979).

AHP trajectories at low discharge rates in the subprimary range often contained a region of flattened slope following the scoop and ramp. The variability of human motor-unit discharge is relatively greatest at recruitment, decreasing with discharge frequency (Moritz et al. 2005). Analysis of ISI variability at low frequencies near recruitment indicates that AHP trajectories in human motoneurons approach threshold gradually, consistent with an exponential decay, unlike the final ramp in cat motoneurons (Matthews 1996). The characteristics of the AHP trajectory observed for rat hindlimb motoneurons are consistent with that suggested for human motoneurons and the discharge variability of human motor units at low discharge frequencies.

Association of discharge properties with input conductance

The association of recruitment order and the current required for recruitment with size-related motoneuron parameters is well known (Binder et al. 1996). Minimum and maximum discharge rates are also associated with motor-unit properties (Button et al. 2006; Kernell 1979). Moreover, the tendency of motoneuron discharge to accelerate or decelerate at larger currents and ΔI was also associated with input conductance, such that motoneurons with larger input conductance were more likely to exhibit adapting discharge patterns. A variety of studies have shown that tendencies toward adaptation and accommodation are more pronounced in large type F motoneurons, whereas properties of smaller motoneurons promote continued activity and PIC activation (Burke and Nelson 1971; Button et al. 2007; Kernell and Monster 1982; Lee and Heckman 1998b). Our results are consistent with these findings.

However, previous work has provided mixed evidence for an association between size-related parameters and f–I gain. In cat motoneurons, f–I gain is correlated neither with input resistance over the range of commonly observed values (Kernell 1966; Schwindt and Calvin 1972), nor with contractile motor-unit properties (Kernell 1979). The f–I gains do not differ significantly in type S and type F rat hindlimb motoneurons classified according to AHP half-decay time (Button et al. 2006). However, the f–I gain of turtle motoneurons varies with size, decreasing with somatic and dendritic size parameters, as does input resistance (McDonagh et al. 2002). An inverse correlation between f–I gain and input conductance has also been reported for decerebrate cat motoneurons (Lee et al. 2003). Decreases of f–I gains in both subprimary and primary ranges with increasing input conductance found here are consistent with these latter studies. This decrease in f–I gain with size is functionally significant, since the current required for a given increase in frequency would scale with motoneuron size, surface area, and the amount of synaptic current that could potentially be applied to the motoneuron (Kernell 2006). Consequently, we consider the inverse relation between f–I gain and input conductance to be an organizing principle of discharge within motoneuron pools.

Our sample contained only one motoneuron with an AHP half-decay time >20 ms. The use of ketamine–xylazine anesthesia tends to reduce AHP amplitude and half-decay time (Button et al. 2006) and the reliability with which AHP half-decay time distinguishes types S and F depends on whether motor units are classified by response to an unfused tetanus (Gardiner 1993) or twitch contraction time (Bakels and Kernell 1993b). Nonetheless, type S motoneurons were probably underrepresented in our sample, suggesting that the association between f–I gain and input conductance applies to the entire motoneuron pool and likely within type F motoneurons.

Since we used current ramps of fixed duration and scaled ramp amplitude according to each cell's rheobase currents, the rate of current injection varied systematically with size, which may have affected our results. We do not expect that this effect was large; previous work indicates that the speed of relatively slow ramps has little influence on discharge responses (Moore and Appenteng 1990). Although the rate of current injection affects discharge during injection of faster ramps, the tendency of discharge to increase with ramp speed (Baldissera et al. 1982) would produce a direct correlation of f–I gain with ramp amplitude and input conductance, opposite to that found here.

The range of observed transition frequencies corresponded to rates in the steep portion of motor-unit force–rate curves, as noted earlier, and these frequencies were better correlated with AHP amplitude than with input conductance. Previous studies have shown an association between AHP parameters and muscle-unit contraction time (Bakels and Kernell 1993a,b; Gardiner 1993; Zengel et al. 1985), but this association is stronger for AHP half-decay time than that for AHP amplitude and depends primarily on type S–type F differences (however, see Bakels and Kernell 1993b). The variation in transition frequency would seem most useful if the transition frequency of a motoneuron matched the force–rate relation of its innervated muscle unit, which is correlated with contraction time (Kernell et al. 1983). Given these uncertainties in the relations of AHP parameters with contraction times and associated force–rate relations, however, it is uncertain how well variations in transition frequency match those of force–rate relations.

The factors that produce the inverse relation between f–I gain and input conductance remain unknown. Input conductance is not a direct determinant of f–I gain (Meunier and Borejsza 2005). Rather, the AHP is of primary importance and AHP conductance, duration, and drive potential (spike threshold to K⁺ reversal potential) largely determine f–I gain (Manuel et al. 2006; Meunier and Borejsza 2005; Wilson et al. 2004). AHP conductance is not correlated with input conductance in cat motoneurons (Manuel et al. 2005), whereas AHP amplitude and half-decay time vary with motor-unit type (Zengel et al. 1985). Since longer AHPs are found in type S motoneurons with smaller input conductances, the variation in AHP parameters with type would tend to produce a relation between f–I gain and input conductance opposite of that observed. Thus other factors must contribute to this relation. One possibility is that f–I gain varies with the distribution of voltage-activated currents across the motoneuron pool. The potential contributions of persistent currents to f–I gain and motoneuron discharge properties are considered in the following text.

Contributions of PICs and outward currents to motoneuron discharge properties

Neurons with only fast voltage-activated currents would have only highly nonlinear f–I relations, characterized by a limited range of high discharge rates (Stein 1967). Addition of AHP conductances produces a linear f–I relation (Kernell and Sjöholm 1973); this conversion of the f–I relation by mechanisms of adaptation is a general feature of neurons (Ermentrout 1998). Thus AHP currents are of primary importance in determining discharge characteristics of motoneurons and other neurons, including f–I gain, as noted earlier. They can also produce secondary range characteristics in f–I relations (Meunier and Borejsza 2005; Wilson et al. 2004). However, other currents, activated by depolarization, also influence discharge. Thus motoneurons enter the secondary range of the f–I relation with activation of Ca²⁺ PICs (Elbasiouny et al. 2006; Li et al. 2004; Schwindt and Crill 1982) and blocking L-type Ca²⁺ currents eliminates the secondary range in rat sacrocaudal motoneurons (Li et al. 2004). Our results support a role for PICs in the formation of f–I characteristics and ranges, within not only the secondary range but also the subprimary range.

As noted in the introduction, PICs are targets of neuromodulation, particularly by monoamines. We often administered modest amounts of norepinephrine to maintain blood pressure (see methods). Although norepinephrine does not seem to pass the blood–brain barrier (MacKenzie et al. 1976), repeated electrode tracks may have compromised this barrier. Consequently, the neuromodulatory state associated with the discharge properties described here and the level of PIC activation described in Hamm et al. (2010) remain unknown.

PICs are initially activated at membrane potentials below threshold, serving to initiate discharge and sustain it at low frequencies (Li et al. 2004). In mouse motoneurons, depolarizing oscillations likely produced by PIC activation create the variable discharge of the subprimary range. Although some features of the subprimary range in rat motoneurons are similar, the combination of flattened AHP trajectory and depolarization-activated fluctuations in membrane potential are not sufficient to account for the subprimary range in rat motoneurons. Instead we found that the subprimary range coincided with a region in which the slope of the AHP ramp increased and in which the AHP trajectories traversed potentials at which prespike depolarizing potentials were produced, which are likely produced by initial PIC activation (Hamm et al. 2010). The inward current that produces prespike potentials likely increases f–I gain (Kernell 1999); such currents could increase the rate of AHP repolarization, as observed in this study. We propose that the larger gain of the subprimary range is produced by progressive activation of PICs given that membrane potential depolarizes with increasing current and frequency of discharge. The transition from subprimary to primary range occurs as PICs are activated maximally preceding further activation that may occur at the start of the secondary range.

Predischarge depolarizations started at membrane potentials about 8 mV negative to spike threshold, consistent with their production by persistent Na⁺ currents (Crill 1996). PICs are initially activated during voltage ramps at potentials that are similarly hyperpolarized relative to spike threshold and the onset of the negative slope region in the I–V relation of hindlimb motoneurons (Hamm et al. 2010). Similar differences between the thresholds of persistent Na⁺ and L-type Ca²⁺ currents and spike threshold have been observed in rat sacrocaudal motoneurons (Li and Bennett 2003). These results strongly suggest that the initial predischarge depolarization and prespike potentials are produced by persistent Na⁺ currents, likely in somatic and perisomatic regions, whereas PICs responsible for secondary-range discharge are L-type Ca²⁺ currents, probably with dendritic locations (Bui et al. 2006; Elbasiouny et al. 2005; however, see Moritz et al. 2007). If these suggestions are correct, then persistent Na⁺ currents would be a key factor in determining the gain and characteristics of the f–I relation in the subprimary range.

Adaptation was a prominent feature of discharge in our studies, despite the evidence for PIC activation. If PICs activated in the subprimary range are mainly somatic and perisomatic persistent Na⁺ currents with fast kinetics, they might do little to produce counterclockwise f–I relations and negative ΔI values. Some discharge rate adaptation would be expected from inactivation of fast Na⁺ currents, which probably occurred without strong signs of accommodation in most cases, as suggested by Fig. 7. Moreover, the AHP is prolonged by a preceding spike train in cat motoneurons (Wienecke et al. 2009); a similar prolongation in rat motoneurons would lower frequencies during repetitive discharge and contribute to adaptation.

The possible contributions of persistent outward currents to adaptation and f–I gain should also be considered. As shown in the companion article (Hamm et al. 2010), rat hindlimb motoneurons produce a long-lasting voltage-activated outward current that determines in part the difference between recruitment and derecruitment currents. A possibility is that progressive activation of this current with depolarization reduces f–I gain in the primary range. The combination of persistent Na⁺ currents in the subprimary range and outward current in the primary range could set f–I gains in concert with AHP currents. These outward currents vary with input conductance, whereas persistent inward currents become relatively smaller as input conductance increases (Hamm et al. 2010). These variations with size are consistent with the size dependence of f–I gains and the contributions of voltage-activated currents to f–I gains.

Our findings and those of several studies cited in this discussion indicate that motoneuron discharge properties are determined by a variety of intrinsic currents in addition to the K⁺ SK currents that produce the mAHP. As noted in the introduction, a variety of mechanisms are available to modulate intrinsic conductances, emphasizing the possibility that discharge properties are state dependent and may be altered by events such as spinal injury. Considering this possibility in relation to the dependence of discharge properties on motoneuron size, this organization may be subject to control and reorganization and disruption in the case of spinal injury.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant R01-NS-054282 to R. Jung and a Barrow Neurological Foundation grant to T. M. Hamm.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).