Interspike Interval Analyses Reveal Irregular Firing Patterns at Short, But Not Long, Intervals in Rat Head Direction Cells

Abstract

Previous studies have shown that a subset of neurons in the rat anterodorsal thalamus discharge as a function of the animal's head direction (HD) in the horizontal plane, independent of the animal's location and behavior. These cells have consistent firing properties across a wide range of conditions and cell discharge appears highly regular when listened to through a loudspeaker. In contrast, interspike interval (ISI) analyses on cortical cells have found that cell firing is irregular, even under constant stimulus conditions. Here, we analyzed HD cells from the anterodorsal thalamus, while rats foraged for food pellets, to determine whether their firing was regular or irregular. ISIs were measured when the animal's HD was maintained within ±6° of the cell's preferred firing direction. ISIs were highly variable with a mean coefficient of variation (CV) of 0.681. For each cell, the CV values at HDs ±24° away from the cell's preferred direction were similar to the coefficient measured at the cell's preferred direction. A second recording session showed that cells had similar coefficients of variation as the first session, suggesting that the degree of variability in cell spiking was a characteristic property for each cell. There was little correlation between ISIs and angular head velocity or translational speed. ISIs measured in HD cells from the postsubiculum and lateral mammillary nuclei showed higher CV values. These results indicate that despite the appearance of regularity in their firing, HD cells, like cortical cells, have irregular ISIs. In contrast to the irregular firing observed for ISIs, analyses over longer time intervals indicated that HD cell firing was much more regular, more nearly resembling a rate code. These findings have implications for attractor networks that model the HD signal and for models proposed to explain the generation of grid cell signals in entorhinal cortex.

INTRODUCTION

An important issue in neurobiology is how information is encoded within single neurons. Two fundamental codes have been postulated: a rate code and a spike timing code. In a rate code information is encoded as the average firing rate of the neuron over a specified time interval. In a spike timing code information is encoded at the level of single spikes and what becomes important is precisely when the neuron fires relative to other neurons. These codes are often referred to as rate (or frequency) coding and temporal coding. Different investigators have favored particular models (rate code: Adrian and Zotterman 1926; Shadlen and Newsome 1994; temporal code: Gray et al. 1989; Softy and Koch 1993). By examining the interspike interval (ISI), studies have examined how regular, or irregular, firing patterns are in various cell types when a stimulus is applied. ISI analyses on cortical cells, particularly in visual areas, have found that cell firing is highly irregular, even under constant stimulus conditions (Dean 1981; Shadlen and Newsome 1994; Softky and Koch 1993; Tomko and Crapper 1974; Vogels et al. 1989). The variation in the ISI is often described by using the coefficient of variation (CV), which is the SD of the ISI divided by the mean ISI. Small values close to 0 indicate regular firing, whereas large values close to or >1 indicate irregular firing. The CV for visual cortical neurons was generally between 0.5 and 1.0, indicating irregular firing (Softky and Koch 1993). In contrast, both regular and irregular spiking patterns have been reported for different neurons within the vestibular nuclei (Goldberg and Fernandez 1971).

Previous studies have shown that a subset of neurons in the rat anterior dorsal thalamic nucleus (ADN) discharge as a function of the animal's head direction (HD) in the horizontal plane, independent of the animal's location and behavior (Taube et al. 1990; reviewed in Sharp et al. 2001a; Taube 2007). These cells have consistent properties across a wide range of conditions. There is little adaptation in firing when the head remains pointed in the cell's preferred firing direction (PFD; Taube and Muller 1998). Each cell has its own characteristic peak firing rate that changes little across most types of manipulations. Mean peak firing rates across cells range from 5 to 150 spikes/s. HD cells are found in several brain areas throughout the limbic system, but are most abundant in the ADN (Taube 1995). HD cells are dependent on an intact vestibular system because neurotoxic lesions or temporary inactivation of the labyrinth disrupts direction-specific discharge (Stackman and Taube 1997; Stackman et al. 2002). Most network models of HD cell firing use rate models where neuronal firing is based on an average firing rate and assume a smooth temporal distribution of firing across the population, such that neurons may fire regularly are out of synchronization with one another. These models have been based on attractor network dynamics (e.g., Blair and Sharp 1995; Redish et al. 1996; Skaggs et al. 1995; Xie et al. 2002; Zhang 1996). In contrast, spiking models use irregular firing rates and two studies were able to generate an HD cell tuning curve using a spiking model with irregular firing that did not contain recurrent excitation (Boucheny et al. 2005; Song and Wang 2005).

Recent recordings from dorsomedial caudal entorhinal cells have identified a unique spatial correlate referred to as grid cells (Hafting et al. 2005). These cells fire in multiple locations, where the pattern of locations forms a regular, repeating tessellated grid. In addition, in vitro recordings from entorhinal cells have shown that many cells contain subthreshold membrane oscillations that vary between 4 and 7 Hz (Giocomo et al. 2007). Recent models proposing to explain how grid cell firing patterns are generated from their dendritic inputs, resulting in the subthreshold membrane oscillations, use smooth changes in the continuous firing rate onto the dendrites of entorhinal cells (Burgess et al. 2007; Hasselmo et al. 2007). One of the primary inputs onto the dendrites of these entorhinal cells originates in the postsubiculum (PoS) and is thought to convey HD information via the ADN (Kohler 1985; Segal 1977; Shibata 1993; van Groen and Wyss 1995). Thus it would be interesting to determine how regular the firing is of HD cells when the animal is pointing its head continuously in the cell's PFD.

When spikes from an HD cell in the ADN are fed through an audio system and listened to with a loudspeaker, the firing pattern sounds relatively regular when the head passes through the cell's PFD, particularly for cells with high peak firing rates (>75 spikes/s). Further, although a previous study reported that ADN HD cells contained little adaptation in firing rate when the animal held its head pointing in the cell's PFD (Taube and Muller 1998), the study did not report whether the instantaneous firing rate varied over the interval. To determine whether HD cells had regular or irregular firing patterns we analyzed the ISIs of ADN HD cells when the animal's head direction was maintained within a ±6° arc of the cell's PFD. We report that all HD cells, like other cortical cells examined, contain relatively irregular firing patterns. A second issue that was investigated was the amount of firing variation across different episodes when the head was pointing in the cell's PFD. In contrast to the ISI variability, we report that cell firing was relatively constant when measured over longer time intervals, suggesting that the neural code more nearly follows a rate code than a temporal code. These findings have implications for computational models that are designed to generate both HD and grid cell firing patterns. Some of these data were previously reported at the 2004 Annual Meeting of the Society for Neuroscience.

METHODS

Cell sample, behavioral apparatus, surgery, electrical recording

HD cells from the ADN were selected from a larger set of HD cells recorded in earlier studies. Only cells that were well isolated from background noise and from other units recorded on the same electrode were used. The results were obtained from 32 ADN HD cells in 24 animals. All cells were from female Long–Evans rats (aged 3–6 mo) that were on food-restricted diets (∼15 g/day). The animals foraged for 20 mg food pellets scattered randomly in a gray, 76 cm diameter, 51 cm high cylinder. The only intentionally introduced asymmetry in the cylinder was a white cue card that subtended about 100° of arc in the cylinder. The cylinder was surrounded by a cylindrical set of black curtains to provide visual isolation. Attached to the animal's head stage were two light-emitting diodes (LEDs; one red, one green) about 10 cm apart along the midline of the head. Cell activity was recorded while a charge-coupled-device video camera (Sony XC-711) suspended 3 m above the floor monitored the positions of the two LEDs. Recording sessions were 8 min in length. Based on the video data, the x and y coordinates of the two LEDs were read into a computer at 60 Hz. Each spike that occurred was timestamped from the beginning of the session in tens of microseconds. Each spike was also assigned to a 1/60th-s time bin, which corresponded in time to the video data.

Surgeries and electrode array placements were conducted as previously reported (Taube 1995). Electrode arrays were stereotaxically targeted to the ADN and all electrode placements were confirmed at the end of the experiment using histological techniques. All procedures involving the rats were performed in compliance with institutional standards as set forth by the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the Society of Neuroscience.

Measures of directional cell firing

HD cell properties were determined using methods discussed previously (Taube et al. 1990) and are only briefly summarized here. The animal's horizontal head direction was calculated from the relative positions of the two LEDs with respect to one another and sorted into one of 60 (6°) bins. The total time and the number of spikes discharged at each head direction were then summed from the collected samples. The cell's firing rate for each HD bin was computed based on the total number of spikes divided by the total time in that bin. Graphs of the cell's firing rate as a function of head direction in 6° bins were then constructed. Head direction angles are defined using a polar coordinate system, such that increasing angles indicate counterclockwise (CCW) turns and decreasing angles indicate clockwise (CW) turns. From the firing rate/head direction functions eight parameters were computed that characterized the properties for each HD cell: 1) the background firing rate (the mean firing rate at head directions ≥24° outside the directional firing range), 2) the PFD (the head direction associated with maximal discharge), 3) the peak firing rate (the firing rate at the PFD), 4) the directional firing range (the range of head directions in which the neuronal firing rate was greater than background level), 5) Gaussian r (how well the firing rate vs. HD function fit a Gaussian distribution), 6) the mean vector r using circular statistics (this value varies between 0 and 1, with 0 indicating no directional variation and 1 indicating perfect directional variation) (Batschelet 1981), and 7) the information content, which was calculated as

$$IC=\sum p_i({\lambda }_i/\lambda ){\log }_2({\lambda }_i/\lambda )$$

where p_i is the time spent with the head pointing in the ith bin divided by the total time (probability that the head pointed in the ith bin); λ is the the mean firing rate of the cell in the ith bin; and λ_i is the overall firing rate of the cell for the entire recording session. The eighth property was the cell's anticipatory time interval (ATI), which is a measure of the amount of time that cell firing best predicts where the animal will be pointing its head in the future. Positive values indicate anticipation, whereas negative values indicate lag, where cell firing best predicts where the head was in the past. ATI values are determined according to the methods of Blair and Sharp (1995). Briefly, firing rate versus HD tuning curves are constructed for CW and CCW head turns. The difference in PFD for these two curves, referred to as the separation angle, is computed. Then the spike time series for the session is shifted incrementally ±16.67 ms relative to the HD time series and the separation angle is recomputed. The separation angle is computed for each of six shifts in the positive direction and each of six shifts in the negative direction. Then a scatterplot is constructed of the separation angle versus its corresponding time shift. The x-intercept of the best-fit line for this relationship is defined as the ATI.

Angular head velocity (AHV) was determined by calculating the first derivative of the head direction time series. The direction time series was first smoothed by calculating a five-point running average. After smoothing, instantaneous AHV was calculated as the slope of the least-squares line fitted to the point, the two preceding points, and the two subsequent points. Positive angular velocities are for CCW turns and negative angular velocities are for CW turns.

Given the occurrence of a spike, there are two corresponding ISIs: one that precedes the current spike and one that follows the current spike. For the analyses described in the following text we used a combination of these values. For a series of spikes that fell within a given head direction range, we used all the ISIs in between the series of spikes, plus the preceding interval of the first spike in the series and the succeeding interval of the last spike in the series. For example, if five spikes occurred within a range of directional headings, then the ISIs for that episode were composed of: 1) the preceding ISI for spike 1; 2) the intervals between spikes 1 and 2, 2 and 3, 3 and 4, and 4 and 5; and 3) the succeeding ISI for spike 5. However, we also ran analyses using interspike spike intervals that were strictly defined as either preceding or succeeding ISIs. These analyses produced very similar results to those reported in the following text.

Based on the timestamped sample data ISI histograms were constructed for each cell based on spikes that occurred within ±6° of the cell's PFD. ISI analyses were also conducted for head direction ranges of ±3° and ±12°. These analyses gave similar results to those reported in the following text for ±6° and only the ±6° data are used for analyses concerned with AHV. We also calculated the mean ISI and its SD and from these values we then computed the CV (σ)

$$\sigma =\mathrm{s}/\mu$$

where s is the SD of the ISI and μ is the mean ISI.

For some cells there were occasional spurious ISI values that were much larger than 100 ms (10 Hz). Because inclusion of these values led to significantly larger CV values and distorted the overall mean values, these large values were not included in the analyses. To avoid inclusion of these values in the calculations, we defined an upper ISI limit of 0.25-fold the cell's peak firing rate. For example, if a cell had a peak firing rate of 60 spikes/s, the upper limit of acceptable ISIs was 0.25 × 60 = 15 spikes/s, which is equivalent to an ISI of 66.6 ms, and intervals >66.6 ms were excluded from analyses. In general, the number of excluded values was small; they averaged 17.8 ± 2.0 samples per cell and were always <6% of the total number of ISI samples (mean: 2.35 ± 0.27%).

We also determined the amount of higher-order temporal variability by computing the CV value for ISI intervals using the nth spike before and after a spike at t = 0. This analysis yielded results for the second-, third-, fourth-, and fifth-orders and we then plotted σ along with all the higher-order CV values as a function of order to reveal particular features in the regularity/irregularity of spike firing.

Because previous studies have shown that σ is sensitive to changes in the cell's mean firing rate (a finding verified in the current results), Holt et al. (1996) developed an alternative method for determining a cell's firing rate variability that was less sensitive to the cell's mean firing rate. This alternative, referred to as CV₂, is defined as

$${\text{CV}}_2=[2(|{\text{ISI}}_{\text{After}}-{\text{ISI}}_{\text{Before}}|)]/({\text{ISI}}_{\text{After}}-{\text{ISI}}_{\text{Before}})$$

where for each given spike, ISI_After is the ISI to the next spike and ISI_Before is the ISI to the previous spike. CV₂ is computed for every spike and then the mean CV₂ is determined. For this analysis, CV₂ is computed using the entire spike train from the session and not just for times when the animal's head is pointing in the preferred direction.

Comparison between observed firing and expected firing

Cell firing variability can also be measured over longer time intervals and one can determine the variability in the cell's firing rate over different episodes when the head passes through the cell's PFD. The measure we used is referred to as the Fano factor, defined as

$$\text{Fano factor}=\text{Variance}\left[\mathrm{T}\right]/\mu \left[\mathrm{T}\right]$$

where μ[T] is the mean number of spikes observed over some specified time interval (T) across different episodes, when the rat's head was pointing in the PFD, and Variance[T] is the variance for this mean number. Fano factor values near 1 are consistent with an underlying Poisson process. Using episodes when the animal's HD was within ±6° of the cell's preferred direction we computed the Fano factor for time intervals (T) ranging from 50 to 500 ms.

We also used a second procedure to determine the amount of firing variability across different episodes. For each cell we compared the number of spikes that fired in each episode when the rat's head was within the cell's PFD to the expected number of spikes based on the overall firing rate at that HD over the entire session. This analysis assumes that the underlying spiking is a Poisson process and is similar to that used by Fenton and Muller (1998) on hippocampal place cells and is reviewed here only briefly (consult the cited article for further details).

In theory, if HD cell firing over discrete intervals obeys a normal distribution then the observed number of spikes for an episode when the head passes through the cell's preferred direction is a random deviation from the expected normal distribution. From this model we can calculate a Z score for each episode that represents the deviation from the expected number of spikes and then examine the distribution of Z scores for all episodes and compare it to a standard normal curve. We performed this analysis on all ADN HD cells using the same sessions as the above mentioned ISI analyses. For this analysis we defined a pass through the cell's PFD as any episode when the rat's head pointed within ±6° of the preferred direction for six consecutive samples (100 ms). From the firing rate versus HD function we determined the expected number of spikes for HDs within this 12° range. From these data, the Z score was calculated as

$$Z=(S-N-0.5)/\sqrt{N}\hspace{1em}\text{for}\hspace{1em}S\ge N$$

$$Z=(S-N+0.5)/\sqrt{N}\hspace{1em}\text{for}\hspace{1em}S<N$$

where S is the number of observed spikes for a single pass of the head through the cell's preferred direction, N is the number of expected spikes for the episode based on the session averaged directional tuning curve, and Z is the number of SDs separating the observed and expected values. We plotted the distribution of Z scores for all cells and episodes and compared the distribution to the unit normal distribution.

All data analysis was performed off-line using LabVIEW 5 software (National Instruments, Austin, TX). Unless otherwise noted, all mean values are reported with the SE. Statistical tests used ANOVAs and post hoc Newman–Keuls tests. Significance was defined as P < 0.05.

RESULTS

Cell sample

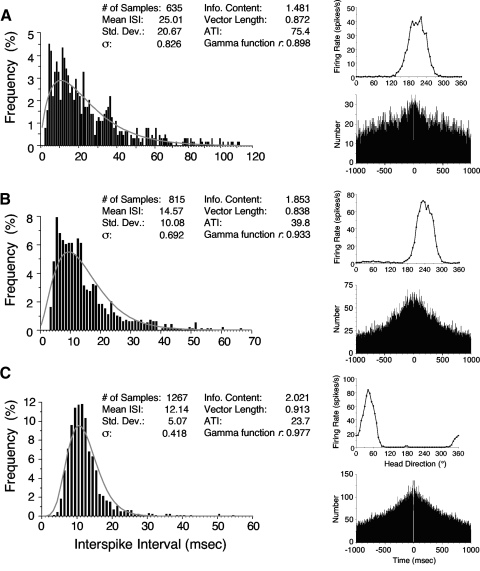
Results were obtained from 32 HD cells from the ADN. All cells were well isolated and most (26 of 32) had background firing rates <1 spike/s. All tuning curves had high information content and Rayleigh values (mean information content = 1.750 ± 0.079; mean vector length = 0.872 ± 0.012) and fit a Gaussian distribution well (mean r = 0.982 ± 0.003). The mean ATI for this group was 48.56 ± 5.25 ms, which is higher than the almost 25 ms of previous reports (Blair and Sharp 1995; Taube and Muller 1998). Table 1 shows a summary of cell characteristics and indicates that the cell population was representative of previously reported HD cells in the ADN (Taube 1995). Representative tuning curves from three cells and their associated autocorrelograms are shown in Fig. 2 (right). None of the cells' autocorrelograms reveals any rhythmical firing corresponding to theta rhythm. This finding stands in contrast to autocorrelograms for hippocampal place cells, showing significant rhythmicity at the theta frequency (Mizumori et al. 1990; O'Keefe and Recce 1993).

Table 1.

HD cell firing properties across different brain areas

	ADN (n = 32)			PoS (n = 16)			LMN (n = 15)
Property	Mean	SE	Range	Mean	SE	Range	Mean	SE	Range
Peak firing rate, spikes/s	68.31	6.36	17.3–174.1	18.43	1.67	11.44–38.51*	69.04	17.99	11.24–239.27
Background firing rate, spikes/s	0.649	0.146	0.023–4.384	1.108	0.26	0.140–3.531	>2.524	0.550	0.010–6.682*
Signal-to-noise ratio	343.40	72.20	21.4–1,458	34.00	6.40	6.10–88.8*	143.20	76.10	4.64–1,124
Directional firing range, deg	99.80	2.60	75.2–137.9	100.3	10.40	69.0–201.6	168.30	9.50	80.0–217.3*
Information content, bits/spike	1.750	0.079	0.907–2.665	1.200	0.147	0.308–1.974*	0.912	0.175	0.236–1.549*
Raleigh r	0.872	0.012	0.633–0.946	0.685	0.039	0.348–0.871*	0.654	0.045	0.377–0.945*
Gaussian r	0.982	0.003	0.929–0.998	0.951	0.011	0.808–0.991*	0.949	0.013	0.804–0.990*
ATI, ms	48.56	5.25	−11.46 to 101.76	−6.91	13.05	−59.34 to 65.30*	89.74	11.47	−20.92 to 147.30*

^* Significantly different compared with ADN (P < 0.05, post hoc Student–Newman–Keuls test).

Fig. 2.

Interspike interval (ISI) histograms from the same 3 representative cells depicted in Fig. 1. The right column depicts each cell's firing rate vs. HD tuning curve and the autocorrelation plot. Cells were selected to represent the range of coefficients of variation observed. A: cell with a large CV (0.826). B: cell with an intermediate CV (0.692). C: cell with a small CV (0.418). The best-fit gamma function for each ISI histogram is shown in gray. HD cell firing properties are shown for each cell. Note that the autocorrelation plots show no evidence of theta rhythmicity.

ISI analyses

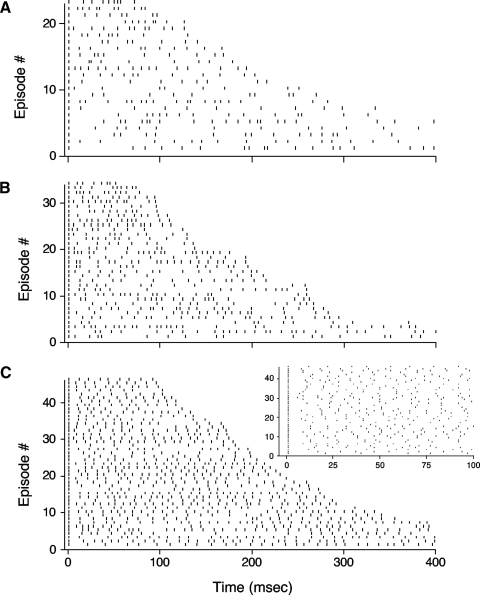
In general, ISIs were rather irregular and variable. Figure 1 shows the firing patterns of different episodes from three cells where the animal's HD was maintained within ±6° of the cell's preferred direction. The irregular firing is quite apparent across all three cells, although it is more robust for the top two cells. Selecting smaller or larger ranges of firing (e.g., ±3° or ±12°) did not qualitatively affect the overall irregular firing patterns (data not shown).

Fig. 1.

Rastergram plots from 3 representative head direction (HD) cells showing spike occurrences across different episodes when the head was pointing in the cell's preferred firing direction (PFD; ±6°). Each episode starts with a spike occurrence at 1 ms. Cells had high (A), medium (B), or low (C) coefficients of variation (CVs). Note the general irregularity of firing across all 3 cells and the absence of any appreciable adaptation throughout an episode. The cell in C had the highest degree of firing regularity of all cells recorded. For purposes of comparison and clarity, all episodes >400 ms were truncated at 400 ms. The plot to the top right in C is a magnified view of the first 100 ms for the episodes shown in the larger plot of C. Given that the first spikes of each episode are all aligned, note the high degree of variability for the occurrence of the second spike across these episodes. For each cell, episodes were arranged in order according to episode length (duration) from top (shortest episode) to bottom (longest episode).

ISI histograms were plotted for each HD cell. The ordinate for each histogram was expressed as a percentage of the total number of spikes. At least 250 spikes had to occur within the ±6° range of the cell's preferred direction for it to be included in the analysis. The mean number of spikes for each histogram was 1,009.7 ± 110.4 (range: 270–2,495). Figure 2 depicts the ISI analyses for the three HD cells shown in Fig. 1 (with the top cell in Fig. 1 corresponding to Fig. 2A, the middle cell in Fig. 1 corresponding to Fig. 2B, etc.). All of the ISI histograms appeared to be unimodal and there was no hint of a bimodal distribution for any HD cell. Each of the ISI histograms could be well fit to a gamma function and each histogram in Fig. 2 shows the best-fit gamma function for that particular cell. The mean best-fit correlation (r) to a gamma function across the population of cells was 0.918 ± 0.012 (range: 0.670–0.992).

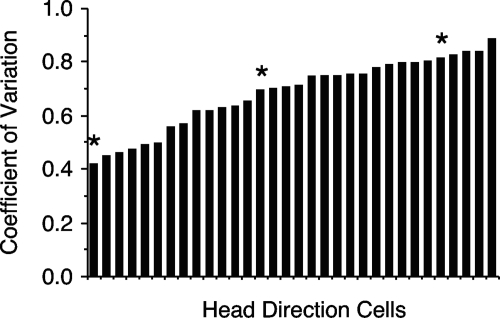
CV values (σ) ranged from 0.418 to 0.887, with the mean equal to 0.681 ± 0.023. Recall that a regular, uniform rate of firing would have a σ score of 0 and a score ≥1 would indicate a cell with a highly irregular rate of firing. Figure 3 is a histogram showing the distribution of σ values across the 32 cells. The three cells depicted in Fig. 2 were selected to represent the broad continuum of scores observed for σ. Thus the cell depicted in Fig. 2C represents the cell with the lowest σ and contains the most “regular” pattern of firing observed. The cell depicted in Fig. 2A represents a cell with one of the higher σ scores; the cell shown in Fig. 2B represents a cell that contained an intermediate σ. Defining the ISI for each spike as either the time that preceded or succeeded each spike did not change the overall σ value; mean σ = 0.679 ± 0.025 for ISI defined as preceding time; mean σ = 0.682 ± 0.024 for ISI defined as succeeding time. Further, lessening or expanding the acceptable firing range from ±6° to ±3 or ±12° led to minimal changes in the mean σ values (mean σ for ±3° = 0.678 ± 0.024; mean σ for ±12° = 0.691 ± 0.021) (Table 2). There was no trend for individual cells to have smaller or larger σ values using ±3° or ±12° analyses.

Fig. 3.

A: plot depicting the distribution of CV values from all analyzed anterior dorsal thalamic nucleus (ADN) HD cells. Each bar represents the CV for one HD cell. Cells are arranged from lowest to highest CV values. Asterisks denote cells used for constructing Figs. 1 and 2.

Table 2.

Coefficient of variation properties for ADN HD cells (n = 32)

Property	Mean	SE	Range
ISI (μ), ms	19.500	2.040	5.970–66.01
SD(s)	14.190	1.890	3.690–30.05
Gamma function fit (r)	0.918	0.012	0.670–0.992
Coefficient of variation (σ) ± 6°	0.681	0.023	0.418–0.887
CV2	0.651	0.028	0.355–0.946
Coefficient of variation (σ) ± 6° using only preceding ISI	0.679	0.025	0.400–0.884
Coefficient of variation (σ) ± 6° using only succeeding ISI	0.682	0.024	0.408–0.921
Coefficient of variation (σ) ± 3°	0.678	0.024	0.411–0.886
Coefficient of variation (σ) ± 12°	0.691	0.021	0.472–0.884
Coefficient of variation (σ) at 24 ± 6° CW of preferred direction	0.671	0.019	0.452–0.925
Coefficient of variation (σ) at 24 ± 6° CCW of preferred direction	0.692	0.019	0.415–0.916

The mean CV₂ using the entire spike train was 0.651 ± 0.028 and is similar to the mean σ (0.681), suggesting that cell firing was not occurring in periodic bursts. The relatively high mean CV₂ value again supports the view that overall HD cell firing is rather irregular.

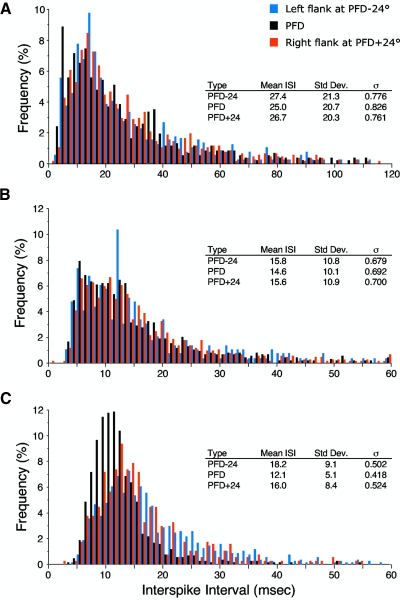
ISIs at head directions within the cell's directional firing range, but away from the cell's preferred direction, also show similar variability compared with the variability observed at the cell's PFD. Figure 4 depicts the same three cells with ISI histograms for ranges of head directions that fell on either side of the cell's PFD (middle graph, referred to as the fundamental ISI histogram). For this analysis, we selected a head direction on each side of the tuning curve that was 24° away (±6°) from the PFD. These points corresponded to firing rates that were roughly 50% of the cell's peak firing rate. For each of these points we constructed the ISI histograms and computed the corresponding σ. For example, if a cell had a PFD of 180° with a directional firing range of 90°, we constructed ISI histograms for cell firing at head directions (±6°) of 156° and 204°; the first value represents a graph for the left portion of the tuning curve and the second value represents a graph for the right portion of the tuning curve. The fundamental ISI histogram was constructed at the cell's PFD using the head direction range surrounding 180° (i.e., 174–186°).

Fig. 4.

ISI histograms are depicted at 3 different head directions for the same 3 cells shown in Fig. 2. Black bars represent the ISI histogram at the cell's PFD (±6°). Blue and red bars represent the ISI histogram at PFD −24° (±6°) and PFD +24° (±6°) from the cell's PFD, respectively. The 60th bin in the middle plot contains a few occurrences that were >60 ms.

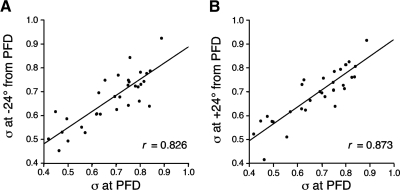
As expected, the ISI histograms for head direction values on the flanks of the cell's tuning curve had larger ISIs as a consequence of their lower firing rates (data not shown). However, the variability at these flanking head directions, as measured by σ, was similar to that observed at the cells' PFDs. The mean σ values computed for head directions at +24° and −24° were 0.692 ± 0.019 and 0.671 ± 0.019, respectively. These values are similar to the 0.681 mean value for σ at the cells' PFDs (t-test, values of P > 0.05). Further, when comparing the σ values at the +24 and −24° head directions to the σ at the cell's PFD, there was a high degree of similarity for values at −24° (Pearson's r = 0.826) and for values at +24° (r = 0.873). Figure 5 depicts scattergrams plotting σ at the cell's PFD versus σ at −24 and +24° away from the cells' PFDs. These results indicate that the σ was relatively constant throughout the cell's directional firing range and suggests that each cell has a characteristic degree of firing variability that is different for each cell.

Fig. 5.

Scattergrams showing the relationship between a cell's CV at the cell's PFD and the CV −24° (A) and +24° (B) away from the cell's PFD. The best-fit lines with high r values indicate that the CV was relatively stable throughout each cell's directional firing range, suggesting that each cell has a characteristic CV value.

Coefficient of variation versus cell firing properties

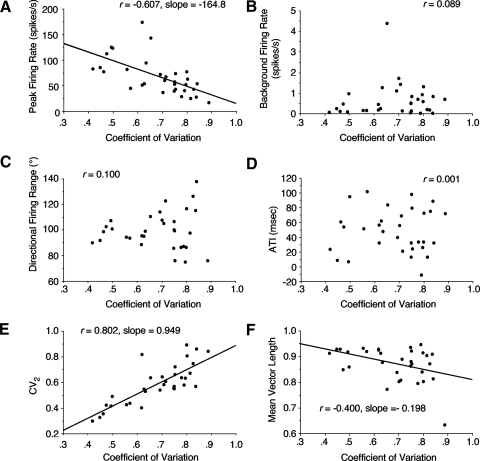
We also plotted scattergrams of various HD cell properties compared with their corresponding CV. Figure 6 shows the correlation for several of these properties along with the slopes of the best-fit lines for plots that had significant correlations. The correlation was low for most properties (background firing rate, directional firing range, ATI), but was relatively good with a significant slope for peak firing rate (r = −0.607; slope = −164.8) (Fig. 6A), indicating that cells with higher peak firing rates tended to have lower CV values (i.e., more regularity in their firing), as predicted by Holt et al. (1996). As expected, there was a good correlation (0.802) between σ and CV₂ (Fig. 6E) and a moderate correlation (−0.400) between σ and mean vector length (Fig. 6F).

Fig. 6.

Scattergrams showing the relationship between a cell's CV and various cell properties. A: peak firing rate. B: background firing rate. C: directional firing range. D: anticipatory time interval (ATI). E: CV₂. F: mean vector length. Best-fit lines and slope values are shown for plots in A, E, and F that had relatively high correlation values.

Reliability of the ISI: comparison across sessions

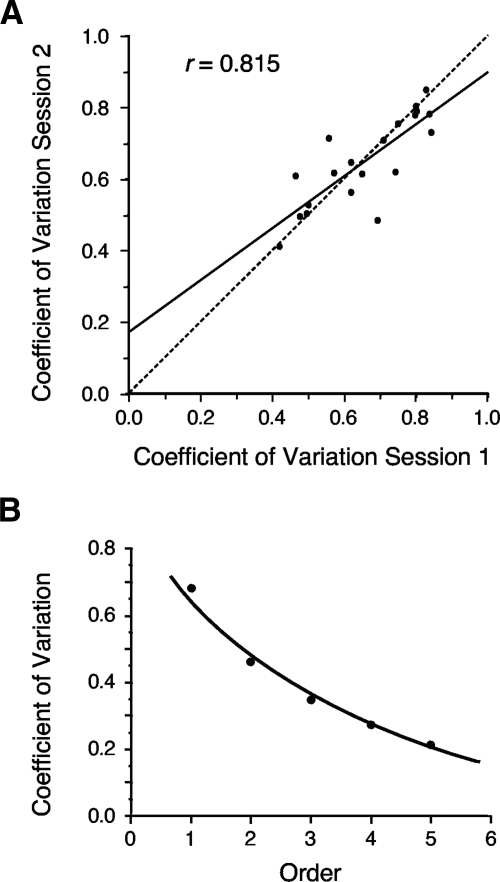
Is the CV value a property for each cell, such that subsequent recording sessions would yield a similar σ compared with the initial session? In other words, how reliable is the CV across recording sessions? To address this issue a second recording session was available for analysis for 20 of the 32 ADN cells. These second sessions generally occurred within 1 h after the initial recording session and were 8 min in length. Using samples within ±6° of the cell's PFD, the mean σ for the second sessions was 0.650 ± 0.028 (range: 0.410–0.850) and is comparable with the mean obtained for the first sessions (0.681). In general, there was a good correlation between σ values for the first and second sessions (r = 0.815). Figure 7A plots a scattergram of this relationship. These results again suggest that the CV is an individual property for each HD cell.

Fig. 7.

A: scattergram showing the consistency of the CV across 2 recording sessions separated by 10–30 min. The solid line shows the best-fit line for the data; the dashed 45° line shows the hypothetical perfect correlation. B: plot showing the CV as a function of higher-order ISIs. As the ISI order increases, the CV decreases exponentially, indicating that cell firing is becoming more regular.

ISI and higher-order analyses

Higher-order ISI analyses yielded an interesting outcome. Figure 7B plots the σ as a function of order number and shows that the degree of firing variability decreased exponentially as a function of order (r = 0.994; r for linear fit = 0.926). This result suggests that as the time window over which cell firing is analyzed lengthens, the cell will appear to fire more regularly and has implications for whether the system is using a rate code or a temporal code. Specifically, the more regular the firing is, the more likely the system is using a rate code over a temporal code. This issue is addressed further in the following text when firing over an entire episode is analyzed with respect to when the rat is pointing its head in the cell's preferred direction.

ISI and AHV analyses

Previous studies have shown that ADN HD cells show a small secondary correlate to the animal's AHV (Taube 1995; Taube and Muller 1998). Further, information from AHV cells in the dorsal tegmental nucleus (DTN) is projected rostrally via the lateral mammillary nuclei (LMN) to the ADN (Bassett et al. 2001; Sharp et al. 2001b). This secondary correlate was usually positive, indicating that HD cells fired slightly faster when the animal turned its head through the cell's PFD at faster speeds. Cells were generally not modulated by the direction of head turn; thus faster head turns in either the CW or CCW direction led to similar increases in firing rates. Because of this AHV correlate, we examined the extent to which the ISI was correlated with the animal's AHV using several different measures. These analyses included determining the correlation between the ISI and 1) the animal's overall AHV, 2) the animal's angular head speed (the absolute value of the AHV term), 3) the animal's angular head speed for CCW head turns (positive AHV values), and 4) the animal's angular head speed for CW head turns (negative AHV values). Because AHV may relate directly to the animal's immediate past or impending head turn, for each of these four analyses, we defined the ISI in two ways: 1) the ISI that preceded the occurrence of a spike and 2) the ISI that succeeded the occurrence of a spike.

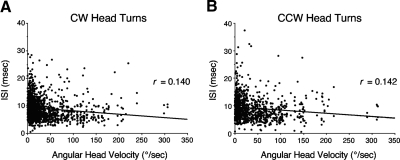
Correlating the ISI with the corresponding AHV generally did not lead to a good correlation for the vast majority of cells. This result was true for each of the four measures used and for whether the ISI was defined as using the preceding spike or the succeeding spike. The mean values for all correlations were <0.075. Even for cells that consistently had correlations between 0.10 and 0.20 for different measures of ISI and AHV, the scattergrams did not reveal any striking relationships. For example, Fig. 8 shows a scattergram plotting the ISI (using the interval of the preceding spike) as a function of AHV for CW and CCW head turns. This cell was selected because it consistently had r values between 0.1 and 0.2 across the different methods of analysis. Both plots have r values of about 0.15 for the best-fit lines. Note, however, that neither plot depicts a discernible relationship between ISI and AHV.

Fig. 8.

Scattergrams plotting ISI as a function of angular head velocity (AHV) for clockwise (CW, A) and counterclockwise (CCW, B) head turns. The data shown are from a cell that had one of the higher-correlation coefficients (r). Note that even for this cell the relationship between ISI and AHV is very weak.

Similar poor correlations were found when correlating CV₂ with AHV, where all mean correlations were <0.030 and all individual cell correlations <0.090.

ISI and linear head velocity analyses

ADN HD cell firing rates have been reported to mildly correlate with the animal's translational (linear) head velocity (Taube 1995). In addition, the oscillatory interference models for entorhinal grid cells requires that HD cell firing be modulated by the animal's translational speed (Hasselmo et al. 2007). We therefore determined the correlation of the ISI to the animal's translational velocity when the animal's head was within ±6° of the cell's preferred direction. This analysis revealed that the mean correlation values were very low: ISI for preceding spike: r = −0.0160 ± 0.0117 (range: −0.171 to 0.123); ISI for succeeding spike: r = −0.0019 ± 0.0097 (range: −0.074 to 0.134). These low correlation values were also obtained when correlating CV₂ with translational head velocity; mean correlation = 0.0242 ± 0.0066 (range: −0.043 to 0.125).

ISI analyses for HD cells in other brain areas

HD cells are also found abundantly in several other brain areas, including the LMN and PoS. These two structures lie immediately afferent and efferent to the ADN, respectively, and serve as the primary connections into and out of the ADN. The LMN → ADN → PoS pathway is thought to serve as the principal means by which directional heading information that originates in the DTN is conveyed to the entorhinal cortex and subsequently to the hippocampus. Thus it was of interest to determine whether the CV was similar for HD cells in the LMN and PoS.

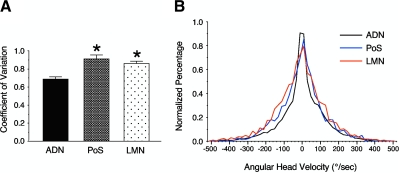
Similar analyses to those described earlier for ADN HD cells were conducted for 15 LMN HD cells and 16 PoS HD cells. The mean σ values for PoS and LMN HD cells were 0.911 ± 0.044 and 0.859 ± 0.027, respectively. Both of these values are significantly greater than the 0.681 mean value for ADN HD cells [F_(2,60) = 16.84, P < 0.05] (Fig. 9A); there was no significant difference between PoS and LMN cells (post hoc Newman–Keuls test).

Fig. 9.

A: differences in mean CV values compared across 3 brain areas containing HD cells. * indicates P < 0.05 compared with ADN cells. B: histogram displaying the frequency of different AHV values across the HD cells used for analyses in the ADN, postsubiculum (PoS), and lateral mammillary nuclei (LMN). A frequency histogram was constructed for each HD cell and then normalized. The mean frequency histogram was then determined from the population of cells from the particular brain area.

It is important to note, however, that several firing properties of LMN and PoS cells were different compared with values obtained from ADN cells (Table 1) and this difference could have contributed to the higher coefficients of variation. The number of cells that were available for analyses from LMN and PoS was more limited than the number of cells drawn for the ADN analyses. Consequently, we could not be as selective in choosing cells with high-quality tuning curves for the LMN and PoS cells; thus PoS and LMN tuning curves were generally less robust and distinct than those for ADN cells. This result is reflected in the lower signal-to-noise ratios, higher directional firing ranges, and lower information content and Rayleigh values in PoS and LMN cells. Importantly, however, if the cells judged to have the poorest tuning curves (∼5 for each brain area) were removed from the analyses, the σ values for both PoS and LMN changed very little (data not shown). Thus it is unlikely that the different CV values for PoS and LMN compared with the ADN are attributed to the less robust tuning curves.

To determine whether the differences in the CV values were due to differences in how the animals turned their heads during the episodes used for the analyses, we compared AHV frequency histograms across cells from the three different groups. The mean histograms (Fig. 9B) reveal a small difference between the normalized distribution for the ADN group compared with that of the PoS and LMN groups, where there are more samples with lower AHV values for the ADN group compared with the PoS and LMN groups (note the heightened function for values around 0°/s for the ADN group). Conversely, there was a larger percentage of time that PoS and LMN animals spent turning their heads at higher velocities compared with the ADN group (note that the flanks of the functions for the PoS and LMN groups lie above the flanks for the ADN function). Although this difference is not striking, the more frequent faster head turns in the PoS and LMN groups could have contributed to a higher variability in firing rate for these cells and commensurate higher CV values, although the earlier AHV analyses for ADN cells indicated that there was little correlation between ISI and AHV. As with ADN cells, there was a poor correlation between the ISI and AHV for PoS and LMN cells; all r values were <0.06 for all measures of correlating the two variables (i.e., AHV or absolute value of AHV vs. ISI preceding spike or ISI succeeding spike). Similarly, there were poor correlations between ISI and linear velocity for PoS and LMN cells (all r values <0.03).

Firing variability across individual episodes in the cell's PFD

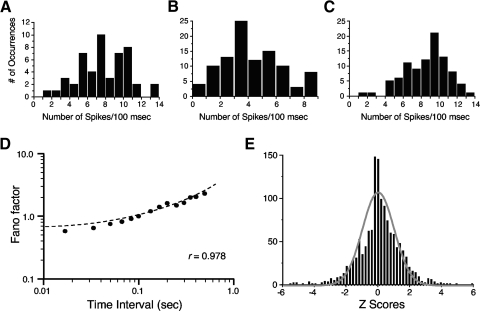
The higher-order ISI analyses described earlier indicated that firing was more regular over longer intervals. Indeed, if the number of spikes that occurred in every 100-ms episode, when the head was pointed in the preferred direction, is plotted for the three cells in Fig. 1, firing appears more regular and the histograms appear more Gaussian (Fig. 10, A–C). A 100-ms period was selected because not only is this about 10-fold longer than an excitatory postsynaptic potential (EPSP), but also because it represents the approximate time interval (120 ms) over which Singer and Sheinberg (2010) showed that temporal cortical neurons integrated form and motion information in visual pathways.

Fig. 10.

A–C: histograms plotting the number of episodes that contained a specified number of spikes over a 100-ms interval from the 3 HD cells in Fig. 1 when the animal's head was within ±6° of the cell's PFD. D: mean Fano factors determined for all episodes in 32 cells in which the HD was within ±6° of the cell's PFD plotted as a function of the time interval length. E: frequency distribution of Z scores comparing observed firing with expected firing. The gray curve plots the unit normal distribution based on the total number of episodes (1,346) and indicates that the distribution of Z scores did not fit the unit normal curve very well, which is mostly attributed to the increased incidence of values around zero.

A more proper analysis that examines variability across episodes is a Fano factor analysis. Using a time window of 100 ms, we computed the Fano factor for each ADN cell for all episodes when the cell's preferred direction was within ±6°. Fano factor values ranged between 0.421 and 1.692, with the mean = 1.034 ± 0.056 for the 32 cells. There were poor correlations between a cell's Fano factor and its peak firing rate (r = 0.0436), σ (r = 0.010), and CV₂ (r = 0.0678). Computing the Fano factor using other time intervals from 16.6 to 500 ms led to the relationship depicted in Fig. 10D plotted on a log scale, where the Fano factor increased relatively linearly (r = 0.978) when increasing the time window length. The Fano factor slope is nearly 1 for observational times around 100 ms, which is compatible with a Poisson process.

Comparison between observed firing and expected firing

For each cell and episode, we also compared the amount of observed firing to the expected firing based on each cell's mean firing rate. This analysis assumes that firing is based on a Poisson process, which may not be accurate based on the ISI results reported earlier. However, this analysis provides a useful comparison to the results reported for hippocampal place cells by Fenton and Muller (1998) who used a similar analysis. In all, 1,346 episodes were analyzed from 32 HD cells in ADN, with an average of 42.1 ± 2.9 episodes per cell. The mean Z score was 0.174 ± 0.0356 and Fig. 10E plots the distribution of Z scores from all episodes. The gray curve is the unit normal distribution and represents the expected distribution. Note that the distribution of episode Z scores falls outside the unit normal curve, particularly at Z scores on either side of zero, which represent episodes when the observed firing was near the expected firing. This result indicates that the cells responded more consistently than expected based on a normal curve, suggesting that the neural code for these cells favors a rate code rather than a temporal code. Indeed, a chi-square test using 20 intervals indicated that these Z scores were not normally distributed χ₍₁₇₎² = 228.3, P < 0.001]. There was a relatively poor relationship between a cell's peak firing rate and its mean Z score (r = 0.191).

DISCUSSION

Two forms of variability in HD cell responses were analyzed over different timescales: 1) variability in the ISI when the head was pointing at the cell's PFD and 2) variability in total firing across different episodes. We first discuss the firing variability that occurred on a short timescale (the ISI) and then discuss the firing variability that occurred over longer intervals involving the entire episode.

ISI analyses on ADN HD cells showed that firing was irregular at both the cell's PFD and throughout the cell's directional firing range. Only 6 of 32 cells had CV values <0.5, and even these 6 cells had coefficients >0.4. The irregular firing of HD cells does not differ significantly from findings in other brain areas including visual, auditory, and parietal cortices (Burns and Webb 1976; Dean 1981; Noda and Adey 1970; Softky and Koch 1993; Vogels et al. 1989), thalamus (Poggio and Viernstein 1964), and retinal ganglion cells (Croner et al. 1993). The results are consistent with the known firing properties of AHV cells in the DTN, where these cells contain irregular firing patterns (Bassett and Taube 2001). The two major sources of information into the DTN are from the nucleus prepositus and supragenual nuclei, each of which receives inputs from the vestibular nuclei (Biazoli Jr et al. 2006; Liu et al. 1984). Interestingly, the vestibular nuclei contain a heterogeneous population of neurons, in which some fire regularly and some fire irregularly (Goldberg and Fernandez 1971), although it is not known which cell type projects to the nucleus prepositus or supragenual nucleus. Information from dorsal tegmental AHV cells projects onto ADN cells via intervening cells in the LMN. Our analyses also showed that LMN HD cells contained irregular firing patterns. Thus although it is unknown whether regular or irregular cell types within the vestibular nuclei project to the HD cell system, the HD circuit is characterized by irregular firing cell types from the DTN all the way to PoS.

All cell firing patterns were analyzed during random foraging behavior by the animal for small food pellets. This task does not have a high spatial demand, in the sense that animals are required to keep track of their spatial orientation when performing the task. One might consider whether a more regular pattern of firing would emerge if the animals were performing a spatial task. This view is unlikely though, when considered with findings that HD cell firing is generally independent of the animal's ongoing behavior (Dudchenko and Taube 1997; Taube et al. 1990). Specifically, Dudchenko and Taube showed that HD cell firing properties, in terms of peak firing rate, directional firing range, PFD, and background firing, did not change during the course of learning to perform a spatial radial arm maze task. Although not definitive, this finding makes it unlikely that regular firing patterns would emerge when performing a more demanding spatial task.

Variability across episodes and comparison with hippocampal place cells

In contrast to the high variability observed for the ISI, variability across an entire episode within the cell's preferred direction was much less and cell firing was more consistent (regular) and predictable. This view is supported by the higher-order ISI analyses, Fano factor values, and the observed versus expected Z score analyses. Although the observed versus expected Z score analysis did not fit a Gaussian distribution well, the poor fit can be primarily attributed to the high incidence of Z scores around zero, which is indicative of a high number of episodes where observed firing rates were similar to the expected firing rate. The more regular firing seen over longer-length time epochs is consistent with the view that HD cell firing is more based on a rate code than a temporal one. In sum, even if individual cells fire irregularly over short ISI intervals, their firing over longer intervals is more regular and a population of such cells would yield an even distribution of spiking activity over time.

Casual observations of complex spiking in place cells with an oscilloscope suggest a regular firing pattern with a fixed ISI. Moreover, when rats run continuously in place on a running wheel, both place cell discharge rate and theta phase remain relatively constant over long time intervals, although a close look at individual cell firing records indicates considerable variability in ISI (see Fig. 1 of Czurkò et al. 1999). To examine firing variability across different episodes Fenton and Muller (1998) analyzed individual passes through a cell's place field. These authors reported excess variance in discharge rate, even on nearly identical trajectories through the cell's place field that matched not only position and direction, but also speed and dwell time at each location. Indeed, Fig. 1 in Fenton and Muller (1998) depicts the cell firing 18 spikes on one occasion and zero spikes on another occasion for highly similar paths, a pattern of activity that was rarely seen for HD cells. The authors attributed the excess variability to other behavioral, attentional, or motivational factors. However, internal state factors were ruled out by showing that when two place cells that had relatively coincident place fields were recorded simultaneously, the discharge of the two cells did not cross-correlate very well. Interestingly, a further study revealed that the excess variance was lessened when the rat was continuously forced to use a single spatial reference frame, as opposed to conditions that did not control for this factor as in the foraging task (Olypher et al. 2002). Jackson and Redish (2007) obtained similar results using three different behavioral tasks and concluded that different cell ensembles were encoding different reference frames and that these cell ensembles were active at different times throughout the tasks. They suggested that it was the switching back and forth between different reference frames as the animal moved about its environment that contributed to firing variability. In sum, place cells display considerable variability across different episodes. In contrast, our results demonstrate that HD cells, which are generally thought of as projecting information to place cells, displayed much less variance in their discharge and fired reliably for each episode every time the animal's head passed through the cell's PFD. Thus even if HD cell firing is irregular over short time intervals such as the ISI, their summed activity over each pass through the cell's preferred direction is relatively constant and more consistent compared with that of place cells.

Two hallmarks of hippocampal place cell firing are complex spikes (Fox and Ranck Jr 1981) and theta precession, where place cell firing occurs time-locked to theta such that each burst of spikes occurs at an earlier portion of the theta cycle as the animal traverses the place field (O'Keefe and Recce 1993). Although the hippocampal EEG was not monitored during our unit recordings, there was no evidence of theta rhythm in the ISI graphs or autocorrelation functions. Thus in contrast to hippocampal place cells, the absence of any theta rhythmicity in HD cells indicates that HD cells do not display any theta precession as an animal turns its head through the cell's PFD.

Computational models and HD cell activity

Numerous attractor networks have been postulated to model HD cell firing (Boucheny et al. 2005; Goodridge and Touretzky 2000; McNaughton et al. 2006; Redish et al. 1996; Sharp et al. 2001a; Skaggs et al. 1995; Song and Wang 2005; Xie et al. 2002; Zhang 1996). In general, these models, with the exception of those by Boucheny et al. (2005) and Song and Wang (2005), use regular firing patterns and rate codes, which do not capture the true firing patterns of HD cells. However, attractor networks operate effectively with irregular firing of individual neurons because the networks are modeled in a manner where the summed activity across a population of irregular spiking cells can result in a regular, rate-like firing code. HD cells are often characterized as a good example of persistent firing, in that the cells are capable of firing indefinitely over time when the animal's head is continually pointing in the cell's PFD. Indeed, little adaptation is observed in HD cell discharge over the relatively short time periods (∼1 s) that have been studied (Taube and Muller 1998). What generates and drives this persistent firing? Two mechanisms are possible: either external inputs into the network can sustain the discharge as well as trigger it or intrinsic cellular mechanisms can tonically maintain activity within the ionotropic channels involved and may include calcium channels (Major and Tank 2004). These two possibilities are not mutually exclusive. Most HD attractor networks are modeled in a way where the hill of activity (cell discharge) is sustained without external inputs (e.g., Skaggs et al. 1995; Zhang 1996). In these models the role of external inputs is primarily to move the hill of activity around when the animal turns its head. When the animal's head is stationary, the activity hill is maintained either by recurrent excitatory circuitry within the network or by intrinsic cellular mechanisms.

Does an irregular, variable ISI in HD cells lend support to one mechanism or the other for how the hill of activity is shifted around the ring attractor? A high amount of variability may suggest external input because the irregularity of synaptic transmission due to synaptic noise could create different times in which a cell reaches threshold to initiate a spike. Consistent with this view, Holt et al. (1996) reported that when depolarizing currents were injected into visual cortical neurons using an in vitro preparation, the ISIs of the resultant spike trains were much more regular than those found in vivo. Indeed, in general ISIs are relatively regular in neocortical neurons following injections of depolarizing current (Mainen and Sejnowski 1995), supporting the notion that irregularity occurs in vivo because of external inputs onto the cell (for a discussion of possible intrinsic sources, see Softky and Koch 1993). Interestingly, Yoshida and Hasselmo (2009) recently recorded from PoS neurons in vitro following injections of brief (0.2–2 s) depolarizing currents and reported that 25% of the cells, which were initially “silent,” went into a sustained firing mode following the current injections. Moreover, the percentage of cells exhibiting this response increased to almost all cells when they were exposed to a cholinergic agonist (carbachol, 10 μM) and that the persistent firing could last for >2 min. Of particular interest was the finding that the mean σ was 0.209 (range: 0.069–0.355), considerably smaller than the σ values reported here (Zilli and Hasselmo, personal communication based on Zilli et al. 2009). This result suggests that PoS cells fired relatively regularly when injected with current and that this regularity was due to intrinsic membrane properties rather than synaptic inputs. Taken together, most evidence points to external synaptic inputs as the most likely source of the high variability in ISIs, rather than intrinsic cellular properties.

Implications for models of grid cell firing in entorhinal cortex

Our results also have important implications for computational models proposed to account for grid cell firing patterns in the entorhinal cortex. Recordings from the dorsomedial caudal entorhinal cortex in freely moving rats have identified cells that fire at multiple locations, such that the locations form a regular repeating tessellated pattern; these cells have been referred to as grid cells (Hafting et al. 2005). Recent computational models have proposed that grid cell responses are generated through an oscillatory interference model where bands of different oscillatory inputs, both dendritic and somatic, are summed at the soma to generate the observed firing patterns (Burgess et al. 2007; Hasselmo et al. 2007). These inputs are modeled based on firing patterns that contain regular oscillations and have rates that approximate the theta rhythm. Interestingly, several studies have reported that entorhinal cells in the same areas where grid cells are found contain intrinsic subthreshold membrane oscillations that are also within the theta frequency band (Alonso and Llinás 1989; Erchova et al. 2004; Giocomo et al. 2007). Frequencies of these oscillations are relatively regular and vary according to the dorsal–ventral depth within the entorhinal cortex, where cells with higher frequencies occur at more dorsal levels and cells with lower frequencies occur at ventral levels (Giocomo et al. 2007). Importantly, these oscillatory frequencies vary along the same dimension as the spatial scale (size) of the grid cell pattern within the entorhinal cortex. One way to achieve the regular firing pattern in entorhinal cells, which is necessary to form the regular, repeating grid patterns of grid cells, is to use smooth changes in continuous firing rate onto the grid cell dendrites. Although individual HD cells have irregular firing patterns over short intervals, their firing when considered over longer intervals is more regular (Fig. 7B). This finding, coupled with the fact that the activity from a population of irregular spiking cells yields a more even distribution of discharge onto the dendrites over time, indicates that the irregular firing of HD cells is not a problem for grid cells to achieve a regular firing pattern. Furthermore, it is likely that the regular oscillations observed in grid cells arise from their intrinsic membrane properties, given that rhythmic subthreshold oscillations were still present in cells from this area in in vitro recordings with synaptic transmission blocked (Dickson et al. 2000). In addition, in vitro studies of layer II, layer III, and layer V neurons in medial entorhinal cortex show that exposure to muscarinic cholinergic agonists, such as carbachol, or agonists for the metabotropic glutamate receptor (mGluR), shift the cells into a persistent firing mode that is calcium dependent (Egorov et al. 2002; Fransèn et al. 2006; Klink and Alonso 1997; Yoshida et al. 2008). These findings suggest that small excitatory inputs onto the cells, even if irregular, can initiate voltage events that bring the cells into a sustained firing mode driven by intrinsic membrane channels. In this case, even irregular firing of the ADN/PoS inputs could trigger events in entorhinal cells that result in sustained firing that is more regular than the synaptic inputs.

Finally, it is noteworthy that the ISIs did not correlate very well to either the animal's angular or translational head velocity. Oscillatory interference models for grid cells postulate that a “speed signal” must be present that projects onto the entorhinal cells. Although these velocity analyses were conducted on ADN HD cells, similar analyses for PoS HD cells also did not find any strong correlations (data not shown). Because both the ADN and PoS project directly to the area of entorhinal cortex where grid cells have been identified (Beckstead 1978; Kohler 1985; Shibata 1993; van Groen and Wyss 1995), the absence of a strong speed signal in this projection presents a problem for these theoretical models.

Conclusions

In sum, our results indicate that despite the appearance of regularity in their firing, HD cells throughout the Papez circuit, like cells elsewhere in the cortex, have irregular firing patterns when measured over short timescales. However, HD cell firing appears more regular when measured over longer timescales that include the entire episode when the head is pointing in the cell's preferred direction. The relatively large variability seen in cellular firing over short epochs suggests that just as neural representations of head direction and location in the spatial domain operate through population vector dynamics (Salinas and Abbott 1994; Wilson and McNaughton 1993), the temporal domain for cell firing also most likely operates as a population vector, where a cell's responses are averaged over some finite time interval. This time interval could be the duration on the order of several EPSPs occurring serially, which would correspond to the time interval of 120 ms postulated for the integration of form and motion information in temporal cortical visual pathways (Singer and Sheinberg 2010).

GRANTS

This work was supported by National Institutes of Health Grants MH-48924, MH-01286, and NS-053907.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author.