Alteration of Cortical Functional Connectivity as a Result of Traumatic Brain Injury Revealed by Graph Theory, ICA, and sLORETA Analyses of EEG Signals

Abstract

In this paper, a novel approach to examine the cortical functional connectivity using multichannel electroen-cephalographic (EEG) signals is proposed. First we utilized independent component analysis (ICA) to transform multichannel EEG recordings into independent processes and then applied source reconstruction algorithm [i.e., standardize low resolution brain electromagnetic (sLORETA)] to identify the cortical regions of interest (ROIs). Second, we performed a graph theory analysis of the bipartite network composite of ROIs and independent processes to assess the connectivity between ROIs. We applied this proposed algorithm and compared the functional connectivity network properties under resting state condition using 29 student-athletes prior to and shortly after sport-related mild traumatic brain injury (MTBI). The major findings of interest are the following. There was 1) alterations in vertex degree at frontal and occipital regions in subjects suffering from MTBI, (p < 0.05); 2) a significant decrease in the long-distance connectivity and significant increase in the short-distance connectivity as a result of MTBI, (p < 0.05); 3) a departure from small-world network configuration in MTBI subjects. These major findings are discussed in relation to current debates regarding the brain functional connectivity within and between local and distal regions both in normal controls in pathological subjects.

I. Introduction

Over the last two decades, the advances in brain imaging methodologies have revealed important information regarding both structural and functional properties of the human brain both in normal controls and pathological populations. However, “traditional” analysis of brain correlates of behavior is mostly implemented by focusing on alteration of brain signals within the focal regions of interest (ROI). For example, numerous imaging studies have documented the involvement of prefrontal cortex in execution of working memory tasks [1]–[5]. Similarly, supplementary motor area (SMA) and anterior cingulate cortex (ACC) have been ascribed to “vocal-motor planning” [6]. A number of our own studies documented differential sensitivity of electroencephalographic (EEG) signal primarily at primary motor cortex (PMC) and SMA towards kinematic [7] and kinetic [8] properties of human movement. It should be noted, however, that human brain has two contradictory properties: 1) segregation which means localization of specific functions and 2) integration, which means combining all the information and functions at a global level within conceptual framework of a “globally integrated network” [9], [10]. The existence of a “default network” in the brain during the resting state was proposed by Greicius et al. 2003 [11]. Moreover, it has been suggested that neural network of the brain has a small-world structure, namely, high cluster coefficients and low average path length allowing the optimization of information processing [10]. Accordingly, synchronized activation between prefrontal, frontal, and central sites has been shown to be correlated with the efficiency of working memory and speed of information processing [12]. Overall, the segregation method, although still commonly used in brain research, can not explain the whole issues of integration phenomena observed in both resting states and during high level information processing in the brain.

It is believed that effective connectivity and optimal network structure is essential for proper information processing in the brain. Indeed, functional abnormalities of the brain are found to be associated with the pathological changes in connectivity and network structures. For example, a few recent functional magnetic resonance imaging (fMRI) reports have indicated predominant loss of long-distance functional connections under resting state in patients suffering from Alzheimer’s disease (AD), [13], [14]. Moreover, recent EEG and MEG studies have also indicated a significant increase in the focal connectivity within the low-frequency band (delta and theta) and decrease in the long-range connectivity within the high-frequency band (alpha and beta) in resting state [15], and during a visual oddball paradigm [16]. Similarly, increased focal EEG coherence within the low-frequency band and reduced long-distance coherence in the high-frequency band were observed in Autistic patients [17]. In contrast, higher long-distance synchronization scores in EEG delta, theta, and lower gamma frequency bands along with decline in synchronization likelihood in the lower alpha frequency band have been reported in patients suffering from low-grade glioma (LGG) [18]. Also, the less small-world like and more random network organization of the functional network during resting state (EEG data within beta frequency band) have been observed in the Alzheimer’s disease (AD) patients [19]. Overall, alteration of the neural network structure with the tendency of departure from the small-world like network organization is assumed to be a common feature of the brain functional abnormalities [10].

The EEG and MEG based signals have been traditionally used to examine the functional cortical connectivity due to its high temporal resolution. Several measurements of functional connectivity using scalp recording EEG and MEG signals include the Pearson coefficient of correlation, coherence, phase lag, and synchronization likelihood [20]. However, it should be noted that both the nonzero reference effect [21], [22] and the volume conduction effect [23] may be serious confounding factors when functional connectivity assessed based on the scalp recording EEG signals. Specifically, high coherence values between two EEG channels may be merely caused by: 1) linear propagation of the independent processes and 2) synchronization between two EEG channels that may not be directly caused by synchronized activation between two corresponding brain areas of interest 3) the biased, non-neural references. Using the imaginary part of the coherence between multiple EEG sites can partially overcome the first problem [23], and using the reference electrode standardization technique (REST) based on equivalent dipole sources can overcome the third problem [21], [22]. However, the second problem may still remain, because the synchronization between two EEG channels can be caused by synchronized activities in some other brain regions rather than in the corresponding regions of interest under study.

Another approach to deal with volume conduction problem has been proposed by Thatcher et al. [24]. They have suggested acquiring the genuine electrical source distribution of EEG signal by solving the linear inverse problem first, and then, calculating the synchronization between the time series of averaged current densities within two regions of interest (ROI). There are, however, several shortcomings of this approach. First, the efficacy of this approach heavily relies on accurate estimation of the current density. Although there are many models proposed for EEG source reconstruction, [25]–[27], all of them are based on certain assumptions. Thus, they only provide the optimized solution under certain conditions due to the ill-conditioning problem [28]. Some algorithms based on distributed source model, such as LORETA and sLORETA, can provide accurate estimation of the sources location to a certain degree, but accurate estimation of current density is not necessarily guaranteed. Second, EEG artifacts, such as eye blinking and/or heart beating can significantly contaminate the recorded electrical potential on the scalp resulting in incorrect estimation of the source distribution [29]. The plausible attempts to overcome these shortcomings are 1) to apply source principle component analysis (sPCA) in order to separate the different compound systems composed by interacting sources and 2), to localize these systems by minimum overlap component analysis (MOCA), similar to LORETA [30]. It should be noted that this approach, although promising, can not provide a direct noninvasive measurement of functional connectivity between various brain regions.

To date, it is not yet clear what is the optimal way to convert/combine imaging data derived from EEG to graph analysis and/or brain functioning assessment tools [10]. Partly to address this quest, we propose a novel EEG based approach to estimate the functional connectivity among brain regions at rest which combines independent component analysis (ICA), sLORETA, and graphical analysis tools. Considering the notion that functional network revealed by graph analysis of EEG data might represent a “physiological substrate for segregated and distributed information processing” [31]–[34], we aimed to provide additional evidence regarding long-lasting neuronal dysfunction and alterations of brain dynamics as a result of mild traumatic brain injury (MTBI). In our previous research, we examined the feasibility of EEG wavelet entropy measures (EEG-WE) to monitor the differential rate of functional recovery in subjects suffering from single versus recurrent concussions [35]. Clearly, EEG-WE values remained significantly reduced primarily at temporal, parietal and the occipital regions at least 30 days post-MTBI. Most importantly, rate of recovery of EEG-WE measures was significantly lower in subjects suffering from recurrent MTBI compared to subjects suffering from a single concussion episode, even though none of these MTBI subjects were clinically symptomatic beyond 10 days postinjury. In this study, we examine the alterations of cortical functional connectivity within and between local and distal areas in the same athletes before and shortly after MTBI.

II. Algorithms

A. Independent Components Analysis

According to the ICA model, the EEG signal recorded on the scalp is a mixture of the electrical potentials generated by temporally independent cerebral and artifactual bioelectrical processes [36]. The summation of potentials arising from various sources in the brain, scalp, and body is linear at all electrodes, and that propagation delays from the sources to the electrodes are negligible. The ICA model can be written as

$$\text{EEG}(\text{t})=\mathit{M}·\text{S}(\text{t})$$ (1)

where EEG(t) is the EEG signal recorded on the scalp with n by 1 dimension, n is the number of electrodes, M ∈ R^n×m is the mixing matrix, S(t) ∈ R^m×1 is independent process (or brain functional property), m is the number of independent processes. Each column of the M is the topography of corresponding independent process on the scalp. M and S(t) can be estimated from EEG(t) by several algorithms, such as fastICA [37]. In the proposed algorithm, independent components (ICs) corresponding to artifacts were excluded manually and all nonartifact components were chosen for further analysis. More specifically, the artifactual components were identified by three factors: 1) the scalp map, 2) the configuration of time series, and 3) spectrum. For example, the ICs corresponding to EMG activity from temporalis muscle are highly concentrated around the temporal region and thus can be easily identified by the scalp map. Similarly, ICs related to the ocular artifact are highly concentrated around the frontal region. In addition, the configuration of the time series of these components is highly analogous to the configuration of the EOG signal. Moreover, the spectrum of these components exhibit low dominant frequency (< 2 Hz).

B. ICA-sLORETA

The next step in the proposed algorithm is to localize the cerebral bioelectrical processes that actually originate in the brain. This is accomplished by using the topography of independent processes (the columns of the matrix M) as the input of source reconstruction algorithms such as LORETA [38]. In our proposed algorithm, sLORETA instead of LORETA was used due to its better localization accuracy [39]. The result of the ICA-sLORETA revealed the cortical regions involved in a certain functional activity (i.e., independent process). For each process, a voxel is considered to be involved in the process if the amplitude of the standardized current density of this voxel is greater than the threshold T. In this report, T was set to be the 70th percentile of the amplitudes corresponding to standardized current density of all of the voxels.

C. Graph Analysis of Brain Connectivity at Resting State

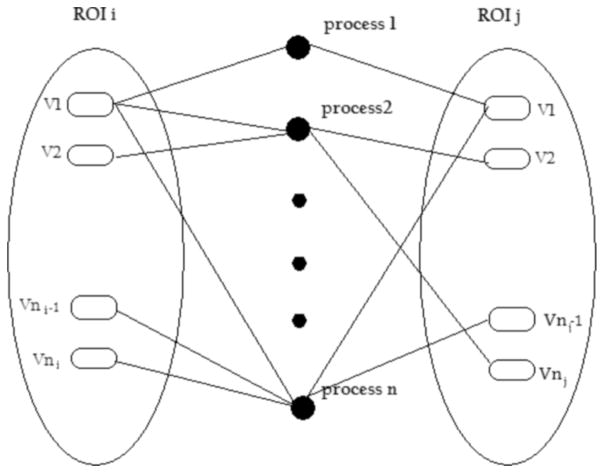
At the third step of the algorithm, an undirected bipartite graph is used to describe the relationship between the voxels at rest (i.e., independent processes). The voxels can be considered as type I vertices, and the processes can be considered as type II vertices. If type I vertices are linked to type II vertices with one edge, then it is assumed that identified voxels are playing a role in certain independent processes. The ROIs consist of a group of type I vertices and are not overlapped with each other. The structure of this graphical analysis is depicted in Fig. 1.

Fig. 1.

Bipartite network of the ROIs and independent processes obtained by ICA.

The connectivity between two type I vertices can be calculated as follows:

$$c_{i,j}^v=\frac{n_p}{n_{ij}}$$ (2)

where n_p is the number of the processes (type II vertices) that are connected with both vertex i and vertex j. n_ij is the number of the processes that at least connected with one of the two vertices.

The connectivity between two ROIs is the mean of the connectivity over all pairs of nonisolated vertices between these two ROIs

$$C_{i,j}^R=\frac{1}{n_i\ast n_j}\sum _{k=1}^{n_i}\sum _{l=1}^{n_j}{c}_{k,l}$$ (3)

where n_i is the number of the nonisolated vertices of ROI_i and n_j is the number of the nonisolated vertices of ROI_j.

D. Graphical Analysis of the Functional Network

A weighted network can be built based on the connectivity between ROIs. The nodes of the network are ROIs, and the edges of the network are weighed by the connectivity. The vertex degree k_i of node i of the weighted network is the sum of the weights of the edges attached to it [40]

$$k_i=\sum _j{C}_{ij}^R..$$ (4)

To compute the local cluster coefficient C_l,, averaged cluster coefficient C_p and averaged path length L_p, we first transfer the weighted network into a binary graph by setting all edges with a weight above a certain threshold T to 1, and the others to 0 [41]. The threshold T was chosen such that for each individual network the averaged number K of connections per vertex is 3, 4, and 5, respectively, [42]. To avoid the disconnection problem, the harmonic mean instead of arithmetic mean of the shortest path length over all pairs of vertices d_ij was used to compute the average path length L_p

$$L_p=\frac{N\ast (N-1)/2}{{\sum }_{i\ne j}1/d_{ij}}.$$ (5)

To explore the small-world network properties, the ratios Cp/C_p–s and L_p/L_p–s were also calculated. In this calculation, C_p–s and L_p–s denote the values of C_p and L_p for appropriate ensembles of random reference graphs with the same degree distribution of the EEG signals. The details of this procedure can be found in [42].

III. Subject and Data Acquisition

Subjects

A total of 160 subjects were initially recruited for the sport-related concussion study. All subjects were Pennsylvania State University athletes at high risk for traumatic brain injury (collegiate rugby, football, and ice hockey players), aged between 18 and 25 years, male (n = 84, mean age = 20.9 years) and female (n = 76, mean age = 21.4 years). None of these subjects had a concussion history at the time of preinjury baseline testing. Twenty nine of these subjects (female, n = 14; male, n = 15) have suffered from grade 1 MTBI (Cantu Data Driven Revised Concussion Grading Guideline, 2006) within six months after baseline testing and were tested on day seven postinjury. These subjects were clinically symptomatic at the day of testing based upon neurological assessments (Co-operative Ataxia Rating Scale, World Federation of Neurology, Trouillas et al. 1997). A detailed description of inclusion criteria for MTBI can be found in [43].

EEG Procedure

Subjects were seated with eyes closed in an electrically shielded and dimly lit environment. The continuous EEG was recorded using Ag/AgCl electrodes mounted in a 19-channel spandex Electro-cap (Electro-cap International Inc., Eaton, OH). The electrical activity from the scalp was recorded at 19-sites: FP1, FP2, FZ, F3, F4, F7, F8, CZ, C3, C4, T3, T4, T5, T6, PZ, P3, P4, O1, O2, according to the International 10–20 system [44]. The ground electrode was located 10% anterior to FZ, linked earlobes served as references and electrode impedances were below 5 kΩ. EEG signals were recorded using a programmable dc coupled broadband SynAmps amplifier (NeuroScan, Inc., El Paso, TX). Data were analog filtered from dc to 70 Hz and recorded with a sampling rate of 1000 samples/s. The impedances were maintained below 10 kΩ and data stored for offline analysis with 24 bit A/D resolution (3 nV/bit precision).

The EEG data were initially processed offline using EEGLAB 5.03 [45] using Matlab open source toolbox (Mathworks, Natick, MA). Imported data were down sampled to 250 Hz to reduce computing time and epoching from 0 to approximately 4 s and at least 3 min of artifact free EEG signal were subjected to further analysis for each subject.

Nineteen ROIs were constructed with the “all nearest voxels” method centered at 19 electrode sites (O1, O2, etc.) using sLORETA software [46]. For each subject, the connectivity between ROIs was first calculated within each selected epoch, and then was averaged over all of the selected epochs. The vertex connectivity degree of each ROI was calculated based on the averaged connectivity. Statistical comparison of functional connectivity and small-world like network properties (i.e., C_p, L_p, Cp/C_p–s and L_p/L_p–s values) before and after MTBI was achieved using two tailed within subjects t-tests. The significance level was set at p < 0.05.

IV. Results

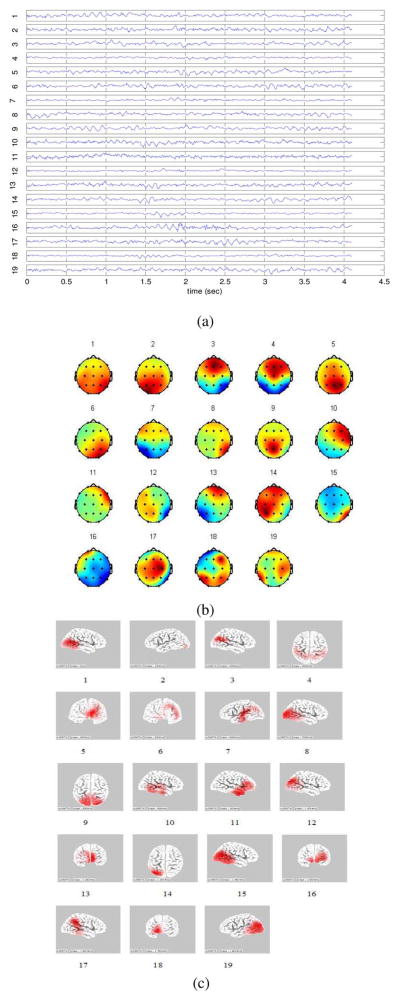
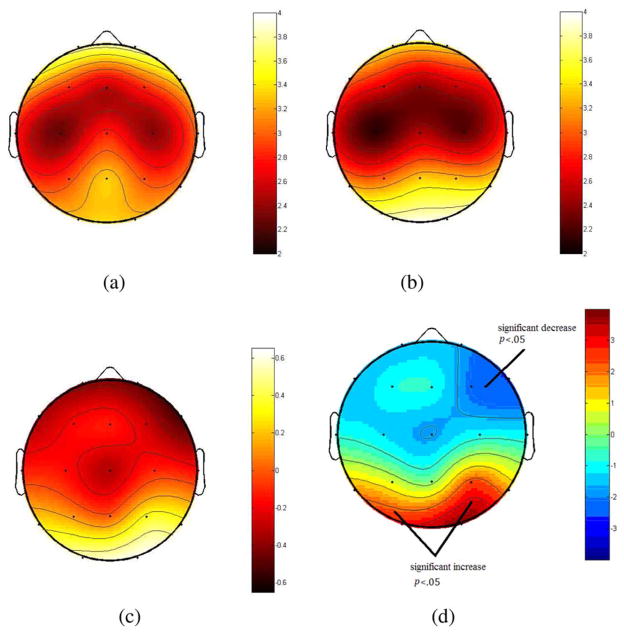
The independent components with respective scalp maps and source distribution on the cortex which are estimated by sLORETA from a single EEG epoch are shown in Fig. 2. It should be noted that although many of these ICs have single-dipole-like source distributions, some of the ICs, such as components 4, 5, 6, 9, 13, and 16, have truly distributed sources. Moreover, the time series of the components which have distributed sources are similar to the rest of components, indicating they are real sources of observed brain activation patterns rather than pure noise. The group means of the vertex degree (k_i) for each ROI are listed in Table I and illustrated in Fig. 3. As can be seen from this Table I, the vertex degrees at occipital and parietal areas significantly increased as a result of MTBI in the ROIs centered at O2 (t = 3.91, d.f. = 28, p < 0.01), O1 (t = 2.95, d.f. = 28, p < 0.01), and P4 (t = 2.35, d.f. = 28, p < 0.01) electrode sites. In contrast, vertex degrees (k_i) at frontal areas significantly decreased particularly in the ROIs centered at F4 (t = −2.64, d.f. = 28, p < 0.01) and F8 (t = −2.14, d.f. = 28, p < 0.01) electrode sites.

Fig. 2.

(a) The time series of the ICs extracted from a single EEG epoch. (b) The topographies of these ICs. (c) The respective source distributions of the ICs obtained from sLORETA. The ICs, the associated topographies and source distributions are labeled by numbers. It is shown in (c) that, some of the ICs, such as 4, 5, 6, 9, 13, and 16, have truly distributed sources.

TABLE I.

T-Test Results of the Vertex Degree (K_i) for Each ROI

ROI Centered	Prior to MTBI	After MTBI	t-score	P value
O2	3.92	3.29	3.91	0.0005**
O1	3.86	3.30	2.95	0.0063**
Pz	3.31	3.31	−0.01	--
P4	3.28	2.94	2.35	0.026*
T4	2.89	3.07	−1.10	--
C4	2.25	2.36	−1.00	--
T3	2.68	2.81	−0.84	--
Cz	2.48	2.80	−1.74	0.093
C3	2.11	2.27	−1.28	--
Fz	2.39	2.52	−0.89	--
F4	2.56	2.83	−2.14	0.042*
F8	2.88	3.41	−2.64	0.014*
F3	2.64	2.83	−0.91	--
Fp2	3.38	3.86	−1.76	0.089
F7	3.08	3.43	−1.64	--
Fp1	3.41	3.84	−1.68	--
T6	3.47	3.11	1.61	--
T5	3.23	2.96	1.75	0.092
P3	3.03	2.92	0.67	--

^**Denotes P < 0.01,

^*Denotes P < 0.05,

-- Denotes P > 0.05

Fig. 3.

(a) Group means of the vertex degree prior to MTBI (b) after MTBI. (c) Difference of mean degree between testing date. (d) t scores of the difference before and after MTBI. The bipartite network of the ROIs and independent processes obtained by ICA.

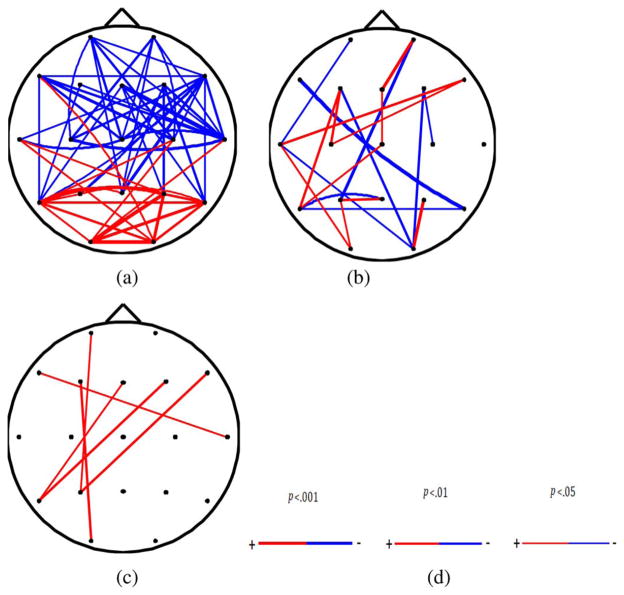
The connectivity between the ROIs is shown in Fig. 4. There was significant increase of short-distance connectivity within the occipital and parietal areas (t = 2.1, d.f. = 28, p < 0.01) as a result of MTBI. In contrast, long-distance connectivity between frontal areas and other areas of the brain was significantly reduced (t = 2.2, d.f. = 28, p < 0.01). Overall, the results demonstrated significant decrease in the long-distance connectivity and significant increase in the short-distance connectivity in MTBI subjects postinjury. The mean Euclidean distance of the ROI pairs with significantly decreased connectivity was 9.2 ± 1.68 cm cm whereas the mean distance of the ROI pairs with significant increased connectivity was 6.5 ± 2.46 cm.

Fig. 4.

(a) significant changes in connectivity due to concussion (p < 0.05). Color “blue” indicates significant decrease due to concussion and “red” indicates significant increase due to concussion. The thickness of the lines indicates the significant level (b) significant changes in the iCOH within alpha band due to MTBI (p < 0.01). (c) Significant changes in the COH within alpha band due to MTBI (p < 0.01). (d) Color “blue” indicates significant decrease due to MTBI and “red” indicates significant increase due to concussion. The thickness of the lines indicates the significant level from 0.05 to 0.001.

Similar patterns of brain connectivity were observed using imaginary part of coherence (iCOH) within alpha frequency band [23]. See Fig. 4(a)–(c) to compare results of connectivity analyses, including those traditionally used in clinical practice. As can be seen from Fig. 4(a)–(c), alterations of functional connectively of distant brain areas in subjects suffering from MTBI can be depicted more clearly using our proposed algorithm. Specifically, the decrease of distant functional connectivity in subjects suffering from MTBI cannot be observed when traditional coherence analysis of scalp recorded EEG was implemented [see Fig. 4(c)].

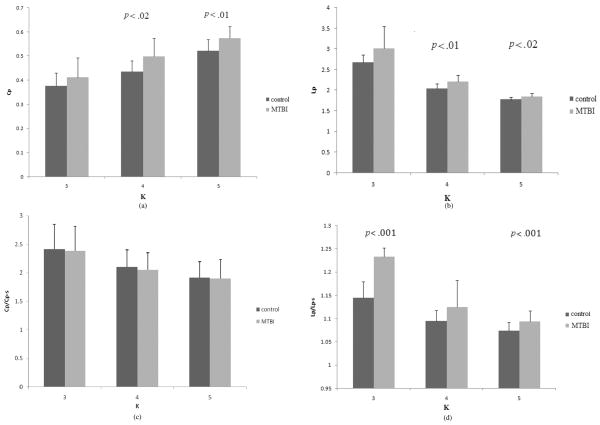
Finally, the global graphic properties of the brain functional network configuration are shown in Fig. 5(a)–(d). As can be seen from these figures, there were significantly higher C_p values for K = 4, 5 (t = 2.6, d.f. = 28, p < 0.01, t = 3.0, d.f. = 28, p < 0.01) and L_p values for K = 4, 5 (t = 3.4, d.f. = 28, p < 0.01; t = 2.5, d.f. = 28, p < 0.01) along with the higher L_p/L_p–s ratio for K = 3, 5 (t = 8.4, d.f. = 28, p < .001; t = 4.31, d.f. = 28, p < 0.01) in subjects postinjury. In contrast, C_p/C_p–s ratio remained unchanged (p > 0.01). Moreover, the C_p/C_p–s ratio was significantly larger than 1 (t = 30.1, d.f. = 14, p < 0.001) along with L_p/L_p–s ratio remained to be close to 1 before and after MTBI, indicating that the functional networks are small world-like networks [47] regardless of injury status. However, the increased L_p/L_p–s, C_p, and L_p in MTBI subjects may indicate that the functional network configuration is less small world-like in subjects postinjury. Overall, there were significant alterations of C (the clustering coefficient as an index of local structure) and L (path length as an index how well integrated a graph) as a result of MTBI.

Fig. 5.

(a) The cluster coefficient (C_p) before and after MTBI when the functional networks have different values of K. The C_p is significantly increased after MTBI when K = 4 and 5. (b) The averaged path length (L_p) before and after MTBI when the functional networks has different values of K. The L_p after MTBI significantly increased when K = 4 and 5. (c) The C_p/C_p–S ratio before and after MTBI. No significant differences for all Ks. (d) The L_p/L_p–S ratio before and after MTBI. There is a significant increase after MTBI, when K = 3 and 5.

V. Discussion

To the best of our knowledge this is the first study to examine the alteration of the brain functional connectivity in the same individuals before and shortly after sport-related mind traumatic brain injury (MTBI). The novel features of our EEG based approach to assess the cortical functional connectivity is that, unlike traditional coherence analysis of EEG raw signal and/or using imaginary part of coherence [23], we proposed a source based measures using graph theory in conjunction with ICA and sLORETA in the same subjects prior to and shortly after brain injury. In addition, instead of calculating the connectivity within certain frequency bands (i.e., commonly used in EEG research [48]), our proposed algorithm does not depend and/or focus on a certain frequency band, and, therefore provides an estimation of the cortical connectivity over the whole range of frequencies.

Our proposed algorithm has three major advantages. First, unlike traditional methods based on correlation or coherence analyses of scalp recorded EEG raw signals, our method is based on estimating the sources of EEG signals, therefore it is most likely not affected by the volume conduction effect. Second, the proposed algorithm is artifacts-free, since artifacts such as eye blinking and muscle activity etc., can be identified and excluded by the ICA composition. Third, instead of directly using the current density obtained from the inverse methods, our algorithm only requires accurate estimation of the location of the sources, which is much easier to be achieved. In fact sLORETA can localize both single [49] and multiple sources [50] with good accuracy, which is very suitable for our algorithm. Therefore, we believe that our algorithm can at least partially overcome the problems with previous methods.

Moreover, in our algorithm, a simple cutoff criterion was applied to localize the source of EEG raw signals using a standardized current density power estimates provided by sLORETA. We assume that more sophisticated and robust analysis of source localization can be potentially used to improve the efficacy of our proposed algorithm. For example, the 3-D cortex surface can be flattened into 2-D surface in order to establish the edge detection and to achieve the image segmentation similar to computer vision and image analysis prototypes [51].

It should be noted that there is a possibility to assess the cortical connectivity within certain frequency bands under the framework of our proposed algorithm by proper selection of independent processes obtained from the ICA. Another possibility is to modify the ICA model itself. According to currently used ICA model, the independent components are assumed to be instantaneously mixed, indicating that the mixing matrix M within each subband is identical. In order to assess the connectivity within different subbands the convolutive mixture model may be applied. The convolutive mixture model can be written as follows [52]:

$$x_i(t)=\sum _{j=1}^n\sum _k{a}_{ij}(t)s_j(t-k)\text{for}i=1,\dots ,n.$$ (5)

In the frequency domain, the model in (5) becomes

$$X_i(\omega )=\sum _{j=1}^m{A}_{ij}(\omega )S_j(\omega )\text{for}i=1,\dots ,n$$ (6)

where X_i(ω), S_j(ω) and A_ij(ω) are the Fourier transform of x_i(t), s_j(t) and a_ij(t) respectively.

The convolutive mixture problem can be transformed into the instantaneous BSS/ICA models at each frequency band. Thus, our algorithm can be extended to assess connectivity within certain frequency bands by using A(ω) as the input of the sLORETA in the complex domain.

There are several findings of interest with regards to alteration of cortical functional connectivity as a result of sport-related concussion. First, the decrease of long-distant functional connectivity was consistently observed in concussed athletes. This finding is consistent with previous brain imaging research, including EEG and fMRI, indicating the same trends in patients suffering from Alzheimer disease [13]–[16], [19], Autism [17], and low-grade glioma [18]. Moreover, long-lasting abnormal patterns of EEG coherence, particularly between distant brain regions, were documented in patients suffering from MTBI up to eight-years postinjury [53]. Taking into consideration that effective connectivity between various brain regions and optimal network structure is essential for proper information processing [10], it is not surprising that MTBI subject under study experienced cognitive deficits on the day of EEG testing, as revealed by neuropsychological evaluations. Overall, our results indicating the alteration of long-distant cortical functional connectivity in MTBI patients is in agreement with “disconnection hypothesis” [54] previously proposed to explain disturbed connectivity between different brain areas in neurological patients.

Second, clear departure from small world like network configuration was observed in subjects after MTBI. Specifically, there was a reduction of the clustering coefficient (C_p) as an index of local structure and enhancement of path length (L_p) as an index of graph integration a graph as a result of concussion. These results seem to be in agreement with “network randomization” hypothesis [41], as a general framework of abnormal brain functions commonly observed in neurological subjects, including those suffering from low-grade tumor and/or epilepsy. It is worth noting that these patients commonly experience disturbed cognition [10], [55], similarly to our MTBI athletes at least in acute stage of injury [56], [57].

Third, the alterations of vertex degrees, as an index of functional cortical connectivity [10] in concussed subjects were consistently observed in ROIs centered at frontal, occipital, and parietal sites. Overall, this finding is consistent with a number of studies indicating the cognitive impairment in concussed individuals due to dysfunctions of frontal and parietal lobes [58]–[60]. It should be noted that the general pattern that emerged from neurological patients is that the abnormalities are the most outspoken to frontal areas [61], [62], [64], [10]. Specifically, the frontal, temporal and parietal lobes are shown to be associated with efficacy of retrieving the declarative memories [63] and/or intact sustained and directed attention [64]. Accordingly, damage to the frontal, temporal and parietal areas is believed to be associated with memory lost and attention problems which are typical symptoms of MTBI [65]. It is important to note that most of our subjects have suffered from memory and attention deficits as revealed by neuropsychological evaluation prior to EEG testing. The reason for altered local connectivity in the occipital areas is not clear at this time.

A possible confusion about this algorithm may arise from the fact that ICs by definition are temporally independent to each other and in most of ERP studies the ICs usually have a single-dipole-source-like scalp distribution. However, we would like to stress that in our study we focused on the spontaneous brain activity at “resting state.” Our approach and obtained findings are consistent with a number of recent brain imaging (fMRI) studies reporting that highly significant synchronization/connectivity may exist between anatomically disconnected brain regions at rest [66]–[68]. Moreover, two temporary “independent” brain activation patterns may have overlapped anatomic region of sources [68].

Overall, this report provides evidences regarding the efficacy of our proposed algorithm to examine alteration of cortical functional connectivity in concussed individuals. Whether the observed alterations are relatively transient in acute stage of brain injury or a long-term persistent residual functional abnormality is yet to be determined. Nevertheless, the proposed approach, in conjunction with other modern approaches (e.g., brain imaging studies including fMRI/MRS/DTI collectively with analysis of biomechanical impact at the time of brain injury, duration of the neurocognitive symptoms and its rate of resolution) can be potentially used by clinicians for more accurate diagnosis and return-to-sport participation criteria after concussive blows.

Biographies

Cheng Cao (M’09) received the Ph.D. degree from the Department of Kinesiology, and M.S. degree from the Department of Electrical Engineering, at the Pennsylvania State University, College, Park, in 2009.

His research involves brain–computer interface, time-frequency analysis, blind signal separation, and the application of modern signal methods in quantitative analysis of EEG.

Mr. Cao won the Presidential Scholarship of the Pennsylvania State University in 2003 and the third prize of excellent student of University of Science and Technology of China in 1999–2002.

Semyon Slobounov received the Ph.D. degree from the Department of Psychology, University of Leningrad, Leningrad, USSR (now St. Petersburg State University, St. Petersburg, Russia), in 1978 and the Ph.D. degree from the Department of Kinesiology, University of Illinois, Urbana-Champaign, in 1994.

He is Professor in the Department of Kinesiology, College of Health of Human Development and Adjunct Professor of Orthopaedics and Medical Rehabilitation with Hershey Medical College at Pennsylvania State University, with primary responsibilities to teach undergraduate and graduate courses in the areas of psychology of injury, neural basis of motor behavior, and psychophysiology. He is an adjunct investigator with the National Institute of Heath, National Institute of Neurological Disorders and Stroke. He also is an Adjunct Professor of the Neuroscience Program, Life Science Consortium, and an Affiliate Professor of Gerontology Center at Pennsylvania State. His research focused on neural basis of human movements with special emphasis on rehabilitation medicine, psychology, and neurophysiology, including traumatic brain injuries.