Factor Structure of Planning and Problem-solving: A Behavioral Genetic Analysis of the Tower of London Task in Middle-aged Twins

Abstract

We examined the genetic architecture of a Tower of London test of planning and problem-solving in 690 middle-aged male twins. Phenotypic analyses revealed only one general factor, but the best-fitting genetic model indicated two correlated genetic factors: speed and efficiency. One variable—number of attempts required to mentally figure the puzzles—loaded on both factors. Shared environmental effects could be dropped with virtually no reduction in model fit. Despite significant nonshared environmental correlations across measures, there was no discernable nonshared environmental factor structure. The correlation between genetic factors (r = 0.46) and the variable loading on both factors could reflect modulation of planning, testing alternatives, and working memory that are required to perform the test. Such coordinated activity is consistent with the notion of a supervisory attentional system, a central executive, or metacognitive ability. The different phenotypic and genetic factor results suggest that relying solely on the former could obscure genetic associations.

Introduction

Planning and goal-directed problem-solving are neuro-cognitive abilities that are important for successful functioning in everyday life. These abilities are typically considered to fall within the broad category of executive functions that are closely linked to prefrontal brain regions (Stuss and Benson 1986; Fuster 1989). Shallice (1982) created the Tower of London task to assess planning ability in patients with frontal lobe lesions, and since that time, this task or variants of it have become widely used in a Edited by Danielle Posthuma. variety of populations.¹ There is variability in planning ability within the general population, and strengths or deficits in planning ability may be important factors in successful aging (Robbins et al. 1998). Planning deficits on variants of the Tower of London may also be found in individuals with frontal lobe lesions (Owen et al. 1990; Levin et al. 1996), in individuals with damage in brain regions that are strongly connected to prefrontal cortex (Owen et al. 1992), and in psychiatric disorders such as schizophrenia (Andreasen et al. 1992).

Individual differences in many cognitive functions are substantially influenced by genetic factors (Bouchard and McGue 2003). Swan and Carmelli (2002) found evidence for a common latent phenotype underlying executive function in older twins; that is, there were shared genetic influences contributing to individual differences in a handful of executive function measures. However, we are unaware of any studies of genetic and environmental influences on planning ability specifically.

Non-genetically informed studies have examined correlates thought to be important for adequate performance in order to gain further understanding of Tower of London tasks. Most often, this has included measurement of the relationship between Tower of London performance and tests of working memory, cognitive inhibition, or fluid intelligence (Welsh et al. 1999; Unterrainer et al. 2004; Zook et al. 2004). Two of these studies have suggested that only fluid intelligence was a significant predictor of Tower of London performance (Unterrainer et al. 2004; Zook et al. 2004). Welsh et al. (1999) did not examine fluid intelligence but found that measures of both working memory and inhibition were significantly correlated with Tower of London performance.

Others have sought to examine components or parameters within the Tower of London task itself (Levin et al. 1996; Unterrainer et al. 2004; Berg and Byrd 2002; Ward and Allport 1997). As reviewed by Berg and Byrd (2002), performance components may include: (1) success or accuracy of solution (how many problems are solved or are solved with the minimum number of moves); (2) efficiency of solution (number of moves to solve the problems or the number of moves taken relative to the minimum needed); (3) speed of performance and planning; and (4) frequency of rule breaks.

Another way to address the components of the Tower of London would be to factor analyze the test parameters. The sample size in most studies has, however, been too small to allow for factor analytic approaches. Levin et al. (1996) conducted a factor analytic study of executive functions tests, including the Tower of London, in 81 children with closed head injuries. Tower of London variables loaded on factors that were labeled as planning, inhibition, and schema (ability to maintain a mental representation). Substantial loadings on the planning factor came only from Tower of London variables, whereas the other two factors included substantial loadings from other tests as well as the Tower of London. The volume of frontal lobe lesions in the head injury group was a significant predictor of the planning and inhibition factors, as well as another factor that did not include Tower of London variables. This study did shed some light on possible Tower of London components, but the goal was to examine this test in head-injured children. To learn more about the basic components underlying the Tower of London, it would be useful to study this test in a larger sample that was composed of non-patients, and to factor analyze Tower of London variables only. We are also unaware of factor analytic studies of the Tower of London in adults. Finally, nothing is known about the genetic architecture of this task.

The goal of this article was to discern the factor structure of Tower of London performance in a behavior genetic context. To accomplish this goal, we examined both the genetic and environmental factor structures of the Tower of London in a sample of middle-aged male–male twins. Because our sample is a community sample, our results may be generalized to middle-aged men in the population. These results in midlife can also set the foundation for future studies on age-related changes in the genetic and environmental influences on dimensions of planning ability. There are not sufficient grounds for hypothesizing a specific factor structure for the Tower of London, nor whether or not a factor structure would be equivalent for the genetic and environmental elements; however, in our view, there are three factor solutions that are most likely. Our scoring of both the time and the number of moves used to complete the puzzles suggests that two basic factors would be speed and efficiency/accuracy. It is possible that speed and efficiency could emerge in a single speed-efficiency trade-off factor, rather than as separate factors. There could also be a separate general ability factor in addition to a speed-efficiency factor, or perhaps just a single overall general ability factor.

Methods

Participants

Twins participated in a study of vulnerability to alcoholism in which they were randomly selected (with one exception) from 3,322 twin pairs (6,644 individuals) who had been interviewed by telephone in the now completed Harvard Drug Study (Tsuang et al. 2001). Harvard Drug study participants were drawn from the Vietnam Era Twin Registry, a nationally distributed sample of male–male twin pairs in which both members served in the military during the Vietnam era (1965–1975). The aforementioned exception was that only those without service in Vietnam were recruited for the alcohol vulnerability study. This constraint was instituted because another study of the registry using only Vietnam veterans was being conducted at the same time, and in order to avoid the potential confounding influence of combat exposure.

Zygosity was assigned to registry members using questionnaire and blood group methods (Eisen et al. 1989) that have approximately 95% accuracy compared with DNA analysis (Nichols and Bilbro 1966; Peeters et al.1998). Previous articles by Eisen et al. (1987) and Henderson et al. (1990) contain a complete description of the registry’s construction.

There were 693 individuals in the present study. To be included, both members of a pair had to agree to participate. Participants were flown in from around the country for a day-long series of assessments at the University of California, Davis in Sacramento, CA and Harvard Medical School in Boston. Participants were given their choice of study site. After complete description of the study to participants, written informed consent was obtained at the study sites. There were 176 monozygotic (MZ) and 169 dizygotic (DZ) pairs; 181 pairs were tested in Boston, 163 pairs in Sacramento, and 1 pair in their hometown. In virtually all cases, both members of a pair came together to the same site. We also included data from three additional MZ twins whose co-twins ended up being unable to participate. The mean age of all participants was 47.9 years (SD = 3.3; range = 41–58); 92.2% were non-Hispanic white, 5.5% were African–American, 1.9% were Hispanic, and 0.4% were other; 97% graduated high school or obtained a GED, 33% were college graduates; 98% were employed full-time and 1.7% were employed part-time.

Tower of London procedures

We modified the Tower of London test that was included in the computer-administered Colorado Neuropsychological Tests (Davis et al. 1994); this package allows for easy modification of tests. Given our nonpatient sample, we wanted to make the test more difficult to reduce potential ceiling effects. In our version, Test 1 had 14 trials;² these included puzzles with 3, 4, or 5 pegs. Three trials had a minimum of 4 moves, 3 trials had a minimum of 5 moves, 2 trials each had a minimum of 6, 7, 8, and 9 moves.

Like the Shallice Tower of London task, the rightmost peg on each trial could hold only one ball, and moving leftward, each successive peg could fit one additional ball. Participants were instructed to move the balls in the “working area” as quickly as possible and in as few moves as possible until they were exactly the same as the “goal arrangement” (see Fig. 1 for specific rules). The balls were moved by means of the computer mouse.

Fig. 1.

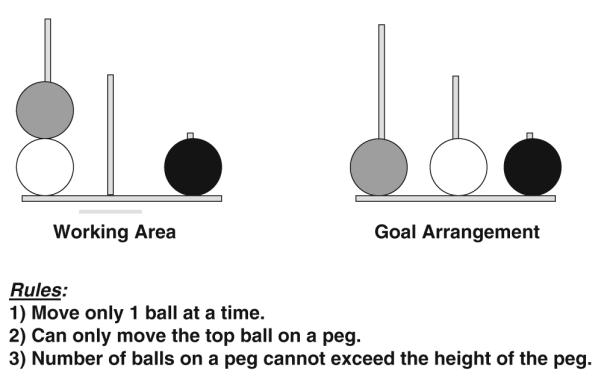
Tower of London display and rules. Object is to rearrange balls in the working area to achieve the goal arrangement in as few moves and as little time as possible

Test 2 had 15 trials, each puzzle again had 3, 4, or 5 pegs. Three trials had a minimum of 2 moves, 4 trials each had a minimum of 3, 4, and 5 moves. Test 2 was performed the same way as Test 1 with one additional dimension. Participants had to mentally figure the minimum number of moves to solve each puzzle before actually solving the puzzle by moving the balls. As soon as a participant thought he figured the correct number of moves, he reported that number to the examiner. If he was correct, the examiner said “that’s right,” and the participant immediately began moving the balls to reach the goal arrangement as in Test 1. If he was incorrect, the examiner said “no” and the participant continued to figure out the number of moves needed until he got the correct number. Participants were strongly discouraged from blind guessing. For example, if someone was told “no” after saying “five moves,” he could not just say “six, seven, eight….” In such cases, the examiner would tell the participant that he needed to try to figure it out and not just guess. This procedure was gone over during practice trials for Test 2. If in the examiner’s judgment, a participant was simply guessing, that portion of the test was scored as missing; this occurred for only two of the participants.

A few key points are worth noting here. Speed and efficiency (accuracy) were given equal emphasis. There were no time limits, and the programs only advanced to the next trial after the current trial was successfully completed. Therefore, all participants successfully solved all of the puzzles presented. Test 2 included instructions for participants to mentally plan ahead, but Test 1 did not. In Test 2 the minimum number of moves was limited to 5 on any given trial because of the requirement to solve the puzzle mentally before actually executing the puzzle.

Tower of London scores

For the present analyses, we focused on six total scores: execution time for Tests 1 and 2; planning time for Test 2; percent above minimum for Tests 1 and 2; and number of attempts for Test 2. Execution time (speed) is the average time in seconds to complete the trials. For Test 2, this score reflected only the time used when actually moving the balls to attain the goal arrangement, just as it did in Test 1. Planning time is the average time in seconds required to mentally figure the minimum number of moves required for each trial in Test 2 (before actually moving the balls). Percent moves above minimum (efficiency) reflects the average number of moves above the minimum needed. If the goal arrangement was reached in the minimum number of moves, this score was 100%. If, for example, a twin took six moves on a trial that required only four moves, this score was 150% (i.e., 6/4). Because all participants successfully completed all trials, these scores were measures of efficiency, not accuracy. Number of attempts is the number of tries it took a twin to mentally figure the minimum number of moves required on each trial summed over all 15 trials in Test 2.

Statistical analysis

Phenotypic factor analysis

We performed a phenotypic factor analysis of the Tower of London variables using SAS Proc Factor (SAS Institute 2000). We utilized the phenotypic factor analysis to compare and contrast it with our model fitting results, as well as for comparisons of phenotypic results with other studies. The phenotypic factor analysis was for descriptive purposes. Because the underlying structure of genetic and environmental covariance may vary from the underlying phenotypic covariance structure, the phenotypic factor analysis does not serve as a guide in evaluating the genetic and environmental factor structures, as there is no necessary correspondence between the two.

Genetic modeling

In the basic twin model (Eaves et al. 1978; Neale and Cardon 1992), phenotypic variation is decomposed into three latent sources of variance: additive genetic influences (A); shared or common environmental influences (C); and nonshared or individual-specific environmental influences (E). These models are typically referred to as “ACE” models. Relationships across twins in the models are as follows: (1) additive genetic factors correlate 1.0 for MZ twins because they share 100% of their segregating genes, and 0.5 for DZ twins because they share, on average, 50% of their genes; (2) shared environmental factors correlate 1.0 across twins regardless of zygosity; these are factors that contribute to twin similarity; (3) nonshared environmental factors are uncorrelated across twins; these are factors that contribute to differences between twins. Measurement error is included in the nonshared environmental variance because it is also assumed to be uncorrelated between twins (given that it is assumed to be random).

Basic genetic and environmental covariance structure

We performed biometric modeling of the raw data with Mx, a maximum-likelihood-based structural equation modeling program (Neale et al. 2003). Analyses were conducted in a stepwise fashion in order to systematically evaluate aspects of the separate covariance structures. In Step 1, we performed a Cholesky decomposition of the variance components in order to provide a saturated model of the general genetic and environmental covariance structure. We also tested whether dropping all genetic influences and/or all shared environmental influences resulted in a significant deterioration in fit, in order to obtain the simplest and most parsimonious model against which subsequent factor models would be compared.

Genetic and environmental factor structure

Although Cholesky models yield estimates of the genetic and environmental correlations across variables, they are not very useful in determining whether there are any meaningful patterns underlying the genetic and environmental covariance across variables. Therefore, in Step 2, we explored whether either the genetic and/or the nonshared environmental influences on covariance across measures could be simplified into a set of more parsimonious factors, using a series of independent pathways models. With six variables, we were able to test upto three factors for each of the A, C, and E components (M. Neale, personal communication, April, 2008). This seemed reasonable based on our initial conceptualization of the Tower of London task. However, we did not try to simplify the shared environmental covariance structure because–as can be seen in the results section–dropping the C effects from the Cholesky structure in Step 1 resulted in virtually no change in model fit, thereby obviating any need for further testing of the shared environmental structure.

We began by testing the genetic factor structure without imposing any constraints on the nonshared environmental covariance structure. A model with three independent factors, as well as subsequent 2- and 1-factor models, including a 2-correlated factors model, was tested. All of the factor models initially allowed for variable-specific (i.e., residual) genetic influences. For 2- and 3-factor models, constraints on factor loadings need to be imposed so that the models are identified. The selection of these factor loadings was not based on their magnitude or any substantive criteria. We simply set the first factor loading on the second factor, and the first two factor loadings on the third factor to zero. Specification of alternate factor loadings did not result in changes in the overall model fit or the rotated factor solutions.³

The estimated factor pattern from the output in Mx was then rotated in SAS to obtain orthogonal factors which are allowed to load on each of the six variables. The 2-correlated factors model further allows for the possibility that the factors are not orthogonal. After obtaining the most parsimonious model for the genetic factor structure that adequately recaptured the genetic variance–covariance structure, we then tried to simplify the nonshared environmental covariance structure in a similar manner to the approach just described.

Model comparisons

Models were compared using the likelihood-ratio chi-square test (LRT) statistic, the Akaike Information Criterion (AIC), and the Baysian Information Criterion (BIC) (Akaike 1987; Williams and Holahan 1994). The LRT is obtained by taking the difference between the −2 log-likelihood (−2LL) of one model and that of a reduced (nested) model, and is distributed as a χ². A reduced model refers to a model from which one or more nonsignificant components have been dropped. If the LRT between two models is nonsignificant, the reduced model is generally accepted as a better (more parsimonious) fit. When the LRT is nonsignificant for two or more competing models, the AIC and BIC are used to determine the preferred model. The AIC, which is calculated as Δχ² – 2Δdf, indexes both goodness-of-fit and parsimony; the more negative the AIC, the better the balance between goodness-of-fit and parsimony. The BIC is similar to the AIC, except that it also adjusts for sample size. Based on Markon and Krueger (2004), when there was a discrepancy, preference was given to the BIC (adjusted for sample size). We present all three fit statistics.

Results

Descriptive statistics

Table 1 shows the means and standard deviations for the different measures. For Tests 1 and 2, we also rank ordered the puzzles within each test according to the percent moves above the minimum needed (not shown in tables). This measure serves as an index of difficulty for each trial, with higher scores reflecting greater difficulty. The correlations between difficulty ranking and minimum number of moves were 0.19 (N = 14; P = 0.37) for Test 1 and 0.60 (N = 15; P < 0.004) for Test 2. These correlations were based on Kendall’s Tau-b because there were many ties for the rankings of minimum number of moves.

Table 1.

Tower of London variables (Ns vary due to missing data)

Measures	N	M	SD
Test 1: Execution time (speed, s)	676	30.25	9.53
Test 2: Execution time (speed, s)	670	12.92	4.90
Test 2: Planning time (speed, s)	670	19.25	9.59
Test 1: Percent moves above minimum  (efficiency)	676	41.99	23.39
Test 2: Percent moves above minimum  (efficiency)	670	17.91	12.78
Test 2: Number of attempts to mentally figure  puzzle	674	1.51	0.33

Phenotypic correlations and factor analysis

Table 2 shows the phenotypic correlations among the Tower of London variables. All correlations were positive, and the phenotypic factor analysis yielded only a single factor with an eigenvalue greater than one. All of the variables had positive loadings on this factor, ranging from 0.46 to 0.73. The eigenvalue for this factor was 1.88 and the factor accounted for 83% of the variance; the next largest eigenvalue was 0.61. For comparisons with the multivariate results below, we also calculated a summary score based on factor scores from the single phenotypic factor and estimated its heritability. The MZ correlation for the factor score was 0.58 and the DZ correlation was 0.38. Standard univariate ACE models revealed that genetic influences accounted for 40% of the variance, shared environmental influences accounted for only 18% of the variance, and nonshared environmental influences accounted for 42% of the variance.

Table 2.

Tower of London phenotypic correlation matrix

	Test 1: Execution time (speed)	Test 2: Execution time (speed)	Test 2: Planning time (speed)	Test 1: % Moves above minimum (efficiency)	Test 2: % Moves above minimum (efficiency)	Test 2: number of attempts to mentally figure puzzle
Test 1: Execution time (speed)	1.0
Test 2: Execution time (speed)	0.608**	1.0
Test 2: Planning time (speed)	0.390**	0.385**	1.0
Test 1: % Moves above  minimum (efficiency)	0.273**	0.146**	0.178**	1.0
Test 2: % Moves above  minimum (efficiency)	0.046	0.407**	0.093*	0.376**	1.0
Test 2: Number of attempts to  mentally figure puzzle	0.171**	0.255**	0.325**	0.363**	0.359**	1.0

% Moves above minimum, higher scores indicate less efficiency

^*p < .05;

^**p < .001

The full Cholesky model

Table 3 shows the estimated genetic and environmental variance components for each of the six Tower of London measures (on the diagonal) as well as the estimated genetic and environmental correlation matrices across variables from the full Cholesky. There were modest heritabilities for each measure (range 0.17–0.31). Genetic correlations varied from 0.32 to 0.99. In contrast, estimates of shared environmental influence on each measure were weaker (range 0.05–0.18). The 95% confidence intervals for the shared environmental correlations contained both zero and one; this situation can arise when overall shared environmental influences are weak, making the interpretation of any overlap of shared environmental influence meaningless. Finally, nonshared environmental influences accounted for the majority of variation in all six measures (range 0.51–0.78). Nine of the 15 nonshared environmental correlations were significant, although they were substantially smaller than their respective genetic correlations.

Table 3.

Results from the full Cholesky model

	Test 1: Speed	Test 2: Speed	Test 2: Planning time	Test 1: Efficiency	Test 2: Efficiency	Test 2: Number of attempts
Genetic effects
Test 1: Speed	0.28*
Test 2: Speed	0.96*	0.31*
Test 2: Planning time	0.59	0.62	0.21
Test 1: Efficiency	0.41	0.40	0.27	0.22*
Test 2: Efficiency	0.52	0.49	0.32	0.99*	0.17*
Test 2: Number of attempts	0.81*	0.87*	0.52	0.79*	0.84*	0.28
Shared environmental effects
Test 1: Speed	0.15
Test 2: Speed	0.92	0.18
Test 2: Planning time	0.71	0.57	0.10
Test 1: Efficiency	0.33	0.46	0.67	0.15
Test 2: Efficiency	0.43	0.40	0.87	0.71	0.05
Test 2: Number of attempts	0.15	0.29	0.54	0.67	0.86	0.17
Nonshared environmental effects
Test 1: Speed	0.58*
Test 2: Speed	0.34*	0.51*
Test 2: Planning time	0.27*	0.26*	0.69*
Test 1: Efficiency	0.21*	−0.03	0.07	0.63*
Test 2: Efficiency	−0.14*	0.41*	−0.03	0.18*	0.78*
Test 2: Number of attempts	−0.11	−0.08	0.21*	0.11	0.15*	0.55*

Speed, execution time; efficiency, % moves above minimum (higher scores indicate poorer efficiency); number of attempts, number of attempts to mentally figure puzzle

Variance components shown on the diagonals. Correlations shown on the off-diagonals

^*P < 0.05

Simplifying genetic and environmental influences

Step 1 was to fit the various Cholesky models as shown in Table 4. Compared to the full Cholesky with both A and C influences (model 1), neither dropping all A elements (model 2) nor dropping all C elements (model 3) resulted in a significantly worse fit to data. However, dropping both A and C simultaneously (model 4) resulted in a very poor fit to the data, indicating that there is some familial overlap between measures. This result indicates that we were underpowered to distinguish between A and C, which was confirmed in formal power analyses (power to detect A = 0.65; power to detect C = 0.19). The C estimates were small, and having 80% power to detect a significant reduction in model fit after dropping C would have required 1,426 twin pairs. The estimates shown in Table 3 suggest that overall, genetic influences are important and shared environmental influences are not. The model without C influences in Table 4 (model 3) also had lower AIC and BIC values compared to the model without genetic influences. Therefore, we concluded that the AE model was the most parsimonious model in Step 1 and utilized it as the comparison model for Step 2.

Table 4.

Model fitting results—testing the Cholesky structure: Step 1

Model	A	C	E	−2LL	df	LRT	Δ df	P-value	AIC	BIC
1	Ch	Ch	Ch	10,231.865	3,967	–	–	–	–	−188.241
2	0	Ch	Ch	10,252.517	3,988	20.652	21	0.480	−21.348	−205.994
3	Ch	0	Ch	10,239.639	3,988	7.774	21	0.996	−34.226	−212.433
4	0	0	Ch	10,427.073	4,009	195.208	42	<0.001	111.208	−146.794

A additive genetic influences, C shared (common) environmental influences, E nonshared (unique) environmental influences, −2LL −2 log-likelihood, LRT likelihood ratio chi-square test, Δdf change in df, AIC Akaike information criterion, BIC Baysian information criterion, Ch Cholesky structure, 0 variance structure omitted

Models 2–4 are tested against the full Cholesky model (model 1). Most parsimonious (best-fitting) model indicated in boldface type

Simplifying the genetic and environmental covariance structure

Table 5 shows Step 2 of the model testing in which we tested the genetic factor structure, using the AE Cholesky model from Step 1 as our comparison model. The 3-independent-factors model had the same number of degrees of freedom as the comparison model so the change in model fit could not be assessed on the basis of the significance of the likelihood ratio test. Nonetheless, the fact that AIC and BIC values for the 3-independent-factors model (model 2) are only slightly higher than the AIC and BIC values from the comparison AE Cholesky model indicates that three common genetic factors plus residual genetic influence on each measure comes quite close to recapturing the observed genetic variance–covariance structure estimated by the Cholesky. Moreover, the 2-independent-factors model (model 3) did not have a significantly poorer fit compared to the 3-independent-factors model (LRT = 4.2, df = 4, P = 0.38), and it also had lower AIC and BIC values compared to either the Cholesky or the 3-factor model. Thus, this 2-factor model was more a parsimonious model than either the 3-factor or the comparison Cholesky model. In contrast, the 1-factor model (model 4) resulted in a highly significant change in model fit compared to the 2-factor model (LRT = 30.3, df = 5, P < 0.001), and generated AIC and BIC values larger than any previous model. It was, therefore, disregarded as a viable factor solution, and the model with two independent genetic factors was regarded as the best model.

Table 5.

Model fitting results—testing the genetic factor structure: Step 2

Model	A	C	E	−2LL	df	LRT	Δ df	P-value	AIC	BIC
1	Ch	0	Ch	10,239.639	3,988	–	–	–	0.000	−212.433
2	3 Independent factors	0	Ch	10,240.747	3,988	n/a	n/a	–	1.108	−211.879
3	2 Independent factors	0	Ch	10,243.873	3,992	4.233	4	0.38	−3.767	−215.665
4	1 Independent factor	0	Ch	10,274.193	3,997	34.554	9	<0.001	16.554	−207.189
5	2 Independent factors (reduced factor structure)	0	Ch	10,267.368	3,996	23.495	4	<0.001	11.729	−209.265
6	2 Correlated factors (reduced factor structure)	0	Ch	10,246.702	3,995	2.829	3	0.42	−6.937	−218.261

A additive genetic influences, C shared (common) environmental influences, E nonshared (unique) environmental influences, −2LL −2 log-likelihood, LRT likelihood ratio chi-square test, Δdf change in df, AIC Akaike information criterion, BIC Baysian information criterion, Ch Cholesky structure, 0 variance structure omitted; reduced factor structure, loadings accounting for <10% of the genetic variance omitted; n/a, not available

Models 2–8 are tested against the reduced Cholesky model (model 1). Most parsimonious (best-fitting) model indicated in boldface type

Because models 2 and 3 have the same degrees of freedom (as do models 4 and 5), it was not possible to test one model as a nested model of the other. Therefore, we tested all of the models against the best-fitting model from Step 1

Rotating the genetic factor loadings from the 2-independent-factors model (model 3) revealed factors that appeared to broadly represent speed (Factor 1) versus efficiency (Factor 2). The result was close to simple structure (variables with substantial loadings on one factor not having substantial loadings on the other factor) except that the number of attempts score from Test 2 loaded on both factors. In Table 5, model 5 we tested this simple structure more formally by dropping factor loadings that accounted for less than ten percent of the variance (i.e., loadings < 0.32). Doing so resulted in a very substantial reduction in fit. The latter outcome was somewhat puzzling because one would not expect that dropping factor loadings that were so small would have a much effect on the fit of the model. This suggested that there might be additional correlations that were not included in the model. Consequently, we added a parameter to this reduced 2-factor model to allow for a correlation between the two genetic factors. This model (model 6) yielded a nonsignificant P-value for the LRT in comparison to the full 2-independent-factors model, and it had the lowest AIC and BIC values of any of the models tested in Table 5.

After obtaining the most parsimonious model for the genetic covariance structure we attempted to simplify the nonshared environmental factor structure in a similar manner, using the 2-correlated factors model from Step 2 as our comparison model. These results are shown in Table 6. In contrast to the results for the genetic factor structure, all of these models had very poor fits to the data. Thus, although there are significant nonshared environmental correlations across measure, there was no discernable pattern to the correlations. Because we were unable to simplify the nonshared environmental factors, we concluded that the most parsimonious model was the model with two correlated genetic factors and a Cholesky structure on the nonshared environmental factors (model 6 from Table 5. The genetic structure of this model is shown in Fig. 2.

Table 6.

Model fitting results—testing the nonshared environmental factor structure: Step 3

Model	A	C	E	−2LL	df	LRT	Δ df	P-value	AIC	BIC
1	2 Correlated factors	0	Ch	10,246.702	3,995	–	–	–	–	−218.261
2	2 Correlated factors	0	3 Independent factors (with residuals)	10,279.424	3,995	32.722	0	–	32.722	−201.900
3	2 Correlated factors	0	2 Independent factors (with residuals)	10,315.307	3,999	68.605	4	<0.001	60.605	−189.306
4	2 Correlated factors	0	1 Independent factors (with residuals)	10,421.058	4,004	174.356	9	<0.001	156.356	−143.117

A additive genetic influences, C shared (common) environmental influences, E nonshared (unique) environmental influences, −2LL −2 log-likelihood, LRT likelihood ratio chi-square test, Δdf change in df, AIC Akaike information criterion, BIC Baysian information criterion, Ch Cholesky structure, 0 variance structure omitted

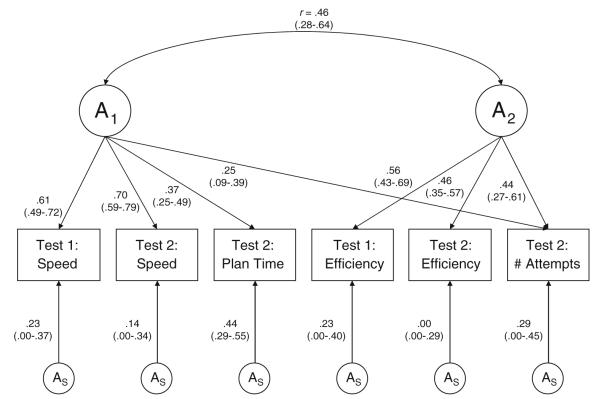
Fig. 2.

Best-fitting (most parsimonious) genetic factor model for the Tower of London A₁ (speed) and A₂ (efficiency) = first and second genetic factor, respectively; A_S = specific genetic influences. Efficiency = % moves above the minimum. Number of attempts = number of attempts to mentally figure a puzzle. Parameter estimates and 95% confidence intervals are shown. Squaring these parameter estimates provides the contribution of each measure to the genetic variances. Arrows from A₁ and A₂ to the measured variables depict the factor loadings of those variables on each genetic factor. The correlation between the factors is, by definition, a genetic correlation because only genetic factors are represented in this figure

Figure 2 shows that the first genetic factor (A1) loads primarily on Test 1 and Test 2 speed, with small, albeit significant, loadings on plan time for Test 2 and number of attempts for Test 2. The second genetic factor (A2) is defined by efficiency on Test 1 and Test 2, as well as number of attempts at Test 2. The correlation between the two genetic factors was 0.46. As with any standard phenotypic factor analysis, it is possible to calculate the proportion of variance accounted for by the two genetic factors using the factor loadings shown in Fig. 2. The total phenotypic variance was 6.01, derived by summing the diagonals of the standardized variance–covariance matrix from the best-fitting model. This process is equivalent to summing the eigenvalues in a standard phenotypic factor analysis; the total equals the number of variables (with rounding error). We then calculated the total amount of variance accounted for by the two factors by summing the diagonals of the genetic variance–covariance matrix derived from two common genetic factors; this total was 1.88. Because the factors included genetic influences only, dividing this amount by the total phenotypic variance (1.88/6.01) yields the proportion of variance in the six Tower of London measures that is accounted for by the genetic factors only (31%). The diagonals of the variance–covariance matrix derived from the variable-specific (residual) genetic influences summed to 0.40. Adding the variance accounted for by the common genetic factors (1.88) to the residual genetic variance (0.40) yields the total genetic variance (including latent genetic factors plus residuals) of 2.28. Therefore, total genetic influences accounted for 38% (i.e., 2.28/6.01) of the variance in the six Tower of London measures. Thus, 0.38 is essentially the same as the overall heritability of these six measures. The two genetic factors accounted for 82% of the genetic variance (i.e., 0.31/0.38).

With regard to the residuals, it can be noted that only one of the Tower of London variables had any significant specific genetic influences. From Fig. 2, it can be calculated that 41% of the genetic variance of planning time was contributed to by the genes underlying factor 1 (0.37/[0.37 + 0.44]), whereas 59% was accounted for by genes that were specific to planning time and independent of either genetic factor (0.44/[0.37 + 0.44]).

Discussion

The present study used biometrical factor models to better understand the covariance between different measures obtained from the Tower of London task. Interestingly, the phenotypic factor analyses indicated that a single factor could adequately account for most of the covariance across measures, but the biometrical models indicated that the genetic and environmental influences responsible for covariance across measure were more complex. Our results suggested that a 2-correlated-factors model was the best-fitting (most parsimonious) model for genetic covariance on performance on the Tower of London in middle age. Factor 1 (A₁) was essentially a speed factor. Factor 2 (A₂) was essentially an efficiency factor. There was also a moderate correlation of .46 between the speed and efficiency factors, indicating that these were not independent dimensions. The commonality between these two dimensions suggests that there could be a higher-order genetic general ability factor.

In addition, the only variable with significant loadings on both factors may provide some clue as to what accounts for the partial link between them. That variable was the number of attempts required to mentally figure the puzzles. This measure may reflect some sort of working memory/monitoring ability. Mentally solving the puzzle clearly places demands on working memory because one must temporarily hold several moves in mind while contemplating the next move, as would be needed for planning moves in a chess game. Fewer attempts to determine the minimum number of moves required to solve a Tower of London puzzle may be associated with greater working memory capacity, but it is not simply a question of storing information. Thinking through a puzzle requires continuous monitoring during the period in which the information is being stored. Such monitoring would involve decision making and inhibition of irrelevant response choices. Given some evidence that working memory is associated with general intelligence (Kyllonen and Christal 1990), this ability could be a component of general ability.

Our design allowed us to examine planning in different ways. In Test 1, the extent of planning was left to the discretion of each participant; in contrast, participants had to plan ahead Test 2. Efficiency scores on Test 2 appeared to be better than those on Test 1; the percentage of moves above the minimum for Test 2 was only 17.91, compared with 41.99 for Test 1 (see Table 1). This efficiency difference could be due to differences in planning, or it could simply reflect difficulty level. Considering the small correlations between Test 2 planning time and efficiency on Test 2 (r = 0.10, P < 0.01) and Test 1 (r = 0.18, P < 0.0001), it does not seem that the time taken to pre-plan one’s strategy confers much beneficial effect on actual performance. However, the association between the number of attempts required to figure the puzzles and efficiency does suggest that working memory and monitoring components of planning are more strongly associated with efficiency of performance than speed of planning. Correlations between the number of attempts required to mentally figure a puzzle on Test 2 and efficiency on Test 2 and Test 1 were 0.34 and 0.35, respectively (both P < 0.0001). Although it may well be the case that such working memory/monitoring functions have a causal relationship to test performance, these correlational results could simply reflect the same underlying processes in both planning and carrying out the test.

On the other hand, Test 1 puzzles might be more difficult because they required a minimum of 4–9 moves, whereas the minimums for Test 2 puzzles ranged from only 2 to 5 moves. There was mixed support for the idea that efficiency is affected by the minimum number of moves required to solve a puzzle. The Kendall’s tau-b correlation between ranked efficiency and minimum moves required was nonsignificant for Test 1 (r = 0.19, P = 0.37), but it was statistically significant for Test 2 (r = 0.60, P < 0.004). It may be the case that this relationship holds only within a range of relatively smaller numbers of moves required (as in Test 2). One possibility is that short-term/working memory capacity might be a factor with smaller minimum numbers of moves, whereas it may be less relevant when the test gets beyond a person’s memory span capacity. However, post hoc analyses showed that the correlations between short-term memory measures and Tower of London efficiency were very similar for Tests 1 and 2. The similarity of these correlations argues against a differential impact of short-term/working memory capacity depending on the number of moves required.

Unterrainer et al. (2004) found that longer planning times were associated with both greater efficiency and shorter execution times. On the other hand, Phillips et al. (2001) did not find a relationship between efficiency and planning time in the test conditions that were analogous to the present study. Unterrainer et al. suggested that the results of Phillips et al. might be due to their use of a version of the task in which all of the pegs were of equal length, thus resulting in fewer rearrangement restrictions. We found small, but significant relationships between planning time and efficiency (r = 0.10 and 0.18), but in the opposite direction to that of Unterrainer et al. In our study, longer planning time was associated with less efficiency (i.e., higher % above minimum; r = 0.34 and 0.35). Planning time was also positively correlated with actual execution time on both Test 2 and Test 1 in our study (r = 0.36 and 0.37, respectively, P < 0.0001). Thus, these relationships were not very different whether or not participants were specifically instructed to solve the problem mentally first. Also, all of the speed variables loaded on the same genetic factor, indicating that they were, to a large extent, influenced by the same set of genes. Taken together, these findings suggest that these genes are more related to speed than to planning per second. In contrast, the number of attempts required to mentally figure the puzzles was more strongly correlated with both speed and efficiency, and it loaded on both genetic factors. These results suggest that the number of attempts required to mentally figure the puzzles provides a better index of planning ability than does planning time.

We are not aware of other studies that have included a variable like the number of attempts variable. Planning time—the more typical measure—could be long because a person was either being careful or inefficient; short planning times could reflect efficiency or impulsivity. As such, planning time could reflect opposing phenomena in different people. It is of interest that the biometrical modeling results were such that planning time was the only measure with any statistically significant specific genetic influences. Over one-half of the genetic variance for planning time was attributable to genes that were specific to that measure and independent of the speed factor. Because the relationship of planning time to other variables paralleled that of the other speed measures, it seems unlikely that these genes reflect some opposing process. Planning time is a mental activity, whereas the other speed measures include a substantial motor component. This distinction suggests that genes that are specific to planning time might be genes that specifically influence thinking speed rather than motor speed. Processing speed is a key variable in the cognitive, particularly cognitive aging, literature. Separating cognitive from motor speed is conceptually easy, but difficult to do in practice. Our results suggest that there may be different genes underlying these two different types of processing speed.

The number of attempts may serve as a crude index of how effective a person’s planning is that is not captured by planning time. On the other hand, it must be acknowledged that we cannot be entirely certain whether participants were truly trying to mentally solve the puzzle with each new attempt or whether they were simply guessing. The fact that this putative index of planning (i.e., number of attempts to mentally figure the puzzles) loads on both genetic factors is consistent with the need to coordinate the appropriate modulation and monitoring of working memory, decision making, and speed of processing in order to maximize efficiency. This implies a form of metacognition responsible for coordinating the influences underlying each of the two genetic factors. Metacognition refers to “knowing about knowing” and it involves both monitoring and control (Nelson and Narens 1990; Shimamura and Metcalfe 1994). Interestingly, metacognitive abilities and cognitive abilities vary independently (Koren et al. 2006; Koriat and Goldsmith 1998). For example, having certain abilities does not necessarily mean having good judgment. On the other hand, individuals lacking in particular abilities may still function reasonably well if they are able to accurately evaluate their limitations and make good decisions about when to change strategies or ask questions to obtain key information.

Individuals who tend to be impulsive or disinhibited would be likely to sacrifice efficiency for speed because they do poorly at regulating their behavior and making good decisions. This pattern may tend to be the case for people with attention deficit hyperactivity disorder. On the other hand, some elderly individuals may be able to compensate for age-related processing speed deficits by invoking strategies that involve working more slowly in order to increase efficiency, i.e., maximally coordinating speed and efficiency. Thus, age-related cognitive slowing does not have to reduce the practical benefits of good planning or metacognitive ability and problem-solving. The fact that most of the variance in Tower of London performance was accounted for by nonshared environmental factors, suggests that strategies for effective regulation of performance and processing speed in the service of planning and problem-solving can be learned as well.

It is interesting that there were two correlated genetic factors underlying a single phenotypic factor on the Tower of London. If the genetic and environmental factor structures were similar, it might be expected that the phenotypic factor analysis would parallel the results of the biometrical modeling. But, as shown in the results section, the genetic and nonshared environmental factor structures were not the same. In fact, there was no discernable nonshared environmental factor structure. The different structures are noteworthy, in part, because the structure of genetic and environmental covariance is usually assumed to be parallel (e.g., in more typical biometrical approaches such as independent or common pathways models). From a cognitive or neuropsychological perspective, the two components of speed and efficiency are relatively intuitive. The biometrical perspective tell us that two sets of partially overlapping genes influence each component, but there appears to be no such pattern for environmental influences.

The genetic factors were not independent of one another, and the correlation of 0.46 does indicate that there is some genetic overlap between them. On the other hand, this correlation also indicates a substantial amount of nonshared genetic influences. We have raised two possibilities regarding this overlap. It may reflect a form of general ability, in part, because general ability often emerges as a higher-order factor underlying more specific cognitive abilities (Bouchard and McGue 2003). It could also reflect monitoring functions that would serve to coordinate and modulate the working memory, selective attention, inhibition, and processing speed components of the task. This metacognitive function is also consistent with the description of the supervisory attentional system (Shallice 1982) or the central executive (Baddeley 1986).

Genetic influences accounted for 40% of the variance in the factor that emerged from the phenotypic factor analysis, and genetic influences accounted for 38% of the variance based on the genetic factor analysis. The total variance accounted for by genetic influences is about the same in both cases, but the genetic factor analysis showed that there are actually two partially related sets of genetic influences on the Tower of London scores. The distinction between these two approaches is an important one because the more traditional approach of performing a phenotypic factor analysis and then estimating the heritability of the factor(s) would have missed these two underlying semi-independent processes. Elucidating the genetic factor structure also has implications for genetic association studies. Our findings suggest that using a summary test score as a phenotype in a genetic association study could be misleading because the underlying genetic structure may not correspond to what one observes at the phenotypic level. There may also be differential changes in the two genetic factors (e.g., with aging) that could be missed if one were looking only at a single summary phenotypic score.