Connecting energy landscapes with experimental rates for aminoacyl-tRNA accommodation in the ribosome

Abstract

Using explicit-solvent simulations of the 70S ribosome, the barrier-crossing attempt frequency was calculated for aminoacyl-tRNA elbow-accommodation. In seven individual trajectories (200–300 ns, each), the relaxation time of tRNA structural fluctuations was determined to be ~ 10 ns and the barrier-crossing attempt-frequency of tRNA accommodation is ~ 1–10 µs⁻¹. These calculations provide a quantitative relationship between the free-energy barrier and experimentally-measured rates of accommodation, which demonstrate that the free-energy barrier of elbow-accommodation is less than 15 k_BT, in vitro and in vivo.

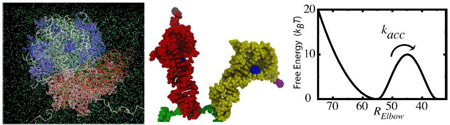
Using explicit-solvent simulations of the 70S ribosome (3.2 million atoms for an aggregate 2.1 µs. Table 1), we provide a quantitative relationship between free-energy profiles and experimentally determined kinetics for aminoacyl-tRNA (aa-tRNA) accommodation in the ribosome during tRNA selection (Figure 1). After initial selection, where the incoming aa-tRNA associates with the messenger RNA (mRNA) on the ribosome,¹ accommodation displaces the encoded amino acid ~90 Å from outside of the ribosome to the peptidyltransferase center (PTC), where it is added into the nascent protein chain. When near-cognate aa-tRNA molecules successfully associate during initial selection, accommodation acts as a “kinetic proofreading” step,² where incorrect tRNAs are often rejected by the ribosome. This kinetic process is governed by the underlying thermodynamics, which have been the focus of experimental^3,4 and theoretical^5,6 investigations.

Table 1.

Summary of diffusion coefficient calculations.

conf	length (ns)	drift (Å/ns)	<ΔR2> (Å2)	<τ> (ns)	D1 (µm2/s )	D2
A/T	301	1.5×10−2	3.27	13.3	1.2	1.1
A/T	262	3.3×10−2	5.79	35.4	0.8	0.9
A/T	260	−3.0×10−2	4.07	17.3	1.2	0.6
A/T	261	4.5×10−4	1.91	8.46	1.1	0.3
A/A	208	1.1×10−2	2.76	19.7	0.7	1.0
A/A	205	9.4×10−3	1.36	11.7	0.6	0.3
A/A	213	2.7×10−2	1.47	7.64	1.0	0.2

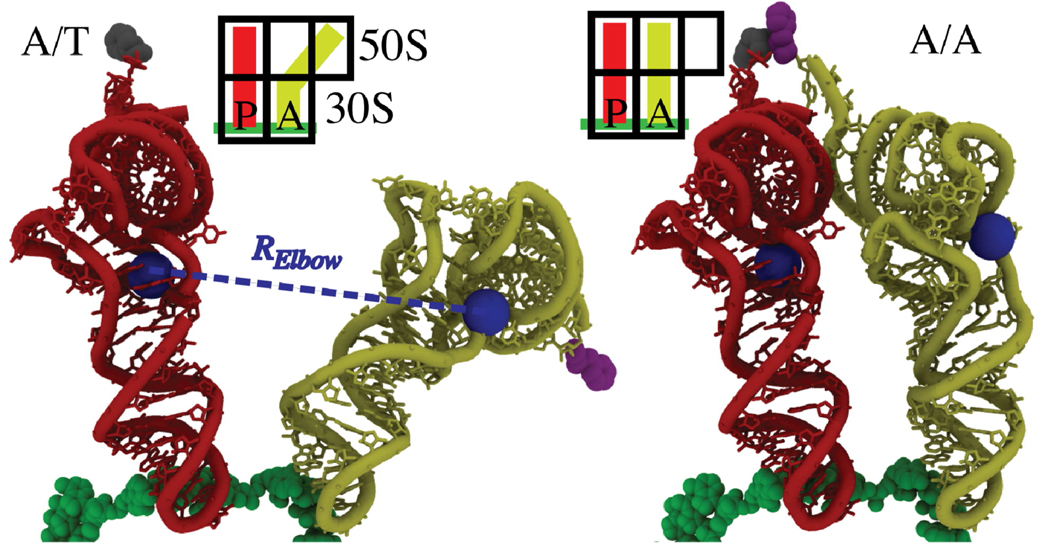
Figure 1.

Structural representation of the aa-tRNA (yellow), p-tRNA (red), mRNA (green), and the associated amino-acids (grey, purple), in the partially-bound A/T conformation (left) and fully-bound A/A conformation (right). Elbow-accommodation is measured by R_Elbow: the distance between the O3’ atoms of U8 on p-tRNA and U47 on aa-tRNA (blue spheres).

Simulations and theoretical models have the potential to provide a structural/energetic framework for interpreting rapid kinetic and single-molecule measurements, though comparison is rarely direct. Specifically, kinetics are measured in bulk experiments, while free-energy profiles are far more difficult to obtain.⁷ In contrast, many molecular simulation methods are available to calculate the potential of mean force (i.e. the free energy along a specific degree of freedom) for biomolecular processes,⁸ while it is not feasible to directly measure rates. Consequently, calculations often focus on the fluctuations about particular configurations.⁹

To connect experimental accommodation kinetics and the free-energy profile, one may use the relationship¹⁰

$$\frac{1}{k_a}=\langle {\tau }_a\rangle ={\displaystyle {\int }_{Q_{A/T}}^{Q_{A/A}}\mathit{\text{dQ}}}{\displaystyle {\int }_{\mathrm{\infty }}^Q\mathit{\text{dQ}}\prime \frac{\text{exp}\left[\left(G(Q)-G(Q\prime )\right)/k_{B}T\right]}{D(Q)}}$$ [1]

where k_a is the rate of accommodation,¹ 〈τ_a〉 is the mean-first passage time, Q is the reaction coordinate, G(Q) is the Gibb’s free-energy, D(Q) is the diffusion in Q-space and Q_A/T and Q_A/A are the values of Q that define the A/T and A/A configurations (SI). If G(Q) has a single barrier, and D(Q) is constant (see SI), Equation 1 is approximated as

$$\frac{1}{k_a}\approx \frac{1}{C_a}\text{exp}(\mathrm{\Delta }{G}_{\mathit{\text{TSE}}}/k_{B}T)$$ [2]

where ΔG_TSE is the difference in the free-energy of the A/T ensemble and the transition state ensemble (TSE). C_a is the barrier-crossing attempt frequency. While this general relationship relates kinetic rates and the free-energy profile, the attempt frequency C_a is process-specific. The barrier-crossing attempt frequency is determined by the diffusion and the distance between the endpoints (both in Q-space).

While accommodation is likely a multistep process,⁶ here the discussion is restricted to tRNA-elbow accommodation (measured by R_Elbow; Fig. 1), for comparison to single-molecule data.^6,11 To determine the attempt frequency, we calculated D_Elbow(R_Elbow) (diffusion coefficient in R_Elbow) from explicit-solvent simulations, set Equations 1 and 2 equal to each other and numerically integrated Equation 1. Since free-energy profiles of accommodation have not previously been determined, the functional form of G(R_Elbow) was varied to establish robustness of the results (SI).

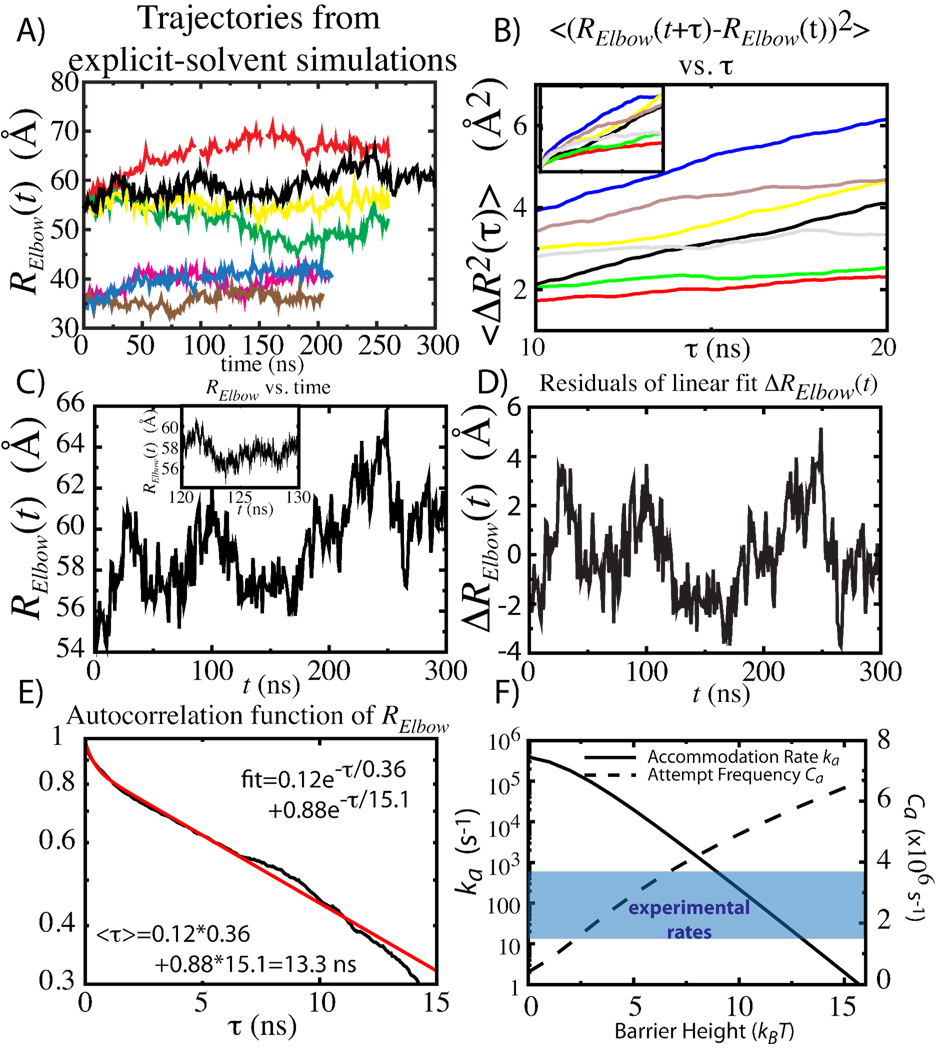
Simulations of the 70S ribosome, fully-solvated with physiological concentrations of ions, were performed (Table 1). The diffusion coefficient in elbow distance, D_Elbow, was determined using 2 different strategies. The first approach was to use the quasi-harmonic approximation to the dynamics, as employed in protein folding studies,¹² where $D_{\mathit{\text{Elbow}}}=\langle \mathrm{\Delta }{R}_{\mathit{\text{Elbow}}}^2\rangle /(2{\tau }_{\mathit{\text{Elbow}}}).\langle \mathrm{\Delta }{R}_{\mathit{\text{Elbow}}}^2\rangle$ is the mean-squared fluctuations in distance and τ_Elbow is the decay time associated with the fluctuations (Figures 2C–E). With this procedure, D_Elbow (labeled D₁ in Table 1) for the A/T and A/A ensembles (SI) was 1.1 ± 0.1 µm²/s and 0.8 ± 0.1 µm²/s. The second strategy employed¹³: $D_{\mathit{\text{Elbow}}}=\underset{t\to \mathrm{\infty }}{\text{lim}}\frac{\partial }{\partial t}\langle |R_{\mathit{\text{Elbow}}}(t)-R_{\mathit{\text{Elbow}}}(0){|}^2\rangle /2$ The mean-squared displacement is linear from 10 and 20 ns, yielding diffusion coefficients (labeled D₂ in Table 1) of 0.8±0.2 µm²/s (A/T) and 0.5±0.2 µm²/s (A/A). In the case of infinite sampling, the two approaches should yield identical values. Here, the two values of D_Elbow are within the statistical uncertainty. In solution, the diffusion coefficient of ternary complex has been estimated at 0.3–2.5 µm²/s.¹⁴ Since diffusion is determined by the degree of roughness in the landscape, the striking similarity between the diffusion in solution and inside the ribosome suggests there is a low degree of roughness in the energy landscape of accommodation.

Figure 2.

A) Time traces of R_elbow from 7 explicit-solvent simulations. B) Mean-squared displacement $\langle \mathrm{\Delta }{R}_{\mathit{\text{elbow}}}^2(\tau )\rangle$ as a function of time delay τ. D_Elbow waṣestimated by the slope between 10 and 20 ns. Inset shows $\langle \mathrm{\Delta }{R}_{\mathit{\text{elbow}}}^2(\tau )\rangle$ for τ=0–30 ns. C) 300 ns trajectory, displayed at 1 ns intervals. Inset shows subset at 5 ps intervals. D) Dispersion and relaxations were calculates from the residuals of linear fit (slopes in Table 1), ΔR_elbow. E) Autocorrelation function of ΔR_elbow fitted to sum of 2 exponentials (SI). D_Elbow was calculated from the average decay time <τ>. F) Accommodation rate k_a and attempt frequency C_a, for D_Elbow=1.1µs²/s, versus the free-energy barrier height. Range of experimentally-determined rates shaded in blue.

Figure 2F shows the accommodation rate k_a as a function of barrier height, obtained through numerical integration of equation 1 (SI), with D_Elbow=1.1 µm²/s. The attempt frequency C_a was also calculated as a function of barrier height. The attempt frequency is proportional to the curvature of the initial and final basins.¹⁵ Since the curvature of the basins increases with increasing barrier height (see SI), the observed increase in attempt frequency (Figure 2F) is expected.

Depending on the barrier height and functional form (SI), the attempt frequency for elbow-accommodation is ~ 1–8 µs⁻¹, which is in the same range of values as for small RNA (0.1–1.6 µs⁻¹)¹⁶ and protein (0.1–20 µs⁻¹)¹⁵ folding.

Here, we employed D_Elbow=1.1 µm²/s, which is our upper-bound estimate. Accordingly, the rate for a given barrier height, and the barrier height for a given rate, should be considered upper bounds. Bulk kinetic experiments have reported the rate of full accommodation to range from 10s to 100s per second^3,4 (Shaded blue in Fig 2F). These rates suggest barrier heights of ~9–13 k_BT.² Since accommodation is not barrier-less, targeting its TSE^6,11 is a viable approach for gaining quantitative control of translation. Finally, this study establishes the conversion between kinetics and free-energy profiles. With this conversion, it is now possible to validate the details of the free-energy profiles obtained from smFRET and simulations through comparison with kinetic data for large-scale conformational rearrangements in the ribosome.