Abstract
Purpose: The current inverse planning methods for intensity modulated radiation therapy (IMRT) are limited because they are not designed to explore the trade-offs between the competing objectives of tumor and normal tissues. The goal was to develop an efficient multiobjective optimization algorithm that was flexible enough to handle any form of objective function and that resulted in a set of Pareto optimal plans.
Methods: A hierarchical evolutionary multiobjective algorithm designed to quickly generate a small diverse Pareto optimal set of IMRT plans that meet all clinical constraints and reflect the optimal trade-offs in any radiation therapy plan was developed. The top level of the hierarchical algorithm is a multiobjective evolutionary algorithm (MOEA). The genes of the individuals generated in the MOEA are the parameters that define the penalty function minimized during an accelerated deterministic IMRT optimization that represents the bottom level of the hierarchy. The MOEA incorporates clinical criteria to restrict the search space through protocol objectives and then uses Pareto optimality among the fitness objectives to select individuals. The population size is not fixed, but a specialized niche effect, domination advantage, is used to control the population and plan diversity. The number of fitness objectives is kept to a minimum for greater selective pressure, but the number of genes is expanded for flexibility that allows a better approximation of the Pareto front.
Results: The MOEA improvements were evaluated for two example prostate cases with one target and two organs at risk (OARs). The population of plans generated by the modified MOEA was closer to the Pareto front than populations of plans generated using a standard genetic algorithm package. Statistical significance of the method was established by compiling the results of 25 multiobjective optimizations using each method. From these sets of 12–15 plans, any random plan selected from a MOEA population had a 11.3%±0.7% chance of dominating any random plan selected by a standard genetic package with 0.04%±0.02% chance of domination in reverse. By implementing domination advantage and protocol objectives, small and diverse populations of clinically acceptable plans that approximated the Pareto front could be generated in a fraction of 1 h. Acceleration techniques implemented on both levels of the hierarchical algorithm resulted in short, practical runtimes for multiobjective optimizations.
Conclusions: The MOEA produces a diverse Pareto optimal set of plans that meet all dosimetric protocol criteria in a feasible amount of time. The final goal is to improve practical aspects of the algorithm and integrate it with a decision analysis tool or human interface for selection of the IMRT plan with the best possible balance of successful treatment of the target with low OAR dose and low risk of complication for any specific patient situation.
Keywords: multiobjective optimization, evolutionary algorithm, radiation oncology, IMRT
INTRODUCTION
Intensity modulated radiation therapy (IMRT) uses inverse planning optimization to determine complex radiation beam configurations that will deliver dose distributions to the patient that are better than could be achieved using three-dimensional (3D) conformal radiation therapy. The problem is inherently multiobjective with competing clinical goals for a high uniform target dose and low doses to the organs at risk (OARs). IMRT inverse planning algorithms commonly optimize a single objective function (also known as “penalty function”) that is a linear combination of many separate organ and tumor-specific objective (penalty) functions. The solution of this problem is one point in the space of feasible treatment plans. To find another point in this space, the user can vary any one of the parameters that make up the penalty function. Current clinical algorithms do not provide methods for efficiently searching this space of feasible plans. The search is complicated by the fact that in comparing plans, one plan may have achieved superior values for some objectives but inferior values for other objectives.
A multiobjective optimization (MOO) algorithm is one method for searching through the space of feasible plans. Such an algorithm varies the parameters that define an objective function and calculates a new plan for each new function. For each plan created, the algorithm calculates objective values that characterize its quality. If all of the objective values of one plan are better or the same as the values of a second plan, the first plan is said to dominate the second (see Sec. 2A1). A plan is said to be Pareto optimal if there are no plans that dominate it.
A problem that has only a single objective might have only one optimal plan; however, in the case of a problem with multiple competing objectives, Pareto optimality refers to the set of plans such that for any one objective value to improve, at least one other must get worse. A Pareto front describes the set of individuals that are Pareto optimal. It is impossible for any individual on the Pareto front to be dominated by any other possible individual.
The true Pareto front of a multiobjective problem is a multidimensional surface that contains an infinite number of points and, hence, there is the potential for the production of Pareto populations that are too large for practical purposes. Methods for handling this issue, called niche functions, come in many forms, but are all designed to limit the number of individuals that can survive in a population while maintaining diversity. For stochastic multiobjective algorithms to be practical, the use of an appropriate niche function may be quite important.
The nature of the separate objective functions used in the MOO plays an important role in the optimization. Those functions that are convex may be optimized using deterministic algorithms. Stochastic optimization methods are needed for optimizing those functions that are not convex to avoid becoming trapped in local minima. In selecting a multiobjective optimization approach, the user may have to make a decision between using a deterministic method that is fast but limits the type of objectives and a stochastic method that is very flexible but slower. If different objective functions are used to evaluate the quality of dose distributions than are used in the single penalty function that optimizes beamlet intensities, it is possible that some parts of the optimization can be done deterministically, while other parts may use stochastic methods.
One type of stochastic optimization algorithms is an evolutionary algorithm that uses concepts based on genetics and natural selection to create a population of new solutions and to select the fittest among them. An “individual” is described by a set of genes. New individuals are created through recombination of genes from two “parent” individuals selected from the existing population. Random mutations can occur, which help prevent the population from becoming trapped in local minima. Natural selection of superior individuals, followed by reproduction using their genes leads the algorithm to find the Pareto optimal solutions. In practice, further heuristic methods are often needed to speed up this process.
This paper describes the development of a multiobjective optimization algorithm that combines an evolutionary method to search feasible plan space with a deterministic method using a single objective penalty function that quickly finds the optimal beamlet intensities for that function. While the penalty function must be convex, the hierarchical method allows us to use any fitness objective (convex or nonconvex) to evaluate plan quality without losing too much in speed. Utilization of a MOO algorithm requires the selection of one plan from the Pareto optimal set to be used for IMRT treatment of the patient. There are many methods for doing so. We have selected an a posteriori method of multiobjective optimization where plan selection is done after the Pareto front is found by either an influence diagram1, 2 or inspection by a radiation oncologist. With both of these approaches, it is best to restrict the set of plans to a relatively small number, e.g., 10–20, and this is reflected in our MOO algorithm.
In Sec. 2, the hierarchical algorithm is described with the emphasis on the evolutionary element and how it interacts with the deterministic step. In Sec. 3, performance of the algorithm is characterized using two clinical prostate cancer cases.
METHODS AND MATERIALS
A multiobjective evolutionary algorithm (MOEA) has been developed for the top level of a hierarchical IMRT optimization method. The lower level is a deterministic algorithm that incorporates a constrained quadratic optimization (BOXCQP) algorithm. We have used a hierarchical process because there are two sets of variables we would like to optimize: (1) beamlet intensities (deterministic optimization) and (2) the objective parameters such as maximum dose, dose homogeneity, etc. (stochastic optimization). At the stochastic level of the algorithm, an individual is created and each individual is characterized by a set of genes that determine the relative weighting between OARs and targets and a set of genes that describe the OAR penalty functions. The deterministic algorithm incorporates these genes into a quadratic objective function, which is then solved for the beamlet intensities. The MOEA uses a separate set of objectives to determine the quality of each individual treatment plan. As mentioned above, considerations of speed have led us to incorporate several heuristic stages in our algorithm, which results in a faster convergence to a clinically acceptable set of Pareto optimal plans. The following sections provide more details of the algorithm as well as descriptions of the methods used to characterize the performance of the MOEA.
Multiobjective evolutionary algorithm
An evolutionary algorithm was chosen as the stochastic component of the multiobjective method because of its effectiveness in searching large regions of solution space while still incorporating techniques for focusing the search on regions more likely to produce better plans.3, 4, 5, 6, 7 A number of characteristics of the IMRT optimization problem guided the development of our MOEA. The critical factors were (1) the very large search space, (2) the relatively large number of objectives, (3) the need for solutions to conform to “clinically acceptable” criteria, and (4) the time constraints for clinical use. In short, our modified MOEA was designed for faster and more effective convergence to the Pareto front inside the clinically acceptable space. The elements of the MOEA and highlights of the impact of these critical factors are described below.
Enhancements to the MOEA
Our MOEA uses no fixed number of individuals per generation, no summary single fitness function, and no tournament-style selection method (as are common in traditional genetic algorithms). Instead, individuals are created one at a time and are eliminated if they are Pareto dominated by any existing individual or if they violate any clinical constraints. Conversely, if the new individual dominates any of the current population, those dominated individuals will be eliminated. If the individual survives, its genes become candidates for recombination in the next individual. In addition to these algorithmic modifications, various parameters of the multiobjective method, such as mutation rate, have been optimized for performance.
We also implemented a specialized niche function, called domination advantage. When determining if plan A dominates plan B, a small value, ε, is temporarily added to all of plan B’s objectives to give plan A a greater chance of domination. In our MOEA, lower objective values are more optimal and “domination” using domination advantage works as follows:
| 1 |
This domination advantage, ε, can be thought of as the difference in objective values below which the clinical significance cannot be determined. Thus, it provided a means to avoid clustering of solutions so that the Pareto optimal set spans the entire clinically relevant space. It was also used to limit the total number of plans. The ε used in domination advantage was not a constant but was set equal to c⋅(ncurrent−ngoal). The constant c was adjusted so that the final number of plans was approximately the desired number, ncurrent≈ngoal.
If two individuals were being compared to test for domination and were very close together, i.e., with all objective values within ε of each other, both individuals would “dominate” the other using domination advantage. In this rare case, a single fitness function was used that was a weighted sum of fitness objectives using importance weighting predetermined by the user. The individual with the worse single fitness function would be eliminated and the other would survive. Note that the result is different from what might occur in traditional evolutionary algorithms where two individuals from different regions of the objective space would be forced into such a comparison. In our algorithm, these two individuals are so close together, the assumption is that little information of clinical value would be lost by the undesirable, but necessary, use of a single fitness function elimination.
We used two sets of objectives in the stochastic part of the algorithm, which we call fitness objectives and protocol objectives. Fitness objectives are the dosimetric functions that best represent the clinical goals and are used to determine plan quality. Protocol objectives are functions that delineate certain dosimetric cutpoints that need to be met usually because of clinical protocol restrictions. Protocol objectives will restrict the search space such that the final set of plans is guaranteed to meet all clinical criteria. As will be described in more detail below, these two sets of objective functions are distinct and play different roles during the optimization.
Fitness and protocol objectives
In multiobjective optimization, smaller numbers of fitness objectives tend to result in greater selective pressure and better performance. Thus, it is desirable to have only one fitness objective for each structure. We chose equivalent uniform dose (EUD) as an appropriate objective for OARs; other functions such as complication probability functions or mean dose could also be used. Unlike for OARs, we did not find target EUD to be an effective objective because a uniform target at prescription dose could be deemed equivalent to a dose distribution with a high variance and a higher mean dose. Typically, target dose distributions must meet minimum dose requirements as well as limits on inhomogeneity. We removed the minimum dose objective by prioritizing it and scaling the dose distributions to meet all minimum dose requirements, thereby leaving maximum dose (dose homogeneity) as the sole target objective.
The two sets of objective functions that were used are as follows:
- Fitness objectives
where m is the number of target fitness objectives and n is the number of OAR fitness objectives,
where dj is the dose to jth OAR voxel, nvoxi is the number of voxels in the ith OAR, is the maximum dose to any voxel within the ith target, and ai is a constant (>1) that characterizes the radiation response of each of the n OARs.8, 9, 102 - Protocol objectives
where p is the number of target protocol objectives and q is the number of OAR protocol objectives,
where Dprot,k is the maximum dose allowed to the structure associated with the kth protocol objective, nvoxviolate,k is the number of voxels in the OAR associated with the kth protocol objective that receive doses that exceed the allowed dose of a dose-volume constraint (DVC), nvoxk is the total number of voxels in the OAR associated with the kth protocol objective, and VOAR,k is the maximum fraction of the OAR associated with the kth protocol objective allowed over the dose for a DVC. Minimum target dose constraints are achieved by scaling the dose distribution if necessary.3
Stages of the MOEA
There are three stages of the MOEA that correspond to (1) a broad search for the feasible plan space, (2) a focusing of the search to a region of space that meets protocol requirements, and (3) a search for the Pareto front within the protocol constraints. Throughout the last two stages, the domination advantage procedure is used to both spread the plans out (avoiding clustering near local minima) and to limit the number of plans. As the optimization proceeds, the current set of solutions approaches the true Pareto front defined by the fitness objectives.
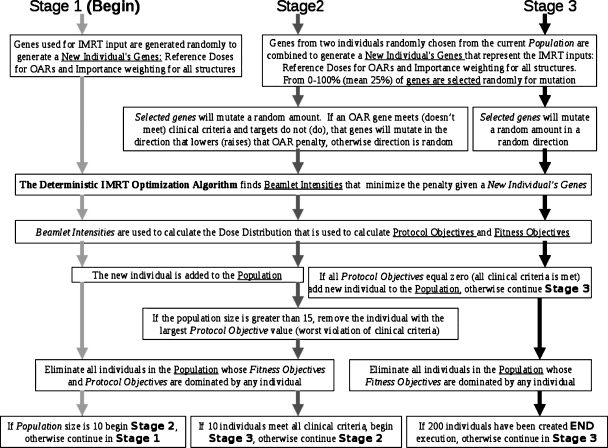
Figure 1 is a diagram that describes the multiple stages. The figure highlights those algorithmic steps that are common among stages and those that are unique to a stage. This diagram is meant to be read from top to bottom, starting with stage 1 and then continuing to the following stages according to the decision box at the bottom. Text boxes that span more than one stage indicate those elements that are common.
Figure 1.
A diagram of our method for all three stages. Stage 1 follows the light gray arrows, stage 2 follows the dark gray arrows, and stage 3 follows the black arrows. This diagram is meant to be read from top to bottom, starting with stage 1 and then continuing to the following stages according to the decision box at the bottom. Text boxes that span more than one stage indicate those steps in the algorithm that are common to more than one stage.
In stage 1, the individuals are created by random selection of genes. The genes are used to construct the quadratic objectives of the deterministic part of the algorithm (see Sec. 2B). Then the fitness and protocol objective values are calculated, and the individual is added to or rejected from the current population, whose size is ncurrent. When ncurrent equals the predefined number of desired plans determined by the decision procedure, ngoal, stage 1 ends.
In stage 2, new individuals are created by recombination of current genes and mutation. During this stage, the directions of mutations are guided, depending on whether or not the parent plan meets the protocol objectives in order to more quickly search relevant space. Selection proceeds as in stage 1 with the addition of the domination advantage procedure. In this stage, the population is allowed to grow larger than ngoal. Stage 2 ends when there are ngoal individuals who meet all of the clinical criteria (protocol objective values=0), at which time, all individuals who do not meet these objectives are eliminated.
Stage 3 proceeds similarly as stage 2 except that the protocol objectives are converted to constraints, mutation direction is not guided, and Pareto optimality is determined only by the fitness objectives. This stage runs for a predetermined number of iterations.
One reason to separate the objectives into two sets is to reduce the dimensionality of the final solution space. As the number of fitness objectives considered in Pareto domination increases, the probability of domination is reduced by a factor of the order of ∼0.5nobjectives and, hence, selective pressure is reduced. By converting protocol objectives into constraints, the solution space is restricted to a smaller number of dimensions equal to the smaller number of fitness objectives.
A multiobjective optimization algorithm needs to be paired with a decision making component. This will have an impact on the number and variation in the solution set. In our case, the decision maker is either a human or an influence diagram, neither of which can handle large numbers of solutions or very nearly identical solutions. Hence, our algorithm is designed to produce on the order of ngoal plans, i.e., 10–15 plans for ngoal=10. The algorithm can be adjusted to produce any size solution set.
Deterministic algorithm
For the beamlet intensity optimization, we employed a modification of the bound constrained convex quadratic problem (BOXCQP) algorithm.11, 12, 13 This efficient method was implemented to minimize a quadratic objective function with the bound constraint that all beamlet intensities are non-negative and less than some maximum allowed beamlet intensity xmax. Nonzero penalty factors were assigned to OAR voxels that had exceeded the OAR dose parameter in each iteration. A short description is provided.
To compute optimal beamlet intensities, BOXCQP minimized the matrix form of the penalty function defined by each individual’s genes summed with a smoothing function as described below,
| 4 |
where fdet is the objective function for the deterministic component of the algorithm, is the vector of the beamlet intensities, B is the precalculated matrix storing the dose to each voxel from each beamlet, P is a diagonal matrix of all importance weighted penalty factors for each voxel, κ is the smoothing constant, S is the smoothing penalty matrix, and xb represents any element in vector
A smoothing term was introduced because BOXCQP depends on solving a well-posed problem.11, 12 It is also desirable to find the deliverable solution for a beamlet weight vector that is not excessively modulated due to delivery limitations, i.e., MLC movement. The smoothing term was based on the fact that the smaller the second derivative of a fluence map, the easier it is to deliver in practice. Therefore, S was the second derivative matrix by finite difference method and κ was a smoothing coefficient that was found empirically. The algorithm was implemented using MATLAB (The MathWorks, Natick, MA). Since this code was executed many times during the course of the optimization, considerable effort was taken to speed up execution.
Treatment planning platform
A treatment plan consists of a set of beams, which describes the geometry of radiation delivery. Each radiation beam was divided into a 2D array of beamlets. Each beamlet represents a 0.6 cm×1 cm area of the beam. A beamlet length of 1 cm was selected because of the size of the collimator leaf, and a width of 0.6 cm was used as a compromise between speed and resolution. Beamlet intensities were the variables optimized in the deterministic IMRT optimization algorithm.
The patient was considered as a collection of 3D voxels that are segmented into a set of targets and critical normal tissues (OARs). A model of radiation transport mapped each beamlet intensity to the dose it deposited at each voxel; this was stored in a beamlet-to-voxel dose contribution matrix, which was calculated once before the optimization. Typically the number of beamlets ranged from 1000 to 5000, while the number of voxels ranged from 104 to 105. The entire system was modeled using the Prism treatment planning system14, 15, 16 that was augmented with a pencil beam dose calculation algorithm.17 The optimization algorithms interacted with Prism via file input∕output.
Experiments
Though the hierarchical method has been used to effectively optimize complex prostate and head and neck example cases with 7–16 objectives, the focus of this work is to introduce this multiobjective method while clinical evaluation of its performance is the subject of ongoing research. As such, results are shown for only two prostate cancer example cases that use only one target and two OARs for simple, quantifiable, and easily displayed results. Case 1, used in all experiments, was selected to be challenging and had a PTV that was ∼8.5 cm across at the widest point and had 39% overlap with the bladder and 32% overlap with the rectum. Case 2, used only in Secs. 3E, 3F, had a PTV that was ∼7 cm in diameter with only 9% overlap with the bladder and 17% overlap with the rectum. Though the volume of OAR overlapping the target is excluded from the fitness objective calculation in the MOEA optimization, this volume is included in the DVH analysis for these two cases. All plans used seven equally spaced 6 MV photon beams.
Three fitness objectives were used in all of the optimizations: Bladder (or bladder wall) EUD, rectal wall EUD, and target maximum dose. OAR voxels inside the PTV were excluded from objective calculation. All dose distributions were scaled to meet minimum target dose requirements, thereby making the target maximum dose a measure of target variance. The protocol objectives represented a maximum allowed target dose and OAR DVH constraints. A comparison was also made for two example prostate patients between the MOEA and a plan generated using a commercial deterministic IMRT optimization algorithm with the current clinical protocol. Of all possible MOEA plans, we chose the one plan from the MOEA output that most closely matched the clinical plan’s target dose distribution.
It should be noted that stochastic algorithms do not guarantee convergence to the Pareto optimal set. The degree to which this algorithm approximates that set is the subject of several of the result sections described below.
The following experiments were performed to evaluate individual aspects of the algorithm:
demonstration of the evolution of a population of IMRT plans toward the Pareto front through the three stages of a multiobjective optimization (Sec. 3A);
a multiobjective comparison of performance between a standard genetic algorithm package and the modified evolutionary algorithm (Sec. 3B);
demonstration of the role of domination advantage in controlling population size, maintaining diversity, and improving performance (Sec. 3C);
evaluation of the performance of the MOEA with and without protocol objectives (Sec. 3D);
a DVH comparison between plans produced by the MOEA and plans produced using our current clinical protocol and a commercial planning system (Sec. 3E); and
assessment of the ability of the MOEA to approximate the true Pareto front (Sec. 3F).
A common method for comparing two different algorithms is to select the “best” plan from each population and do DVH comparisons; however, such a method is not a multiobjective metric that can compare algorithms that produce populations of plans. It focuses on only a small subset of the results, does not lead itself to quantitative or statistical analysis, and, given the multiobjective nature of the problem, selection of the plan used for comparison is subjective.
As previously discussed, in multiobjective optimization a plan can only be deemed superior to another if it is better in all of its objectives, which is the definition of Pareto domination. We used a metric based on Pareto dominance that we term “domination comparison” DC. If is the set of plans generated using method A and is the set of plans using method B, DC(A,B) is the probability for a plan randomly selected from to dominate a plan randomly selected from . Domination comparison is noncommutative, and if DC(A,B)>DC(B,A), this implies that is closer to the Pareto front than . Notice that DC(A,B)+DC(B,A)+ND(A,B)=100%, where ND(A,B)=ND(B,A) is the probability that no domination will occur between two randomly selected plans. In mathematical form, the domination comparison metric DC(A,B) can be calculated as follows:
| 5 |
where f(Ai,Bj)=1 if Ai dominates Bj and f(Ai,Bj)=0 otherwise.
Domination comparison does not give a measure of the diversity of the population or coverage of the Pareto front. For this reason, we included 3D Pareto plots for graphical display of the final populations for the two prostate examples. For greater ease, we made all of these plots uniform, with rectum objective on the x axis, bladder objective on the y axis, and target objective in color scale.
RESULTS
Stages of the MOEA
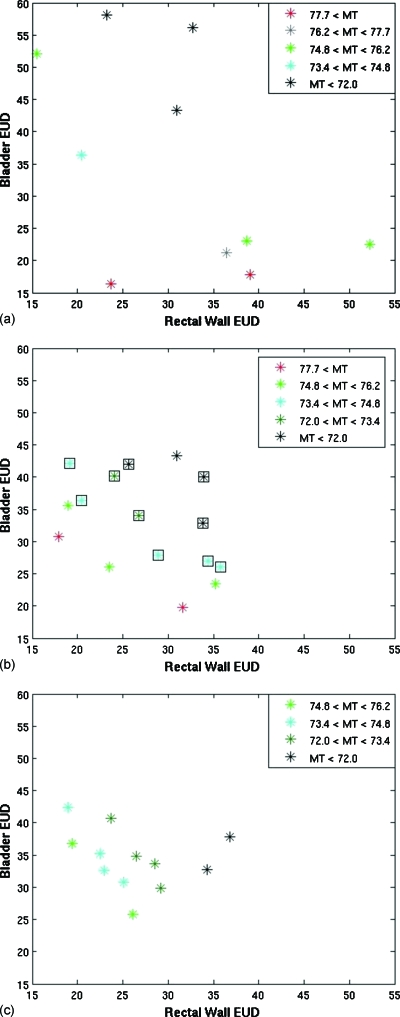
A population of plans for case 1 was tracked through the three stages of the evolutionary algorithm [Figs. 2a, 2b, 2c]. Three fitness objectives were used: Rectal wall EUD, bladder EUD, and maximum target (MT) dose. Only OAR voxels outside the target were used in the calculation of the fitness objectives.
Figure 2.
Plots of the objective values of the plans at the end of (a) stage 1, (b) stage 2, and (c) stage 3 for a MOEA optimization of patient case 1. The colors represent different values for the target objective, MT. In (b), the square icons represent plans that met the clinical protocol objectives.
Often Pareto optimality is demonstrated using only two objectives which makes determining the Pareto front visually easy. Given that we used three fitness objectives, we used color to indicate the value of the third axis. For uniformity, rectal wall EUD was always plotted on the x axis, bladder EUD on the y axis, and the value of the MT dose was represented in color scale. The plots illustrate the difficulty in visualizing even a three-dimensional fitness objective space, which is small compared to the dimensions of most IMRT planning which highlights our decision to present relatively simple examples.
Dose distributions were scaled to meet all minimum target dose requirements to eliminate the need for a minimum target dose fitness objective. The maximum target dose represents clinically undesirable hot spots and is a measure of target variance. Throughout the presentations of these results, lower fitness objective values correspond to more optimal plans. We used ngoal=10 throughout this work.
The population after the first ten iterations obtained from completely random genes has relatively poor objective values. Stage 2 was completed after 53 iterations, and objectives values have improved. The ten clinically acceptable plans are shown with a black box outline. All other plans were removed before stage 3 began. For this example, the greatest amount of improvement is seen in a small number of iterations during stage 2 as the initial population was not close to Pareto optimal. Stage 3 was completed after a total of 200 iterations. Further improvement is observed in the objective space during stage 3.
Performance of the hierarchical evolutionary algorithm
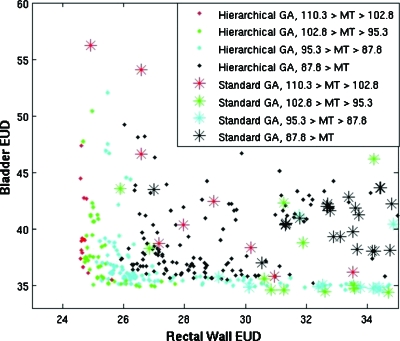
The modified evolutionary algorithm was compared to the MATLAB standard genetic algorithm package that used a single stage, a set population size, and a tournament-style selection method with a single fitness function. Both algorithms used the previously described deterministic algorithm. To isolate differences in the algorithms, domination advantage and protocol objectives were not used in either multiobjective optimization. Important differences included the selection method, allowed population size, and mutation rates. Bladder EUD, rectal wall EUD, and MT dose were used as the fitness objectives.
Twenty-five multiobjective optimizations that each produced a set of 11–15 plans were performed for both situations to establish statistical significance, and each multiobjective optimization executed a total of 200 BOXCQP iterations in ∼10 min. Objective values (OAR EUD and target maximum dose) for individual plans resulting from two optimizations are shown in Fig. 3.
Figure 3.
Plot comparing the objectives of the final populations of plans for case 1, resulting from the hierarchical approach with that of a standard genetic algorithm. The standard genetic algorithm is shown as asterisks, and the hierarchical approach is shown as solid diamonds. The color reflects the MT dose, the target variance objective. Lower values in all objectives are more optimal.
Populations resulting from our MOEA dominated populations resulting from the standard genetic algorithm (GA) DC(MOEA,GA)=11.3%±0.7% of possible comparisons versus DC(GA,MOEA)=0.04%±0.02% in reverse. Results indicate that the new evolutionary algorithm was able to produce a population of plans with lower OAR EUD values and lower target variance in a short amount of time.
Domination advantage
Our MOEA does not have a set population size or limit and does not use a single objective fitness function for selection. The resulting populations could potentially be very large even with a relatively small number of objectives. To keep the population size in the desired range, to increase selective pressure, and to promote diversity in the population, a specialized niche effect, domination advantage, was used (see Sec. 2A1). A comparison of two multiobjective optimizations of a prostate case (with and without domination advantage) was performed to demonstrate the effect on a single population (Fig. 4). Twenty-five multiobjective optimizations were performed with and without domination advantage to establish statistical significance.
Figure 4.
Plot demonstrating the effect domination advantage has on a population of plans for case 1. The plans resulting from the hierarchical approach without using domination advantage are shown as asterisks, and those using domination advantage are shown as open squares. MT dose, the target variance objective, is displayed in color. Lower values in all objectives are more optimal.
The average population size without domination advantage (NDA) was 68.7±2.1 versus 13.2±0.2 with domination advantage (DA). The population generated using the niche effect dominated an average of DC(DA,NDA)=1.73%±0.35% of the population generated without it and only DC(NDA,DA)=0.17%±0.04% of dominations occurred in reverse. When domination advantage was used, there were fewer individuals for a more manageable final population size. The distribution of individuals was diverse and closer to the true Pareto front possibly due to the increase in selective pressure from the niche effect. Domination advantage did not allow searching in regions that give only a small improvement in one objective at great cost to other objectives. This speeds up the optimization; however, it also means that some of the Pareto front may not be mapped.
Effect of protocol objectives
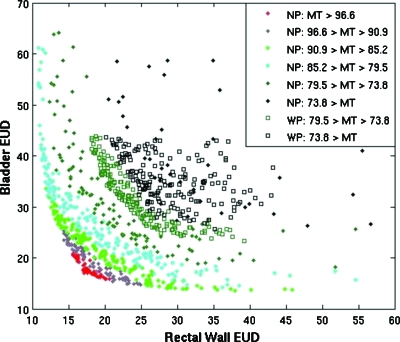
Protocol objectives were used to focus the search to a region of objective space that met predetermined clinical dosimetric requirements. The performance of multiobjective optimizations was evaluated for an example prostate case with and without protocol objectives that reflected constraints from a clinical protocol. The effectiveness of the preference space guidance algorithm is shown in Fig. 5.
Figure 5.
Plot comparing multiobjective optimization for case 1 with (WP) and without (NP) using protocol objectives. Bladder EUD and Rectal Wall EUD are plotted for the sum of 25 full optimizations with and without using protocol objectives to restrict the search space. MT dose, the target variance objective, is plotted in color. The solid diamonds show the full Pareto front, and the open squares display the optimizations using protocol objectives.
In terms of Pareto domination the protocol objectives did not improve or degrade results; however, without protocol objectives, the search focused on too wide a search space. Of all individual plans generated without using protocol objectives, only 4.4%±0.8% met the clinical criteria and only 68% of the full multiobjective optimizations had at least one plan that met all clinical requirements. In other words, 32% of the optimization procedures did not yield a usable plan when the protocol constraints were not considered, whereas all of the plans generated using the protocol objectives met all of the clinical criteria.
Two clinical DVH comparisons
The MOEA was compared to our clinical planning methods for the two prostate cases. IMRT plans were optimized using a 200 iteration MOEA optimization and using our standard clinical inverse planning procedure (Pinnacle,3 Philips Medical Systems). The MOEA plan whose target dose distribution most closely matched the plan using the clinic’s deterministic algorithm was chosen from each multiobjective population for each case. A DVH comparison was made between these plans and the corresponding clinical plans. None of the example patient studies included femur and unspecified tissue objectives, and the MOEA plans were not translated into deliverable beams. This comparison is only a demonstration of the potential of this algorithm and not designed to be a comparison of plans ready to be used in the clinic.
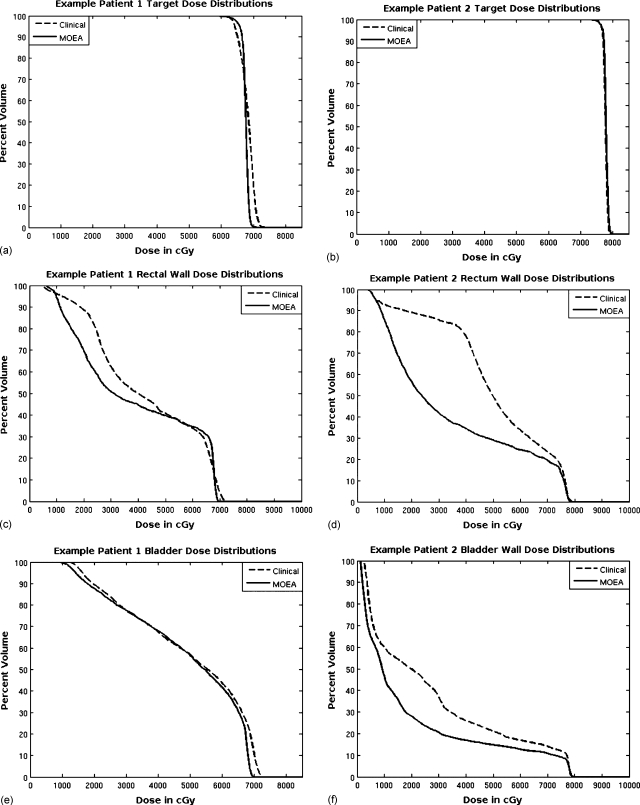
The DVH comparisons for the target, rectal wall, and bladder for case 1 are shown in Figs. 6a, 6c, 6e. The minimum target dose requirements were matched for these plans; however, the uniformity of the target dose distribution and lower maximum target dose was better for the MOEA plan. This patient was more difficult especially with regard to the volume of bladder at close proximity to (but just outside) the target, so improvement of the MOEA OAR distributions over the clinical plan was modest. In addition, 32% of the volume of the rectum was inside the target, and some of this volume received higher dose than the MOEA plan as it was not considered in the fitness objectives. Once outside the PTV, the dose to the rectum dropped off more quickly for the MOEA than for the plan produced using the current clinical protocol.
Figure 6.
DVH comparisons for bladder, bladder wall, rectal wall, and PTV are made between plans selected from the population produced by the MOEA and plans produced using the current clinical inverse planning method. Results for case 1 are on the left [(a), (c), and (e)] and results for case 2 are on the right [(b), (d), and (f)].
The DVH comparisons for the target, rectal wall, and bladder wall for case 2 are shown in Figs. 6b, 6d, 6f. For this prostate patient example, there was more separation between the OARs and the target, and this resulted in a greater potential for improvement using the MOEA. The target distributions nearly overlap, with the clinical plan’s coldest 1% of voxels below 75.5 Gy versus 75.4 Gy for the MOEA plan, and the clinical plan’s hottest 1% of voxels above 79.1 Gy versus 79.3 Gy for the MOEA plan. Dose levels for both the bladder and especially the rectum are much lower for the MOEA plan over the entire DVH.
Estimation of the Pareto front
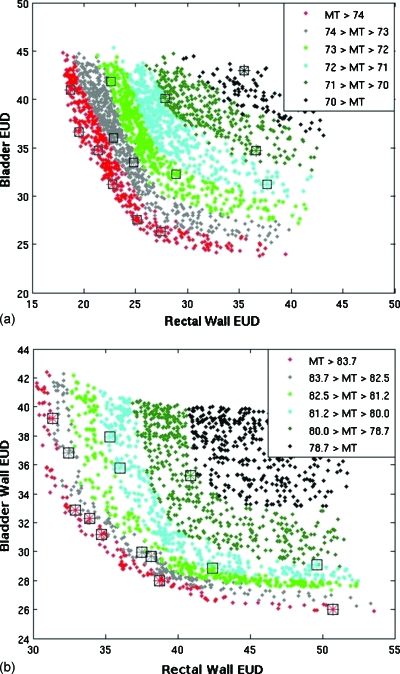
The same two cases were used to investigate the ability of the MOEA to approximate the true Pareto front. For case 1, a long multiobjective optimization generated 9118 individuals in 12.6 h without domination advantage in order to approximate the true Pareto front. Results were compared to 25 shorter optimizations that each generated 200 individuals using domination advantage. Figure 7a plots the results from one of the 25 short runs performed using domination advantage against the long optimization without using it. A similar comparison using case 2 was also performed using both a long (5000 individuals) run and 25 short runs (200 individuals) each. Results from one of the short runs are plotted with results from the long run (LR) in Fig. 7b.
Figure 7.
Plots for short multiobjective optimizations mapped onto an approximation of the Pareto front for case 1 [top, (a)] and case 2 [bottom, (b)]. Rectum and bladder objective values are plotted with the target variance objective (MT) shown in color. The plans from the long optimization runs are represented as solid diamonds that make up most of the graphs. The plans resulting from the quick optimization are shown with asterisks using the same color scale and surrounded by a black square for easier viewing.
For case 1, each individual in the LR dominated only DC(LR,SO)=0.20%±0.05% of the population generated using the short optimization (SO). For case 2, each individual in the true Pareto front dominated an average of only DC(LR,SO)=0.14%±0.04% of the population generated using the short optimization. This demonstrates how quickly the algorithm with domination advantage approaches the Pareto front. The smaller populations were diverse and covered a wide range of the Pareto front, but certain regions characterized by diminishing returns were missed when using the domination advantage feature. In both of the above cases, DC(SO,LR)=0.
In order to see if the small performance improvement using domination advantage in short runs (Sec. 3C) translated to longer runs, the long optimization runs described in the previous paragraph were repeated with and without domination advantage. For case 1, each individual in the long optimization using domination advantage (LDA) dominated only DC(LDA,LNDA)=0.009% of the population generated using the long optimization without domination advantage (LNDA) with DC(LNDA,LDA)=0.004% in reverse. For case 2, each individual produced using domination advantage dominated only DC(LDA,LNDA)=0.005% of the population generated using the long optimization without domination advantage, and the comparison was DC(LNDA,LDA)=0.028% in reverse. Results suggest that for very long runs that closely approximate the Pareto front, domination advantage may slow convergence slightly, but differences are very small. Note that without the single fitness function domination advantage feature described in Sec. 2A2, the MOEA would never get within ∼ε of the Pareto front using domination advantage because all new individuals only slightly better than the existing population would have been eliminated.
DISCUSSION
We have reported on the development of a hierarchical multiobjective optimization algorithm that couples a stochastic evolutionary algorithm with a fast deterministic one. The multiobjective nature of the algorithm reflects our view that IMRT planning requires exploring possible trade-offs between competing clinical goals. The decision making strategy that must be coupled with the multiobjective optimization has a profound influence on the structure of the algorithm. The current standard clinical decision making strategy supported by commercial inverse planning systems takes an interactive approach in which a plan is generated, evaluated by a human user, and a new search is made if necessary. Unfortunately, these systems do not provide any method for performing an efficient and effective search for all possible trade-offs between objectives. While the result is usually better than that achievable with 3D conformal techniques, the decision maker is not aware of the large number of other feasible solutions that may be better.
Another multiobjective method is the a posteriori approach in which a set of Pareto optimal plans are found first, and then this set is evaluated by a decision maker to select one. This is the nature of our MOEA and is a fairly popular approach for multiobjective problems in general.5, 18 It has the advantage that the user does not have to determine the relative importance among objectives before achievable trade-offs are known. However, this comes at the price of time since there is little guidance in the search procedure. We have used several heuristic methods to focus the search. In addition, the domination advantage niche effect is designed to limit the final number of plans to the number that our decision process can handle. Bortfeld and co-workers19, 20, 21, 22, 23 devised an alternative approach in which only convex objectives are used, the Pareto front is systematically mapped and calculation times are reduced by interpolating solutions. Specially designed software allows the decision maker to steer between solutions on the Pareto front and observe the trade-offs of the different regions. Another systematic search approach was taken by Lahanas and co-workers24, 25 in which attention was focused on the method of completely mapping the Pareto front with a simple decision making approach used a posteriori. An early paper by Yu, which focused on brachytherapy and radiosurgical planning, presented an excellent discussion of multiobjective optimization in radiation therapy.26 He devised a plan ranking system that required some a priori importance input but used a simulated-annealing method to introduce some fuzziness and to broaden the search space. He also included a “satisfying” condition that functioned similar to our protocol objectives.
An a priori approach to multiobjective decision making in multiobjective optimization is the third alternative. Prior methods have the advantages of being among the fastest and providing a single solution. Jee et al.27 described a method using the technique of lexigraphic ordering in which prior ranking of objectives leads to a sequence in which the first objective is satisfied and then turned into a constraint as the second objective is optimized and so on for the remainder. This is somewhat similar to our shifting of the use of our protocol objectives between the second and the third stages, but we make no preference between the objectives and all are satisfied simultaneously before transforming them to constraints.
Our use of an evolutionary algorithm was determined by its extensive use in multiobjective optimization in other fields5 and because this type of algorithm can handle a much wider range of objective types than can deterministic algorithms. As with other aspects of our approach, the trade-off hinges on the speed of convergence. We used a hierarchical approach, coupled with the multiple stages in order to mitigate this issue, and our results demonstrate that the performance is acceptable in a clinical setting. Wu and Zhu4 used a genetic algorithm for 3D conformal optimization to optimize the weighting factors. Although they did not explicitly use Pareto optimality, their choice of a genetic algorithm was based on a recognition of the multiobjective nature of the problem and a desire to be flexible with respect to single objectives. Evolutionary algorithms have found their greatest use for the solution of explicitly nonconvex objectives, such as the problem of number and orientation of the radiation beams7, 25, 28, 29 and the integration of leaf sequencing and intensity optimization.30, 31 Many other objectives in IMRT planning are also nonconvex such as dose-volume objectives. For certain situations, it has been found that becoming trapped in local minima may be unlikely32 or mathematical techniques are able to be applied to linearize nonconvex objectives or approximate them with a convex surrogate.20, 33
A critical component of any multiobjective optimization is the means by which two objects with multiple characteristics are compared or rated. A common example is the comparison of a dose-volume histogram from two different plans. When the DVHs do not cross, one can determine which is clearly better; when they do cross, “better” depends on the decision variables. This is the essence of Pareto optimality. In our IMRT optimization, we removed plans that were dominated within some epsilon since those plans were clinically similar or worse in every aspect when compared to other plans. When comparing algorithms or optimization methods, a similar multiobjective approach can be taken. In our evaluation of different versions of our algorithm, we found it more useful to base our definition of better on a statistical comparison using Pareto dominance as the defining criterion. A flexible multiobjective algorithm as described in this paper is the ideal means for making such comparisons which are more convincing than alternatives that are commonly used.
CONCLUSION
A multiobjective evolutionary algorithm was developed to find a diverse set of Pareto optimal and clinically acceptable IMRT plans. The novel selection method, flexible population size, and optimized mutation rates improved performance. The population diversity and size was effectively controlled using a niche effect, “domination advantage.” The protocol objectives and multiple stages used in reproduction and selection guided the optimization to those regions of plan space that met clinical criteria. Key features of the algorithm are the ability to use any functional form of individual objectives and the ability to tailor the number and diversity of the output to the decision making environment.
ACKNOWLEDGMENTS
Thanks are due to Stephanie Banerian for the computer and technical support. This work was supported by NIH Grant No. 1-R01-CA112505.
References
- Meyer J., Phillips M. H., Cho P. S., Kalet I., and Doctor J. N., “Application of influence diagrams to prostate intensity-modulated radiation therapy plan selection,” Phys. Med. Biol. 49, 1637–1653 (2004). 10.1088/0031-9155/49/9/004 [DOI] [PubMed] [Google Scholar]
- Smith W. P., Doctor J., Meyer J., Kalet I. J., and Phillips M. H., “A decision aid for IMRT plan selection in prostate cancer based on a prognostic Bayesian network and a Markov model,” Artif. Intell. Med. 46, 119–130 (2009). 10.1016/j.artmed.2008.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ezzell G. A., “Genetic and geometric optimization of three-dimensional radiation therapy treatment planning,” Med. Phys. 23, 293–305 (1996). 10.1118/1.597660 [DOI] [PubMed] [Google Scholar]
- Wu X. and Zhu Y., “An optimization method for importance factors and beam weights based on genetic algorithms for radiotherapy treatment planning,” Phys. Med. Biol. 46, 1085–1099 (2001). 10.1088/0031-9155/46/4/313 [DOI] [PubMed] [Google Scholar]
- Coello C. A. C., Van Veldhuizen D. A., and Lamont G. B., Evolutionary Algorithms for Solving Multi-Objective Problems (Kluwer Academic, Dordrecht: /Plenum, New York, 2002). [Google Scholar]
- Osyczka A., Evolutionary Algorithms for Single and Multicriteria Design Optimization (Physica-Verlag, Heidelberg, 2002). [Google Scholar]
- Schreibmann E., Lahanas M., Xing L., and Baltas D., “Multiobjective evolutionary optimization of the number of beams, their orientations and weights for intensity modulated radiation therapy,” Phys. Med. Biol. 49, 747–770 (2004). 10.1088/0031-9155/49/5/007 [DOI] [PubMed] [Google Scholar]
- Niemierko A., “Reporting and analyzing dose distributions: A concept of equivalent uniform dose,” Med. Phys. 24, 103–110 (1997). 10.1118/1.598063 [DOI] [PubMed] [Google Scholar]
- Niemierko A., “A generalized concept of equivalent uniform dose (EUD),” Med. Phys. 26, 1100 (1999). [DOI] [PubMed] [Google Scholar]
- Luxton G., Keall P. J., and King C. R., “A new formula for normal tissue complication probability (NTCP) as a function of equivalent uniform dose (EUD),” Phys. Med. Biol. 53, 23–26 (2008). 10.1088/0031-9155/53/1/002 [DOI] [PubMed] [Google Scholar]
- Breedveld S., Storchi P. R. M., Keijzer M., and Heijmen B. J. M., “Fast, multiple optimization of quadratic dose objective functions in IMRT,” Phys. Med. Biol. 51, 3569–3579 (2006). 10.1088/0031-9155/51/14/019 [DOI] [PubMed] [Google Scholar]
- Voglis C. and Lagaris I. E., “BOXCQP: An algorithm for bound constrained convex quadratic problems,” Proceedings of the First International Conference: From Scientific Computing to Computational Engineering, 2004. (unpublished).
- Phillips M., Kim M., and Ghate A., “SU-GG-T-121: Multiobjective optimization for IMRT using genetic algorithm,” Med. Phys. 35, 2753 (2008). 10.1118/1.2961873 [DOI] [Google Scholar]
- Kalet I. J., Jacky J. P., Austin-Seymour M. M., and Unger J. M., “Prism: A new approach to radiotherapy planning software,” Int. J. Radiat. Oncol., Biol., Phys. 36, 451–461 (1996). 10.1016/S0360-3016(96)00322-7 [DOI] [PubMed] [Google Scholar]
- Kalet I. J., Unger J. M., Jacky J. P., and Phillips M. H., “Prism system capabilities and user interface specification, version 1.2,” Technical Report No. 97-12-02 (Radiation Oncology Department, University of Washington, Seattle, WA, 1997).
- Kalet I. J., Unger J. M., Jacky J. P., and Phillips M. H., “Experience programming radiotherapy applications in Common Lisp,” in Proceedings of the 12th International Conference on the Use of Computers in Radiation Therapy, edited by Leavitt D. D. and Starkschall G. (Medical Physics Publishing, Madison, Wisconsin, 1997).
- Phillips M. H., Singer K. M., and Hounsell A. R., “A macropencil beam model: Clinical implementation for conformal and intensity modulated radiation therapy,” Phys. Med. Biol. 44, 1067–1088 (1999). 10.1088/0031-9155/44/4/018 [DOI] [PubMed] [Google Scholar]
- Collette Y. and Siarry P., Multiobjective Optimization: Principles and Case Studies (Springer, New York, 2003). [Google Scholar]
- Craft D. L., Halabi T. F., Shih H. A., and Bortfeld T. R., “Approximating convex Pareto surfaces in multiobjective radiotherapy planning,” Med. Phys. 33, 3399–3407 (2006). 10.1118/1.2335486 [DOI] [PubMed] [Google Scholar]
- Craft D., Halabi T., Shih H. A., and Bortfeld T., “An approach for practical multiobjective IMRT treatment planning,” Int. J. Radiat. Oncol., Biol., Phys. 69, 1600–1607 (2007). [DOI] [PubMed] [Google Scholar]
- Hong T. S., Craft D. L., Carlsson F., and Bortfeld T. R., “Multicriteria optimization in intensity-modulated radiation therapy treatment planning for locally advanced cancer of the pancreatic head,” Int. J. Radiat. Oncol., Biol., Phys. 72, 1208–1214 (2008). 10.1016/j.ijrobp.2008.07.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monz M., Küfer K. H., Bortfeld T. R., and Thieke C., “Pareto navigation,” Phys. Med. Biol. 53, 985–998 (2008). 10.1088/0031-9155/53/4/011 [DOI] [PubMed] [Google Scholar]
- Thieke C., Küfer K. H., Monz M., Scherrer A., Alonso F., Oelfke U., Huber P. E., Debus J., and Bortfeld T., “A new concept for interactive radiotherapy planning with multicriteria optimization: First clinical evaluation,” Radiother. Oncol. 85, 292–298 (2007). 10.1016/j.radonc.2007.06.020 [DOI] [PubMed] [Google Scholar]
- Lahanas M., Schreibmann E., and Baltas D., “Multiobjective inverse planning for intensity modulated radiotherapy with constraint-free gradient-based optimization algorithms,” Phys. Med. Biol. 48, 2843–2871 (2003). 10.1088/0031-9155/48/17/308 [DOI] [PubMed] [Google Scholar]
- Lahanas M., Schreibmann E., and Baltas D., “Intensity modulated beam radiation therapy dose optimization with multiobjective evolutionary algorithms,” in Proceedings of the Second International Conference on Evolutionary Multi-Criterion Optimization (EMO 2003), Faro, Portugal, 8–11 April 2003, edited by Fonseca C. M. (Springer-Verlag, Faro, Portugal, 2003), pp. 439–447.
- Yu Y., “Multiobjective decision theory for computational optimization in radiation therapy,” Med. Phys. 24, 1445–1454 (1997). 10.1118/1.598033 [DOI] [PubMed] [Google Scholar]
- Jee K. W., McShan D. L., and Fraass B., “Lexicographic ordering: Intuitive multicriteria optimization for IMRT,” Phys. Med. Biol. 52, 1845–1861 (2007). 10.1088/0031-9155/52/7/006 [DOI] [PubMed] [Google Scholar]
- Hou Q., Wang J., Chen Y., and Galvin J. M., “Beam orientation optimization for IMRT by a hybrid method of the genetic algorithm and the simulated dynamics,” Med. Phys. 30, 2360–2367 (2003). 10.1118/1.1601911 [DOI] [PubMed] [Google Scholar]
- Li Y., Yao J., and Yao D., “Automatic beam angle selection in IMRT planning using genetic algorithm,” Phys. Med. Biol. 49, 1915–1932 (2004). 10.1088/0031-9155/49/10/007 [DOI] [PubMed] [Google Scholar]
- Li Y., Yao J., and Yao D., “Genetic algorithm based deliverable segments optimization for static intensity-modulated radiotherapy,” Phys. Med. Biol. 48, 3353–3374 (2003). 10.1088/0031-9155/48/20/007 [DOI] [PubMed] [Google Scholar]
- Cotrutz C. and Xing L., “Segment based dose optimization using a genetic algorithm,” Phys. Med. Biol. 48, 2987–2998 (2003). 10.1088/0031-9155/48/18/303 [DOI] [PubMed] [Google Scholar]
- Llacer J., Deasy J. O., Bortfeld T. R., Solberg T. D., and Promberger C., “Absence of multiple local minima effects in intensity modulated optimization with dose-volume constraints,” Phys. Med. Biol. 48, 183–210 (2003). 10.1088/0031-9155/48/2/304 [DOI] [PubMed] [Google Scholar]
- Romeijn H., Ahuja R., Dempsey J., Kumar A., and Li J., “A novel linear programming approach to fluence map optimization for intensity modulated radiation therapy treatment planning,” Phys. Med. Biol. 48, 3521–3542 (2003). 10.1088/0031-9155/48/21/005 [DOI] [PubMed] [Google Scholar]