Detailed analysis of latencies in image-based dynamic MLC tracking

Abstract

Purpose: Previous measurements of the accuracy of image-based real-time dynamic multileaf collimator (DMLC) tracking show that the major contributor to errors is latency, i.e., the delay between target motion and MLC response. Therefore the purpose of this work was to develop a method for detailed analysis of latency contributions during image-based DMLC tracking.

Methods: A prototype DMLC tracking system integrated with a linear accelerator was used for tracking a phantom with an embedded fiducial marker during treatment delivery. The phantom performed a sinusoidal motion. Real-time target localization was based on x-ray images acquired either with a portal imager or a kV imager mounted orthogonal to the treatment beam. Each image was stored in a file on the imaging workstation. A marker segmentation program opened the image file, determined the marker position in the image, and transferred it to the DMLC tracking program. This program estimated the three-dimensional target position by a single-imager method and adjusted the MLC aperture to the target position. Imaging intervals ΔT_image from 150 to 1000 ms were investigated for both kV and MV imaging. After the experiments, the recorded images were synchronized with MLC log files generated by the MLC controller and tracking log files generated by the tracking program. This synchronization allowed temporal analysis of the information flow for each individual image from acquisition to completed MLC adjustment. The synchronization also allowed investigation of the MLC adjustment dynamics on a considerably finer time scale than the 50 ms time resolution of the MLC log files.

Results: For ΔT_image=150 ms, the total time from image acquisition to completed MLC adjustment was 380±9 ms for MV and 420±12 ms for kV images. The main part of this time was from image acquisition to completed image file writing (272 ms for MV and 309 ms for kV). Image file opening (38 ms), marker segmentation (4 ms), MLC position calculation (16 ms), and MLC adjustment (52 ms) were considerably faster. For ΔT_image=1000 ms, the total time from image acquisition to completed MLC adjustment increased to 1030±62 ms (MV) and 1330±52 ms (kV) mainly because of delayed image file writing. The MLC adjustment duration was constant 52 ms (±3 ms) for MLC adjustments below 1.1 mm and increased linearly for larger MLC adjustments.

Conclusions: A method for detailed time analysis of each individual real-time position signal for DMLC tracking has been developed and applied to image-based tracking. The method allows identification of the major contributors to latency and therefore a focus for reducing this latency. The method could be an important tool for the reconstruction of the delivered target dose during DMLC tracking as it provides synchronization between target motion and MLC motion.

INTRODUCTION

Most tumors move during radiotherapy treatment delivery. This intrafraction motion is usually accounted for by treating a static volume that includes both the tumor and its anticipated motion with a high probability.¹ An alternative to this static volume approach is tumor tracking, where real-time tumor position monitoring is used for repeated realignment of the treatment beam to the tumor position. Tracking is attractive because it could reduce irradiation of healthy tissue and eliminate the risk of tumor motion outside the predesigned high-dose volume.

The proposed methods for target tracking with a conventional linear accelerator include continuous couch position corrections² and dynamic multileaf collimator (DMLC) tracking.^{3, 4, 5, 6, 7, 8} DMLC tracking has been demonstrated with real-time target position monitoring based on either an external optical system,⁹ implantable electromagnetic transponders,^{10, 11, 12} or x-ray images of an implantable fiducial marker.^{13, 14, 15}

In all tracking systems, there is a latency τ between the target motion and the beam-target realignment. For DMLC tracking, continuous portal imaging has previously been used to measure the average latency τ_av between the target motion and the MLC motion.^{9, 10, 12, 13} Portal imaging is an attractive method for measurement of τ_av because both target motion and MLC motion are captured at the same time in the images.

The reported values of τ_av for DMLC tracking varied from 160 to 570 ms.^{9, 14} It was largest for image-based DMLC tracking, where the latency was found to be the main contributor to geometrical errors in tracking of respiratory target motion.¹⁶ Here, latency reduction would be a clear pathway to accuracy improvements.¹⁶ Such latency reduction would rely on detailed knowledge about individual latency contributions. However, portal imaging does not, by itself, provide knowledge about the latency contributions.

In this study, we will develop a markedly improved method for tracking latency analysis by synchronization of portal imaging with two other data streams: (1) MLC positions recorded in MLC log files (Dynalog files¹⁷) and (2) tracking events recorded in tracking log files. Several studies have validated that the Dynalog files accurately reflect the actual MLC positions.^{18, 19, 20} The synchronization method enables tracing of the events that constitute the tracking process from image acquisition to the completion of the resulting MLC adjustment. It provides useful insight into the tracking process and the relationship between individual latency contributions and the overall latency τ_av of a tracking system. Furthermore, the synchronization allows analysis of the MLC leaf adjustment dynamics on a time scale that is much finer than the temporal resolution of the Dynalog files.

METHODS AND MATERIALS

DMLC tracking procedure

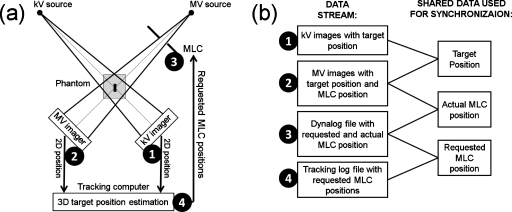
The DMLC tracking experiment is sketched in Fig. 1a. A phantom with an embedded cylindrical gold marker (3 mm length and 1 mm diameter) was placed on a motion stage.²¹ The motion stage performed a sinusoidal motion with a 10 s period in the superior-inferior (SI) direction. The peak-to-peak amplitude was 20 mm.

Figure 1.

(a) Image-based DMLC tracking experiment. (b) Four different data streams collected during the tracking experiments (left) and synchronized off-line by utilizing pairwise shared data (right). The numbers 1–4 indicate the four data streams in both (a) and (b).

A 6 MV field with 10 cm circular aperture, 45° gantry angle (IEC coordinates), and the MLC leaves aligned parallel to the target motion was delivered to the phantom by a Trilogy linear accelerator with a 120 leaf Millennium MLC controlled by MLC Workstation version 7.0 (Varian Medical Systems, Palo Alto, CA). The accelerator was equipped with a PortalVision AS1000 portal imager system and a kV On-Board Imager system (Varian Medical Systems) for acquisition of MV portal images and orthogonal kV x-ray images, respectively.

During field delivery, DMLC tracking of the phantom motion was performed based either on kV or MV images. When a new image was acquired, an image file was written to the hard disk of the kV or MV imaging workstation. An in-house computer program opened the image file, segmented the marker, and transmitted the projected marker position to a DMLC tracking program on a dedicated tracking computer.¹³ The tracking program estimated the 3D marker position by a single-imager method,²² fitted the MLC positions to the updated target position, and requested the updated MLC positions from the MLC controller. In the current experiments, the single-imager target position estimation relied on prior knowledge of the probability density function for the target position.²²

For kV imaging, the imaging interval ΔT_image could be adjusted in steps of 1.024 ms. Single-imager kV tracking was performed with ΔT_image approximately equal to 150 (146×1.024 ms), 200 (195×1.024 ms), 500 (488×1.024 ms), and 1000 ms (977×1.024 ms). It corresponded to imaging frequencies of 6.67, 5, 2, and 1 Hz. The exposure settings were 55 kV, 40 mA, and 12 ms independent of ΔT_image. During kV-based tracking MV portal images needed for the time analysis were acquired at 5.2 Hz.

Single-imager MV tracking was also performed with nominal ΔT_image values of 150, 200, 500, and 1000 ms. Unlike kV imaging, where the exposure duration could be set by the user, the exposure duration for MV imaging was set automatically by the system approximately equal to ΔT_image. For ΔT_image=1000 ms, the target motion between subsequent images occasionally exceeded the allowed 5 mm tolerance between requested and actual MLC position. In such cases a beam-hold was asserted resulting in delayed image acquisition and increased ΔT_image. Beam-holds also occurred for kV-based tracking at 1 Hz, but it did not affect the tracking signal (i.e., the kV images).

The source-imager-distance was 180 cm for the kV imager and 150 cm for the MV imager. The pixel lengths scaled to isocenter distance were 0.216 (kV images) and 0.261 mm (MV images).

Data acquisition and synchronization

The following four data streams were recorded during the tracking process (as indicated by numbers in Fig. 1): (1) kV images showing the target position in kV beam’s eye view, (2) MV images showing the target position and MLC position in MV beam’s eye view, (3) Dynalog file with the requested and the actual MLC leaf positions recorded every 50 ms, and (4) tracking log files with recordings of each requested MLC update by the tracking program as well as the start and end times for image file opening, marker segmentation, and MLC position calculation for each image with a time resolution of 15.625 ms (1∕64 s).

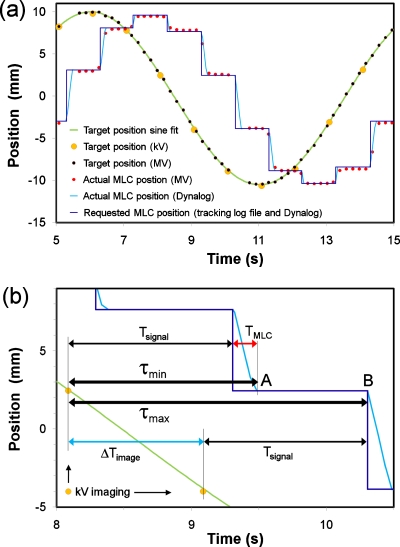
Each of the four data streams was recorded with relative time stamps for each data point, but without synchronization between the data streams. After the experiments, the data streams were therefore pairwise synchronized by utilizing common information content as indicated in the right part of Fig. 1b. Figure 2a shows an example of the synchronization method for 1 Hz kV-based tracking. Here, the large dots indicate the target position in the SI direction as captured in the kV images. This was fitted to the known sinusoidal target motion which, in turn, was fitted to the SI target position in the MV images (black dots). This procedure provided a common time axis for both kV and MV images. Note that we define the acquisition time for an image by the captured target position in the image. In other words, the acquisition time is the midexposure time (approximately).

Figure 2.

(a) Example of synchronization of four data streams recorded during DMLC tracking with kV images acquired at 1 Hz. (b) Excerpt from (a). The thick arrows in (b) indicate the minimum latency τ_min immediately after a MLC adjustment (point A) and the maximum latency τ_max immediately before a MLC adjustment (point B). The thinner arrows indicate the signal processing duration T_signal, the MLC adjustment duration T_MLC, and the imaging interval ΔT_image.

Next, the MLC aperture center position was estimated in each MV image by fitting the aperture to a circle with 10 cm diameter.⁹ The aperture center position was estimated similarly for each recorded set of actual MLC positions in the Dynalog file. The two aperture center trajectories (in MV images and in Dynalog files) were then used for manual time synchronization between the MV images [small dots in Fig. 2a] and the Dynalog file (light curve).

Finally, recordings of the requested MLC adjustments in the Dynalog file were synchronized with the requested MLC adjustments in the tracking log file as follows: Whenever the requested MLC position at a time t in the Dynalog file differed from the previously requested MLC position at time t−50 ms the tracking program must have requested a MLC adjustment in the time interval between t−50 ms and t. Fulfilling this requirement for all requested MLC adjustments in an experiment locked the time scale of the tracking log file with the time scale of the Dynalog file within 1–2 ms. This synchronization provided the starting time for each MLC adjustment on the Dynalog time axis with an uncertainty that varied from <1 to 15.625 ms [step-like curve in Fig. 2a].

Latency contributions

As illustrated in Fig. 2a, the motion of the MLC aperture center consisted of a series of discrete steps, each step being the result of a new image acquisition. This discrete MLC motion was seen in all experiments because the imaging interval ΔT_image always was sufficiently long to allow completion of a MLC adjustment before the next MLC adjustment was requested (i.e., ΔT_image>T_MLC, where T_MLC denote the MLC adjustment duration).

As a consequence of the discrete MLC motion, the latency between the target position and the MLC center position was not constant, but varied during the experiment. The latency had its minimum value τ_min right after completion of a MLC adjustment, i.e., at point A in Fig. 2b. As shown by the upper thin arrows in Fig. 2b, τ_min was given by

$${\tau }_{\text{min}}={\text{T}}_{\text{signal}}+{\text{T}}_{\text{MLC}},$$ (1)

where the signal processing time T_signal is the elapsed time from image acquisition to initiation of the resulting MLC adjustment. The maximum latency τ_max occurred just before initiation of a MLC adjustment, i.e., at point B in Fig. 2b. As seen by the lower thin arrows in Fig. 2b, the maximum latency was

$${\tau }_{\text{max}}={\text{T}}_{\text{signal}}+\Delta {\text{T}}_{\text{image}}.$$ (2)

In the time interval from τ_min to τ_max after an image acquisition, the MLC aperture remained in a constant position centered at the target position that was captured in the image. To first order the average latency is simply the average of Eqs. 1, 2, i.e.,

$${\tau }_{\text{av}}=⟨{\text{T}}_{\text{signal}}⟩+0.5\times ⟨\Delta {\text{T}}_{\text{image}}⟩+0.5\times ⟨{\text{T}}_{\text{MLC}}⟩.$$ (3)

Here, 0.5×⟨ΔT_image⟩ is the mean waiting time from the occurrence of a target position change until it is observed by the next coming image. Note that ⟨T_MLC⟩ only contributes with a factor of 0.5 to the average latency. The reason for this is that each MLC adjustment was completed before the next MLC adjustment was requested in these experiments (i.e., T_MLC<ΔT_image). This result—that the beam-target alignment duration only contributes with a factor of 0.5 to τ_av—is valid in general for all tracking systems when the beam-target alignment is completed before the next beam-target alignment is initiated.

As seen in Eq. 3, τ_av had three contributions: T_signal, ΔT_image, and T_MLC. Here, ΔT_image was given by the imaging frequency and T_MLC was estimated as described in Sec. 2D. Since the data stream synchronization provided a common time scale for each recorded event during the tracking experiments, it directly gave T_signal for each image. T_signal was further subdivided into the following four contributions: (1) Image acquisition and image file writing, (2) image file opening for marker segmentation, (3) marker segmentation, and (4) MLC position calculation. The first of these contributions consisted of both image acquisition and image file writing as these two events could not be separated by our method.

Estimation of T_MLC

Most requested MLC aperture adjustments were completed within 50–100 ms. Therefore, the 50 ms time resolution of the Dynalog file was too coarse to give any details of the MLC dynamics for individual MLC adjustments. However, the synchronization between the Dynalog file and the tracking log file provided the elapsed time from each MLC adjustment request to the subsequent MLC position recordings in the Dynalog file. The limited time resolution of the tracking log file means that the elapsed time was known to be within a certain range only. The width of the time range was 15.625 ms in most cases, but shorter if the tracking log file time stamp appeared close to the border of the 0–50 ms range, in which the MLC adjustment request was known to have happened.

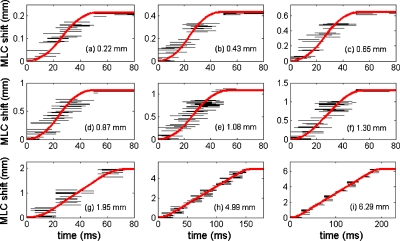
In Fig. 3, each black line segment corresponds to one MLC adjustment during the DMLC tracking experiments based on kV imaging at 1 or 2 Hz. Each line segment shows the MLC aperture center shift in the Dynalog file versus the possible range of elapsed time after the request of the MLC adjustment. Each subfigure in Fig. 3 contains data for several tens of MLC adjustments of nearly identical size Δx (mean standard deviation of 0.003 mm).

Figure 3.

Horizontal line segments in each subfigure: MLC aperture center shift for several tens of requested MLC adjustments of identical magnitude shown as a function of possible elapsed time interval since the adjustment was requested. Thick curves: Functional fit. For each graph, the requested adjustment magnitude is specified. [(a)–(f)] Results from 2 Hz kV-based tracking experiment. [(g)–(i)] Results from 1 Hz kV-based tracking experiment.

The reason for the recurring requests of nearly identical MLC adjustments during the kV-based tracking is that each requested MLC adjustment was an integer value of the 0.216 mm kV imager pixel length. Therefore, several tens of MLC adjustments of N×0.216 mm (N=1,2,3,4,5,6) occurred during the experiment with 2 Hz kV-based tracking [Figs. 3a, 3b, 3c, 3d, 3e, 3f]. Similarly, MLC adjustments of 1.95 (9 pixels), 4.99 (23 pixels), and 6.29 mm (29 pixels) occurred frequently during the experiment with kV imaging at 1 Hz [Figs. 3g, 3h, 3i].

In this study, we will assume that the MLC dynamics were identical for all requested adjustments of a given magnitude Δx in an experiment. Consequently, the MLC motion for an adjustment Δx can be estimated by a curve that crosses all the line segments in Figs. 3a, 3b, 3c, 3d, 3e, 3f, 3g, 3h, 3i. In this way, the MLC adjustment can be analyzed with a time resolution that is considerably finer than the 50 ms resolution of the Dynalog files. In order to quantify T_MLC, the following functional form was assumed for the MLC adjustment Δx:²³ (1) (Large Δx): Constant acceleration a followed by constant speed v_max and constant deceleration −a. (2) (Small Δx): Constant acceleration a followed by constant deceleration −a. The maximum leaf speed v_max was determined from the recorded MLC motion in 50 ms intervals in Dynalog files for large adjustments of several hundred ms duration. It was 3.60±0.08 cm∕s (one standard deviation). An adjustment Δx was categorized as “large” [i.e., functional form (1) above] if a fit to the functional form (2) resulted in violation of the 3.60 cm∕s speed limit.

For each adjustment size Δx, the MLC acceleration a and the MLC adjustment duration T_MLC were estimated by fitting this functional form to the experimental data.²³ Each fit was performed by minimizing the sum of squared distances between the fit function and the closest point on the line segments in Fig. 3. The resulting functional fits are shown as thick curves in Fig. 3.

Average latency measured by portal images

The synchronization method in this study allowed determination of the average latency τ_av by Eq. 3. For comparison, the average latency was also quantified by a previously applied method based on the phase difference between target motion and MLC motion in the portal images.^{9, 13} The advantage of this method is that no data stream synchronization is needed as both the target and the MLC position are captured and visible in the MV images. For MV-based tracking, the MV image frequency was the one under investigation (1, 2, 5, or 6.67 Hz). For kV-based tracking, the MV image frequency was 5.2 Hz.

The latency quantified by this method will be termed the “latency in MV images” in this paper. It is equal to τ_av in Eq. 3 provided that the latency captured in the MV images is a good representation of the average latency. This might not be the case for MV-based tracking because the MV images always will be acquired at the same location relative to the staircase-shaped MLC motion in Fig. 2b, e.g., close to point A (giving an underestimation of τ_av) or close to point B (giving an overestimation of τ_av).

RESULTS

MLC adjustment duration

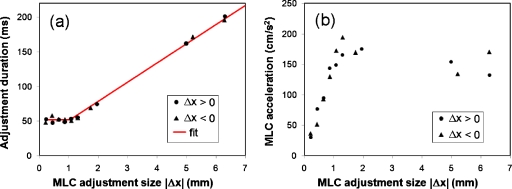
The measured and fitted MLC aperture positions during MLC adjustment were shown in Fig. 3. The adjustment duration T_MLC was around 50 ms for the six smallest adjustment sizes Δx (0.22–1.30 mm) and started to increase for the larger Δx. Figure 4 shows T_MLC and the acceleration a as estimated by functional fits for both the nine positive MLC adjustments in Fig. 3 and nine negative adjustments. The nearly constant T_MLC for |Δx|≤1.3 mm [Fig. 4a] was caused by a large decrease in the MLC acceleration with decreasing |Δx| [Fig. 4b]. The curve in Fig. 4a is a piecewise linear fit to the T_MLC with confined slopes of 0 for small |Δx| and 1∕v_max for large |Δx|. The functional form is

$${\text{T}}_{\text{MLC}}=\{\begin{array}{ll}52\text{ms}\hfill & \text{for}0<\left|\Delta \text{x}\right|<1.05\text{mm}\hfill \\ 23\text{ms}+\frac{\left|\Delta \text{x}\right|}{v_{\text{max}}}\hfill & \text{for}\left|\Delta \text{x}\right|\ge 1.05\text{mm}\hfill \end{array}\phantom{\}}.$$ (4)

In the following it will be assumed that T_MLC can be estimated by Eq. 4 for all Δx in the experiments.

Figure 4.

(a) MLC adjustment duration T_MLC and (b) MLC acceleration a determined by functional fits to the nine positive MLC aperture shifts in Fig. 3 (circles) and nine similar negative MLC aperture shifts (triangles). The curve in (a) is a piecewise linear fit to T_MLC.

Latencies

Figure 5 shows the sinusoidal target motion and the MLC aperture center position in four DMLC tracking experiments based on kV or MV imaging with imaging frequencies of 6.67 and 1 Hz. The latency was larger for kV imaging than for MV imaging and it increased markedly with the imaging interval ΔT_image. Table 1 summarizes the latency contributions and the average latency in MV images for all eight experiments. The image interval ΔT_image was equal to the nominal value of 1∕frequency for all experiments except low frequency MV-based tracking (1 and 2 Hz). Here, ΔT_image was slightly larger due to occasional beam-holds when the target motion between subsequent images exceeded 5 mm. Large motion between subsequent images was also the reason for the prolonged marker segmentation duration for both kV and MV imaging at 1 Hz: If the marker segmentation program did not find the marker in a confined region of 41 pixels×41 pixels centered at the previous marker position, then it extended its search to a larger (and more time consuming) region. The MLC adjustment duration was essentially identical for kV and MV tracking at the same imaging frequency. It increased with the decreasing imaging frequency because of larger MLC adjustments between subsequent images. On the other hand, the latency contributions from image file opening and MLC position calculation did not depend on the imaging frequency.

Figure 5.

Sinusoidal target motion and synchronized motion of MLC aperture center during tracking based on MV or kV imaging at 6.67 Hz (thin staircase curves) and at 1 Hz (thick staircase curves).

Table 1.

Mean and standard deviation of latency contributions. All units are milliseconds.

Image frequency (Hz)	MV-based tracking				kV-based tracking
	6.67	5	2	1	6.67	5	2	1
0. Image interval ΔTimage	150±0	200±0	502±1	1016±3	150±0	200±0	500±0	1000±0
1. Image acquisition and file writing	272±10	313±13	410±16	826±23	309±18	359±12	624±12	1126±13
2. Image file opening	36±7	35±7	35±7	38±8	39±8	40±8	39±8	39±8
3. Marker segmentation	4±7	5±7	5±7	12±16	4±7	4±7	3±6	22±17
4. MLC position calculation	16±6	17±11	19±11	18±9	16±5	14±7	17±7	15±9
5. MLC adjustment	52±0	54±3	82±23	137±61	52±0	53±3	82±22	134±51
Min latency τmin [Eq. 1, sum of 1–5 above]	380±9	420±12	550±26	1030±66	420±12	470±11	770±24	1340±54
Max latency τmax [Eq, 2, sum of 0–4 above]	480±9	570±12	979±17	1910±39	520±12	620±11	1180±24	2200±54
Calculated average latency τav [Eq. 3]	430±9	500±12	760±17	1470±39	470±12	540±11	970±15	1770±42
Measured latency in MV images	450	490	820	1270	480	550	980	1790

As seen in Table 1, a considerable part of τ_min (between 72% and 84%) was caused by image acquisition and file writing to the hard disk. Linear fits resulted in the following mean durations of image acquisition and file writing: 160 ms+0.63×ΔT_image for MV images and 160 ms+0.95×ΔT_image for kV images.

The two last rows in Table 1 compare the average latency as calculated from Eq. 3 to the latency observed in MV images. The two latency estimations showed good agreement for all kV frequencies and for MV-based tracking at 5 and 6.67 Hz. For less frequent MV imaging (1 and 2 Hz), some discrepancies between the two methods occurred because the latency captured in the low frequency MV images gave a poor representation of the average latency between the target and the MLC. As an example, the MV images at 1 Hz tended to capture the MLC aperture near the end of the MLC aperture adjustments [point A in Fig. 2b], which resulted in the underestimation of the average latency.

DISCUSSION

In this study, a method for detailed time and latency analysis in image-based DMLC tracking was developed. Knowledge of individual latency contributions is essential in order to reduce the latency, which is the major error contributor in image-based DMLC tracking of respiratory motion.¹⁶ A relationship between the individual latency contributions and the average system latency τ_av was derived, showing that the MLC adjustment duration T_MLC and the image interval ΔT_image contribute with at factor of 0.5 to τ_av while the signal processing duration T_signal contributes with a factor of 1 [Eq. 3]. Although this result was derived for image-based DMLC tracking, it applies in general for any tracking system when the beam-target alignment duration (T_MLC in this study) is shorter than the target position sampling interval (ΔT_image in this study). The current study did not investigate the case where the beam-target alignment duration is longer than the position sampling interval. Here, τ_av will depend on the response of the tracking system to new alignment requests arriving during an alignment procedure. Since T_MLC was 50 ms or longer for the current prototype DMLC tracking system, this situation occurs for DMLC tracking based on target localization frequencies above 20 Hz such as for electromagnetic transponders^{10, 11} or an optical marker.⁹

A prediction algorithm for latency compensation should have a look-ahead time equal to the average latency τ_av in Eq. 3 and not simply the time interval from image acquisition to completed MLC adjustment [τ_min in Eq. 1]. If the prediction algorithm only compensated for the time interval from image acquisition to completed MLC adjustment, the MLC would just catch up with the target at the moment of completed MLC adjustment. Then the MLC would stand still until the arrival of the next position measurement while the target would move ahead of the MLC. The MLC would fluctuate between being synchronized with the MLC and lagging behind the MLC. Instead, the prediction look-ahead time should be equal to the τ_av, causing the MLC to fluctuate between being ahead of the MLC and lagging behind the MLC.

The largest latency contribution of the investigated tracking system was image acquisition and image file writing. This contribution increased linearly with the imaging interval ΔT_image approximately being 160 ms+0.95×ΔT_image for kV images and 160 ms+0.63×ΔT_image for MV images. Extrapolation to ΔT_image=0 suggests that both imager systems used around 160 ms for image-frequency independent operations such as panel read-out, image correction, and image file writing. For kV imaging, the latency scaling with ΔT_image indicates that a kV image file was not written to the hard disk until the subsequent kV image had been acquired. It gives an unnecessary long delay that could easily be reduced with design improvements. It should be noted that the current imaging system was not designed for real-time tracking.

Unlike kV images, the MV images were exposed over an extended period approximately equal to ΔT_image. Therefore, a MV image contained information that already had a mean age of 0.5×ΔT_image right after completed exposure. We would therefore expect the time from MV image acquisition to completed image file writing to increase roughly as 0.5×ΔT_image. This is in reasonable accordance with our finding that the MV acquisition and file writing duration increased as 0.63×ΔT_image. Potential design improvements for MV images include a reduced image exposure duration that is independent of ΔT_image, which would reduce both latency and motion blurring in the images. Both kV and MV imaging would benefit from direct access to the memory of the imaging computer rather than image file writing to and reading from the hard disk.

MLC adjustment was the second largest contributor to the latency. The MLC adjustment duration was constant around 52 ms for adjustments below ∼1.1 mm and increased linearly with the distance to travel for larger adjustments. Since this variation is predictable, it might be incorporated into prediction algorithms for improved performance. The constant adjustment duration for small MLC adjustments is a consequence of the current MLC system being designed for the delivery of predefined MLC sequences. Here, the MLC system knows the planned MLC positions 50 ms ahead of time and aims at reaching these positions in 50 ms. For tracking, the system should instead aim at reaching the MLC positions as fast as possible.

The latency analysis in this work agrees with previous average latency measurements based on portal images (450 ms latency for 6.67 Hz kV∕MV-based tracking¹³ and 570 ms latency for 5 Hz kV-based tracking¹⁴). Compared to the portal image measurements, the present method provides substantially more details and it extends the applicability to low frequent MV-based tracking, where the portal imaging method fails (cf., Table 1). Although the proposed method was used for image-based tracking the synchronization method could be applied for tracking based on any real-time target position signal if a radio-opaque marker is placed on the target for target-MLC synchronization.

Synchronization of target motion and MLC motion is a critical component to verify the accuracy of treatment delivery in DMLC tracking. While continuous portal imaging provides a straightforward way to achieve this goal, the temporal and spatial resolution of the MV images is often limited. In this sense, the proposed synchronization of target motion with MLC log file information provides record and verify of tracking treatments in a highly accurate way. The resulting knowledge of the mutual motion of target and MLC could be an important tool for reconstruction of the delivered target dose during DMLC tracking.

A limitation of this study was the relatively coarse time resolution of 15.625 ms in the tracking log files. For this reason, the MLC dynamics was modeled very simply by a universal maximum speed that was independent of the requested adjustment size Δx and an acceleration that did depend on Δx. This analysis was sufficient for our purpose of estimating the MLC adjustment duration on a ms time scale. However, a better time resolution in the tracking log files and a more systematic study of MLC adjustments would allow more detailed investigation of the MLC dynamics assessing, for example, differences between acceleration at motion start and deceleration at motion end²³ as well as overshooting of the MLC motion.

CONCLUSION

A method for detailed latency analysis of each individual real-time position signal for DMLC tracking was developed and applied for image-based tracking. This method allows identification of major contributors to latency and therefore a focus for reducing this latency. The method enables analysis of the MLC dynamics on a time scale that is much finer than the time resolution of the MLC log files. It could be an important tool for reconstruction of the delivered target dose during DMLC tracking.