Optimizing principal component models for representing interfraction variation in lung cancer radiotherapy

Abstract

Purpose: To optimize modeling of interfractional anatomical variation during active breath-hold radiotherapy in lung cancer using principal component analysis (PCA).

Methods: In 12 patients analyzed, weekly CT sessions consisting of three repeat intrafraction scans were acquired with active breathing control at the end of normal inspiration. The gross tumor volume (GTV) and lungs were delineated and reviewed on the first week image by physicians and propagated to all other images using deformable image registration. PCA was used to model the target and lung variability during treatment. Four PCA models were generated for each specific patient: (1) Individual models for the GTV and each lung from one image per week (week to week, W2W); (2) a W2W composite model of all structures; (3) individual models using all images (weekly plus repeat intrafraction images, allscans); and (4) composite model with all images. Models were reconstructed retrospectively (using all available images acquired) and prospectively (using only data acquired up to a time point during treatment). Dominant modes representing at least 95% of the total variability were used to reconstruct the observed anatomy. Residual reconstruction error between the model-reconstructed and observed anatomy was calculated to compare the accuracy of the models.

Results: An average of 3.4 and 4.9 modes was required for the allscans models, for the GTV and composite models, respectively. The W2W model required one less mode in 40% of the patients. For the retrospective composite W2W model, the average reconstruction error was 0.7±0.2 mm, which increased to 1.1±0.5 mm when the allscans model was used. Individual and composite models did not have significantly different errors (p=0.15, paired t-test). The average reconstruction error for the prospective models of the GTV stabilized after four measurements at 1.2±0.5 mm and for the composite model after five measurements at 0.8±0.4 mm.

Conclusions: Retrospective PCA models were capable of reconstructing original GTV and lung shapes and positions within several millimeters with three to four dominant modes, on average. Prospective models achieved similar accuracy after four to five measurements.

INTRODUCTION

Treatment-related normal tissue toxicity is a major concern in lung cancer radiotherapy, whether in hypofractionated treatment for early stage disease^{1, 2} or in conventional fractionation for locally advanced cases.^{3, 4} Mitigating the effect of respiration-induced tumor motion—with a variety of techniques such as gating, tracking, or breath-hold—can reduce the amount of normal tissue irradiated.^{5, 6, 7, 8} However, day-to-day changes in respiration and mean tumor position within the lung^{9, 10, 11, 12} cannot be directly managed with these same techniques (except, potentially, by tracking). Instead, direct localization of the soft-tissue target afforded by image guidance is required and can reduce the required margin by several millimeters.^{13, 14, 15}

Existing online image guidance tools correct for localization error by shifting the patient position, presuming a rigid target object. However, shape and volume change of the tumor (due to therapeutic response) and normal anatomy are not well-controlled with couch corrections prior to treatment. Several options to manage the residual variability (after correction of rigid error) currently exist including accounting for the residual variability explicitly in a margin¹⁶ and implicit compensation with probabilistic treatment planning.^{17, 18, 19} Furthermore, shape and volume variation during treatment varies substantially between patients,^{20, 21, 22, 23, 24, 25} which implies that adaptive replanning to compensate for patient-specific volume and shape change may be important for managing residual variability in lung radiotherapy.

Both probabilistic treatment planning and adaptive radiotherapy require a means to accumulate and evaluate dose in deforming anatomy. Acquired patient images can be used for such a purpose, but this places a large radiographic dose and time burden on the patient and makes the planning process unnecessarily complex and resource intensive. Statistical patient models that can be efficiently and easily updated as new information about the patient becomes available would reduce these burdens by enabling construction of likely anatomical poses of a given patient directly from the model. Furthermore, as accumulated error could quickly overwhelm the benefit of the adaptation, statistical models that are relatively insensitive to imaging and registration error are highly desirable.

A variety of statistical models have been explored,^{26, 27, 28, 29, 30, 31, 32, 33} with statistical shape model (SSM) or statistical deformation model (SDM) meeting the requirements denoted above. Both are statistical representations of the patient anatomy over time, where small, uncorrelated displacements that likely represent error have been removed from the models. SSM and SDM differ in that SSMs track homologous point locations between surfaces (i.e., of organs or tumors) whereas SDMs track voxel locations between images. SSMs have been previously used to model patient-specific geometric variation in radiotherapy.^{31, 34} Söhn et al.³¹ proposed a SSM as a simple model of geometric variability for adaptive radiotherapy in prostate cancer. Zhang et al.³³ proposed a patient-specific SDM as a free-breathing respiratory model that parametrized the 3D deformation fields with a surrogate signal.

While the general use of SDM or SSM as a patient model for adaptive radiotherapy has been introduced, the model requirements including the number of dominant statistical modes that must be used, the required number of samples, and the sampling frequency have not been defined. Furthermore, most models to date have been formed for pelvic organs or for intrafraction thoracic motion. For lung cancer and other regressing tumors, time-trends in tumor volume change may place greater demands on the modeling requirements.

The purpose of this study is to optimize an SSM approach for lung cancer in terms of model accuracy by evaluating the number of principal components (termed in this study as dominant eigenmodes that are ordered with respect to variation), number of samples, sampling frequency, and update requirements. A population of active breathing control (ABC) patients was used, as high-frequency CT imaging during radiotherapy exists in these patients, image artifact is minimal, and deformable image registration results are of good quality. Multivariate statistical principal component analysis (PCA) was used to determine the most dominant modes of correlated motion and deformation of tumor and lung surface geometries during radiotherapy treatment. Multiple models were generated for each patient and used to assess sensitivity and accuracy in reconstructing original structures.

METHODS

Data acquisition and delineation

Sixteen patients with locally advanced nonsmall cell lung cancer undergoing curative radiotherapy gave informed consent and were enrolled on a trial to perform weekly helical CT imaging during treatment. During simulation and once per week of treatment, CT images were acquired using an ABC technique at the end of normal inspiration. Three CT scans were acquired to assess breath-hold reproducibility during each session; the total number of images acquired for each patient varied from 12 to 21 (corresponding to 4–7 weeks of treatment) over all patients. The CT voxel size was 1.2×1.2×2.0 mm³. The scanning and breath-hold protocol is described in detail in Ref. 23. A physician delineated the gross tumor volume (GTV) and each lung separately on the first breath-hold CT image from the first week, which was defined as the reference image using the research version of a commercial treatment planning system (PINNACLE v8.1x, Philips Oncology, Fitchburg,WI). A small deformation, inverse consistent, linear elastic deformable registration algorithm³⁵ was used to register each image to the first CT image acquired during the first week. The GTV and lung structures delineated on the reference image were propagated using the registration to all other images by its corresponding displacement vector field (DVF). The resulting deformed structures were reviewed by the same physician. This method provided homologous point correspondence for GTV and lung structures between all images and a representation of the change in each structure shape and position over time. This homologous point correspondence specifies the movements of the different structure surface points over treatment time.

Principal component modeling of interfraction variation

A PCA was performed on the structure surface points following the method of Söhn et al.³¹ For each delineated image, surface point positions were formed into a vector p,

$$\mathbf{p}={\left[x_1{y}_1{z}_1{x}_2{y}_2{z}_2\dots x_M{y}_M{z}_M\right]}^T,$$ (1)

where x, y, and z in Eq. 1 are the coordinates of the point location (position), M is the number of surface points, and the dimensionality of p is 3M. If a vector p is generated for each image for an individual patient, this vector can be thought of as a time-varying vector p(t) for each patient. Entries of vector p at different times hold coordinates of the corresponding points. Since only the observed instances of p are available at the discrete time points at which images are acquired, a set of N vectors {p(t₁),p(t₂),…,p(t_N)} was created, representing the discrete instances of the observed anatomy over the treatment course. For an individual structure, such as GTV, ipsilateral lung (IL), or contralateral lung (CL), the dimensionality of p was M_GTV, M_IL, or M_CL, respectively, which varied between patients. Modeling deformation∕motion of more than one structure, a vector p_all was created that contained concatenated points of M_GTV, M_IL, and M_CL. The dimensionality of the composite vector p_all was 3(M_GTV+M_IL+M_CL), which represents the composite geometry of the structures under consideration.

PCA decomposes and reassembles p(t) into the mean vector (over time) plus the sum of a set of orthonormal basis functions for reconstruction as

$$\mathbf{p}\left(\mathit{t}\right)=\overline{\mathbf{p}}+\sum _{\mathit{l}=\mathbf{1}}^{\mathit{N}}{\mathit{c}}_{\mathit{l}}\left(\mathit{t}\right){\mathbf{q}}_{\mathit{l}},\parallel {\mathbf{q}}_{\mathit{l}}\parallel =\mathbf{1},$$ (2)

where $\overline{\mathit{p}}$ in Eq. 2 is the mean of p(t) over time (for the number of images N used in each model), {q₁,q₂,…,q_N} is the set of orthonormal basis vectors, {c₁(t),c₂(t),….,c_N(t)} is the set of principal component (PC) coefficients (or PC weights) that reconstruct each specific time instance t of p(t), and N is the number of statistically independent modes of deformation that is equal to the number of sample geometries in the model. Each basis vector q_l, along with its corresponding variance, represents a mode of statistically independent deformation. The mode variance is the variance of the N original geometry samples projected on the lth eigenvector. In PCA, the modes are ordered by decreasing variance, with mode l=1 capturing the largest correlated variance in the model.

Assuming that the variabilities of interest (e.g., respiration, tumor regression, and other true anatomical shape and volume changes) are large compared to the errors in model construction (e.g., imaging artifact, discrete low-frequency sampling of the anatomy, and deformable registration error), a reduced model can be formed by keeping only the L dominant modes (L<N) that represent some portion of the variability by taking the summation in Eq. 2 from l=1 to L,

$${\mathbf{p}}^{\prime }\left(\mathit{t}\right)=\overline{\mathbf{p}}+\sum _{\mathit{l}=\mathbf{1}}^{\mathit{L}}{\mathit{c}}_{\mathit{l}}\left(\mathit{t}\right){\mathbf{q}}_{\mathit{l}},$$ (3)

where p^′(t) is the reconstructed instance of the anatomy at time t from the reduced model. Essentially, uncorrelated and small magnitude variability (assumed to be error) is truncated from the model. In this study, reduced models were formed from modes representing at least 95% of the variability.

PCA was performed by singular value decomposition (SVD). The mean geometry $\overline{\mathit{p}}$ was calculated by averaging the corresponding homologous points across all N samples. The surface point vectors were centered around the mean and scaled by $1∕\sqrt{N-1}$,

$$\mathbf{d}\mathbf{p}\left(\mathit{t}\right)=\frac{\mathbf{1}}{\sqrt{\mathit{N}-\mathbf{1}}}{\left(\mathbf{p}\left(\mathit{t}\right)-\overline{\mathbf{p}}\right)}^{\mathit{T}},$$ (4)

where dp(t) is the mean-centered surface point vector describing the displacements of the geometry at any time t. Next, the set of mean-centered vectors is formed to create the mean-corrected variability matrix DP,

$$\mathbf{D}\mathbf{P}=\left\{\mathbf{d}\mathbf{p}\left({\mathit{t}}_1\right)\left|\dots \dots \right|\mathbf{d}\mathbf{p}\left({\mathit{t}}_{\mathit{N}}\right)\right\}.$$ (5)

Here, DP is the mean-centered anatomical variability matrix of dimension 3M×N and contains the homologous displacement point sequence through N weekly samples.

SVD and PCA are related, and SVD provides a computationally efficient method of finding the PCs, as illustrated by Jolliffe.³⁶ PCA (as used by Söhn et al. and others) decomposes the covariance matrix of the organ geometry samples into eigenmodes, while SVD directly decomposes the mean-centered and corrected anatomical variability matrix, DP, as follows:

$$\mathbf{D}\mathbf{P}=\mathit{US}{\mathit{V}}^T,$$ (6)

where S is a diagonal, square matrix of singular values of dimension N×N, with non-negative diagonal elements in decreasing order, U is a matrix of dimension 3M×N containing the orthogonal eigenvectors basis set {q_l}, in its leftmost columns, and V is an orthogonal (V⁻¹=V^T) matrix of dimension N×N. The SVD MATLAB (MathWorks version 7.6.0.324, R2008a) implementation³⁷ was used here. As 3M>N, we used the economy size decomposition for fast implementation directly on the DP matrix without reduction, smoothing, or further processing to our raw data. The eigenvector basis set, {q_l}, l from 1 to L, which are orthonormal, represent a new coordinate system with reduced dimensionality. The singular values along the diagonal of S are equal to the eigenvalues λ_l calculated by the standard PCA decomposition of the covariance matrix as in Söhn et al. Each λ_l is the statistical variance $\left({\mathbf{\sigma }}_{\mathit{l}}^{\mathbf{2}}={\lambda }_{\mathit{l}}\right)$ of the N original geometry samples projected on the lth eigenvector as a new basis vector. Eigenvalues resulting from the SVD algorithm after multiplying the original centered vector by $1∕\sqrt{N-1}$ in Eq. 4 are equal to that resulted from a covariance matrix (as the standard PCA approach illustrated in Söhn et al. and others). The SVD algorithm is computationally efficient in dealing with vectors of long length as it computes only the first N columns of U.

Retaining the eigenvectors associated with the largest eigenvalues (λ_l), the M-dimensional structure model can be represented in a lower-dimensional subspace. Generally, this is formulated by calculating the cumulative sum of variance values that is larger than some fraction of the total sum of variance values. In this way, the lower-dimensional subspace defined by the retained eigenvectors (L) can be said to capture a percentage of cumulative variance. In this framework, we aimed to capture at least 95% of the cumulative variance, as stated above, which required retaining only a few eigenvectors.

Equation 3 is used to reconstruct each instance of the observed geometry p(t) to form a reconstructed geometry p^′(t). To do so, the PC coefficients c_l(t) must be determined. The standard method used by Söhn et al. was followed, whereby the weights are the dot product of the mean-centered surface point vector and the basis vector,

$${\mathit{c}}_{\mathit{l}}\left(\mathit{t}\right)=\left(\mathbf{p}\left(\mathit{t}\right)-\overline{\mathbf{p}}\right)\cdot {\mathbf{q}}_{\mathit{l}}.$$ (7)

This process of Eq. 7 is repeated for l=1 to L in order to get the set of PC coefficients for all dominant modes.

Experimental model parameters

Models were formed for each individual structure (GTV, RL, and LL), and a composite model was formed using all structures simultaneously (using p_all). For each individual structure and for the composite structure model, two PCA models were created for each patient: The first consisted of a single first image from each weekly session (N=4→7 images per patient and will be termed W2W). Thus, the W2W model included interfraction variability. The second (termed as allscans) consisted of all three repeat images per weekly session (N=12→21 samples per patient). Thus, the allscans model included intrafraction variation due to breath-hold to breath-hold variation in addition to interfraction variability. Thus, a total of four models was generated for each patient.

• (1)Individual models for the GTV and each lung from one image per week (W2W);
• (2)A composite model of all structures (GTV, lungs) together from one image per week (W2W);
• (3)Individual models using all images (allscans); and
• (4)Composite model using all images (allscans).

All models were constructed retrospectively, meaning that the model was constructed after all data were acquired for the patient, at the end of treatment, using imaging from all weeks of treatment.

Retrospective modeling is useful for analysis of the existing data, but is of little use for patient-specific adaptation as the adaptation must be performed while the patient is still under treatment, unless a model can be formed from limited data early in treatment and then holds throughout the treatment course. For adaptive radiotherapy, future data are obviously not available for incorporating into the model. To simulate this limitation, we developed a method for prospective modeling. A prospective or “updatable” model could be formed from early data and then updated with new modeling data, and the model regenerated, as new data become available upon treatment. To evaluate these two different models, we constructed prospective models by changing N, starting with N=2 (first 2 weeks of treatment for the W2W model) or N=6 (first 2 weeks for the allscans model), and creating models by incrementing N until the retrospective model was achieved (where N is the maximum number of images available for each model).

Residual error in the model was calculated by reconstructing the shape of the GTV and lungs from each of the PCA models and comparing the point locations in the reconstructed structures to the locations in the original, observed structures (samples used for PCA modeling). Euclidean surface distance measure between corresponding points in original and reconstructed geometries was used to calculate the residual error. The local residual error is the error between the corresponding reconstructed point position and the observed point position for one sample vector of M points. The average local residual error is calculated by averaging residual errors of N local sample vector residual errors (at the corresponding points). Overall average residual error is averaging error over all M points of average local residuals. Overall average residual error is considered as a measure of quality of PCA reconstruction.

Two types of residual errors were calculated. For the first type—which we term the training error—the reconstruction errors were calculated using only the data that generated the model. The second error type, the testing error, is the reconstruction error calculated from all available data, whether or not used for modeling. For example, for a given patient with 6 weeks of imaging, PCA models were generated and reconstruction error calculated using the first 3 weeks data for the training error and then residual error evaluated with the full 6 weeks dataset to calculate the testing error. Overall residual errors and standard deviations for reconstruction using only L dominant modes were calculated and compared between the four models.

RESULTS

Twelve of the 16 patients enrolled were analyzed. One patient was excluded due to the development of a collapsed lung and another due to treatment termination after 1 week. Neither development was study related. Two patients were excluded due to the inability to obtain accurate deformable registration results. Table 1 shows population characteristics of GTV volume (cc), number of surface points (M) for GTV and composite models, tumor location, tumor stage, and number of weeks of imaging for the 12 analyzed patients. Distance between contour points in mm varies from case to case due to the manual delineation, where complex, irregular axial contours require more points to model. For example, patient 1 GTV has 26 contours (5.2 cm maximum length) of 1624 total points, which translates to an average of 62 points per contour in a slice.

Table 1.

Study population characteristics. Only the 12 patients analyzed are included here.

Subject	GTV volume (cc)	M, GTV only	M, composite model	Tumor location	Stage	Weeks of imaging
1	23.8	1624	75 436	LUL	IIIA (T2N2M0)	6
2	100.3	5215	91 553	Bilat+mediastinum	IIIB (T4N2M0)	6
3	65.0	2675	69 056	LLL	IIB (T2N1M0)	7
4	0.6	127	70 301	RUL∕supraclavicular	IIIB (T1N3M0)	6
5	241.9	8389	63 263	RLL	IIIA (T2N2M0)	5
6	11.3	851	88 366	RUL	IIB (T2N1M0)	4
7	40.1	1246	47 898	RUL	IIIA (T2N2M0)	5
8	80.2	3394	99 388	Bilat	IIIB (T4N1M0)	7
9	37.4	2318	72 594	RML	IIIA (T2N2M0)	5
10	376.4	14796	135 572	LUL	IIIA (T3N2M0)	5
11	74.0	2470	63 795	LUL	IIA (T1N1M0)	6
12	216.2	5864	97 452	RUL	IIIA (T3N1M0)	7
Mean	105.6	4081	81 223
SD	114	4114	22 996

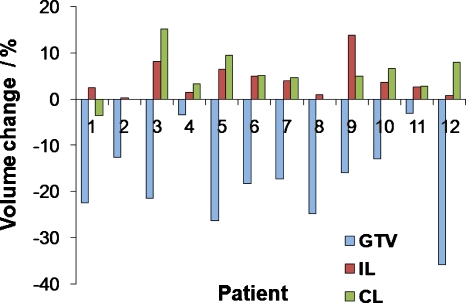
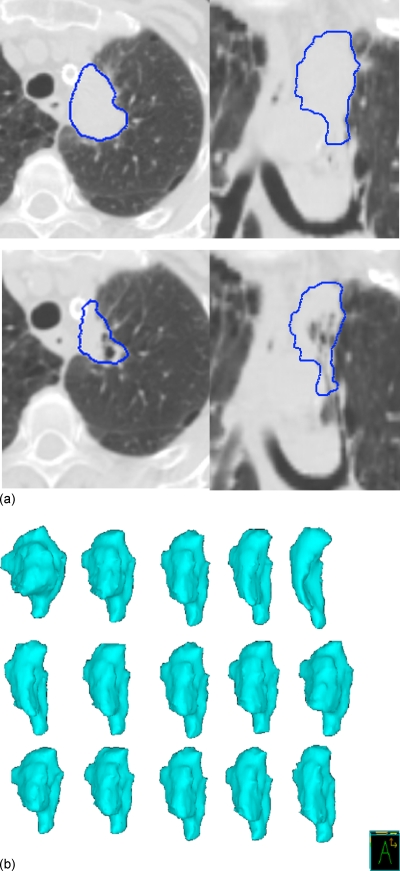
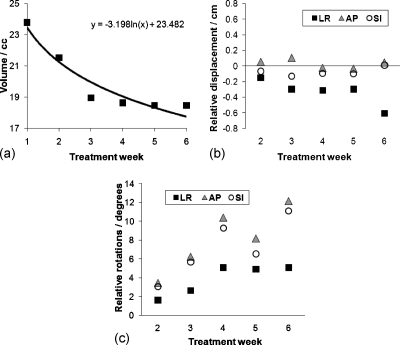
Figure 1 shows the volume change during treatment for all 12 patients for all individual structures (GTV, ipsilateral lung, and contralateral lung). As evident from Fig. 1, the amount of volume change was patient specific; GTVs were of different size, shape, and location. Tumor shrinkage was evident in most patients and showed an exponential decaying trend that varied from patient to patient. Relative displacement and volume regression in this subject population was explored in more detail in Ref. 23. Structures during treatment demonstrated various types of transformations such as translational shifts (measured by centroids), rotations (measured around principal axes), and deformations (volume and shape change). Figure 2 shows CT images of an example subject with a left upper mediastinal tumor with visualization of individual W2W GTV structure first three dominant deformation modes, shown as $\left(\overline{\mathit{p}}-3{\sigma }_l\cdot {\mathit{q}}_l\right)$, $\left(\overline{\mathit{p}}-{\sigma }_l\cdot {\mathit{q}}_l\right)$, $\overline{\mathit{p}}$, $\left(\overline{\mathit{p}}+{\sigma }_l\cdot {\mathit{q}}_l\right)$, and $\left(\overline{\mathit{p}}+3{\sigma }_l\cdot {\mathit{q}}_l\right)$ 3D models reconstructed by deforming the mean geometry $\overline{\mathit{p}}$ by its respective scaled eigenvector q_l. The tumor had a volume reduction of 22.4% from the first to sixth week of treatment. Figure 3 shows the change in volume of the GTV over treatment for subject 1, with logarithmic fit with parameters (y=−3.198 ln(x)+23.482), where y is the volume (cc) and x is the treatment week index.

Figure 1.

Volume change (%) from fifth to first week of treatment for GTV, IL, and CL. For patient 6, the volume change after the fourth week of treatment is shown, as this patient did not have imaging on the fifth week.

Figure 2.

Breath-hold images from an example subject. (a) Top: First week of treatment. Bottom: Sixth week of treatment. The GTV is delineated in each image. (b) First three dominant modes of the W2W retrospective GTV model from six weekly geometries. Each row on the right shows deformation modes $\left(\overline{\mathit{p}}-3{\sigma }_l\cdot {\mathit{q}}_l\right)$, $\left(\overline{\mathit{p}}-{\sigma }_l\cdot {\mathit{q}}_l\right)$, $\overline{\mathit{p}}$, $\left(\overline{\mathit{p}}+{\sigma }_l\cdot {\mathit{q}}_l\right)$, and $\left(\overline{\mathit{p}}+3{\sigma }_l\cdot {\mathit{q}}_l\right)$ reconstructed by deforming the mean geometry $\overline{\mathit{p}}$ by its respective eigenvector q_l scaled by the standard deviation σ_l.

Figure 3.

(a) GTV volume over treatment for subject 1 with logarithmic fit parameters shown. (b) The relative displacement of the GTV centroid, relative to week 1. (c) GTV rotations around the principal axes relative to week 1.

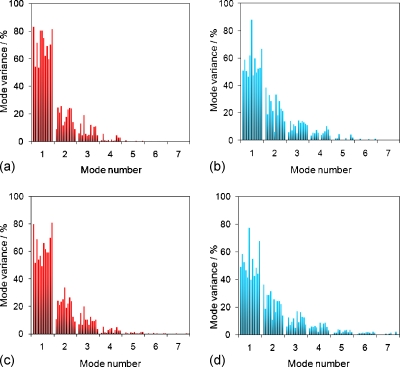
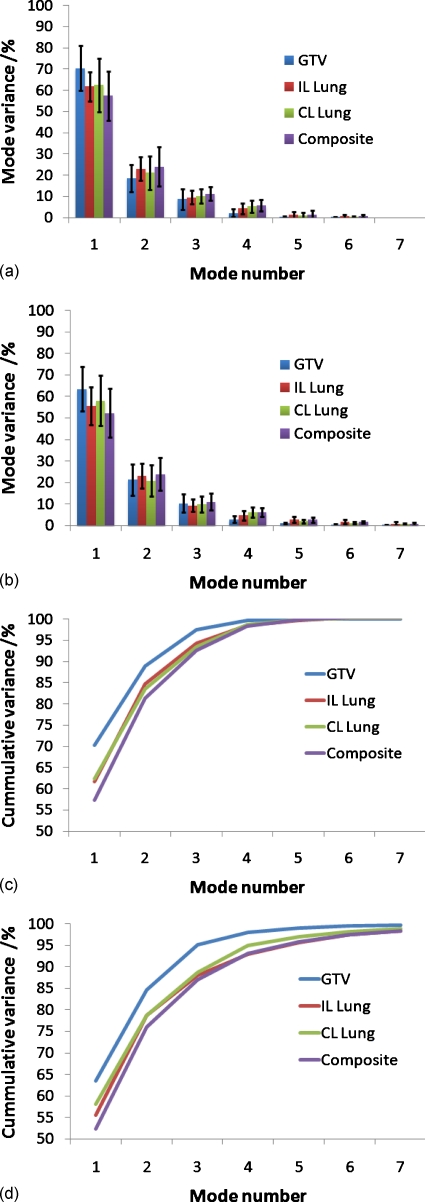
Figure 4 shows the PCA eigenvalue (variance) spectrum of the W2W and the allscans models for all subjects, for the GTV and composite retrospective models. All eigenvalues for the W2W models are shown, and only the first 7 eigenvalues (out of a maximum of 21) for allscans models are shown. The spectra between the W2W and allscans models had similar patterns for most patients.

Figure 4.

Eigenvalue spectrum (as percent of the total variance), retrospective models for all subjects. W2W (a) and allscans, displaying only first 7/21 modes (b), GTV only models. W2W (c) and allscans (d) composite models.

Figure 5 shows all patient’s mean and standard deviation of the eigenvalue spectrum and its cumulative variance for all individual (GTV and CL and IL lungs) and composite structures. Two to seven eigenmodes were necessary to capture at least 95% of the variability over all patients (Table 2). For the GTV only models, the average number of principal components increased from 2.9 for the W2W model to 3.4 for the allscans model due to the increased burden of modeling intrafraction variability in the allscans model. The W2W model required one less mode in 6 of 12 patients, and the same number of modes in the remaining 6 patients for both the GTV and lung models. For the composite models, an average of 3.8 modes was required for the W2W models, compared to 4.9 modes for the allscans models. From Table 2, the number of principal components in the composite model is substantially less than the sum of the number of principal components from modeling structures individually. A mean reduction from 9.9 to 3.8 was obtained for the W2W models and from 12.6 to 4.9 for allscans models. This result implies some interaction and correlation between the individual structures.

Figure 5.

Average eigenvalue spectrum (variance of each mode as a percentage of the total variance) for the retrospective W2W (a), allscans displaying only first 7/21 modes (b), average cumulative variance W2W (c), and cumulative variance allscans.

Table 2.

Number of dominant modes, retrospective models of all individual, and composite structures.

Subject	W2W models (max N=7)					Allscans models (max N=21)
	GTV	IL	CL	Totala	Composite	GTV	IL	CL	Totala	Composite
1	3	3	4	10	3	3	3	4	10	4
2	3	4	3	10	4	3	4	4	11	4
3	3	4	3	10	4	3	4	4	11	4
4	3	4	4	11	4	3	5	4	12	5
5	3	4	3	10	4	4	5	5	14	5
6	2	3	2	7	3	3	5	2	10	4
7	3	3	3	9	3	4	5	4	13	5
8	3	4	3	10	4	3	7	5	15	7
9	3	4	4	11	4	3	5	4	12	5
10	3	3	4	10	4	4	4	4	12	4
11	3	4	4	11	4	4	7	7	18	7
12	3	3	4	10	4	4	4	5	13	5
Mean	2.9	3.6	3.4	9.9	3.8	3.4	4.8	4.3	12.6	4.9
SD	0.3	0.5	0.7	1.1	0.5	0.5	1.2	1.2	2.3	1.1

^a“Total” is the sum of GTV, IL, and CL from the individual models.

Table 3 shows the cumulative variance captured by the retrospective models. As the cutoff was 95% of the total variance, all models capture at least this percentage of the total variance. However, as an integer number of modes must be selected, some models capture a higher percentage of the variance. The average percentage of cumulative variance captured ranged from 96.4% (composite, allscans model) to 97.7% (GTV only, W2W model).

Table 3.

Cumulative variance captured by the dominant modes (percent of the total variance) corresponding to the number of modes in Table 2.

Subject	GTV only, W2W	Composite, W2W	GTV only, allscans	Composite, allscans
1	99.02	96.14	98.41	97.54
2	98.92	98.44	97.49	96.88
3	98.08	97.03	97.53	95.61
4	99.25	95.27	98.47	96.90
5	98.46	100	96.30	95.54
6	95.47	98.54	98.54	96.30
7	98.34	95.82	97.01	96.96
8	98.39	96.90	97.03	96.00
9	98.95	100	95.97	96.73
10	95.01	100	98.64	95.48
11	96.21	95.66	96.14	96.71
12	95.76	96.15	97.22	95.86
Mean	97.66	97.50	97.40	96.37
SD	1.57	1.81	0.96	0.67

Table 4 shows the mean testing error, and Table 5 shows the 90th percentile testing error (level at which 90% of the testing error was below) for the retrospective modeling (all available images used). The difference between the testing error and training error was minimal for the retrospective models, so only the testing error is presented here. For the composite W2W model, the mean testing error averaged over all patients was 0.7±0.2 mm, which increased to 1.1±0.5 mm when the allscans model was used. The 90% error level was 1.0±0.3 mm for the W2W model and 1.6±0.7 for the allscans model. If only the first four dominant modes from the weekly (W2W) model are used, 90% of the error was less than 3 mm for 11 of the 12 patients and less than 2 mm for 8 of the 12 patients. Comparing the individual models to the composite models, the 90th percentile error averaged over all patients and all individual structures was 1.2±0.3 mm for the W2W model, which was not significantly different from the testing error for the composite model (p=0.15, two-sided paired t-test). Similar results were observed for the allscan s models.

Table 4.

Mean residual testing error (mm) for each patient, for the retrospective composite model.

Subject	W2W model				Allscans model
	3 modes	4 modes	5 modes	All modesa	3 modes	4 modes	5 modes	All modesa
1	1.3	0.9	0.5	0.5	1.3	0.9	0.9	0.9
2	2.2	1.5	0.8	0.8	2.2	1.5	0.9	0.9
3	2.0	1.4	1.0	1.0	2.0	1.4	1.0	1.0
4	1.3	1.0	0.7	0.5	1.3	1.0	0.8	0.8
5	2.3	1.8	1.4	1.0	2.7	2.3	1.8	1.8
6	1.1	0.8	0.6	0.6	1.2	0.8	0.8	0.8
7	2.0	1.4	0.9	0.6	2.0	1.3	1.3	1.3
8	2.8	2.3	1.9	1.0	3.1	2.5	2.2	2.2
9	1.6	1.0	0.7	0.5	1.6	1.2	0.9	0.9
10	1.4	0.9	0.5	0.5	1.4	1.0	0.5	0.5
11	1.3	1.1	0.9	0.4	1.4	1.2	1.0	1.0
12	1.8	1.4	1.0	0.8	1.9	1.4	1.2	1.2
Mean	1.8	1.3	0.9	0.7	1.9	1.4	1.1	1.1
SD	0.5	0.4	0.4	0.2	0.6	0.5	0.5	0.5

^a“All modes” refers to all dominant modes (≥95% total variability).

Table 5.

90th percentile of residual testing error (mm) for each patient, for the retrospective composite model.

Subject	W2W model				allscans model
	3 modes	4 modes	5 modes	All modesa	3 modes	4 modes	5 modes	All modesa
1	2.0	1.5	0.8	0.8	2.0	1.5	1.5	1.5
2	3.8	2.1	1.3	1.3	3.8	2.1	1.4	1.4
3	2.7	2.1	1.4	1.4	2.8	2.1	1.4	1.4
4	1.8	1.4	1.0	0.6	1.8	1.5	1.1	1.1
5	3.1	2.4	1.8	1.2	3.8	2.9	2.3	2.3
6	1.7	1.2	0.9	0.9	1.7	1.2	1.2	1.2
7	2.7	1.9	1.2	0.8	2.8	2.2	2.2	2.2
8	4.0	3.4	2.8	1.6	4.4	3.9	3.3	3.3
9	2.3	1.6	1.2	0.7	2.3	1.9	1.4	1.4
10	2.1	1.3	0.8	0.8	2.1	1.5	0.7	0.7
11	1.8	1.4	1.2	0.6	1.9	1.7	1.5	1.5
12	2.8	2.0	1.6	1.2	2.9	2.1	1.7	1.7
Mean	2.6	1.9	1.3	1.0	2.7	2.1	1.6	1.6
SD	0.8	0.6	0.6	0.3	0.9	0.7	0.7	0.7

^a“All modes” refers to all dominant modes (≥95% total variability).

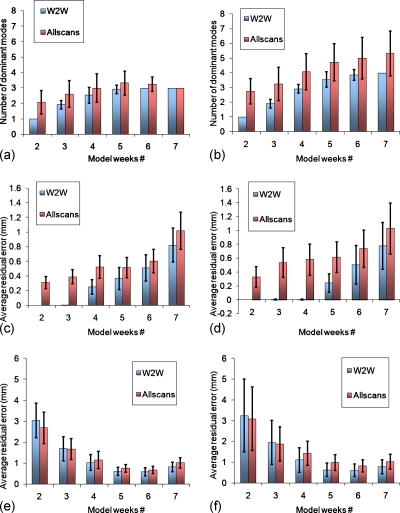
For the prospective models, Fig. 6 shows the average number of dominant modes and associated training and testing errors, for GTV and composite, and W2W and allscans models, for all 12 patients. As the number of weekly measurements increase, the number of dominant modes and the testing error demonstrated a marked stabilization for the GTV model at around four weekly measurements and three dominant modes. For the composite model, testing error stabilized at around 5 weeks but the number of dominant modes appeared to increase with weekly measurements without stabilizing. Modeling with the first four weekly images, the average testing errors were 1.2±0.5 mm for the GTV W2W and allscans models, and 1.3±0.6 mm for the composite models. At 5 weeks, the errors diverged slightly, with 0.9±0.3 mm for the GTV W2W and allscans models, 0.8±0.4 mm for the composite W2W model, and 1.1±0.4 mm for the composite allscans model.

Figure 6.

Prospective GTV (a) and composite (b) model dominant modes and the corresponding residual errors for training [(c) and (d)] and testing [(e) and (f)], averaged over all 12 patients.

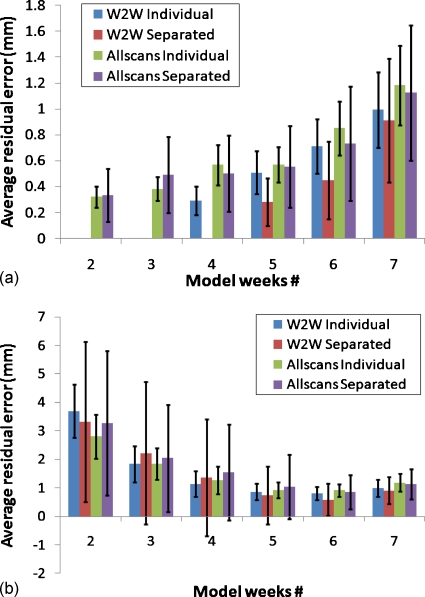
The residual error results for the composite model include error from the GTV and both lungs together. To compare the error in reconstructing the GTV alone between the individual and composite models, the residual error was calculated from the composite model for only the reconstructed GTV (lungs were excluded from the calculation). Figure 7 shows this comparison of average residual error between the individual GTV models and composite models (only GTV reconstructed). The residual error for GTV only as a substructure separated from composite model has higher average overall standard deviations values than the individual GTV models for both training and testing. The reason for the increased error is because the GTV represents only a small number of points in the composite model. Thus, it has less effect in modeling and therefore will have more error.

Figure 7.

Prospective GTV only (individual) and GTV separated from composite model (separated) training (a) and testing (b) errors.

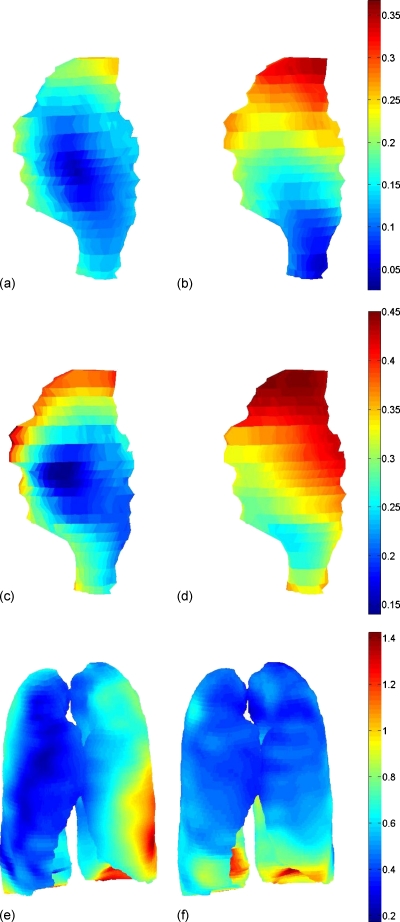
As an example, Fig. 8 visualizes training average residual error spatial distributions on the mean geometry shape of its corresponding models, all for patient 1. Figure 8 (left) shows the W2W individual GTV model (L=3, N=6) and W2W GTV only separated from its composite model (L=3, N=6) average residual errors. The middle row shows allscan individual GTV model (L=3, N=18) and allscan GTV only separated from its composite model (L=4, N=18) average residual errors. The bottom row shows W2W composite model (L=3, N=18) and allscan composite model (L=4, N=18) average residual errors. In all of the GTV models, the largest errors were distributed in the superior regions. For the composite models in the lungs, the largest errors were distributed in the inferior regions (near diaphragm) and mainly in the IL lung. These error distributions are specific to this patient 1 and vary from patient to patient, depending on the size of the tumor and its anatomical location.

Figure 8.

Average residual error distribution in mm for GTV and lung surfaces (retrospective models, training errors) of example patient 1, displayed on its corresponding mean shape. Top row: (a) W2W individual GTV (average overall error of 0.13 mm) and (b) W2W GTV only separated from its W2W composite model (average overall error of 0.2 mm). Middle row: (c) Allscans individual GTV (average overall error of 0.25 mm) and (d) allscans GTV only separated from its allscans composite model (average overall error of 0.36 mm). Bottom row: (e) Composite W2W model (average overall error of 0.5 mm) and (f) composite allscans model (average overall error of 0.52 mm).

For the GTV models that were reconstructed retrospectively including all dominant L modes, the volume percentage difference and centroid difference between the reconstructed GTV and the observed (original) GTV were computed. The average volumetric differences (between original and reconstructed GTVs over all patients, all samples) were 3.3±2.7% and 2.6±1.8% for W2W and allscans models, respectively. The average centroid differences were 0.2±0.2 and 0.2±0.1 mm for W2W and allscans models, respectively.

DISCUSSION

The results of this study demonstrate that complex geometric variations including gross tumor regression can be represented using only a few dominant modes from PCA due to the high degree of correlation in tumor and organ variability from day to day. Positions of tissue elements are highly correlated spatially as motion or deformation of one region of a structure generally is associated with motion or deformation of other regions. These results are in line with those of other groups,^{30, 31, 34} which demonstrate that geometric tissue variability during radiotherapy can be represented with a few dominant modes for error levels on the order of 1 mm. These other studies have been performed mainly on pelvic organs, which do not demonstrate substantial time-trends such as gross tumor regression. However, accounting for the interfraction deformations due to organ filling and emptying, which was not a factor in the current study, could offset the additional modeling required in the thorax for regression.

Including or excluding the effect of intrafraction change due to breath-hold to breath-hold variability (through the W2W and allscans models) made a minimal impact on the residual testing error. This result is likely due to the small breath-hold to breath-hold changes observed in this population in a previous study (breath-hold to breath-hold variation in the GTV position was less than 2 mm).²³ Using the W2W model, the out of sample structures from the repeat CT studies could be reconstructed, which implies that the dynamics of breath-hold to breath-hold variation is not substantially different than day-to-day variations.

Residual error for the individual organ and tumor models and the composite model was not significantly different. The dimensionality of the allscan composite model (around 4.9) is always larger than that of the GTV only model (around 3.4), as more modes are required to capture the additional lung variability. However, the composite model required less than the sum of the dominant modes for the individual structures (summing the number of dominant modes for the GTV only, IL only, and CL only models), which implies some interaction between the GTV and lungs, and between each lung in a patient. This result is as expected, as lung tumor motion during both free-breathing and breath-hold can be predicted to first order by changes in lung volume or diaphragm position.^{8, 33, 38, 39}

Retrospective modeling is useful for generating population statistics or analyzing the types and magnitude of correlated and uncorrelated variabilities. For example, one use of the retrospective model would be to classify and separate variabilities from different sources such as positional changes due to breath-hold level changes and volume change due to tumor regression. Prospective modeling is more suited to adaptive replanning and prediction, where the model would be used to estimate future target and organ shapes and adjust the treatment plan to compensate for such shape variation. It is important to note that we did not test the predictive strength of the prospective models in this study. The current study demonstrated that prospective models can be used to reconstruct known samples acquired at a later time. This result implies that the types and relative magnitudes of variabilities do not change much during treatment. For adaptation, the PCA model is generally used as a basis for a statistical model such as an SSM or an SDM. To do so, in the case of time-trends such as regression would require a time-trending predictive model to be incorporated into the strategy. As the results imply, the type of variability does not change much over the treatment course (since the prospective models could be used to reconstruct later samples), a predictive model of only the principal components may be sufficient. This hypothesis remains to be tested in a subsequent study.

Our SSM in this study was generated by extracting displacement vectors from a set of dense DVFs generated from a set of intensity-driven deformable registrations. An SDM could have been generated from this set of DVFs; however, we chose to focus on the SSM approach for this paper due to the ease of working with the smaller dataset to emphasize the concept. The limitation of the SSM approach is that it cannot be used directly for dose accumulation in deforming anatomy. Approaches for generating a dense DVF from a set of surfaces have been developed (for example, by Kaus et al.⁴⁰) and could be incorporated into an SSM to enable dose accumulation.

Zhang et al.³³ also used principal component analysis to reconstruct imaged anatomy in the thorax, using an SDM approach, and reported an average displacement error of 2–3 mm in GTV centroid for four patients. Our reported average centroid difference values of 0.2±0.2 mm over all 12 patients, between the original and reconstructed geometries, are less than the difference in the predicted and observed GTV centroid of 2.6±1.8 mm (corresponding to 1.1±0.6 mm LR, 1.8±1.0 mm AP, and 1.6±1.4 mm SI) of Zhang et al. respiration modeling SDM study; however, they proposed a model differently with added prediction step of the displacement field using surrogate signals. The larger error in their study may be explained by the selection of dominant modes, as they kept only the two main principal components (two PCs out of ten samples) only, which corresponded to at least 83% of the total variance. In addition, their modeling data are for full respiration cycle (inspiration and expiration), while our current data are for ABC study at the end of normal inspiration only. In the current study, we kept a higher total variance of at least 95%, which corresponded to higher dominant dimensionality (approximately three to four modes for GTV out of 7–21 samples for W2W or allscans model) and less overall error. Of course, a 95% variance cutoff, being itself arbitrarily selected, does not confirm that all variability within the dominant modes is truly organ motion and the remaining variability is all uncorrelated noise. It is an assumption like most other SSM and SDM studies and is specifically justified in our study by the residual error between the reconstructed and the original geometries being low. However, it may be possible to lower the cutoff (i.e., keep less modes), but the error level will increase, as demonstrated in Tables 4, 5.

Several deficiencies with the study must be mentioned. Two patients were excluded due to large errors in deformable registration that were caused by dissolving atelectasis and development of a pleural effusion, as mentioned in Sec. 3. As these pathologies are common in nonsmall cell lung cancer patients, methods to improve deformable registration to account for them are needed. Also, only weekly imaging was available, so we were unable to test the actual number of fractions required to stabilize the number of dominant modes and testing error. Finally, typical risk structures such as the spinal cord, esophagus, and heart were not evaluated. It would be interesting to determine how the number of dominant modes changed if these structures were included in a composite model.

CONCLUSIONS

Intrapatient PCA models are capable of representing the dominant modes of deformation of the GTV and lungs including GTV regression and positional variation during radiotherapy. Three to four dominant modes were required to model the original structure positions and shapes with mean errors of 1–2 mm, on average. Modeling inclusive of intrafraction breath-hold to breath-hold variation did not improve model accuracy or robustness. Models created with individual structures or a composite of all structures had similar accuracy and robustness in reconstructing the original structures. Prospectively modeling GTV variability during treatment demonstrated accuracy that stabilized with four measurements.