Abstract
Purpose: This article considers the problem of reconstructing cone-beam computed tomography (CBCT) images from a set of undersampled and potentially noisy projection measurements.
Methods: The authors cast the reconstruction as a compressed sensing problem based on ℓ1 norm minimization constrained by statistically weighted least-squares of CBCT projection data. For accurate modeling, the noise characteristics of the CBCT projection data are used to determine the relative importance of each projection measurement. To solve the compressed sensing problem, the authors employ a method minimizing total-variation norm, satisfying a prespecified level of measurement consistency using a first-order method developed by Nesterov.
Results: The method converges fast to the optimal solution without excessive memory requirement, thanks to the method of iterative forward and back-projections. The performance of the proposed algorithm is demonstrated through a series of digital and experimental phantom studies. It is found a that high quality CBCT image can be reconstructed from undersampled and potentially noisy projection data by using the proposed method. Both sparse sampling and decreasing x-ray tube current (i.e., noisy projection data) lead to the reduction of radiation dose in CBCT imaging.
Conclusions: It is demonstrated that compressed sensing outperforms the traditional algorithm when dealing with sparse, and potentially noisy, CBCT projection views.
Keywords: cone-beam computed tomography, compressed sensing, weighted least-squares, Nesterov's first order method
INTRODUCTION
There is growing interest in using on-board cone-beam computed tomography (CBCT) in radiation therapy for patient setup and adaptive replanning.1, 2, 3, 4, 5 While the onboard volumetric imaging offers welcome on-treatment patient anatomy, there is critical concern over the risk associated with the excessive radiation dose when it is used repeatedly.6, 7, 8, 9 The risk is invisible, long term, and cumulative; every scan compounds the dose and the risk. The 2006 report of the Biological Effects of Ionizing Radiation provides a framework for estimating the lifetime attributable risk of cancer incidence from radiation exposure using the most current data on the health effects of radiation. In general, the risk is significantly modulated by polymorphism of genes involved in DNA damage and repair (such as the BRCA1-BRCA2 mutation). It has been reported7, 8 that the dose delivered to the patient is more than 3 cGy for central tissue and about 5 cGy for most of the peripheral tissues from a kV-CBCT scan with current clinical protocols. When a patient is imaged daily, this amounts to more than 100 cGy dose to the region inside the field of view during a treatment course with a conventional fractionation scheme. The risk is exacerbated by the frequent use of other modern x-ray imaging modalities such as 4D simulation CT and fluoroscopic imaging in modern radiation oncology clinics.10 Given that the radiological dose is directly and linearly related to risk and based on the as low as reasonably achievable principle, the unwanted kV-CBCT dose must be minimized in order for the patient to truly benefit from the modern image guidance technology.9
In CBCT literature, a variety of filtered back-projection (FBP) algorithms are popularly used for image reconstruction from projection data. A FBP-type algorithm, originally proposed by Feldkamp, Davis, and Kress (FDK),11 and its derivatives12, 13, 14, 15 are widely used for CBCT reconstruction. When FBP or FDK algorithms are applied to undersampled projection data, the quality of resultant images degrades dramatically due to incomplete information in the Fourier domain. Several methods are under investigation for tomographic image reconstruction from sparse samples.16, 17, 18, 19, 20 For cone-beam geometry, in contrast to its counterpart of parallel-beam scan, obtaining Fourier-domain samples from the projection data is less straightforward. This process is typically done by approximation algorithms, e.g., Fourier rebinning, which interpolate the projection data and may result in some distortion.20, 21, 22, 23, 24, 25 Total variation based CBCT recovery has recently been proposed.26, 27, 28, 29, 30, 31, 32 Heuristic iterative algorithms, such as projection on convex sets26 (POCS) and random search,29 are developed to find solutions and the results are very encouraging. In the statistics and signal processing, ℓ1-regularization for compressed sensing (CS) is a well-established approach for signal recovery. Computationally, while the standard second-order methods work well, it is necessary to solve a large system of linear equations in order to compute the Newton steps.33, 34, 35 A great number of first-order methods are available to tackle the problem of compressed sensing.36, 37, 38 In this work, we apply this technique to solve the problem of CBCT image reconstruction from a set of highly undersampled and noisy CBCT projection measurements. We show that high quality CBCT images are attainable under the condition of sparse and even noisy projection data.
The contribution of this work spans several knowledge areas. First, our compressed sensing problem formulation, i.e., total-variation (TV) norm minimization with a quadratic inequality constraint, mitigates the manual parameter selection in previous approaches by enabling the physical interpretation of data. Second, we investigate a first-order method for solving the large-scale imaging problem to reduce the computational burden. Compared to conventional second-order iterative methods, our implementation avoids excessive usage of computer memory by iterative forward and back-projections. Additionally, our method outperforms the other memory-saving methods, such as POCS, in that it leads to an order of magnitude faster convergence. In Sec. 2, we first introduce the cost function for image reconstruction of CBCT with consideration of the noise properties of the projection data. We then describe our compressed sensing model and the first-order method for solving the problem. In Sec. 3, the proposed algorithm is evaluated by using a 3D Shepp–Logan digital phantom and an anthropomorphic head phantom. The discussion is followed in Sec. 4. We conclude in Sec. 5.
METHODS AND MATERIALS
CBCT sinogram noise model
In this subsection, we introduce a widely investigated x-ray noise model39, 40, 41, 42 which is not new but makes our work self-explanatory. The line integral of attenuation coefficients is given by
| (1) |
where Ni0 and Ni is the incident photon number and the detected photon number at detector bin i, respectively. In a real x-ray CBCT system, the measured signal is total energy deposit on the flat-panel detector, from which we calculate detected photon number Ni. In the following, we refer to the value of yi as the sinogram datum at the detector bin i. Noise in x-ray CT projection data after logarithm transform follows approximately Gaussian distribution and the variance of the noise can be determined by an exponential formula39, 40, 41, 42
| (2) |
where and are defined as the mean and the variance of noisy sinogram datum yi, respectively. This noise model considers the signal-to-noise ratio (SNR) of the line integrals. The measurement associated with a larger SNR will contribute more to the solution, as we describe in Sec. 2B.
Compressed sensing with statistically weighted CBCT projection data
Based on the noise properties of the projection data, a cost function in the image domain can be constructed.
| (3) |
where y is the vector of sinogram data and x is the vector of attenuation coefficients to be reconstructed. The operator P represents the system or projection matrix. The (i,j)th entry P[i,j] is the length of the intersection of projection ray i with voxel j. The symbol T denotes the transpose operator, and thus, PT is the back-projection matrix. The matrix Σ is a diagonal matrix with ith element of , i.e., an estimate of the variance of noise of line integral at detector bin i which can be calculated from the measured projection data according to Eq. 2. The element of the diagonal matrix, which characterizes the contribution of each measurement, plays the role of weighting in the weighted least square (WLS) cost function.
For the standard least-squares formulation, we introduce A=Σ−1∕2P and , rewrite Eq. 3 as
| (4) |
Introducing the tolerance level of measurement inconsistency ε, we can formulate the image reconstruction problem as a quadratically constrained problem
| 5 |
where f is an ℓ1-norm related regularization function depending on prior assumption about the image x. The quadratic constraint here can be interpreted as the Euclidian distance between the detection and estimation is not greater than ε. The Euclidian distance ε quantifies the tolerable uncertainty level about the noisy projection measurements. This concept will be discussed in Sec. 4.
Among many possible candidates for CS penalty function,43, 44, 45 we select 3D TV of the reconstructed image, i.e., f(x)=∥x∥TV, defined by
to form the objective function, where ∇x[i,j,k]∊R3 is the difference vector at each position (i,j,k) of the object image defined by
Operators D1, D2, and D3 are the directional differences as
in x-, y-, and z-axis, respectively. Therefore, our CBCT reconstruction problem is
| 6 |
where we minimize the total variation of reconstructed image in the sublevel set with measurement inconsistency tolerance ε. We will discuss the advantage of the TV minimization with a quadratic constraint in Sec. 4.
A first-order method for compressed sensing
Problems of the form Eq. 6 can be solved using a variety of algorithms, including interior point methods,34, 46 projected gradient methods,47 homotopy methods,48 Bregman iterative regularization algorithms,37, 49 and a first-order method based on Nesterov’s algorithm.38, 50 We describe here a first-order method developed by Nesterov, which provides an accurate and efficient solution to large-scale compressed sensing reconstruction problems using a smoothing technique38, 50, 51
We first rewrite the TV norm
| (7) |
where u=[u1,u2,u3] is in the dual feasible set Qd if and only if for each voxel at position (i,j,k). With this formulation, Eq. 6 can be recast as the following saddle point problem as:
| (8) |
where Qp denotes the primal feasible set satisfying the data inconsistency cost constraint, i.e., Qp={x:∥Ax−b∥ℓ2≤ε}, for the given tolerance level ε.
Following Nesterov’s approach, we smooth the regularization function as
| (9) |
where we can set μ sufficiently small as to fμ≈f. Then, we have
| (10) |
where
for a∊{1,2,3}.
Our compressed sensing reconstruction method can be summarized as
| given tolerance ε>0, parameter μinitializek≔0, x0=FDK(y)while stop criterion is invalid |
| k≔k+1gk≔∇fμ(xk)xk≔τkzk+(1−τk)yk, m∊Njend |
We update yk and zk using the Karush–Kuhn–Tucker conditions as follows:38, 46
| (11) |
| (12) |
where the Lagrange multipliers λy and λz equal to
with
For more details on parameter selections, see the NESTA tech report.38
Here we use CBCT projection function call rather than the matrix-vector product. Storing the projection matrix requires excessive memory space which can be problematic for large-scale CBCT imaging problems. With efficient CBCT forward and back-projection functions, we can solve problems with much larger numbers of variables (voxels to be determined) and measurements (CBCT projection data) as compared to conventional approaches. For example, when calculating ATAx, we cast the product to PTΣ−1Px. The matrix-vector product Px can be equivalently calculated by CBCT projection function call with parameter x. Also, Σ−1y is the elementwise product of two vectors and y rather than matrix-vector product. Similarly, PTy is calculated by CBCT back-projection function call with parameter y. Similar approaches to avoid excessive memory requirement can be found in previous works.26, 52, 53
Evaluation
We first used a 3D Shepp–Logan phantom to evaluate the proposed method. The size of 3 phantom is 256×256×256, where the size of one voxel is assumed 1×1×1 mm3. The distance between the cone-beam source and detection panel is 1500 mm and the distance between the object image and detection panned is 500 mm. The size of detection panel is 512×512 mm2 and the size of a projection image is 256×256 pixels. The code is written in MATLAB (version 7.8) running on a Linux workstation with a 2.33 GHz Intel Xeon CPU and 4 GB memory.
Without any loss of generality, we can fix the weighting matrix Σ with exponential values of the actual line integrals which determines the principal directions of the ellipsoidal quadratic constraint. Here we assume a constant incident photon number Ni0=N0 across every bin i in the digital phantom study. The quadratic constraints can be commonly factorized by N0. By adjusting the infidelity tolerance level ε, the volume of the ellipsoid is set corresponding to each incident photon number.
For the purpose of performance evaluation, we compare the convergence speed of the proposed method to that of POCS. The POCS algorithm implemented in this work relies on the projections onto the hyperplanes with a constant step size for the quadratic constraints and the steepest decent gradient with back-tracking line search to decrease the TV norm. For more details on the implementation of POCS algorithm, we refer the readers to Ref. 26. As a criterion for performance comparison, we incorporate an unconstrained least absolute shrinkage and selection operator (LASSO) expressed as
| (13) |
where λ is the shrinkage parameter to control the biobjectives.
An anthropomorphic phantom experiment was also carried out. The experimental CBCT projection data were acquired by using an Acuity simulator (Varian Medical Systems, Palo Alto, CA). The number of projections for a full 360° rotation is 680 and the total time for the acquisition about 1 min. The dimension of each acquired projection image is 397×298 mm2, containing 1024×768 pixels.
We use two protocols for the performance comparison. For the low-dose CBCT protocol, the x-ray tube current was set at 10 mA and the duration of the x-ray pulse at each projection view was 10 ms during the projection data acquisition. For the high-dose CBCT protocol, the tube current was set at 80 mA and the duration of the x-ray pulse was set at 10 ms. The tube voltage was set to 125 kVp for both protocols. The projection data were acquired in full-fan mode with a bowtie filter. The distance of source-to-axis is 100 cm and source-to-detector distance of 150 cm. The size of reconstructed image is 700×700×16 voxels, where the voxel size is 0.320×0.320×0.320 mm3.
RESULTS
Digital phantom study
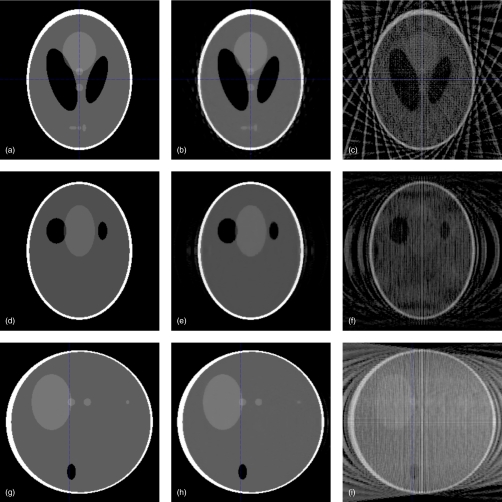
We first reconstruct 3D Shepp–Logan phantom from 32 projection views along a circular orbit uniformly distributed in [0,2π]. In this case, the number of beamlet measurements is only 1∕8 of the number of voxels to be determined. Compressed sensing based on statistically weighted least square (CS-WLS) reconstruction results are compared to the traditional reconstruction using FDK algorithm.11 Several representative slices of the original phantom and reconstructed images are shown in Fig. 1. To further illustrate the edge information, Fig. 2 shows 1D profiles of the original phantom and reconstructed images in x, y, and z directions. It is seen that CS-WLS recovers the object image with high fidelity from the highly sparse and noiseless projection data. However, the same is not true for FDK algorithm.
Figure 1.
Representative axial/frontal/sagittal slices of the digital phantom, CS-WLS reconstruction, and FDK reconstruction. For CS-WLS and FDK-based reconstructions, 32 noiseless projection views are used. (a) Original phantom (axial); (b) CS-WLS (axial); (c) FDK algorithm (axial); (d) original phantom (frontal); (e) CS-WLS (frontal); (f) FDK algorithm (frontal); (g) original phantom (sagittal); (h) CS-WLS (sagittal); and (i) FDK algorithm (sagittal). Display window: [0,0.1] mm−1.
Figure 2.
1D profiles of the digital phantom, CS-WLS reconstruction, and FDK-based reconstruction. For CS-WLS and FDK reconstructions, 32 noiseless projection views are used. (a) Horizontal profiles of the axial slices; (b) vertical profiles of the axial slices; and (c) longitudinal profiles along with the lines in the sagittal slices in Fig. 1.
The convergence speed of the proposed method and the existing POCS method is shown in Fig. 3 in term of the number of iterations. For 500 iterations, the proposed method and POCS took about 25 643 and 25 196 s, respectively. To evaluate the vicinity to the optimal solution, we estimate the normalized difference between fLASSO(x(k)) the LASSO regression value at each iteration and LASSO regression value for the digital phantom for each iteration.
Figure 3.
Convergence comparison between POCS and Nesterov in the first 500 iterations. For fair comparison, POCS algorithm uses a back-tracking line search rather than constant step size. The compared criterion f is the unconstrained LASSO regression value and f∗ is the LASSO value with the digital phantom.
Using the noise model introduced in Sec. 2, the noise simulation results for the digital phantom are shown in Figs. 45. We assume the incident photon number is constant, i.e., Ni0=N0, for all bin i, and the N0 takes 103, 104, 105, and 106, respectively, to simulate clinical CBCT radiation intensity.39, 42 As expected from the noiseless results, FDK results from 32 noisy projection views show very poor images (Fig. 4) and failed to hold the piecewise constant property of the digital phantom as seen in the 1D profiles in Fig. 5. On the other hand, compressed sensing shows the robustness even for the high level of noise with N0=104. It is useful to mention that the clinical noise level is generally ∼105, indicating the validity of the proposed method in a practical situation. We acknowledge here that the effects of the bowtie filter and the compound Poisson sampling due to the polyenergetic spectrum were omitted in the simulation studies.
Figure 4.
Comparison of representative slices of the digital phantom reconstructed by FDK and CS-WLS using 32 projection views with different incident photon numbers. (a) FDK reconstruction with N0=103; (b) CS-WLS reconstruction with N0=103; (c) FDK reconstruction with N0=104; (d) CS-WLS reconstruction with N0=104; (e) FDK reconstruction with N0=105; (f) CS-WLS reconstruction with N0=105; (g) FDK reconstruction with N0=106; and (h) CS-WLS reconstruction with N0=106. Display window: [0,0.1] mm−1.
Figure 5.
1D profiles of the digital phantom, CS-WLS reconstruction, and FDK-based reconstruction with different incident photon numbers. (a) Vertical profiles with N0=103; (b) vertical profiles with N0=104; (c) vertical profiles with N0=105; and (d) vertical profiles with N0=106.
Table 1 lists the contrast-to-noise ratio (CNR) of soft tissue and inner objects for different incident photon numbers. It can be observed that the CNR increase with the incident photon number in both reconstruction algorithms. The CNR of the image reconstructed using compressed sensing remains high with N0≥104.
Table 1.
CNRs of the soft tissue and inner objects in the digital phantom study.
| N0 | 103 | 104 | 105 | 106 | Noiseless |
|---|---|---|---|---|---|
| FDK | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 |
| CS-WLS | 1.34 | 2.96 | 3.38 | 3.41 | 3.46 |
Experimental phantom study
Figures 67 show a representative slice of the reconstructed head phantom images based on the projection data of Acuity measurements. The reconstructed images based on the low-dose and high-dose protocol using FDK and CS algorithms are shown in Figs. 67, respectively. As can be seen from the figures, the CS technique efficiently suppresses noise in the low-dose protocol resulting in images with sharper edges compared to the FDK reconstruction. Figure 8 compares a region of interest (ROI) in the images reconstructed using CS-WLS and the conventional FDK algorithms. The CS-WLS result clearly preserves the edge even when reconstructed from undersampled and noisy projection data. Figure 9 shows the central 1D profiles of the slices in x and y directions. The results are very close to that obtained using high-dose protocol. Compressed sensing thus provides a useful method to reduce effectively the imaging dose with minimal compromise in the resultant image quality. The CNRs for the anthropomorphic phantom study are listed in Table 2.
Figure 6.
Comparison of representative slices of the anthropomorphic head phantom reconstructed by FDK and CS-WLS using 10 mA tube-current projection data. (a) FDK reconstruction using 56 projection views; (b) CS-WLS reconstruction using 56 projection views; (c) FDK reconstruction using 113 projection views; (d) CS-WLS reconstruction using 113 projection views; (e) FDK reconstruction using 226 projection views; (f) CS-WLS reconstruction using 226 projection views; (g) FDK reconstruction using 339 projection views; (h) CS-WLS reconstruction using 339 projection views; (i) FDK reconstruction using 678 projection views; and (j) CS-WLS reconstruction using 678 projection views. Display window: [0,0.045] mm−1.
Figure 7.
Comparison of representative slices of the anthropomorphic head phantom reconstructed by FDK and CS-WLS using 80 mA tube-current projection data. (a) FDK reconstruction using 56 projection views; (b) CS-WLS reconstruction using 56 projection views; (c) FDK reconstruction using 113 projection views; (d) CS-WLS reconstruction using 113 projection views; (e) FDK reconstruction using 226 projection views; (f) CS-WLS reconstruction using 226 projection views; (g) FDK reconstruction using 339 projection views; (h) CS-WLS reconstruction using 339 projection views; (i) FDK reconstruction using 678 projection views; and (j) CS-WLS reconstruction using 678 projection views. Display window: [0,0.045] mm−1.
Figure 8.
Comparison of ROIs in Figs. 67. (a) and (b) show the FDK and CS-WLS reconstructions using 339 projection views with 10 mA tube current, respectively. (c) and (d) show the FDK and CS-WLS reconstructions using 678 projection views with 80 mA tube current, respectively. Display window: [0,0.045] mm−1.
Figure 9.
Central 1D profiles of anthropomorphic head slice images reconstructed using 339 projection views with 10 mA tube current (low-dose protocol) and 678 projection views with 80 mA tube current (high-dose protocol): (a) Horizontal profiles of the axial slices and (b) vertical profiles of the axial slices.
Table 2.
CNRs in the anthropomorphic phantom study.
| Projection views | 56 | 113 | 226 | 339 | 678 |
| 80 mA FDK | 2.90 | 3.92 | 4.48 | 4.69 | 4.89 |
| 80 mA CS-WLS | 3.79 | 4.47 | 5.23 | 5.56 | 5.58 |
| 10 mA FDK | 1.31 | 1.83 | 2.38 | 2.68 | 3.18 |
| 10 mA CS-WLS | 3.22 | 3.55 | 3.92 | 5.00 | 5.56 |
DISCUSSION
The classical Shannon–Nyquist sampling theorem specifies that to avoid losing information when capturing a signal, one must sample at least two times faster than the signal bandwidth. In many applications, including digital image and video cameras, the Nyquist rate is so high that too many samples result, making samples compressible for efficient storage or transmission. In other applications, such as medical imaging systems and high-speed analog-to-digital converters, increasing the sampling rate is either impractical or too expensive. Recently, an alternative theory of compressive sampling or compressed sensing has emerged, which shows that super-resolved signals and images can be reconstructed from far fewer data∕measurements than what is usually considered necessary.43, 44, 45
Briefly, compressed sensing is a technique for acquiring and reconstructing a signal that is known to be sparse or compressible. A mathematical manifestation of a sparse signal is that it contains many coefficients close to or equal to zero, when represented in some appropriate transform domain, such as Fourier domain, total-variation norm, and wavelet domain. Effective utilization of this type of prior knowledge of the system can potentially reduce the required number of measurement samples determined by the Shannon–Nyquist theorem. Most CT images represented by the x-ray attenuation coefficients are sparse, and thus, CT imaging recovery is a good application of compressed sensing. The x-ray attenuation coefficient often remains (almost) constant within organs and sharp variations are usually confined to the borders of internal tissue structure so that images have sparse gradient-magnitude images.26
Even though solving a sparsity problem is mathematically NP-hard, it is shown that a good approximate approach for a sparse recovery problem can be obtained using a convex optimization of an ℓ1 norm.43, 44, 45, 46 A variety of algorithms have been proposed for solving problems in the form of least-squares plus ℓ1 norm, including interior point methods,34, 46 projected gradient methods,47 homotopy methods,48 and first-order methods.37, 38, 50, 51 In CBC imaging literature, a POCS algorithm has been widely used.26, 27, 28, 29, 30, 31, 32 In the implemented first-order method, we calculate the next step using the previous step as well as the decent gradient of the current point. An advantage of this two-step method compared to the one-step method is that it converges to the optimal solution much faster with similar memory requirement.38, 50, 51 Nesterov’s algorithm is a well-known two-step method and the required number of the iterations to reach |f(x)−f∗|≤ε is ,50, 51 whereas one-step methods based on the steepest decent gradient require O(1∕ε) iterations in general.46 A fast convergence speed is highly desirable in solving large-scale problems. The cost for the proposed two-step method in improving the convergence speed is the additional registers to store the history of some of previous iterations regardless of the size of the problem.38, 50, 51 It has been proved that this additional memory requirement can be reduced into just one more register while holding the same order of convergence speed.50, 51
A few algorithms based on regularized least-squares have been applied to solving the image reconstruction problem presented.39 Such quadratic penalty simply encourages the equivalence between neighbors without considering discontinuities in the image and may lead to oversmoothing around sharp edges or boundaries.46 In the presented compressed sensing technique, we use a total variation to consider the potential inequivalence of the neighbors. In general, total variation can remove much of the noise, while preserving any possible rapid variation in the original signal.46 Compressed sensing is known as a tool for robust denois43, 45 and the study here strongly supports the conclusions drawn from the previous investigation in noise reduction. In the digital phantom study, the piecewise constant images were recovered accurately from sparse and noisy projection views with N0≥104. In reality, the incident x-ray intensities with 80 mA tube current and 10 ms pulse time are in the order of 105 across the field of view39, 42 and the noise simulation results support the robustness of compressed sensing against noise. The robust denoising property becomes clearer in the anthropomorphic head phantom study. High quality was achieved even when the tube current and number of projection views were reduced by factors of 1∕8 and 1∕2, respectively. The result with our low-dose protocol setting shows the efficacy of the proposed method. It is interesting to point out that the same amount of dose reduction may be achieved by reducing the number of projection views by a factor of 1∕16 while maintaining the tube current at 80 mA. In reality, fewer projection views with high tube current can be an inefficient strategy in the sense of SNR.
TV-based CBCT reconstructions based on the minimization of TV norm with a quadratic constraints have been reported.26, 27 However, these projection-based algorithms with a constant step size are incapable of utilizing the statistical weights across the measurement data since it is not straightforward to incorporate the statistical weights into each hyperplane projection. In this work, a statistically weighted quadratic constraint is directly used for calculating the decent direction according to the relative importance of the consistency (or fidelity) of the measurements. This formulation makes the determination of the system parameter easy: The physical meaning of the measurement inconsistency tolerance ε can be perceived in terms of the inconsistency level of the normalized sinogram which has a chi-square distribution. The constrained least-squares can be interpreted as a sublevel set in the form of a solid ellipsoid. The volume of the ellipsoid is directly related to the measurement inconsistency tolerance level ε. The proposed method explores the ellipsoid by minimizing the ℓ1 norm. Here, we choose ε by the noise level of the sinogram data, which is estimated based on our experiment settings since the tolerance is associated with the variance of the sinogram.
Despite intense efforts in the developments of iterative CBCT reconstruction algorithms over the years and all the potential benefits of these new algorithms, FDK∕FBP based algorithms remain the workhorse in clinical CT scanner mainly for their computational efficiency.27 The widespread adoption of compressed sensing based reconstruction will be difficult, if not impossible, without a dramatic improvement in its computational efficiency. The improvement in convergence behavior and memory usage from this work represents a valuable incremental step in reducing the gap between the state-of-the-art research and clinical practice. Combined with technical advancements in computer hardware, such as the GPU-based computing, it is foreseeable that compressed sensing based large-scale CBCT reconstruction will enter the routine clinical applications, at least for some special applications, in the not too distant future.
CONCLUSION
A compressed sensing technique using a first-order method has been developed for CBCT image reconstruction with sparse and potentially noisy low-dose projection data. In this method, the weight for each measurement was chosen based on sinogram datum variance. By eliminating the intermediate step of mapping CBCT projection data to the Fourier domain, the proposed method allows high quality reconstruction of object. The performance of the proposed method is demonstrated by both simulation and experimental phantom studies. It is demonstrated that compressed sensing outperforms the traditional algorithm when dealing with sparse CBCT projection views in the presence of relatively high noise due to low tube current. The results indicate that it is possible to reduce CBCT radiation dose by more than an order of magnitude without loss of useful information for radiotherapy.
ACKNOWLEDGMENTS
Kihwan Choi is supported by Kwanjeong Educational Foundation, South Korea. This project was supported in part by grants from the National Science Foundation (Grant No. 0854492), National Cancer Institute (Grant No. 1R01 CA104205), and Global R&D Resource Recruitment and Support Program, Korean Ministry of Education, Science, and Technology (Grant No. K20901000001-09E0100-00110).
This work was presented in 16th International Conference on the Use of Computers in Radiation Therapy (ICCR), Amsterdam, The Netherlands, June 2010.
References
- Timmerman R. D. and Xing L., Image Guided and Adaptive Radiation Therapy (Lippincott Williams and Wilkins, Baltimore, 2009). [Google Scholar]
- Jaffray D. A., Siewerdsen J. S., Wong J. W., and Martinez A. A., “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
- Xing L., Thorndyke B., Schreibmann E., Yang Y., Li T. -F., Kim G. -Y., Luxton G., and Koong A., “Overview of image-guided radiation therapy,” Med. Dosim. 31, 91–112 (2006). 10.1016/j.meddos.2005.12.004 [DOI] [PubMed] [Google Scholar]
- Yang Y., Schreibmann E., Li T. F., Wang C., and Xing L., “Evaluation of on-board kV cone beam CT (CBCT)-based dose calculation,” Phys. Med. Biol. 52, 685–705 (2007). 10.1088/0031-9155/52/3/011 [DOI] [PubMed] [Google Scholar]
- Lee L., Le Q. T., and Xing L., “Retrospective IMRT dose reconstruction based on cone-beam CT and MLC log-file,” Int. J. Radiat. Oncol., Biol., Phys. 70, 634–644 (2008). 10.1016/j.ijrobp.2007.09.054 [DOI] [PubMed] [Google Scholar]
- Brenner D. J. and Hall E. J., “Computed tomography—An increasing source of radiation exposure,” N. Engl. J. Med. 357, 2277–2284 (2007). 10.1056/NEJMra072149 [DOI] [PubMed] [Google Scholar]
- Islam M. K., Purdie T. G., Norrlinger B. D., Alasti H., Moseley D. J., Sharpe M. B., Siewerdsen J. H., and Jaffray D. A., “Patient dose from kilovoltage cone beam computed tomography imaging in radiation therapy,” Med. Phys. 33, 1573–1582 (2006). 10.1118/1.2198169 [DOI] [PubMed] [Google Scholar]
- Wen N., Guan H. Q., Hammoud R., Pradhan D., Nurushev T., Li S. D., and Movsas B., “Dose delivered from Varian’s CBCT to patients receiving IMRT for prostate cancer,” Phys. Med. Biol. 52, 2267–2276 (2007). 10.1088/0031-9155/52/8/015 [DOI] [PubMed] [Google Scholar]
- Murphy M. J., Balter J., Balter S., J. A.BenComo, Jr., Das I. J., Jiang S. B., Ma C. M., Olivera G. H., Rodebaugh R. F., Ruchala K. J., Shirato H., and Yin F. F., “The management of imaging dose during image-guided radiotherapy: Report of the AAPM Task Group 75,” Med. Phys. 34, 4041–4063 (2007). 10.1118/1.2775667 [DOI] [PubMed] [Google Scholar]
- Li T., Schreibmann E., Thorndyke B., Tillman G., Boyer A., Koong A., Goodman K., and Xing L., “Radiation dose reduction in four-dimensional computed tomography,” Med. Phys. 32, 3650–3660 (2005). 10.1118/1.2122567 [DOI] [PubMed] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A Opt. Image Sci. Vis 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- Hu J. C., Tam K., and Qi J. Y., “An approximate short scan helical FDK cone beam algorithm based on mutating curved surfaces satisfying the Tuy’s condition,” Med. Phys. 32, 1529–1536 (2005). 10.1118/1.1916077 [DOI] [PubMed] [Google Scholar]
- Tang X. Y., Hsieh J., Nilsen R. A., Dutta S., Samsonov D., and Hagiwara A., “A three-dimensional-weighted cone beam filtered backprojection (CB-FBP) algorithm for image reconstruction in volumetric CT-helical scanning,” Phys. Med. Biol. 51, 855–874 (2006). 10.1088/0031-9155/51/4/007 [DOI] [PubMed] [Google Scholar]
- Mori S., Endo M., Komatsu S., Kandatsu S., Yashiro T., and Baba M., “A combination-weighted Feldkamp-based reconstruction algorithm for cone-beam CT,” Phys. Med. Biol. 51, 3953–3965 (2006). 10.1088/0031-9155/51/16/005 [DOI] [PubMed] [Google Scholar]
- Cho S., Xia D., Pelizzari C. A., and Pan X. C., “Exact reconstruction of volumetric images in reverse helical cone-beam CT,” Med. Phys. 35, 3030–3040 (2008). 10.1118/1.2936219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye J. C., “Compressed sensing shape estimation of star-shaped objects in Fourier imaging,” IEEE Signal Process. Lett. 14, 750–753 (2007). 10.1109/LSP.2007.898342 [DOI] [Google Scholar]
- Jung H., Ye J. C., and Kim E. Y., “Improved k-t BLAST and k-t SENSE using FOCUSS,” Phys. Med. Biol. 52, 3201–3226 (2007). 10.1088/0031-9155/52/11/018 [DOI] [PubMed] [Google Scholar]
- Song J., Liu Q. H., Johnson G. A., and Badea C. T., “Sparseness prior based iterative image reconstruction for retrospectively gated cardiac micro-CT,” Med. Phys. 34, 4476–4483 (2007). 10.1118/1.2795830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaRoque S. J., Sidky E. Y., and Pan X., “Accurate image reconstruction from few-view and limited-angle data in diffraction tomography,” J. Opt. Soc. Am. A Opt. Image Sci. Vis 25, 1772–1782 (2008). 10.1364/JOSAA.25.001772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Provost J. and Lesage F., “The application of compressed sensing for photo-acoustic tomography,” IEEE Trans. Med. Imaging 28, 585–594 (2009). 10.1109/TMI.2008.2007825 [DOI] [PubMed] [Google Scholar]
- Seger M. M., “Three-dimensional reconstruction from cone-beam data using an efficient Fourier technique combined with a special interpolation filter,” Phys. Med. Biol. 43, 951–959 (1998). 10.1088/0031-9155/43/4/022 [DOI] [PubMed] [Google Scholar]
- Defrise M., Kinahan P. E., Townsend D. W., Michel C., Sibomana M., and Newport D. F., “Exact and approximate rebinning algorithms for 3-D PET data,” IEEE Trans. Med. Imaging 16, 145–158 (1997). 10.1109/42.563660 [DOI] [PubMed] [Google Scholar]
- Matej S., Karp J. S., Lewitt R. M., and Becher A. J., “Performance of the Fourier rebinning algorithm for 3D PET with large acceptance angles,” Phys. Med. Biol. 43, 787–797 (1998). 10.1088/0031-9155/43/4/008 [DOI] [PubMed] [Google Scholar]
- O’Connor Y. Z. and Fessler J. A., “Fourier-based forward and back-projectors in iterative fan-beam tomographic image reconstruction,” IEEE Trans. Med. Imaging 25, 582–589 (2006). 10.1109/TMI.2006.872139 [DOI] [PubMed] [Google Scholar]
- Mazin S. R. and Pelc N. J., “Fourier rebinning algorithm for inverse geometry CT,” Med. Phys. 35, 4857–4862 (2008). 10.1118/1.2986155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky E. Y. and Pan X. C., “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Phys. Med. Biol. 53, 4777–4807 (2008). 10.1088/0031-9155/53/17/021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan X., Sidky E. Y., and Vannier M., “Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?,” Inverse Probl. 25, 123009 (2009). 10.1088/0266-5611/25/12/123009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G. -H., Tang J., and Leng S., “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys. 35, 660–663 (2008). 10.1118/1.2836423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J., Nett B. E., and Chen G. H., “Performance comparison between total variation (TV)-based compressed sensing and statistical iterative reconstruction algorithms,” Phys. Med. Biol. 54, 5781–5804 (2009). 10.1088/0031-9155/54/19/008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leng S., Tang J., Zambelli J., Nett B., Tolakanahalli R., and Chen G. H., “High temporal resolution and streak-free four-dimensional cone-beam computed tomography,” Phys. Med. Biol. 53, 5653–5673 (2008). 10.1088/0031-9155/53/20/006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herman G. T. and Davidi R., “On image reconstruction from a small number of projections,” Inverse Probl. 24, 045011 (2008). 10.1088/0266-5611/24/4/045011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., Yu H., and De Man B., “An outlook on x-ray CT research and development,” Med. Phys. 35, 1051–1064 (2008). 10.1118/1.2836950 [DOI] [PubMed] [Google Scholar]
- Candes E. and Romberg J., “ℓ1-magic: Recovery of sparse signals via convex programming,” Technical Report (California Institute of Technology, 2007).
- Kim S. J., Koh K., Lustig M., Boyd S., and Gorinevsky D., “A method for large-scale ℓ1-regularized least squares,” IEEE J. Sel. Top. Signal Process. 1, 606–617 (2007). 10.1109/JSTSP.2007.910971 [DOI] [Google Scholar]
- Saunders M. A. and Kim B., “PDCO: Primal-dual interior method for convex objectives,” Technical Report (Stanford University, 2002).
- Hale E. T., Yin W. T., and Zhang Y., “Fixed-point continuation for ℓ1-minimization: Methodology and convergence,” SIAM J. Optim. 19, 1107–1130 (2008). 10.1137/070698920 [DOI] [Google Scholar]
- Yin W., Osher S., Goldfarb D., and Darbon J., “Bregman iterative algorithms for ℓ1-minimization with applications to compressed sensing,” SIAM J. Imaging Sci. 1, 143–168 (2008). 10.1137/070703983 [DOI] [Google Scholar]
- Becker S., Bobin J., and Candes E. J., “NESTA: A fast and accurate first-order method for sparse recovery,” Technical Report (California Institute of Technology, 2009).
- Wang J., Li T. F., and Xing L., “Iterative image reconstruction for CBCT using edge-preserving prior,” Med. Phys. 36, 252–260 (2009). 10.1118/1.3036112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L., Wang J., and Xing L., “Noise suppression in scatter correction for cone-beam CT,” Med. Phys. 36, 741–752 (2009). 10.1118/1.3063001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li T., Li X., Wang J., Wen J. H., Lu H. B., Hsieh J., and Liang Z. R., “Nonlinear sinogram smoothing for low-dose x-ray CT,” IEEE Trans. Nucl. Sci. 51, 2505–2513 (2004). 10.1109/TNS.2004.834824 [DOI] [Google Scholar]
- Wang J., Lu H. B., Liang Z. R., Eremina D., Zhang G. X., Wang S., Chen J., and Manzione J., “An experimental study on the noise properties of x-ray CT sinogram data in Radon space,” Phys. Med. Biol. 53, 3327–3341 (2008). 10.1088/0031-9155/53/12/018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candes E. J., Romberg J., and Tao T., “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory 52, 489–509 (2006). 10.1109/TIT.2005.862083 [DOI] [Google Scholar]
- Candes E. J. and Tao T., “Near-optimal signal recovery from random projections: Universal encoding strategies?,” IEEE Trans. Inf. Theory 52, 5406–5425 (2006). 10.1109/TIT.2006.885507 [DOI] [Google Scholar]
- Donoho D. L., “Compressed sensing,” IEEE Trans. Inf. Theory 52, 1289–1306 (2006). 10.1109/TIT.2006.871582 [DOI] [Google Scholar]
- Boyd S. P. and Vandenberghe L., Convex Optimization (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Figueiredo M. A. T., Nowak R. D., and Wright S. J., “Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems,” IEEE J. Sel. Top. Signal Process. 1, 586–597 (2007). 10.1109/JSTSP.2007.910281 [DOI] [Google Scholar]
- Hastie T., Rosset S., Tibshirani R., and Zhu J., “The entire regularization path for the support vector machine,” J. Mach. Learn. Res. 5, 1391–1415 (2004). [Google Scholar]
- Osher S., Burger M., Goldfarb D., Xu J. J., and Yin W. T., “An iterative regularization method for total variation-based image restoration,” Multiscale Model. Simul. 4, 460–489 (2005). 10.1137/040605412 [DOI] [Google Scholar]
- Nesterov Y., “Gradient methods for minimizing composite objective function,” Technical Report [Center for Operations Research and Econometrics (CORE), Universite Catholique de Louvain, 2007].
- Nesterov Y., “A method for unconstrained convex minimization problem with the rate of convergence O(1∕k2) ,” Dokl. Akad. Nauk UzSSR 269, 543–547 (1983). [Google Scholar]
- Sidky E. Y., Kao C. -M., and Pan X., “Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT,” J. X-Ray Sci. Technol. 14, 119–139 (2006). [Google Scholar]
- Thibault J. -B., Sauer K. D., and Bouman C. A., “A three-dimensional statistical approach to improved image quality for multislice helical CT,” Med. Phys. 34, 4526–4544 (2007). 10.1118/1.2789499 [DOI] [PubMed] [Google Scholar]