The time course of cochlear gain reduction measured using a more efficient psychophysical technique

Abstract

In a previous study it was shown that an on-frequency precursor intended to activate the medial olivocochlear reflex (MOCR) at the signal frequency reduces the gain estimated from growth-of-masking (GOM) functions. This is called the temporal effect (TE). In Expt. 1 a shorter method of measuring this change in gain is established. GOM functions were measured with an on- and off-frequency precursor presented before the masker and signal, and used to estimate Input∕Output functions. The change in gain estimated in this way was very similar to that estimated from comparing two points measured with a single fixed masker level on the lower legs of the GOM functions. In Expt. 2, the TE was measured as a function of precursor duration and signal delay. For short precursor durations and short delays the TE increased (buildup) or remained constant as delay increased, then decreased. The TE also increased with precursor duration for the shortest delay. The results were fitted with a model based on the time course of the MOCR. The model fitted the data well, and predicted the buildup. This buildup is not consistent with exponential decay predicted by neural adaptation or persistence of excitation.

INTRODUCTION

Like other sensory systems, the auditory system may adjust to the changing environment. Psychophysical evidence for dynamic adjustment to sound comes from a phenomenon called overshoot (Zwicker, 1965) or the temporal effect (Hicks and Bacon, 1992). The temporal effect (TE) exists when a signal at the onset of a masker is more detectable if it is preceded by an additional sound. This additional sound may be an extension of the masker, or a separate stimulus (called a “precursor”), presented before the masker’s onset.

Although the TE may be a sum of effects at multiple levels of the auditory system, considerable evidence suggests that it may be partially due to changes in the active process in the cochlea. The active process is thought to be due to amplification by the outer hair cells (OHCs). This results in amplification at low intensities, and increases frequency selectivity. The TE is reduced by temporary (Champlin and McFadden, 1989; McFadden and Champlin, 1990) or permanent (Bacon and Takahashi, 1992; Strickland and Krishnan, 2005) cochlear hearing loss, which may affect the active process. Studies of the TE have shown that a precursor also reduces estimates of cochlear gain and frequency selectivity (Strickland, 2001, 2004; Strickland and Krishnan, 2005; Strickland 2008).

A decrease in the gain of the active process could be mediated by the medial olivocochlear reflex (MOCR). The MOCR results from stimulation of the medial olivocochlear bundle, a pathway that feeds back from the level of the superior olivary complex to the outer hair cells in the cochlea (Warr and Guinan, 1979; Warr, 1980). Physiological studies in animals have shown that the MOCR turns down the gain of the active process in the cochlea in response to sound (Guinan and Gifford, 1988; Cooper and Guinan, 2006) and also leads to a release from adaptation in auditory nerve fibers responding to a tone in noise (Kawase et al., 1993).

Because the MOCR is a possible physiological mechanism for the psychophysical TE, researchers have examined other evidence that may link the TE and the MOCR. One aspect of the two types of data that has been compared is the time course. Although early studies of the MOCR involved invasive procedures that could be used only in animals, the MOCR also may be measured as a change in the level of otoacoustic emissions (OAEs) in humans (Kim et al., 2001). OAEs are sounds that can be measured coming out of the ear, and are by-products of the active process in the cochlea.

There are several types of OAEs that may be measured. The time course of the MOCR in humans has been measured in detail by Backus and Guinan (2006) for stimulus frequency otoacoustic emissions (SFOAEs). The clearest time course may be measured by suppressing the SFOAEs with contralateral acoustic stimulation (CAS), which takes advantage of the crossed nature of the MOCR. Backus and Guinan identified four segments in the time course of the MOCR. There is an onset delay of approximately 25 ms from the onset of the CAS to the initiation of a rise in MOC effect. This is followed by buildup of the MOCR. The buildup can be fitted with fast (70 ms), medium (300 ms) and slow (25 s) time constants. There is an offset delay, from the offset of the CAS to the start of the decay of the MOCR, which is approximately equal to the onset delay. This is followed by the decay of the MOCR, which has an average time constant of approximately 160 ms. This time course appears to be independent of CAS level and to be the same for ipsilateral acoustic stimulation. Most SFOAE studies have been done around 1 kHz, where MOCR effects are large.

Approximately the same time course has been found using distortion-product otoacoustic emissions (DPOAEs) (Kim et al., 2001; James et al., 2005). These studies have found large MOCR effects around 4 kHz, which is a frequency often used in psychophysical studies. A new nonlinear version of SFOAEs (nSFOAEs) also has been used to measure the response to a tone in a noise masker, which may reflect the MOCR as well (Walsh et al., 2010b). That study reported buildup time constants that were dependent on the windowing used. With a 40-ms analysis window, buildup time constants were 70–90 ms, whereas with a 20-ms analysis window, buildup time constants were 23–39 ms. Walsh et al. reported much slower decay than Backus and Guinan (2006). While most studies have used long MOCR elicitors, James et al. (2005) and Walsh et al. (2010b) also have examined shorter elicitor durations.

In a parallel manner, we can talk about the time course for the TE in psychophysics. In simultaneous masking, the size of the TE has been measured by delaying a signal from the onset of a masker. The reference condition is the signal (or masker) threshold when the signal is at the onset of the masker, and the TE is the difference between this threshold and other thresholds. The buildup time course of the TE is the decrease in signal threshold (or increase in masker level) as the signal is delayed from the onset of the masker. The TE seems to plateau after roughly 200 ms or so (Zwicker, 1965; Bacon and Moore, 1986). Assuming the masker onset elicits the MOCR, any TE in the first 25 ms from the onset of the masker should not be due to gain reduction by the MOCR, because of the onset delay documented by Backus and Guinan (2006) and Walsh et al. (2010b). Given the time steps that have been used, as well as variability in the data, it is often not possible to determine precisely how much of a change in threshold there is within the first 25 ms. The plateau of the buildup of the TE after 200 ms or so would be consistent with the onset delay plus buildup time constant (100–200 ms) reported for the MOCR.

The decay time course for the psychophysical TE also has been measured for a signal at the onset of a masker as a function of delay from the offset of a precursor (Carlyon, 1987, 1989; McFadden, 1989; Schmidt and Zwicker, 1991; Overson et al., 1996). In this case, the precursor would be presumed to elicit the MOCR. The time course is in the same range as has been reported for the MOCR, if it is assumed that this includes the combined time of the offset delay plus decay.

Recently we have moved to forward-masking techniques to study the TE (Krull and Strickland, 2008; Jennings et al., 2009), to avoid the effects of suppression. While the TE may decrease simultaneous masking (by increasing the signal to masker ratio) it may contribute to forward masking (that is, make a signal less detectable) (Strickland, 2008, Fig. 3). Gain reduction cannot account for all of forward masking, because forward masking is seen for masker durations shorter than 20 ms, which would be shorter than the onset delay of the MOCR. Thus there also must be what we will call “excitatory masking.” By this we mean what has traditionally been called persistence of excitation, which is different from gain reduction. Assuming that gain reduction is due to the MOCR, we can take advantage of the sluggish time course to at least partially separate these two mechanisms, which is not possible in simultaneous masking.

We have developed a forward-masking technique in which a 20-ms masker and a 6-ms signal are used as tools to measure growth of masking (GOM) functions and psychophysical tuning curves (PTCs). GOM functions and PTCs can be used to estimate cochlear gain and frequency selectivity, which are related to the active process. The 20-ms masker should be short enough that the MOCR will not be activated, so it produces only excitatory masking. A long-duration precursor at the signal frequency is presented before the masker, which should cause gain reduction. The control condition may be no precursor, or a precursor well below the signal frequency. The TE is the amount of gain reduction. Long (2.5 s) tonal elicitors have been found to be effective in eliciting an MOC effect in SFOAE studies but are less effective than wider band elicitors or tone pips (e.g., Lilaonitkul and Guinan, 2009b). Short tonal precursors (≤160 ms) have elicited the TE in forward masking in previous studies. A tonal precursor was used in the present study to allow for precise control of the frequency region stimulated.

The magnitude of the gain of the Input∕Output (I∕O) function estimated from the GOM function can be reduced by an on-frequency precursor (Krull and Strickland, 2008; Jennings et al., 2009), which also can broaden the PTC and cause the tip to shift to a lower frequency (Jennings et al., 2009). These results are consistent with a decrease in the gain of the active process, and support the idea that the TE in forward masking also may be due to the MOCR. Measuring the entire GOM function with an on-frequency and an off-frequency (or no) precursor has been useful in showing that a precursor reduces the gain of the active process. However, it is a time-consuming technique. The first goal of this study was to develop a more efficient technique to measure the gain reduction caused by the precursor.

The buildup time of the TE also has been examined using the forward-masking technique described above, but with a 40-ms masker. Krull and Strickland (2008) found that a 40-ms on-frequency precursor reduced the gain of the GOM function as much as a 160-ms one. This was surprising given that previous studies of the TE in simultaneous masking suggested that the 40-ms precursor should have less effect (Bacon and Healy, 2000). Due to the presence of the 40-ms masker, however, the delay from the onset of the 40-ms precursor to the signal onset was 80 ms, while in the Bacon and Healy study the delay from the precursor onset was only 40 ms. Krull and Strickland (2008) suggested that both precursor duration and the delay from precursor onset to signal onset might be important in determining the size of the TE, because of the relatively slow time course of the MOCR. As noted above, only two OAE studies have examined the effects of elicitor duration. James et al. (2005) found that elicitors as short as 5 ms may be effective in evoking the MOCR.

The second goal of the present study was to measure the effects of precursor duration and signal delay independently to map the time course of the TE. Measurements of the time course of gain reduction (the TE) were made while keeping excitatory masking as constant as possible. This was done by using the more efficient method for measuring the change in gain of the I∕O function developed in Expt. 1.

EXPERIMENT 1: Growth-of-Masking Functions

In previous studies, we have estimated the cochlear I∕O function using a GOM technique first described by Oxenham and Plack (1997). In this technique, forward-masked thresholds for a masker approximately one octave below the signal frequency are compared to thresholds for an on-frequency masker to derive the I∕O function. In both the Oxenham and Plack (1997) study and our previous studies, the masker level was varied to find threshold. With short delays between masker offset and signal onset, the GOM function for the on-frequency masker has a slope close to one, and thus the off-frequency GOM is a direct estimate of the I∕O function (Oxenham and Plack, 1997). Therefore, for efficiency, we have measured only the off-frequency GOM function (Krull and Strickland, 2008; Jennings et al., 2009). Our studies have shown that an on-frequency precursor shifts the lower leg of the GOM function to higher signal levels, consistent with a decrease in cochlear gain. In the present study, we wanted to find a more efficient technique to estimate the decrease in cochlear gain produced by a precursor.

GOM also may be measured with the masker level fixed and the signal level varied (e.g., Plack and Oxenham, 1998). This technique would allow us to better define changes in the lower leg of the GOM function. The purpose of Expt. 1 was to determine whether the change in gain estimated with a fixed masker level on the lower leg of the GOM function was a reasonable estimate of the change in gain estimated from fitting an I∕O function to the whole GOM function. This was done for a subset of listeners. For all listeners, Expt. 1 established the masker level to be used for Expt. 2.

Methods

Subjects

Six listeners participated in the study. The age range was from 21 to 50 years, with a median of 22.5. All listeners had pure tone thresholds ≤15 dB Hearing Level for octave frequencies from 250–8000 Hz, and were within the normal range on measures of acoustic immittance and DPOAEs. The right ear of each listener was tested for the study. The listeners were paid for their participation except for S1 and S4, the first and second authors.

Stimuli

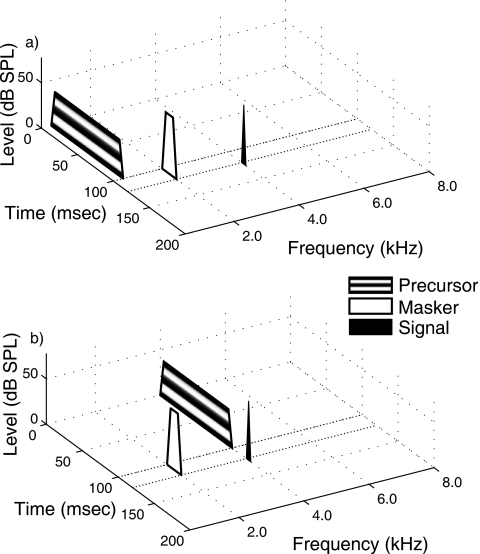
During each observation interval, three stimuli were presented sequentially: precursor, masker, and signal. These are shown in Fig. 1. Varying the signal and masker allowed us to trace a GOM function and the precursor was intended to elicit the MOCR. The signal was a 4-kHz sinusoid, 6 ms in duration including 3-ms cos² onset and offset ramps. A signal frequency of 4 kHz has been shown to yield large temporal effects in simultaneous masking (e.g., Bacon and Takahashi, 1992) and forward masking (Krull and Strickland, 2008; Jennings et al., 2009). The forward masker was a 2-kHz sinusoid, 20 ms in duration including 5-ms cos² ramps. The masker was assumed to have a linear response at the signal frequency place (Oxenham and Plack, 1997). There was no delay from masker offset to signal onset. The precursor was either a 0.8 or 4.0 kHz sinusoid set at a level of 40 dB SPL. The precursor duration was 100 ms, including 5-ms cos² ramps. There was no delay from precursor offset to masker onset. Studies from our laboratory have shown that a 0.8-kHz precursor results in similar thresholds to those measured with no precursor present (Jennings et al., 2009). Thus, thresholds measured with a 0.8-kHz (off-frequency) precursor served as a control to those measured with a 4-kHz (on-frequency) precursor while keeping the same temporal characteristics between the two conditions. Preliminary data suggested the stimulus parameters described above were effective in producing a TE in all subjects tested. In all conditions, high pass noise was presented to limit off-frequency listening (e.g., Nelson et al., 2001); it began 50 ms prior to precursor onset and ended 50 ms after signal offset. The spectrum level of the noise varied with signal level, but always was 50 dB below the signal level, and had lower and upper cutoff frequencies of 4.8 and 8.0 kHz, respectively. The noise included 5-ms cos² ramps.

Figure 1.

Schematic depicting spectral and temporal characteristics of the precursor, masker and signal in Expt. 1. Panels (a) and (b) show off-frequency and on-frequency precursor conditions, respectively. Highpass noise (not shown) also was present in all conditions; it began 50 ms before the precursor and ended 50 ms after signal offset. The spectrum level of the noise varied with signal level, but always was 50 dB below the signal level, and had lower and upper cutoff frequencies of 4.8 and 8.0 kHz, respectively.

The stimuli were generated digitally, and passed through four separate D∕A channels (TDT DA3–4), low-pass filtered at 10 kHz (TDT FT5 and FT6–2) and adjusted in level by programmable attenuators (TDT PA4). The stimuli were mixed (TDT-SM3), routed to a headphone buffer (TDT HB6), and presented to the listener through one of two ER-2A insert earphones. These earphones have a flat frequency response at the eardrum from 250 to 8000 Hz.

Procedures

Testing took place in a double-walled, sound-attenuating booth. Thresholds were measured with either signal or masker level fixed in different blocks of trials. A two-up, one-down (signal fixed) or two-down, one-up (masker fixed) stepping rule was used to estimate a threshold of 70.7% correct (Levitt, 1971). A three-interval forced-choice procedure was used, with visual representation of each interval on a computer screen. Listeners indicated the interval containing the signal via a keystroke. Visual feedback was provided after each correct or incorrect response. The step size was 5 dB until the second reversal, and then was decreased to 2 dB. Threshold in any given run was defined as the average of the last even number of reversals at the smaller step size in a set of 50 trials. Any individually measured thresholds resulting in standard deviations of 5 dB or greater were discarded. Final thresholds in all conditions were averages from at least 2 runs. Learning effects were observed for some listeners. If the initial thresholds differed by more than 5 dB from the average of subsequent thresholds, the initial thresholds were discarded.

For all listeners, thresholds first were measured with the signal level fixed across a range of levels, and with the off-frequency precursor. For three subjects, thresholds also were measured with signal level fixed, with an on-frequency precursor. The upper end of the signal range was limited by the ability to determine a masker threshold within the limits of the system (95 dB SPL). For all subjects, one to three masker levels on the lower leg of the off-frequency GOM function were selected. These masker levels were fixed and estimates of threshold with both off- and on-frequency precursors were obtained by varying signal level in the manner described above.

Results

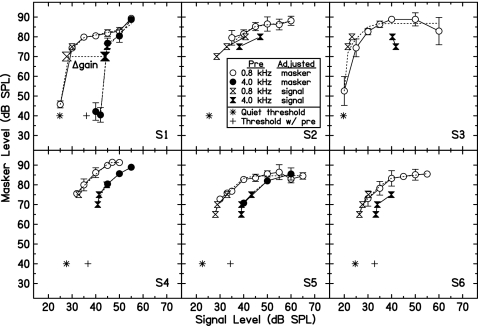
Figure 2 shows GOM functions for all subjects. Open symbols depict thresholds measured with the off-frequency precursor, and filled symbols with the on-frequency precursor. Circles and hourglasses indicate thresholds measured with the signal or masker level fixed, respectively. For the off-frequency precursor data, thresholds measured with signal level fixed or with masker level fixed appear to be tracing the same functions, as would be expected. This function should mirror the cochlear I∕O function. The on-frequency precursor shifted the lower leg of the GOM function to higher signal levels, as we have shown in previous studies (Krull and Strickland, 2008; Jennings et al. 2009). S3 showed a decrease in masker threshold at the highest signal levels. This also has been seen in our previous studies. We suspect that this may be due to suppression by the highpass noise, which varied in level with the signal.

Figure 2.

GOM functions for off-frequency (open symbols) and on-frequency (filled symbols) precursor conditions. Circles indicate thresholds obtained when the signal level was fixed and masker level varied. Hourglasses represent thresholds obtained when the masker level was fixed and the signal level varied. Asterisks show each subject’s signal threshold with no masker or precursor (the symbols are arbitrarily placed at 40-dB masker level). Plus symbols show signal threshold in the presence of an on-frequency precursor with 20 ms of silence in place of the off-frequency masker. Dashed lines are model fits described in the text.

GOM functions were fitted with functions used by Jennings and Strickland (2010). This is a piecewise linear function used by Yasin and Plack (2003), which has been modified by the addition of an internal noise parameter to account for the steep roll off near quiet threshold.

The equations used by Yasin and Plack (2003) were

$${\text{L}}_{\text{out}}={\text{L}}_{\text{in}}+\text{G},{\text{L}}_{\text{in}}\le \text{BP}1,$$ (1)

$${\text{L}}_{\text{out}}=\text{c}\times {\text{L}}_{\text{in}}+{\text{BP}}_1\times \left(1-\text{c}\right)+\text{G},\text{BP}1<{\text{L}}_{\text{in}}\le \text{BP}2,$$ (2)

$${\text{L}}_{\text{out}}=\text{c}\times {\text{L}}_{\text{in}}+{\text{BP}}_1\times \left(1-\text{c}\right)+{\text{BP}}_2\times \left(\text{c}-1\right)+\text{G},\text{BP}1<{\text{L}}_{\text{in}}\le \text{BP}2,$$ (3)

where L_in is the input signal level, L_out is the masker level estimate, G is gain, c is compression, and BP1 and BP2 are breakpoints. An estimate of internal noise, α, also was included in the fits. The input levels of L_in, BP₁, and BP₂ were adjusted for the internal noise by the following equation, where each of these parameters is substituted for X_orig

$$\text{X}=10\times {\text{log}}_{10}\left({10}^{\wedge }\left({\text{X}}_{\text{orig}}∕10\right)-{10}^{\wedge }\left(\alpha ∕10\right)\right).$$ (4)

BP2 was set at 100 dB SPL. The MATLAB function “fminsearch” adjusted the parameter estimates to minimize the RMS error of the fits.

The fits are plotted as dashed lines in Fig. 2. The gain estimates from the I∕O functions, as well as the reduction in gain between the two conditions for the three subjects with complete GOM functions in both conditions (S1, S4 and S5), are shown in Table 1. A change in gain results in a parallel shift in the lower leg of the I∕O function if it is assumed that internal noise also shifts (see Jennings and Strickland, 2010). This parallel shift can be seen in the fits (dashed lines) in Fig. 2. Thus, the amount of gain reduction also may be estimated by fixing the masker level and measuring the difference between points on the lower leg of the GOM function. We define this value as the TE. For all subjects, the two-point estimate of the change in gain (and the masker level used to estimate it) is shown in Table 1. 95% confidence intervals were constructed for the gain change estimate with the fixed-masker method. It can be seen that the fitted function gain change estimate lies within the confidence interval for S1, S4 and S5. This result supports the uniformity of these two methods of predictions. For the remainder of this report, thresholds measured with on- and off-frequency precursors were estimated for a single fixed masker level on the lower leg of each subject’s GOM function. The difference between these two thresholds was assumed to reflect the reduction in gain.

Table 1.

Estimates of gain change from two methods (fourth and fifth columns). The gain with a 0.8-kHz Pre was estimated from I∕O functions fitted to each subject’s GOM data using Eqs. 1, 2, 3, 4. For S1, S4, and S5, I∕O functions also were fitted to GOM data measured with an on-frequency precursor. The difference between these two estimates of gain is shown as gain change. The two-point gain change estimates were obtained by subtracting signal thresholds for on- and off-frequency precursor conditions with a single fixed masker level. The fixed masker level used is indicated in parentheses. A 95% confidence interval (CI) was constructed for the two-point gain change estimates. The sixth and seventh columns compare the additivity-of-forward-masking (AFM) threshold predictions (when data were available) and measured on-frequency precursor thresholds.

Subject	Gain, 0.8-kHz Pre	Gain, 4.0-kHz Pre	Gain change	Two-point gain change	Two-point 95% CI	Additivity pred	Measured value
S1	45.37	29.50	15.86	16.17 (70 dB)	14.60, 17.74	38.47	43.93
S2	41.75	–	–	9.10 (80 dB)	4.95, 13.23	–	47.00
S3	55.60	–	–	20.28 (75 dB)	16.29, 24.60	–	41.79
S4	45.66	37.05	8.60	8.56 (75 dB)	7.81, 9.31	38.15	41.38
S5	43.33	32.54	10.79	12.03 (65 dB)	10.34, 13.72	35.28	39.03
S6	44.89	–	–	9.62 (75 dB)	7.96, 11.28	34.74	39.86

Similar to Jennings et al. (2009) we compared the size of the TE to predictions assuming that there is no gain reduction and that the excitatory effects of the precursor and masker simply add. This is called additivity of forward masking (AFM) (e.g., Penner and Shiffrin, 1980; Plack and O’Hanlon, 2003). For S1, S4, S5 and S6 signal thresholds were measured with an on-frequency precursor alone and a 20-ms delay in place of the masker (plus symbols in Fig. 2). Thresholds in the off-frequency precursor condition were assumed to represent thresholds with the off-frequency masker only (for a particular fixed level). The processing by the auditory periphery can be modeled with each subject’s fitted I∕O function. After passing each of the single-masker thresholds through the subject’s I∕O function, the intensities of these output values were summed and passed inversely through the I∕O function to derive threshold predictions. As shown in Table 1, AFM under-predicted true thresholds with both precursor and masker. This result is consistent with results reported in Krull and Strickland (2008), and Jennings and Strickland (2010).

EXPERIMENT 2: PRECURSOR DURATION AND SIGNAL DELAY

The goal of Expt. 2 was to measure the time course of the TE. With the more efficient technique established in Expt. 1, a single masker level was selected and held constant for the remainder of the study. We assume that this masker produces primarily excitatory masking. There was no delay between masker offset and signal onset, so that the excitatory masking was held constant. The TE is the change produced by the precursor. It is assumed that the precursor does not affect the masker, because the masker response at the signal place should be linear, and thus wouldn’t be affected by a decrease in gain. The time course of the TE was measured by varying the precursor duration and the delay of the masker-signal complex from the precursor. These two parameters were varied independently.

Methods

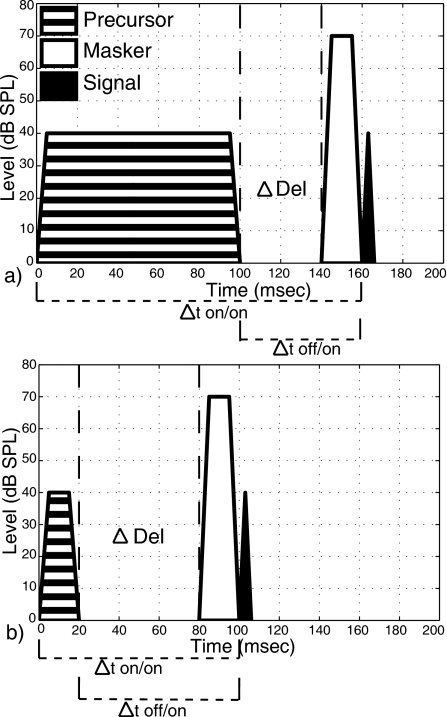
The subjects were the same as those in Expt. 1. Data from S6 are not shown for the signal-delay experiment because a complete set of stable thresholds could not be obtained due to time constraints. The masker level selected for each subject from Expt. 1 was fixed and signal level was varied to estimate signal threshold. The precursor duration was set from 5–100 ms. Five ms cos² ramps were used for all durations except 5 ms, where ramps were 2.5 ms. Figure 3 shows a schematic of the stimulus conditions for Expt. 2. Two ways of measuring the time delay between the precursor and the masker-signal complex are shown in Fig. 3. One metric, Δt_off∕on, is the time between the offset of the precursor and the onset of the signal. For this metric the delays were constant across precursor duration, so it is useful for describing the conditions. It is also the appropriate metric for examining whether the results are consistent with a simple decay of the TE after the precursor. The other metric used for the time course is Δt_on∕on. This is the time delay between the onset of the precursor and the onset of the signal. This metric is more relevant for comparing the time course of the TE to the time course of the MOCR, assuming the precursor elicits the MOCR.

Figure 3.

Schematic showing spectral and temporal characteristics of stimuli used in Expt. 2. Panels (a) and (b) show two example conditions. For precursors of various durations, a delay was inserted between the precursor and masker. Delays are specified in terms of precursor offset to signal onset (Δt_off∕on) or precursor onset to signal onset (Δt_on∕on). The minimum-delay condition is Δt_off∕on=20 ms due to the presence of the masker. As in Expt. 1, highpass noise was present in all conditions.

For each precursor duration, Δt_off∕on was set between 20–140 ms. The shortest delay was 20 ms because of the presence of the masker (see Fig. 3) and this will be referred to as the minimum-delay condition. The specific precursor durations and signal delays (in units of Δt_off∕on) are shown in Table 2. Not all precursor duration-signal delay conditions were used for all subjects. Each precursor condition was tested with an off- and an on-frequency precursor to control for attentional effects.

Table 2.

Conditions used in Expt. 2. Not all delays were used for all precursor durations. The average off-frequency precursor thresholds for all duration and delay conditions (used to derive the temporal effect) are presented with their standard deviations (SD). *Note that for S5 and S6 off-frequency precursor thresholds were not obtained for all conditions and, thus, the average standard deviations are higher.

	Off-frequency precursor average (SD)	Fixed masker level	Precursor duration	Δtoff∕on
S1	27.87 dB (0.84)	70	100, 50, 20, 10, 5	20, 40, 60, 100, 120, 140
S2	37.60 dB (0.59)	80	100, 50, 20, 10, 5	20, 40, 60, 100
S3	22.00 dB (0.59)	75	100, 50, 20, 15, 10, 5	20, 40, 60, 100
S4	32.82 dB (0.70)	75	100, 50, 20, 10	20, 22, 24, 26, 40, 60, 100
S5	26.60 dB (2.46)*	65	100, 50, 20, 15, 10, 5	20, 40, 50, 60, 70, 100, 120
S6	29.77 dB (2.02)*	75	100, 50, 30, 20, 10, 5	N∕A

Results

Precursor Duration

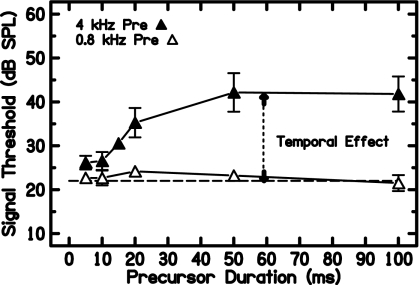
In Fig. 4, representative data from one subject are plotted as a function of precursor duration in the minimum-delay condition. On-frequency precursor thresholds increased with precursor duration up to 50 ms. No systematic differences were evident in off-frequency precursor thresholds as a function of duration. This also was true for the other delay conditions (not shown). For each subject, a grand average (across precursor duration and delay) was taken of the off-frequency precursor thresholds. This value was subtracted from that subject’s on-frequency precursor thresholds to obtain the TE.

Figure 4.

Thresholds for S3 in the on-frequency (filled symbols) and off-frequency (open symbols) precursor conditions as a function of precursor duration. No systematic differences were seen for off-frequency precursors across conditions (including delay, not shown), so a grand average was taken of all off-frequency precursor thresholds. The temporal effect is defined as the difference between on-frequency precursor thresholds and the average off-frequency precursor thresholds (dashed line).

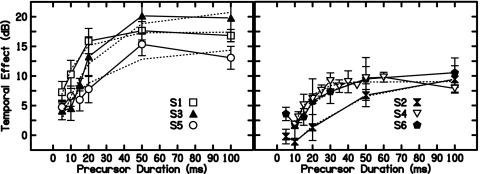
In Fig. 5, the TE as a function of precursor duration is plotted for each subject for the minimum-delay condition. With the 40-dB SPL precursor used in this study, maximum TEs ranged from approximately 10 to 20 dB. All subjects showed a rapid buildup in TE as precursor duration increased from 5 to 20 ms. For some subjects the TE plateaus or rolls over for further increases in precursor duration. For others no plateau was reached at the maximum duration measured. The dotted lines are exponential rising fits and will be discussed later.

Figure 5.

The TE for each subject as a function of precursor duration for the minimum-duration condition. The TE is the difference between on-frequency precursor and off-frequency precursor conditions. Data are divided into two panels for clarity. Dotted lines are fits with exponentially rising functions [Eq. 6].

Signal Delay

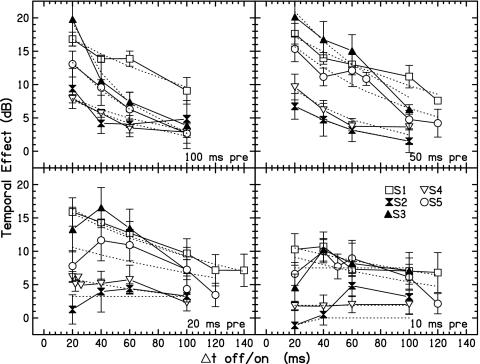
In Fig. 6, the TE for all subjects is plotted as a function of Δt_off∕on. Each panel shows all subject data for a different precursor duration. This way of plotting the data fits with traditional interpretations of the effect of the precursor, which would be that its masking adds to that produced by the masker (AFM). Masking models which assume persistence of excitation provide a framework for this interpretation and predict that the TE will decay monotonically as a function of Δt_off∕on. With precursor durations of 100 and 50 ms (upper panels), subjects show a monotonic decrease in TE as signal delay is increased. With shorter precursor durations some subjects show an increase followed by a decrease in TE with delay.

Figure 6.

The TE as a function of Δt_off∕on for four precursor durations (across panels). Dotted lines are fits to the data with exponentially decaying functions [Eq. 5].

The data in Fig. 6 were fitted with exponential decay functions (dotted lines), which will be called the Exponential Decay Model. The estimate of the TE over time is given by

$$\text{TE}\left(\text{t}\right)=\text{G}\times \text{exp}\left(-\text{t}∕{\tau }_{\text{off}∕\text{on}}\right),$$ (5)

where t is time (adjusted to begin at 20 ms), G is the peak TE and is an estimate of maximum gain change, and τ_off∕on is the time constant. Estimates of τ_off∕on and the RMS error of the fits for 100, 50, 20 and 10 ms precursor durations are presented in Table 3. For most subjects, data for shorter precursor durations were not as well fit with an exponential decay function as were the longer precursor durations. This is indicated by increasing RMS errors and very large estimates of τ_off∕on. Of course, the exponentially decaying fits miss the nonmonotonic changes occurring with the shorter precursor data.

Table 3.

Estimates of time constants from the fits of an exponential decay function [Eq. 5] to the individual data in Fig. 6. Also shown are the RMS errors. Very large time constants and∕or larger RMS errors are seen for shorter precursors for most subjects.

	100-ms precursor		50-ms precursor		20-ms precursor		10-ms precursor
	τoff∕on	RMS error	τoff∕on	RMS error	τoff∕on	RMS error	τoff∕on	RMS error
S1	142.72	0.74	143.66	0.89	141.90	0.48	203.57	0.82
S2	85.00	1.61	53.61	0.05	>10 000	1.19	>10 000	2.30
S3	40.82	0.89	83.92	1.43	148.95	2.24	>10 000	2.05
S4	65.17	0.46	60.16	0.84	109.43	0.77	>10 000	0.12
S5	53.51	0.28	89.75	1.50	175.94	2.27	152.33	1.89

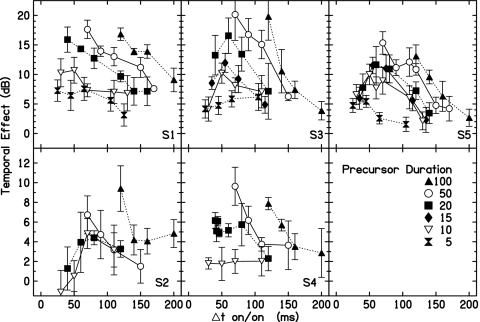
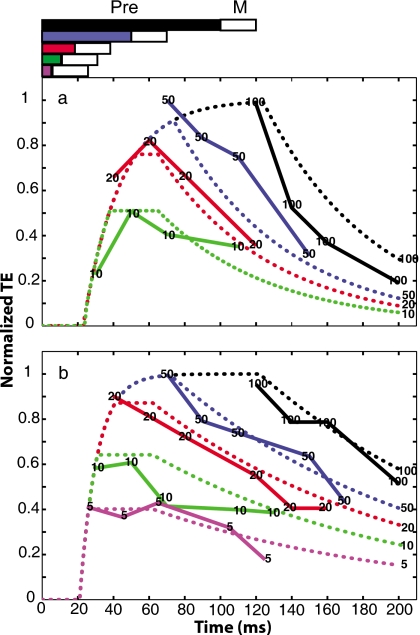
As was mentioned in the Introduction, physiological data examine the time course of the MOCR (suppression of OAEs) relative to acoustic elicitor onset. If the precursor is an elicitor of MOCR activity, Δt_on∕on is the relevant metric. In Fig. 7 the TE is plotted as a function of Δt_on∕on across durations and delays. The bottom two panels show data for S2 and S4, who have small TEs and thus a different ordinate scale from the top three panels. For S2, S3 and S5, the TE does not decay in a simple manner as a function of Δt_on∕on for shorter precursor durations. Instead, there is a buildup in the TE followed by a decay. The peaks of the shorter precursor functions all occur within a time window between 25 and 75 ms. For all subjects, thresholds in the minimum-delay condition increase as a function of duration. Thus the TE may increase with precursor duration and with signal delay. Both of these effects may be consistent with an MOCR hypothesis, as will be examined in the next section.

Figure 7.

The TE as a function of Δt_on∕on for all precursor durations. Each listener’s data are presented within a panel. Note that the ordinate scales are different in the top and the bottom rows.

Modeling

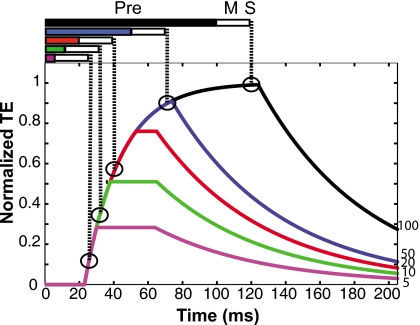
For the short precursors, all listeners showed either an increase (S2, S3 and S5) or no change (S1 and S4) in the TE for short delays rather than a simple decrease. This is not easily explained by hypotheses such as neural adaptation or persistence of excitation, both of which predict a decrease in TE with delay. However, it may be consistent with the sluggish onset of the MOCR. A model was developed to explore a gain reduction explanation of the data quantitatively based on the four segments of the time course measured by Backus and Guinan (2006), described in the Introduction. A schematic of this model is shown in Fig. 8. In this model we assume that the precursor elicited the MOCR, and that the TE can be interpreted as a reduction in gain.

Figure 8.

Schematic depicting the MOCR model of predicted TE with different precursor durations. Bars above the figure panel represent precursors of different durations, followed by a 20-ms masker (open bar). The highlighted points in the figure show the predicted TE for the signal with each precursor duration in the minimum-delay condition. The maximum value in the model is normalized to each subject’s maximum TE.

The precursor durations are shown above the figure panel in Fig. 8. In all cases there is a 20-ms gap between precursor offset and signal onset because of the presence of the masker, represented as open bars above the figure panel. This is the minimum-delay condition. Of interest is the size of the TE at the onset of the signal for each precursor duration, shown by circles in the schematic. The first two segments of the schematic are the onset delay and exponential buildup in the TE. The onset delay is shown by the flat line starting from the beginning of the precursor. This is followed by exponential buildup over some time. The schematic suggests that the buildup of the MOCR may be traced by the thresholds across precursor duration in the minimum-delay condition. Fitting these thresholds may give an estimate of the buildup time constant.

The minimum-delay data across precursor duration were fitted with the following equation:

$$\text{TE}\left(\text{t}\right)=\text{G}\times \left(1-\text{exp}\left(-\left(\text{t}-\text{o}\right)∕{\tau }_{\text{on}∕\text{on}}\right)\right)$$ (6)

with G, o, and τ_on∕on as free parameters. Parameter G represents the peak value and is an estimate of maximum gain change, t is time from the onset of the precursor, o is an estimate of the onset delay, and τ_on∕on is the buildup time constant. The estimates of gain change, onset delay and buildup time constant are presented in Table 4. The fits are shown by the dashed lines in Fig. 5. The onset delays are roughly similar to those reported by Backus and Guinan (2006), and the buildup time constants are consistent with those reported by Walsh et al. (2010b) with the short analysis window.

Table 4.

Parameter estimates from exponentially rising fits to the minimum-delay data [Eq. 6]. The minimum-delay fits provide parameter estimates for generating MOCR models (i.e., Fig. 9).

	Gain (G)	Onset delay (o)	τon∕on	RMS error
S1	17.39	20.06	9.74	0.61
S2	10.47	34.15	36.63	0.18
S3	20.92	22.21	20.76	1.39
S4	8.74	27.88	9.46	0.67
S5	14.59	16.80	25.14	1.43

The schematic also shows how the data for longer delays were fitted. For the 100- and 50-ms precursors it was assumed that the MOCR built up over the duration of the precursor, followed by an offset delay and exponential decay. The offset delay is the time from the offset of the precursor to the start of the decay of the function and is equal to the onset delay [estimated from the fits with Eq. 5]. The exponential decay was estimated by the average of the 100- and 50-ms precursor decay fits (shown in Table 3). These are faster than the 160-ms decay time constants reported by Backus and Guinan (2006).

For precursor durations of 20 ms and less, some assumptions had to be made based on the data of James et al. (2005). That study found that for elicitors of 40 ms or shorter, the MOCR did not begin to decay until approximately 40 ms after the onset delay. It is not clear from that study if the size of the MOCR built up for longer than the elicitor duration, or whether the offset delay was longer and dependent on elicitor duration.

As shown in the schematic, a model has been created that includes the time segments described by Backus and Guinan (2006), with the addition of a minimum-duration plateau for short precursors based on findings by James et al. (2005). This is called the MOCR Model. For each listener, it was assumed that the buildup time constant and the decay time constant were the same across precursor duration. These values were already determined using Eqs. 5, 6. What remained to be determined were the buildup time and the duration of the offset delay for precursor durations of 20 ms and less. Initially the data in the present study were fitted with the buildup time constrained to be equal to the duration of the precursor, and the offset delay lengthened to extend the TE for 40 ms after the onset delay. However, this did not fit the data well. Therefore, a parameter was added that made the buildup time proportional to the precursor duration, but still adjusted the offset delay so that the duration from the onset delay was 40 ms. For example, when the buildup fraction was 1.5, the 20-ms precursor effect was allowed to build up for 30 ms (1.5×20), and the plateau following was 10 ms (40-ms minimum duration minus 30-ms buildup). The same buildup fraction was applied to 15, 10, and 5 ms precursors. The buildup fraction resulting in the smallest RMS error was determined. The fractional buildup is shown for each subject in Table 5. The schematic (Fig. 8) shows that maximum TE grows with precursor duration. Walsh et al. (2010b) (Fig. 9) reported a similar effect of elicitor duration in their nSFOAE study.

Table 5.

RMS errors of fits to the data from two models. Corrected RMS errors were obtained by dividing total RMS error by degrees of freedom, where degrees of freedom is given by number of data points (n) minus number of parameters (p). The exponential decay model fits are presented as dotted lines in Fig. 6. The uncorrected RMS errors did not take into account number of model parameters. For the exponential decay model RMS errors were obtained by combining RMS errors for the exponentially decaying fit (Table 3) across durations.

	Exponential decay model			MOCR model
	Uncorrected RMS error	Degrees of freedom (n-p)	Corrected RMS error	Fractional buildup	Uncorrected RMS error	Degrees of freedom (n-p)	Corrected RMS error
S1	0.80	15	0.05	1.03	1.17	20	0.06
S2	1.76	8	0.22	1.95	1.70	11	0.15
S3	1.65	12	0.14	1.50	2.19	19	0.12
S4	0.65	11	0.06	0.38	1.23	14	0.09
S5	1.84	18	0.10	2.40	1.75	25	0.07

Figure 9.

(a) Data for S3 (number symbols and solid lines) and MOCR model predictions (dotted lines). Number symbols indicate the precursor duration. Numbers to the right of the dotted lines indicate the duration of precursor corresponding to the predicted effect size. For clarity, the 15-ms precursor condition was omitted from this figure. Bars above the figure panel show the temporal characteristics of the precursor and masker. (b) Data for S1 and the MOCR model predictions.

Figure 9 shows model predictions and measured data for two subjects. As noted previously, for the short precursor durations, listeners showed either a buildup (S2, S3 and S5) or no change (S1 and S4) in the TE for short delays. Panel a shows the predicted and measured data for S3. The model predicts a buildup in the TE at short delays for 10- and 20-ms precursors. Model predictions and measured data for S1 are shown in panel b. The model predicts decay or a plateau at short delays for all precursor durations for S1. RMS error values of the fits are presented in Table 5.

We used a procedure described by Rosen et al. (1992) to compare the MOCR Model to the Exponential Decay Model. In this procedure RMS errors may be compared after accounting for the number of model parameters. In the Exponential Decay Model, G and τ_off∕on were allowed to vary for each precursor duration, resulting in a total of 8–12 parameters depending on the number of precursor durations tested. In the MOCR Model the fit is constrained to a total of five parameters that have been described above: G, τ_on∕on, τ_off∕on, buildup fraction, and o (which was both onset and offset delay). A corrected RMS error was calculated by dividing the total RMS error for each method by the degrees of freedom. The corrected RMS error values are shown in Table 5.

For the subjects that show buildup in their data (S2, S3, and S5) the MOCR model resulted in a lower corrected RMS error than the Exponential Decay Model, although all RMS values are small. The MOCR Model predicts the buildup in the data and the Exponential Decay Model does not. However, because the buildup effect occurs over only a few decibels, missing this trend does not significantly increase the RMS error. It is apparent from Fig. 8 that capturing this buildup, essentially a moving target, is dependent on a window of a few milliseconds. Individual variability in onset delays and time constants, and∕or amount of gain from trial to trial easily could influence how well the buildup was captured. These factors also could explain variability in thresholds that remained despite repeated trials for shorter precursors with shorter delays. With shorter onset delays the entire predicted MOCR function could be shifted left-ward on the abscissa. This would mean that the signal would be predicted to fall on the plateau or decay part of the function, which could lead to unusually fast buildup time-constant estimates (as seen for S1 and S4). This is demonstrated for S1 in Fig. 9b. Subjects who did show buildup within precursor duration for short delays (S2, S3 and S5) had buildup time constants similar to those reported by Walsh et al. (2010b) for nSFOAEs when a 20-ms analysis window was used. This suggests that the minimum-delay points for these subjects are positioned as shown in Fig. 9a (not on the plateau) and are capturing the buildup phase of the MOCR.

DISCUSSION

New technique to measure the TE

Expt. 1 established an efficient method for measuring the TE that can be directly interpreted as a change in gain. This technique assumes there are two mechanisms of forward masking, excitatory masking and gain reduction, each of which follows a distinct time course. The masker duration was approximately equal to the onset delay of the MOCR. We assumed the masker produced a fixed amount of excitatory masking throughout the experiment. The precursor offset was 20 ms before the signal onset and was at least 5 ms in duration, and thus it was assumed that it was activating the MOCR, based on the findings of James et al. (2005). The I∕O function fits to the GOM functions supported the idea that the precursor was causing a change in gain.

The more efficient technique established in Expt. 1 is an improvement over other measurements of the TE in simultaneous and forward masking. For example, in Strickland (2004), the TE was measured for a short tone in a long simultaneous masker, as a function of the onset of the signal relative to the masker. The size of the temporal effect depended on signal level, varying from 0 dB at low and high signal levels to as much as 20 dB at mid signal levels. In that paper, the whole range of TEs could be fitted by a single change in the gain of the I∕O function. In the forward-masking technique used in the present paper, the TE itself is an estimate of the change in gain. The maximum change in gain observed in the present study was 20 dB, which is consistent with estimates from previous studies using simultaneous masking (Strickland, 2004; Strickland and Krishnan, 2005; Strickland, 2008) as well as physiological studies of the MOCR (Murugasu and Russell, 1996). The consistency in the maximum gain change across different psychophysical studies supports the idea that they may be measuring the effect of the MOCR, and that this effect is of considerable magnitude.

Time course of the TE

Expt. 2 was designed to separate the effects of precursor duration from the effects of signal delay in determining the time course of the TE. Although previous studies have examined this time course, the surprising finding in this study was the observation of the buildup of TE with delay for short precursors. This is important in differentiating the gain-reduction effect from the effects of neural adaptation and temporal integration (i.e., the “temporal window”). Neither of these latter mechanisms would be expected to show an increase in TE with signal delay.

The buildup with precursor duration for the minimum-delay condition (Fig. 5) has been seen in a previous study. Oxenham and Plack (2000) examined the effects of masker duration for a noise masker and a 6-kHz sinusoid. The sinusoid onset was delayed either 0 or 20 ms from the masker offset. In the 20-ms delay condition, the effect of masker duration was very similar to what is shown in Fig. 5, with signal threshold reaching a plateau above 30 ms. In the 0-ms delay condition, where excitatory masking also would play a role, thresholds continued to increase to the longest masker duration tested, 200 ms. In the Oxenham and Plack paper, the temporal-window model was able to provide a reasonable fit to the overall data, but did not capture the change in slope of the growth of threshold with duration between the two delay conditions. In the first paper establishing the present technique, Krull and Strickland (2008) found that a 40-ms precursor produced as large a TE as a 160-ms precursor, consistent with the present study.

The buildup with signal delay seen in Fig. 7 was seen only for short precursors and delays near 20 ms. As far as we know, no other studies have examined these particular conditions, where this surprising effect is found. In studies of the TE in simultaneous masking, the typical approach has been to find the precursor duration that produces a large effect, then use that (long) precursor duration to look at effects of delaying the signal and simultaneous masker.

Three listeners showed a decrease in the TE as the precursor duration increased from 50 to 100 ms. This also is in accord with the gain-reduction explanation. The precursor itself should be reduced in level by the gain reduction after a long enough time course. Again, this decrease is not predicted by models of neural adaptation or persistence of excitation.

The results of Expt. 2 show that an acoustic stimulus as short as 5 ms can produce a TE, but a 20- to 50-ms precursor is required to produce the maximal effect, as shown in Fig. 5. The maximal TE is reached 70–75 ms after the onset of the precursor (Fig. 7). The results were fitted well with a model incorporating the four time segments for the MOCR described by Backus and Guinan (2006) with the addition of a fractional buildup for precursor durations ≤20 ms. The onset and offset delays are in the range reported by Backus and Guinan (2006), although the buildup and decay time constants in the present study were shorter. Buildup time constants we report are similar to those reported by Walsh et al. (2010b) for nSFOAEs using their short analysis window.

It is possible that the paradigm used in the present study precluded measuring the time course as accurately as has been possible in OAE studies. First, the TE had not fully decayed at the longest delays we measured, and thus the decay time constant must be viewed with some caution. Second, in our study the off-frequency masker duration may have been longer than the onset delay. This could prevent us from capturing the buildup and could lead to abnormally short estimates of buildup time constants as discussed above.

Relationship between the TE and the MOCR

This buildup, together with the reduction in the gain of the GOM function shown in Expt. 1, and the decrease in frequency selectivity shown in Jennings et al. (2009) support the hypothesis that the TE in forward masking is mediated by the MOCR. The reduction in gain and decrease in frequency selectivity seen in simultaneous masking (Strickland 2001, 2004; Strickland and Krishnan, 2005; Strickland, 2008) support the idea that the same TE is being measured in simultaneous and forward masking. The simultaneous masking condition is probably more ecologically relevant, and gain reduction in this case generally produces an improvement in the signal-to-noise ratio, which would be a benefit while listening in noisy conditions.

Psychophysical studies have shown larger overshoot at 4 kHz than 1 kHz (e.g., Strickland, 2001), a finding consistent with physiological studies in animals that show larger MOCR effects at high frequencies than low frequencies (e.g., Kawase et al., 1993). Conversely, Lilaonitkul and Guinan (2009a) have found larger MOCR effects at 1 kHz than 4 kHz in sFOAEs. The reason for this discrepancy is not clear, but is considered in detail in their paper. Two recent studies have attempted to more directly correlate psychophysical overshoot and MOC effects observed in OAEs using a 4-kHz tone in broadband noise. Walsh et al. (2010a) suggested a link between their psychophysical and physiological results, while Keefe et al. (2009) did not. This method of more direct comparison across techniques may shed more light on whether the TE is mediated by efferent processes or by more central mechanisms.

CONCLUSIONS

• 1.A more efficient method of measuring the TE in forward masking predicts the same gain change as measuring the entire GOM function.
• 2.A buildup in the TE with signal delay can be observed for some listeners, for short precursors and short delays, which is not consistent with neural adaptation or persistence of excitation. In the minimum-delay condition, a buildup also is seen with precursor duration.
• 3.Both of these outcomes can be modeled by gain reduction that follows the time course of the MOCR.