Abstract
Bernstein and Trahiotis [(2009). J. Acoust. Soc. Am. 125, 3234–3242] reported threshold interaural temporal disparities (ITDs) conveyed by the envelopes of 4-kHz-centered “raised-sine” stimuli. A raised-sine stimulus consists of a carrier modulated by a sinusoid raised to an exponent. Such stimuli permitted Bernstein and Trahiotis to vary, independently, stimulus modulation frequency, modulation depth, and “relative peakedness∕deadtime.” An interaural correlation-based model that included stages mimicking peripheral auditory processing captured most of the data save for an overestimation of threshold ITDs obtained when the depth of modulation was 25% and the raised-sine exponent was 8.0. The purpose of the present study was: (1) to present a quantitative evaluation of how well other measures, including normalized envelope fourth moment, envelope peakwidth, and envelope “deadtime” might also account for the data reported by Bernstein and Trahiotis and (2) to present new threshold ITDs measured while varying, factorially, depth of modulation, raised-sine exponent, and modulation frequency. Quantitative analyses of both the prior and the new data showed that the normalized interaural correlation, computed subsequent to peripheral auditory processing, provided the most accurate predictions. Importantly, the overestimation of threshold ITDs did not occur when it was assumed that listeners can employ information within “off-frequency” auditory filters.
INTRODUCTION
Historically, the processing of interaural temporal disparities (ITDs) conveyed by the envelopes of high-frequency signals has been found to be less efficient than the processing of ITDs conveyed by the waveforms (i.e., fine-structure and envelope) of low-frequency signals (e.g., Klumpp and Eady, 1956; Zwislocki and Feldman, 1956; McFadden and Pasanen, 1976; Nuetzel and Hafter, 1976; Henning, 1980; Bernstein and Trahiotis, 1982, 1994; Blauert, 1983). Over the last decade, experiments employing special, “transposed,” stimuli have consistently revealed that ITD-processing at high frequencies can be enhanced in terms of resolution of ITDs, extents of ITD-based laterality, and resistance to binaural interference (e.g., Bernstein and Trahiotis, 2002, 2003, 2004, 2005). Such enhancements indicate that ITDs conveyed by the envelopes of high-frequency, complex signals can approach, and often rival, the potency of ITDs conveyed by low-frequency stimuli.
Recently, we reported the results of an investigation employing “raised-sine” high-frequency stimuli (Bernstein and Trahiotis, 2009). The generation of raised-sine stimuli, originally described by John et al. (2002), entails raising a DC-shifted sine-wave to a power greater than or equal to 1.0 prior to multiplication with a carrier. The equation used to generate such stimuli and published in Bernstein and Trahiotis (2009) is
| (1) |
where fc is the frequency of the carrier, fm is the frequency of the modulator, and m is the index of modulation. The exponent, n, denotes the power to which the DC-shifted modulator is raised and is the parameter that directly determines the peakedness or “sharpness” of the individual “lobes” of the envelope.
What may be a more intuitive form of Eq. 1 was recently suggested to us by Dr. William M. Hartmann:
| (2) |
In Eq. 2, the expression enclosed within the square brackets represents the modulator; the quantity to the left of the bracketed expression represents the carrier. Examples of raised sine waveforms generated with m=1.0 and values of n of from 1.0 to 8.0 can be found in Bernstein and Trahiotis (2009).
The advantage of using raised-sine stimuli is that they permit one to manipulate, independently, the modulation frequency, the modulation depth, and the relative “peakedness∕deadtime” of the envelope of a high-frequency waveform while also suitably restricting its spectral content. These are features that cannot be varied independently with conventional stimuli such as sinusoidally amplitude-modulated (SAM) tones, repeated Gaussian clicks (e.g., Buell and Hafter, 1988; Stecker and Hafter, 2002) or the transposed tones employed in our previous studies.
Using these types of stimuli, Bernstein and Trahiotis (2009) found that increases in raised-sine exponent, depth of modulation, and rate of modulation generally led to decreases in threshold ITD. For the most part, those changes in threshold ITD were captured well by a model based on the normalized interaural correlation (i.e., the index of the normalized interaural correlation, which is the value of the normalized cross-correlation function at lag-zero) calculated subsequent to stages mimicking peripheral auditory processing. An important exception was the model’s overestimation of threshold ITDs obtained when m equalled 0.25 (i.e., the depth of modulation was 25%) and the raised-sine exponent was 8.0.
The present study had two purposes. The first was to present a quantitative evaluation of how well, in addition to the normalized interaural correlation, other measures might also account for the data reported by Bernstein and Trahiotis (2009). The measures evaluated were normalized envelope fourth moment, envelope peakwidth, and envelope deadtime (all defined in detail below). The second purpose was to obtain new threshold ITDs measured while varying, factorially, depth of modulation, raised-sine exponent, and modulation frequency. It will be seen that, of the measures explored, normalized interaural correlation, computed subsequent to peripheral auditory processing, provided the most accurate predictions for both the prior and the new data. In addition, it will be shown that the shortcoming of the normalized interaural correlation-based model mentioned above can be remedied if it is assumed that listeners can employ information within “off-frequency” auditory filters.
BACKGROUND AND GENERAL METHODS
The motivation for investigating the predictive value of envelope fourth moment, envelope peakwidth, and envelope deadtime, stems from the recognition that the normalized interaural correlation is a statistic that can reflect the influence(s) of many aspects of the physical stimuli. Therefore, models based on interaural correlation do not provide information concerning whether, or to what degree, other measures quantifying the envelopes of the stimuli might account for sensitivity to changes in ITD. The purpose of this study was to begin to provide such information.
The envelope measures that are the focus of this study are quantifiable variables that have, in prior published investigations conducted across several laboratories, been hypothesized to account for or to explain differences in the efficiency of envelope-based ITD-processing. For example, Dye et al. (1994) suggested that the binaural processing of ITDs conveyed by high-frequency stimuli could, in general, be accounted for by considering the degree to which the envelopes of the stimuli fluctuate. The measure Dye et al. used to quantify the degree of fluctuation of the envelope was the fourth moment of the envelope normalized by the square of the power (the second moment) of the envelope:
| (3) |
That statistic had been described in two earlier papers by Hartmann (1987) and Hartmann and Pumplin (1988). Dye et al.’s (1994) appeal to the utility of Y was that it accounted qualitatively for the fact that their listeners’ threshold ITDs were inversely proportional to Y. Subsequently, Bernstein and Trahiotis (2007) demonstrated that Y did not provide a successful explanation for variations in threshold ITDs obtained with a limited set of transposed stimuli, while the normalized interaural correlation did so.
Deadtime gains its status as a potentially useful measure based upon Hafter’s (1977) cogent discussion concerning how sensitivity to ITDs conveyed by the envelopes of high-frequency SAM tones might be determined by the “respites” (i.e., the pauses) between successive lobes of the envelope. In addition, it has long been argued that it is the lack of deadtime between the envelope lobes of conventional high-frequency complex stimuli, such as SAM tones, that is responsible for their yielding relatively large threshold ITDs and relatively small extents of ITD-based laterality (e.g., Blauert, 1983; Bernstein and Trahiotis, 1985). One important characteristic of many types of transposed and raised-sine stimuli is that they do have distinct deadtimes. Based on Hafter’s arguments, such deadtimes could enhance the processing of envelope-based ITDs. For the purposes of the analyses carried out here, the calculation of deadtime for each stimulus was made by finding the length of time over which the magnitude of the envelope (having a maximum possible value of 2.0) remained essentially at zero (i.e., zero ±0.005).
Relative peakedness∕sharpness of the envelope gains its status via ideas put forth by Blauert (1983). He suggested that the larger extents of ITD-based laterality typically obtained with low-frequency tones vs high-frequency SAM signals could result from peripheral auditory processing. Specifically, Blauert stated that “…a low-frequency signal undergoes a sort of half-wave-rectification during the signal processing in the inner ear, while the envelope of a high-frequency carrier is maintained as a full-wave signal. A half-wave-rectified signal may provide more distinct time cues than a full-wave signal, due to its transient features (p. 318).” In our view, the words “transient features” can be interpreted to encompass two distinct temporal aspects of the processed stimuli. On the one hand, they could refer to the relative peakedness∕sharpness of the transduced waveform during its “on-time.” On the other hand, they could refer to the “respites” (deadtime) discussed by Hafter (1977). For the purposes of this investigation, peakwidth was defined as the duration over which the magnitude of the individual lobes of the envelope is greater than or equal to 80% of its maximum value.
It occurred to us that all three measures could be relevant to understanding sensitivity to changes in ITD because, depending on the particular measure, increases or decreases in their values would, following peripheral auditory processing, result in distributions of neural responses that are relatively tightly synchronized. In turn, more tightly synchronized neural responses would be expected to foster greater precision in the discrimination of changes in ITD (see Batra et al., 1997).
In order to determine the extent to which changes in the three measures described above can account for the threshold ITDs reported by Bernstein and Trahiotis (2009), the values of all three measures were computed for their set of raised-sine stimuli. The computations were carried out on the physical stimuli and, separately, on the stimuli as processed via stages of a model (described in detail below) which were designed to emulate peripheral auditory filtering, rectification, and compression. In addition, the same type of analyses were conducted for new measures of threshold ITD that were obtained while varying, factorially, depth of modulation, the exponent of the raised-sine, and the frequency of modulation. The new data represent an extension of the conditions employed by Bernstein and Trahiotis. The parameters of the stimuli were chosen to shed further light on how sensitivity to changes in envelope-based ITD is affected by simultaneous variation of modulation frequency, modulation depth, and the exponent of the raised sine.
RELATION OF QUANTITATIVE ENVELOPE MEASURES TO THRESHOLD ITDS OBTAINED IN Bernstein and Trahiotis (2009)
Bernstein and Trahiotis (2009) measured threshold ITDs for 100% modulated (m=1.0) raised-sine stimuli having exponents (n) of 1.0 (equivalent to a SAM tone), 1.5, 2.0, 4.0, and 8.0 and for transposed-tones [see Eq. 2 above]. All stimuli were centered at 4 kHz. Thresholds were measured at rates of modulation ranging between 32 and 256 Hz. The duration of the stimuli was 300 ms, including 20-ms cos2 rise-decay ramps, and they were presented via Etymotic ER-2 insert earphones at a level of 70 dB SPL. A low-pass diotic noise (spectrum level equivalent to 30 dB SPL) was continuously present in order to preclude listeners’ use of low-frequency distortion products.
Threshold ITDs were measured using a two-cue, two-alternative, forced choice, adaptive task targeting 70.7% correct performance. Each trial consisted of a warning interval and four 300-ms observation intervals. The stimuli in the first and fourth intervals were diotic. The listener’s task was to detect the presence of an ongoing ITD (left-ear leading) that was presented with equal a priori probability in either the second or the third interval. Four normal-hearing adults served as listeners. Final values of threshold for each listener and stimulus condition were obtained by computing the median of 12 estimates. See Bernstein and Trahiotis (2009, p. 3235) for more details.
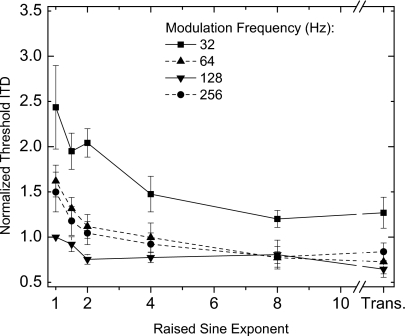
Figure 1 shows the data obtained by Bernstein and Trahiotis (2009) and presented in their Fig. 2. It displays mean “normalized” threshold ITDs, calculated across the four listeners. The normalization was accomplished by dividing each listener’s threshold ITD by his or her threshold ITD obtained when the stimulus was a SAM tone (raised-sine exponent equal to 1.0) having a frequency of modulation of 128 Hz. The error bars represent plus and minus one standard error of the mean normalized thresholds. Note that, for all four rates of modulation, threshold ITDs decreased with increases in the exponent of the raised-sine and approximated threshold ITDs obtained with transposed stimuli when the exponent was 8.0. In addition, threshold ITDs decreased with increases in rate of modulation from 32 to 128 Hz and then increased slightly when the rate of modulation was increased to 256 Hz.
Figure 1.
A re-plotting of the results of Fig. 2 from Bernstein and Trahiotis (2009). Mean normalized threshold ITDs, calculated across four listeners as a function of the exponent of the 4-kHz-centered raised-sine stimuli. Normalized threshold ITDs obtained with 4-kHz-centered transposed stimuli are plotted at the far right. The normalization was accomplished by dividing an individual listener’s threshold ITDs by that listener’s threshold ITD obtained with an SAM tone (raised-sine exponent equal to 1.0) having a frequency of modulation of 128 Hz. Error bars represent plus and minus one standard error of the mean normalized thresholds.
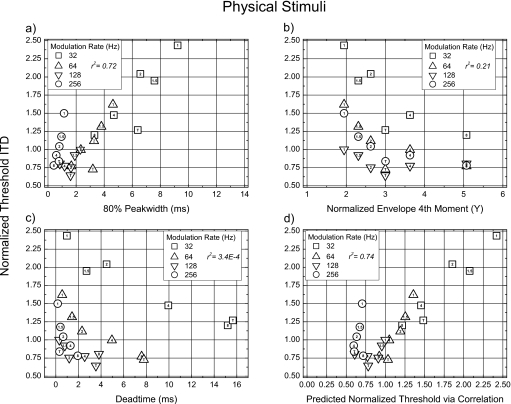
Figure 2.
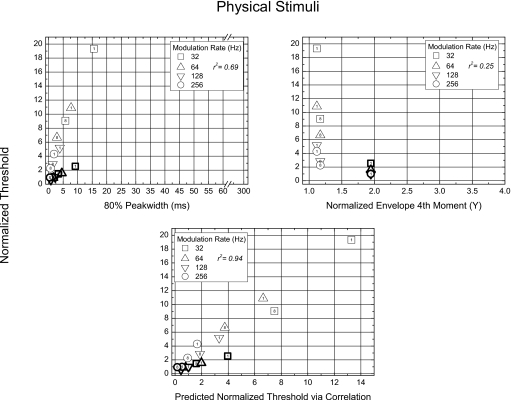
Normalized threshold ITDs plotted as a function of the values of each of four candidate envelope measures computed on the physical stimuli (see text). The parameter in each plot is rate of modulation and the value of the exponent of the raised-sine is indicated within each symbol. Threshold ITDs obtained with transposed tones are identified by a “T” within the symbol. The relevant value of the coefficient of determination, r2, is given in each panel.
We now turn to an evaluation of how well each of the measures described above, as well as the normalized interaural correlation, can account for these variations in the data. In what follows, each of the measures was calculated on the envelope of the stimulus as computed via the Hilbert transform. The parameter in each plot of Fig. 2 is rate of modulation and the value of the exponent of the raised-sine is indicated within each symbol. Threshold ITDs obtained with transposed tones are identified by a “T” within the symbol. The relevant value of the coefficient of determination, r2, is given in each panel.
Panel a relates mean normalized threshold ITDs to the value of peakwidth. The underlying goal here (and in panels b and c) is to evaluate how well changes in the parameters of the physical stimuli, per se, map to changes in obtained threshold ITDs. Save for the data corresponding to a rate of modulation of 256 Hz (circles), the predicted thresholds provide a good fit to the behavioral thresholds. In fact, when the “256-Hz data” are excluded, the value of r2 increases from 0.72 to 0.87.
Panel b relates mean normalized threshold ITD to the normalized fourth moment of the envelope (Y). At each rate of modulation, normalized threshold ITDs are essentially inversely related to the value of Y. It is the case, however, that the measure Y does not account for the data taken across rates of modulation. For example, raised-sine stimuli with an exponent of 2.0 all have values of Y near 2.6 but, depending on the rate of modulation, yield normalized threshold ITDs ranging from about 0.75 to just over 2.0. Clearly, Y is not a suitable measure for accounting for threshold ITDs obtained with the set of raised-sine and transposed stimuli employed. That impression is quantified by the relatively low r2 value of 0.21.
Panel c relates mean normalized threshold ITD to the duration of the deadtime. As was the case for the measure Y, deadtime does not account for the data taken across rates of modulation although, at each rate of modulation, deadtime and threshold ITDs are essentially inversely related. The value of r2 for these measures is, for all practical purposes, zero.
Panel d relates obtained normalized threshold ITDs to predicted normalized threshold ITDs. The predictions were made by assuming that, in order to perform the discrimination, a listener required a single, constant-criterion change in the normalized interaural correlation of the envelope (from the reference envelope correlation of 1.0 produced by an ITD of zero). To clarify, our assumption is that, to the extent that normalized correlation underlies performance, the obtained values of threshold ITD would reflect a single, threshold, value of change in interaural correlation brought about by changes in the ITD of the physical waveform.
In order to make the predictions, functions relating ITD to normalized interaural correlation were first determined for each particular combination of frequency of modulation and exponent. Sixth order polynomials were then fit to the paired values of normalized correlation and ITD using a least-squares criterion. The procedure determined the criterion value of normalized interaural correlation that maximized the amount of variance accounted for between predicted and obtained values of normalized threshold ITD. The patterning within the plot is extremely similar to that observed in panel a. This impression is bolstered by the fact that the r2 based on all of the data was found to be 0.74 and, once again, was found to increase (to 0.92) when the data obtained at rate of modulation of 256 Hz were excluded. The similarity between the results presented in panels a and d was expected because the relative peakedness of the lobes of the envelope determine the rate of decrease in the normalized correlation of the envelope with increasing values of ITD. Thus, based on both visual impressions and statistical analyses, it appears that the patterning of threshold ITDs in Fig. 2 is captured fairly well by stimulus-based measures of 80% peakwidth and normalized interaural correlation, but not by stimulus-based measures of the normalized envelope fourth moment or deadtime.
Let us now consider whether and how well envelope measures computed on the same stimuli as processed via stages of the normalized interaural correlation model used by Bernstein and Trahiotis (2009) can account for the threshold ITDs. Specifically, the model incorporates an initial stage of gammatone-based bandpass filtering at 4 kHz (see Patterson et al., 1995), envelope compression (exponent=0.23), half-wave square-law rectification, and low-pass filtering at 425 Hz to capture the loss of neural synchrony to the fine-structure of the stimuli that occurs as the center frequency is increased (Weiss and Rose, 1988). The model also includes a first-order (6 dB∕oct) Butterworth low-pass filter designed to attenuate spectral components of the envelope above 150 Hz. This type of filtering is in accord with Kohlrausch et al. (2000) and Ewert and Dau (2000) who measured and accounted for temporal modulation transfer functions using sinusoidally amplitude-modulated stimuli. The reader is referred to Bernstein and Trahiotis (2002, 2009) for further details.
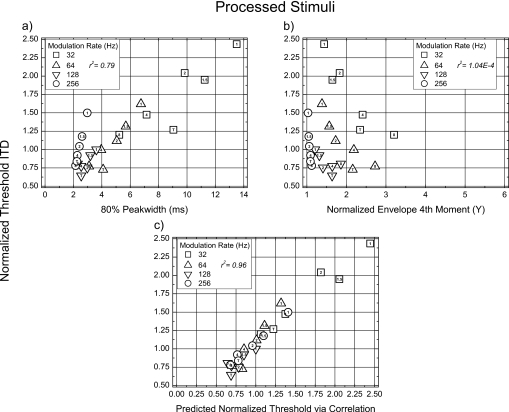
Figure 3 contains the relevant plots. It contains three panels, rather than four, because the stimuli as processed contained no deadtimes as defined above. This occurred primarily because the envelopes resulting from the peripheral processing of the stimuli included DC components that maintained their magnitudes substantially above zero. Rather than change the definition of deadtime in what would be an arbitrary and ad-hoc manner, it was decided to omit consideration of that measure.
Figure 3.
Similar to Fig. 2 with the exception that the envelope measures were computed on the stimuli as processed via stages of a model designed to mimic features of peripheral auditory processing. In contrast to Fig. 2, the measure “deadtime” was excluded because processing via the model rendered that measure invalid (see text).
Panel a of Fig. 3 relates normalized threshold ITD to the 80% peakwidth of the processed stimuli. Note that the relative ordering of the data is like that observed with the physical stimuli (panel a of Fig. 2) even though the values of peakwidth are now larger and extend over a greater range. The value of r2 between the threshold ITDs and the peakwidths of the processed stimuli is slightly larger than that found with the physical stimuli (0.79 vs 0.72). As was true for the physical stimuli, removing the data obtained at a rate of modulation of 256 Hz improves the degree of association between the variables, yielding an r2 of 0.90.
Panel b of Fig. 3 reveals that the processed stimuli are characterized by both smaller overall values of Y and a smaller range of values of Y than their unprocessed counterparts. Nevertheless, it is still the case that Y is a poor predictor of the data. In fact, the value of r2 for the processed stimuli approaches zero, indicating that the degree of association of Y and threshold ITD is substantially lower than that (r2=0.21) found with the unprocessed, physical stimuli.
Panel c of Fig. 3 relates normalized threshold ITDs to predictions of normalized threshold ITDs which were obtained by assuming a constant-criterion change in the normalized interaural correlation of the processed stimuli. These predictions, which were presented in a different format in Fig. 4 of Bernstein and Trahiotis (2009), are much more accurate than their counterparts computed on the physical stimuli. The value of r2 utilizing the processed stimuli is 0.96, indicating that almost all of the variance in the behavioral threshold ITDs is accounted for. The principal change in the patterning of the data is the alignment of the threshold ITDs obtained with a rate of modulation of 256 Hz with the threshold ITDs obtained with each of the three other rates of modulation. This result stems from the operation, within the model, of the 150-Hz low-pass filtering of the envelopes.
It is important to note that the similarities in the patterning of the data between panels a and d of Fig. 2 (for measurements on the physical stimuli) do not obtain for the panels a and c of Fig. 3 (for measurements on the processed stimuli). Specifically, the departure of the data collected at a rate of modulation of 256 Hz remains for measures of 80% peakwidth of the processed stimuli. It is absent, however, when normalized interaural correlation is used to predict the thresholds. This difference reflects the fact that the 150-Hz low-pass “envelope filter” increases the relative magnitude of the DC component at 256 Hz. That, in turn, affects the normalized interaural correlation such that a larger change in ITD is required to attain the criterion change that represents threshold. In contrast, alterations in the relative magnitudes of the DC components of the stimuli do not affect their 80% peakwidths. Thus, the relative placement of the measures of peakwidth for stimuli having a rate of modulation of 256-Hz is very similar for the physical stimuli and their processed counterparts.
Two general conclusions appear to follow: (1) as determined by Bernstein and Trahiotis (2009), the normalized interaural correlation of the stimuli as processed provides an excellent accounting of the patterning of the set of data and (2) normalized threshold ITDs do change systematically with measures of peakwidth, normalized fourth moment, and deadtime of the envelope within, but not across, rates of modulation. Therefore, these three measures do not appear, in and of themselves, to account for sensitivity to changes in envelope-based ITD obtained with parametric changes in rate of modulation and exponent of raised-sine stimuli. This is not to say that future research could not reveal some combination of the three measures, perhaps in conjunction with others, that will prove successful in accounting for threshold ITDs measured with the types of stimuli employed in this study. That eventuality notwithstanding, it seems to us that one could consider the normalized interaural correlation to be an index that, at least for the stimuli employed here, suitably incorporates the influence of not only peakwidth, deadtime, and normalized fourth moment, but perhaps also the influence of other measures that may be described∕discovered in the future.
FURTHER EXAMINATION OF THE INFLUENCE OF CHANGES IN MODULATION DEPTH
In this section, the results of a new experiment are compared to model predictions. In the new experiment, the parameters of the stimuli were chosen to test the generality of the earlier finding (Bernstein and Trahiotis, 2009) that the normalized interaural correlation model overestimated threshold ITDs when the frequency of modulation was 128 Hz, the depth of modulation was 25% and the raised-sine exponent was 8.0. Specifically, threshold ITDs were obtained with factorial combinations of four frequencies of modulation (32, 64, 128, or 256 Hz), two depths of modulation (25 or 100%), and two exponents of the raised-sine (1.0 or 8.0). All other parameters of the stimuli (duration, overall level, etc.) and the psychophysical procedure used to obtain the thresholds were the same as those used by Bernstein and Trahiotis and described above in section 2.
Four normal-hearing adults served as listeners, three of whom had participated in the earlier study. Particular stimulus combinations were chosen pseudo-randomly and three consecutive estimates of threshold were obtained for each of the 16 stimulus combinations (four frequencies of modulation X two depths of modulation X two values of the exponent of the raised sine) before moving on to the next one. Then, three more thresholds were obtained by re-visiting the same stimulus conditions in reverse order. The entire procedure was repeated, yielding twelve estimates of threshold for each stimulus condition. Values of threshold exceeding one-quarter period of the rate of modulation (rounded to the nearest 100 μs) were excluded. Across listeners and conditions, no more than three of the 12 individual measures of threshold were excluded for any single condition, save for one instance. For one of the listeners, threshold values could not be obtained that were less than or equal to one-quarter period of the 256-Hz rate of modulation when the depth of modulation was 25% and the exponent of the raised-sine was 1.0. For that condition and listener, the maximum “allowable” value of 1000 μs was recorded as the threshold ITD. The final values of threshold for each listener and stimulus condition were obtained by computing the median of the nine to twelve valid estimates that remained.
RESULTS AND DISCUSSION
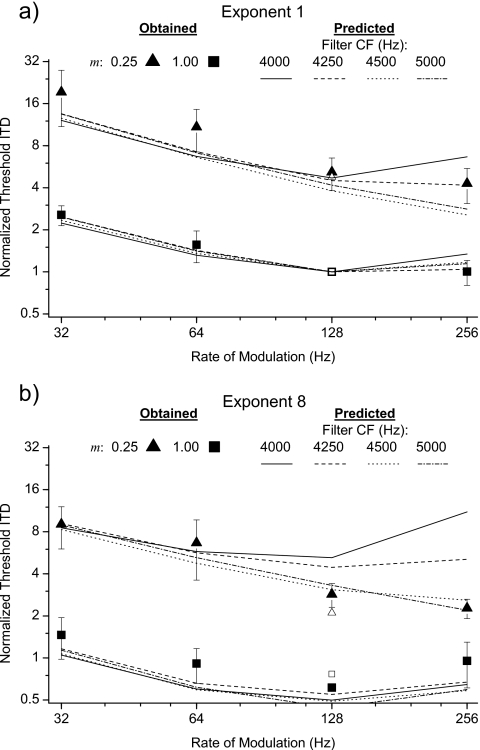
The mean normalized threshold ITDs are plotted in panels a and b of Fig. 4 as a function of rate of modulation for raised-sine exponents of 1.0 and 8.0, respectively. Closed triangles represent threshold ITDs obtained when the depth of modulation was 25% and closed squares represent threshold ITDs obtained when the depth of modulation was 100%. The error bars represent plus and minus one standard error of the mean. The lines in both panels represent predicted normalized threshold ITDs and will be discussed below. The open triangles and squares represent the earlier data from Bernstein and Trahiotis (2009) which were obtained with a rate of modulation of 128 Hz. The similarity between those thresholds and the ones obtained in the current experiment indicates successful replication.
Figure 4.
Mean normalized threshold ITDs as a function of rate of modulation, for raised-sine exponents of 1.0 and 8.0, respectively. Closed triangles represent thresholds obtained when the depth of modulation was 25%; closed squares represent thresholds obtained when the depth of modulation was 100%. Error bars represent plus and minus one standard error of the mean. The open triangles and squares represent data from Bernstein and Trahiotis (2009) which were obtained with a rate of modulation of 128 Hz. Solid and broken lines represent predicted values of threshold computed via an interaural correlation-based model and while employing auditory filters centered at the frequencies indicated in the legends.
Visual inspection of panels a and b reveal three general outcomes. First, threshold ITDs generally decreased when rate of modulation was increased from 32 to 256 Hz. When modulation depth was 100% (squares) and the exponent of the raised-sine was 8.0 (panel b), however, thresholds increased slightly when the modulation rate was increased from 128 to 256 Hz. A similar outcome had been reported in a number of prior studies (see Bernstein and Trahiotis, 2009). Second, for both values of the exponent, thresholds increased by about a factor of six when depth of modulation was reduced from 100 to 25%. Third, comparing panels a and b, increasing the exponent from 1.0 to 8.0 resulted in decreases in threshold of just slightly under a factor of two independent of rate and depth of modulation.
Note that the ordinate in both panels a and b is logarithmic. Consistent with that, the data in Fig. 4 were first transformed by computing their (base-2) logarithms and were then subjected to a three-factor (four modulation frequencies X two exponents X two modulation depths), within-subjects analysis of variance (ANOVA). The error terms for the main effects and for the interactions were the interaction of the particular main effect (or the particular interaction) with the subject “factor” (Keppel, 1991). In addition to testing for significant effects, the proportions of variance accounted for (ω2) were determined for each significant main effect and interaction (Hays, 1973).
Consistent with visual inspection of the data, the main effect of rate of modulation was significant (assuming an α of 0.05) [F(3,9)=17.2, p<0.001] and accounted for 15% of the variability of the data. This reflects the fact that, on average, threshold ITDs were lower for higher modulation frequencies. The main effect of depth of modulation was also significant [F(1,3)=174.1, p=0.001] and accounted for 56% of the variability in the data. This stems from the fact that, on average, threshold ITDs were smaller when the depth of modulation was 100% than when it was 25%. The main effect of raised-sine exponent was also significant [F(1,3)=115.5, p=0.002] and accounted for 6% of the variability in the data. This reflects the fact that, on average, threshold ITDs decreased when the value of the exponent was increased from 1.0 to 8.0. The interaction between rate of modulation and depth of modulation was significant [F(3,9)=5.1, p=0.024] and accounted for 1% of the variability in the data. This reflects the finding that the magnitudes of the relative changes in threshold ITD produced by changes in the rate of modulation depended, statistically, upon the depth of modulation. Overall, the statistical analysis reveals that 78% of the variability in the relative magnitudes of the threshold ITDs calculated across the four listeners is accounted for by the stimulus variables.
The solid lines in both panels depict predictions obtained using the model described earlier. That analysis assumed that the listener monitors the auditory filter centered at 4 kHz, the center frequency of the stimuli. The criterion change in normalized interaural correlation used to make the predictions was the same one used by Bernstein and Trahiotis (2009) in their earlier study and the one used to provide the fit to the data in panel a of Fig. 4.1 Recall that Bernstein and Trahiotis found that the model (and several variations of it) overestimated threshold ITDs for a rate of modulation of 128 Hz when the exponent of the raised-sine was 8.0 and the depth of modulation was 25%. Panel b of Fig. 4 indicates the same outcome. In addition, the new data obtained with a modulation depth of 25% reveal that overestimates of the model do not occur at rates of modulation of 32 and 64 Hz, but do occur at a rate of modulation of 256 Hz independent of whether the exponent is 1.0 or 8.0.
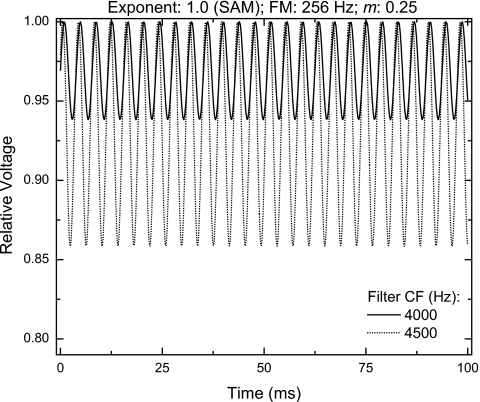
It occurred to us that the predictions of the model might be improved by assuming that the listener monitors activity in an auditory filter centered above the 4-kHz center frequency of the stimulus. In order to understand how such an improvement could occur, let us consider a SAM tone (equivalent to a raised-sine stimulus having an exponent of 1.0), a rate of modulation of 256 Hz, and a depth of modulation of 25%. For this stimulus, the amplitude of each of the pair of sidebands surrounding the 4-kHz carrier is 18 dB below the level of the carrier. The envelope of this stimulus, as “recovered” by peripheral auditory processing when the frequency of the auditory filter is 4000 Hz, consists, essentially, of a single 256-Hz component accompanied by a large DC offset. The resulting waveform, calculated via the “front-end” of the model described above is depicted as the solid function in Fig. 5. In contrast, the output of the model when the center frequency of the auditory filter was set to 4500 Hz is depicted by the dotted function in Fig. 5. Note that the two outputs have been normalized to their respective maximum values. This was done in order to make clear the fact that the output of the model resulting from the use of the higher frequency filter has a substantially lower relative DC offset than does its on-frequency counterpart. Now, within the model, all other things being equal, reducing the relative DC offset increases sensitivity to ITD because it increases the degree to which an ITD reduces the normalized interaural correlation from its base value of 1.0 (zero-ITD). This happens because the normalized interaural correlation includes and is sensitive to the value of the DC offset in each monaural input (see Bernstein and Trahiotis, 1996). Computer simulations revealed that similar effects also occur for the raised-sine stimulus having an exponent of 8.0, but those effects differed in their detail because the larger number of sidebands (as compared to when the exponent is 1.0) were affected differentially by the combined effects of the individual stages included in the model. The proposed use of ITD-information within auditory filters centered above the center frequency of a high-frequency complex stimulus is not ad-hoc. Rather, it has been shown to be consistent with data obtained in experiments concerning sensitivity to envelope-based ITDs (van de Par et al., 2000; Bernstein and Trahiotis, 2008).
Figure 5.
Waveforms resulting from processing via the “front-end” of the normalized interaural correlation model (see text). The stimulus was a 4-kHz-centered raised-sine having an exponent of 1.0 (SAM tone) and modulated at 256 Hz. The solid line depicts the waveform resulting from centering the (gammatone) bandpass filter at 4000 Hz; the dotted line depicts the waveform resulting from centering the (gammatone) bandpass filter at 4500 Hz.
In order to explore the viability of this line of reasoning, we re-computed predictions of the model utilizing gammatone-based bandpass filters (see Patterson et al., 1995) centered at 4250, 4500, or 5000 Hz. The results are shown in Fig. 4 as the dashed, dotted, and dash-dotted lines, respectively. Visual inspection reveals that utilizing a filter centered above 4 kHz brings the predictions of the model and the data into closer register. Specifically, with a raised-sine exponent of 8.0 and a 25% depth of modulation (panel b), increasing the center frequency of the filter to either 4500 or 5000 Hz removes the overestimates of threshold at rates of modulation of 128 and 256 Hz. The same type of improvements occurred when the raised-sine exponent was 1.0 and the rate of modulation was 256 Hz (panel a). Furthermore, these improvements occur without any appreciable change in the accuracy of the predictions for the remaining stimulus conditions. Quantitatively, considering all of the conditions tested, the amounts of variance accounted for in the empirical normalized threshold ITDs by the model with filters centered at 4000, 4250, 4500, or 5000 Hz, were 58, 85, 81, and 86%, respectively.2 This confirms the original intuition that utilizing an “off-frequency” filter could improve the predictions of the model.
It is worthwhile considering that the stimulus as processed through an off-frequency filter would have less power than its counterpart processed through the on-frequency filter. Calculations using gammatone filters centered at either 4000 or 4500 Hz revealed that, for stimuli having a 25% depth of modulation, the power in the off-frequency filter was about 11 dB less than the power in the on-frequency filter. This difference was essentially constant for all four rates of modulation and both values of the exponent of the raised sine. The results of previous studies concerning the effects of overall level and conducted with similar high-frequency stimuli that were 100% modulated are inconsistent. Some (e.g., McFadden and Pasanen, 1976; Nuetzel and Hafter, 1976; Smoski and Trahiotis, 1986) have shown that reducing the overall level of the stimulus from 70 dB SPL (the level we employed) to about 59 dB SPL resulted in, at most, about a 30–40% increase in threshold ITDs. Others (Dreyer and Oxenham, 2008; Bernstein and Trahiotis, 2008) have reported little or no effect. To our knowledge, there are no data relating threshold ITDs to overall level for high-frequency stimuli having low depths of modulation. Therefore, one cannot be certain that level effects akin to those discussed above for 100% modulated stimuli occur for 25% modulated stimuli.
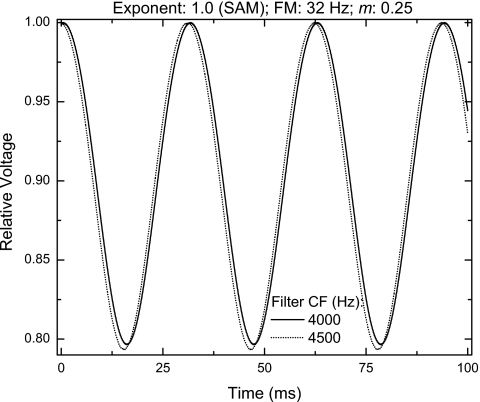
One might wonder why the predictions of the model do not appear to be appreciably affected by the use of an off-frequency filter when the rate of modulation is low (i.e., 32 and 64 Hz). In such cases, the envelope recovered from a stimulus having a low rate of modulation, here 32 or 64 Hz, would not be affected by the 150-Hz low-pass envelope filter that affects temporal processing in high-frequency channels. Additionally, there would little or no advantage to utilizing an off-frequency auditory filter because the proximity of the sidebands to the carrier would preclude substantial differential attenuations of the respective components. Figure 6 parallels Fig. 5 and shows functions computed when the rate of modulation of a 4-kHz-centered SAM tone was 32 Hz. As in Fig. 5, the solid function represents the output of the model resulting from “on-frequency” bandpass filtering at 4000 Hz; the dashed function represents the output of the model resulting from “off-frequency” bandpass filtering at 4500 Hz. Clearly, as expected, the output of the model is essentially the same for on- and off-frequency filters.
Figure 6.
Same as Fig. 5 except that the rate of modulation of the raised-sine stimulus was 32 Hz.
One might also wonder why the predictions of the model do not appear to be appreciably affected by the use of an off-frequency filter when the depth of modulation is 100%, independent of the rate of modulation. This is so because, even when the rate of modulation is 128 or 256 Hz, the relative attenuation of the resulting envelope components by the 150-Hz low-pass filter would still contain sufficient power to result in a processed stimulus having an envelope with a relatively small DC offset. This type of output corresponds to a stimulus input having a substantial depth of modulation. Empirically, in this case, one would not expect sensitivity to ITDs to be adversely affected. This is so because sensitivity to ITDs conveyed by high-frequency complex stimuli is not substantially affected by reductions in depth of modulation until the depth of modulation falls well below 50% (see McFadden and Pasanen, 1976; Nuetzel and Hafter, 1981).
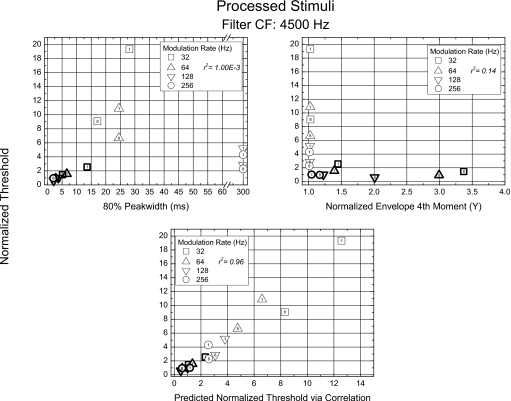
For completeness, Figs. 78 show the predictive utility of three of the measures used in Figs. 23 (peakwidth, normalized fourth moment, and normalized interaural correlation) for the normalized threshold ITDs plotted in Fig. 4. As before, separate figures are used for comparisons based on the physical stimuli (Fig. 7) and for comparisons based on the processed stimuli (Fig. 8). The thicker-edged symbols represent data obtained when the depth of modulation was 100%; the thinner-edged symbols represent data obtained when the depth of modulation was 25%. The predictions for the processed stimuli were made while employing, within the model, an off-frequency auditory filter centered at 4500 Hz. For reasons discussed above for the processed stimuli (Fig. 3) and because there is no deadtime in the envelopes of the physical stimuli modulated at 25%, comparisons with that measure are omitted.
Figure 7.
Normalized threshold ITDs from Fig. 4, plotted as a function of the values of each of three candidate envelope measures computed on the physical stimuli (see text). The parameter in each plot is rate of modulation and the value of the exponent of the raised-sine is indicated within each symbol. Thicker-edged symbols represent data obtained when the depth of modulation was 100%; thinner-edged symbols represent data obtained when the depth of modulation was 25%.
Figure 8.
Same as Fig. 5 with the exception that the envelope measures were computed on the stimuli as processed via stages of a model designed to mimic features of peripheral auditory processing. The center frequency of the auditory filter employed within the model was 4500 Hz.
Visual inspection of the plots and their accompanying values of r2 reveal that, once again, neither 80% peakwidth nor normalized envelope fourth moment is a good predictor of threshold ITDs. In contrast to what was observed in Figs. 23, for this set of data, threshold ITDs predicted on the basis of normalized correlation are accurately predicted independent of whether the computations are made using the physical or the processed stimuli. Further analyses suggested that the increase in r2 from 0.79 to 0.94 (Fig. 2 vs Figure 7), found for predictions made via normalized interaural correlation and using the physical stimuli, resulted principally from the much larger range of values over which predictions could be made. When the data are considered in their totality, however, it is clear that the normalized interaural correlation calculated on the processed stimuli yields excellent predictions of threshold ITDs, while the other measures do not.
SUMMARY
The purpose of this study was to evaluate, quantitatively, how well envelope fourth moment, envelope peakwidth, envelope deadtime, and normalized envelope interaural correlation could account for threshold ITDs obtained by Bernstein and Trahiotis (2009) using raised-sine stimuli centered at 4 kHz. Of the four measures, only interaural correlation was found to provide highly accurate predictions of the threshold ITDs and those predictions were most accurate when peripheral auditory processing was included. New threshold ITDs were measured while varying, factorially, depth of modulation raised-sine exponent, and modulation frequency. The motivation was to understand Bernstein and Trahiotis’ (2009) finding that a model based on normalized interaural correlation substantially overestimated threshold ITDs when the exponent of the raised sine was 8.0 and the depth of modulation was 25%. A quantitative analysis of the new data suggests that, if it is assumed that listeners can employ information within “off-frequency” auditory filters centered above 4 kHz, then an interaural correlation-based model can accurately predict threshold ITDs obtained with such stimuli.
ACKNOWLEDGMENTS
This research was supported by research grant NIH DC-04147 from the National Institute on Deafness and Other Communication Disorders, National Institutes of Health. The authors thank Dr. H. Steven Colburn, one anonymous reviewer, and the Associate Editor, Dr. Michael Akeroyd, for their insightful comments and suggestions that served to strengthen the presentation. In addition, the authors are grateful to “Reviewer 2” for comments that led us to a detailed consideration of how and whether changes in level resulting from “off-frequency listening” might be expected to influence the results.
Footnotes
The predictions in terms of ITD for the filter centered at 4000 Hz (solid lines) in Fig. 4 differ slightly from those appearing in Bernstein and Trahiotis (2009). This is because, although the criterion (threshold) change in correlation was assumed to be the same as that used by Bernstein and Trahiotis, the form of the function used to fit the empirical values of normalized correlation vs ITD for each stimulus was different than that employed in that study. The new form (the spline fitting function supplied within MATLAB®) was chosen because it proved more robust over a broader range of stimulus parameters than did the previous function.
The formula used to compute the percentage of the variance for which our predicted values of threshold accounted was where Oi and Pi represent individual observed and predicted values of threshold, respectively, and represents the mean of the observed values of threshold (e.g., Bernstein and Trahiotis, 1994).
References
- Batra, R., Kuwada, S., and Fitzpatrick, D. C. (1997). “Sensitivity to interaural temporal disparities of low- and high-frequency neurons in the superior olivary complex. II. Coincidence detection,” J. Neurophysiol. 78, 1237–1247. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1982). “Detection of interaural delay in high-frequency noise,” J. Acoust. Soc. Am. 71, 147–152. 10.1121/1.387254 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1985). “Lateralization of sinusoidally-amplitude-modulated tones: Effects of spectral locus and temporal variation,” J. Acoust. Soc. Am. 78, 514–523. 10.1121/1.392473 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1994). “Detection of interaural delay in high-frequency SAM tones, two-tone complexes, and bands of noise,” J. Acoust. Soc. Am. 95, 3561–3567. 10.1121/1.409973 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1996). “On the use of the normalized correlation as an index of interaural envelope correlation,” J. Acoust. Soc. Am. 100, 1754–1763. 10.1121/1.416072 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2002). “Enhancing sensitivity to interaural delays at high frequencies by using transposed stimuli,” J. Acoust. Soc. Am. 112, 1026–1036. 10.1121/1.1497620 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2003). “Enhancing interaural-delay-based extents of laterality at high frequencies by using ‘transposed stimuli’,” J. Acoust. Soc. Am. 113, 3335–3347. 10.1121/1.1570431 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2004). “The apparent immunity of high-frequency ‘transposed' stimuli to low-frequency binaural interference,” J. Acoust. Soc. Am. 116, 3062–3069. 10.1121/1.1791892 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2005). “Measures of extents of laterality for high-frequency ‘transposed’ stimuli under conditions of binaural interference,” J. Acoust. Soc. Am. 118, 1626–1635. 10.1121/1.1984827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2007). “Why do transposed stimuli enhance binaural processing?: Interaural envelope correlation vs. envelope normalized fourth moment,” J. Acoust. Soc. Am. 121, EL23. 10.1121/1.2401225 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2008). “Discrimination of interaural temporal disparities conveyed by high-frequency sinusoidally amplitude-modulated tones and high-frequency transposed tones: Effects of spectrally flanking noises,” J. Acoust. Soc. Am. 124, 3088–3094. 10.1121/1.2980523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2009). “How sensitivity to ongoing interaural temporal disparities is affected by manipulations of temporal features of the envelopes of high-frequency stimuli,” J. Acoust. Soc. Am. 125, 3234–3242. 10.1121/1.3101454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blauert, J. (1983). Spatial Hearing (MIT Press, Cambridge, MA: ), pp. 316–321. [Google Scholar]
- Buell, T. N., and Hafter, E. R. (1988). “Discrimination of interaural differences of time in the envelopes of high-frequency signals: Integration times,” J. Acoust. Soc. Am. 84, 2063–2066. 10.1121/1.397050 [DOI] [PubMed] [Google Scholar]
- Dreyer, A. A., and Oxenham, A. J. (2008). “Effects of level and background noise on interaural time difference discrimination for transposed stimuli,” J. Acoust. Soc. Am. 123, EL1–EL7. 10.1121/1.2820442 [DOI] [PubMed] [Google Scholar]
- Dye, R. H., Jr., Niemiec, A. J., and Stellmack, M. A. (1994). “Discrimination of interaural envelope delays: The effect of randomizing component starting phase,” J. Acoust. Soc. Am. 95, 463–470. 10.1121/1.408341 [DOI] [PubMed] [Google Scholar]
- Ewert, S. D., and Dau, T. (2000). “Characterizing frequency selectivity for envelope fluctuations,” J. Acoust. Soc. Am. 108, 1181–1196. 10.1121/1.1288665 [DOI] [PubMed] [Google Scholar]
- Hafter, E. R. (1977). “Lateralization model and the role of time-intensity tradings in binaural masking: Can the data be explained by a time-only hypothesis?” J. Acoust. Soc. Am. 59, 1259–1265. [DOI] [PubMed] [Google Scholar]
- Hartmann, W. M. (1987). “Temporal fluctuations and the discrimination of spectrally dense signals by human listeners,” in Auditory Processing of Complex Sound, edited by Yost W. A. and Watson C. S. (Erlbaum, Hillsdale, NJ: ), pp. 126–135. [Google Scholar]
- Hartmann, W. M., and Pumplin, J. (1988). “Noise power fluctuations and the masking of sine signals,” J. Acoust. Soc. Am. 83, 2277–2289. 10.1121/1.396358 [DOI] [PubMed] [Google Scholar]
- Hays, W. L. (1973). Statistics for the Social Sciences (Holt, Rinehart, and Winston, New York: ), pp. 417–419. [Google Scholar]
- Henning, G. B. (1980). “Some observations on the lateralization of complex waveforms,” J. Acoust. Soc. Am. 68, 446–453. 10.1121/1.384756 [DOI] [PubMed] [Google Scholar]
- John, M. S., Dimitrijevic, A., and Picton, T. (2002). “Auditory steady-state responses to exponential modulation envelopes,” Ear Hear. 23, 106–117. 10.1097/00003446-200204000-00004 [DOI] [PubMed] [Google Scholar]
- Keppel, G. (1991). Design and Analysis: A Researchers Handbook (Prentice-Hall, Englewood Cliffs, NJ: ), p. 494. [Google Scholar]
- Klumpp, R. G., and Eady, H. R. (1956). “Some measurements of interaural time difference thresholds,” J. Acoust. Soc. Am. 28, 859–860. 10.1121/1.1908493 [DOI] [Google Scholar]
- Kohlrausch, A., Fassel, R., and Dau, T. (2000). “The influence of carrier level and frequency on modulation and beat-detection thresholds for sinusoidal carriers,” J. Acoust. Soc. Am. 108, 723–734. 10.1121/1.429605 [DOI] [PubMed] [Google Scholar]
- McFadden, D., and Pasanen, E. G. (1976). “Lateralization at high frequencies based on interaural time differences,” J. Acoust. Soc. Am. 59, 634–639. 10.1121/1.380913 [DOI] [PubMed] [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1976). “Lateralization of complex waveforms: Effects of fine-structure, amplitude, and duration,” J. Acoust. Soc. Am. 60, 1339–1346. 10.1121/1.381227 [DOI] [PubMed] [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1981). “Discrimination of interaural delays in complex waveforms: Spectral effects,” J. Acoust. Soc. Am. 69, 1112–1118. 10.1121/1.385690 [DOI] [Google Scholar]
- Patterson, R. D., Allerhand, M. H., and Giguere, C. (1995). “Time-domain modeling of peripheral auditory processing: A modular architecture and a software platform,” J. Acoust. Soc. Am. 98, 1890–1894. 10.1121/1.414456 [DOI] [PubMed] [Google Scholar]
- Smoski, W. J., and Trahiotis, C. (1986). “Discrimination of interaural temporal disparities by normal-hearing listeners and listeners with high-frequency, sensorineural hearing loss,” J. Acoust. Soc. Am. 79, 1541–1547. 10.1121/1.393680 [DOI] [PubMed] [Google Scholar]
- Stecker, G. C., and Hafter, E. R. (2002). “Temporal weighting in sound localization,” J. Acoust. Soc. Am. 112, 1046–1057. 10.1121/1.1497366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Par, S., Trahiotis, C., and Bernstein, L. R. (2000). “The use of off-frequency information in a high-frequency binaural discrimination task,” Acustica 86, 526–531. [Google Scholar]
- Weiss, T. F. and Rose, C. (1988). “A comparison of synchronization filters in different auditory receptor organs,” Hear. Res. 33, 175–179. 10.1016/0378-5955(88)90030-5 [DOI] [PubMed] [Google Scholar]
- Zwislocki, J., and Feldman, R. S. (1956). “Just noticeable differences in dichotic phase,” J. Acoust. Soc. Am. 28, 860–864. 10.1121/1.1908495 [DOI] [Google Scholar]