A model for the dynamics of ultrasound contrast agents in vivo

Abstract

The Rayleigh-Plesset (RP) equation for a clean gas bubble in an incompressible and infinite liquid has previously been applied to approximately simulate the behavior of ultrasound contrast agents (UCA) in vivo, and extended RP equations have been proposed to account for the effects of the UCA shell or surrounding soft tissue. These models produce results that are consistent with experimental measurements for low acoustic pressure scenarios. For applications of UCAs in therapeutic medicine, the transmitted acoustic pulse can have a peak negative pressure (PNP) up to a few megapascals, resulting in discrepancies between measurements and predictions using these extended RP equations. Here, a model was developed to describe the dynamics of UCAs in vivo while taking account of the effects of liquid compressibility, the shell and the surrounding tissue. Liquid compressibility is approximated to first order and the shell is treated either as a Voigt viscoelastic solid or a Newtonian viscous liquid. Finite deformation of the shell and tissue is derived. Dynamics of UCAs with a shell of lipid, polymer, albumin and liquid are investigated for typical therapeutic ultrasound pulses. The effects of liquid compressibility and shell and tissue parameters are analyzed.

INTRODUCTION

Interest in ultrasound contrast agents (UCA) has recently increased both in the fields of ultrasound imaging and drug and gene delivery (Lindner, 2004; Ferrara et al., 2007; Newman and Bettinger, 2007). A typical UCA is a gas bubble with a diameter from 1 to 5 μm that is encapsulated by a shell. The low density and high compressibility of the gas core allow the bubble to oscillate and result in a unique nonlinear signature that can be distinguished from that of the surrounding tissue. Diffusion limits the life-time of a clean air bubble (an air bubble without a shell) in a gas-saturated liquid to less than 1 s (Epstein and Plesset, 1950, Ferrara et al., 2007). By encapsulating a high molecular weight and low solubility gas such as perfluorocarbon and adding a shell, the lifetime of an UCA can be several orders of magnitude greater than a clean bubble. The UCA shells can be albumin, as in the case of Optison^™ (GE Healthcare System, Princeton, NJ 08540, USA), lipid, as in the case of MP1950 or Definity (Bristol-Myers Squibb, New York, NY), oil, as with MRX-552, or polymer (POINT Biomedical, San Carlos, CA). For ultrasound-mediated UCA drug delivery, therapeutic drugs can be incorporated into the UCAs or attached to the shell surface. When the UCAs arrive at the target site after intravenous injection, a series of ultrasound pulses with a pressure amplitude up to a few megapascals is transmitted to induce violent oscillation or fragmentation of UCAs. The drug is therefore locally released and∕or microvascular permeability is enhanced (Ferrara et al., 2007).

An important consideration for such a model is whether the output can easily predict the likelihood of biological effects. The mechanical index (MI), which is defined by the peak negative pressure in megapascals divided by square root of the center frequency in megahertz, is frequently used to summarize the potential for biological effects. We and other groups have previously observed that microbubble expansion follows an inverse dependence on the center frequency rather than the square root of frequency and thus we evaluate this dependence here (Forsberg et al., 2006; Qin and Ferrara, 2006).

In vivo, the oscillation of UCA is constrained by soft tissue and blood cells. Theoretical and experimental investigations have demonstrated that for typical medical ultrasound pulses the presence of blood cells has a negligible effect upon UCA dynamics and hence acoustic response (Stride and Saffari, 2004). In order to understand the behavior of an UCA insonified by high intensity ultrasound in therapeutic medicine in vivo, it is necessary to model the UCA as a shelled gas bubble surrounded by soft tissue. To our knowledge, existing models for UCAs roughly fall into two categories: the single clean gas bubble (without a shell) oscillating in a homogenous and Newtonian liquid or viscoelastic media with or without the compressibility of the liquid accounted to first order (Rayleigh, 1917; Gilmore, 1952; Keller and Miksis, 1980; Prosperetti and Lezzi, 1986; Yang and Church, 2005, Freund, 2008) and a shelled bubble in an infinite incompressible fluid (Roy et al., 1990; Dejong et al., 1994; Church, 1995; Hoff et al., 2000; Morgan et al., 2000; Allen et al., 2002). These models produce results that are consistent with experimental measurements for low acoustic pressure scenarios such as those typically encountered in acoustic imaging. For applications of UCAs in therapeutic medicine, the bubble shell wall velocity can reach up to 1000 m∕s, which is on the same order as the speed of sound in a liquid (Allen et al., 2002). Under this scenario, the assumption of the incompressible liquid is not valid and the effects of acoustic radiation and the shell on the behavior of UCAs are substantial. In this work, we developed a new model to describe the dynamics of UCAs in vivo while taking account of liquid compressibility and shell and soft tissue effects. Liquid compressibility is approximated to first order as in the Keller equation (Keller and Miksis, 1980; Prosperetti et al., 1988) and the shell is treated either as a layer of Voigt viscoelastic solid or a viscous liquid (Church, 1995; Hoff et al., 2000; Allen et al., 2002). Soft tissue is modeled as a Voigt viscoelastic medium, approximating the effect of blood and soft tissue (Stride and Saffari, 2004; Yang and Church, 2005). Finite deformation of the shell is included and a related theoretical expression is derived. In the simulated in vivo environment, the dynamics of typical UCAs with a lipid, albumin, oil or polymeric shell are investigated and the effects of the shell and soft tissue are examined.

THEORY AND METHOD

The following derivation will develop a single, general equation for the dynamics of a shelled spherical bubble in either liquid or tissue. Considering the compressibility of the surrounding liquid to first order, the governing equation for a clean spherical gas bubble in an infinite homogeneous Newtonian liquid is given by the Keller equation as follows (Prosperetti and Lezzi, 1986; Brenner et al., 2002):

$${\rho }_L\left[\left(1-\frac{\dot{R}}{c}\right)R\ddot{R}+\frac{3}{2}{\dot{R}}^2\left(1-\frac{1}{3}\frac{\dot{R}}{c}\right)\right]=\left(1+\frac{\dot{R}}{c}\right)\left[p_L\left(R,t\right)-p_I\left(t\right)\right]+\frac{R}{c}\frac{d{p}_g\left(t\right)}{dt}.$$ (1)

The definitions of all symbols in this paper are summarized in the Nomenclature. For violent oscillation of the agent, the effect of the van der Waals hard core should be included and therefore the equations of state are given by (Löfstedt et al., 1993; Barber et al., 1997)

$$p_g\left(t\right)=\left(p_0+\frac{2{\sigma }_1}{R_{10}}+\frac{2{\sigma }_2}{R_{20}}\right){\left[\frac{1}{{\left(\frac{R_1}{R_{10}}\right)}^3-\frac{b}{V_m}}\right]}^{\gamma },$$$$T_g\left(R\right)=\frac{T_0}{{\left[{\left(\frac{R_1}{R_{10}}\right)}^3-\frac{b}{V_m}\right]}^{\gamma -1}}.$$ (2)

Liquid compressibility effects do not substantially alter the effects of the shell and the viscoelasticity of the surrounding medium. Therefore, when deriving the effects of the shell and surrounding medium viscoelasticity, we neglect the liquid compressibility. The continuity equation and the radial linear momentum equation for Newtonian liquids or viscoelastic media are (Prosperetti, 1982; Church, 1995)

$$u_r=\frac{R_2^2}{r^2}{\dot{R}}_2=\frac{R_1^2}{r^2}{\dot{R}}_1,$$$$\rho \left(\frac{\partial u_r}{\partial t}+u_r\frac{\partial u_r}{\partial r}\right)=-\frac{\partial p}{\partial r}+\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{\tau }_{rr}\right)-\frac{{\tau }_{\theta \theta }+{\tau }_{\varphi \varphi }}{r}.$$ (3)

Because the trace of the stress tensor is zero for incompressible materials, the momentum equation can be written as

$$\rho \left(\frac{\partial u_r}{\partial t}+u_r\frac{\partial u_r}{\partial r}\right)=-\frac{\partial p}{\partial r}+\frac{\partial {\tau }_{rr}}{\partial r}+\frac{3{\tau }_{rr}}{r}.$$ (4)

Integrating both sides of Eq. 4 from R₁ to R₂ leads to

$${\rho }_S\left[\frac{R_2\left(R_2-R_1\right)}{R_1}{\ddot{R}}_2-\frac{3R_1^4-4R_2{R}_1^3+R_2^4}{2R_1^4}{\dot{R}}_2^2\right]={\tau }_{S,rr}\left(R_2\right)-p_S\left(R_2\right)-\left({\tau }_{S,rr}\left(R_1\right)-p_S\left(R_1\right)\right)+3{\int }_{R_1}^{R_2}\frac{{\tau }_{rr}}{r}dr.$$ (5)

For finite deformation of an incompressible shell or a Voigt viscoelastic medium, we have

$${\dot{\epsilon }}_r=\frac{\partial u_r}{\partial r}=-\frac{2R_2^2{\dot{R}}_2}{r^3},$$$${\epsilon }_r=-\frac{2}{3r^3}\left(R_2^3-R_{20}^3\right),$$ (6)

and the radial component of the stress tensor τ_rr can be written as

$${\tau }_{rr}=2\left(G{\epsilon }_r+\mu {\dot{\epsilon }}_r\right)=-\frac{4G}{3r^3}\left(R_2^3-R_{20}^3\right)-\frac{4\mu R_2^2{\dot{R}}_2}{r^3}.$$ (7)

Integrating Eq. 7 from R₁ to R₂ and R₂ to infinity, respectively, we get

$$3{\int }_{R_1}^{R_2}\frac{{\tau }_{rr}}{r}dr=-\frac{4}{3}{G}_S\frac{V_S}{R_2^3-V_S}\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]-4{\mu }_S\frac{V_s}{R_2^3-V_s}\frac{{\dot{R}}_2}{R_2},$$$$3{\int }_{R_2}^{\infty }\frac{{\tau }_{rr}}{r}dr=-\frac{4}{3}{G}_L\frac{R_2^3-R_{20}^3}{R_2^3}-4{\mu }_L\frac{{\dot{R}}_2}{R_2}.$$ (8)

For a viscoelastic medium, the boundary conditions at the inner and outer surface of the shell are

$$p_S\left(R_1,t\right)-{\tau }_{S,rr}\left(R_1,t\right)=p_g-\frac{2{\sigma }_1}{R_1},r=R_1,$$$$p_S\left(R_2,t\right)-{\tau }_{S,rr}\left(R_2,t\right)=p_L\left(R_2,t\right)+\frac{2{\sigma }_2}{R_2}-{\tau }_{L,rr}\left(R_2,t\right),r=R_2.$$ (9)

Substituting for the pressure at infinity (Yang and Church, 2005) $p_I\left(t\right)=p_0+p_i\left(t\right)+{\tau }_{L,rr}\left(R_2,t\right)-3{\int }_{R_2}^{\infty }\left({\tau }_{rr}∕r\right)dr$ and Eq. 9 into Eq. 5 leads to

$$p_L\left(R_2,t\right)-p_I\left(t\right)=p_g-\frac{2{\sigma }_1}{R_1}-\frac{2{\sigma }_2}{R_2}-{\rho }_S\left[\frac{R_2\left(R_2-R_1\right)}{R_1}{\ddot{R}}_2-\frac{3R_1^4-4R_2{R}_1^3+R_2^4}{2R_1^4}{\dot{R}}_2^2\right]-\frac{4}{3}{G}_S\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]\frac{V_S}{R_2^3-V_S}-4{\mu }_S\frac{V_s}{R_2^3-V_s}\frac{{\dot{R}}_2}{R_2}-\frac{4}{3}{G}_L\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]-4{\mu }_L\frac{{\dot{R}}_2}{R_2}-p_0-p_i\left(t\right).$$ (10)

Substituting Eqs. 2, 10 into Eq. 1, we get

$$\left[{\rho }_L\left(1-\frac{{\dot{R}}_2}{c}\right)+{\rho }_S\left(1+\frac{{\dot{R}}_2}{c}\right)\left(\frac{R_2}{R_1}-1\right)\right]R_2{\ddot{R}}_2+\left\{\frac{3}{2}{\rho }_L\left(1-\frac{1}{3}\frac{{\dot{R}}_2}{c}\right)+{\rho }_S\left(1+\frac{{\dot{R}}_2}{c}\right)\left[-\frac{3}{2}+2\left(\frac{R_2}{R_1}\right)-\frac{1}{2}{\left(\frac{R_2}{R_1}\right)}^4\right]\right\}{\dot{R}}_2^2=\left(1+\frac{{\dot{R}}_2}{c}\right)\left\{p_g\left(t\right)-\frac{2{\sigma }_1}{R_1}-\frac{2{\sigma }_2}{R_2}-\frac{4}{3}{G}_S\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]\frac{V_S}{R_2^3-V_S}-4{\mu }_S\frac{V_s}{R_2^3-V_s}\frac{{\dot{R}}_2}{R_2}-\frac{4}{3}{G}_L\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]-4{\mu }_L\frac{{\dot{R}}_2}{R_2}-p_0-p_i\left(t\right)\right\}-3\gamma \frac{{\dot{R}}_2}{c}{\left(\frac{R_2}{R_{10}}\right)}^3\frac{p_g\left(t\right)}{{\left(\frac{R_1}{R_{10}}\right)}^3-\frac{b}{V_m}},$$ (11)

where R₁=(R₂−V_S)^1∕3. When R₂₀=R₁₀, Eq. 11 becomes the governing equation for a clean gas bubble oscillating in soft tissue, which is similar to the equation obtained by Yang and Church (2005). When R₂₀=R₁₀ and G_L=0, Eq. 11 reduces to Eq. 1, which is the typical Keller equation for a gas bubble oscillating in a viscous Newtonian liquid. Noticing that

$$\frac{4}{3}{G}_S\left[1-{\left(\frac{R_{20}}{R_2}\right)}^3\right]\frac{V_S}{R_2^3-V_S}=-4G_S\frac{V_S}{R_2^3}\left(1-\frac{R_{10}}{R_1}\right)+O\left({\left(R_1-R_{10}\right)}^2\right)$$

when G_L=0 and ${\dot{R}}_2∕c\approx 0$, Eq. 11 becomes the governing equation for shelled bubbles with infinitesimal deformation obtained by Church (1995) and Hoff et al. (2000). Therefore we integrate models for microbubble oscillations in different scenarios into one general formula [Eq. 11]. In order to minimize computation errors, Eq. 11 was first non-dimensionalized by using $R_2^{*}=R_2∕R_{20}$, t^*=ωt, ${\dot{R}}_2^{*}={\dot{R}}_2∕R_{20}\omega$. A MATLAB code (Version 7.1, MathWorks, Inc., El Segundo, CA 90245, USA) was developed to solve Eq. 11 using the built-in function ode45 which is based on the Runge-Kutta algorithm. The initial conditions are R₂(0)=R₂₀, R₁(0)=R₁₀ and ${\dot{R}}_2\left(0\right)=0$.

RESULTS

We first validated our model and code by reproducing previously published results by setting appropriate parameter values in Eq. 11, including a clean gas bubble oscillating in an infinite liquid [supplementary figures a and b reproducing Figs. 3 and 4(a) in Versluis et al., 2000 and Fig. 2(b) in Matula, 1999], a gas bubble with a elastic solid shell oscillating in soft tissue (supplementary figure c reproducing Fig. 5 in Yang and Church, 2005) and a gas bubble with a liquid shell oscillating in infinite liquid (supplementary figure d reproducing Figs. 1 and 6 in Allen et al., 2002) [see supplementary material].

We next apply our model to examine ultrasound contrast agents with a layer of liquid, polymer, albumin and lipid using the formalism in Sec. II. The following physical parameters were applied: ρ_L=1060 kg∕m³, p₀=1.01×10⁵ Pa, c=1540 m∕s, b=0.1727 l∕mol, V_m=22.4 l∕mol and γ=1.4. The mechanical properties of tissue vary with tissue type and composition, where the shear modulus of tissue spans from 0.5 to 1.5 MPa (Frizzell et al., 1976; Madsen et al., 1983). In our current computation, the values of shear modulus and viscosity of tissue considered are G_L=0,0.5,1.5 MPa and μ_L=0.015 Pa s (Yang and Church, 2005) to represent blood, soft tissue and relatively stiff tissue. Referring to Hoff et al., 2000 and Stride and Saffari, 2004, the agent parameters used in this work are summarized in Tables 1, 2. The typical pulses used in drug delivery are simulated as 7-cycle “almost Gaussian” weighted sound waves (Ayme-Bellegarda and Church, 1989; Allen et al., 2002).

Table 1.

Material properties applied in all analyses.

Parameter	Symbol	Value				Unit
		High shear modulus-viscosity (lipid)	Albumin	Polymer	Liquid
Density	ρS	1000	1100	1150	1150	kg m−3
Shear modulus	GS	122	88.8	11.7	0	MPa
Viscosity	μS	2.5	1.77	0.45	0.028	Pa s
Surface tension	σ2	0.056	0.056	0.056	0.056	N m−1
	σ1	0.04	0.04	0.04	0.04	N m−1

Table 2.

Shell thickness and radius.

	Parameter	Symbol	High shear modulus-viscosity	Albumin	Polymer	Liquid	Unit
Hypothetical agents (Figs. 2345)	Outer radius	R20	1.0	1.0	1.0	1.0	μm
	Thickness	R20−R10	10	10	10	10	nm
Previously reported commercial or experimental agents (Figs. 16789)	Outer radius	R20	1.0 (lipid)	1.5	2.5	2.45	μm
	Thickness	R20−R10	1.5 (lipid)	15	125	500	nm

The results are organized as follows. First, we compared the predictions of different models for a lipid-shelled and polymer-shelled agent within soft tissue. Second, in order to delineate the effects of the mechanical properties of the agents and tissue on bubble oscillation, we investigated four hypothetical agents with an identical size and shell thickness but with different shell materials. Finally, our model is used to simulate oscillation using shell parameters that have been previously reported for commercial or experimental agents.

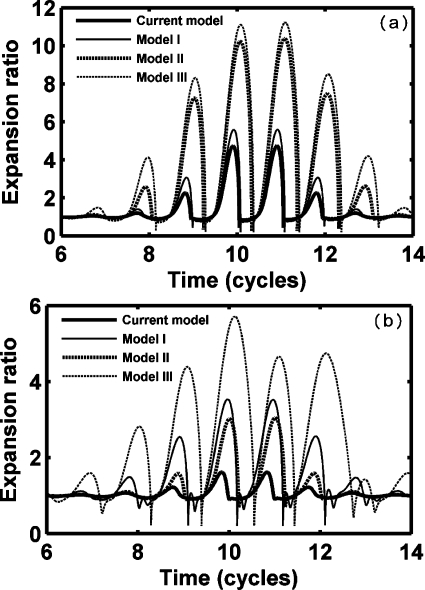
The oscillation amplitude of an UCA in soft tissue is affected by the liquid compressibility and the presence of soft tissue and the agent shell for both a lipid shell [Fig. 1a] and a polymer shell [Fig. 1b], here shown by the evaluation of Eq. 11. Model I simulates a clean gas bubble oscillating in a soft tissue [G_L=0.5 MPa, R₁₀=R₂₀ in Eq. 11], which is similar to the scenario described by Yang and Church (2005). Model II simulates a shelled gas bubble oscillating in an incompressible liquid [G_L=0.0 MPa, ${\dot{R}}_2∕c=0$ in Eq. 11], which is modeled by Church (1995) and Hoff et al. (2000). Model Ш simulates a gas bubble oscillating in a compressible liquid [G_L=0.0 MPa, R₁₀=R₂₀ in Eq. 11], as described by the Keller equation. Finally, the new model proposed here combines the effect of liquid compressibility, tissue, and shell [in Eq. 11G_L=0.5 MPa and the shell parameters are as given in Tables 1, 2 lower row]. For a thin lipid shell layer of 1.5 nm, expansion decreases slightly with the inclusion of a shell (current model versus model I and model II versus model Ш); however, with the thicker polymer shell (125 nm), oscillation is initially smaller and significantly damped by the inclusion of the shell. For both the lipid agent and the polymer agent, the presence of the surrounding tissue reduces the expansion amplitude by a factor of two (current model versus II and model I versus model Ш).

Figure 1.

Expansion ratio of UCAs within soft tissue (G_L=0.5 MPa) predicted by different models with a PNP of 1.5 MPa and a center frequency of 1.0 MHz. Model I simulates a clean gas bubble oscillating in soft tissue (R₁₀=R₂₀). Model II simulates a shelled gas bubble oscillating in an incompressible liquid (G_L=0.0 MPa, ${\dot{R}}_2∕c=0$). Model III simulates a gas bubble oscillating in a compressible liquid (R₁₀=R₂₀, G_L=0.0 MPa). (a) A lipid-shelled agent; (b) a polymer-shelled agent. UCA parameters are in Table 1 and lower row of Table 2.

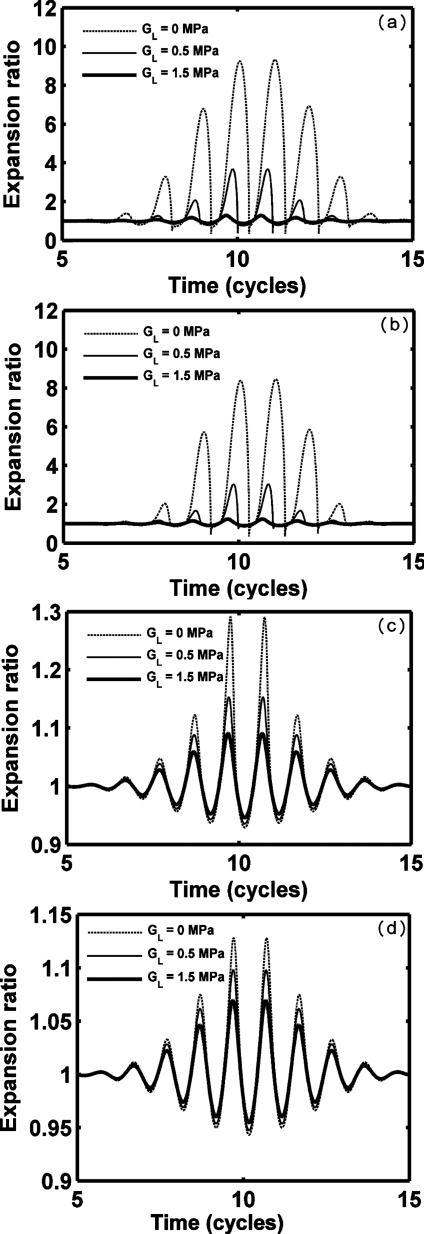
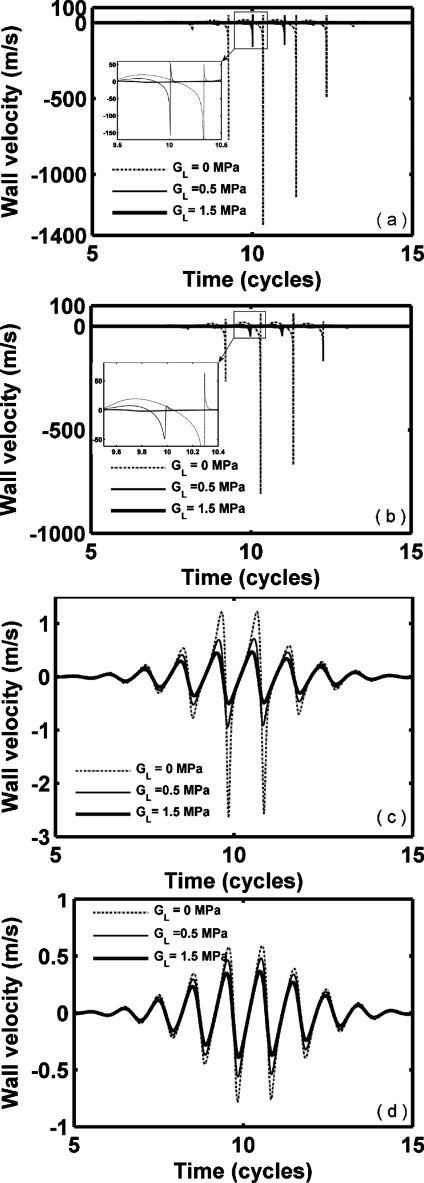
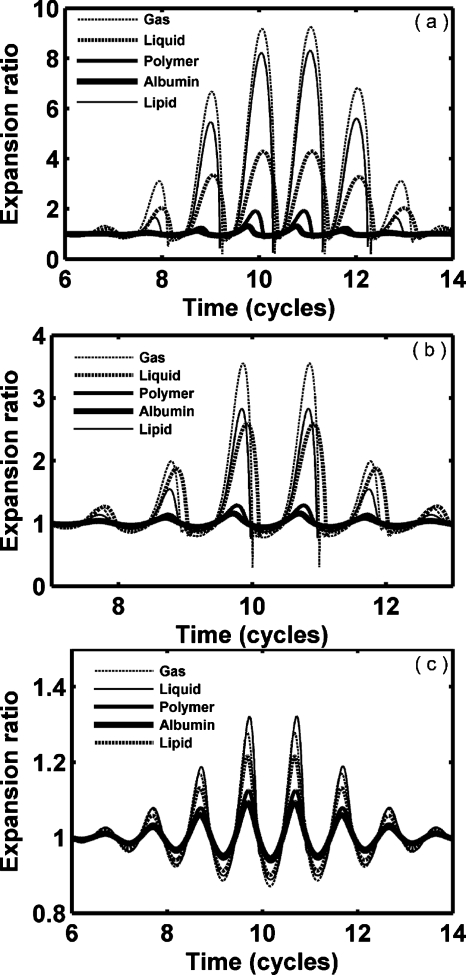
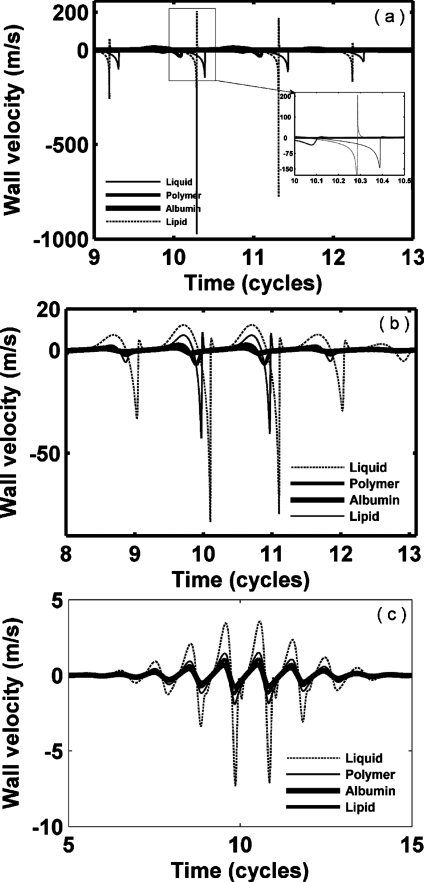
We next consider oscillation for a set of hypothetical agents with a consistent radius (1 μm) and shell thickness (10 nm) (Figs. 2345 and Table 3), noting that monolayer lipid membranes are substantially thinner. Thus, the resulting oscillation of an agent with a stiffness and viscosity that would otherwise be relevant for a lipid does not correspond to that of a commercial lipid-shelled agent. Nonlinear oscillation, where the amplitude of expansion is much larger than the amplitude of contraction, is predicted for our parameters; wall velocity during contraction is much larger than that during expansion (Figs. 23 and Table 3). With a smaller value of G_L, nonlinearity increases. The maximum expansion and wall velocity decrease with increasing shear modulus of the shell and∕or surrounding tissue. Within a stiff tissue (G_L=1.5 MPa), the maximum expansion ratio of all four types of agents is less than 2 and therefore inertial cavitation is not predicted (expansion ratio of 2 is used as the cavitation threshold as in Apfel and Holland, 1991). For a stiff shell with G_S=88.8 and 122 MPa, respectively, agents are not predicted to demonstrate inertial cavitation for G_L from 0 to 1.5 MPa [Figs. 2c, 2d]. In contrast, polymer- and liquid-shelled agents are predicted to experience inertial cavitation within soft tissue (G_L≤0.5 MPa) [Figs. 2a, 2b]. The maximum expansion ratio and wall velocity are greatest for liquid-shelled agents (similar to clean gas bubbles which are not shown) among the examined agents [Figs. 2a, 3a]. The difference between the oscillation of liquid-shelled agents and others show that the presence of an intact shell substantially decreases bubble oscillation. The maximum expansion ratio decreases from 9.3 to 1.13 and wall velocity from 1135.7 to 0.78 m∕s when a 10 nm high shear modulus and viscosity shell was added to a clean gas bubble [Figs. 2a, 2d, 3a, and 3d Table 3]. Within a soft tissue with G_L≤0.5 MPa, the maximum wall velocity of the liquid-shelled and polymer-shelled agents approaches the speed of sound in blood and therefore a model including the liquid compressibility is more appropriate [Figs. 3a, 3b].

Figure 2.

Expansion ratio of UCAs within blood (G_L=0.0 MPa), soft tissue (G_L=0.5 MPa) and stiff tissue (G_L=1.5 MPa). UCAs with an outer radius of 1 μm and a thickness of 10 nm are insonified by pulses with a PNP of 1.2 MPa and a center frequency of 1.0 MHz: (a) liquid-shelled agent (b) polymer-shelled agent, (c) albumin-shelled agent, and (d) high shear modulus and viscosity agent.

Figure 3.

Bubble wall velocity of UCAs within blood (G_L=0.0 MPa), soft tissue (G_L=0.5 MPa) and stiff tissue (G_L=1.5 MPa). UCAs with an outer radius of 1 μm and a thickness of 10 nm are insonified by pulses with a PNP of 1.2 MPa and center frequency of 1.0 MHz: (a) liquid-shelled agent (b) polymer-shelled agent, (c) albumin-shelled agent, and (d) high shear modulus and viscosity agent.

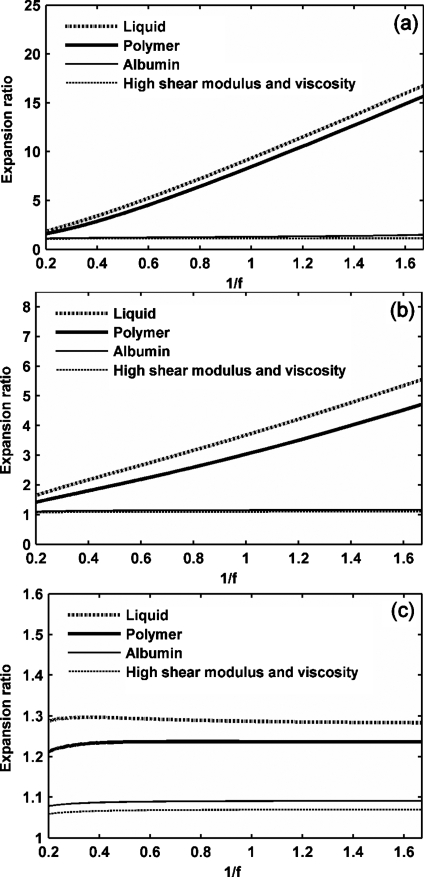
Figure 4.

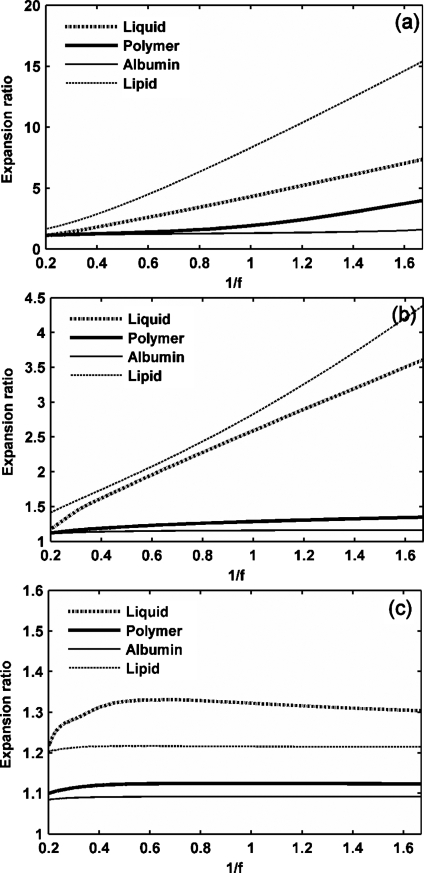
Expansion ratio of UCAs versus 1∕f. UCAs with an outer radius of 1 μm and a thickness of 10 nm are insonified by pulses with a PNP of 1.2 MPa and a center frequency from 600 kHz to 5 MHz: (a) G_L=0 MPa, (b) G_L=0.5 MPa, (c) G_L=1.5 MPa.

Figure 5.

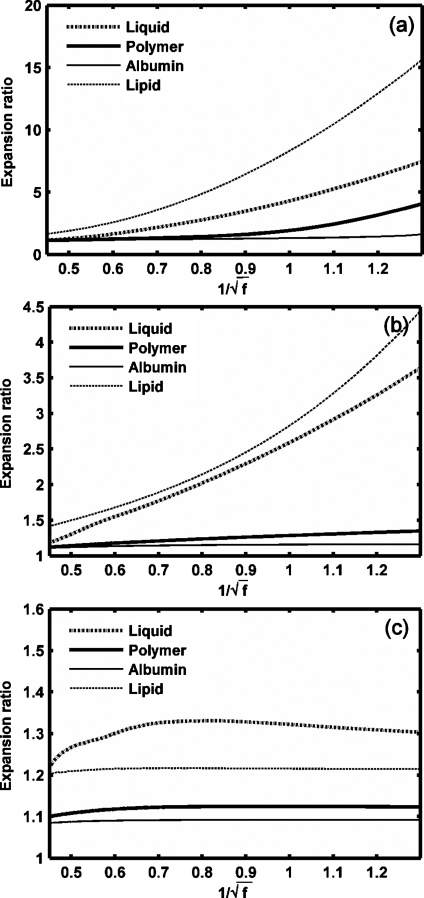
Expansion ratio of UCAs versus $1∕\sqrt{f}$ (frequency dependence as in the MI). UCAs with an outer radius of 1 μm and a thickness of 10 nm diameter are insonified by pulses with a PNP of 1.2 MPa and center frequency 600 kHz to 5 MHz: (a) G_L=0 MPa, (b) soft tissue (G_L=0.5 MPa), (c) rigid tissue (G_L=1.5 MPa).

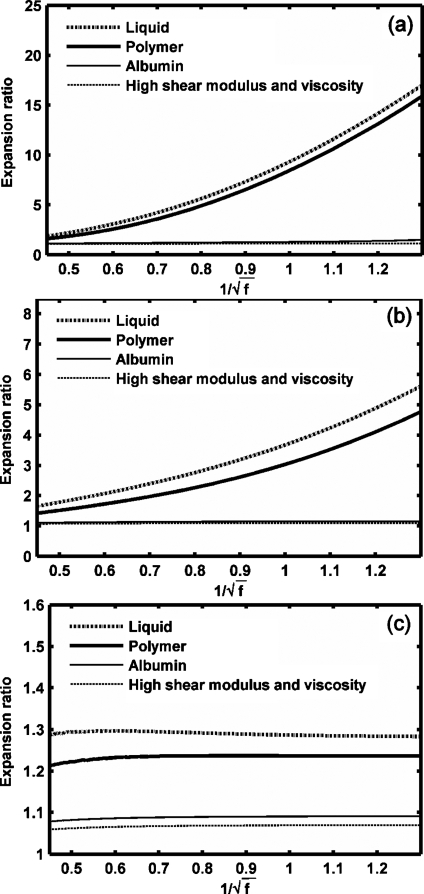
Table 3.

Maximum expansion ratio, wall velocity and cavitation for hypothetical agents with 1 μm radius and 10 nm shell thickness as a function of material properties. Inertial cavitation is assumed to be present if the ratio of maximum to initial radius exceeds two.

	High shear modulus and viscosity			Albumin			Polymer			Liquid			Unit
GL	0.0	0.5	1.5	0.0	0.5	1.5	0.0	0.5	1.5	0.0	0.5	1.5	MPa
δmax	1.13	1.10	1.07	1.29	1.15	1.09	8.47	3.03	1.24	9.34	3.68	1.29	m∕s
$V_{2\text{\hspace{0.17em}max}}^{+}$	0.59	0.48	0.37	1.22	0.71	0.47	63.9	7.8	1.2	51.3	54.2	1.4	m∕s
$V_{2\text{\hspace{0.17em}max}}^{-}$	0.78	0.56	0.39	2.64	0.94	0.50	810.9	48.9	1.4	1135.7	158	1.7	m∕s
Cavitation	No	No	No	No	No	No	Yes	Yes	No	Yes	Yes	No	N∕A

The effect of an ultrasound frequency ranging from 600 kHz to 5 MHz on microbubble expansion is examined in Figs. 45 with G_L increasing from 0 to 1.5 MPa, noting that the dependence on frequency is nearly linear with 1∕f rather than $1∕\sqrt{f}$. When the tissue stiffness is relatively small as compared to the ultrasound PNP, the maximum bubble expansion is linearly related to the inverse of ultrasound center frequency (in units of MHz) [Figs. 4a, 4b]. The effect of the frequency on UCA oscillation decreases with increasing stiffness of the surrounding tissue. When the tissue stiffness is relatively large as compared to the ultrasound PNP, maximum bubble expansion is nearly independent of ultrasound center frequency or MI [Figs. 4c, 5c]. Within a stiff tissue (G_L=1.5 MPa), inertial cavitation is not predicted at the PNP of 1.2 MPa and the corresponding maximum bubble expansion is nearly constant for ultrasound center frequencies from 600 kHz to 5 MHz [Figs. 4c, 5c]. However, when the tissue stiffness is relatively small as compared to the ultrasound PNP, the relationship between the maximum bubble expansion ratio and MI is no longer linear [the liquid-shelled and polymer-shelled agents in Figs. 5a, 5b].

The analysis of expansion and wall velocity was repeated for reported commercial or experimental agents, with G_L increasing from 0 to 1.5 MPa (Figs. 67); here, the agent diameter and shell thickness were individually tailored to match reported values (Tables 1, 2). When the lipid-shell thickness is decreased to 1.5 nm in order to approximate experimental agents, the lipid shell oscillation approaches that predicted for a clean gas bubble (Fig. 6). Choosing parameters for the albumin-shelled agent to approximate Albunex and Optison (and assuming this shell to remain intact) results in a predicted oscillation amplitude that is the smallest considered here. For G_L=0, 0.5 and 1.5 MPa, the maximum expansion ratio of a lipid-shelled agent reaches 8.07, 2.67 and 1.21, respectively, and an albumin-shelled agent reaches 1.31, 1.16 and 1.09. The maximum wall velocity of lipid-shelled agents during compression reaches 929.5 m∕s, and therefore the liquid compressibility effect is important. The presence of tissue has the largest effect on the lipid-shelled agent in Fig. 6, and the smallest effect on the albumin-shelled agent (Fig. 6 and Table 4). The relationship between bubble expansion and the inverse of ultrasound frequency for the commercial or experimental agents is also linear (Fig. 8). However, within soft tissue (G_L=0 and 0.5 MPa), liquid-shelled and lipid-shelled agents demonstrate a nonlinear relationship between maximum bubble expansion ratio and the inverse of the square root of frequency or equivalently the MI [Figs. 9a, 9b].

Figure 6.

Expansion ratio of UCAs versus ultrasound pulse cycles. UCAs with a mean radius and thickness of the corresponding type are insonified by pulses with a PNP of 1.2 MPa and a center frequency of 1.0 MHz: (a) G_L=0 MPa, (b) G_L=0.5 MPa, (c) G_L=1.5 MPa.

Figure 7.

Bubble wall velocity of UCAs versus ultrasound pulse cycles. UCAs with a mean radius and thickness of the corresponding type are insonified by pulses with a PNP of 1.2 MPa and a center frequency of 1.0 MHz: (a) G_L=0 MPa, (b) G_L=0.5 MPa, (c) G_L=1.5 MPa.

Table 4.

Maximum expansion ratio, wall velocity and prediction of inertial cavitation for previously-reported commercial or experimental agents using varied dimensions as described in lower row of Table 2. Inertial cavitation is assumed to be present if the ratio of maximum to initial radius exceeds two. The high shear modulus and viscosity is associated with a lipid membrane when the shell thickness is small.

	High shear modulus and viscosity (lipid)			Albumin			Polymer			Liquid			Unit
GL	0.0	0.5	1.5	0.0	0.5	1.5	0.0	0.5	1.5	0.0	0.5	1.5	MPa
δmax	8.07	2.67	1.21	1.31	1.16	1.09	1.91	1.29	1.12	4.20	2.56	1.32	m∕s
$V_{2\text{\hspace{0.17em}max}}^{+}$	208.4	6.7	1.1	1.9	1.1	0.7	7.5	2.9	1.5	20.0	12.0	3.5	m∕s
$V_{2\text{\hspace{0.17em}max}}^{-}$	929.5	35.8	1.2	4.8	1.6	0.8	33.6	7.0	1.9	145.7	81.1	7.2	m∕s
Cavitation	Yes	Yes	No	No	No	No	No	No	No	Yes	Yes	No	N∕A

Figure 8.

Expansion ratio of UCAs versus 1∕f. UCAs with a mean radius and thickness of the corresponding type are insonified by pulses with a PNP of 1.2 MPa and a center frequency from 600 kHz to 5 MHz: (a) G_L=0 MPa, (b) G_L=0.5 MPa, (c) G_L=1.5 MPa.

Figure 9.

Expansion ratio of four types of UCAs versus $1∕\sqrt{f}$ (frequency dependence as in the MI). UCAs with a mean radius and thickness of the corresponding type and are insonified by pulses with a PNP of 1.2 MPa and a center frequency from 600 kHz to 5 MHz: (a) G_L=0 MPa, (b) G_L=0.5 MPa, (c) G_L=1.5 MPa.

DISCUSSION

For ultrasound-mediated drug and gene delivery, UCAs are insonified at high pressure and oscillate with a high amplitude and with the maximum wall velocity approaching∕or exceeding the speed of sound in blood. The full partial differential equations for gas bubble dynamics have been well established (Flynn, 1975). However, due to the numerical complexity, application of the full partial differential equations in biomedical engineering has been limited. Therefore, the Rayleigh-Plesset and its extended family of equations have been widely applied in investigations of UCA dynamics in UCA-assisted drug delivery. However, the difference between experimental results and predictions based on classic Rayleigh-Plesset equation can be large. Our goal is to obtain a relatively simple bubble dynamic equation for large amplitude oscillation while preserving accuracy. Both theory and experimental results have demonstrated that the Keller-like equation written in terms of enthalpy yields results that are in good agreement with those obtained by numerical simulations based on full partial differential equations (Prosperetti and Lezzi, 1986; Lezzi and Prosperetti, 1987; Lin et al., 2002; Qin et al., 2009). Further, the difference between the results obtained by the Keller equation written in terms of enthalpy and in terms of pressure is small. For simplicity, we started our derivation from the Keller equation in terms of pressure [Eq. 1]. The presence of the bubble shell and soft tissue was finally demonstrated in the term describing the boundary condition, Eq. 10. A full and complete derivation would start from the governing equations for a compressible liquid and then obtain a Keller-like equation using a perturbation method or linear acoustic wave approximation as in Prosperetti and Lezzi, 1986; Yang and Church, 2005. The boundary conditions considering the shell and surrounding tissue would then be applied to eliminate integral terms. Under the same assumptions, the final equation should be the same as that shown here. In the literature, the correction term for compressibility [last term in Eq. 1] has different forms for different considerations. In Prosperetti and Lezzi, 1986 and Gaitan et al., 1992, compressibility is written as (R∕c)(dp_L∕dt) and in the work of Rayleigh took the form of (R∕c)d(p_g−p_I)∕dt (Rayleigh, 1917; Löfstedt et al., 1995; Barber et al., 1997). For simplicity, we choose the form (R∕c)(dp_g∕dt) as in Brenner et al., 2002 since the time derivative of the driving pressure is small and not dominant for violent oscillation. Our additional computational results (not shown) indicate that the difference between the use of (R∕c)(dp_g∕dt) and (R∕c)d(p_g−p_I)∕dt is negligible.

In drug delivery, UCAs are driven to cavitate and fragment at the target site. For UCAs with inertial cavitation, the bubble wall velocity can approach or exceed the speed of sound, i.e., $\dot{R}∕c\approx 1$ in Eq. 11, which means that acoustic radiation is substantial. Under this scenario, the effect of surrounding tissue upon the behavior of UCA oscillation is important as demonstrated here in the case of simulated lipid- and liquid-shelled agents in Figs. 1a, 6 and Table 4.

Submerged in a liquid, a clean gas bubble has two types of gas diffusion during insonation. One is called rectified diffusion where the bubble gradually grows from its equilibrium size during insonation (Crum, 1980; Crum and Hansen, 1982); the other is called acoustically driven diffusion in which the bubble gradually diminishes when insonified (Chomas et al., 2001). In medical applications, UCAs are usually observed to shrink or fragment after the administration of long ultrasound pulses. In the current computation, we did not include gas diffusion for the short pulses used here. When the ultrasound pulse is long (greater than 20 cycles), acoustically-driven diffusion is not negligible. The complete governing equations describing gas diffusion should be based on mass diffusion within the agent core, the shell layer and the liquid. Solutions could be obtained by coupling gas diffusion and the bubble radial equation [Eq. 11]. Assuming the velocity of the bubble wall can be neglected, Epstein and Plesset (1950) developed a quasi-stationary model for gas diffusion. Later, Eller and Flynn further developed the model and obtained a solution to the diffusion equation, which is uncoupled from the bubble dynamics (Eller and Flynn, 1965; Eller, 1969; Church, 1988). Eller and Flynn (1965) assumed spherically symmetrical fluid motion only and negligible diffusion during a single oscillation of a clean gas bubble. The bubble equilibrium equation can be written as

$$\frac{d{R}_{10}}{dt}=\frac{D{R}_{g}T}{R_{10}}{\left(p_0+\frac{4{\sigma }_1}{3R_{10}}\right)}^{-1}\left[A+R_{10}{\left(\frac{B}{\pi Dt}\right)}^{1∕2}\right]C_{sn}\left(\frac{C_{\infty }}{C_{sn}}-\frac{A}{B}\right).$$ (12)

The coefficients are defined as follows:

$$A=\frac{1}{T_b}{\int }_0^{T_b}\frac{R_1}{R_{10}}dt,$$$$B=\frac{1}{T_b}{\int }_0^{T_b}{\left(\frac{R_1}{R_{10}}\right)}^{4}dt,$$$$C_{sn}=C_0\left(1+\frac{2{\sigma }_1}{R_{10}{p}_0}\right).$$ (13)

Duncan and Needham (2004) tested the accuracy of the Epstein-Plesset model for the lipid-shelled gas bubble and found that the Epstein-Plesset model over-predicted the dissolution time by 8.2% of the measured dissolution time. Therefore, it would be appropriate to couple Eqs. 11, 13 for the long pulses used in ultrasound-mediated drug delivery.

The results presented here indicate that the occurrence of inertial cavitation is important when considering the effect of tissue on bubble oscillation. When inertial cavitation occurs, bubble oscillation is strongly nonlinear and the presence of the tissue substantially subdues the bubble oscillation amplitude. The oscillation of commercial lipid-shelled and liquid-shelled agents is strongly nonlinear and thus suitable to be used in imaging algorithms such as contrast pulse sequences (CPS), which require nonlinear oscillation [Figs. 6a, 6b]. Within a stiff tissue (G_L≥1.5 MPa), all four agents would be weakly echogenic and a nonlinearity-based imaging modality would be ineffective. In such a stiff tissue, bubble oscillation amplitude is small; the presence of the shell and the ultrasound frequency have little effect on the bubble’s oscillation (Figs. 2367). Finally, we note that oscillation demonstrates a linear dependence on the inverse of the center frequency, rather than the inverse of the square root of frequency and thus such a metric may have substantial value.

CONCLUSION

A theoretical model for a shelled gas bubble submerged in soft tissue or blood is proposed. The model accounts for the compressibility of the liquid to first order. Using a viscoelastic model, the effects of large deformation of the shell and soft tissue on the behavior of the agent was derived. The resulting general form of the equation for microbubble oscillation can be reduced to reproduce previous results by setting shell and tissue parameters to appropriate values. The effects of both liquid compressibility and the mechanical properties of the shell and tissue on the behavior of bubble oscillation are summarized in a single expression. Lipid-shelled, albumin-shelled, polymer-shelled and liquid-shelled UCAs are examined using high-pressure ultrasound pulses. When inertial cavitation occurs, the bubble wall velocity approaches or exceeds the speed of sound in the liquid and nonlinear oscillation dominates. The presence of a shell and surrounding tissue has a larger effect on subduing the bubble’s oscillation when the corresponding clean bubble demonstrates inertial cavitation. The bubble’s maximum expansion ratio is shown to be approximately proportional to the inverse of the ultrasound center frequency for a range of medical ultrasound frequencies.

NOMENCLATURE

Subscripts

b

van der Waals constant

c

Speed of sound in the liquid

C₀

The saturation concentration of gas

C_∞

The concentration of gas dissolved in the medium far from the bubble

D

Gas diffusion constant

δ_max

Bubble maximum expansion ratio

ε_r

Strain in the r direction

${\dot{\epsilon }}_r$

Strain rate in the r direction

f

Ultrasound center frequency

G

Shear modulus

γ

Polytropic gas exponent

μ

Viscosity

p

Pressure

p₀

Hydrostatic pressure

p_g

Gas pressure within the agent

p_i

Ultrasound pressure at infinity

p_I

Pressure at infinity

r, θ, ϕ

The r, θ, ϕ axes in the spherical coordinate system

R

Radius of a clean bubble (without shell)

R₁

Inner radius of agent

R₂

Outer radius of agent

R₁₀

Equilibrium inner radius of agent

R₂₀

Equilibrium outer radius of agent

$\dot{R}$

Wall velocity of a clean bubble (without a shell)

${\dot{R}}_1$

Inner wall velocity of agent

${\dot{R}}_2$

Outer wall velocity of agent

$\ddot{R}$

Wall acceleration of a clean bubble

${\ddot{R}}_2$

Outer wall acceleration of agent

R_g

The universal gas constant

ρ

Density

σ₁

Surface tension at the inner radius

σ₂

Surface tension at the outer radius

t

Time

T

Absolute temperature

T₀

Ambient temperature

T_b

The period of the pulsating bubble

T_g

Temperature within the agent

τ_θθ

Stress in the θ direction

τ_ϕϕ

Stress in the ϕ direction

τ_rr

Stress in the r direction

u_r

Radial velocity

V_m

Universal molar volume

V_S

$R_{20}^3-R_{10}^3$

$V_{2\text{\hspace{0.17em}max}}^{+}$

Bubble maximum outward wall velocity

$V_{2\text{\hspace{0.17em}max}}^{-}$

Bubble maximum inward wall velocity

ω

Angular frequency of ultrasound

L

The surrounding medium

S

The shell