An Optical Method for Evaluation of Geometric Fidelity for Anatomically Shaped Tissue-Engineered Constructs

Abstract

Quantification of shape fidelity of complex geometries for tissue-engineered constructs has not been thoroughly investigated. The objective of this study was to quantitatively describe geometric fidelities of various approaches to the fabrication of anatomically shaped meniscal constructs. Ovine menisci (n = 4) were imaged using magnetic resonance imaging (MRI) and microcomputed tomography (μCT). Acrylonitrile butadiene styrene plastic molds were designed from each imaging modality and three-dimensional printed on a Stratasys FDM 3000. Silastic impression molds were fabricated directly from ovine menisci. These molds were used to generate shaped constructs using 2% alginate with 2% CaSO₄. Solid freeform fabrication was conducted on a custom open-architecture three-dimensional printing platform. Printed samples were made using 2% alginate with 0.75% CaSO₄. Hydrogel constructs were scanned via laser triangulation distance sensor. The point cloud images were analyzed to acquire computational measurements for key points of interest (e.g., height, width, and volume). Silastic molds were within ±10% error with respect to the native tissue for seven key measurements, μCT molds for six of seven, μCT prints for four of seven, MRI molds for five of seven, and MRI prints for four of seven. This work shows the ability to generate and quantify anatomically shaped meniscal constructs of high geometric fidelity and lends insight into the relative geometric fidelities of several tissue engineering techniques.

Introduction

Reproducing geometry has been a goal of tissue engineering since its inception. Early studies began by forming cartilage in the shape of an ear¹ and creating bone cartilage composites in the shape of the mandible joint.² Later works have generated anatomically shaped menisci for the knee,³ cranial segments,⁴ and leaflet valves for the heart.⁵ Ideally, these anatomically shaped constructs would be tailored to meet patient-specific needs, but before patient-specific geometries can be achieved, a method to evaluate the geometric fidelities of various tissue engineering techniques must be developed.

Geometry plays a crucial role in construct identity, function, and effectiveness. The importance of geometry spans across many tissue types. Facial reconstruction marks a cornerstone of plastic surgery, interfacing cosmetic and reconstructive procedures to repair the contours of the nose, cheek bones, and mandible/chin, thus restoring physical and aesthetic identity.⁶ In the heart, the shape and intricate folds of a leaflet for heart valves aid in regulating blood flow.^7,8 Given the diversity of size and surface architecture in articular joints, geometry and size matching are critical for the success and longevity of surgical repair, whether it be for cadaveric allografts^9,10 or more commonly used synthetic implants.

Generating complicated geometries for tissue engineering purposes has become possible by combining computer-aided design (CAD) with a plethora of innovative fabrication methods such as injection molding, solid freeform fabrication (SFF), or three-dimensional (3D) printing, and lithography. At the macrolevel, current efforts have concentrated on generating novel applications for injection molding and SFF technology using CAD programs to generate a variety of shapes to engineer tympanic membrane patches for the ear,¹¹ bone structures,^4,12,13 and heart valves.^5,14 At the microlevel, intricate networks of microchannels can be generated through lithography,¹⁵ and specific cell and matrix deposition can be achieved through inkjet printing techniques for use in hepatic tissue¹⁶ and advance organ printing efforts.¹⁷

As more techniques are developed to generate complex geometries, improved tools to quantify the accuracy of the end product's shape fidelity must be developed. Presently, geometry comparisons of tissue-engineered constructs are made through simple visual inspection and manual measurements using rulers or calipers.^18,19 Visual comparisons are not quantitative, and manual measurements suffer from lack of repeatability. Manual measurements are also time intensive and can result in damage to fragile implants such as hydrogels. Cohen et al.²⁰ developed a method that compared engineered construct geometries using contact points throughout the hydrogel surface, whereby contact with the construct would complete an electrical circuit outputting an x–y–z location in 3D space. Building upon the work done by Cohen et al., a method could be developed that is automated, repeatable, and does not damage or contaminate the construct.

We propose such a method to compare anatomical constructs via a commercially available laser triangulation distance sensor and commercially available software designed to compare geometries. The methods are commonly used practices for nontissue engineering applications such as quality control to verify surface roughness when rolling sheet metal²¹ or to assess the source of vibrations in production equipment.²² Here we focus on the generation of anatomically accurate engineered menisci. The meniscus is pertinent for three reasons: (1) clinical relevance—meniscal lesions are one of the most common injuries in the knee²³ with >1.5 million knee surgeries involving the meniscus and usually resulting in the removal of damaged tissue as opposed to repair or replacement²³; (2) complex geometry—predicting and calculating meniscal shape based on magnetic resonance imaging (MRI) images can be quite time consuming, and the algorithms for making these predictions are continually being modified^24–28; (3) accurate meniscal geometry is crucial for proper mechanical function of the knee joint,²⁹ its primary function being to aid in joint load distribution, thus decreasing contact stresses on the underlying articular cartilage. A deviation by >10% in size matching²⁷ can result in detrimental joint loading and more rapid development of osteoarthritis.

Having generated anatomically shaped menisci via injection molding³ and 3D printing²⁰ in prior studies, our current objective was to quantify and compare shape fidelity between these two fabrication methods and to observe differences in constructs generated from MRI and microcomputed tomography (μCT) imaging modalities.

Materials and Methods

Imaging

Four ovine menisci underwent both MRI and μCT imaging as described previously.³ Briefly, an MRI scan of each knee was performed on a clinical 3T MR unit (Twin Speed, GE Health Care, Milwaukee, WI) using a commercially available, eight-channel, receive-only knee coil (In vivo, Milwaukee, WI). Sagittal 3D spoiled gradient echo sequences were acquired, resulting in a spatial resolution of 253.9 μm (frequency) × 253.9 μm (phase) × 0.5 mm at one excitation.

The medial meniscus was then dissected, soaked in Omnipaque^® Iohexol 300 mg I/mL contrasting agent for 2 h, and scanned using an Enhanced Vision Systems Model Ms-8 In Vitro Micro-CT Scanner. Each scan was taken using short scan X-ray settings with 0.023 mm/pixel resolution. Scans were calibrated via values for bone, air, and saline.

Mold design

Injection molds were designed as previously described.³ Briefly, MRI and μCT datasets were used to render a 3D representation that allowed for formatting and generation of a solid model (Geomagic Studio 4.0, Research Triangle Park, NC). The model was then imported into CAD for mold design for both imaging modalities. Molds were printed using a Stratus FDM 3000 machine (Stratasys, Eden Prairie, MN).

Silastic impression molds were generated via room temperature vulcanizing silicone rubber impression molds³⁰ (Silastic^® brand; Dow Corning Corporation, Midland, MI) of the same ovine menisci that underwent MRI and μCT imaging.

Injection molding

Alginate hydrogel was prepared by mixing 2% weight low viscosity, high G-content alginate with 2% CaSO₄.³ Alginate hydrogel was then injected into the molds and allowed to gelate for 20 min in 2% CaCl₂ solution. Constructs were manually demolded.³

3D printing

Alginate hydrogel was prepared by mixing 2% weight low viscosity, high G-content alginate with 0.75% CaSO₄ crosslinker. Alginate hydrogel was immediately loaded into a disposable plastic syringe and allowed to crosslink for 7 min before being loaded into a custom, stepper motor-driven syringe pump. The pump was mounted onto a custom gantry robot that had 25 μm accuracy in the x–y plane. Accuracy in the z-axis is equal to the tip diameter from which the hydrogel was extruded. Alginate hydrogel was extruded layer wise, through 0.5 mm diameter syringe tips (EFD, East Providence, RI) along paths planned by custom STL-slicing software.

To support overhangs, the construct was printed on top of a contoured substrate generated from the medical imagery (the substrate was fabricated before the start of the print using the Stratasys platform). After printing, the constructs were allowed to further cross link in 2% CaCl₂ solution.

Geometric analysis

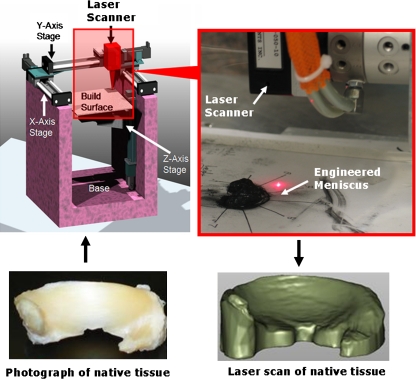
The native tissue was set on a transparency where an outline was made of the tissue and then placed onto the gantry robot's z-platform to be scanned via laser triangulation distance sensor (Microtrak II; MTI Instruments, Albany, NY). Alginate hydrogels were then placed on the transparency to fit the outline as best as possible and then laser scanned. The distance sensor resolution was 50 × 50 × 1 μm (x−y−z), and the data were at 40 KHz. Operations performed in Qualify v8.0 (Geomagic) included importing a point cloud of the scan data, reconstructing the surface, and running a shape autoregistration function to allow for proper alignment between the native and engineered laser scan for analysis of % error volume (Fig. 1). Key dimensions were measured, and % errors were calculated based on specific points established by Haut and coworkers^24,28 (Fig. 2). Manual and computational measurements were taken and showed similar trends and values. Manual measurements were taken after the completion of the laser scan. Samples were aligned on a transparency to take all key dimensions (height, width, span, depth, etc.) using calipers. Manual and computational measurements showed similar trends and values to within 2%–10%. Only computational data are presented here.

FIG. 1.

Custom gantry robot with laser triangulation distance sensor capturing surface of native and engineered sample. Note the projected surface of the native tissue overhangs on its respective laser scan (right). Color images available online at www.liebertonline.com/ten.

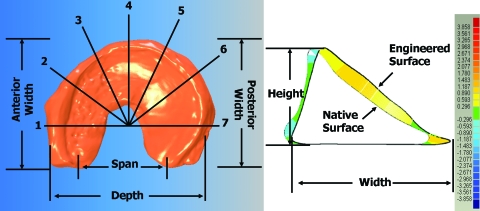
FIG. 2.

Key dimensions that were measured physically and computationally (left). Heights and widths were measured at the seven radial locations (1–7). Height was measured from the base of the meniscus to the topmost point of the cross section, and the width was measured across the thickest portion of the cross section (right). Colored striations denote surface-to-surface deviations between native tissue and engineered hydrogel. Color images available online at www.liebertonline.com/ten.

Errors associated with importing geometry would be caused by reconstruction of surfaces with radii of curvature less than the resolution of the scanner (∼50 μm). As a result, Qualify-based reconstruction did not represent surface roughness accurately. However, surface deviations were binned at 300 μm, which is six times larger than the resolution of the process. All key measurements (volume, height, width, span, depth, etc.) were automated to be taken from both native and engineered samples. Autoregistration was used to generate surface-to-surface deviation heat maps in Qualify to denote differences in overall surface geometry. Errors in autoregistration were determined by performing this task multiple times with varying starting positions. The effect of starting position was minimal, compared with the 300 μm bins used to generate frequency histograms.

Statistics

A total of six replicates were made from each animal's medial meniscus (n = 4) for each fabrication method based on MRI, μCT, or silastic impression mold, resulting in a total of 120 engineered samples. Both one-way and two-way analyses of variance were performed to determine significant differences with Tukey post hoc comparison using Sigmastat version 3.0. All data are presented as mean ± standard deviation with significance at p < 0.05.

Results

Quantification of gross anatomy

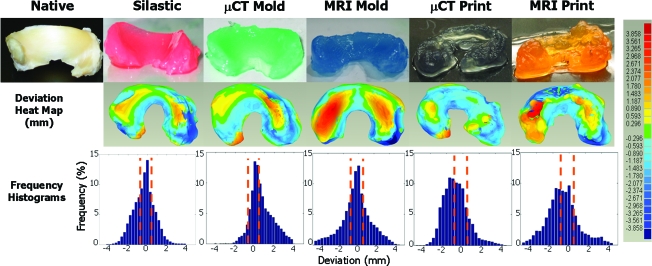
Visual inspection showed that both 3D printing and injection molding were capable of generating meniscal-shaped constructs of grossly comparable accuracy (Fig. 3). Similarly, initial observations of MRI and μCT samples showed that both imaging modalities can be used to design menisci. Samples produced from silastic molds had superior surface quality compared with those produced from acrylonitrile butadiene styrene plastic molds and 3D printed samples. Laser scans captured surface geometry well, but contained additional volume due to the projection of overhanging surfaces (Fig. 1).

FIG. 3.

Photographs of engineered menisci (top row) and respective deviation color heat maps (middle row). Hot colors (reds) designate positive errors and cool colors (blues) designate negative errors relative to the native tissue surface. The bottom row contains % error frequency histograms, where bars located between the orange dashed lines are within ±10% error. μCT, microcomputed tomography. Color images available online at www.liebertonline.com/ten.

Computationally rendered images of the surface-to-surface deviation between native tissue and engineered constructs indicated errors ranging from −4 to 3.8 mm (Fig. 3). Heat maps of deviation show the most extreme errors in samples molded and printed from MRI scans. Printed samples produced from μCT scans had a prevalence of negative deviations, as indicated by cooler colors. Samples produced from silastic or μCT-based molds had similar deviation maps, with slightly hotter patterns in μCT-based samples (Fig. 3).

Frequency histograms of the deviation data indicate the fraction of points within ±10% of the target height. Distributions of deviation were Gaussian for samples generated from silastic molds. Samples generated from MRI molds had minor skew from Gaussian, and all other had significant skews. All samples made from molds had deviation distributions centered at 0 mm, whereas those of printed samples were centered at approximately −1 mm (Fig. 3).

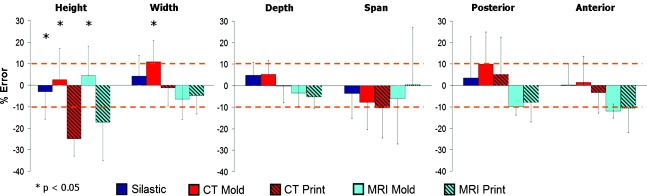
Pooled measurements

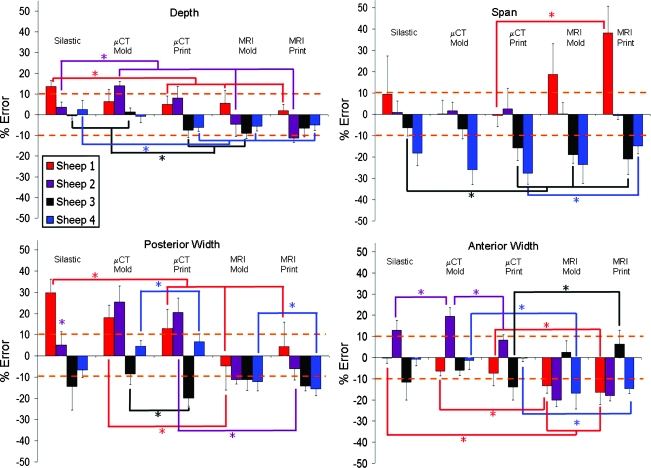
Measurements of key dimensions (i.e., height, width, depth, span, posterior, and anterior width) were pooled for all sheep to compare imaging and fabrication techniques (Fig. 4). All imaging and fabrication techniques produced desired dimensions for depth, span, anterior width, and posterior width to within ∼10% of target sizes. The seven heights and widths were pooled (Fig. 2), because only a significant difference existed among groups. Molding was more accurate in achieving desired heights than printing (p < 0.05) (Fig. 4). The μCT molds were less accurate in replicating the desired width than MRI molds and both printed groups (p < 0.01) (Fig. 4). Overall, the samples made from silastic molds were within the ±10% range for seven of seven measurements, μCT molds for six of seven, μCT print four of seven, MRI mold five of seven, and MRI print four of seven.

FIG. 4.

Average % error across key dimensions as a function of fabrication method. The height and width errors are pooled averages across the seven radial positions because no significant difference was present on location, but was dependent on fabrication method. Color images available online at www.liebertonline.com/ten.

When data were pooled across all sheep (Table 1), no significant difference in volumetric error was found between fabrication groups (p = 0.08), despite a three- to four-fold difference between MRI molds and silastic molds. These trends in volumetric error (Table 1) are consistent with the heat map and frequency histogram data. As denoted by the orange dotted lines in the frequency histograms (Fig. 3), 43%–50% of points fell within ±10% of the intended heights (Table 1). There was no difference in the number of points that fell within ±10% between groups (p = 0.931).

Table 1.

Average Volumetric Error, Percentage of Points from Deviation Heat Maps That Fell Within ±10% of the Native Tissue, and Repeatability Error of Fabrication Methods

	Silastic	μCT mold	μCT print	MRI mold	MRI print
Volumetric error (%)	−8.3 ± 19.5	−8.7 ± 31.4	−21.7 ± 19.0	−19.8 ± 7.7	−30.7 ± 9.4
±10% (%)	49.1 ± 3.8	48.4 ± 10.7	45.9 ± 9.9	47.4 ± 13.8	43.5 ± 7.7
Repeatability error (±%)	7.7	6.7	8.0	7.1	8.7

Lower repeatability error denotes higher repeatability of the technique.

MRI, magnetic resonance imaging.

To compare reproducibility, the standard deviation of the error for all key measurements was averaged for each sample, sheep, and then for all sheep. The resulting value, denoted as repeatability error, indicates how consistently each technique can generate the desired geometry (i.e., a lower reproducibility error value means the technique is more consistent). For all techniques, the repeatability error was <10% (Table 1), indicating that sample-to-sample construct generation was highly consistent.

Individual sample analysis

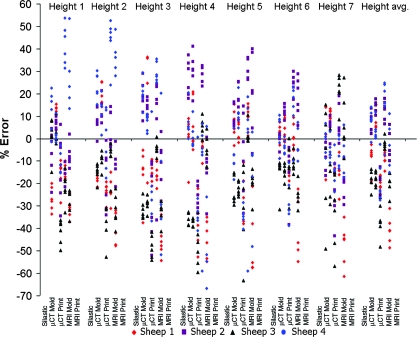
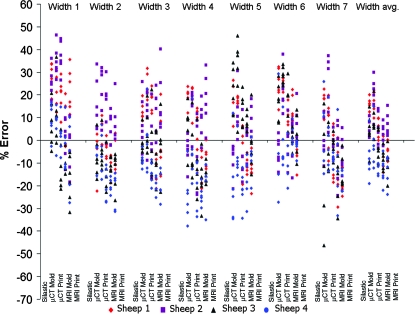
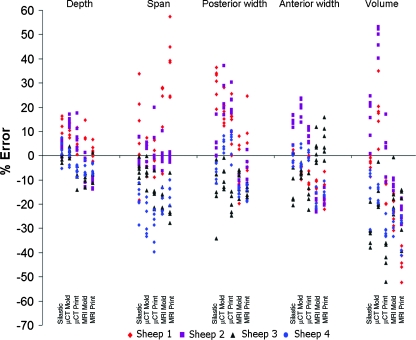
Despite low average errors, high variances were observed for some key dimensions (Fig. 4). The origin of this variance is unclear, but may be due to image source, fabrication process, or animal-to-animal variability. To elucidate the origin of this variation, scatter plots of percent error for height (Fig. 5), width (Fig. 6), and depth, span, posterior width, anterior width, and volume (Fig. 7) were constructed for all fabrication methods. Noticeable shifts in error and increases in variance of scatter profiles were observed for different fabrication processes. This was particularly noticeable for height measurements of MRI mold groups and both printed groups compared with the silastic mold and μCT mold groups (Fig. 5). Across all seven width measurements, there was little variation due to fabrication method (Fig. 6). The trend of increased variance and error for MRI and printed groups were also observed for other measurements, particularly depth and span (Fig. 7). The opposite trend was found for posterior width, anterior width, and volumetric error, for which there was a decrease in the scatter profile for both the MRI mold and MRI print groups (Fig. 7).

FIG. 5.

Scatter plot of height errors showing significant deviation mostly dependent on animal variation and fabrication technique, but not located along the seven radial positions. Color images available online at www.liebertonline.com/ten.

FIG. 6.

Scatter plot of width errors showing significant deviation mostly dependent on animal variation and fabrication technique, but not located along the seven radial positions. Note width data scatter had less variance than height data in Figure 5. Color images available online at www.liebertonline.com/ten.

FIG. 7.

Scatter plot of depth, span, volume, and posterior and anterior width errors showing significant deviations dependent on animal, fabrication technique, and location, specifically span and volumetric errors. Color images available online at www.liebertonline.com/ten.

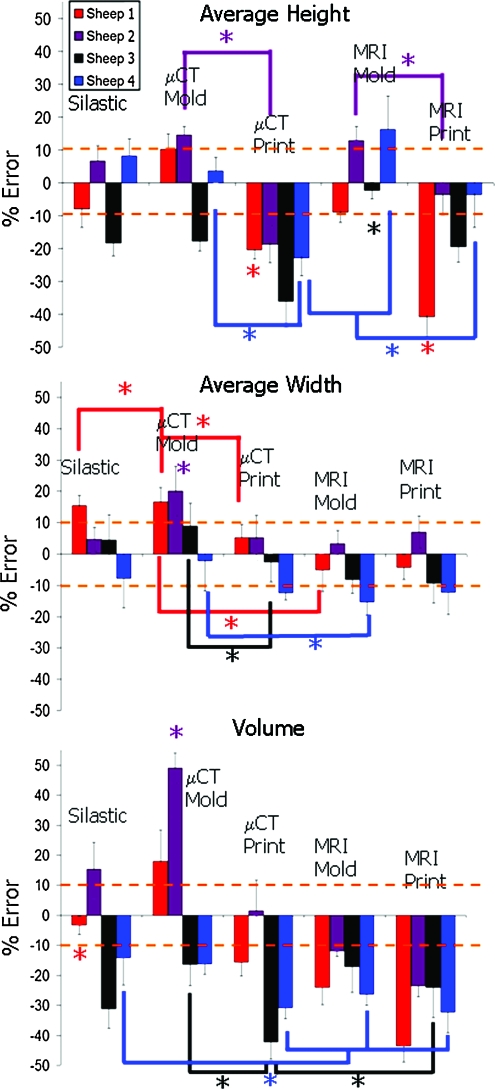
The ability to accurately reproduce geometry varied significantly from animal to animal (Fig. 8) (p < 0.01). Sheep 1 and 3 had more accurate MRI molds than MRI prints (p < 0.01), whereas sheep 2 and 4 had the opposite trend (p < 0.01). On the basis of the average height measurements (Fig. 8), all μCT molded groups were more accurate than μCT printed groups (p < 0.01).

FIG. 8.

Average % error for height width and volume across different sheep and fabrication methods. Height and width data were pooled averages across the seven radial positions. Note differences between animals where sheep 3 was consistently negative for height, volume, and in most cases for width. Color images available online at www.liebertonline.com/ten.

Average width data (Fig. 8) showed that printed samples generated the desired widths very well from both MRI and μCT images. μCT molds were more accurate than μCT prints for sheep 1, 2, and 3 (p < 0.01). MRI scans also provided accurate reproduction of width, as seen by the MRI mold group, being more accurate than the μCT mold groups for sheep 1, 2 and 4 (p < 0.05).

Volumetric error (Fig. 8) was most dependent on imaging and fabrication method. MRI and printed groups were more consistently undersized for all sheep. μCT and silastic mold groups were more likely to be accurately sized or oversized. Depth data were at or near ±10% for all fabrication methods for all sheep (Fig. 9).

FIG. 9.

Average % error across different sheep and fabrication methods for depth, span, and posterior and anterior widths. As noted in Figure 8, sheep 3 and 4 are consistently more negative compared with the native tissue across the different points of interest regardless of fabrication technique or imaging modality. Color images available online at www.liebertonline.com/ten.

Span data were more variable from animal to animal (Fig. 9). Sheep 3 and 4 were consistently undersized, whereas sheep 2 matched the target dimension very well. Silastic and μCT methods were most accurate for sheep 1, whereas MRI-based samples were oversized.

For posterior width, MRI-based samples were consistently undersized for all sheep, but absolute errors were relatively low (Fig. 9). In contrast, μCT-based samples were variable, with some oversizing and undersizing that was sheep specific. Trends in anterior width data (Fig. 9) were similar to posterior width trends. MRI-based samples were also undersized with slightly more absolute error.

Success criteria

Matching key dimensions to within 10% is an established criterion for use of meniscal allografts.²⁷ We evaluated the fraction of data points that met this criterion for each sheep. The fraction of points that fell within ±10% error was greater than 33% for all sheep across all fabrication methods (Table 2). Silastic and μCT molded samples were the most consistent with 40%–64% of points meeting the ±10% error criterion. In comparison, printed and MRI-based samples were more variable with 33%–66% of points meeting the ±10% criterion.

Table 2.

Percentage of Points That Fell Within ±10% Deviation from Native Tissue

	±10% (%)
	Silastic	μCT mold	μCT print	MRI mold	MRI print
Sheep 1	48.3 ± 5.8	45.9 ± 2.8	48.0 ± 2.3	66.3 ± 4.4	44.8 ± 3.5
Sheep 2	52.1 ± 3.1	40.7 ± 4.8	41.4 ± 5.4	33.5 ± 5.9	43.8 ± 4.6
Sheep 3	52.0 ± 2.0	64.1 ± 3.9	58.6 ± 4.6	47.2 ± 3.0	52.1 ± 3.0
Sheep 4	44.1 ± 4.2	42.8 ± 5.3	35.5 ± 3.3	42.5 ± 5.4	33.4 ± 3.3

Note that with the exception of sheep 2 MRI mold and sheep 4 printing groups, most engineered samples were near 50% of the point being within the threshold.

Repeatability error (Table 3) for all methods for all sheep was quite low (5.9%–11.0%). As might be expected from other data, repeatability was consistently lowest in all molded groups (5.9%–8.7%). Printed samples were slightly less consistent with repeatability errors ranging from 5.9% to 11.0%.

Table 3.

Repeatability Error for Each Sheep Meniscus and Fabrication Method

	Repeatability error (±%)
	Silastic	μCT mold	μCT print	MRI mold	MRI print
Sheep 1	7.1	6.9	6.7	7.0	8.5
Sheep 2	7.1	7.6	10.7	7.3	8.0
Sheep 3	8.7	6.5	8.9	5.9	7.5
Sheep 4	8.1	6.7	5.9	8.1	11.0

All samples except for sheep 4 MRI print had a repeatability error below 10%.

Discussion

This work is one of the first studies to present a method to quantitatively compare the geometry of tissue-engineered constructs. The technique presented here uses a commercially available laser scanner and commercially available software that allows for automated measurements and quantitative geometric comparisons. This protocol was used to assess the geometry of the meniscus, a highly complex anatomic structure. The meniscus is a tissue where rudimentary techniques have been developed to quantify geometry as a standard for tissue transplantation.^24,27,28,31 Using this new process enabled automated comparisons to these standards and yielded a host of additional data about other tissue dimensions and sample volume. Although these results are specific to regeneration of the meniscus, this approach is widely applicable to other tissues with complex geometry such as the ear, bones, and heart valve.

The technique described above was used to quantify the geometry of meniscal constructs designed from MRI and μCT scans and fabricated via tissue injection molding and 3D tissue printing. The feasibility of using medical imaging data to design tissue-engineered constructs has only been investigated very recently.^3,32 Similarly, over the past decade a number of efforts have demonstrated the utility of injection molding^3,11,30,33 and 3D tissue printing^17,20 in fabricating engineered tissues with complex geometry. Despite all this work there is limited information on the geometric accuracy of these techniques and how this geometric accuracy might compare between techniques. This article directly compares the geometric fidelity of meniscal constructs produced by tissue injection molding and 3D printing designed from MRI and μCT data.

Both imaging modalities and both fabrication techniques produced anatomically shaped constructs of high geometric fidelity. Injection molded samples were more accurate and reproducible than 3D printed samples. Constructs based on μCT images were more accurate than MRI-based samples, likely due to the difference in resolution based on the chosen scan parameters. It is true that this method may not be a fair comparison of the MRI scan's ability to provide an accurate model of the meniscus because it is in a loaded condition. However, MRI molds did yield samples with a significant fraction of key dimensions within ±10% error with respect to the native tissue. This suggests that the effect of loading may not be large for these measurements. Further, this study also aimed to find out whether a simulated in vivo MRI scan of the native meniscus could compete with a high-resolution μCT scan of excised tissue. We chose not to do an in vivo μCT scan as μCT does not readily view soft tissue without the use of a contrast agent. Delivery of a contrast agent to a sheep meniscus in vivo would prove quite cumbersome such that it was not thought to be a medically relevant option for this method of image-based tissue engineering. Instead we wished to implement a method that could be clinically relevant and noninvasive, as MRI obviates the need for ionizing radiation and avoids the potential of adverse contrast reactions.

Silastic impression molds were used as a benchmark because it is a widely used method for replicating complex geometries (e.g., dental records) and has been used to generate molded engineered tissue.^3,30,34 Comparing deviation heat maps and frequency histograms of injection molds using either MRI or μCT showed that both were very close to silastic impression molds (Fig. 3). However, global trends across the seven points of interest^24,28 showed that injection molds were close to or within ±10% range (Fig. 4). Further, observations from pooled values across the seven height and width locations showed that each sheep had a distinct error pattern regardless of imaging or fabrication method (Fig. 8). Although MRI-based molds were more accurate at generating desired widths compared with the μCT-based molds, all imaging and fabrication methods for all sheep were close to the acceptable error range with respect to the width values. Current printing techniques still suffer in achieving the desired heights. These findings were supported by volumetric error data (Table 1 and Fig. 8), which were largest in the printed tissues, most likely due to the stochastic print errors. μCT molds tended to be larger than native tissue, possibly due to swelling after the tissue was excised and soaked in contrast agent before imaging.

Silastic and μCT-fabricated constructs showed less deviation than MRI-generated constructs. This finding was not surprising due to the much higher image resolution of μCT. MRI samples were consistently undersized, possibly due to the in vivo loading conditions that occur naturally when these joints are being imaged (Fig. 7). Another factor that could cause inaccurate amplification of deviation measurements is projection-based 3D image reconstruction from the laser scans (Fig. 1). This is especially problematic with rigid native tissue that did not sit flat on the platform. Errors that can arise as a result of the projection-based 3D image reconstruction from laser scans will only affect height measurements near the horns, the volume estimate of the native tissue, and the deviation heat maps will be affected near the horns and white zone for some samples. These errors were consistent for all comparisons for a given sheep meniscus. This could be corrected with the addition of a second laser that would spiral around the menisci to gather radial data along the z-axis so that overhanging and elevated surfaces could be viewed and accounted for during the modeling process.

Further evidences of large differences between individual sheep menisci are also evident in the number of points that fell within ±10% (Table 2). For example, sheep 1 had its highest score of 66.3% for MRI mold, whereas sheep 2 had its lowest score of 33.5% for the same method. Sheep 3 had μCT mold as its highest score of 64.1%, and sheep 4 had no imaging modality or fabrication method that scored above 50% (Table 2).

The most promising result was that all fabrication methods and imaging modalities had repeatability errors below 10%, a necessary threshold to validate the practicality of this method for clinical purposes (Tables 1 and 3). The high repeatability is extended to all sheep as well, because all methods were below 10% with the exception of sheep 2 μCT print and sheep 4 MRI print (Table 3). Having low repeatability error is more important than low linear error because simple linear errors can be addressed in the CAD portion of the fabrication process. Because the templates for these geometries are based on CAD software, geometries can be scaled accordingly to increase or decrease volume and thus compensate for shrinkage due to phase change (i.e., liquid to gel). Altering the geometries in this way will allow deviation histograms to be centered about 0% error (Fig. 2).

A major challenge to the image-based approaches to recreating patient-specific geometry is that the structure in need of replacement may not be intact or have the original or correct shape. In such cases there are at least three scenarios for image-guided tissue engineering: (1) the use of data on the geometry of the meniscus from the contralateral knee; (2) the use of data from the target knee obtained before an injury; and (3) the development of a database of meniscal geometry from a large number of patients that could be used to find a match for a specific patient based on the anatomy of other structures in the knee. Obtaining meniscal data from the contralateral knee would require the assumption that both joints are symmetric. Although this is not likely a perfect assumption, this approach would likely be more accurate than matches generated from available cadaveric donor tissue. This information might then be used to compare intact and deficient meniscal geometries in the setting of collagen meniscal scaffold replacement or more accurately sizing meniscal transplantation. Poor matching of native meniscal geometry has been implicated in failure of transplantation.^35,36 If the patient has prior scans of the knee where the meniscus was undamaged (as might be the case for elite athletes or military personnel or individuals scanned for other reasons such as extensor tendon pathology), the relevant geometry could be extracted using the same technique we have presented here, even if MRI data were not as high a resolution as our scans. The last possibility is using current meniscal designs and scaling them to fit dimensions of the knee based on the tibial plateau, contralateral knee, or other knee dimensions. The third option is using work already being explored by Haut and coworkers to develop proper parameters to match cadaveric donor tissue to patients in need of a total meniscal replacement.

With the method presented here, many steps can be taken to improve geometric fidelity in tissue-engineered scaffolds. Future efforts should focus on the development of higher resolution 3D printing of tissues implementing control feedback to prevent stochastic deposition print errors. Given its lack of ionizing radiation and no requirement for contrast agent (with the attendant risks of contrast reaction), MRI holds several advantages over CT for projected clinical use. Newer, more efficient 3D pulse sequences that provide sufficient boundary recognition and isotropic voxels will likely be more amenable to semiautomatic segmentation algorithms and more efficient generation of MRI-derived datasets.³⁷ The future of this methodology still lies in further development of both 3D printing and MRI technology to generate high-resolution scans in a relevant clinical practice time frame and then print them with minimal deviation from the native tissue.

Acknowledgments

The authors would like to thank the Alfred P. Sloan Foundation, Clark & Kirby Foundation, Soft Tissue & Sports Medicine Funds, MRRCC Core grant: AR046121, NSF Fellowship Program, and Cornell University.

Disclosure Statement

No competing financial interests exist.