Pore Characteristics of Chitosan Scaffolds Studied by Electrochemical Impedance Spectroscopy

Abstract

In this study, a novel approach, electrochemical impedance spectroscopy (EIS), was used to examine the pore characteristics of chitosan scaffolds under aqueous conditions. The EIS was run with a constant current of 0.1 mA with the frequency sweep of 10⁶ to 10⁻⁴ Hz. The resulting complex impedance measurement was then used to calculate porosity, which was determined to be 71%. Scanning electron microscopy (SEM) and mercury intrusion porosimetry (MIP), two commonly used methods for scaffold characterization, were used to independently evaluate the pore characteristics and compare with that of EIS. The SEM and MIP were performed and analyzed under standard conditions. The pore diameter values found by SEM and MIP are 107 μm and 82 μm, respectively, indicating that both the image-based (SEM) and pressure-based (MIP) analyses provide similar results. The porosity of 73% calculated by MIP is comparable to that of EIS. From these results, it can be suggested that EIS, a relatively nondestructive test, is able to obtain comparable data on pore characteristics, as compared to SEM and MIP. The advantage of the EIS as an nondestructive test is that it can be performed under physiologically relevant conditions, whereas SEM and MIP require dry samples and vacuum conditions for measurement. These benefits make EIS a viable option for the characterization and long-term observation of tissue-engineered scaffolds.

Introduction

In the United States, thousands of individuals are in critical need of an organ or tissue transplant, and many of those will not be matched with a suitable donor.¹ Due to the incredible need for donor organs and tissue as well as the difficulty in procurement and compatibility, tissue engineering could provide an alternative source of transplant tissue with reduced risk of immune rejection.^2–4 The engineering of tissue requires three critical components: the cells, adequate levels of soluble and insoluble biofunctional molecules, and the scaffold for the support of cell growth and tissue formation. The scaffold acts as a temporary extracellular matrix allowing cell attachment and acclimation to the environment. To achieve the ultimate goal of tissue formation, the scaffold must possess several characteristics, including biocompatibility, nontoxic formation of degradation by-products, cell accessible pore structure, and scaffold degradation rates with appropriate time scales that allow for cell invasion and tissue remodeling.⁵ To accommodate cell infiltration into the scaffolds, the pore diameter must be large enough for cell invasion and migration within the scaffold. Porosity and interconnectivity of the pores must be large enough for adequate cell distribution and small enough to prevent cell detachment by fluid flow.⁵

Due to the pore requirements for successful implementation of a tissue-engineered scaffold, it is important to appropriately design a scaffold as well as evaluate its structure upon fabrication. There are several methods for determining pore structure and porosity such as scanning electron microscopy (SEM), mercury intrusion porosimetry (MIP),⁶ gas adsorption, and X-ray microtomography (μCT)⁷; however, these methods all have distinctive drawbacks that can prevent continued evaluation of the scaffold. SEM can provide observation of the pore geometry and allow for diameter determination, but it also requires cutting of the dried sample, sputtering with gold, and exposure to high vacuum. Similarly, MIP can be used to determine porosity and interpret pore size. Vacuum operating conditions are required to force mercury into the pores of the dried sample, thus resulting in sample loss. Vacuum conditions are also required for gas adsorption, while nitrogen adsorption throughout the sample is recorded. Finally, microtomography can be performed on samples under aqueous conditions but requires radiation exposure.⁷ Consequently, these techniques are not useful quality-control methods for large-scale scaffold production or for long-term in situ monitoring.

Electrochemical impedance spectroscopy (EIS) has been used to study the microstructural properties of a variety of porous materials ranging from cement to ceramics while resulting in negligible damage to the sample.^8,9 EIS allows for the study of the effects of various composites added to a central material as well as long-term evaluation of material stability under different conditions.^8,9 In addition to porous materials, EIS has also been used as an evaluation tool for tissues providing information regarding the status of the tissue over time¹⁰ as well as tissue morphology.¹¹

EIS uses a two or four conductive probe setup in samples filled with conductive fluid. When alternating current passes between the probes through the sample, it travels the path of least resistance, which is, in this case, the pores filled with conductive media. Because the source current is alternating, it can be sent over a specified frequency range. The resistance along the currents path at each frequency is recorded as the complex impedance, which consists of both the real and imaginary components, as well as the phase shift that can be translated to porosity.^8,12 Despite the introduction of small metal probes, EIS does not cause any immediate or long-term damage to the sample being tested. As a result of EIS's usefulness in studying porous structures, it was chosen as a method for the evaluation of tissue engineering scaffolds in a nondestructive manner.

The model scaffold material chosen for evaluation is chitosan. Chitosan is produced through the deacetylation of chitin, which is the naturally occurring polysaccharide comprising the exoskeletons of crustaceans. The resulting chitosan contains charged end groups that allow it to dissolve readily in weak organic acids and forms a regular structure of a porous sponge-like matrix upon redessication. Chitosan has demonstrated a high level of biocompatibility when used as an implant material as well as resistance to bacteria.¹³ The pore structure of chitosan scaffolds has been shown to be larger in diameter than that of an average chondrocyte.¹⁴ Additionally, chitosan scaffolds exhibit high porosity and interconnected pore structure. The biocompatibility and predetermined pore characteristics of chitosan suggest its appropriateness as a cell scaffold material.¹⁴

The ability to nondestructively characterize and monitor scaffolds under in vivo conditions offers a great advantage for engineering tissues. In our studies, EIS was first used to characterize the pore geometry of chitosan scaffolds. The results were compared to the more common scaffold characterization methods of SEM and MIP to determine its viability as a nondestructive technique for evaluating porosity and pore interconnectivity. The overall goal of this comparison is to demonstrate that EIS is a comparable effective method that can be used for both initial characterization and continuous monitoring.

Materials and Methods

Scaffold fabrication

Chitosan scaffolds were fabricated by dissolving 2% weight per volume dry chitosan powder from crab shells in 2% volume per volume acetic acid, purchased from Sigma (St. Louis, MO), heated to 50°C. The chitosan solution was cast into a specimen container to an approximate fill level of 3 cm in height and frozen at −20°C for 24 h. Once thoroughly frozen, the scaffold was lyophilized for 24 to 36 h, resulting in a foam-like three-dimensional matrix. The sample was ensured to be completely dry by piercing the center of the scaffold with a 20-gauge needle to feel for irregularities indicative of insufficient freeze drying. A total of eight bulk scaffolds were fabricated from separate batches to test the consistency of the results acquired from EIS.

Characterization

SEM

Three completely dry scaffolds were removed from the lyophilizer and cut into wedges, thereby exposing their interior surfaces. The sample slices were kept with desiccant before sputter coating with gold. The sample was then imaged on an SEM (Amray 1830, Bedford, MA) using an accelerating current of 25 kV and recorded at resolutions of 60 × to 200 × . Eight of the obtained images were analyzed using the NIH Image J software. Twenty-five usable pores per image were outlined, and the two-dimensional area was determined by measuring at the same orientation across the visible pore diameters. Statistical analysis (average and standard deviation) was performed.

MIP

Mercury intrusion determines pore geometry and pore volume by introducing mercury, which is a nonwetting liquid, into the dry scaffold under pressurized conditions. Samples placed in a penetrometer are subjected to high vacuum. Once the minimal pressure is achieved inside the glass penetrometer, mercury flows to surround the sample. This initial volume of mercury subtracted from the known volume of the penetrometer provides the volume of the sample if it were completely solid. Pressure is then applied to the reservoir of mercury in the penetrometer stem at increasing incremental installments. With increased pressure, the mercury enters increasingly smaller pores. The total volume of mercury forced into the sample is used to determine the overall porosity, while the mercury at each pressure interval allows for the estimation of pore size.

Three wedge portions were sliced from three separate chitosan scaffolds and analyzed with a mercury porosimeter (Micromeritics Autopore IV, Norcross, GA). Correspondence to the SEM was facilitated by using the same batch of scaffolds. First, a vacuum of 50 μm of mercury was pulled on each sample, thereby completely removing the air from the sample. Mercury then surrounded the sample and was forced into the pores with increasing pressure from 0.22 up to 30 psi. The weight of the sample in the penetrometer was determined both before and after the introduction of mercury. The difference in weight divided by the density of mercury at room temperature gives the total volume used. By dividing the total pore volume by the external volume of the sample, porosity or percent pore volume was determined. The pore size was estimated using the Washburn equation:

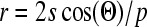(1)

where r is the pore radius, s is the surface tension of mercury, Θ is the contact angle of the mercury, and p is the pressure applied. A built-in algorithm automatically calculated this value at each pressure interval, and average values were obtained after all points were recorded.

EIS

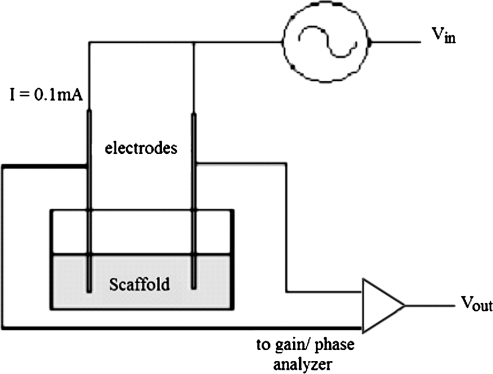
The electrochemical impedance spectrometer (Fig. 1) consists of an AC generator, the left and right sample electrodes, and the impedance analyzer, which also inputs the signal into the computer for data collection. The AC generator operates at a constant current while sweeping across a predetermined frequency range starting with the highest to the lowest. At each frequency, the impedance analyzer measures the complex impedance. Each data point consists of the impedance magnitude, the real and imaginary impedance, and the phase shift.

FIG. 1.

Electrochemical impedance spectroscopy setup showing parallel electrodes introducing a constant current of 0.1 mA into the chitosan scaffold.

EIS was initially performed on two dry scaffold samples using 6Al 4V ELI medical-grade titanium wire probes (Small Parts, Miramar, FL) attached to an impedance analyzer (Solartron 1260A, Hampshire, England). The sides and bottom of four scaffolds were sealed with wax to prevent current leakage. A constant current of 0.1 mA was used for the evaluation, and scanning was performed over the frequency range of 10⁻² to 10⁴ Hz. The scaffolds were then loaded with deionized (DI) water until reaching total saturation equivalent to a fully swollen state, followed by EIS using the same current and frequency range. EIS was performed on scaffolds swollen with phosphate-buffered saline (PBS) at 20% dilution, followed by 29%, 50%, and 100%. Identical experimental parameters were used for all dilutions. Five remaining scaffolds were each sealed with wax and swelled with nondiluted PBS. Each was evaluated with EIS with a constant current of 0.1 mA over the frequency range of 10⁻² to 10⁴ Hz.

Data analysis

The magnitude of impedance was plotted against the frequency. The impedance of the sample was observed over the frequency range and the effect of ionic composition on the shift of the impedance magnitude was examined. The tangent of this phase shift is the ratio of the imaginary permittivity (ɛ′′) to the real permittivity (ɛ′):

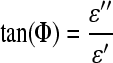(2)

The imaginary permittivity is the loss permittivity that is related to the resistive nature of the sample while the real permittivity is the storage permittivity related to the capacitive nature of the sample. The tangent of the absolute value of phase shift was computed for the frequency range, thereby providing the ratio of resistive to capacitive components.

By plotting the real versus imaginary impedance in a Nyquist plot, the bulk resistance was acquired. Using a form of Archie's law, porosity was estimated from the bulk resistance by first calculating the effective conductivity according to Neithalath et al.⁹:

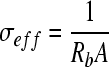(3)

where σ_eff is the effective conductivity, R_b is the bulk resistivity, A is the cross-sectional area, and l is the sample length. Archie's law was used to determine the porosity by the following equation:

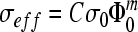(4)

where σ₀ is the conductivity of saline, which is known to be 1.2 S/m,¹⁵ Φ₀ is the pore volume or porosity, C is the coefficient of saturation ranging from 0.1 to 1, and m is the cementation factor typically in the range of 1.5 to 4.

Once the sample porosity was calculated, the pore connectivity was determined. There is a connectivity factor for the pores as well as the solid material, which is related to the effective conductivity of the saturated scaffold as seen in the following equation.⁹

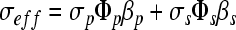(5)

where σ_eff is the effective conductivity, and σ_p and σ_s, Φ_p and Φ_s, and β_p and β_s represent the pore and scaffold conductivities, the pore and scaffold volume fractions, and the pore and scaffold connectivity factors, respectively.

Results and Discussion

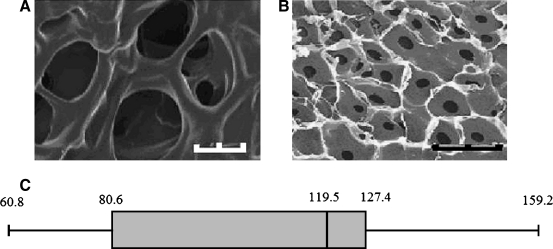
SEM analysis showed a consistent pore structure throughout the scaffold (Fig. 2A) with the exception of the slicing location. As a result, regions where samples were sliced were eliminated from the data analysis, and only regions in which pores appeared completely intact were analyzed. Under the assumption that the pores are sectioned past the midpoint and the opening remains circular but decreases consistently in size (Fig. 2B), the diameters were determined for 25 pores on 8 different representative images. The average diameter was determined to be approximately 107.31 ± 24.05 μm, and the median value was 119.45 μm. Pore diameter ranged from 60.8 to 159.23 μm (Fig. 2C). Some aberrant larger pores were noted; however, these are likely the result of being present on the uppermost surface during lyophilizing. Internal sections fall primarily within the aforementioned range.

FIG. 2.

(A) Scanning electron microscopy scan of chitosan scaffold at 25 kV showing pores with average diameter of 107.31 ± 24.05 μm. (B) Scanning electron microscopy scan of chitosan scaffold at 20 kV showing consistent decreasing circular cross section. (C) Distribution of pore sizes determined from image analysis (n = 8 images with 25 pores per image). Scale bar = 100 μm (A) and 50 μm (B).

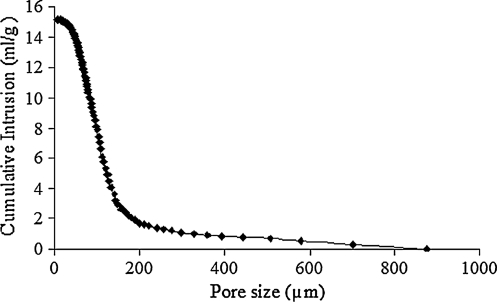
With a mercury contact angle of 130° and a density of 15.53 g/mL, the average porosity was found to be 72.9 ± 0.5% using MIP. The average of the three samples gave a pore diameter average of 82.2 ± 4.8 μm. These values are consistent with the results of previous studies.¹⁴ A sample plot of cumulative intrusion volume versus pore size for one of the three samples illustrates a steep drop initially followed by a plateau indicative of a narrow parameter range (Fig. 3), further corroborating the SEM images.

FIG. 3.

Cumulative intrusion volume per pore size determined from mercury intrusion porosimetry analysis of a chitosan scaffold (n = 3 scaffolds with three wedges per scaffold).

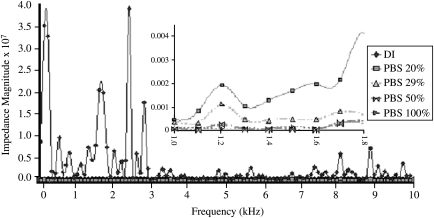
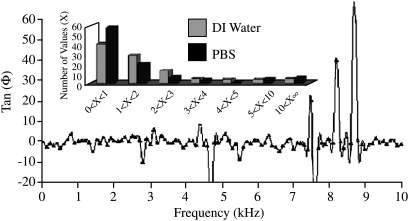
Altering the PBS concentration resulted in the shifts in impedance noted in five EIS data sets (Fig. 4). The first sample was run without the addition of any liquid and resulted in expected high impedance across the frequency (data not shown). The addition of deionized (DI) water reduced the impedance values from the previous dry sample because of the presence of charged species from the dissociation of water molecules into hydronium and hydroxyl ions; however, the values were still high. With each increase in ionic strength, the overall impedance of the sample was reduced. These are expected results due to the increase in the number of ionic species in the solution, thus rendering a lowered resistance.

FIG. 4.

Impedance magnitude over the frequency range as determined by electrochemical impedance spectroscopy with titanium probes showing decreasing magnitude with increasing ionic concentration (n = 4 scaffolds each of which has five dilutions). Inset: close-up view of frequency under 2 kHz (dry sample not shown).

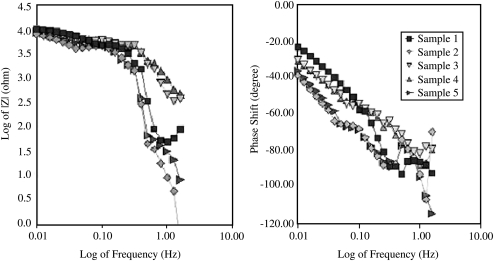
The data for the samples containing 100% PBS and DI water were also compared over the same frequency range for the phase shift. The phase shift is the change in phase angle between the input and output waveform. The signal is altered by the material the current passes through, resulting in a phase shift from the emitted signal to the resultant signal. While no correlation could be made to the frequency, the distribution of the permittivity ratio showed considerably higher values between 0 and 1 for the 100% PBS sample as compared to the DI water (Fig. 5). The values between 0 and 1 indicate that the resistivity of the sample is lower than the capacitance; therefore, the sample saturated with DI water is far more resistive than the PBS. Perhaps, the increase in ionic species in PBS results in a capacitive effect, whereas in the case of DI water, due to the lack of ionic species, the system acts as a nonconductor that dissipates electricity. The next set of EIS data from five separate samples was collected and compared for consistency by two Bode plots. The Bode plots of the phase shift and the magnitude showed close grouping of the points, indicating uniformity in both the sample and the testing method (Fig. 6). Additionally, the two Bode plots took on the standard curvature for EIS for a single time constant system.¹⁶ All samples were run under the conditions stated previously with the exception of sample 5. After the previous four had been run, it became apparent that the Nyquist plot required further scanning of the lower frequency range.

FIG. 5.

Phase shift as a function of frequency of chitosan scaffolds swollen in deionized water. Inset: distribution ratio values for the tangent of the phase shift (n = 4).

FIG. 6.

Bode plot of the impedance magnitude (left) and the phase shift (right) as a function of frequency (n = 5).

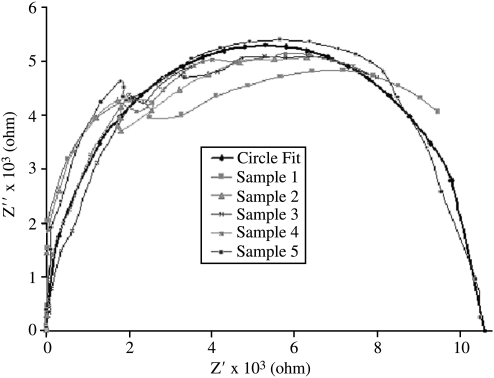
The Nyquist plots showing the real versus imaginary impedance of the five sequential samples took on the characteristic semicircle shape for the lower frequency values (Fig. 7). Given the normality of the shape, the bulk resistance (R_b) can be estimated as the point at which the semicircle crosses the x-axis. Because only one of the samples was allowed to cross the x-axis, the others were fitted to a semicircle to determine their approximate cross. To anticipate the x-intercept of the Nyquist plots, an approximate radius was estimated by taking the average of the real and imaginary impedance values at the visually observed center point, x = 5300. Different samples gave slightly different values (Table 1). The average of the values totaled approximately 5300 ± 140 ohms. Using 5300 as the radius, a semicircle was plotted (Fig. 7) along with the impedance values showing a good fit, which, therefore, suggests that the x-intercept of the semicircle is approximately that of Nyquist plots (x-intercept = 10,600 ohms). As a result the new R_b was determined to be 10,600 ohms. A simple DC resistance evaluation was performed confirming the EIS-determined R_b (data not shown).

FIG. 7.

Nyquist plot of the real versus the imaginary impedance for chitosan scaffolds (n = 5). Geometric projection of the semicircle (circle fit) indicates a bulk resistance value of 10,600 ohms (n = 5).

Table 1.

Estimated Radii of Nyquists Plots for Chitosan Scaffolds from Approximate Center Point of Each Arc (n = 5)

Sample	Estimated radius × 103
1	5.20
2	5.28
3	5.19
4	5.29
5	5.53
Average	5.3 ± 0.14

While the formulas and interpretations of Archie's law have been widely published for a number of different types of rocks,¹⁷ the use of EIS to characterize tissue scaffolds is novel. Consequently, the behavior of the scaffold must be taken into account to obtain the correct equation format. Because the scaffold becomes completely swollen with PBS, it can be assumed that C is at or near a value equal to 1.0 due to total saturation. The cementation factor is harder to estimate from physical observation. Previous studies of a fused glass bead experiment have reported a relationship between porosity and the inverse of the formation factor (F), which is σ_eff/σ_o.¹⁸ The experimental setup included the development and characterization of physical porosity models composed of three different-sized glass beads. The data collected showed that the physical models fit the mathematical model proposed with the use of C = 1 and m = 2.¹⁸ This model also applies to physical systems with porosity in the anticipated range of the chitosan scaffold justifying the values of C = 1 and m = 2 in the characterization.

Using the R_b determined from the Nyquist plot, the effective conductivity was determined to be 0.605 S/m. Introducing the effective conductivity into Archie's law, the porosity was estimated to be 71.0%. The pore connectivity factor cannot be determined from either of the previously discussed methods; however, evaluating the connectivity is important to assess fluid flow through the scaffold. When the scaffold is saturated with an electrolytic solution, the contribution of the pore to the effective conductivity far exceeds the contribution of the solid components of the scaffold. As a consequence, the solid portion of the equation can be considered null and the equation can be rewritten in the following format to solve for the connectivity.

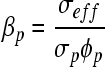(6)

The effective conductivity was once again used to determine the pore connectivity factor, which is 0.71, a reasonable value given the relationship between porosity and pore connectivity.⁹

Based on physical observation of the scaffold before, during, and after the performance of EIS analysis, it became apparent that the physical damage from the testing was minimal. The purpose of the wax technique is solely to prevent current leakage. For use in vivo, this wax coating would not be necessary due to modification in the casting procedure. The ionic strength variation experiments resulted in the expected correlation of lowered resistance with increased ionic strength. The results of these findings include the assessment that the primary contributor to the EIS data is the fluid in the pores and that the testing can be optimally performed under subtly varying in vivo conditions. The phase shift evaluation confirms once again the critical effect of the pore fluid as well as the overall slight capacitive nature of the scaffold when filled with PBS. Based on the testing parameters with PBS, the scaffold can be evaluated under in vivo conditions.

The SEM data for pore diameter agree with previously published data¹⁴ and corresponds to the value of pore diameter provided by the MIP (Table 2). By comparing the visual data with the physical intrusion data, we can further legitimize the results of the MIP providing confidence in the value of 72.9% for porosity. While the EIS technique does not provide pore diameter data, SEM and MIP results are comparable. The calculated value for porosity of 71.0% from EIS is therefore not only close to the value acquired from the proven method but also legitimate. The additional value of 0.71 for the pore connectivity factor provides characterization that heretofore was unattainable by the commonly used methods. This pore connectivity factor indicates a high level of connectivity that can be associated with appropriate flow of nutrients and waste to and from regions of the scaffold. Ultimately, the porosity and pore connectivity values are more useful for rapid nondestructive quality-control analysis due to their representation of the whole scaffold as opposed to selected regions.

Table 2.

Pore Size and Porosity Comparison for Scanning Electron Microscopy, Mercury Intrusion Porisimetry, and Electrochemical Impedance Spectroscopy

Method	Pore diameter (μm)	Porosity	Comments
SEM	107.31	–	Not tested for porosity
MIP	82.22	72.9%	Dry sample in vacuum
EIS	–	71.0%	Sample in aqueous conditions

SEM, scanning electron microscopy; MIP, mercury intrusion porosimetry; EIS, electrochemical impedance spectroscopy.

Conclusions

In summary, the data acquired and interpreted from the EIS compare favorably to the more commonly used characterization methods of SEM and MIP. This comparison indicates that the EIS provides an effective nondestructive way of characterizing the physical properties of the chitosan scaffold. Further, EIS provides the opportunity to monitor the scaffold long term under in vivo conditions. The successful implementation of the EIS for swollen chitosan scaffolds strongly suggests that this technique is applicable as a characterization method for other fluid-filled tissue engineering scaffolds.

Acknowledgments

The authors would like to thank the National Institute of Health (P20 R16456) for partial funding. Stephanie Tully-Dartez is partially funded by the National Science Foundation's GK12 Teaching Fellows program under NSF Award Number EEC 0803821 awarded to Dr. David K. Mills.

Disclosure Statement

No competing financial interests exist.