Dynamic Contrast Enhanced-MRI with Extravasating Contrast Reagent: Rat Cerebral Glioma Blood Volume Determination

Abstract

The accurate mapping of the tumor blood volume (TBV) fraction (v_b) is a highly desired imaging biometric goal. It is commonly thought that achieving this is difficult, if not impossible, when small molecule contrast reagents (CRs) are used for the T₁-weighted (Dynamic-Contrast-Enhanced) DCE-MRI technique. This is because angiogenic malignant tumor vessels allow facile CR extravasation. Here, a three-site equilibrium water exchange model is applied to DCE-MRI data from the cerebrally-implanted rat brain U87 glioma, a tumor exhibiting rapid CR extravasation. Analyses of segments of the (and the entire) DCE data time course with this “shutter-speed” pharmacokinetic model, which admits finite water exchange kinetics, allow TBV estimation from the first-pass segment. Pairwise parameter determinances were tested with grid searches of 2D parametric error surfaces. Tumor blood volume (v_b), as well as v_e [the extracellular, extravascular space volume fraction], and K^trans [a CR extravasation rate measure] parametric maps are presented. The role of the Patlak Plot in DCE-MRI is also considered.

Introduction

For (Dynamic-Contrast-Enhanced) DCE-MRI, the paramagnetic contrast reagent (CR) is detected indirectly, through its ability to reduce the tissue ¹H₂O longitudinal relaxation time constant, T₁. Thus, effects of equilibrium intercompartmental water exchange on the pharmacokinetic analysis have to be considered. Though the potential for such exchange effects has long been recognized (1–4), most early MRI pharmacokinetic models assumed a linear relationship between ¹H₂O (T₁)⁻¹ [≡ R₁] and CR concentration [the signature Standard Model (SM) characteristic] (5–7). However, this is tantamount to assuming that equilibrium water exchange between tissue compartments is effectively infinitely fast, a corollary known to be invalid. This assumption makes MRI pharmacokinetic modeling incorrectly analogous to that of nuclear medicine, where the radiotracer is detected directly but its compartmentalization is not intrinsic to its signal. To enfranchise such modeling, some exchange-desensitized DCE-MRI approaches have been proposed (4,8), but these usually incur the expense of decreased sensitivities to other parameters (9). Thus, during the information-rich CR bolus first-pass, the magnitude of the DCE-MRI water exchange effect is largely unexplored. A comprehensive DCE-MRI model BALDERO [Blood Agent Level Dependent and Extravasation Relaxation Overview], which admits three-site water exchange, has been described (10). This “Shutter-Speed” Model (SSM) includes the SM as a limiting case. Simplified two-site special cases include: only equilibrium transendothelial water exchange when the extent of CR extravasation is small (11) and only transcytolemmal water exchange when CR extravasation is extensive (12). Recent studies demonstrate that significantly increased breast cancer tumor specificity obtains when the latter exchange is taken into account (13–15).

The accurate determination of tumor blood volume fraction (v_b) is a highly desired imaging biometric goal. This is commonly thought difficult, if not impossible, for small molecule CR DCE-MRI because angiogenic malignant tumor vessels allow rapid CR extravasation. This has led to the use of macromolecular CRs for DCE-MRI, which are assumed to remain intravascular (16). However, analyses of the latter type of study usually assume effectively infinitely fast equilibrium transendothelial water exchange and this could cause significant incorrect ¹H₂O signal-weighting attributions during the indirectly-detected CR bolus passage and affect pharmacokinetic parameter value determination (8–10). Starting with the Bloch rate law modified for simultaneous relaxation of the blood, interstitial, and intracellular ¹H₂O signals, the Three-Site-Two-eXchange (3S2X) shutter-speed pharmacokinetic model BALDERO (10) accounts for these aspects. Here we report the use of BALDERO to measure v_b and other parameter values in rat brain gliomas exhibiting significant CR extravasation.

Methods

Seven male athymic nude rats (rnu/rnu, 220–330 g, from the OHSU Blood-Brain Barrier Program in-house colony) were anesthetized with intraperitoneal (IP) ketamine (60 mg/kg) and IP diazepam (7.5 mg/kg). Human U87 cells (~1.5 × 10⁶ cells in 15 µL) were stereotactically injected into the right caudate nucleus. Four to ten weeks later, tumor-bearing animals were anesthetized using IP medetomidine (0.6 mg/kg) and ketamine (15 mg/kg). Following tail vein catheter insertion, coronal-equivalent MRI scans of the head were performed with an ultra-high field (11.75 T) instrument (Bruker; Billerica, MA). For each animal, a dose of only 50 µmol/kg of GdDTPA-BMA (Omniscan, after 1:2 dilution) was injected via the tail vein catheter, followed by ~ 0.24 mL saline flush, with a flow rate of 1 mL/min. A quadrature volume RF transmit coil was used along with a surface RF receive coil placed on the animal’s head. The three-slice, fast-gradient-echo DCE-MRI sequence parameters were: TR/TE, 25/1.4 ms, flip angle 20°, slice thickness 1.0 mm, rectangular FOV (4.48 × 2.24) cm², a complex image matrix of 128 × 64, and a 1.6 s intersampling interval. Thus, the nominal spatial resolution is 1.0 × 0.35 × 0.35 mm³.

For the Arterial Input Function (AIF) of each animal, data were taken from an ROI in the sagittal sinus (SS) using custom-written code that is capable of arbitrary multi-pixel selection. The time-course of two-to-four pixel ROI-averaged DCE signal intensity (an extensive property) was used to estimate the temporal features of that of the blood ¹H₂O longitudinal relaxation rate constant, R_1b(t). The blood plasma CR concentration, [CR_p](t), was adjusted by iterating between changing it in the SS time-course and fitting the eight minute time-course of a reference tissue (17) temporalis muscle ROI within the head FOV. This minimizes inflow effects introduced errors. This was done until the muscle v_e [Extracellular, Extravascular Space (EES) volume fraction] value converged on 0.11, and K^trans [volume-weighted CR extravasation rate constant] was generally around 0.03 min⁻¹ (18). The value of r_1p [plasma CR relaxivity - relates [CR_p] to R_1b] was assumed to be 3.32 mM⁻¹s⁻¹. The v_e and K^trans values were assumed to have no significant shutter-speed effects because of the low CR dose (10,12,14) used at this high field (see below). The use of the rat SS ¹H₂O MR signal for AIF determination has been very well-validated by gold standard Gd(¹⁴C)DTPA²⁻ radiotracer measurements, though the poor temporal resolution of the latter does not allow detection of the first-pass (19). To the extent that any varying transverse relaxation of the ¹H₂O_b signal (see below) does not significantly affect this, R_1b is an intensive property directly related to the plasma CR concentration, [CR_p]. Each AIF was synchronized with each tumor DCE time-course before fitting the latter.

The tumor pre-contrast T₁ value (T₁₀) was determined using a spin echo inversion recovery (IR) sequence (TR/TE: 9000/5.1 ms) with seven TI values (0.14, 0.3, 0.6, 1.2, 2.5, 5.0, and 8.5 s). The IR data were modeled with three adjustable parameters: R₁, M₀ (Boltzmann magnetization), and α (imperfect inversion correction). The ¹H₂O T₁₀ values calculated from the tumor ROI were then used for the pharmacokinetic modeling. Since only one T₁ is measured for each voxel, R_1o0 = R_1i = 1/T₁ is assumed (these symbols are defined in Table 1). R_1b0 is calculated the same way from a small ROI within the SS.

Table 1.

PARAMETER		Numerical value	Reference
blood CR relaxivity	r1p (mM−1 s−1)	3.32	this study
EES CR relaxivity	r1o (mM−1 s−1)	3.32	this study
blood 1H2O R1 before CR (in the absence of exchange)	R1b0 (s−1)	0.33	this study
EES 1H2O R1 before CR (in the absence of exchange)	R1o0 (s−1)	0.52 (for rat # 1)	this study
intracellular 1H2O R1 (in the absence of exchange)	R1i (s−1)	0.52 (for rat # 1)	this study
tissue density	ρ [(g (tissue))(cm)−3]	1.0
tissue volume fraction accessible to mobile aqueous solutes	fw	0.8	(40)
macrovascular hematocrit	hv	0.45	(41)
microvascular hematocrit	hs	0.3	(41)
water vascular average lifetime	τb (s)	0.3	(18)
intracellular water average lifetime	τi (s)	0.3	(15)
blood volume fraction	vb	varied for first pass fixed at first pass   fitted values   elsewhere
EES volume fraction	ve	0.2 (if not a fitting   parameter)
CR extravasation rate constant	Ktrans (min−1)	varied

Subsequent to the DCE-MRI study, each animal was sacrificed by an intracardiac overdose of sodium pentobarbital. The brain was excised, fixed in formalin, and vibratome-sectioned into 100 µm coronal-equivalent planes. The slices were incubated with mouse antihuman mitochondrial antigen (Abcam, Cambridge MA), followed by biotinylated secondary antibody, and visualized with the Vectastain ABC kit (Vector Laboratories, Burlingame, CA) using diaminobenzidine. Dark brown staining is specific for the presence of human tumor cells derived from those implanted.

The compartmental CR relaxivity quantity (r_1p, r_1o in the interstitium) was determined using a phantom sample containing tubes with saline solutions having different [CR] values.

Results

Fitting the Data

A) Nonlinear Fitting

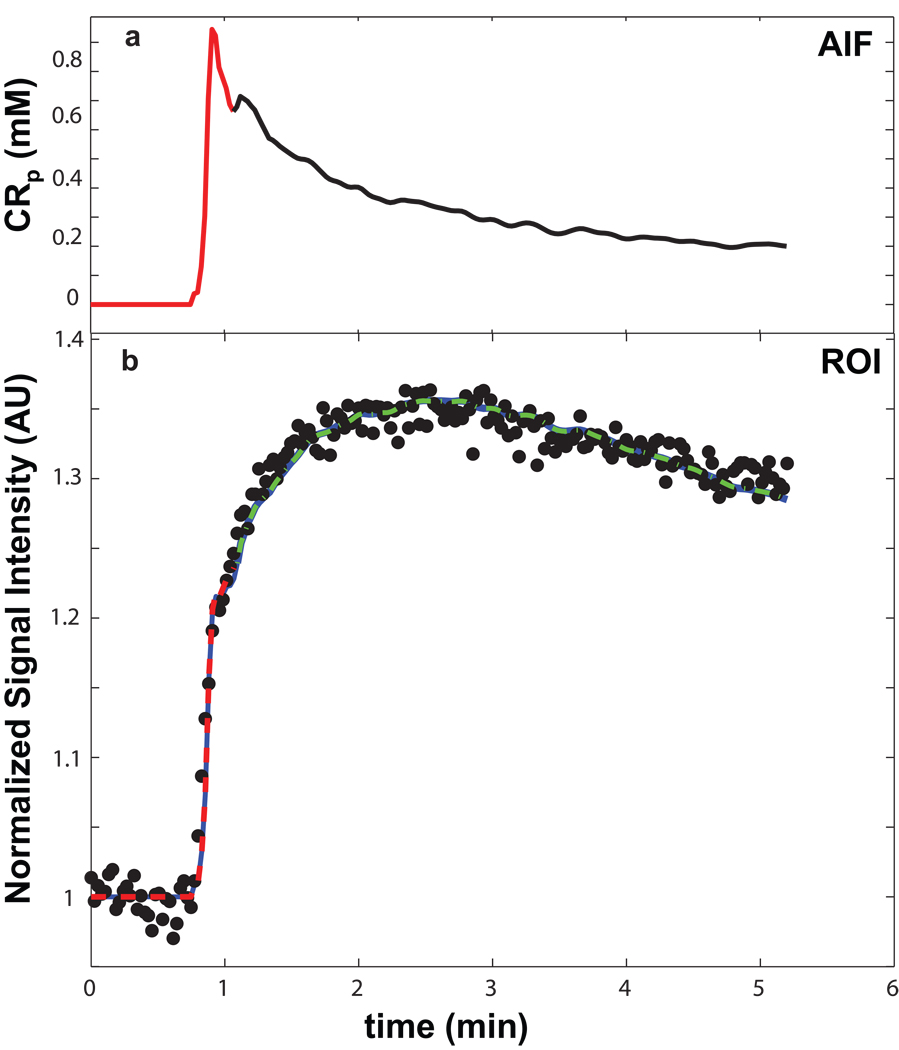
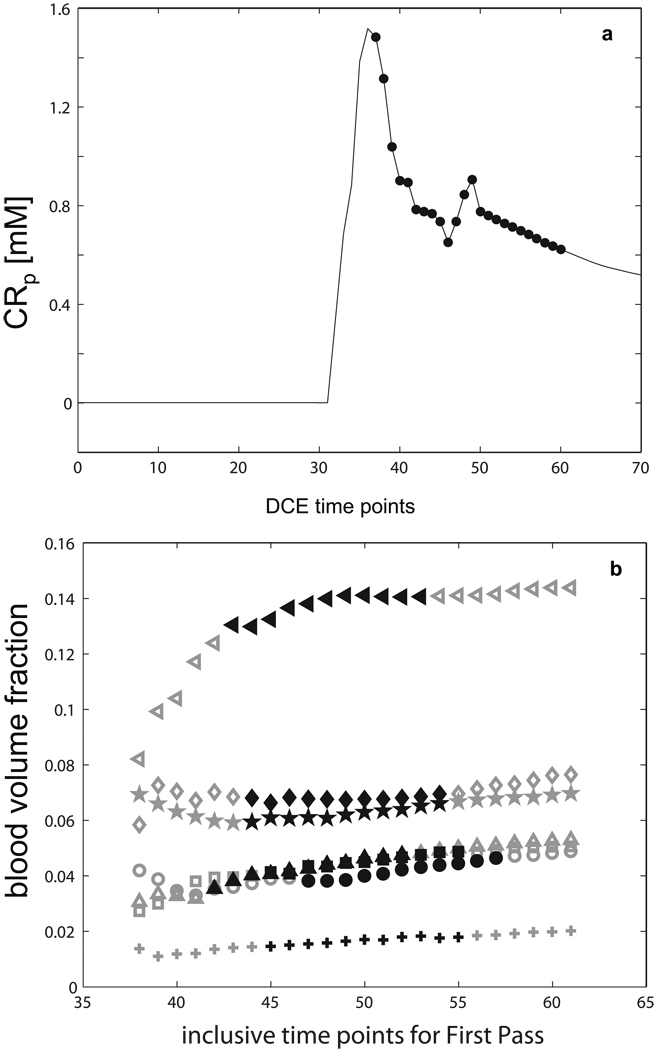
The AIF for animal #1 is plotted (solid curve) as the plasma CR concentration, [CR_p], in Figure 1a. [More precisely, AIF should be termed PCF (Plasma Concentration Function).] It was determined from SS and temporalis data as described in Methods. The AIF was temporally registered with the tumor data time-course before fitting the latter. The Fig. 1b points report the time-course of the mean tumor ROI signal intensity (divided by that before CR arrival; S/S₀) for the same animal. Three colored solid curves represent successive BALDERO fittings of different DCE time-course segments. The red curve, covering only the first-pass (also red in the AIF), shows the fitting using only two variable parameters: K^trans and p_b (v_b/f_W), the mole fraction (“population”) of tissue water in blood. The τ_b⁻¹ (unidirectional rate constant for water extravasation) value was fixed at 3.3 s⁻¹ (20) [more on this below]. All other parameters (which are common to the Standard [intrinsically] and Shutter-Speed Models) were held fixed at the values listed in Table 1, where they are also defined and their precedents cited. Only R₁₀ values differ among the animals. With the thus-fitted K^trans (0.092 min⁻¹) and p_b (0.073) as initial starting value and fixed, respectively, the green curve shows the BALDERO fitting of the data points occurring only after the first-pass. This was accomplished using only K^trans and p_o (v_e/f_W), the mole fraction of tissue water in (“outside”) EES, as fitting parameters. The blue curve, which largely overlaps the red and green ones, is a K^trans,p_o fitting of the entire time-course. The negligible differences between these curves and the relative continuity of the fitted segments reflects the dominance of different model parameters at different CR passage periods, as predicted in (10). This result suggests little is to be gained if iterative fitting approaches are adopted (in general, no more than three successive approximations were required for convergence; not shown). Thus, in this case the successive curve segment fitting procedure was halted after the entire time-course fitting was completed. The K^trans values determined for the first-pass data only, for those only after the first-pass, and for those from the entire time-course are: 0.092 min⁻¹, 0.091 min⁻¹, and 0.091 min⁻¹, respectively. The p_o values returned for the latter two are each 0.19. The “texture” of the fitted curves arises from that of the AIF, which is numerically incorporated (12) into the analytical BALDERO. The green and blue fitted curves exhibit a very slight mismatch underestimating the data between 1 and 2 minutes. This may be due to the second pass peak evident in the SS AIF, which might be absent in the local tissue AIF. Perhaps this highlights the problem of using a large vessel [CR_p](t) when the model wants the voxel capillary [CR_p](t) (21).

Figure 1.

Panel a shows the Arterial Input Function (AIF) derived from sagittal sinus and temporalis data for animal #1. It is used for pharmacokinetic model fitting of the U87 glioma tumor tissue data. The panel b points trace the time-course of the mean tumor ROI signal intensity for animal #1. The three solid curves represent successive BALDERO fittings of different DCE time-course segments. The red curve, covering only the first-pass (also red in panel a), shows the fitting using only two variable parameters: K^trans and p_b. With the thus-fitted K^trans (0.092 min⁻¹) and p_b (0.073) as initial starting value and fixed, respectively, the green curve is a fitting (K^trans = 0.091 min⁻¹, p_o = 0.19) of the data points occurring only after the first-pass. The blue curve shows the BALDERO fitting, which largely overlaps the other curves, of the entire time-course using only K^trans and p_o as fitting parameters – returned as 0.091 min⁻¹ and 0.19, respectively. Other parameter values are as enumerated in Table 1.

The above recursive fitting procedure could result in v_e,v_b correlation. This was investigated with simulations using different v_e values (v_e start values) fixed for first-pass fittings. Fifteen steps, with v_e evenly spaced between 0.04 and 0.79 (p_o from 0.05 to 0.98), were used for each animal studied. The set of parameter values for the curve fitted to the entire time-course (blue, in Fig 1b) was then used for each subject. For each v_e value, random Gaussian noise was added each time to the discretized, simulated (entire) time-course, and then 200 fittings were performed. Different initial guess v_b, K^trans values were used for each of the 15 v_e steps. Each fitting proceeded in the same way as described for Fig 1b (first-pass to determine v_b with potential v_e bias, then entire time-course for v_e with v_b fixed at the fitted value). Within experimental error, the first-pass fitted v_b value is v_e-insensitive for v_e fixed above 0.2. Correlation coefficients of the fitted v_b (from first-pass) and v_e (from entire time-course) values were comparable to those of other fitting parameter pairs (never greater than 0.4) as long as the constant v_e value for the first-pass K^trans,v_b fitting is not fixed too small or too large. Thus, v_e = 0.2 was used for our first-pass fittings.

Another way to describe the almost universally used Standard Model pharmacokinetic analysis family is that it incorporates the [Fast eXchange Limit] FXL constraint for all equilibrium intercompartmental water exchange systems. If the animal #1 data are fitted with the SM (by setting τ_b to be 1 ms), the model curve is perfectly superimposed on those in Fig. 1b (not shown), but the parameter values returned are: K^trans = 0.094 min⁻¹, p_b = 0.062, and p_o = 0.19. This 15% v_b underestimation by the SM is an indication of a water exchange effect similar to that reported previously for intravascular CR studies (4).

B) Linear Fitting

One can illustrate this systematic error using a Patlak Plot (PP) – the popular linearization technique codified more than 25 years ago (22) for graphical analyses of tracer pharmacokinetic data – recently reviewed and used for glioma MRI (23) and for myocardial perfusion MRI (24). The integral pharmacokinetic rate law upon which the PP is generally based is given in Equation [1], where [CR_o] is the interstitial CR concentration (10). The Eq. [1]

$${\mathrm{v}}_e[{\mathit{\text{CR}}}_o](T)+{\mathrm{v}}_p[{\mathit{\text{CR}}}_p](T)={\mathrm{K}}^{\text{trans}}{\displaystyle {\int }_0^T[{\mathit{\text{CR}}}_p]}(t)e^{(-{\mathrm{K}}^{\text{trans}}{\mathrm{v}}_{\mathrm{e}}^{-1}(T-t))}\mathit{\text{dt}}+{\mathrm{v}}_p[{\mathit{\text{CR}}}_p](T)$$ [1]

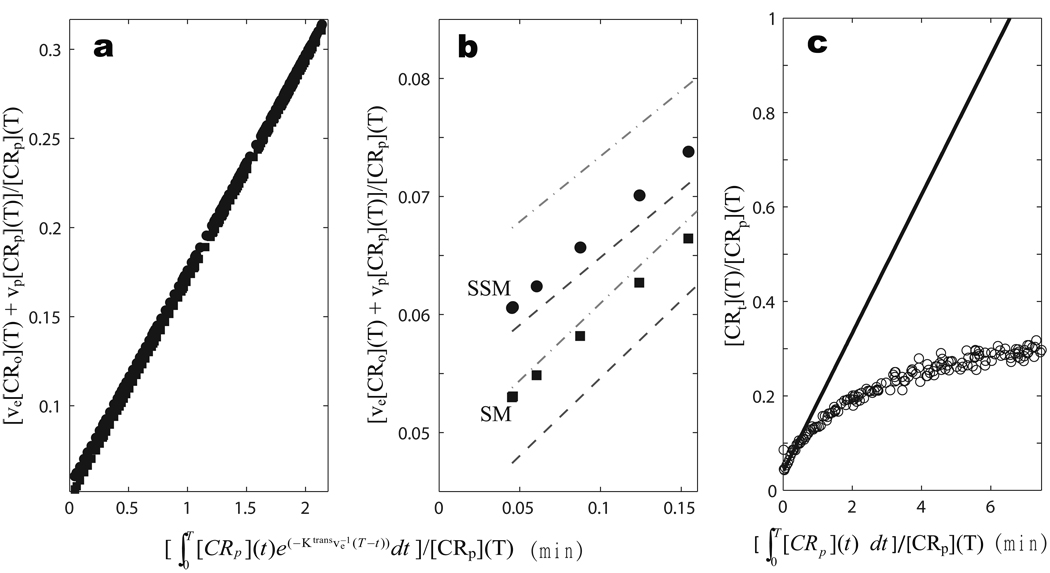
left hand side is the tissue (voxel) CR concentration, [CR_t]. This is what is measured with a tracer, for which the signal is not compartment-specific. The v_e[CR_o] and v_p[CR_p] products represent [CR_t]_o and [CR_t]_p, the concentrations corresponding to interstitial and plasma CR, respectively, as if diluted into the entire voxel. Positron Emission Tomography [PET] tracers (combined PET/MRI is an active field) and hyperpolarized MRS metabolites have the same property. Though subvoxel compartmentalization may be assumed from prior knowledge, it is not intrinsic to the pharmacokinetic signal. The PP has {[v_e[CR_o](T) + v_p[CR_p](T)]/[CR_p](T)} as ordinate and $\{[{\displaystyle {\int }_0^T[{\mathit{\text{CR}}}_p](t)e^{(-{\mathrm{K}}^{\text{trans}}{\mathrm{v}}_{\mathrm{e}}^{-1}(T-t))}\mathit{\text{dt}}]/[{\text{CR}}_{\mathrm{p}}](\mathrm{T})\}}$ as abscissa - a graphical manifestation of Eq. [1]. Though Eq. [1] is valid for two compartment tracer and MRS metabolite studies, its simple application in DCE-MRI analyses requires assuming that [v_e[CR_o](T) + v_p[CR_p](T)] bears a linear relationship to the tissue ¹H₂O R₁(T) that is measured, via the relaxivity (r₁) coefficient, and that (1 − h_s)v_p[CR_p](T) is linearly related to the blood ¹H₂O R_1b(T) (5). Though the latter is almost always a good approximation, the first assumption implies the FXL constraint for both the equilibrium transcytolemmal and transendothelial water exchange systems. Furthermore, the simple addition of the “indicator dilution” v_p[CR_p] term on the right hand side also implies that the equilibrium transendothelial water exchange system is in the FXL condition (9,10). Mimicking these Standard Model assumptions [by fixing τ_b (= τ_i) = 1 ms] for the animal #1 tumor ROI-averaged results leads to the Patlak Plot of the discretized, SM-estimated concentrations as filled squares in Figure 2a [T is incremented between zero and 5.3 minutes]: the zoomed initial portion is re-plotted in Fig. 2b. It is linear with a slope corresponding to K^trans ~0.12 min⁻¹, and an intercept to v_p = 0.048 (v_b = [v_p/(1 − h_s)] = 0.068).

Figure 2.

Panel a shows Patlak Plots (PPs) of the animal #1 results analyzed with τ_b (= τ_i) = 300 ms (filled circles, the Shutter-Speed Model [SSM]) and with τ_b (= τ_i) = 1 ms (filled squares, the Standard Model [SM]). Though the two PPs have almost the same slope (K^trans = 0.12 min⁻¹), they have different intercepts ([v_p/(1 − h_s)] = 0.055 and 0.048 for SSM and SM, respectively). The entire PP is a straight line in each case. Panel b enlarges the initial portion of panel a. The gray dot-dashed and dashed curves trace the ± 1SD boundaries measuring agreement of the SSM and SM PPs, respectively, with experimental data. Panel c shows the PP of the animal #1 data (open circles) when CR re-intravasation is ignored (by assuming K^transv_e⁻¹ is zero). Clearly, there is significant CR reentry into the blood in these tumors, and it becomes noticeable quite quickly.

In order to use Eq. [1] for DCE-MRI and admit the possibility of exchange effects, the [CR] values must be determined beforehand using a shutter-speed pharmacokinetic model – BALDERO here – which allows that the [CR] terms can potentially transiently determine tissue ¹H₂O R₁ nonlinearly during the bolus time-course. Panel 2a also shows the PP that results when the same data were analyzed with τ_b (= τ_i) = 300 ms (filled circles). Though the plot has almost the same slope, it has a different intercept: v_p = 0.055 (v_b = 0.079), seen clearly in the zoomed display of Fig. 2b. The entire PP is a straight line in each case. Just like nonlinear data-fitting (as above): PP linearity itself is not probative of the exchange condition. The shift of this line is a measure of the shutter-speed (water exchange) effect on v_b. Here, this systematic difference (a 23% increase) lies outside the one Standard Deviation (SD) boundaries [dot-dashed and dashed gray Fig. 1b curves for SSM and SM, respectively] that measure agreement with the experimental data. [A Monte Carlo method was used similar to that described above for testing v_e,v_b correlation.] The intercept (proportional to v_b) uncertainty is smaller because it results from the extrapolation of many points. Only v_b is affected here because of the small CR dose (10,12,14) [allowed by the ultra-high field strength (25)] used here. However, with the larger CR doses required at clinical fields, there can be substantial shutter-speed effects on any or all parameter biomarkers (10,12–15,18). For example, the use of larger CR doses often leads to shutter-speed effects on the K^trans value (12) [i.e., the PP slope (results not shown)]. The slopes in Fig. 2a are only barely discernibly different (the SSM K^trans is slightly smaller) here because the CR dose is so small. Of course, no parameter should be CR dose-, dose delivery rate-, or magnetic field strength-dependent: they have fundamental pharmacokinetic definitions and should vary only with tissue and/or temperature (14). For the same data, it is SM parameter values that are more dependent on dose, dose delivery rate, and/or magnetic field (14). Thus, the common use of the Standard Model (FXL-constrained) may be a cause for considerable literature DCE-MRI parameter irreproducibility. To recapitulate this point, all SM formulations involve the assumptions that τ_b → 0 and τ_i → 0 in Table 1, and this can impart systematic errors in any or all of the biomarkers (v_b, v_e, K^trans) normally desired. Assuming the Eq. [1] LHS to be linearly proportional to R₁(T) yields an inappropriate functional form for modeling DCE-MRI data. Of course, if accessible, τ_b⁻¹ and τ_i⁻¹ would also be important new intrinsic biomarkers in their own rights.

The Fig. 2a,b results show the necessity of incorporating the MR equilibrium exchange kinetics before the pharmacokinetics in the model derivation (10): though finite, exchange kinetics are faster than pharmacokinetics. Standard Model derivations always begin with the pharmacokinetic rate law. The Patlak Plot can be used, but the first step for DCE-MRI must address the nature of S(t) [or R₁(t)] = f([CR](t)). Since this function can be spatiotemporally variant in tissue, nonlinear data fitting must be accomplished before Patlak Plotting. It seems only prudent to use the unified shutter-speed DCE-MRI pharmacokinetic model (10). If exchange effects are negligible, the model handles this in stride.

Panel 2c shows the PP of the animal #1 tumor ROI-averaged data when CR re-intravasation, described by the exponential factor within the integrand on the Eq. [1] RHS, is ignored [by assuming K^transve⁻¹ is zero] (open circles). The nonlinearity suggests clearly that there is significant blood CR reentry in these tumors, and its neglect becomes noticeable quite quickly.

The BALDERO SSM used here does assume that the ¹H₂O_b, ¹H₂O_o, and ¹H₂O_i signals each contribute proportionately, modified only by equilibrium water exchange effects. If there is disproportionate "quenching" of any signal - because of differential transverse relaxation (T₂*) - then BALDERO can underestimate shutter-speed effects actually present in the data (14). Disproportionate quenching is quite likely (14), especially at higher field. Analysis of the Fig. 1b data with a BALDERO version (26) admitting modest ¹H₂O_b quenching (not shown) does indicate a further increase of v_b and possibly a K^trans increase. Thus, the v_b values reported here should be considered lower limits.

Investigating Fitting Uncertainties

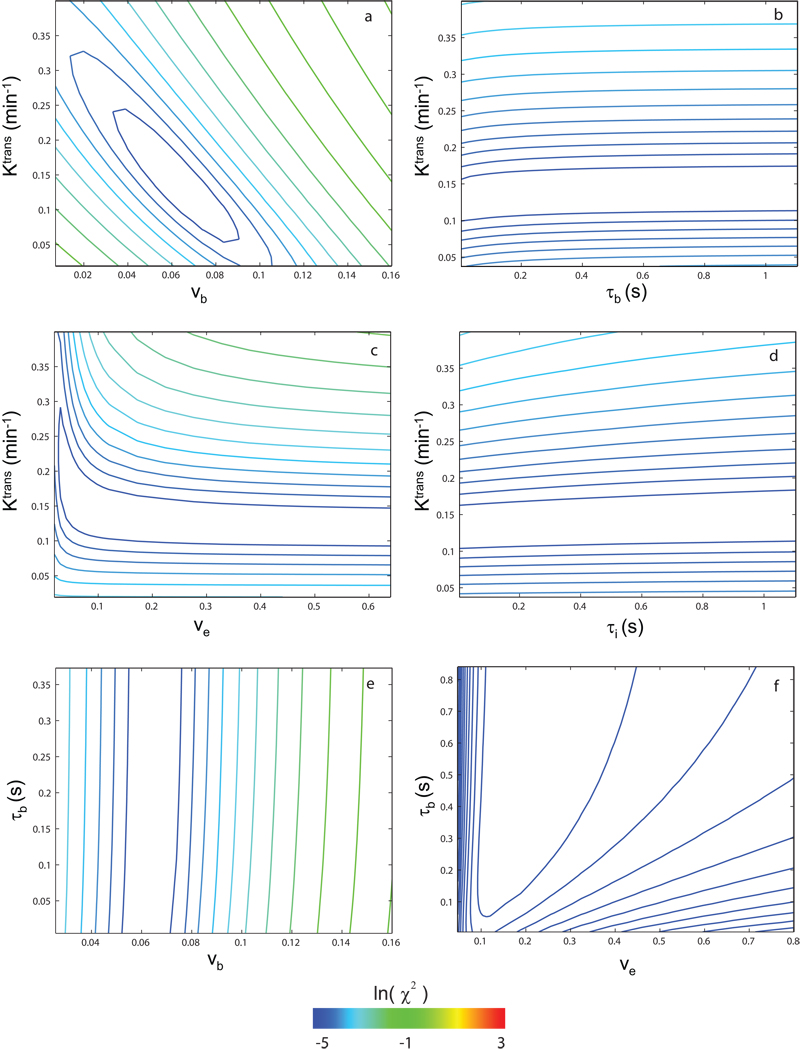
To gain confidence in these multi-parametric fittings, DCE data sensitivities to various parameters were tested using comparisons that effected parametric grid searches of error surfaces (27). Figure 3 shows contour plots of the natural logarithm of the chi square statistic, χ² = Σ[S_data(t) − S^model(t)]², for the first-pass data of animal #2 (first ~ 1.2 min, similar to the Fig.1b red fitting). The ln(χ²) color scale used for all panels is shown at the bottom. For each panel, the only two parameters varied are those labeled on the ordinate and the abscissa. Thus, in panel a, only K^trans and v_b (= p_b•f_W) were varied while the others were fixed at the reasonable values given in Table 1 (except for R₁₀ = 0.52 s⁻¹). Other parameters tested in the same pair-wise manner were: K^trans, v_b, τ_b, v_e (= p_o•f_w), and τ_i (mean intracellular water molecule lifetime). These could be called “chi-by-eye” contours, since they measure the χ² value (“goodness”) of comparisons with the data of different model curves calculated for the parameter values given by the coordinates. The χ² value decreases as the contour color shifts in the blue direction. With the six most likely fitting parameter pairs tested and shown in panels a – f for the first-pass data alone, only the K^trans,v_b pair exhibited consistently (for all animals) the well-defined funnel-shaped surface (28) required. The v_e value is not determinate. In Fig. 3c, there is no focal minimum (i.e., no unique solution), but mostly a “trench” [centered on K^trans = 0.13 min⁻¹] that parallels the v_e axis. The corollary of this is that the exact value at which v_e is fixed (as long as it is greater than ~0.1) has no influence on the K^trans value returned. The same is true for τ_b: though for a different animal, Fig. 3b is consistent with Fig. 2a,b: the K^trans value is reasonably independent of the τ_b value. In Fig. 3e, one does see a slight indication of the τ_b-sensitivity to v_b evident in Fig. 2b. The lowest (darkest blue) contour trends slightly toward larger v_b values with increasing τ_b and seems closer to closing as τ_b vanishes. The Patlak Plot (Fig. 2) is a sensitive way to display shutter-speed effects (and to check SSM computer coding).

Figure 3.

Grid searches of error surfaces were performed to examine (animal #2) DCE data sensitivities to model parameter values. Contour plots of the natural logarithm of the chi square statistic, χ² = Σ [S_data(t) − S_model(t)]², for only the first-pass data (~ first 1.2 min, similar to red portions of Fig. 1) are shown. The ln(χ²) color scale used for all panels is shown at the bottom. For each panel, the only two parameters varied are labeled on the ordinate and the abscissa. Using panel a as an example, only K^trans and v_b were varied while others were fixed at the reasonable values in Table 1. Parameters tested in this pair-wise manner were: K^trans, v_b, τ_b, v_e, and τ_i. These could be called “chi-by-eye” contours, since they measure the χ² value (“goodness”) of comparisons of the data with model curves calculated for the parameter values given by the coordinates. The χ² value decreases as the contour color shifts in the blue direction. With the six most likely fitting parameter pairs tested for first-pass data alone, and shown in panels a – f, only the K^trans,v_b pair (panel a) exhibited consistently (for all animals) the well-defined funnel-shaped surface required.

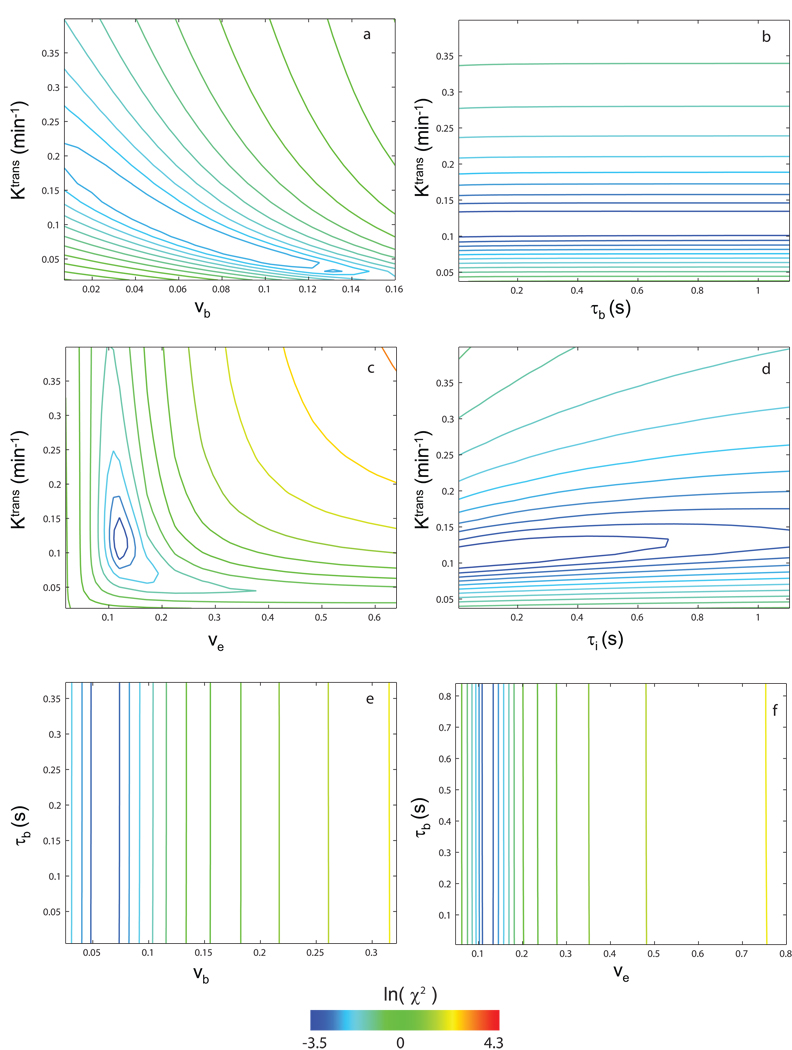
Figure 4 shows the analogous six 2D chi square statistic error surfaces for the entire data time-course (in Fig. 1b, the blue fitting) for animal #2. The p_b value was fixed at that (0.066) from the first-pass fitting. In this case, the only well-behaved surface (i.e., with a funnel shape) is now seen for the K^trans,v_e pair, in panel c. The fact that the funnel surface switches from Fig. 3a to Fig. 4c when the entire time-course data are used confirms the prediction of our earlier simulation [Fig. 4 of (10)]: different parameters dominate different portions of the DCE-MRI time-course. Though considerable CR is present in the blood throughout the entire DCE-MRI experiment, the ¹H₂O_b signal contribution is greatly diminished after CR extravasation is significant. Thus, v_b is indeterminate for most of the time-course. Notice that the Fig. 4 color scale covers a range of larger ln(χ²) values than that in Fig. 3 since all time points are used for this ln(χ²) calculation instead of only the first 45 points covering the first-pass for Fig. 3.

Figure 4.

Variations of the natural logarithm of the chi square statistic for comparison with the entire time-course (animal #2) data are shown. If not varied, the p_b value was fixed at that from the first-pass fitting. The only well-behaved surface when the entire time-course data are used is now that of K^trans and v_e, panel c. Notice that the color scale covers a range of larger ln (χ²) values than that in Fig. 3, due to the increased number of data points (entire time-course vs. first-pass only) for these comparisons.

Since the primary goal for the current study is to estimate TBV using DCE-MRI, a low CR dose is used (for better v_b determination and for minimizing high field T₂* effects). This also minimizes transendothelial shutter-speed [the site pair relaxation rate constant difference (10)] effects. Principally because of this, the exact kinetics of each water exchange process remains indeterminate. This does not mean, however, that one should use the SM (τ_b → 0) to analyze data, especially those obtained using the larger CR doses required at lower clinical fields. We have already seen a shutter-speed effect on v_b (Fig. 2a,b) with even the low dose used here.

The reliability of the tumor ROI-averaged v_b determination is investigated by fitting increasing numbers of the initial DCE time-course data points. As for the Fig. 1b red fitting, K^trans and v_b are the only variable parameters. The Figure 5a [CR_p] curve indicates the span of terminal data point indices (from the 38^th to the 61^th for rat # 6, filled circles) for the 24 truncations used for these fittings. The Fig. 5b gray symbols plot v_b values for each of these fittings (24 for each animal), with each symbol representing one animal. The spans of black symbols represent the starts and finishes of the second passes (recirculation) detected in the AIFs. The value of v_b is fairly well defined if the entire first-pass (e.g., before about the first 45 data points, or 1.2 min into the study for rat #6) is used. For the span of the initial ~18 s of the CR 2^nd pass, we obtain constant v_b values for ROI data.

Figure 5.

The v_b determination reliability is investigated by fitting the initial DCE time-course data with incremental numbers of data points subjected to the model analysis. The filled circles of 5a [CR_p](t) indicate the truncation data points (from the first 38 to the first 61 points for rat #6) used for these fittings. Figure 5b summarizes v_b results (24 fittings for each animal), with each symbol representing one animal. The symbol, animal correspondences are: , #1; ♦, #2; ▲, #3; ✚, #4; ■, #5; ●, #6; and ◄, #7. The spans of black symbols represent the starts and finishes of the second passes (recirculation) detected in the AIFs.

Collating the Fittings

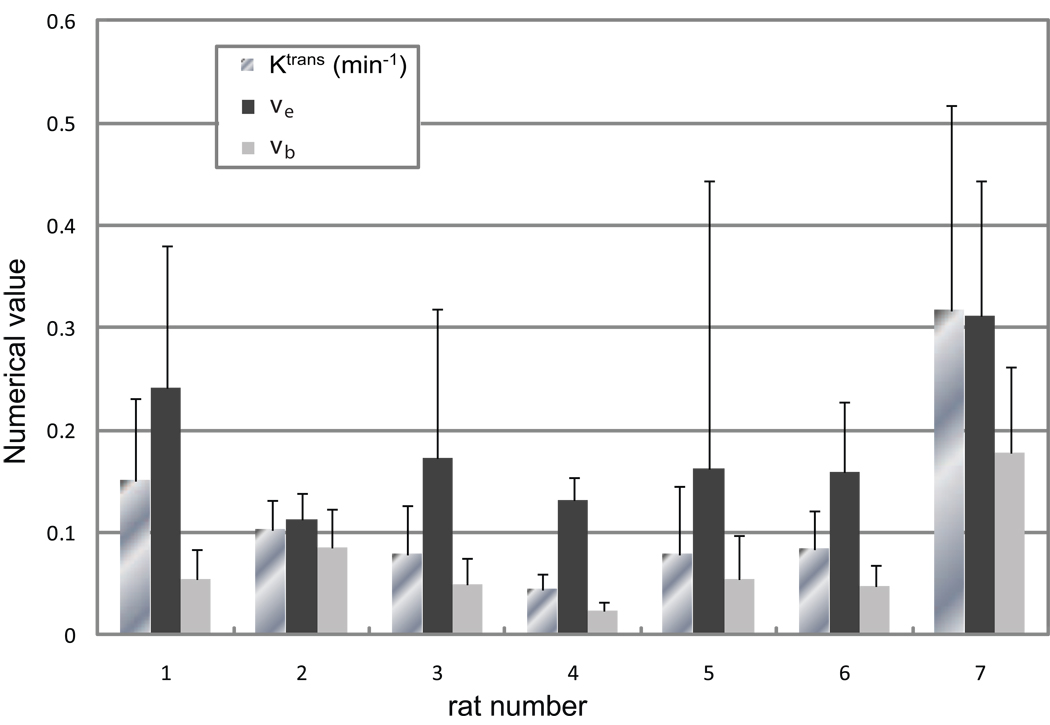
Figures 3–5 confirm the feasibility of the successive fittings approach used here. The (interanimal) average parameter values returned by this method for the seven tumor ROI fittings are [mean (± SD)]: v_b = 0.056 (± 0.038), v_e = 0.15 (± 0.07), and K^trans = 0.13 (± 0.11) min⁻¹. It should be noted that v_i ≡ 1 − (v_b + v_e). These SD values represent mostly tumor variations between animals: the fitting SDs from ROI averaged data are much smaller. Further details of these tumor ROIs are illustrated in Figure 6, where the mean pixel-by-pixel fitting parameter values for the contrast-enhanced tumor ROI of each individual are summarized in bar graphs. Values of v_b resulted from fittings of only the first-pass tissue time-courses, while K^trans and v_e were from the complete time-courses. Mean ROI values are given as the bar lengths, and the error bars represent SDs within the tumor ROIs, somewhat an indication of tumor heterogeneity. The animal index number labels the abscissa, and the parameter numerical values are given on the ordinate. The K^trans unit is (min⁻¹): the v_b and v_e volume fractions have no units. Though tumor heterogeneity cannot be directly represented, this bar graph gives an overall view of the results. From it, we see greater absolute variability for the K^trans and v_e parameters. This could reflect different progression stages for the individual tumors. All animals exhibit moderate pixel-by-pixel correlation coefficients (r = −0.26 to 0.29) between the v_b and v_e fitting parameters (not shown).

Figure 6.

The mean pixel-by-pixel fitting parameter values within ROIs that cover the entire contrast-enhanced tumor areas are shown for all animals. Values of v_b are from fittings of the first-pass data only, while K^trans and v_e are from the complete time-courses. ROI means are given as the bar lengths, and the error bars represent the standard deviation (SD) within the tumor ROI, somewhat an indication of tumor heterogeneity. The animal number labels the abscissa and the parameter values are given on the ordinate. The unit of K^trans is (min⁻¹): the v_b and v_e volume fractions have no units.

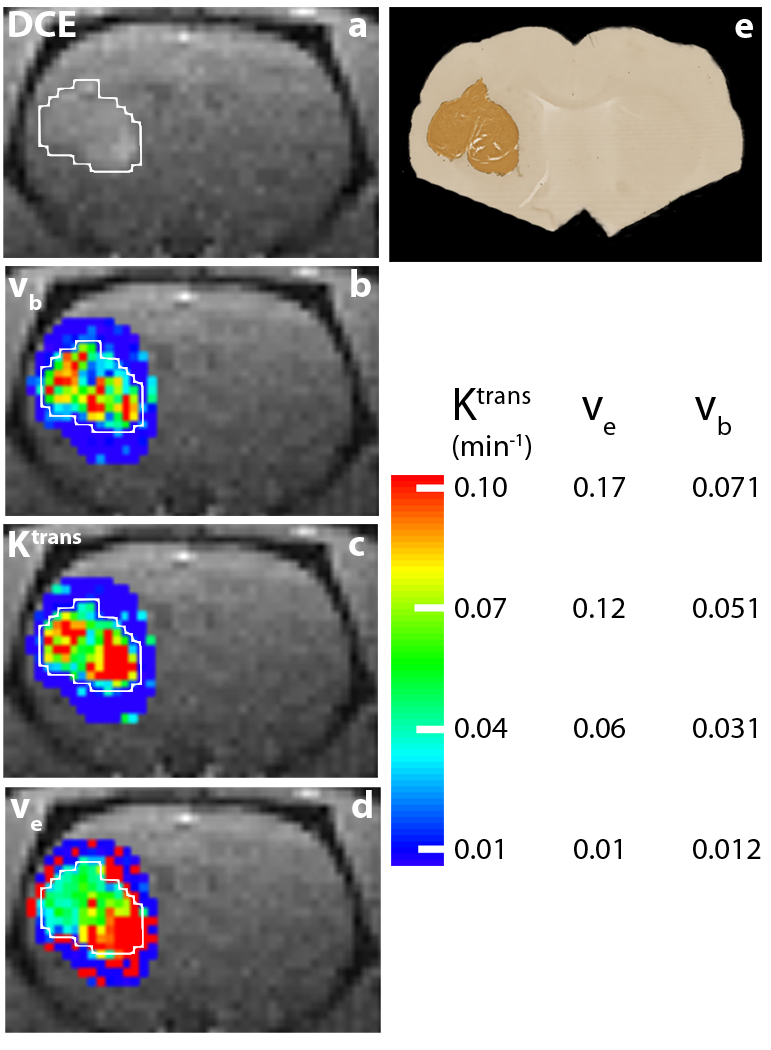
Figure 7a shows the 1.2 min DCE coronal-equivalent image of the head of animal #6. The enhanced U87 tumor is on the right side of the brain (left side of the image), and the lesion ROI is circumscribed with a white border. Tumor heterogeneity can be seen in parametric maps shown in the other panels. The color bar at the bottom right of Fig. 7 shows scales for the three parameters mapped. Panel b shows the v_b map, derived from fitting the CR first-pass DCE data (spanning the first ~1.2 min of acquisition) with two variable parameters: K^trans and v_b. The other parameters were held fixed at the values given in Table 1. Elevated v_b values are seen within the tumor area, compared with those of surrounding brain parenchyma (dark blue, v_b ~ 0.01). With p_b and K^trans held fixed and set as the initial guess, respectively, at the first-pass fitted values for each pixel, two parameter BALDERO fittings of the entire (~5 minute) data time-courses were performed, with K^trans and v_e as variables and all others fixed as in Table 1 (except pre-CR R₁, R₁₀). Panels c and d show the K^trans and v_e maps from these. The panel d map demonstrates detectable v_e (~ 0.15) in the tumor with elevated values in the inferior lobe. Patterns showing elevated tumor rim v_e values were seen in cerebrally-implanted rat GS-9L gliosarcoma (12) and mouse 4C8 glioma (29). The surrounding normal-appearing brain parenchyma [v_e ~ 0.1] exhibits sporadic, artifactual individual red pixels. These reflect the fact that the v_e parameter is the most poorly determined (Fig. 6) and can not be successfully measured in regions with almost no CR extravasation (10,12,14). The panel c map shows the large K^trans values (>0.1 min⁻¹) characteristic of a malignant tumor [especially compared with the surrounding dark blue parenchyma (where K^trans is < 10⁻³ min⁻¹)] in both lobes. The parameter K^trans has contributions from CR permeability (the permeability surface area product, P_CRS) as well as from blood perfusion (9,12). Thus, one might expect increased K^trans values in regions where v_b is elevated.

Figure 7.

Panel a shows the 1.2 min DCE coronal-equivalent image of the head of animal #6. The U87 tumor is clearly visible in the left brain (right side of image), and the lesion ROI is circumscribed with a white border. Panel b shows the v_b map derived from fitting the CR first-pass DCE data (spanning the first ~ 1.2 min of acquisition) with two variable parameters: K^trans, and v_b. The tumor v_b values are elevated from those of surrounding brain parenchyma (dark blue, ~0.01). With v_b and K^trans held fixed and set as the initial guess, respectively, at the first-pass fitted values for each pixel, two parameter BALDERO fittings of the entire (~5 min.) data time-courses were performed with K^trans and v_e as variables. Panels c and d show the K^trans and v_e maps from these. The panel d map demonstrates the detectable v_e in the tumor (~0.15) and poor v_e parameter definition outside of the tumor. It is particularly interesting that K^trans is more extensively at its maximum (~ 0.17 min⁻¹) in the inferior lobe, as is v_e. The color bar at the bottom right shows the scales for all three parametric maps. The darker brown color in panel e shows human mitochondria staining of the same animal brain in a histological slice comparable to that of the DCE image slice.

Panel e shows anti human mitochondria immunohistochemical staining results for the histological brain slice of animal #6 that matches the DCE image slice. Since the stain is targeted for human cells, the tumor shows very clearly as darker brown color. There is excellent agreement between the DCE-MRI maps and the histopathology image.

Discussion

Our results demonstrate that with proper modeling v_b can be estimated from first-pass T₁-weighted DCE-MRI data even in the presence of rapid CR extravasation. This approach for v_b determination is not particularly sensitive to first-pass cutoff selection, and the v_b,v_e correlation is generally low if v_e is set neither too high nor too low during the first-pass v_b fitting. The range depends on the v_e of the particular tumor under study (Figs. 6,7). As extravascular CR accumulates with time, the contribution of the blood ¹H₂O signal diminishes (10). [This is different from tracer techniques, where the blood tracer contribution is significant during the entire time-course.] During the CR first-pass (even with some CR extravasation), however, its importance probably cannot be neglected. Water exchange effects can be important in DCE-MRI modeling. If τ_b is held vanishingly small [1 ms] (as in most other analyses – the Standard Model), the values returned for v_b are typically underestimated by 15% – 30% here. Analogously, with sufficient CR extravasation, holding τ_i vanishingly small (again, as in most other analyses) leads to significant v_e and K^trans underestimations (12–15). Since the current study is designed to measure blood volume with DCE-MRI, the relatively low dose (about half the standard for humans) adopted was insufficient to drive the equilibrium transcytolemmal water exchange system out of the FXL. As a result, τ_i remained indeterminate. The transendothelial water exchange rate constant plays a significant role in the data modeling although its actual value is also indeterminate (30). This shows that the SM can return erroneous parameter values - v_b here. However, the general indeterminacy of the actual τ_b value itself in Figs. 3b,e,f is disappointing. Access to this parameter could be very useful. The ratio v_b/τ_b is equal to the capillary wall water permeability coefficient surface area product, P_WS (9). This, in turn, could be a valuable biomarker for the high interstitial fluid pressure known to exist in solid tumors (31,32).

At ultra-high field, due to the strong T₂^* effect introduced by the CR bolus, sequences other than those with ultra small TE values (33) preclude the effective use of the higher CR doses normally adopted at the smaller clinical field strengths. This implies that a high field advantage (reduced detectable [CR] threshold facilitating detection of interstitial CR in normal brain (25)) for DCE-MRI can be fully appreciated only when T₂^* effects are minimized. Also, with the generally low CR concentrations used at high field, CR extravasation can hardly reach a level that would make transcytolemmal water exchange appear slow.

As usually applied, and as applied here, the BALDERO formalism assumes that there is negligible transverse relaxation (T₂^* time constant) of the blood, interstitial, and intracellular ¹H₂O signals or at least no disproportionate transverse relaxation of these during the CR bolus passage. Thus, they contribute proportionately, modified only by exchange effects (10,14,15). However, we have found that disproportionate T₂* relaxation (relative “quenching”) of compartmental ¹H₂O signals can cause significant changes in biomarker parametric values returned by modeling (14,15,26). Thus, we tried fitting some of these DCE-MRI data as if there was modest quenching of the blood ¹H₂O signal. Because of the presence of paramagnetic CR in the plasma space, this signal – tiny to begin with - is the most sensitive to magnetic susceptibility-induced T₂* relaxation, especially at the ultra-high field strength used here. We had hopes that this might yield a focal χ² minimum (say, in Fig. 3b) at a reasonable τ_b value. However, we found that such quenching doesn’t change the indeterminate nature of τ_b in these particular data though there was a noticeable v_b increase (not shown). Quantification of the extent of quenching requires measuring the TE-dependence (14,26). Perhaps acquisition pulse sequence parameter adjustments can increase the exchange sensitivity (14,26).

It is important to note that tumor perfusion flow (F) can also be directly determined [employing BALDEROF (9)] from data such as those used here, when the AIF is also well determined.

The accuracy of AIF estimation plays an important role in all DCE-MRI parameter determinations (12,14,30). Since the rat brain AIF is hard to measure well, the v_b, K^trans, and v_e values returned could include systematic errors. However, large lesion-averaged v_e values (Fig. 6) could be expected (32,34) for the aggressive U87 glioma, which can harbor extensive necrotic regions: v_e is related to the “cellularity” complement. [Interestingly, K^trans is smaller in the interlobe region (Fig. 7c) where v_e is also small.] When fast MR imaging with pure T₁-weighted (33) DCE-MRI acquisitions and/or "blind" estimations (21) become widely practical, better AIFs and thus even more accurate K^trans, v_b, v_e, and F determinations will result, especially at high field.

The high temporal resolution (1.6 s) of these DCE-MRI studies came at the cost of spatial resolution, which is only adequate for these tiny tumors. Pixelation is evident in the Fig. 7 images and maps. One can obtain data with increased spatial resolution while retaining sufficient temporal resolution with better MRI technology such as parallel imaging acquisition (35).

Parameter correlation is expected to vary with K^trans. For heavy CR extravasation, clear distinction between v_b and v_e is expected to become poorer, and this in turn will result in weaker v_b determination (10).

It is not easy to ascertain the absolute accuracies of DCE-MRI biomarker parameters. Indeed, it has been opined that “In fact, there is no ‘ground truth’ (or gold standard) that can confirm correctness of the fitted parameters” (36). One way to approach this, however, is by measuring the parameters of the same system by more than one “modality” – with all the errors (co-registration, etc.) attendant to such an effort. Comparable approaches lie in the families of radiotracer methods. We have found that the (two orders of magnitude) smaller normal brain transfer constant for Gd(HP-DO3A) determined for the human by DCE-MRI even at 4T (37) agrees with that for ⁵⁷CoDTPA²⁻ (22) and that for Gd(¹⁴⁷Pm)DTPA²⁻ (38) determined by gold standard, sacrificial radiotracer techniques (that cannot be applied in humans) in the normal rat brain only if the transendothelial water exchange system is allowed to sortie out of the FXL and into the FXR (Fast-eXchange-Regime) during the CR bolus passage. If this system is constrained to the FXL (the SM), the transfer constant is overestimated by ~50% in the DCE analysis and thus shifted out of agreement with the nuclear medicine results.

An abstract of work on the comparison of transfer constants measured after a cerebral ischemic period - by DCE-MRI using GdDTPA²⁻ and by Quantitative AutoRadiography (QAR) using Gd(¹⁴C-)DTPA²⁻ - in the same rat brains has been reported (39). However, the way the investigators used the Patlak Plot to analyze the DCE-MRI data embodied only the assumption that the trans- endothelial and cytolemmal water exchange systems be constrained to their FXL conditions (the SM). The DCE transfer constant was found to agree with the QAR transfer constant [at least to within 25%] (39). However, no mention was made of the respective v_p values. As we have seen in the brain tumor model here, the shutter-speed effect can change v_b and not K^trans (Fig. 2a,b).

Conclusion

Using a three-site water exchange model, the possibility of v_b determination with extravasating CR is demonstrated. This presents a potential new way of estimating blood volume, CR extravasation rate constant, and extracellular, extravascular space in a single DCE-MRI experiment.