Simulations of calcium channel block by trivalent cations: Gd³⁺ competes with permeant ions for the selectivity filter

Abstract

Current through L-type calcium channels (Ca_V1.2 or dihydropyridine receptor) can be blocked by micromolar concentrations of trivalent cations like the lanthanide gadolinium (Gd³⁺). It has been proposed that trivalent block is due to ions competing for a binding site in both the open and closed configuration, but with possibly with different trivalent affinities. Here, we corroborate this general view of trivalent block by computing conductance of a model L-type calcium channel. The model qualitatively reproduces the Gd³⁺ concentration dependence and the effect that substantially more Gd³⁺ is required to produce similar block in the presence of Sr²⁺ (compared to Ba²⁺) and even more in the presence of Ca²⁺. Trivalent block is explained in this model by cations binding in the selectivity filter with the charge/space competition mechanism. This is the same mechanism that in the model channel governs other selectivity properties. Specifically, selectivity is determined by the combination of ions that most effectively screen the negative glutamates of the protein while finding space in the midst of the closely-packed carboxylate groups of the glutamate residues.

INTRODUCTION

L-type calcium channels (Ca_V1.2) have an extremely high affinity for divalent cations like Ca²⁺, Sr²⁺, and Ba²⁺. Even at micromolar concentrations these ions can occupy and block the pore often enough to significantly reduce monovalent cation current [1, 2]. However, these divalents are conducted by the pore and therefore the channel is never completely blocked (i.e., current is never zero, no matter how large the concentration of divalents). The story is different for trivalent cations like the lanthanide gadolinium (Gd³⁺). These can completely block the current through an open channel at concentrations <10 μM [3-8].

Block by trivalents has been divided in two categories, tonic and use-dependent. These are distinguished during whole-cell recordings from cells expressing L- and T-type calcium channels. After two voltage pulses in the presence of trivalent cations, the peak current after the onset of the second pulse I₂ is less than the peak current after the onset of the first pulse I₁ (use-dependent block), and the ratio I₂/I₁ is extremely sensitive to the trivalent concentration. The peak current after the first pulse (I₁) also decreases as trivalent concentration increases. This is tonic block.

Tonic block is the result of trivalents binding inside the pore of closed channels (see, for example, [7, 8]). The reduction of current at the beginning of a voltage pulse in the presence of trivalent cations (compared to the 0 trivalent concentration) is a reflection of the percentage of all calcium channels in the cell that bound a trivalent cation while closed. Use-dependent block, on the other hand, is a reflection of trivalents binding in the pore of open channels. The reduction of current after the initial peak current is due to trivalent cations binding to channels not already blocked, in addition to the normal inactivation of the calcium channels (which can occur on the same timescale as the binding of Gd³⁺ at submicromolar concentrations) [7, 8]. Experiments imply that the trivalent binding to the same site is responsible for both tonic and use-dependent block, although this binding site may have a higher trivalent affinity in the open pore than in the closed [3, 7, 8].

In this paper we investigate trivalent block with a model of the L-type calcium channel to compute the conductance of the channel in the presence of Gd³⁺. The site of action appears to be the same, the selectivity filter, in our view, since mutations of the EEEE locus substantially reduce both kinds of block [8]. (Babich et al. [8] disagree about the location.) Since only the apparent affinity for Gd³⁺ changes between the open and closed states, we assume that to first order the mechanism of tonic and use-dependent block are the same. Therefore, we attempt to qualitatively reproduce the experimental findings, understanding that the exact results will differ for the open and closed state of the channel.

We find that the concentration effect of Gd³⁺ block is well reproduced with the model pore by the same charge/space competition selectivity mechanism responsible for the channel's other selectivity properties. In our model pore, Gd³⁺ selectivity occurs because cations are electrostatically attracted to the negatively charged pore, but they must compete for space within the selectivity filter. This is because the filter is crowded with the side chains of four flexible glutamate residues that move freely within the filter to coordinate the cations.

This very reduced model has successfully reproduced both the conductance and selectivity properties of the L-type channel, including micromolar Ca²⁺ block of Na⁺ current, anomalous mole fraction effects in mixtures of Ca²⁺ and Ba²⁺, and selectivity in other ion mixtures [9-12]. While this approach does not explain specific contributions for the individual glutamates or the role of nonglutamate residues, it does provide an intuitive, leading-order interpretation of permeation and selectivity. Additional atomic details will refine the results of this model, but not change its big-picture findings because those details will only tweak the leading-order physics. Moreover, a similar reduced model has correctly reproduced all the permeation and selectivity data—as well as predicting other, counterintuitive data—of the ryanodine receptor calcium channel [13-16].

THEORY AND METHODS

Model of the L-type calcium channel

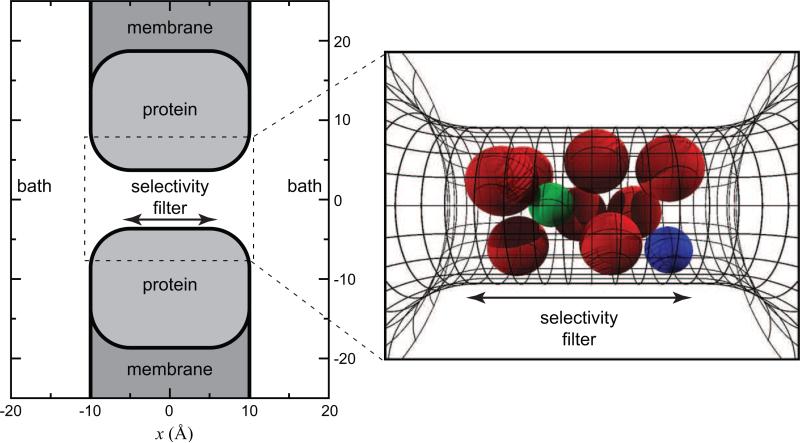
The model of the L-type calcium channel pore is the simplest possible: a selectivity filter between two uncharged vestibules that connects two baths. This is shown in Fig. 1. The selectivity filter is a hard cylinder that is 10 Å in length and 3.5 Å in radius. The radius of our pore is consistent with the lower bound of 3 Å measured by McCleskey and Almers [17]. However, our results are (to a first-order approximation) not dependent on the specific dimensions. A recent study showed that it is the volume of the selectivity filter—and not the aspect ratio (e.g., long and narrow versus short and wide)—is the major determinant of binding selectivity in this model [18].

1.

Geometry of the model pore. At left, a cross section of the pore is shown. The baths and simulations cell are several times larger than shown here. At right, the selectivity filter containing the eight oxygens (large (red) spheres) is shown in a simulation snapshot. Also, in the filter are one Ca²⁺ (green sphere) and one Na⁺ (blue sphere). The region of confinement of the oxygens (–5 < z < 5 Å) is shown with the span of the arrows.

The selectivity filter contains the four glutamates that produce the steady-state (i.e., long-time) selectivity of this channel [19, 20], assuming there is sufficient time for the ions to accumulate in the pore. We model each of these as only their negatively charged terminal carboxyl (COO^–) group, and each of these as two half-charged, independent oxygens (O^1/2–). The glutamates face the permeation pathway and the carboxyl groups are probably relatively free to move within the filter, but are tethered to the protein by the CH₂ groups of the side chain. We model this freedom of movement with infinite flexibility: the eight oxygens are free to move anywhere within the selectivity filter cylinder, but cannot leave the cylinder. Except for that constraint, the oxygens are subject to all the same forces as all the permeating ions, namely thermal motion, Coulombic interactions, and dispersion forces.

The dispersion forces are modeled very crudely by having all the particles (oxygens, Cl^–, and permeant cations) be charged, hard spheres. Therefore any two particles interact Coulombically and they cannot overlap. The size of each hard sphere is the Pauling radius: Na⁺ 0.95 Å, Ca²⁺ 0.99 Å, Sr²⁺ 1.13 Å, Ba²⁺ 1.35 Å, Gd³⁺ 0.94 Å, Cl^– 1.81 Å, and O^1/2– 1.40 Å.

The particles also interact electrostatically with the pore itself. Specifically, the dielectric constant of the protein is different from that of the permeation pathway (10 and 80, respectively) so that the ions induce a surface charge on this dielectric interface (image charges). Each ion induces charges that would normally repel it from the pore. This approximates the dehydration energy needed for the ion to strip waters off to enter the pore. However, cations go into the pore because not only are there four negative glutamates to draw them in, but also because of the negative induced charges of these glutamates; the low dielectric constant of the protein helps to amplify the negative structural charge of the pore [9, 21].

The details of the model pore have been described previously [10, 12].

Computing conductance

The Monte Carlo (MC) simulations that we use (described below) are designed for equilibrium. Therefore, we have two identical baths and no applied voltage. From this situation it is still possible to compute the conductance at zero applied voltage V because, while the current I is zero, the slope conductance dI / dV is not. To compute conductance, we start with the Nernst-Planck (drift-diffusion) equation [10, 16]. In three dimensions, this is

$$-{\mathbf{J}}_i\left(\mathbf{x}\right)=\frac{1}{kT}{D}_i\left(\mathbf{x}\right){\rho }_i\left(\mathbf{x}\right)\nabla {\mu }_i\left(\mathbf{x}\right)$$ (1)

where, for ion species i, J_i(x) is the flux per unit area, D_i(x) is the diffusion coefficient profile from the bath through the pore, ρ_i(x) is the density profile, and μ_i(x) is the electrochemical potential profile. The Boltzmann constant is k and the absolute temperature is T.

As before with this model pore, we assume that the flux is limited only in the selectivity filter (the cylindrical part of our pore) [10, 12]. It has previously been shown that, when a very small driving force is applied so that there is an ohmic current/voltage relation, Eq. (1) can be integrated to give the conductance γ at zero voltage [12]:

$$\gamma =\frac{1}{kT}\sum _i{D}_i{z}_i^2{e}_0^2{\left(\int \frac{dz}{n_i\left(z\right)}\right)}^{-1}$$ (2)

where n_i(z) is the axial number density of ions (i.e., the number of ions of species i in a slice of the pore of width dz centered around axial location z). We take the diffusion constant in the cylinder D_i to be constant in both the axial and radial directions. The valence of species i is z_i and e₀ is the fundamental charge. For the ions we consider here, the normalized conductance is given by

$$\frac{\gamma }{{\gamma }^0}=\frac{\frac{D_{\mathrm{Gd}}}{D_{\mathrm{Na}}}{\eta }_{\mathrm{Gd}}+\frac{D_{\mathrm{M}}}{D_{\mathrm{Na}}}{\eta }_{\mathrm{M}}+{\eta }_{\mathrm{Na}}}{\frac{D_{\mathrm{M}}}{D_{\mathrm{Na}}}{\eta }_{\mathrm{M}}^0+{\eta }_{\mathrm{Na}}^0}$$ (3)

where

$${\eta }_i=z_i^2{e}_0^2{\left(\int \frac{dz}{n_i\left(z\right)}\right)}^{-1}$$ (4)

and the conductance has been normalized with that in the absence of Gd³⁺ (denoted by the 0 superscript).

It is important to note that Eq. (2) is only valid for a small voltage range around zero where the current/voltage curve is linear. Technical details regarding the validity of using the Nernst-Planck equation in this pore have been described previously [10].

Monte Carlo simulations

The conductance, as computed from Eq. (2), requires the line density profile n_i(z) as an input. We use Metropolis MC simulations to compute this profile. The details of the simulations have been described previously [11, 21, 22] and we only review them briefly here.

The Gd³⁺ experiments require very low bath concentrations (e.g., 10^–8 M). These very low concentrations can be achieved in the MC simulations by performing these simulations in the grand canonical ensemble where the bath chemical potential is held fixed, rather than the number of particles in the simulation cell. Because of this, ions are created or deleted (see below) and the average number of ions of one species in the simulation cell can be less than 1. The chemical potentials that make the desired bath concentrations were computed in a separate grand canonical ensemble simulation as described previously [23].

In MC, one ion (permeanting, as well as oxygens and Cl^–) at a time is picked at random and moved to a random (although possibly biased) new location. The energy change of this move is computed and a move is accepted with a probability that ensures microscopic reversibility. Possible moves include: (1) small changes from the old position (for sampling of regions with high densities like the selectivity filter where ~25% of the available space is taken up by oxygens); (2) changes to a new position selected randomly from a uniform distribution anywhere in the cell (for sampling regions with low densities like the baths where the ions have gas densities because of our implicit-solvent model of the electrolyte); (3) moving a particle from a position in the selectivity filter to a position in the baths (or vice versa), a preferential move between subvolumes needed to efficiently sample the pore that takes up only a small fraction of the volume of the simulation cell [22]; (4) insertion or removal of a neutral group of ions (e.g., Na⁺ + Cl^– or Ca²⁺ + 2Cl^–) into or from the simulation cell; and (5) cation insertions or deletions analogous to (4) but directly into or out of the selectivity filter [11] with anions inserted or deleted from the baths. Moves (3), (4), and (5) are necessary in order to have enough configurations with ions at low bath densities (e.g., Gd³⁺).

The results presented here are averages of many simulations performed on multiple processors and with different starting configurations. In total, 6 ×10⁸ to 1.2 ×10⁹ MC moves are attempted for each result we present.

A successful reduced model

This model obviously excludes most the structural details one might deem important. Nevertheless, it seems to capture the essential physics of selectivity of the L-type channel. For example, without adjustable parameters like diffusion coefficients it naturally has micromolar Ca²⁺ affinity. It also reproduces the classical anomalous mole fraction effect of Almers and McCleskey [1, 2]—the only model of this channel to have done so with direct simulations of micromolar [Ca²⁺] [10]. Without changing anything about the structure of the pore, it also reproduces the L-type channel's size selectivity properties (i.e., selectivity among ions of the same charge) in mole fraction [10] and added-Ca²⁺ [12] mixtures of Ca²⁺ and Ba²⁺, as well as mole fraction mixtures of Li⁺ and Na⁺ [12].

The reason for this success is probably that the physics of these phenomena is dominated by electrostatics and dispersion forces (i.e., the excluded volume of the ions forcing them not to overlap), the two forces explicitly included in the model. In that case one would not expect that the details of the arrangement of the amino acids matters, at least to first order. These details do matter for other experimental data that this model fails to reproduce (e.g., that mutating each of the four glutamates does not produce identical results [19]).

The data that we analyze in this paper (i.e., how Na⁺, divalents, and Gd³⁺ competitively bind in the selectivity filter) is the type of data that this model has reproduced well. We do not change any of the parameters of the pore (e.g., radius, length, dielectric coefficients) from previous papers and the ion sizes are fixed to be Pauling radii. Therefore, the results we show are what comes out of the model pore naturally. If the model did not include the correct physics to describe this process (either in the ion binding or in the conductance), the results would most likely be incorrect since we are attempting to reproduce data over a large range (e.g., four orders of magnitude of Gd³⁺ concentration) and since this problem is particularly challenging with three cations competing for the pore.

Relating simulations to experiments

The vast majority of current experiments done on L- and T-type calcium channels are performed using the whole-cell patch clamp method. Single channel recordings with patch clamp or artificial bilayers are extremely difficult because of the small conductances of these channels and for a variety of technical reasons like “run-down” (i.e., channel currents steady decrease to zero) within seconds or, at best, minutes after a membrane patch is removed.

Whole-cell recordings also suffer from difficulties. For example, inactivation of L- and T-type channels decreases the measured current significantly on the millisecond timescale, which is also the time scale of trivalent binding when these cations are at submicromolar concentrations [7, 8]. This makes it difficult to unambiguously separate decreases in current due to inactivation and due to trivalent block of open channels (even assuming there is no effect of trivalents on inactivation).

In our simulations we consider the long-time (steady-state) binding of Gd³⁺ to an open channel and so ideally we would compare with long-time current data of use-dependent block. While such experiments have been done (e.g., [3, 6-8]), the steady-state current values have (to our knowledge) not been published, just peak currents and decay rates. Moreover, only Ca²⁺ and Ba²⁺—but not Sr²⁺—seem to have been used in these experiments. However, we can still connect to the block of open channels from tonic block data (i.e., block of closed channels), as we argue below.

Since the selectivity filter of a closed channel binds Gd³⁺, it has an affinity for ions, as does the selectivity filter of the open channel. Both Obejero-Paz et al. [7] and Babich et al. [8] calculated an increased on-rate (block rate) of trivalents in the open pore compared to the closed pore. (Obejero-Paz et al. [7] determined an Y³⁺ block rate ratio of 7.7 between the open and closed channel for Ca²⁺ and 3 for Ba²⁺. Babich et al. [8] calculated 7.1 for the Gd³⁺ on-rate with Ca²⁺ and 5.7 with Ba²⁺.) This may indicate that the affinity of the open pore for Gd³⁺ is greater than the closed pore which was first described by Biagi and Enyeart [3].

Both the open and closed pores seem to bind ions competitively; Babich et al. [8] calculate that the open-to-closed ratio of Gd³⁺ on-rate with Ca²⁺ is 0.4–0.5 times smaller than with Ba²⁺ in both open and closed pores. This indicates not only that Ca²⁺ competes more effectively with Gd³⁺ than Ba²⁺, but also that the difference between Ca²⁺ and Ba²⁺ is the same in the open and closed channels. Therefore, Ca²⁺ vs. Gd³⁺ and Ba²⁺ vs. Gd³⁺ competition appears to be very similar in both open and closed channels.

We presume that the fundamental mechanism of competition in the open and closed channels is the same, even though they may have different ion affinities. Not only is this the simplest explanation, but our previous work has shown that even small changes in the selectivity filter radius and the dielectric coefficient of the surrounding protein can cause noticeable shifts in affinity [9, 21]. Both of these can be caused by the strong electric field of the Gd³⁺, perhaps constricting the radius and/or exposing more hydrophilic residues depending on the state of the gate to change polarization and ion crowding. On the other hand, our previous work has also shown that only the ion affinity is affected. The selectivity sequence is unaffected unless ion dehydration is substantially changed [9, 12, 14, 18, 21, 24, 25]. The mechanism of ion selectivity is unchanged whether the simulation is done at equilibrium or far from equilibrium [9, 12-14].

If both the block of closed channels (tonic block) and the block of open/non-inactivated channels (use-dependent block) is the result of the same physical process, then we presume that they will give similar qualitative results. Consequently, we choose to compare to tonic block data because tonic block data is the most plentiful and the only one for which Gd³⁺ vs. Sr²⁺ is considered (to our knowledge). We do this to show that the simulations of use-dependent block produce the same qualitative results as tonic block. The purpose of our paper is to show that trivalent block is the result of competitive binding of ions in the selectivity filter by a specific physical mechanism, namely charge/space competition. Therefore, we wish to show trends and not quantitative matching with experiments. This would be impossible anyway, given the very reduced nature of the model pore and the natural differences among calcium channel types (e.g., L- vs. T-type), alternative mixes of subunits in the same channel type [8], and variations among the same channel type among different animal species [7, 8].

RESULTS

Computing block

Babich et al. [8] measured the Gd³⁺ dependence of tonic block in asymmetric solutions. The internal solution contained 155 mM CsCl, 10 HEPES, and 5 mM Mg-ATP, while the extracellular solution contained 150 mM NaCl, 10 mM Tris-Cl, and 10 mM CaCl₂, SrCl₂, or BaCl₂. Gd³⁺ was added to the extracellular side. The MC simulation method is designed for symmetric solutions, so we performed the simulations in symmetric 150 mM NaCl, 10 mM CaCl₂, SrCl₂, or BaCl₂, and the indicated concentration of Gd³⁺. This difference in protocol is not expected to qualitatively affect the general conclusions because the applied voltage in the experiments moved extracellular cations inward, as we have found in previous studies [10, 12].

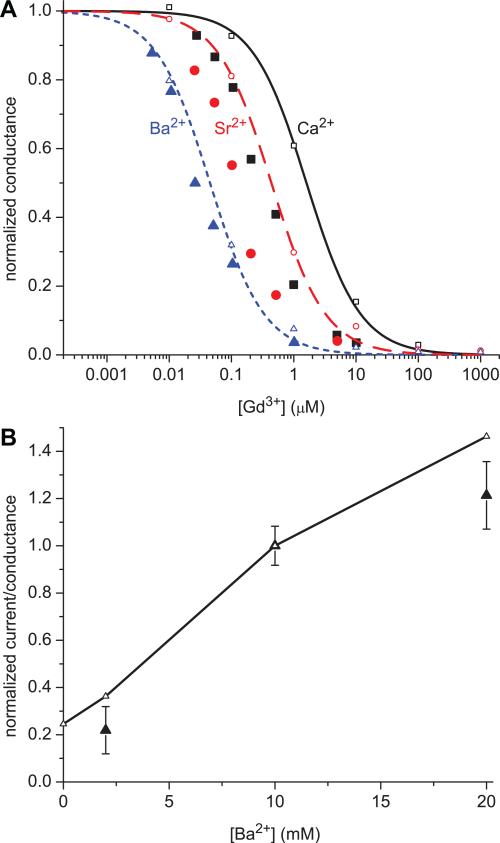
The comparisons of our calculations of normalized conductance to experimental currents are shown in Fig. 2A. Like the experimental currents, our conductance γ is normalized to the conductance in the absence of Gd³⁺ (γ⁰). The model reproduces the differential effect of Gd³⁺ on Ca²⁺, Sr²⁺, and Ba²⁺ qualitatively: Ba²⁺ is initially affected by ~0.01 μM Gd³⁺, Sr²⁺ requires more Gd³⁺ to see an effect, and Ca²⁺ requires even more.

2.

Comparison of the normalized currents from experiments (large, solid symbols) to normalized conductances computed from the model (small, open symbols). (A) In the simulations there is 150 mM NaCl, the indicated concentration of GdCl₃, and 10 mM divalent cation: Ca²⁺ solid (black) curve and square (black) symbols; Sr²⁺ dashed (red) curve and circle (red) symbols; Ba²⁺ dotted (blue) curve and triangle (blue) symbols. The lines are fits of the model results to Eq. (5) with the conductance normalized by the value in the absence of Gd³⁺. (B) In the simulations there is 150 mM NaCl, 25 nM GdCl₃, and the indicated concentration of BaCl₂. The conductances are normalized to the value with [Ba²⁺] = 10 mM.

To give an idea of how the model compares, we fit the model results with the equation

$$\frac{\gamma }{{\gamma }^0}=\frac{1}{1+\frac{\left[{\mathrm{Gd}}^{3+}\right]}{{\mathrm{IC}}_{50}}},$$ (5)

we computed IC₅₀'s for Gd³⁺ in the presence of the divalents (experimental results for tonic block [8] are in parentheses): for Ca²⁺, IC₅₀ = 1.6±0.08 μM (0.29±0.05); for Sr²⁺, 0.44±0.03 μM (0.12±0.02); for Ba²⁺, 0.045±0.003 μM (0.03±0.01). While the IC₅₀ for Ba²⁺ is close to the experimental value, the IC₅₀'s for Sr²⁺ and Ca²⁺ are too large by factors of 3.7 and 5.3, respectively.

Babich et al. also measured the effect of [Ba²⁺] on current, showing that Ba²⁺ can compete with 25 nM Gd³⁺ for the pore. This kind of competitive binding selectivity is predicted by the charge/space competition mechanism, and Fig. 2B shows that the model reproduces the experimental trend. In our model, 25 nM Gd³⁺ is not enough to completely block Na⁺ current and adding Ba²⁺ increases current. This is different than in other contexts where divalents are used as blockers of monovalent current. In this case the divalents are significantly more permeable than Gd³⁺ so increasing Ba²⁺ actually increases current. (This calculation used D_Ba / D_Na = 0.3 , the value previously estimated for this model from independent data [10].)

Given the evident structural differences between our very reduced model of the pore and the real channel, the overall qualitative agreement between the model and experiments is very good; the model includes the simplification of four indistinguishable glutamates of the selectivity filter [19], only approximately takes ion dehydration into account, and uses symmetric ion solutions instead of the real experimental conditions. The experimental difficulties of working with Gd³⁺ also cannot be overlooked. For example, to avoid using buffers (which cause their own difficulties [12]) 1 mM GdCl₃ solutions had to be diluted down to 10 nM. Babich et al. also describe that just switching from glass to polycarbonate containers affected the measurements with “dramatically improved consistency of results at [Gd³⁺] < 1 μM” [8].

Most model results are independent of unknown parameters

One significant (and unexpected) aspect of the normalized conductances in Fig. 2A is that they are independent of the ion diffusion coefficient ratios of Eq. (3). Whereas ion diameters can be estimated with Pauling diameters and the pore parameters (e.g., protein dielectric coefficient and pore radius) can be estimated by matching the experimentally-determined micromolar Ca²⁺ affinity [9], ion diffusion coefficients are the only parameters for which we do not have reliable independent estimates.

The fact that the conductances are independent of the diffusion coefficient ratios comes from two findings:

1. the conductance of Gd³⁺ is always zero because n_Gd (z) ≈ 0 outside the center of the selectivity filter (see Fig. 4 later) and therefore η_Gd = 0 (Eq. (4));

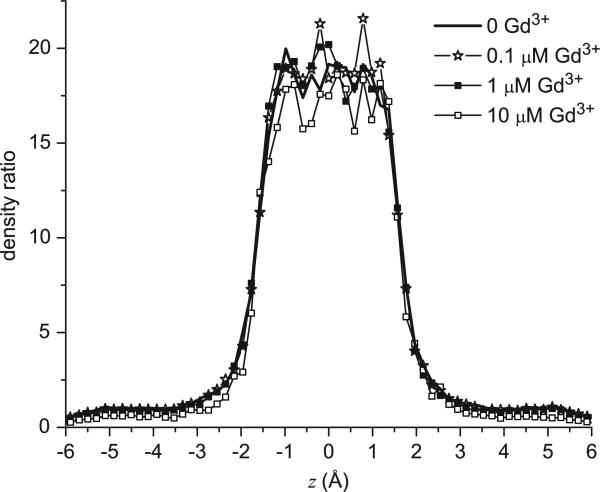
2. the concentration profiles n_i (z) of Na⁺ and the divalents M²⁺ change in the same proportion with varied [Gd³⁺]. That is,

   $$\frac{n_{\mathrm{M}}\left(z\right)}{n_{\mathrm{Na}}\left(z\right)}=\frac{n_{\mathrm{M}}^0\left(z\right)}{n_{\mathrm{Na}}^0\left(z\right)}$$ (6)

   where the function n_i(z) is the line density from Eq. (2) (which depends on [Gd³⁺]) and the superscript 0 refers to the profile when [Gd³⁺] = 0. This is shown in Fig. 3. Because of Eq. (6) and because the conductance of Gd³⁺ is zero, Eq. (3) becomes

   $$\begin{array}{cc}\hfill \frac{\gamma \left(\left[{\mathrm{Gd}}^{3+}\right]\right)}{{\gamma }^0}& \approx \frac{\frac{D_{\mathrm{M}}}{D_{\mathrm{Na}}}{\eta }_{\mathrm{M}}\left(\left[{\mathrm{Gd}}^{3+}\right]\right){\eta }_{\mathrm{Na}}\left(\left[{\mathrm{Gd}}^{3+}\right]\right)}{\frac{D_{\mathrm{M}}}{D_{\mathrm{Na}}}{\eta }_{\mathrm{M}}^0+{\eta }_{\mathrm{Na}}^{}}\hfill \\ \hfill & =\frac{{\eta }_{\mathrm{Na}}\left(\left[{\mathrm{Gd}}^{3+}\right]\right)}{{\eta }_{\mathrm{Na}}^0}=\frac{{\eta }_{\mathrm{M}}\left(\left[{\mathrm{Gd}}^{3+}\right]\right)}{{\eta }_{\mathrm{M}}^0}.\hfill \end{array}$$ (7)

4.

Concentration profiles of ions in the pore: top row (A, D, G) Na⁺; middle row (B, E, H) divalent M²⁺; bottom row (C, F, I) Gd³⁺. The left column (A, B, C) are when the divalent is Ca²⁺, the middle column (D, E, F) Sr²⁺, and the right column (G, H, I) Ba²⁺. The thick black line is when [Gd³⁺] = 0, the thin black line when [Gd³⁺] is 0.1 μM, the long-dashed (red) line when [Gd³⁺] is 1 μM, and the dotted (blue) line when [Gd³⁺] is 10 μM. These concentrations are given in molar instead of the line density used in Eq. (2). The area used to compute this molar concentration from the line density is the cross-sectional area accessible to the center of each ion species.

3.

The line density profile ratio n_Ca(z)/n_Na(z) at different [Gd³⁺]. The results with Sr²⁺ and Ba²⁺ are qualitatively identical.

The consequence of the normalized conductance being independent of the diffusion coefficient ratios is that the normalized pore conductance γ /γ⁰ is determined solely by the ion binding selectivity properties of the model pore through the density profiles n_i(z) in η_i (Eq. (4)). (Of course the absolute conductance γ does depend on the diffusion coefficients.) The model results are then more robust, in that they are not subject to particular choices of parameters that are difficult to estimate independently.

We do, however, consider quantities that depend on the diffusion coefficients. For example, under the conditions of Fig. 2A, we compute the individual Ca²⁺ and Na⁺ conductances to be approximately equal (data not shown) when the diffusion coefficient ratio D_Ca / D_Na is 0.1, reflecting the relative difficulty Ca²⁺ has diffusing within the “stew” of oxygens in the selectivity filter. (This is the value we have used in the past [10, 12, 18] and is consistent with similar models of ryanodine receptor calcium channels that reproduce experimental data [13-16]. A similar value has also been found in recent dynamical simulations of calcium channels that are independent of diffusion coefficients [26].) Therefore, it could be that the model predicts currents of monovalent cations that are dramatically greater than those observed experimentally. Part of this is certainly due to the significantly larger driving force for Ca²⁺ in experiments where Ca²⁺ is generally only present on one side of the membrane. With 1 μM Ca²⁺ intracellularly and 0.1, 1, or 10 mM extracellularly, this corresponds to ~120, 175, 235 mV of driving force, compared to 0 with our symmetric Ca²⁺ distribution [10]. In addition, other parts of the channel that we do not model could affect these conductances.

There may, however, be another explanation. Counterintuitively, after substituting large non-permeating monovalent cations for Na⁺ (as in experiments), preliminary simulations show that the total conductances (which is what is measured in experiments) in both cases are unexpectedly similar (data not shown). Measurement of the same net current in such ion substitution experiments have been interpreted to mean that Na⁺ does not permeate the pore. Since our model seems to give a different interpretation, we will explore this with our model in future work.

Regardless, the ion occupancies of the selectivity filter we calculate (see Fig. 5 later) — and the block by Gd³⁺—are robust, as are the general conclusions of this paper derived from them. The conversion to conductances allow us to compare our calculations with experiments more directly. Specifically, ion occupancy of the selectivity filter is not always proportional to that ion's current [10, 16] and ions move through the filter with different velocities, as recently shown [26]. The conversion of density profiles to conductance around 0 mV attempts to include these two phenomena. The comparison between our conductance in symmetric ion conditions and the experimental current in asymmetric conditions is fairly rough because of the reduced nature of the model pore and the exclusion of the large experimental driving force for Ca²⁺. It is, however, a significant improvement over merely considering ion occupancies in the filter.

5.

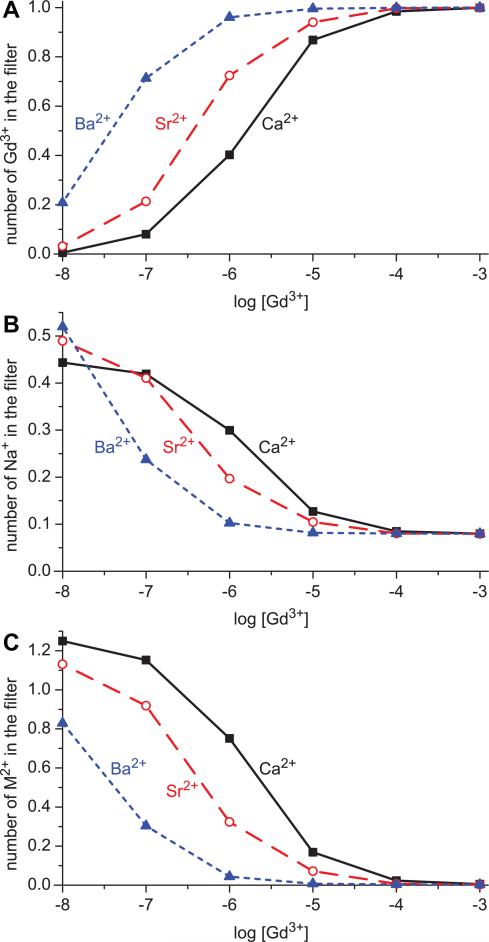
Occupancy of each cation species in the selectivity filter (–5 Å < z < 5 Å in Fig. 1) when different divalents are present: Ca²⁺ solid (black) curves and square (black) symbols; Sr²⁺ dashed (red) curves and circle (red) symbols; Ba²⁺ dotted (blue) curves and triangle (blue) symbols. (A) The number of Gd³⁺ in the filter. (B) Na⁺. (C) divalents M²⁺.

Effect of Gd³⁺ concentration on permeant ions

Because the normalized total conductance γ /γ⁰ is determined by the binding selectivity of the pore for Na⁺ and the divalents M²⁺, we examine the effect [Gd³⁺] has on the distributions of these ions within the pore. Fig. 4 shows the concentration profiles of Na⁺, M²⁺, and Gd³⁺ as Gd³⁺ is added. These show the general behavior of ion binding that have been shown in other studies of this model pore [9, 10, 12, 18, 21]. For example, the high-valence ions like the divalents bind preferentially in the center of the pore with smaller, secondary accumulation sites (“binding sites”) just outside the selectivity filter. In contrast, Na⁺ also accumulates in the center, but has much higher concentrations in the vestibules. It is important to note that these secondary binding sites (similar to those postulated in chemical kinetics models [27]) are not built into the model. Rather, they are a natural result of the physics put into the model pore, namely ions of finite size (not point charges) competing for space in a crowded selectivity filter filled with negatively-charged, flexible side chains. For example, the large peaks of Na⁺ accumulation outside the selectivity filter show that it is more energetically favorable for Na⁺ to screen the charge of the selectivity filter from the outside, rather than find space in the crowded filter. The divalents, on the other hand, can screen the glutamates more efficiently than the Na⁺ ions because they take up less volume for the same amount of charge. This balance of electrostatics and excluded volume of the ions (including the glutamate side chains) was first described by Nonner et al. [28] and is called the charge/space competition mechanism (coined by D. Busath in [29]).

As [Gd³⁺] increases, the general pattern is the same no matter which divalent M²⁺ is present: the peak of Gd³⁺ in the center of the pore increases, the peak of M²⁺ decreases, filter Na⁺ concentration decreases, as do all the ion concentrations in the secondary binding sites in the vestibules. Overall, as Gd³⁺ occupies the center of the pore more often (i.e., with a higher probability), the permeant ions are displaced from both the filter and the vestibules.

Effect of divalent size on Gd³⁺ binding

Despite the general pattern of permeant ions being replaced in the pore by Gd³⁺, there are significant differences in the extent to which the three divalents are displaced from the model pore by increasing [Gd³⁺]. These differences are responsible for the divalent dependence on tonic block shown in Fig. 2A. It can be seen that Ba²⁺ is the divalent most easily displaced by Gd³⁺. The concentration profiles in Fig. 4H reveal that even 0.1 μM Gd³⁺ is enough to displace more than half of the Ba²⁺ from the center of the selectivity filter, compared to when no Gd³⁺ is present (compare thick and thin black lines); Na⁺ is also displaced from the entire pore (Fig. 4G). In contrast, 0.1 μM Gd³⁺ has little effect on Ca²⁺ (Fig. 4B) and an intermediate effect on Sr²⁺ (Fig. 4E). For both Ca²⁺ and Sr²⁺, Na⁺ concentration in the pore is little affected by 0.1 μM Gd³⁺ (Figs. 4A and D, respectively).

A different way of looking at the same thing is to consider the number of each cation species (Na⁺, M²⁺, and Gd³⁺) in the selectivity filter. Fig. 5 shows these filter occupancies as [Gd³⁺] is increased. Each panel shows a different cation (A: Gd³⁺; B: Na⁺; C: M²⁺) when different divalents are present (solid lines: Ca²⁺; dashed lines: Sr²⁺; dotted lines: Ba²⁺). The figure shows that Ca²⁺ competes best with Gd³⁺ for the selectivity filter: the Gd³⁺ occupancy curve when Ca²⁺ is present (Fig. 5A, solid curve) is to the right of both the Sr²⁺ and Ba²⁺ curves (Fig. 5A, dashed and dotted curves, respectively). Similarly, when Ca²⁺ is present, both the Na⁺ occupancy curve (Fig. 5B, solid line) and the Ca²⁺ occupancy curves (Fig. 5C, solid line) are to the right of the same curves when either Sr²⁺ or Ba²⁺ are present (Fig. 5B and C, dashed and dotted curves, respectively); it takes relatively little Gd³⁺ to displace the permeant cations when Ba²⁺ is present, more Gd³⁺ when Sr²⁺ is present, and even more when Ca²⁺ is present.

DISCUSSION

The pattern of ion binding selectivity found in the block experiments (Fig. 2A) is consistent with the L- and T-type calcium channels’ tendency to be more selective for small ions (with the notable exception not considered here that Mg²⁺ is not preferred over the larger Ca²⁺ by L-type, presumably due to ion dehydration effects [30]). In this case, the selectivity sequence Ca²⁺>Sr²⁺>Ba²⁺ mirrors ion size: Ca²⁺ is smallest (radius 0.95 Å) and Ba²⁺ largest (radius 1.35 Å), with Sr²⁺ of intermediate size (radius 1.13 Å).

In modeling the L-type channel to define its selectivity mechanism, we and our co-workers have found that this channel selects ions by the charge/space competition mechanism [9-12, 18, 21, 22, 31], as do other Ca²⁺ selective pores like the ryanodine receptor calcium channel [13-16], mutated and chemically modified OmpF porins [32-34], and negatively-charged synthetic nanopores [24, 35]. The pattern of cations being replaced in the pore by Gd³⁺—with the smaller Ca²⁺ competing much more effectively with Gd³⁺ than the larger Sr²⁺ and Ba²⁺—is consistent with the charge/space competition mechanism of selectivity. In this mechanism, selectivity is determined by a balance of protein charges attracting the cations into the selectivity filter and of the ions finding space in a selectivity filter where ~25% of the available space is taken up by the eight oxygens of the four glutamate side chains. In such a crowded environment it takes less free energy to insert a Ca²⁺ ion than a Ba²⁺ ion because the Ca²⁺ ion has ~40% of the volume of the Ba²⁺ ion; the entropy change is less when a smaller ion is inserted. For both these divalents, even less energy is required to insert a Gd³⁺ ion because it has more charge. Therefore, as [Gd³⁺] increases, it is more likely that a Gd³⁺ enters the pore. However, Gd³⁺ requires more energy to remove a Ca²⁺ from the pore than a Ba²⁺ because of Ca²⁺'s relative stability over Ba²⁺.

As for the change in conductance, we find that Gd³⁺ does not permeate the model pore. This is because Gd³⁺ binds with any appreciable concentration only in the center of the selectivity filter, which creates regions of high resistance to Gd³⁺ current flow elsewhere; the low-concentration regions (depletion zones) have high resistance just like any low-concentration electrolyte solution (as described previously [10, 24, 36]) so the Gd³⁺ current is negligible. When Gd³⁺ is in the filter, then the permeant cations Na⁺ and the divalents M²⁺ do not occupy the pore and therefore do not produce a current.

But, Gd³⁺ is not always in the pore; it has a probability of being in the selectivity filter that depends on [Gd³⁺]. When Gd³⁺ is not in the pore, then Na⁺ and the divalents M²⁺ can conduct through the channel. The calculated current is then a long-time statistical average of this process. Therefore, the reduction of current comes about as the probability of Gd³⁺ being in the selectivity filter increases with [Gd³⁺], blocking permeant ion current more and more of the time. In our approach, we measure this by sampling many states of one channels while the whole-cell experiments sample one state of many channels.

This explanation of current reduction is similar to what has been proposed for Ca²⁺ block of monovalent current [10, 16, 36] (i.e., the classic Ca²⁺ versus Na⁺ anomalous mole fraction effect found by Almers and McCleskey [1, 2]). Like Gd³⁺, Ca²⁺ (and other divalents) occupy the center of the selectivity filter, blocking monovalent current during that time. However, Ca²⁺ is not bound as tightly in the pore as Gd³⁺ and can be displaced by another Ca²⁺ often enough to make an appreciable Ca²⁺ current. Considered in terms of resistors in an equivalent circuit, Ca²⁺ has relatively low resistance in the selectivity filter where its concentration is high, but very high resistance everywhere else because its concentration is low there. Ca²⁺ conductance through the entire pore is low—despite its high occupancy in the selectivity filter—because these resistors are in series. The same principle also holds in the ryanodine receptor calcium channel [16].

CONCLUSION

Trivalent cations alter the permeation properties of calcium channels in general [7, 37, 38], making them useful laboratory tools [3, 39-41]. In fact, trivalents affect many kinds of ion channels (e.g., [42, 43]). Here we described a possible mechanism for one of these effects on calcium channels. Specifically, we showed that the reduction of Na⁺ and divalent currents by increasing [Gd³⁺] can be described by these ions competitively binding within the selectivity filter. Our results also give further evidence that selectivity in the L- and T-type calcium channels stems from a balance of electrostatic attraction of cations into the filter and excluded volume repulsion of the ions from the crowded filter (charge/space competition).