Improving Temporal Resolution of Pulmonary Perfusion Imaging in Rats using the Partially Separable Function Model

Abstract

Dynamic contrast-enhanced MRI (or DCE-MRI) is a useful tool for measuring blood flow and perfusion, and it has found use in the study of pulmonary perfusion in animal models. However, DCE-MRI experiments are difficult in small animals such as rats. A recently developed method known as Interleaved Radial Imaging and Sliding window-keyhole (IRIS) addresses this problem by using a data acquisition scheme that covers (k, t)-space with data acquired from multiple bolus injections of a contrast agent. However, the temporal resolution of IRIS is limited by the effects of temporal averaging inherent in the sliding window and keyhole operations. This paper describes a new method to cover (k, t)-space based on the theory of partially separable functions (PSF). Specifically, a sparse sampling of (k, t)-space is performed to acquire two data sets, one with high temporal resolution and the other with extended k-space coverage. The high temporal resolution training data are used to determine the temporal basis functions of the PSF model, while the other data set is used to determine the spatial variations of the model. The proposed method was validated by simulations and demonstrated by an experimental study. In this particular study, the proposed method achieved a temporal resolution of 32 ms.

INTRODUCTION

Dynamic contrast-enhanced MRI (or DCE-MRI) experiments often involve the acquisition of a time series of images after the bolus injection of a contrast agent. These images are then used to estimate perfusion metrics (such as time of peak contrast enhancement, wash-in rate, and mean transit time) in tissues and blood vessels (1). Many respiratory diseases are known to affect perfusion characteristics in the pulmonary arteries and veins (2–7), and the diagnostic value of perfusion measurements in pulmonary blood vessels has been the topic of DCE-MRI research for many years using genetically bred rat models (2, 5–8). However, imaging these small animals places high demands on signal-to-noise ratio (SNR) and spatiotemporal resolution. To address this problem for pulmonary perfusion imaging, Mistry, et al. proposed a DCE-MRI technique, known as IRIS (Interleaved Radial Imaging combined with a Sliding window-keyhole reconstruction) (8). IRIS collects data over multiple contrast injections (8) acquired with carefully controlled experimental conditions such that the acquisition conditions were repeatable. IRIS is able to achieve much of the needed SNR and spatial resolution for pulmonary studies in rats; however, the temporal resolution is limited by the temporal averaging effect of the sliding window operation. Improved temporal resolution may improve the accuracy of the signal-intensity curves from the DCE-MRI data especially since pulmonary perfusion data from rats contain frequencies as high as twice the heart rate or roughly 12 Hz (see Figure 5a in Ref. (8)) implying a temporal Nyquist criterion of 24 Hz. Also, improved temporal resolution may be traded for increased spatial resolution which could have value in resolving the pulmonary blood vessels.

Improving the temporal resolution can be done by applying a number of imaging acceleration techniques that have been shown to have success in DCE-MRI. Such methods include parallel imaging (9, 10), sparse projection acquisition methods (11, 12), and dynamic imaging methods (13, 14). As an alternative, this paper proposes the application of a spatiotemporal model with temporal eigenbasis functions to perform computationally efficient dynamic imaging. The use of temporal eigenbasis functions for dynamic imaging was first proposed in 2001 (15) as a generalization of DIME (Dynamic Imaging by Model Estimation) (16). The model is based on the theory of partially separable functions (PSF) (17) and has been further investigated over the last few years (18–23). This paper presents a demonstration of the technique for pulmonary perfusion imaging using a non-Cartesian k-space trajectory.

THEORY

The proposed imaging method is based on the use of a specific model, known as partially separable functions (PSF), of the spatiotemporal signal changes in dynamic perfusion imaging (17). This model enables reconstruction of the dynamic images from very sparsely sampled (k, t)-space data. The proposed sampling method is characterized by the acquisition of two complementary data sets: (a) the training data with high temporal resolution but limited k-space coverage and (b) the imaging data with extended k-space coverage but low temporal resolution. The proposed reconstruction method uses the training data set to derive a set of temporal basis vectors that are then fit to the imaging data set to determine the spatial basis vectors of the model. The proposed method is described in detail in the remainder of this section.

Following conventions (24), the acquired data s(k, t) and the desired image function ρ(x, t) are expressed as

$$s(\mathbf{k},t)={\displaystyle {\int }_{-\infty }^{\infty }\rho (\mathbf{x},t)e^{-i2\pi \mathbf{k}·\mathbf{x}}d\mathbf{x}}.$$ [1]

We model s(k, t) using the PSF model as

$$s_{\text{psf}}(\mathbf{k},t)={\displaystyle \sum _{\ell =1}^L{c}_{\ell }(\mathbf{k}){\phi }_{\ell }(t)}$$ [2]

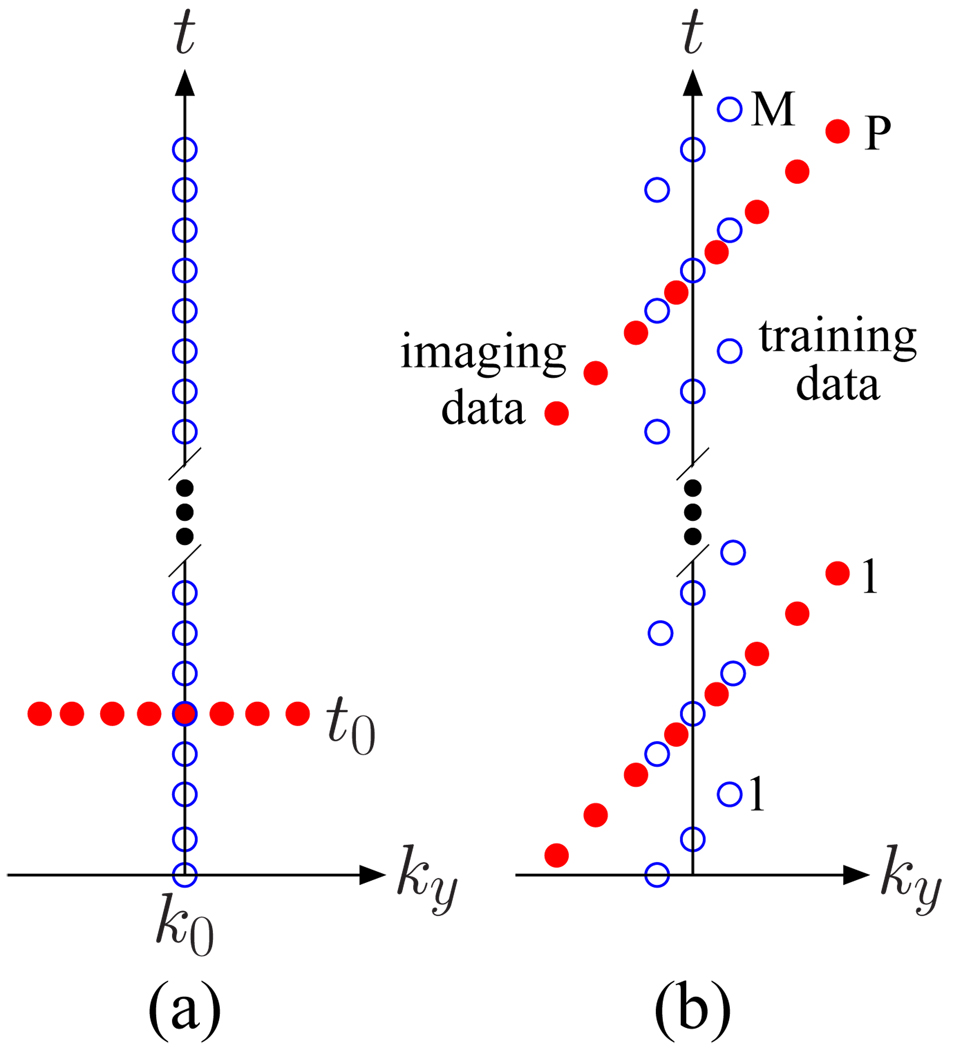
where L is the model order (or separation rank) of the (k, t)-space signal (17). When L is small, such as when many spatial locations share similar temporal characteristics, sparse sampling of (k, t)-space is possible. For example, when L = 1, s_psf(k, t) = c(k)φ(t), so s_psf(k, t) can be recovered from samples along two perpendicular lines such as s(k, t₀) and s(k₀, t) for some constants t₀ and k₀ when s(k₀, t₀) ≠ 0 (see Figure 1 (a)). In practice, L > 1 and we need to collect sufficient data to determine {φ_ℓ(t)} and {c_ℓ(k)}. One strategy is to collect a training data set s₁(k, t) with high temporal resolution to determine {φ_ℓ(t)} and the regular imaging data s₂(k, t) with extended k-space coverage (thus high spatial resolution) to determine {c_ℓ(k)}. One such scheme is shown in Figure 1 (b). We tailor this scheme for dynamic perfusion imaging with radial k-space coverage. Details of this adaptation are giving in the Methods section.

Figure 1.

Sparse (k, t)-space sampling patterns for dynamic imaging of partially separable functions where k_y is the phase encoding axis, and k_x, the frequency encoding axis, is into the page. The open circles represent the training data, s₁(k, t), and the filled circles represent the imaging data, s₂(k, t). (a) A conceptual (k, t)-space sampling pattern for partially separable functions of order 1. (b) A realizable (k, t)-space sampling pattern for higher order partially separable functions.

In general, image reconstruction using Eq. [2] is performed in a four step process: (a) determining the temporal basis functions {φ_ℓ(t)} from the training data, (b) fitting these basis functions to the imaging data to find {c_ℓ(k)}, (c) computing the full (k, t)-space signal, s_psf (k, t), using Eq. [2], and (d) applying an inverse Fourier transform over the k-space. The first step is accomplished by constructing a matrix, C, from the training data as follows:

$$\mathbf{C}=\left[\begin{array}{cccc}\hfill s_1({\mathbf{k}}_1,t_1)\hfill & \hfill s_1({\mathbf{k}}_2,t_1)\hfill & \hfill \cdots \hfill & \hfill s_1({\mathbf{k}}_N,t_1)\hfill \\ \hfill s_1({\mathbf{k}}_1,t_2)\hfill & \hfill s_1({\mathbf{k}}_2,t_2)\hfill & \hfill \cdots \hfill & \hfill s_1({\mathbf{k}}_N,t_2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill s_1({\mathbf{k}}_1,t_M)\hfill & \hfill s_1({\mathbf{k}}_2,t_M)\hfill & \hfill \cdots \hfill & \hfill s_1({\mathbf{k}}_N,t_M)\hfill \end{array}\right]$$ [3]

where each of the N points in k-space has been measured M times. Singular Value Decomposition (SVD) (25) is then used to identify the dominant column subspace for use as {φ_ℓ(t)}. The SVD of C can be expressed as:

$$\mathbf{C}={\displaystyle \sum _{\ell =1}^{\text{min}\{M,N\}}{\sigma }_{\ell }{\mathbf{u}}_{\ell }{\mathbf{v}}_{\ell }^{\mathrm{H}}}$$ [4]

where the {σ_ℓ} are the singular values of C arranged in descending order, {u_ℓ} and {v_ℓ} are the left and right singular vectors, respectively. Then {φ_ℓ(t)} are set equal to the L most significant left singular vectors such that

$${[{\phi }_{\ell }(t_1),{\phi }_{\ell }(t_2),\cdots ,{\phi }_{\ell }(t_M)]}^{\mathrm{T}}={\mathbf{u}}_{\ell }$$ [5]

for ℓ = 1, 2, …,L.

The second step in the method is to determine {c_ℓ(k)} by fitting {φ_ℓ(t)} to the imaging data, s₂(k, t). s₂(k, t) is measured at a series of (k, t)-space locations {(k_q, t_1,q), (k_q, t_2,q), …, (k_q, t_p,q), …, (k_q, t_P,q)} for q = 1, 2, …, Q and p = 1, 2, …, P. The fitting is accomplished by solving a linear system of equations for each k_q from Eq. [2] as follows

$$\left[\begin{array}{ccc}\hfill {\phi }_1(t_{1,q})\hfill & \hfill \cdots \hfill & \hfill {\phi }_L(t_{1,q})\hfill \\ \hfill {\phi }_1(t_{2,q})\hfill & \hfill \cdots \hfill & \hfill {\phi }_L(t_{2,q})\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\phi }_1(t_{P,q})\hfill & \hfill \cdots \hfill & \hfill {\phi }_L(t_{P,q})\hfill \end{array}\right]\left[\begin{array}{c}\hfill c_1({\mathbf{k}}_q)\hfill \\ \hfill c_2({\mathbf{k}}_q)\hfill \\ \hfill ⋮\hfill \\ \hfill c_L({\mathbf{k}}_q)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill s_2({\mathbf{k}}_q,t_{1,q})\hfill \\ \hfill s_2({\mathbf{k}}_q,t_{2,q})\hfill \\ \hfill ⋮\hfill \\ \hfill s_2({\mathbf{k}}_q,t_{P,q})\hfill \end{array}\right],$$ [6]

(or Φ_qc_q = s_q for short). Furthermore, the solution can be stabilized by solving Eq. [6] in the least-squares sense with regularization (26). Regularization helps to avoid the adverse effects of ill-conditioning of the Φ_q matrix caused by the sparse sampling process. Also, the imaging data are acquired such that P > L which makes Eq. [6] overdetermined and helps with the conditioning of Φ_q.

The third step in the general reconstruction procedure is to use Eq. [2] to compute s_psf(k, t) over the full (k, t)-space. This model based reconstruction can be taken as the final estimate of the (k, t)-space signal, s(k, t), or data replacement can be performed such that

$$\widehat{s}(\mathbf{k},t)=\{\begin{array}{cc}s(\mathbf{k},t)\hfill & (\mathbf{k},t)\in \text{measure data}\hfill \\ s_{\text{psf}}(\mathbf{k},t)\hfill & \text{otherwise}\hfill \end{array}$$ [7]

Data replacement ensures that the region of (k, t)-space covered by the sampling pattern is accurately represented, while the main disadvantage of data replacement is a loss of SNR since the SVD truncation operation results in some denoising of the data. The fourth and final step in the general image reconstruction procedure is to apply an inverse spatial Fourier transform to s_psf(k, t) or ŝ(k, t) to produce an estimate of ρ(x, t). This result can be taken as the final reconstruction for ρ(x, t), or alternatively, ρ_psf can be used to regularize the final reconstruction (27) such that

$${\rho }^0(\mathbf{x},t)=\underset{\rho }{\text{argmin}}{\Vert s(\mathbf{k},t)-{ℱ}_{\rho }(\mathbf{x},t)\Vert }_2^2+{\lambda }^2{\Vert W(\rho (\mathbf{x},t)-{\rho }_{\text{psf}}(\mathbf{x},t))\Vert }_2^2$$ [8]

where λ² is the regularization parameter, and W is a weighting function. (ℱ is a Fourier transform from x to k.) In this paper, ρ_psf(x, t) is used as the final reconstruction.

METHODS

Animal Model

A total of 5 DCE-MRI experiments were carried out using a total of 3 rats (2 were examined twice with 1.5 h between scans) using an experimental protocol approved by the Duke Institutional Animal Care and Use Committee. All the rats were healthy female Fischer 344 rats (Charles River Laboratories, Wilmington, MA) weighing 190–225 g. Catheters (3 French) were placed in their right jugular veins, and the animals were intubated and mechanically ventilated at 60 breaths/min (2.0–2.2 ml tidal volume). Anesthesia was administered via 0.05 ml injections of Nembutal every 45 minutes, and body temperature was controlled using a heat source with feedback from a rectal thermistor. Electrodes on the footpads were used to acquire the electrocardiogram (ECG) signal. Physiological signals were continuously collected (Coulbourn Instruments, Allentown, PA) and displayed using LabView software (National Instruments, Austin, TX). These signals were used to trigger the imaging sequences. After the studies were completed, the animals were euthanized with an overdose of anesthesia.

Simulation

The imaging method was validated using a pulmonary perfusion phantom that was created from a denoised experimental image. Compartments within the image were defined to represent the pulmonary artery, left lung parenchyma, right lung parenchyma, pulmonary vein, and descending aorta. Temporal signal changes for each compartment were created by adding a gamma variate curve

$$C(t)=C_0{\left(\frac{e}{\mathit{\text{ab}}}(t-T_0)\right)}^a{e}^{-(t-T_0)/b}$$ [9]

to model the pre-contrast value of each compartment for t ≥ T₀ (1, 28). In Eq. [9], a, and b are shaping parameters. While C₀ is the normalized peak concentration, and T₀ is the time of arrival of the contrast bolus. Typical parameters for rats were used to create the phantom (for example, a = 14 and b = 0.1 s for the descending aorta) (8). The component of the signal caused by cardiac pulsation was modeled by two additive sinusoids with frequencies of 6 Hz and 12 Hz. The cardiac pulsation was added to the gamma variate curve for the descending aorta compartment, while the signal-intensity curves for the other compartments remained unchanged. (k, t)-space data were generated from the phantom with parameters identical to the experiment, and ρ̂(x, t) was reconstructed using both the proposed imaging method and the sliding window based method.

Experimental Procedures

All experimental data were acquired using a GE EXCITE console running version 12M4 (GE Healthcare, Milwaukee, WI) with a 2.0 T horizontal bore Oxford magnet, and a birdcage coil (7 cm diameter, 5.5 cm length) was used for all of the data acquisitions. A single slice containing the pulmonary arteries and veins with a 50 mm field of view and 3 mm thickness was imaged using the radial data acquisition scheme depicted in Figure 2. The readouts were performed with T_R = 4 ms, T_E = 1 ms, 40° flip angle, 62.5 kHz bandwidth, and 256 points. The ECG and respiratory signals were used to trigger each of the 5 contrast injections within a given DCE-MRI experiment with a separation of approximately 15 s. Each injection was triggered by the first ECG R wave identified after suspending the ventilation during end-expiration, and each 20 µl, 50 ms injection delivered 0.05 mmol/(kg of body mass) of Magnevist (Gd-DTPA, Berlex, Montville, NJ) 800 ms after the start of the data acquisition (8). Also, the dosages of Gd-DTPA used in this study have been shown to result in a strongly linear relationship between concentration and signal-intensity (8).

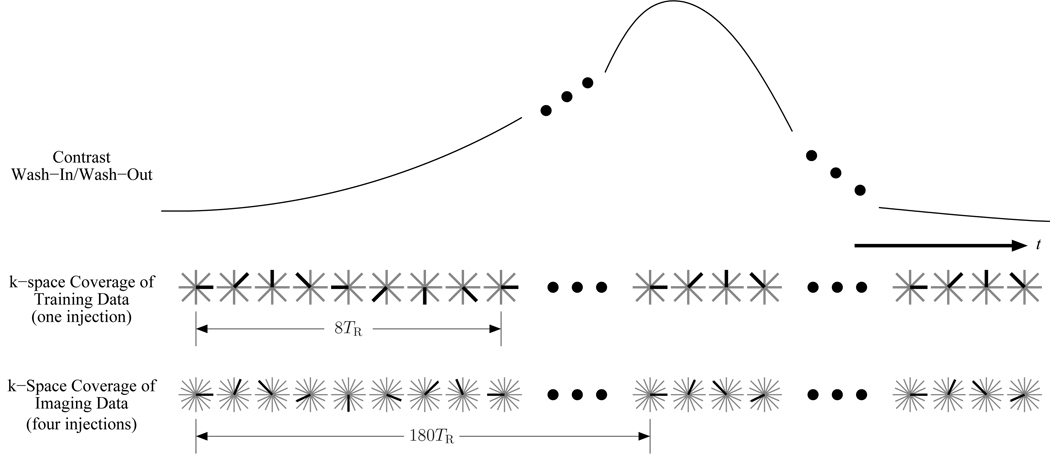
Figure 2.

The k-space sampling over time for the proposed method. The dark radial is the one acquired for that T_R, while the light gray radials represent the full set. The training data cover 8 equally spaced angles and are incremented by 45° every T_R. The imaging data cover 720 equally spaced angles that are divided into 4 unique sets for acquisition during separate contrast injections. The imaging data’s angle step size is 66.5° every T_R.

The data acquisition scheme illustrated in Figure 2 was designed based on the constraints of the application and the needs of the general dynamic imaging method described in the Theory section that uses the PSF model in Eq. 2 to represent the (k, t)-space signal. For this particular application, the radial k-space trajectory is a good choice since its short T_E helps to overcome the fast signal decay caused by the short $T_2^{*}$ in the lung region. The proposed dynamic imaging method requires training data and imaging data, and the training data were designed to satisfy the temporal Nyquist criterion by covering 8 angles in the following order: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°. The temporal resolution is then 8T_R or 32 ms (which is better than the desired 42 ms based on the rate of the cardiac pulsation). The imaging data acquisition was designed such that the number of measurements for each k-space location would be P = 12 since the model order was L = 5 so that P > L would be satisfied. A total of 720 distinct radials were acquired for the imaging data which resulted in an undersampling factor of 2.2 at the outermost region of k-space. The imaging data’s 720 radials were split into 4 unique groups of 180 radials that were acquired during 4 separate injections. Each group of imaging data was acquired in a repeating pattern so that any individual radial was acquired every 180T_R or 720 ms. The pattern for each imaging data acquisition was created by starting with one of the angles 0°, 90°, 180°, or 270° and then incrementing the angle by 66.5° with each T_R, which approximates an optimized radial acquisition order based on the Golden Ratio (29).

Since the order of the imaging data within each repeating pattern is of little consequence to the fitting of the PSF model, a pattern was selected that eliminates the need for a spoiling gradient which helps keep the T_R as short as possible. Such a pattern for radial acquisition can be created by incrementing the angle between successive readouts by a large angle in the 45° to 135° range. The operation of this pulse sequence can be understood by considering the effects of a second readout after a single excitation and radial readout. After the first readout, residual magnetization exists with a phase corresponding to the outer part of k-space. Without spoiling this magnetization, it will decay according to $T_2^{*}$. However, the second RF excitation will cause this residual magnetization to split into two components: one at the tip of the previous radial readout and the other at the same distance from the center of k-space but 180° away (30) (page 126). If the next radial readout is performed at nearly the same angle as the previous (or 180° from it), then one of these two residual magnetizations will refocus toward the center of k-space and cause interference with the desired readout. In contrast, a readout at an angle roughly perpendicular to the first readout will push both residual magnetizations along trajectories only in the high k-space (which naturally has low energy) while they decay according to $T_2^{*}$. As a result, the signal from the residual magnetization can be neglected.

Data Processing

The DCE-MRI data were reconstructed into a time series of images using the general method described in the Theory section. Step (a) of finding the temporal basis functions, φ_ℓ(t), was performed by constructing C from the training data and applying an SVD. It is worth noting that each row of C contains data from one time instant, so temporal interpolation via cubic splines was used to compute C from the time sequentially acquired training data. For this reason, the training data’s acquisition should satisfy the temporal Nyquist criterion. In this case the sampling is fast enough that the readout times were ignored in the interpolation; however, all the training data were interpolated to a temporal spacing of 4 ms to make the construction of Φ_q easier. In the second step, (b), c_ℓ (k) were determined by solving Eq. [6] for each location in the k-space for L = 5 and P = 12. Again, the readout time was approximated as instantaneous, but each T_R was accounted for when constructing Φ_q. Φ_q was inverted using the MATLAB pinv function with its default parameters. pinv performs a truncated SVD pseudo-inverse procedure that stabilizes the solution (26). For step (c), Eq. [2] was evaluated to estimate the (k, t)-space signal. The last step, (d), was accomplished by applying a standard gridding algorithm (31) with a modified Hamming filter for density compensation (H(|k|) = |k|(0.54 + 0.46 cos(|k|π/max(|k|)))) and a Kaiser-Bessel convolution kernel (W = 3 and β = 13.9) (32) to the estimated (k, t)-space signal. Then the temporal signal changes in each region of interest were extracted, and these signal-intensity curves were averaged together within each region of interest. The time of peak contrast enhancement, T_P, and mean transit time, MTT, were calculated by first fitting Eq. [9] to the signal-intensity curves and then using the relations

$$T_{\mathrm{P}}=\mathit{\text{ba}}+T_0$$ [10]

and

$$\text{MTT}=b(a+1)=\frac{{\displaystyle \int tC(t)\mathrm{d}t}}{{\displaystyle \int C(t)\mathrm{d}t}}$$ [11]

where the fitting was accomplished using non-linear least-squares optimization in MATLAB (8). For the sake of comparison, the imaging data were also processed using the sliding window method with a window size of 720 ms and temporal step size of 32 ms. The signal-intensity curves were extracted and analyzed in exactly the same manner as for the model based reconstruction.

RESULTS

Simulation

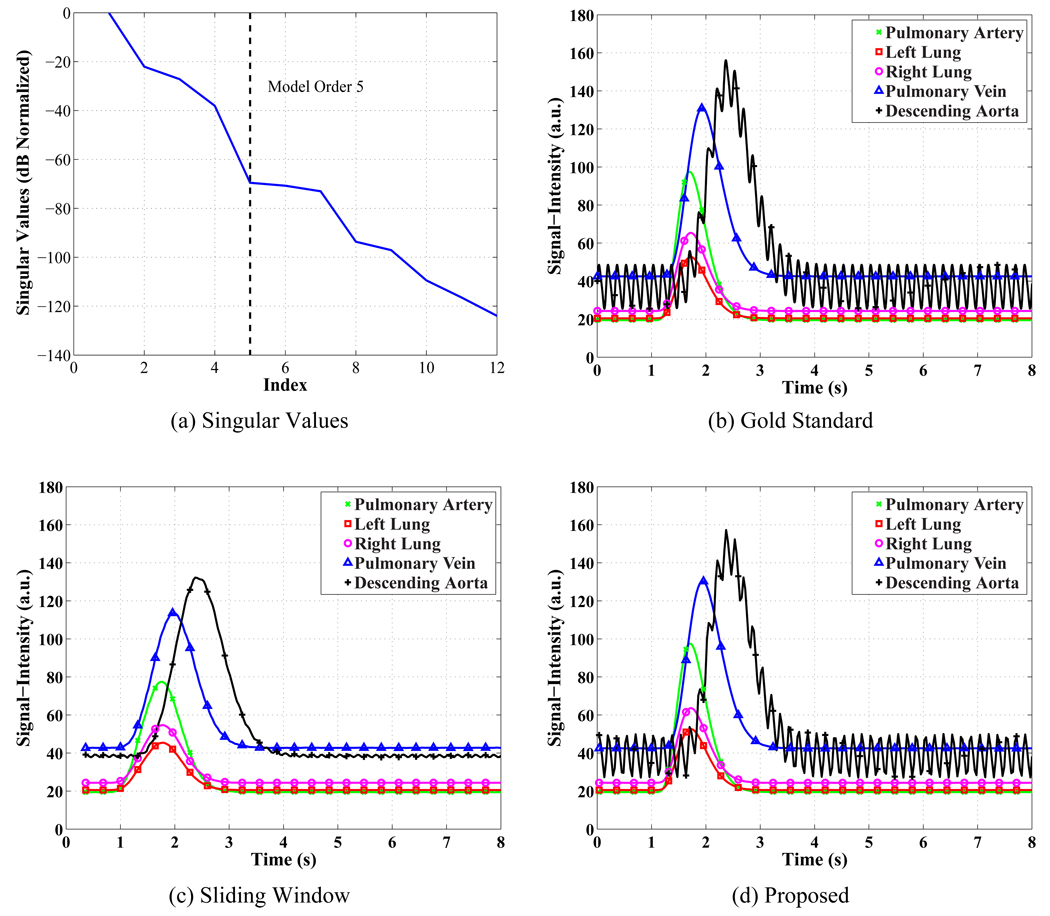
Figure 3 demonstrates that the proposed method produces more accurate signal-intensity curves than the sliding window method in the simulation. The proposed method correctly assigns the cardiac pulsation only to the descending aorta, while the sliding window method’s curves are all fairly smooth. Also, the normalized root mean square error (RMSE) was computed for all of the curves using

$$\sqrt{\frac{{\displaystyle {\sum }_n{|c(t_n)-c_{\text{gs}}(t_n)|}^2}}{{\displaystyle {\sum }_n{|c_{\text{gs}}(t_n)|}^2}}}$$ [12]

where c(t_n) represents the reconstructed signal-intensity curve and c_gs(t_n) is the gold standard curve. The curves from the sliding window method have normalized RMSEs between 7% and 15%, while the proposed method’s curves have between 0.4% and 3.2% normalized RMSE. The mean transit time (MTT) and peak time (T_P) were computed for all the signal-intensity curves from the simulation. The gamma-variate in Eq. [9] was fit to the data shown in Figure 3 (c) and (d), and the results are shown in Tables 1, 2, and 3. The peak times were slightly improved in two cases, while the mean transit time was consistently improved by a small amount by the proposed method. The largest performance increase was in the estimate of the peak concentration where the sliding window method has errors from 9% to 20%, while the proposed method’s errors for peak concentration ranged between 0.2% and 2.4%.

Figure 3.

Results from the pulmonary perfusion simulation reconstructed using the proposed method and the sliding window method. (a) The singular values of the training data normalized by the square root sum of squares of the singular values and converted to dB. The 6^th singular value has a normalized value of −70.8 dB or 0.029%. (b) The gold standard signal-intensity curves shown at 4 ms resolution. (c) The sliding window signal-intensity curves have a normalized RMSE between 7 and 15%. The curves have been reconstructed at 32 ms spacing with a 720 ms sliding window. (d) The proposed method’s signal-intensity curves have a normalized RMSE between 0.4 and 3.2%. The curves have been reconstructed at 32 ms resolution.

Table 1.

Errors in time of peak contrast enhancement (T_P) for the simulation in seconds. Improved measurements are highlighted in bold. Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Gold Standard	Sliding Window	Proposed
PA	1.70 s	−0.01 s	+0.01 s
LL	1.72 s	−0.01 s	+0.00 s
RL	1.72 s	−0.02 s	+0.00 s
PV	1.93 s	−0.01 s	+0.01 s
DA	2.40 s	+0.00 s	+0.02 s

Table 2.

Errors in Mean Transit Time (MTT) for the simulation in seconds. Improved measurements are highlighted in bold. Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Gold Standard	Sliding Window	Proposed
PA	0.80 s	+0.06 s	−0.02 s
LL	0.82 s	+0.05 s	−0.03 s
RL	0.82 s	+0.05 s	−0.02 s
PV	1.03 s	+0.04 s	−0.02 s
DA	1.50 s	+0.02 s	−0.01 s

Table 3.

Errors in peak signal-intensity (C₀ + pre-contrast value) for the simulation in percent. Improved measurements are highlighted in bold. Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Gold Standard	Sliding Window	Proposed
PA	97.5	−20%	−1.0 %
LL	52.7	−13%	−0.2 %
RL	65.4	−16%	−2.4 %
PV	130.8	−13%	−0.4 %
DA	145.4	−9%	+1.0 %

In Vivo Experiments

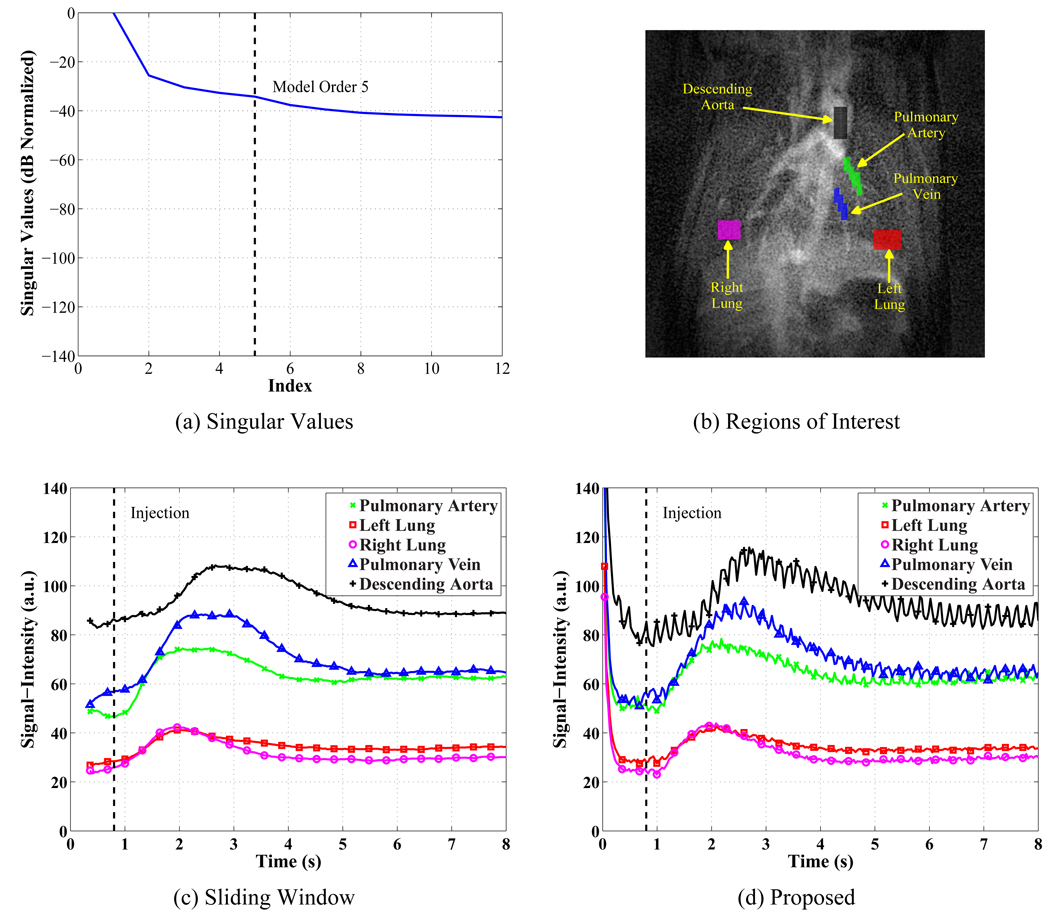
The characteristics of the experimental signal-intensity curves reconstructed using the proposed method and sliding window mimic those observed in the simulation as is seen in Figure 4. The singular values decay quickly as shown in Figure 4 (a) where the model order, L = 5, is shown on the plot. The sliding window and proposed methods are compared in Figures 4 (c) and (d) for the regions of interest in Figure 4 (b). The sliding window method’s curves are generally smooth, because the temporal averaging suppresses the cardiac pulsation. The sliding window’s width of 720 ms means that the first time point reconstructed is at 360 ms as seen in the figure, and the time averaging can distort the pre-contrast signal-intensities as can be seen in Figures 4 (c) and (d). In contrast, the proposed method’s curves are reconstructed for all time points in the experiment and reveal cardiac pulsation in most of the regions because of the improved temporal resolution. Perfusion parameters were estimated by fitting the gamma variate function in Eq. [9] to the signal-intensity curves that were reconstructed at 32 ms time steps for both methods. A comparison between the time of peak contrast enhancement, the Mean Transit Time, and the peak signal intensity is given in Tables 4, 5, and 6 for all 5 regions of interest in the image. The measurements from all 5 experiments were used to test the hypothesis that their means are identical by computing the t test statistic for paired, dependent samples (33) (page 409)

$$t=\frac{\overline{d}\sqrt{N_{\text{exp}}}}{{\sigma }_d}$$ [13]

that compares the differences in the measurements to the standard deviation of the differences. (d̄ is the mean value of the differences in the perfusion parameters for the two methods. σ_d is the standard deviation of the differences of the measurements for the two methods over the N_exp = 5 experiments.) The means are concluded to be different when |t| > t_α/2 where t_α/2 is looked up in a table for the Student’s t distribution using N_exp − 1 degrees of freedom. For a level of significance of 95%, α = 0.05 and t_α/2 = 2.776, so 6 out of 15 cases listed in Tables 4, 5, and 6 imply that the two methods report different means for the perfusion parameters in a statistically significant sense.

Figure 4.

Representative experimental DCE-MRI results. (a) The singular values of the training data normalized by the square root sum of squares of the singular values and converted to dB. The 6^th singular value has a normalized value of −37.7 dB or 1.3%. (b) The regions of interest analyzed to produce the signal-intensity curves. (c) The sliding window method’s signal-intensity curves with 32 ms spacing. (d) The proposed method’s signal-intensity curves at 32 ms resolution.

Table 4.

Time of peak contrast enhancement (T_P) plus or minus one standard deviation for the experiment in seconds. For α = 0.05, t_α/2 = 2.776, and |t| > t_α/2 implies statistically that the means reported by the two methods are significantly different (highlighted in bold). Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Sliding Window	Proposed	Mean Diff.	Std. Dev. Diff.	t test statistic
PA	1.99 ±0.19 s	2.00 ±0.16 s	0.012573 s	0.060362 s	0.4657
LL	1.90 ±0.20 s	1.87 ±0.17 s	−0.022534 s	0.072186 s	−0.6980
RL	1.78 ±0.11 s	1.81 ±0.12 s	0.031202 s	0.034511 s	2.0216
PV	2.32 ±0.17 s	2.25 ±0.19 s	−0.070348 s	0.033758 s	−4.6598
DA	2.77 ±0.23 s	2.75 ±0.29 s	−0.016274 s	0.069806 s	−0.5213

Table 5.

Mean Transit Time (MTT) plus or minus one standard deviation for the experiment in seconds. For α = 0.05, t_α/2 = 2.776, and |t| > t_α/2 implies statistically that the means reported by the two methods are significantly different (highlighted in bold). Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Sliding Window	Proposed	Mean Diff.	Std. Dev. Diff.	t test statistic
PA	2.32 ±0.44 s	1.88 ±0.34 s	−0.43557 s	0.26157 s	−3.7236
LL	1.60 ±0.44 s	1.43 ±0.32 s	−0.16711 s	0.14475 s	−2.5816
RL	1.31 ±0.20 s	1.29 ±0.21 s	−0.015675 s	0.056764 s	−0.6175
PV	1.94 ±0.27 s	2.01 ±0.25 s	0.070813 s	0.038287 s	4.1357
DA	2.07 ±0.32 s	2.45 ±0.42 s	0.37691 s	0.26447 s	3.1867

Table 6.

Peak signal-intensity (C₀ + pre-contrast value) plus or minus one standard deviation for the experiment in arbitrary units. For α = 0.05, t_α/2 = 2.776, and |t| > t_α/2 implies statistically that the means reported by the two methods are significantly different (highlighted in bold). Key: PA - Pulmonary Artery, LL - Left Lung, RL - Right Lung, PV - Pulmonary Vein, DA - Descending Aorta

Region	Sliding Window	Proposed	Mean Diff.	Std. Dev. Diff.	t test statistic
PA	57.67 ±12.27 s	59.37 ±12.08 s	1.6998 s	0.63395 s	5.9955
LL	33.29 ±10.88 s	33.68 ±11.34 s	0.39262 s	0.70342 s	1.2481
RL	35.50 ±6.99 s	35.94 ±7.30 s	0.43356 s	0.5662 s	1.7122
PV	75.18 ±12.73 s	74.13 ±12.77 s	−1.0464 s	0.8097 s	−2.8898
DA	78.03 ±20.53 s	76.73 ±21.45 s	−1.2922 s	2.8812 s	−1.0029

DISCUSSION

Temporal Resolution

The temporal resolution of radial k-space trajectories is difficult to define, because the center of k-space is acquired more often than the outer portion. In this study, the center of k-space is acquired every 4 ms, but the outer part of k-space is acquired every 720 ms. For this reason, the sliding window has a width of 720 ms, so the finest details in the dynamic images have this temporal resolution. In comparison, the IRIS method’s rotating sampling pattern and keyhole operation enables a sliding window width of 400 ms which is a factor of 1.8 better than the multi-injection sliding window method demonstrated here. While the keyhole operation in IRIS improves the SNR and temporal resolution, it does mean that the dynamics come only from the central 1/4^th of the k-space since the outer portion is replaced by its time average. In contrast, the proposed method resolves all points in the k-space to a resolution of 32 ms which is 22.5 times better than sliding window. In the proposed method, the temporal resolution is determined by the training data, while the SNR is a function of how many times, P, each k-space location is acquired during the experiment. Higher P improves the SNR of the model fitting, but increasing P decreases the coverage of the k-space by the imaging data. For phase encoding, this means reduced spatial resolution, while for radial sampling the result is an increase in the level of undersampling artifacts. The proposed method has traded a small amount of SNR for a large increase in the temporal resolution without requiring a large increase in the number of injections. In contrast, sliding window would require 90 injections and IRIS 50 injections to achieve similar temporal resolution. However, these large number of injections cannot be used in practice due to the build up of the contrast agent in the blood (8).

The results show that the proposed method significantly improves the temporal resolution of the signal-intensity curves which leads to more accurate curves and sometimes results in more accurate perfusion parameters. The nature of the improvement in the signal-intensity curve’s accuracy for the proposed method is subject dependent since it depends on the characteristics of the true signal-intensity curves. In the simulation, the improvement in the time of peak contrast enhancement and MTT is relatively small, but there is a significant improvement in the peak contrast intensity value. In the experimental study, several cases of parameter measurements showed different values between the sliding window and proposed methods (in a statistically significant sense). The simulation results imply that these differences correspond to improvements in the parameter estimates.

Practical Considerations

Pulmonary perfusion imaging using the proposed method has two inherent limitations. First, all methods based on the multiple-injection approach assume reproducible data acquisition conditions from one injection to another. Experimental data reveal that the overall intensity of the blood increases slightly with each injection due to build up of the contrast agent, and the cardiac pulsation artifact differs because of the heart-rate variability. But, the magnitudes of these inconsistencies are relatively small, and they do not appear to significantly degrade the quality of the reconstructions. Second, slice selection is a limiting factor on the signal-intensity curve analysis. The slice must be carefully placed to avoid seeing any cardiac motion, and as a result, the roots of the pulmonary artery and vein cannot be imaged. This slice placement makes it difficult to distinguish the time of peak contrast enhancement between the pulmonary artery and the lungs. Also, the slice thickness is large enough that multiple tissues and blood vessels are overlapped in the images. The overlapped anatomy causes a superposition of signal-intensity curves in the data and complicates the selection of the regions of interest.

A key requirement of the proposed method is that the number of data frames must equal or exceed the PSF model order (unless additional constraints are used); otherwise, Eq. [6] is underdetermined. The parameters of the experiment must be chosen carefully to ensure that adequate data are collected based on the empirically determined model order so that P > L. The model order, L, can be chosen in a variety of ways including comparing the noise variance to the singular values, considering the percent of the training data’s energy represented, and sweeping L to examine the resulting spatial coefficients. Choosing L too low will result in blurry, blocky artifacts along the time dimension similar to artifacts observed in SVD image compression schemes, while too high of an L leads to noisy reconstructions. Also, even when Eq. [6] is overdetermined, it can be ill-conditioned. For example, the worst case condition number observed in this study was approximately 20 while the median was approximately 5. Ill-conditioning occurs when the rows of Φ_q are nearly linear combinations of each other as can happen when the samples are taken too densely in time or when the samples are spaced close to the period of a strong sinusoidal component in the data. Severe ill-conditioning will cause some coefficients to have unrealistically large values resulting in image artifacts. However, this issue can be largely avoided by spacing the samples widely over time and then solving Eq. [6] in a regularized least-squares sense as was done in this study.

CONCLUSIONS

A new method for pulmonary perfusion imaging in rats has been presented in this paper. This method adapts the multiple-injection, radial k-space data acquisition scheme from IRIS so that a PSF model of the (k, t)-space can be used to perform dynamic imaging. Specifically, the method covers the (k, t)-space with one high temporal resolution training data set and a second extended k-space data set called imaging data. The sparse (k, t)-space samples are adequate to determine the parameters of the model, which enables reconstruction of the dynamic image sequence in high spatiotemporal resolution. Simulation and experimental results have shown that the proposed method improves the temporal resolution of the signal-intensity curves over the multiple-injection sliding window method. The increased temporal resolution of the proposed method reduces the negative effects of temporal averaging, and it produces estimates of perfusion parameters that are at least consistent with and sometimes improved upon the multi-injection sliding window method. The proposed method may find use in the study of respiratory diseases via pulmonary perfusion imaging, and the general concept of using the PSF model for dynamic imaging may be even more advantageous in other imaging scenarios where the spatiotemporal resolution trade-off is more extreme.