Abstract
An on-line calculator was developed (http://www.bncdnet.ku.edu/cml/info_ccc.vi) to compute phonotactic probability, the likelihood of occurrence of a sound sequence, and neighborhood density, the number of phonologically similar words, based on child corpora of American English (Kolson, 1960; Moe, Hopkins, & Rush, 1982) and compared to an adult calculator. Phonotactic probability and neighborhood density were computed for a set of 380 nouns (Fenson et al., 1993) using both the child and adult corpora. Child and adult raw values were significantly correlated. However, significant differences were detected. Specifically, child phonotactic probability was higher than adult phonotactic probability, especially for high probability words; and child neighborhood density was lower than adult neighborhood density, especially for high density words. These differences were reduced or eliminated when relative measures (i.e., z scores) were used. Suggestions are offered regarding which values to use in future research.
Keywords: vocabulary, neighborhood density, phonotactic probability, developmental research
Many recent studies of spoken language processing by children have considered the role of phonotactic probability, the likelihood of occurrence of a sound sequence, and neighborhood density, the number of phonologically similar words, in word recognition (Garlock, Walley, & Metsala, 2001; Mainela-Arnold, Evans, & Coady, 2008; Metsala, 1997), word production (Edwards, Beckman, & Munson, 2004; Munson, Swenson, & Manthei, 2005; Newman & German, 2005; Zamuner, Gerken, & Hammond, 2004), memory (Gathercole, Frankish, Pickering, & Peaker, 1999; Thomson, Richardson, & Goswami, 2005), and learning (Alt & Plante, 2006; Storkel, 2001, 2003, 2004a, 2009; Storkel, Armbruster, & Hogan, 2006; Storkel & Maekawa, 2005; Swingley & Aslin, 2007). A number of these studies have calculated phonotactic probability and neighborhood density using readily available American English adult corpora and on-line calculators (Balota et al., 2007; Davis, 2005; Vitevitch & Luce, 2004) because comparable child calculators do not exist. However, the validity of the values generated from adult on-line calculators for child research warrants investigation. Moreover, an understanding of the relationship between values generated from child sources compared to those from adult sources is critical for developmental research, which seeks to compare phonotactic probability and neighborhood density effects across different ages as the lexicon grows.
What evidence is there that child phonotactic probability and neighborhood density may differ from adult phonotactic probability and neighborhood density? To our knowledge, no studies have investigated how phonotactic probability may change with development. However, numerous studies have considered how neighborhood density may change from childhood to adulthood as the lexicon grows (Charles-Luce & Luce, 1990, 1995; Coady & Aslin, 2003; Dollaghan, 1994). Thus, we begin by examining what is known about neighborhood density changes and then apply the observed patterns to phonotactic probability. Across studies examining lexical growth, there is clear evidence that the number of neighbors increases from childhood to adulthood, meaning that the child density for a given word will tend to be lower than the adult density for the same word (Charles-Luce & Luce, 1990, 1995; Coady & Aslin, 2003; Dollaghan, 1994). However, it is unknown whether these density differences are constant or variable across words or neighborhoods.
One possibility is that child density differs from adult density by a relatively constant value across neighborhoods. In this case, the difference in density for stimuli identified as sparse versus dense for one age group (e.g., children) will be approximately the same as for an older age group (e.g., adults). Consider the following hypothetical example. The word “mouth,” with only 5 child neighbors, is selected as a sparse word for children and the word “tooth,” with 10 child neighbors, is selected as a dense word for children. The difference between the sparse and dense condition is 5 neighbors for children. If growth in the lexicon is equally distributed across neighborhoods, then two new neighbors may be added to each neighborhood, yielding 7 neighbors for adults for “mouth” and 12 neighbors for adults for “tooth.” Thus, although the child density for each word (i.e., 5 and 10) is smaller than the adult density for each word (i.e., 7 and 12), the difference between the sparse and dense conditions is the same for both the child and the adult (i.e., sparse differs from dense by 5 neighbors).
In contrast, the difference between child and adult density may not be the same across neighborhoods. In fact, there are good reasons to assume that this is the case. In particular, children and adults appear to learn dense words more readily than sparse words (Storkel, 2004a, 2009; Storkel et al., 2006), suggesting that more words may be added to dense neighborhoods than to sparse neighborhoods. To illustrate by continuing the previous hypothetical example, two new neighbors may be added to the neighborhood of “mouth,” yielding an adult density of 7, whereas four new neighbors may be added to the neighborhood of “tooth,” yielding an adult density of 14. Under this scenario, the difference between sparse and dense stimuli is not the same for children (i.e., sparse differs from dense by 5 neighbors) versus adults (i.e., sparse differs from dense by 7 neighbors). While the selected stimuli are sparse and dense for both age groups, it is unclear whether they are equally sparse and dense for each age group. This suggests the need to consider a measure of relative density when selecting stimuli for developmental research (cf. Coady & Aslin, 2003).
One relative measure of neighborhood density that may hold promise for addressing this issue is z scores. Z scores express the distance from a reference point (i.e., the mean) in standard deviation units (i.e., (obtained value – M)/SD). Z scores are commonly used in research to convert scores on different measurement scales to a common scale. In terms of the application to neighborhood density, z scores can quantify how extreme the density of a given word is relative to other words in the child or adult lexicon and express this in units that are comparable across lexicons of different sizes (i.e., standard deviation units). Thus, z scores provide a way of measuring whether a given word is equally sparse or dense for each age group, using a common measurement scale. Storkel (2004b) described procedures for creating z scores for adult phonotactic probability and neighborhood density. Briefly, phonotactic probability and neighborhood density means and standard deviations were computed for all the words of a given length in an adult corpus used for calculating phonotactic probability and neighborhood density, and these values were used to compute z scores for any given word. Thus, the z score for “mouth” and “tooth” in our example might be -1.32 and -0.50, respectively. If we had a comparable reference point for children, we might find a child z score of -1.24 for “mouth” and of -0.55 for “tooth.” In this scenario, the child z scores (i.e., -1.24 and -0.55) are relatively similar to the adult z scores (i.e., -1.32 and -0.50) even though the raw values appeared more discrepant. Therefore, in this example, we might conclude that the words are equally sparse (or dense) for children and adults. Taken together, z scores hold promise for determining whether stimuli are equally sparse or dense for different age groups with different sized lexicons. However, it is unknown whether neighborhood density z scores would show the pattern in the hypothetical example, or whether discrepancies would be identified.
While changes in phonotactic probability from childhood to adulthood have received less attention, the previously described scenarios for neighborhood density are relevant. As with neighborhood density, there is evidence that phonotactic probability influences word learning. In particular, when phonotactic probability is differentiated from neighborhood density, children and adults tend to learn rare sound sequences more readily than common sound sequences (Storkel, 2009; Storkel et al., 2006). Acquisition of rare sound sequences may lower phonotactic probability values for an adult when compared to a child and this lowering could be equivalently or asymmetrically distributed across rare and common sound sequences. It is also possible that differences in raw values could be eliminated when relative measures of phonotactic probability, such as z scores, are used.
The goal of this research was to develop an on-line phonotactic probability and neighborhood density child calculator and compare phonotactic probability and neighborhood density values based on this child calculator to those based on an adult calculator. The words used for comparing child and adult phonotactic probability and neighborhood density were the 380 nouns on the MacArthur-Bates Communicative Development Inventory: Words and Sentences (Fenson et al., 1993) because these words are likely known by both children and adults. Similarity between child and adult phonotactic probability and neighborhood density was examined via correlation to determine whether the relative ranking of the values was similar across children and adults. Child and adult phonotactic probability and neighborhood density also were compared via a t test to determine whether child values were significantly lower or higher than adult values. Based on past work, child phonotactic probability was predicted to be significantly higher than adult phonotactic probability, (Storkel, 2009; Storkel et al., 2006) and child neighborhood density was predicted to be significantly lower than adult neighborhood density (Charles-Luce & Luce, 1990, 1995; Coady & Aslin, 2003; Dollaghan, 1994). In the case of a significant t test, difference scores (i.e., adult value – child value) were computed for each significant variable and correlated with the child value for the same variable to determine whether differences were equivalently distributed across the lexicon (i.e., no correlation between difference scores and child value) or not (i.e., significant correlation between difference scores and child value). Based on word learning research, significant correlations between difference scores and child phonotactic probability (Storkel, 2009; Storkel et al., 2006) and child density (Storkel, 2004a, 2009; Storkel et al., 2006) were expected. A similar set of analyses was performed for relative measures (i.e., z scores) of child and adult phonotactic probability and neighborhood density. Predictions were not made for this set of analyses because few studies have considered relative measures of phonotactic probability or neighborhood density (but see Coady & Aslin, 2003) and none have used z scores.
Method
Child Corpus
Words and frequency of occurrence were taken from two spoken language corpora: (1) Kolson (1960), based on words produced by Kindergarten children at home, school, and in an elicited picture task (n = 3,728 different words), and (2) Moe, Hopkins, and Rush (1982), based on words produced by first grade children during an examiner led interview (n = 6,412 different words). Hard copy data from the original publications were scanned into a computer and converted to text. Scanned data were checked for accuracy by comparing the electronic data to the hard copy data. The two databases were then combined. Words appearing in both databases were combined into one entry by adding the frequency from each database. The remaining procedures were undertaken so that the child corpus would better match the existing adult corpus, which is based on a dictionary. First, the log base 10 of the combined raw frequency counts was calculated. A constant of 1.0 was added to the log value to avoid values of 0, which occur when the raw frequency is 1. Second, a computer readable phonemic transcription (i.e., pronunciation) of each word was obtained from the existing adult corpus. If a word was not available in the adult corpus, a dictionary was consulted (Longman dictionary of American English, 1993). Dictionary transcriptions were altered to follow transcription conventions in the adult corpus, which tended to make greater use of syllabic sonorant consonants. In the event that a word was not found in the dictionary, a native speaker of English provided a transcription for the word following the transcription conventions in the adult corpus. This occurred primarily for proper names (e.g., Allison, Frankenstein, Duluth). Finally, similar forms of words were eliminated for two types of words, words that were grammatically related (i.e., inflected vs. uninflected forms) and words that are pronounced the same but differ in meaning and spelling (i.e., homophones). These procedures are in-line with current theories of the lexicon which assume that only one form of a word is stored and also serve to make the child corpus more comparable to the available adult corpus (described below). More specifically, all inflected forms of a word (e.g., running) were eliminated from the corpus leaving only the uninflected form (e.g., run). This included consideration of both grammatical and ungrammatical inflected forms (e.g., deers). The only exception to this procedure was that inflected forms were retained in the corpus if the uninflected form was absent (e.g., “aces” was retained because “ace” was absent). Likewise, homophonous word forms (e.g., by, bye, buy) were collapsed into one form. These procedures yielded a corpus of 4,832 different words (i.e., types) and 1,028,417 total words (i.e., tokens).
Adult Corpus
The adult corpus for comparison was the Hoosier Mental Lexicon (Nusbaum, Pisoni, & Davis, 1984). This corpus consists of 19,290 different words (i.e., types) from a dictionary (Webster's Seventh Collegiate Dictionary, 1967). For the current study, only the computer readable phonemic transcription and written word frequency (Kucera & Francis, 1967) were used. In terms of overlap between the two corpora, 58% of the words in the child corpus appeared in the adult corpus. In addition, words in the child corpus (M = 4.87 sounds, SD = 1.77 sounds, range = 1-14 sounds) were significantly shorter in length than the words in the adult corpus (M = 6.35 sounds, SD = 2.31 sounds, range = 1-15 sounds), t (24120) = -41.55, p < 0.001. Words in the child corpus (M = 2.04, SD = 0.87, range 1.00 - 5.73) also were significantly higher in log frequency than the words in the adult corpus (M = 1.49, SD = 0.69, range 1.00 - 5.84), t (24120) = 47.71, p < 0.001.
On-line Calculator
An on-line interface was created to calculate phonotactic probability and neighborhood density using either the child or adult corpora. Although on-line calculators for adult corpora already exist, the adult corpus was included in this calculator so that the same interface for computing phonotactic probability and neighborhood density could be applied to each corpus. That is, any programming errors would affect both the child and adult values. The calculator is available at http://www.bncdnet.ku.edu/cml/info_ccc.vi. The prototype software for the calculator was built in LabVIEW as a standalone application with a graphical interface and is compatible with Linux, Mac, and Windows operating systems. The web version uses this same application with the LabVIEW Internet Toolkit, CGI, and an Apache 2 HTTP server on a Linux system. The web interface has been tested with versions of Mozilla Firefox and Microsoft Internet Explorer browsers and requires no additional browser plug-ins.
To use the calculator, a phonemic transcription of a target word (or words) in a computer readable format is entered in a textbox with one word per line, the child or adult corpus is selected, and output variables are selected (described below). Additional detailed instructions and an example item are provided on the calculator website.
Phonotactic probability algorithm
Two measures of phonotactic probability were computed for this analysis: positional segment average and biphone average (Storkel, 2004b; Vitevitch & Luce, 2004). In addition to these two summary variables, the calculator will return the component values that lead to these summary variables, as detailed subsequently. The calculation for positional segment average begins by computing the positional segment frequency, referred to as Pos Seg Freq in the calculator interface. The positional segment frequency is computed for each sound in the target word by iterating over every entry in the corpus that is long enough to have any sound in the corresponding position (counted from the left edge of the word without respect to syllable structure) and checking for matches against each sound in the target word. The log frequency of all the words in the corpus that contain the given sound in a given word position (identified as S1, S2, etc.) is summed and then divided by the sum of the log frequency of all the words in the corpus that contain any sound in the given word position. Thus, the number of positional segment frequencies returned will correspond to the number of sounds in the target word. The positional segment sum (i.e., Pos Sum in the calculator interface) is computed by adding the positional segment frequency for each sound in the target word. The positional segment average (i.e., Pos Ave in the calculator interface) is computed by dividing the positional segment sum by the number of sounds in the word.
The biphone average is computed in a similar manner except that pairs of adjacent sounds are used in the calculations, rather than individual sounds. The calculation for biphone average begins by computing biphone frequency (i.e., Biphone Freq in the calculator interface). The biphone frequency is computed for each pair of sounds in the target word by summing the log frequency of all the words in the corpus that contain the given pair of sounds in a given word position (identified as B1, B2, etc.) and then dividing by the sum of the log frequency of all the words in the corpus that contain any sound in the given word position. Thus, the number of biphone frequencies returned will correspond to the number of sound pairs in the target word. The biphone sum (i.e., Biphone Sum in the calculator interface) is computed by adding the biphone frequency for each sound pair in the target word. The biphone average (i.e., Biphone Ave in the calculator interface) is computed by dividing the biphone sum by the number of sound pairs in the word (which will be the number of sounds minus 1).
Neighborhood density algorithm
Neighborhood density, referred to as Num of Nbors in the calculator interface, is calculated by counting all the words in the corpus that differ from the target word by a one sound substitution, addition, or deletion in any word position (Balota et al., 2007; Storkel, 2004b). To find neighbors, the calculator creates a regular expression and then finds every matching entry in the corpus. For example, to find an addition in the second position for /sɪŋ/, which would be entered as sIG in the calculator input box, the regular expression s.IG is formed with the wild card character (.) in the second position. The wild card character indicates that only one sound may be inserted in the second position so /stɪŋ/ would be identified as a match but /strɪŋ/ would not be because two sounds are inserted in the second position. This process is iterative such that multiple regular expressions are created by the calculator program to search for all possible substitutions, deletions, and additions in any word position. The calculator will show the neighbors by checking the “show neighbors” box. The calculator also provides other details of neighborhood structure (see details at the website).
Phonotactic probability and neighborhood density characteristics of the child and adult corpora are summarized in Appendix A.
Words for Analysis
The words used for comparing child and adult phonotactic probability and neighborhood density were the 380 nouns on the MacArthur-Bates Communicative Development Inventory: Words and Sentences (Fenson et al., 1993) because these words are likely known by both children and adults and have been used in past word learning research (Storkel, 2004a, 2009). In addition, the words in this set vary in the sounds targeted (i.e., all English sounds present), syllable structure (e.g., CV, CCV, CCCV, VC, VCC, CVC, CCVC, CCCVC, CVCC), and word length (i.e., M = 4.42 sounds, SD = 1.56 sounds, range = 1 – 10 sounds), suggesting that the set represents a wide range of word structures learned by young children.
For each of the 380 nouns, positional segment average, biphone average, and neighborhood density were computed using the on-line calculator and the child corpus. In addition to these raw values, z scores were computed for each word following the procedures of Storkel (2004b, (obtained value - mean)/standard deviation) and using the child means and standard deviations for the appropriate word length (see Appendix A). The same raw values also were computed for each word using the on-line calculator and the adult corpus, and then z scores were calculated using the adult means and standard deviations for the appropriate word length (see Appendix A).
A parallel analysis was completed for a set of 310 nonwords, with results shown in Appendix B. Generally, the nonword analysis produced similar results to the real word analysis.
Results and Discussion
Raw values
The first issue to be addressed by this study was the relationship between child and adult phonotactic probability and neighborhood density raw values. Results showed that child and adult raw values were significantly positively correlated for positional segment averages, r (380) = 0.90, p < 0.001, biphone average, r (378) = 0.89, p < 0.001, and neighborhood density, r (380) = 0.94, p < 0.001. As shown in Figure 1, child and adult values for each variable tended to decrease or increase in tandem.
Figure 1.
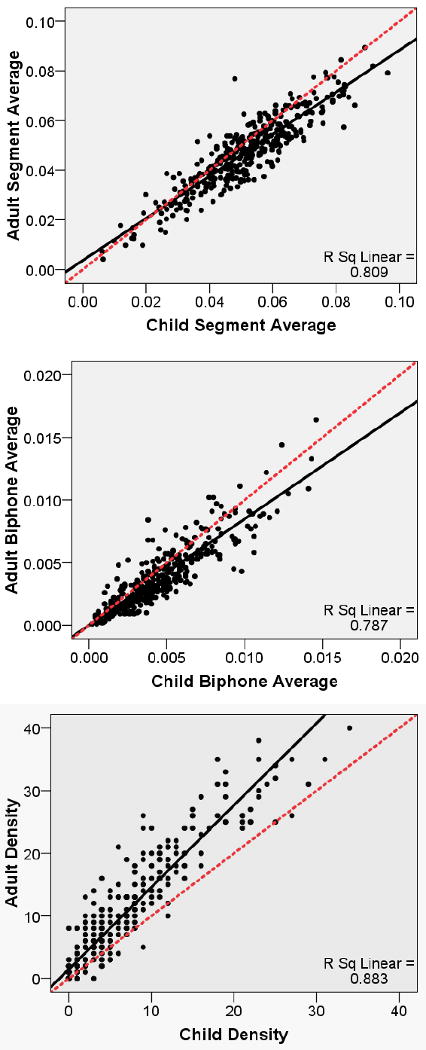
Scatter plots of child versus adult positional segment average (top), biphone average (middle), and neighborhood density (bottom). Solid line indicates the linear regression fit line. Dashed line is a reference line indicating a perfect correlation.
Turning to t test comparisons, child positional segment averages (M = 0.051, SD = 0.015, range = 0.006 - 0.096) were significantly higher than adult positional segment averages (M = 0.047, SD = 0.014, range = 0.004-0.089), t (379) = 12.47, p < 0.001, ηp2 = 0.29. Likewise, child biphone averages (M = 0.0044, SD = 0.0027, range = 0.0002 - 0.0146) were significantly higher than adult biphone averages (M = 0.0038, SD = 0.0026, range = 0.0001 - 0.0164), t (377) = 10.56, p < 0.001, ηp2 = 0.23. These findings are consistent with a priori predictions that ease of learning of rare sound sequences, as has been reported in previous research (Storkel, 2009; Storkel et al., 2006), would lead to a lowering of phonotactic probability from childhood to adulthood. Another factor that accounts for the difference between child and adult phonotactic probability is that the words in the child corpus were significantly higher in frequency than the words in the adult corpus. Because word frequency is used in phonotactic probability computations, the addition of low frequency words to the lexicon also would lead to a lowering of phonotactic probability from childhood to adulthood.
The opposite pattern was observed for neighborhood density. Here, child neighborhood density (M = 5.5, SD = 6.6, range 0 - 34) was significantly lower than adult neighborhood density (M = 8.7, SD = 9.2, range 0 - 40), t (379) = -16.59, p < 0.001, ηp2 = 0.42. This finding is consistent with past studies showing that child neighborhood densities are significantly lower than adult neighborhood densities due to differences in the overall size of the lexicon of children versus adults (Charles-Luce & Luce, 1990, 1995; Coady & Aslin, 2003; Dollaghan, 1994).
Difference Scores
The second issue to be addressed was whether the observed significant differences between child and adult phonotactic probability as well as between child and adult neighborhood density were equivalently distributed across the lexicon. To address this issue, the relationship between these child and adult differences and each child variable was explored. Difference scores were computed for each variable by subtracting the child value from the adult value. In this way, negative difference scores indicate that the child value is larger than the adult, and positive difference scores indicate that the child value is smaller than the adult.
For phonotactic probability, difference scores were significantly negatively correlated with child positional segment average, r (380) = -0.35, p < 0.001, and child biphone average, r (378) = -0.33, p < 0.001. As shown in Figure 2, difference scores decreased (i.e., become more negative) as child positional segment or biphone averages increased. That is, differences between child phonotactic probability and adult phonotactic probability were not equivalently distributed across the lexicon. Instead, differences between child and adult positional segment averages were smaller for lower probability sound sequences (i.e., those at or below the child mean; M difference = -0.0022, SD = 0.0064, range = -0.0016 – 0.0288) than for higher probability sound sequences (i.e., those above the child mean, M difference = -0.0062, SD = 0.0062, range = -0.0250 – 0.0069). Likewise, differences between child and adult biphone averages were smaller for lower probability sound sequences (M difference = -0.0004, SD = 0.0010, range = -0.0027 – 0.0046) than for higher probability sound sequences (M difference = -0.0010, SD = 0.0014, range = -0.0055 – 0.0027). This suggests that the learning of rare sound sequences (Storkel, 2009; Storkel et al., 2006) and low frequency words that occurred with development had a greater impact on higher probability sound sequences than lower probability sound sequences.
Figure 2.
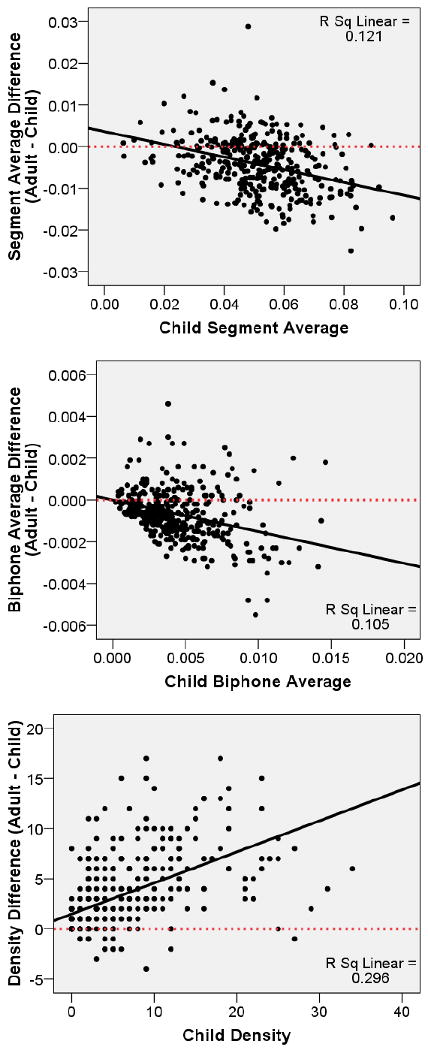
Scatter plots of difference scores (adult – child) versus child positional segment average (top), biphone average (middle), and neighborhood density (bottom). Solid line indicates the linear regression fit line. Dashed line is a reference line indicating a difference score of zero (i.e., adult = child). Points falling below the line (i.e., a negative difference score) indicate that the child value is higher than the adult value. Points falling above the line (i.e., a positive difference score) indicate that the child value is lower than the adult value.
For neighborhood density, difference scores were significantly positively correlated with child neighborhood density, r (380) = 0.54, p < 0.001. As shown in Figure 2, difference scores increased (i.e., became more positive) as neighborhood density increased. As with phonotactic probability, differences between child and adult neighborhood density were not equivalently distributed across the lexicon. Rather, differences between child and adult densities were smaller for sparser neighborhoods (i.e., those at or below the child mean, M = 1.37 neighbors, SD = 2.22, range = -3 – 11) than for denser neighborhoods (i.e., those above the child mean, M = 5.20 neighbors, SD = 4.07, range = -4 – 17). As predicted from word learning research (Storkel, 2004a, 2009; Storkel et al., 2006), more words were added to dense neighborhoods than to sparse neighborhoods as the lexicon grew, leading to larger discrepancies between child and adult densities for dense neighborhoods than for sparse neighborhoods.
Z scores
The third issue to be addressed was whether the patterns observed with raw values also would be observed for relative measures of phonotactic probability and neighborhood density (i.e., z scores). The same set of analyses performed for raw values was performed for the z score data. As with raw values, child and adult z scores were significantly positively correlated for positional segment average z scores, r = 0.88, p < 0.001, biphone average z scores, r = 0.87, p < 0.001, and neighborhood density z scores, r = 0.71, p < 0.001. As shown in Figure 3, child and adult z scores tended to increase or decrease in tandem.
Figure 3.
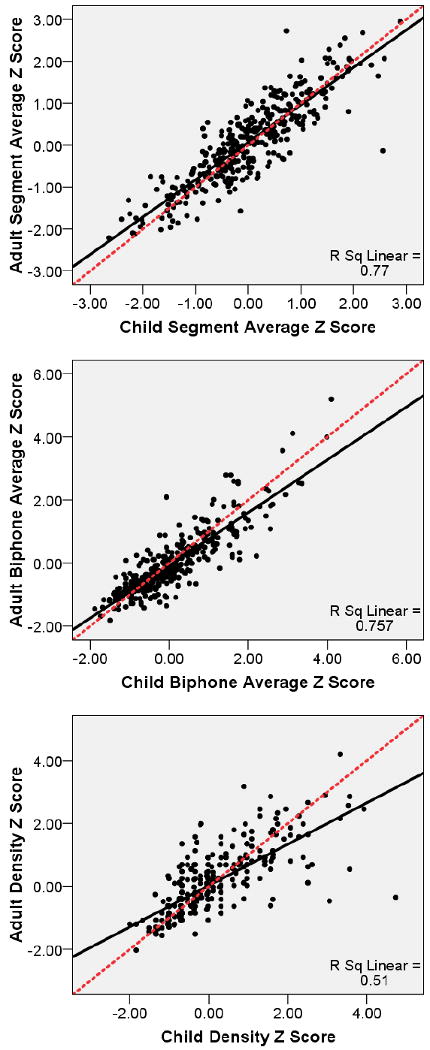
Scatter plots of child versus adult positional segment average z scores (top), biphone average z scores (middle), and neighborhood density z scores (bottom). Solid line indicates the linear regression fit line. Dashed line is a reference line indicating a perfect correlation.
Turning to t test analyses, child positional segment average z scores (M = 0.02, SD = 0.95, range -2.64 – 2.89) were significantly lower than adult positional segment average z scores (M = 0.09, SD = 0.97, range -2.21 – 2.95), t (379) = -2.75, p < 0.01, ηp2 = 0.02 (refer to Figure 3). In contrast, child biphone average z scores (M = 0.03, SD = 1.03, range -1.89 – 4.11) were significantly higher than adult biphone average z scores (M = -0.05, SD = 0.99, range -1.82 – 5.20), t (377) = 2.98, p < 0.01, ηp2 = 0.02 (refer to Figure 3). Although these differences are statistically significant, note that the effect sizes are small and that the difference scores were relatively small for both positional segment averages (M = 0.07, SD = 0.48, range -2.69 – 2.00) and biphone averages (M = -0.08, SD = 0.52, range -1.99 to 2.16). Thus, the distribution of child and adult z scores was largely overlapping.
Moreover, analysis of z score differences (i.e., adult – child) showed a pattern that resembled regression to the mean. Z score differences (i.e. adult z score – child z score) were significantly negatively correlated with child positional segment average z scores, r (380) = -0.22, p < 0.001, and with child biphone average z scores, r (378) = -0.33, p < 0.001. Figure 4 shows difference scores relative to child z scores. When child z scores were negative (i.e., low probability), adult z scores tended to be less negative for positional segment average (M difference = 0.14, SD = 0.43, range -1.42 to 1.31) and for biphone average (M difference = 0.06, SD = 0.43, range -1.29 to 2.16). In contrast, when child z scores were positive (i.e., high probability), adult z scores tended to be less positive for positional segment average (M difference = -0.01, SD = 0.51, range -2.69 to 4.69) and for biphone average (M difference = -0.27, SD = 0.56, range -1.99 to 1.35). In both cases, the adult z score tended to be less extreme than the child z score, a pattern that is consistent with regression to the mean rather than developmental differences between children and adults. Note that the concept of regression to the mean is typically applied to multiple observations or measures on a single person, with the underlying hypothesis being that each observation reflects the person's true score plus some amount of error that will variably influence the obtained score on repeated administration. The effect of the variability is that extreme scores on the first administration will tend to become less extreme on repeated administration. Although the current case is a bit different (i.e., multiple measures on a single set of words), the logic is similar. That is, there is a true phonotactic probability score for each word but there is some amount of error associated with each corpus (or method) used to calculate phonotactic probability. The error across corpora will variably influence the obtained phonotactic probability for a given word such that extreme scores based on one corpus will tend to become less extreme in a second corpus.
Figure 4.
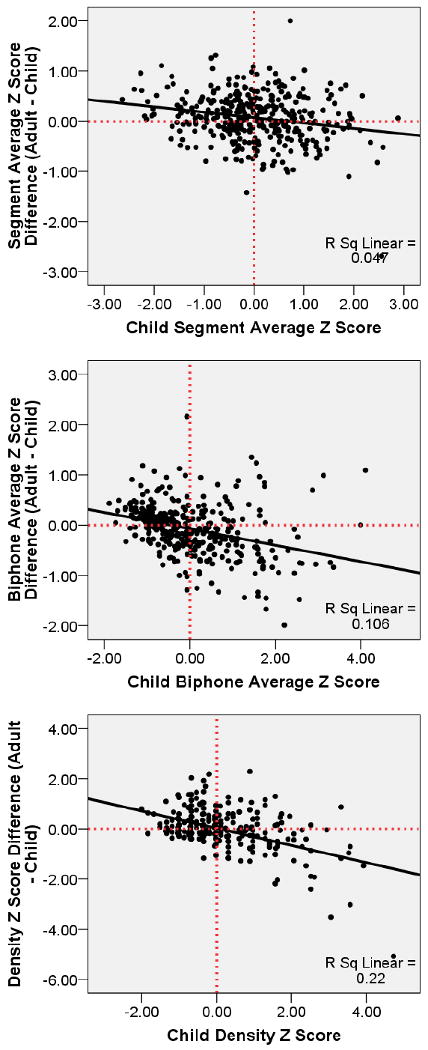
Scatter plots of z score difference (adult – child) relative to the child positional segment average z score (top), the child biphone average z score (middle), and the child neighborhood density z score (bottom). Solid line indicates the linear regression fit line. Horizontal dashed line is a reference line indicating a difference score of zero (i.e., adult = child). Points falling below the line (i.e., a negative difference score) indicate that the child value is higher than the adult value. Points falling above the line (i.e., a positive difference score) indicate that the child value is lower than the adult value. Vertical dashed line indicates a z-score of 0.00, differentiating low probability or density (values below 0.00) from high (values greater than 0.00).
Turning to neighborhood density z scores, child z scores (M = 0.04, SD = 1.04, range -2.00 to 4.73) did not differ significantly from adult z scores (M = 0.05, SD = 0.96, range -2.03 to 4.20), t (379) = -0.336, p > 0.70, ηp2 < 0.001. Likewise, z score differences (i.e., adult – child) were relatively small (M = 0.01, SD = 0.76, range -5.08 – 2.29). As shown in Figure 4, differences between child and adult neighborhood density z scores were consistent with a pattern of regression to the mean.
Summary & Conclusion
Child and adult phonotactic probability and neighborhood density were significantly correlated for both raw values and z scores. This suggests that the corpora used to compute phonotactic probability and neighborhood density may not be critical when only gross or extreme distinctions are made (e.g., “low” versus “high” probability or density). In contrast, t test analysis of raw values showed significant discrepancies between child and adult values. Specifically, child phonotactic probability was higher than adult phonotactic probability, whereas child neighborhood density was lower than adult neighborhood density. Moreover, differences between child and adult phonotactic probability and neighborhood density were not distributed equivalently across the lexicon. In particular, child and adult differences were larger for higher probability sound sequences and for denser neighborhoods. Thus, when more precise or fine-grained distinctions need to be made, it may be more critical to select corpora that are more representative of the words known by the study population. In addition, z scores may be useful in establishing whether the words are equivalently rare or common, sparse or dense given the hypothesized size of the lexicon of the study population. Z scores appeared to reduce differences between child and adult values for phonotactic probability and neighborhood density. Moreover, z scores would be useful in comparing phonotactic probability and neighborhood density across studies that use different corpora to determine whether stimuli are equivalently rare or common, sparse or dense across studies. Results from analysis of nonwords (see Appendix B) generally parallel these results from real words, bolstering these conclusions.
Acknowledgments
This research was supported by NIH Grants DC 08095, DC 00052, DC009135, DC 05803, and HD02528. Douglas S. Kieweg created the web interface and program for the on-line calculator. The following individuals contributed to development of the child corpus and/or data processing and analysis: Shinying Chu, Maki Sueto, and Ashlee Widler.
Appendix A: Phonotactic probability and neighborhood density by word length for child and adult corpora
| Word Length in Sounds (number of words per corpus) | Positional Segment Average | Biphone Average | Neighborhood Density | |||
|---|---|---|---|---|---|---|
| Child M |
Adult M |
Child M |
Adult M |
Child M |
Adult M |
|
| (SD) | (SD) | (SD) | (SD) | (SD) | (SD) | |
| 1 | 0.0082 | 0.0113 | N/A | N/A | 16.80 | 21.40 |
| (n = 5 child; 5 adult) | (0.0042) | (0.0118) | (7.56) | (8.62) | ||
| 2 | 0.0335 | 0.0305 | 0.0018 | 0.0015 | 17.29* | 22.89* |
| (n = 157 child; 194 adult) | (0.0201) | (0.0170) | (0.0014) | (0.0028) | (7.18) | (8.05) |
| 3 | 0.0512* | 0.0449* | 0.0040* | 0.0030* | 12.31* | 18.21* |
| (n = 958 child; 1608 adult) | (0.0175) | (0.0166) | (0.0026) | (0.0026) | (6.14) | (8.47) |
| 4 | 0.0545* | 0.0466* | 0.0049* | 0.0040* | 4.06* | 6.87* |
| (n = 1286 child; 2899 adult) | (0.0147) | (0.0135) | (0.0027) | (0.0027) | (3.04) | (4.53) |
| 5 | 0.0515* | 0.0462* | 0.0046* | 0.0042* | 0.91* | 1.78* |
| (n = 943 child; 3114 adult) | (0.0139) | (0.0121) | (0.0025) | (0.0025) | (1.23) | (1.96) |
| 6 | 0.0498* | 0.0474* | 0.0043 | 0.0046 | 0.22* | 0.53* |
| (n = 639 child; 3039 adult) | (0.0126) | (0.0118) | (0.0022) | (0.0025) | (0.50) | (0.86) |
| 7 | 0.0486 | 0.0483 | 0.0040* | 0.0049* | 0.09* | 0.25* |
| (n = 442 child; 2725 adult) | (0.0112) | (0.0111) | (0.0018) | (0.0023) | (0.30) | (0.54) |
| 8 | 0.0493 | 0.0504 | 0.0041* | 0.0057* | 0.05* | 0.16* |
| (n = 210 child; 2202 adult) | (0.0104) | (0.0108) | (0.0017) | (0.0026) | (0.24) | (0.43) |
| 9 | 0.0512 | 0.0521 | 0.0049* | 0.0069* | 0.04 | 0.15 |
| (n = 117 child; 1534 adult) | (0.0101) | (0.0104) | (0.0018) | (0.0036) | (0.20) | (0.43) |
| 10 | 0.0525 | 0.0570 | 0.0052* | 0.0093* | 0.09 | 0.12 |
| (n = 44 child; 1019 adult) | (0.0107) | (0.0114) | (0.0018) | (0.0059) | (0.29) | (0.34) |
| 11 | 0.0537 | 0.0564 | 0.0055* | 0.0082* | 0.09 | 0.06 |
| (n = 23 child; 526 adult) | (0.0145) | (0.0111) | (0.0021) | (0.0043) | (0.29) | (0.24) |
| 12 | 0.0708 | 0.0603 | 0.0101 | 0.0094 | 0.00 | 0.03 |
| (n = 4 child; 266 adult) | (0.0103) | (0.0118) | (0.0015) | (0.0054) | (0.00) | (0.17) |
| 13 | 0.0743 | 0.0563 | 0.0182* | 0.0077* | 0.00 | 0.00 |
| (n = 2 child; 106 adult) | (0.0330) | (0.0108) | (0.0066) | (0.0036) | (0.00) | (0.00) |
| 14 | 0.1066 | 0.0563 | 0.0324 | 0.0080 | 0.00 | 0.00 |
| (n = 2 child; 37 adult) | (0.0416) | 0.0113) | (0.0135) | (0.0034) | (0.00) | (0.00) |
| 15 | N/A | 0.0629 | N/A | 0.0099 | N/A | 0.00 |
| (n = 0 child; 16 adult) | (0.0114) | (0.0024) | (0.00) | |||
| All Words | 0.0511* | 0.0485* | 0.0044* | 0.0051* | 4.32* | 3.23* |
| (n = 4832 child; 19290 adult) | (0.0151) | (0.0129) | (0.0026) | (0.0034) | (6.16) | (6.39) |
Note. Although the values were re-computed for this study, adult values match those reported in Table 2 of H. L. Storkel, 2004b, Journal of Speech, Language, and Hearing Research, 47, p 1460.
Copyright 2004 by the American Speech-Language-Hearing Association. Reprinted with permission.
Child value differs significantly from adult, p < 0.001.
Appendix B: Analysis of a set of nonwords
Nonwords for Analysis
The nonwords used for comparing child and adult phonotactic probability were 310 nonwords developed in our lab for published, unpublished, and on-going research studies on word learning and word representations. Of these 310 nonwords, 298 were one syllable consonant-vowel-consonant (CVC) sequences and 12 were two syllable CVCVC sequences. Note that these stimuli do not represent a random sample of CVC nonwords because various constraints (e.g., consonants needed to be early acquired) were imposed during stimuli creation, depending on the goals of the study, and, in most cases, the stimuli were selected for extreme values of phonotactic probability and/or neighborhood density based on the adult corpus (i.e., low vs. high was an independent variable in the study).
Raw values
Results of this set of analyses parallel the findings reported for real words: child and adult values were significantly correlated (see Table 1); child phonotactic probability was significantly higher than adult; child neighborhood density was significantly lower than adult (see Table 2).
Table 1. Correlation between child and adult values.
| r | p | |
|---|---|---|
| Positional Segment Average | 0.92 | < 0.001 |
| Biphone Average | 0.85 | < 0.001 |
| Neighborhood Density | 0.90 | < 0.001 |
Table 2. T test between child and adult values.
| t | p | ηp2 | Child M |
Adult M |
|
|---|---|---|---|---|---|
| (SD) | (SD) | ||||
| Range | Range | ||||
| Positional Segment Average | 15.74 | < 0.001 | 0.45 | 0.047 | 0.042 |
| (0.012) | (0.012) | ||||
| 0.015 - 0.082 | 0.014 – 0.085 | ||||
| Biphone Average | 6.99 | < 0.001 | 0.14 | 0.0026 | 0.0022 |
| (0.0017) | (0.0018) | ||||
| 0.0000 - 0.0096 | 0.0001 – 0.0133 | ||||
| Neighborhood Density | -28.97 | < 0.001 | 0.73 | 9.6 | 15.33 |
| (5.3) | (7.4) | ||||
| 0 - 26 | 0 – 39 |
Difference scores
Results of this set of analyses parallel the findings reported for real words: child and adult differences were larger for higher probability sequences and for denser neighborhoods (see Table 3).
Table 3. Correlation of difference scores (adult – child) with each child variable.
| r | p | Low M |
High M |
|
|---|---|---|---|---|
| (SD) | (SD) | |||
| Range | Range | |||
| Positional Segment Average | -0.12 | 0.04 | -0.004 | -0.005 |
| (0.005) | (0.005) | |||
| -0.018 - 0.009 | -0.019 – 0.007 | |||
| Biphone Average | -0.13 | 0.03 | -0.0004 | -0.0004 |
| (0.0007) | (0.0018) | |||
| -0.0021 - 0.0042 | -0.0048 – 0.0040 | |||
| Neighborhood Density | 0.39 | <0.001 | 5.2 | 7.1 |
| (3.1) | (3.9) | |||
| -1 - 15 | -1 – 16 |
Z scores
Results of the correlation analysis parallel the findings reported for real words: child and adult z scores were significantly correlated (see Table 4). In contrast, results of the t test analysis differed from the findings reported for real words (see Table 5). Specifically, significant differences were obtained for all three variables with child z scores being significantly lower than adult z scores for each variable. However, similar to the analysis of real words, effect sizes were lower for z scores than for raw values and differences between child and adult values were relatively small for z scores. Also similar to the analysis of real words, when z score differences were significantly correlated with child z scores (see Table 6), the pattern was consistent with an interpretation of regression to the mean.
Table 4. Correlation between child and adult z scores.
| r | p | |
|---|---|---|
| Positional Segment Average | 0.92 | < 0.001 |
| Biphone Average | 0.86 | < 0.001 |
| Neighborhood Density | 0.88 | < 0.001 |
Table 5. T test between child and adult z scores.
| t | p | ηp2 | Child M |
Adult M |
|
|---|---|---|---|---|---|
| (SD) | (SD) | ||||
| Range | Range | ||||
| Positional Segment Average | -5.94 | < 0.001 | 0.10 | -0.26 | -0.16 |
| (0.71) | (0.78) | ||||
| -2.65 – 1.77 | -2.69 – 2.42 | ||||
| Biphone Average | -10.95 | < 0.001 | 0.28 | -0.55 | -0.32 |
| (0.65) | (0.71) | ||||
| -1.76 – 2.15 | -1.64 – 3.96 | ||||
| Neighborhood Density | -4.43 | < 0.001 | 0.06 | -0.39 | -0.29 |
| (0.80) | (0.80) | ||||
| -1.84 – 2.23 | -2.03 – 2.45 |
Table 6. Correlation of z score differences (adult – child) with each child variable.
| r | p | All M |
Low M |
High M |
|
|---|---|---|---|---|---|
| (SD) | (SD) | (SD) | |||
| Range | Range | Range | |||
| Positional Segment Average | 0.03 | 0.62 | 0.10 | 0.10 | 0.11 |
| (0.30) | (0.29) | (0.32) | |||
| -0.73 – 1.08 | -0.73 – 1.08 | -0.73 – 0.84 | |||
| Biphone Average | -0.11 | 0.05 | 0.23 | 0.23 | 0.22 |
| (0.37) | (0.28) | (0.71) | |||
| -1.46 – 2.00 | -0.42 – 2.00 | -1.46 – 1.92 | |||
| Neighborhood Density | -0.26 | <0.001 | 0.10 | 0.15 | -0.05 |
| (0.39) | (0.34) | (0.46) | |||
| -0.94 – 1.19 | -0.58 – 1.19 | -0.94 – 0.93 |
Contributor Information
Holly L. Storkel, Department of Speech-Language-Hearing: Sciences and Disorders, University of Kansas
Jill R. Hoover, Child Language Doctoral Program, University of Kansas
References
- Alt M, Plante E. Factors that influence lexical and semantic fast mapping of young children with specific language impairment. Journal of Speech, Language, and Hearing Research. 2006;49:941–954. doi: 10.1044/1092-4388(2006/068). [DOI] [PubMed] [Google Scholar]
- Balota DA, Yap MJ, Cortese MJ, Hutchison KA, Kessler B, Loftis B, et al. The English Lexicon Project. Behavior Research Methods. 2007;39:445–459. doi: 10.3758/bf03193014. [DOI] [PubMed] [Google Scholar]
- Charles-Luce J, Luce PA. Similarity neighbourhoods of words in young children's lexicons. Journal of Child Language. 1990;17:205–215. doi: 10.1017/s0305000900013180. [DOI] [PubMed] [Google Scholar]
- Charles-Luce J, Luce PA. An examination of similarity neighbourhoods in young children's receptive vocabularies. Journal of Child Language. 1995;22:727–735. doi: 10.1017/s0305000900010023. [DOI] [PubMed] [Google Scholar]
- Coady JA, Aslin RN. Phonological neighbourhoods in the developing lexicon. Journal of Child Language. 2003;30:441–470. [PMC free article] [PubMed] [Google Scholar]
- Davis CJ. N-Watch: A program for deriving neighborhood size and other psycholinguistic statistics. Behavior Research Methods. 2005;37:65–70. doi: 10.3758/bf03206399. [DOI] [PubMed] [Google Scholar]
- Dollaghan CA. Children's phonological neighbourhoods: Half empty or half full? Journal of Child Language. 1994;21:257–271. doi: 10.1017/s0305000900009260. [DOI] [PubMed] [Google Scholar]
- Edwards J, Beckman M, Munson B. The interaction between vocabulary size and phonotactic probability effects on children's production accuracy and fluency in nonword repetition. Journal of Speech, Language and Hearing Research. 2004;47:421–436. doi: 10.1044/1092-4388(2004/034). [DOI] [PubMed] [Google Scholar]
- Fenson L, Dale PS, Reznick JS, Thal D, Bates E, Hartung JP, et al. The MacArthur Communicative Development Inventories: User's guide and technical manual. San Diego: Singular Publishing Group; 1993. [Google Scholar]
- Garlock VM, Walley AC, Metsala JL. Age-of-acquisition, word frequency, and neighborhood density effects on spoken word recognition by children and adults. Journal of Memory and Language. 2001;45:468–492. [Google Scholar]
- Gathercole SE, Frankish CR, Pickering SJ, Peaker S. Phonotactic influences on short-term memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:84–95. doi: 10.1037//0278-7393.25.1.84. [DOI] [PubMed] [Google Scholar]
- Kolson CJ. The vocabulary of kindergarten children. University of Pittsburgh; Pittsburgh: 1960. [Google Scholar]
- Kucera H, Francis WN. Computational analysis of present-day American English. Providence, RI: Brown University; 1967. [Google Scholar]
- Longman dictionary of American English. White Plains, NY: Longman; 1993. [Google Scholar]
- Mainela-Arnold E, Evans JL, Coady JA. Lexical representations in children with SLI: Evidence from a frequency-manipulated gating task. Journal of Speech and Hearing Research. 2008;51:381–393. doi: 10.1044/1092-4388(2008/028). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metsala JL. An examination of word frequency and neighborhood density in the development of spoken-word recognition. Memory and Cognition. 1997;25:47–56. doi: 10.3758/bf03197284. [DOI] [PubMed] [Google Scholar]
- Moe AJ, Hopkins KJ, Rush RT. The vocabulary of first grade children. Springfield, IL: Thomas; 1982. [Google Scholar]
- Munson B, Swenson CL, Manthei SC. Lexical and phonological organization in children: Evidence from repetition tasks. Journal of Speech, Language and Hearing Research. 2005;48:108–124. doi: 10.1044/1092-4388(2005/009). [DOI] [PubMed] [Google Scholar]
- Newman RS, German DJ. Life span effects of lexical factors on oral naming. Language and Speech. 2005;48:123–156. doi: 10.1177/00238309050480020101. [DOI] [PubMed] [Google Scholar]
- Nusbaum HC, Pisoni DB, Davis CK. In Research on Spoken Language Processing Report No 10. Bloomington, IN: Speech Research Laboratory, Indiana University; 1984. Sizing up the Hoosier mental lexicon; pp. 357–376. [Google Scholar]
- Storkel HL. Learning new words: Phonotactic probability in language development. Journal of Speech, Language, and Hearing Research. 2001;44:1321–1337. doi: 10.1044/1092-4388(2001/103). [DOI] [PubMed] [Google Scholar]
- Storkel HL. Learning new words II: Phonotactic probability in verb learning. Journal of Speech, Language, and Hearing Research. 2003;46:1312–1323. doi: 10.1044/1092-4388(2003/102). [DOI] [PubMed] [Google Scholar]
- Storkel HL. Do children acquire dense neighborhoods? An investigation of similarity neighborhoods in lexical acquisition. Applied Psycholinguistics. 2004a;25:201–221. [Google Scholar]
- Storkel HL. Methods for minimizing the confounding effects of word length in the analysis of phonotactic probability and neighborhood density. Journal of Speech, Language, and Hearing Research. 2004b;47:1454–1468. doi: 10.1044/1092-4388(2004/108). [DOI] [PubMed] [Google Scholar]
- Storkel HL. Developmental differences in the effects of phonological, lexical and semantic variables on word learning by infants. J Child Lang. 2009;36:291–321. doi: 10.1017/S030500090800891X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storkel HL, Armbruster J, Hogan TP. Differentiating phonotactic probability and neighborhood density in adult word learning. Journal of Speech, Language, and Hearing Research. 2006;49:1175–1192. doi: 10.1044/1092-4388(2006/085). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storkel HL, Maekawa J. A comparison of homonym and novel word learning: The role of phonotactic probability and word frequency. Journal of Child Language. 2005;32:827–853. doi: 10.1017/s0305000905007099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swingley D, Aslin RN. Lexical competition in young children's word learning. Cognitive Psychology. 2007;54:99–132. doi: 10.1016/j.cogpsych.2006.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson JM, Richardson U, Goswami U. Phonological similarity neighborhoods and children's short-term memory: typical development and dyslexia. Memory & Cognition. 2005;33:1210–1219. doi: 10.3758/bf03193223. [DOI] [PubMed] [Google Scholar]
- Vitevitch MS, Luce P. A web-based interface to calculate phonotactic probability for words and nonwords in English. Behavior Research Methods, Instruments & Computers. 2004;36:481–487. doi: 10.3758/bf03195594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster's Seventh Collegiate Dictionary. Los Angeles: Library Reproduction Service; 1967. [Google Scholar]
- Zamuner TS, Gerken L, Hammond M. Phonotactic probabilities in young children's speech production. Journal of Child Language. 2004;31:515–536. doi: 10.1017/s0305000904006233. [DOI] [PubMed] [Google Scholar]


