A multi-phase method for estimating cohort effects in age-period contingency table data

Abstract

Purpose

Understanding the effects of age, period, and cohort on disease morbidity and mortality may help identify etiological factors and inform prevention programs. We illustrate a three-phase method that conceptualizes the cohort effect as a partial interaction between age and period. As an example of application, we analyze homicide mortality data for US males, 1935–2004.

Method

The three phased method begins with graphical inspection; second, a median polish is used to remove the log-additive components of age and period effects; third, a linear regression of residuals from the median polish is modeled to quantify the relative magnitude of the cohort effect.

Results

Individuals born after 1960 have a significantly increased rate of homicide relative to those born between 1920–1924. After removal of the log-additive effects of age and period, the estimated homicide rate for men born between 1980–1984 is more than twice the rate for men born 1920–1924 (rate ratio 2.11, 95% confidence interval 1.98–2.25).

Conclusion

The three-phase method presented here offers several advantages, the foremost being an alternative conceptualization of the cohort effect not as an independent component of age and period effects, but as a partial interaction. Further, the strengths of the method include computational simplicity, interpretability, and reliability.

As the life-course perspective increases in utility to understand disease etiology (1), analysis of historical data over time has become imperative for understanding the role of biological and environmental factors in disease distribution. Temporal variation in rates of disease may reflect changes in the nature and magnitude of etiologically important exposures. An attractive method to identify factors influencing risk over time is age-period-cohort analysis, but methodological complexities and interpretational difficulties have reduced its utility for many life-course researchers.

Evaluation of birth cohort effects began as a life-table method with William Farr in 1885 (2), and many conceptual advances in the social sciences have been generated through the idea that a birth cohort is an index of barriers and resources that affect health and development through the lifecourse (3, 4, 5). Graphical approaches were developed throughout the first half of the 20^th century (6, 7, 8), but statistical approaches to effect quantification remained desirable. While some study designs (e.g., cohort sequential) allow for more robust inference regarding the presence of cohort effects (5, 9), conventional statistical models such as generalized linear regressions cannot provide valid estimates of age, period, and cohort effects because of co-linearity among the three variables (10). A variety of methodological approaches have been developed attempting to quantify meaningful effects given this limitation (11, 12, 13, 14, 15, 16, 17, 18), but methods are consistently criticized for unstable assumptions and limited interpretational value (19, 20, 21, 22).

These methodological challenges have limited the application of cohort analysis to increasingly available and rich data sources. We illustrate a computationally simple three-phase method that utilizes and extends the non-parametric median polish method conceptualizing the cohort effect as a partial multiplicative interaction between age and period. This conceptualization originates with Greenberg (23) and deviates from many existing methods in that the cohort effect is not isolated from the age and period effect; instead, the cohort effect is defined as a partial multiplicative interaction quantified in the non-linear component of age and period effects. This conceptualization is consistent with methods assessing linear deviations or curvatures of an unidentified linear slope (13, 15, 24, 25), in that an interaction is a second order effect of age and period.

The median polish was first developed by Tukey (26) and used for age-period-cohort analysis by Selvin (27) to graphically display cohort effects; it is an elegant yet underutilized tool in cohort analysis. The goal of the present paper is to: 1) describe the method proposed by Tukey and Selvin; and 2) extend it to parametrically quantify the magnitude of age-period interaction by calculating the rate ratio of cohort effects across time compared to a reference cohort. We describe and exemplify the conceptual and statistical details of the three-phase method using the homicide data (1935 – 2004) for U.S. males.

Methods

Cohort effect as a multiplicative interaction of age and period

A cohort analysis of aggregated data begins by separating data into m age groups within n periods. The outcome (Y_ij), often a mortality rate or risk for a specific disease, is presented for each i=1,…,m and j=1,…,n on an m × n contingency table (see Table 1 for example). When age and period are grouped with the same time interval (e.g., five years), individuals in the left-to-right diagonals are approximately the same birth cohort. There will be a maximum of m+n−1 cohort categories for which there is any information, and two cohorts (the youngest and the oldest) each has only one data point. For instance, in Table 1, the rate of homicide for individuals aged 0–4 in 2000–2004 is 4.02 per 100 000, the sole data point available for this cohort. Conversely, we have 14 data points for the cohort that was 0–4 in 1935–1939. This cohort had rate of 1.73 per 100 000 at age 0–4, rate of 0.51 per 100 000 at age 5–9 (in 1940–1944), etc. (Table 1). In these data, information was unavailable on those aged 75–79 in 1935–1939; thus, information exists for a total of m+n−2 cohorts.

Table 1.

Age-Period contingency table (redacted) for yearly homicide rate per 100,000 by age (rows) and period (columns) among males in the United States, 1935–2004

	1935–1939	1940–1944	1945–1949	...	1990–1994	1995–1999	2000–2004
0–4	1.73	1.47	1.61		4.41	4.00	4.02
5–9	0.54	0.51	0.55		0.85	0.88	0.68
10–14	0.90	0.86	0.83		2.98	2.06	1.29
15–19	6.82	5.97	6.25		32.53	22.75	15.76
20–24	19.44	14.89	16.30		41.05	32.33	27.78
25–29	23.55	17.10	18.09		31.23	22.85	22.63
30–34	21.32	17.39	16.71		24.42	16.88	15.77
35–39	22.29	16.28	16.84		19.83	13.49	12.69
40–44	17.49	13.20	14.16		15.52	11.59	10.49
45–49	14.70	11.26	12.29		12.69	9.08	8.82
50–54	12.08	9.41	9.80		10.32	7.19	6.87
55–59	9.93	7.84	7.77		8.27	6.35	5.45
60–64	8.81	6.31	6.31		7.20	5.41	4.27
65–69	8.45	5.66	5.81		5.80	4.53	3.80
70–74	6.20	5.05	5.10		5.21	3.61	3.37
75–79	--	3.98	4.65		5.08	3.69	3.14

We have followed the convention in an age-period-cohort analysis of aggregated data to label the cohort intervals by subtracting the youngest age from the earliest year and the latest year in the interval. For instance, for the individuals aged 30–34 in 1955–1959, we subtract 30 from 1955 and 1959 to label the cohort interval, 1925–1929. The convention introduces misclassification as some of the individuals in this category will be born from 1921 to 1924 (e.g., those aged 34 in 1955–59). In aggregated data, mutually exclusive cohort rates cannot be estimated because of overlapping cohorts. This issue is not unique to the median polish method but common to all methods using aggregated data (17, 28). Since the primary purpose of an age-period-cohort analysis is to estimate the presence of cohort effects rather than to precisely quantify a `true' causal rate, the overlap in cohort serves as a caution against over-interpretation of generated estimates.

A general two-factor model for the rate (Y_ij) is that it is a function of the vector (α_i), the ith of m−1 age effects, and the vector (β_j), the jth of n−1 period effects. The natural log of Y_ij is modeled as a constant term (μ) plus α_i, β_j, and error term (ε_ij):

$$\mathrm{Log}\left({\mathrm{Y}}_{\mathrm{ij}}\right)=\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}+{\epsilon }_{\mathrm{ij}}$$ (1)

The error term represents residual unaccounted for by log-additive effects of age and period. Equation 1 can be rewritten as:

$$\mathrm{Log}\left({\mathrm{Y}}_{\mathrm{ij}}\right)=\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}+{\delta }_{\mathrm{ij}}$$ (2)

where δ_ij denotes a multiplicative interaction between the age and period effects. Equation 2 represents the saturated model of the age-period data; the error term in the model is equal to zero. The variance attributable to the multiplicative interaction term in the fully saturated model is then partitioned into systematic and non-systematic components. The systematic component is considered the cohort effect, and the remaining variance is considered random error. Thus, the cohort effect is a partial multiplicative interaction between age and period; we isolate the cohort effect from the error term in equation 1 (or, conversely, we isolate error from the age-period interaction term in equation 2) through a three-phase process.

Phase I: Graphical representation

Examination of the m × n contingency table via graphs is an informative initial step. Graphs can be created for age variation across specific periods or cohorts, cohort variation across specific ages or periods, etc. In examining graphs of rates over time by age, we are first examining whether there is variation over time to be explained. If the age-specific estimates do not change over time, then no cohort or period effects are likely to be operative. If the age-specific estimates for different age groups change in parallel during a specific period, then period effects may be present; if the age-specific estimates for certain age groups change over time in markedly different fashions than for other age groups, then cohort effects may be existent.

Phase II: Median polish

Median polish analysis removes the additive effect of age (row) and period (column) by iteratively subtracting the median value of each row and column. Median polish results can be obtained without mathematical transformation or using any transformation of risks and rates, but it should be noted that log transformation of rate or risk data before median polish (which is common in the analysis of rates) results in the assessment of interaction on the multiplicative scale (or log-additive effect). For the present analysis, we assess interaction on the multiplicative scale by log transforming rates prior to median polish analysis. Results were not dependent on the scale upon which interaction was assessed. After several iterations, the residual values stabilize (the row and column medians approximate zero) and can be considered to contain the cohort effect plus error (i.e. the residual error term in equation 1).

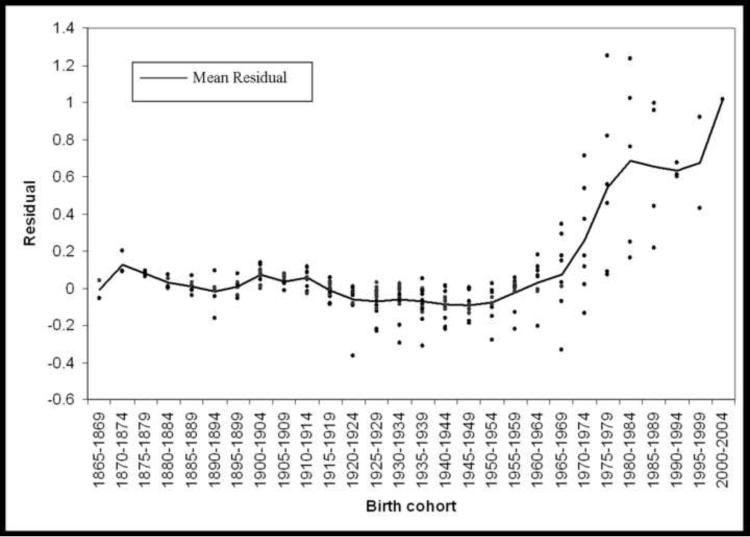
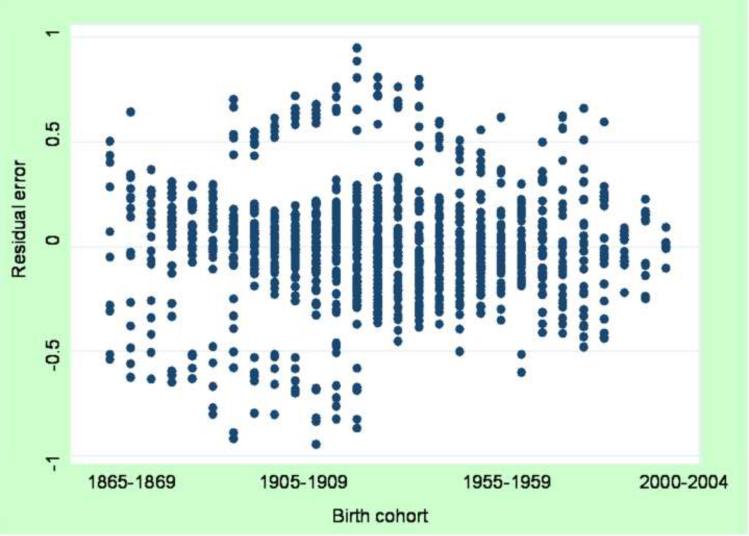
Plotting the residuals against cohort category is an efficient descriptive procedure to assess the presence and size of cohort effects (see Figure 2). If no cohort effects exist, the residuals tend to evenly distribute around zero (the expectation of the residuals should be approximately zero); a marked deviation from zero may indicate the presence of a cohort effect (non-linearity of period and age effects). The residuals can also be subtracted from the cells of the original table, leaving cells reflecting only the additive effects of age and period for qualitative comparison with original contingency table (note: additive on specified scale; for our analyses we assessed the log-additive effect). For a full description and examples of median polish analysis, we refer readers to the excellent texts of Tukey and Selvin (26, 27).

Figure 2.

Residual values from median polish by birth cohort, males in the United States

Phase III: Regression

After residuals are identified from the median polish analysis, the final step to statistically assess the relative magnitude of cohort effects is to regress residuals (e_k) on cohort category (entered as a collection of indicator variables for the m+n−2 cohort, k=1, 2, …, m+n−2) using linear regression, where e_k is a function of intercept μ_k, a vector of cohort effects γ_k, and a vector of error terms e_ijk (the errors term representing the random error unaccounted for by the cohort effect across i age, j period, and k cohort categories):

$${\mathrm{e}}_{\mathrm{k}}={\mu }_{\mathrm{k}}+{\gamma }_{\mathrm{k}}+{\mathrm{e}}_{\mathrm{ijk}}$$ (3)

with the expectation of intercept μ_k approximately equal to zero. This step produces k beta estimates (one for each cohort category) reflecting the log rate that reflects a ratio of cohort effects (i.e., the ratio of the non-additive effect for one cohort to that of the non-additive effect for a reference cohort). The exponentiation of each beta estimate derived from equation three indicates the excess rate attributable to each cohort category. Each cohort category can be then compared to the referent cohort to obtain a relative estimate of the size of the cohort effect. The residuals from this model can be examined for violations of parametric assumptions.

Application of the method to homicide mortality data

Homicide mortality and population data were abstracted from annual Mortality Statistics and later Vital Statistics of the United States volumes made publicly available from 1910 to 2004 by the National Center for Health Statistics, Hyattsville, Maryland (29, 30). Persons over age 80 were excluded because of insufficient numbers of homicide deaths and unavailable data in early years. Definition of homicide was based initially on the International List of Causes of Death, and most recently by the International Classification of Diseases and Related Health Problems (ICD). Though there were seven revisions of the ICD since 1935, categorization alterations had little detectable effect on homicide classification (31, 32, 33, 34, 35, 36). Further details can be found elsewhere (37). Due to considerable gender differences in homicide, the present analysis was restricted to males (808,055 total male homicide deaths). Age and period were categorized into 16 and 14 five-year groups, respectively, resulting in 29 birth cohorts.

Statistical analysis

Median polish analysis was done using spreadsheet software (Excel, Microsoft Office 2006). The regression estimates and confidence intervals were generated using STATA version 9.0 (Stata Corp LP, College Station, Tex).

Results

Graphical Representation

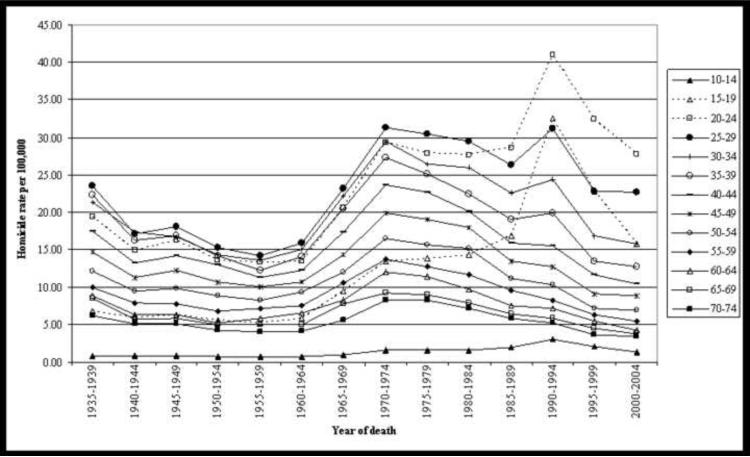
In Figure 1 we graph homicide rates by age across each period (year of death). We redacted age-specific rates for the youngest (0–4 and 5–9) and oldest (75–79) age groups for visual simplicity. Homicide rates by age appear relatively stable over time at parallel across age until 1960. After 1960, homicide rates increase across age, indicative of a period effect. Shown in the dotted line is the homicide rate for those aged 15–19 and 20–24. For these age groups, the post-1960 trends appear non-parallel, as the homicide rate increase is faster for these age groups than for other age groups. This non-parallel increase for certain age groups is indicative of a cohort effect, suggesting that period effects and age effects alone may be insufficient to fully account for the patterns evidenced in the graphically presented data.

Figure 1.

Age-specific homicide mortality rate per 100,000 by year of death, males in the United States.

Median Polish

A median polish procedure was performed on log-transformed rates. The pattern of residuals across cohorts (Figure 2) is indicative of cohort effects for those cohorts born approximately after 1960. There is systematic deviation of the residuals from zero, suggesting positive cohort effects (i.e. greater than expected given log-additive effects of age and period).

By subtracting residuals from original data in the age-period contingency table, comparison is possible between perfectly additive (on a log scale) table and the observed data. For example, the homicide rate for ages 15–19 in 1990–1994 is 32.53 per 100 000 (Table 1): the residual obtained from the log transformed median polish analysis is 1.25 for that cell. To calculate the log-additive rate (i.e. with cohort effect removed), we use the following formula: [32.53 × e^−(1.25)] = 9.32. This indicates log homicide rate in this group is higher than expected if age and period effects were log-additive.

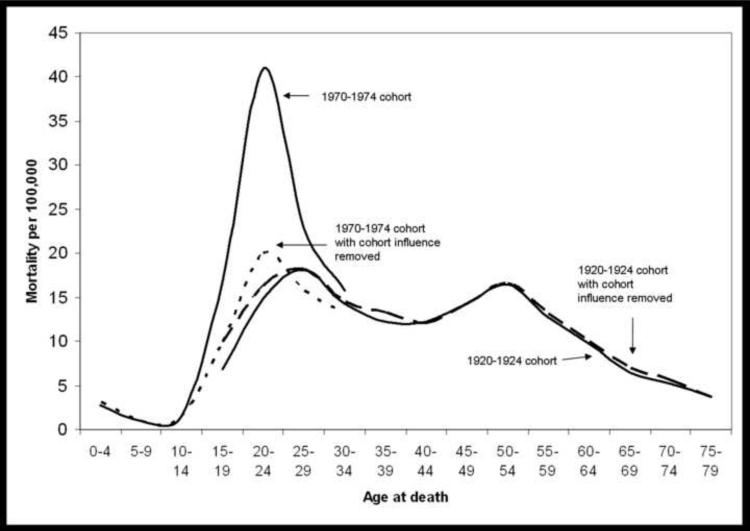
Figure 3 shows the cohort-specific mortality by age with and without cohort influence for two groups: those born approximately 1970–1974 and those born approximately 1920–1924. There is evidence of a cohort effect for those born between 1970 and 1974; the age-specific log homicide rate is greater than expected if age and period were log-additive. The cohort born between 1920 and 1924 demonstrate little evidence of a cohort effect. The 1920–1924 cohort is well-described by age and period acting log-additively, whereas an interaction between age and period is needed to describe the cohort born 1970–1974.

Figure 3.

Homicide rate per 100,000 in the U.S. for the 1970–1974 male birth cohort and the 1920–1924 male birth cohort with and without the cohort effect.

Regression

Residuals obtained via the median polish method were regressed on indicator variables for the m+n−2 cohort categories using a linear regression (shown in Table 2). The exponentiated regression coefficients along with 95% confidence interval from this model are interpreted here as the ratio of the cohort effect for each cohort relative to the cohort effect for the 1920–1924 cohort (i.e., rate ratio), chosen for consistency with Figure 3. The magnitude of the rate ratios indicate that cohorts born prior to the referent cohort of 1920–1924 evidence a slightly higher cohort effect compared to the referent cohort. Beginning with the 1960–1964 cohort, there is evidence of significantly increased cohort effects compared to the referent cohort. The cohorts effect is approximately 2.0 times higher for those born after 1980 compared to the referent cohort, indicating increasingly higher rate of homicide mortality at all ages. For instance, the cohort effect for men born between 1980 and 1984 is 2.11 (95% C.I. 1.98–2.25) times higher than for men born between 1920 and 1924.

Table 2.

Estimated rate ratio and 95% confidence interval for the effect of birth cohort on homicide mortality rate per 100,000, United States, 1935–2004

Birth Cohort	Rate Ratio	95% Confidence interval
1865–1869	1.06	(0.96–1.16)
1870–1874	1.21	(1.12–1.31)
1875–1879	1.15	(1.07–1.23)
1880–1884	1.09	(1.03–1.17)
1885–1889	1.07	(1.01–1.14)
1890–1894	1.05	(0.99–1.11)
1895–1899	1.07	(1.01–1.13)
1900–1904	1.14	(1.08–1.21)
1905–1909	1.10	(1.05–1.16)
1910–1914	1.12	(1.07–1.18)
1915–1919	1.05	(1.00–1.10)
1920–1924	1.00	(reference)
1925–1929	0.99	(0.94–1.04)
1930–1934	1.00	(0.96–1.05)
1935–1939	0.99	(0.94–1.04)
1940–1944	0.97	(0.93–1.02)
1945–1949	0.97	(0.92–1.02)
1950–1954	0.98	(0.94–1.03)
1955–1959	1.04	(0.99–1.01)
1960–1964	1.10	(1.04–1.16)
1965–1969	1.14	(1.08–1.21)
1970–1974	1.37	(1.30–1.46)
1975–1979	1.83	(1.72–1.94)
1980–1984	2.11	(1.98–2.25)
1985–1989	2.04	(1.90–2.19)
1990–1994	2.00	(1.85–2.16)
1995–1999	2.09	(1.91–2.29)
2000–2004	2.94	(2.59–3.34)

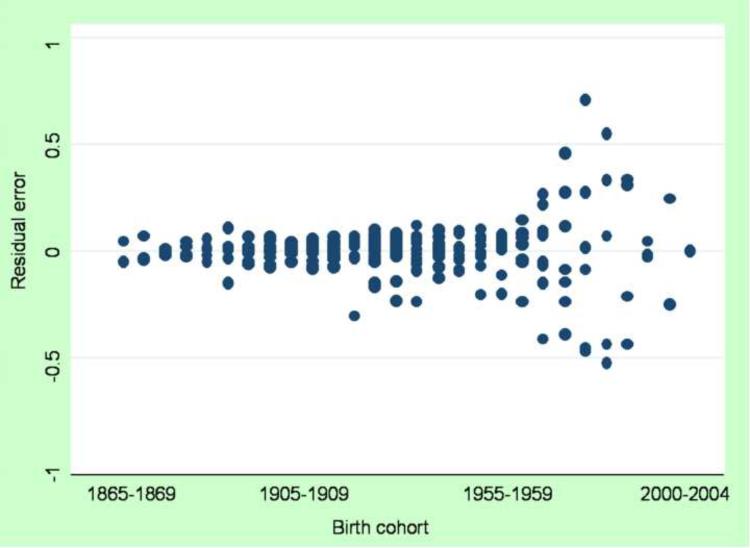
The r-square for the simple linear regression model is 0.69, indicating that multiplicative cohort effects explain approximately 69% of the variance in the age-period interaction, with remaining variance attributable to error. A graph of regression residuals by cohort is shown in Figure 4a (note the distinction between median polish residual, which includes the cohort effect and residual error, and the regression residuals, which includes the remaining variance after accounting for the cohort effect). These errors exhibit heteroscedasticity, evidenced by the increasing variance in the residuals across the birth cohorts. This heteroscedasticity indicates that the confidence bounds around the estimates for later birth cohorts may be unstable. Thus, the implications of this heteroskedascity should be evaluated in the choice of a model that best represents these data.

Figure 4a.

Graph of residual errors from the median polish residual linear regression model by birth cohort, males in the United States

Comparison between the median polish method and two-stage regression

An alternative cohort analysis is a two-factor (age and period) regression model (see Formula (1)), generating the residual matrix, ε_ij. For comparison, we log-transformed the homicide data and fit a two-factor linear regression model of log rates on indicator variables for the m−1 age categories and n−1 period categories (the normal distribution after log transformation appeared to be the best fitting link function). Regressing residuals from the two-factor model on cohort category yielded an r-square of 0.49, substantially lower than that obtained through the median polish approach (0.69). The residual errors from the two-stage regression approach are displayed in Figure 4b. The residual graphs in Figures 4a and 4b include the same number of data points (1,115). Figure 4b appears to have many more data points because of the increased range and variability throughout the scatter plot.

Figure 4b.

Graph of residual errors from the two factor linear regression model by birth cohort, males in the United States

Discussion

The study of disease over the life-course and across generations has benefited from the detection of cohort effects (4, 10). The method described here provides an efficient way to estimate cohort effects as a partial multiplicative interaction between age and period. While the median polish is not the only means through which a cohort effect can be estimated, this method is a reliable, robust, and simple statistical procedure that is based on a conceptual model for the cohort effect as a partial age-period interaction. Previous investigations of homicide have also detected cohort effects using the second-order function approach (37) and proxy variable approach (38, 39); the advantage of the multi-phased approach is that not only can a cohort effect be detected, but the magnitude of the cohort effect as the partial interaction of age and period effects can also be quantified.

The main conceptual difference between this approach and other approaches to cohort-effect modeling (11, 13, 24, 25) is that the median polish approach defines the cohort effect as a special form of multiplicative interaction between age and period; thus, by definition a cohort effect is a second-order effect with no linear component. The “linear components” are attributable to the additive age and period effects, and the cohort effect does not exist independently of the age and period effects. The median polish approach is conceptually similar to the linear contrast method, in that cohort effects are defined as second order effects of age and period effect. However, the linear contrast provides a means to judge the statistical significance of the second order effect, whereas the multi-phased approach additionally provides a quantitative estimate of the magnitude of the second order effect. Further, the multi-phased method provides a clear, conceptual working definition for a cohort effect as an age by period interaction, which aids in the interpretation of results.

While the proposed multi-phase method seems to provide a sound and practical approach to cohort analysis, it does not address other limitations inherent in the age-period contingency table data, namely the overlapping of adjacent cohorts and the inability to incorporate the precision of the underlying rate data into the quantification of effects. Further, there may be circumstances in which various age-period-cohort methods will perform equally (e.g., two-factor regression residual extraction, constraints-coefficients); however, the median polish provides conceptual shift for the definition of a cohort effect, statistically quantified the effect with a minimum of assumptions, and can be applied in a wide variety of aggregated datasets. Further, assumptions of regression models should be evaluated when using the median polish method; for example, the homicide data exhibited heteroscedasticity for younger birth cohorts, indicating that confidence intervals may be unstable. Use of the multi-phased approach is not a guarantor of a valid inference; the approach is one of many potential approaches to examine cohort effects in epidemiologic data. Each model has assumptions that require careful consideration before implementation.

The primary objective of an age-period-cohort analysis is to determine the combination of effects leading to changes over time, but identification of the causes of population effects(40) is the ultimate aim for inference to public health interventions. In the homicide data, several hypotheses have been generated regarding the cause of the cohort effect, including cohort size and composition (38) as well as increases in substance use (41) and exposure to firearms (42). Testing pathways will provide much-needed information regarding phenomena in homicide mortality, but detection of susceptible cohorts is a crucial analytic step in developing and refining hypotheses.