Maximum Flux Transition Paths of Conformational Change

Abstract

Given two metastable states A and B of a biomolecular system, the problem is to calculate the likely paths of the transition from A to B. Such a calculation is more informative and more manageable if done for a reduced set of collective variables chosen so that paths cluster in collective variable space. The computational task becomes that of computing the “center” of such a cluster. A good way to define the center employs the concept of a committor, whose value at a point in collective variable space is the probability that a trajectory at that point will reach B before A. The committor “foliates” the transition region into a set of isocommittors. The maximum flux transition path is defined as a path that crosses each isocommittor at a point which (locally) has the highest crossing rate of distinct reactive trajectories. This path is based on the same principle as the minimum resistance path of Berkowitz et al (1983), but it has two advantages: (i) the path is invariant with respect to a change of coordinates in collective variable space and (ii) the differential equations that define the path are simpler. It is argued that such a path is nearer to an ideal path than others that have been proposed with the possible exception of the finite-temperature string method path. To make the calculation tractable, three approximations are introduced, yielding a path that is the solution of a nonsingular two-point boundary-value problem. For such a problem, one can construct a simple and robust algorithm. One such algorithm and its performance is discussed.

1 Summary

1.1 Introduction

Considered here is the problem of computing transition paths of conformational change, given two different metastable states of a biomolecule. One motivation for this is to facilitate the accurate calculation of free energy differences. Another motivation is to determine the existence and structure of transition states and intermediate metastable states. The latter are possible targets for inhibitors of enhanced specificity in cases where a family of proteins have active sites with very similar structure. A good example of this situation is the Src tyrosine kinase family, ¹ which has long been implicated in the development of cancer. For this system there are already computational results,^2–4 supported by experiment,⁵ for the transition path from an active catalytic domain to an inactive catalytic domain.

Some approaches to this problem generate ensembles of trajectories based on the equations of motion. Notable examples are transition path sampling⁶ and Markov state models.⁷ Applying such methods to large proteins (without compromise) would appear to require exceptional computing capabilities, so here we pursue a more theoretical approach that avoids “direct numerical simulation.” Such an approach seeks to characterize one (or several isolated) “representative” reaction paths connecting two given metastable states, each path representing a bundle or cluster of trajectories. Here we adopt a well developed and tested theory, namely, transition path theory (TPT).^8–11 Additional references on computing transition paths are found in Ref. 12 In general, it may also be of interest to calculate (i) the reaction rate for each bundle, or, at least, the relative rate for different bundles, and (ii) the potential of mean force. Here we consider only the calculation of the path itself.

It happens that the path proposed here is based on the same principle as the minimum resistance path, ¹³ but differs in an important respect. Here, we make the path independent of the choice of coordinates in collective variable space by introducing a metric tensor to measure distance. This enables one to choose these coordinates on the basis of convenience, and, in particular, makes it easier to adapt to limitations imposed by a simulation program. Additionally, an appropriate choice of metric yields differential equations for defining the path that are significantly simpler than those for the minimum resistance path.

The minimum resistance path is offered as an alternative to the minimum energy path (MEP) (also known as the steepest descent path), to capture finite temperature effects. The MaxFlux method¹⁴ computes the minimum resistance path, as does the nudged elastic band implementation of Ref.15 Other temperature-dependent paths have been proposed, including one defined as a most probable stochastic trajectory in the sense of a path integral,¹⁶ one based on mean first-passage times,¹⁷ and one whose tangent is the most probable direction determined from a swarm of trajectories.¹² A compelling case for including temperature effects is given in Ref., ¹⁸ which shows for alanine dipeptide the considerable extent to which the MaxFlux path from α_R to C_7ax1 differs from the minimum free energy path (MFEP).⁹ This same article also shows that this same MaxFlux path well represents an ensemble of trajectories generated with transition path sampling. However, the ability to locate the center of such a bundle depends on a selection of collective variables that avoid fine-grained roughness in the free energy landscape. Otherwise, actual averaging is needed, as in the finite-temperature string (FTS) method (see Sec. IV.B of Ref. 19 and Ref.20).

In a nutshell, this article embraces a certain aspect of TPT and carries it to a logical conclusion, obtaining a formula, an implementation, and a proof of concept. The aim is to compute a path that is closer to the ideal than the MFEP and that, in a couple of respects, is better than the path of the FTS method. Additionally, the formula for the path is computationally more attractive than the formula that underlies either the path of the FTS method or the MFEP.

1.2 Outline and discussion

There are two distinct steps in getting a solution: The first is to define the problem without concern for the methods to be employed (other than taking into account the intrinsic difficulty of the problem). Defining a problem apart from a method gives a more concise definition. Also, by not guessing about what is feasible computationally, one may avoid unnecessary compromises. The second step is to construct a method and algorithm.

Given two metastable states A and B of a biomolecular system, the aim is to calculate the likely paths of the transition from A to B. Such a calculation is more informative and more manageable if done for a reduced set of collective variables, functions of the system configuration x,

$$\begin{array}{cc}{\zeta }_1={\xi }_1(x),{\zeta }_2={\xi }_2(x),\dots ,{\zeta }_{\nu }={\xi }_{\nu }(x),& \text{abbreviated as}\zeta =\xi (x),\end{array}$$

chosen so that paths cluster in collective variable space. The computational task becomes that of computing the “center” of such a cluster. A good way to define the center employs the concept of a committor, whose value at a point in collective variable space is the probability that a trajectory at that point will reach B before A. The committor “foliates” the transition region into a set of committor isosurfaces known as isocommittors. The maximum flux transition path (MFTP) is defined as a path that intersects each isocommittor at a point which (locally) has the highest crossing rate of distinct reactive trajectories. A more detailed account of the problem definition is given in Section 2.

The minimum free energy path has been used for some time to represent reactive trajectories in collective variable space. Only fairly recently has its relationship to reactive trajectories been explained. The article⁹ applies large deviation theory to show that the MFEP is the most probable path in the zero temperature limit of dynamics on a free energy surface defined at finite temperature. Hence, the MFEP (though not the MEP) is an inherently inconsistent construct and it is useful only to the extent that it represents fully finite-temperature trajectories. In fact, it does this fairly well on the simple tests reported here.

To make the calculation tractable, three approximations are introduced. To make the committor a more accessible quantity, the set of paths is approximated by a Brownian dynamics model, resulting in a boundary value problem in ν-dimensional space. Then the number of space dimensions is reduced to one by assuming most of the transition paths are contained in a tube, resulting in a two-point boundary-value problem with 2ν unknowns. A third approximation reduces this to ν unknowns, whose solution is a maximum flux transition path. The resulting equations involve a free energy gradient term and an explicitly temperature-dependent curvature term. Specifically, the maximum flux transition path ζ = Z(s), 0 ≤ s ≤ 1, is defined by the condition that

$$-\beta \nabla F^{+}(Z)-\frac{{\nabla }_{\zeta }c(Z,Z_s)}{c(Z,Z_s)}+\frac{{(D{(Z)}^{-1}{Z}_s)}_s}{c{(Z,Z_s)}^2}\Vert D{(Z)}^{-1}{Z}_s$$

holds for ζ = Z(s), where

$$F^{+}(\zeta )=F(\zeta )-\frac{1}{2\beta }\text{log}(\text{det}D(\zeta )),c(\zeta ,\omega )=({\omega }^{\top }{D(\zeta )}^{-1}{\omega )}^{1/2},$$

β is the inverse temperature, F(ζ) is the free energy profile, D(ζ) is a proto-diffusion tensor depending on masses and ξ, and the subscript s denotes differentiation (d/ds). In the high temperature limit, the path becomes a straight line. In the low temperature limit, the path becomes an MFEP. At zero temperature the path will have cusps at some intermediate local minima, which presents difficulties if free energy profiles or relative reaction rates are to be determined. This formula is a key result of this article. Details are given in Section 3. By contrast the minimum resistance path satisfies a more complicated condition, −β∇F − 2c⁻¹∇_ζc + c⁻²(WD⁻¹Z_s)_s ‖ WD⁻¹Z_s where $W=2I-Z_s(Z_s^{\top }{Z_s)}^{-1}{Z}_s^{\top }$, which differs from the MFTP except in very special cases such as D(ζ) = I.

The temperature-dependent curvature term not only provides a finite temperature correction to the MFEP, but it yields a nonsingular second order ordinary differential equation, amenable to standard techniques—except for the need to do computationally intensive sampling to evaluate terms in the differential equation. An existing set of algorithms for the MFEP^9,21 applies equally well to the MFTP. In Section 4, the equation of a simplified MFTP, Eq. (12) below, is discretized using upwinded differencing and solved using the semi-implicit simplified string method.²² (A notable alternative is the nudged elastic band method, introduced in Ref.23) Algorithmic details are provided in Section 4.

Section 5 compares the MFTP to the MFEP on numerical examples. First, an artificial problem in full configuration space is solved to demonstrate the effect of the curvature term of the MFTP. (A problem in full configuration space is equivalent to a problem in collective variable space with perfect sampling.) In particular, the necessity of using an adaptive mesh for the MFEP is demonstrated. Then alanine dipeptide in vacuum is solved using the ϕ, ψ dihedrals as collective variables. For the transition path from C_7ax to C_7eq as in Ref.,⁹ the computational cost for calculating the MFTP and the MFEP is almost same. However, for a transition path from C_7eq to $C_{7\text{eq}}^{\prime }$ through C_7ax shown in Ref., ¹⁹ the MFEP has a cusp at C_7ax and the computational cost for finding such a cusp is expensive. On the other hand, the MFTP smooths out the cusp and the computational cost is reduced. Finally, the MFTP is calculated for alanine dipeptide in explicit water and for alanine decapeptide.

An open source implementation of the MFTP method is available²⁴ as a relatively simple set of Python modules with examples using pure Python, CHARMM,²⁵ and NAMD.²⁶

1.3 Conclusions

For alanine dipeptide, the MFEP, MFTP, and FTS method paths are quite similar. On a contrived problem with a rough energy landscape, e.g., Figure 2 in Ref., ²⁰ the FTS method path gives a much better result. On a different contrived problem given in Section 5.1, the MFTP gives a much better result. Contrived examples are relevant because computational techniques are sometimes applied in extreme situations for which they may not have been designed. In terms of quality, the MFTP ranks higher than the MFEP but lower than the FTS method path (because the latter addresses the more serious difficulty of multiple local minima).

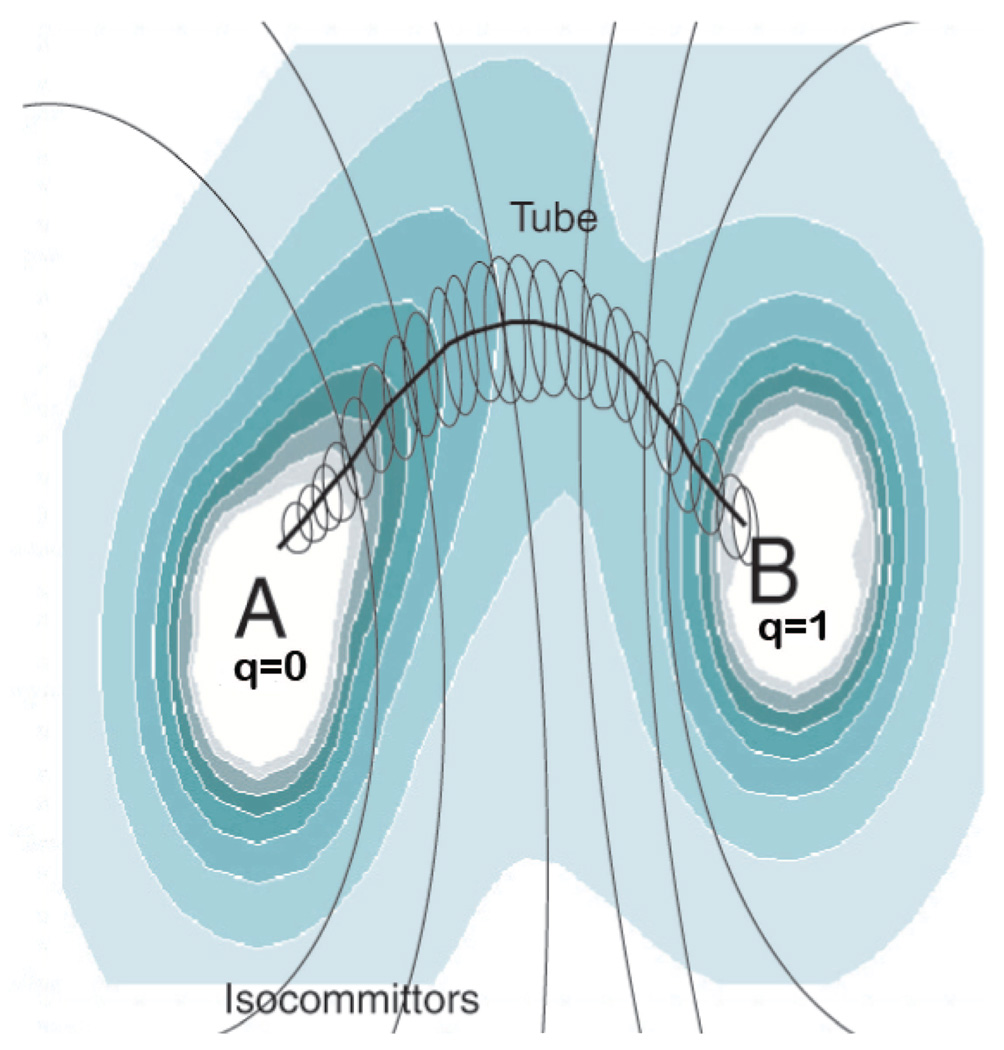
Figure 2.

Shading indicates contours of free energy, thin curves denote isocommittors, ellipses enclose concentrations of crossing points from reactive trajectories, and the thick curve is the center.

The minimum free energy path (and that of the FTS method) can have cusps at local minima of free energy, which makes it unsuitable for defining an isocommittor at these points and harder to compute. Computational difficulties include the need for an adaptive mesh and a greater number of iterations until convergence.

2 What is the problem?

We begin by defining an ensemble of transition paths from A to B: For simplicity, assume the molecular system obeys Newtonian dynamics with potential energy function U(x) and a diagonal matrix M of atomic masses. Positions x and momenta p satisfy x = X(t), p = P(t) where (d/dt)X(t) = M⁻¹P(t) and (d/dt)P(t) = −∇U(X(t)). Initial values are drawn from a Boltzmann-Gibbs distribution ρ (x, p): positions x from probability density const e^−βU(x) and momenta p from a Maxwell distribution. Imagine an extremely long trajectory. The trajectory enters and leaves A and B many times yielding a huge set of reactive paths from A to B. (A reactive path is a piece of the trajectory outside of A and B that comes from A and goes to B.)

Generating an ensemble of trajectories is extremely demanding computationally. And, even if this were possible, what would the user do with all the data? By answering such a question, we might well avoid the task of computing trajectories. It is likely that one would cluster the trajectories to produce a concise description. Therefore, one might instead directly determine such a concise description. Specifically, if the paths cluster into one or several distinct isolated bundles/tubes/channels/pathways, one might compute a “representative path” for each cluster. This idea is developed in the paragraphs that follow.

However, transition paths might not cluster adequately—in full configuration space. Assume, though, there is a smaller set of collective variables, ζ = ξ(x), such that in ζ-space, paths cluster into one or several distinct isolated channels connecting two separated subsets A_ξ and B_ξ of collective variable space. Otherwise, there is little of interest to compute. A typical example of collective variables is ϕ/ψ angles along a peptide backbone. Once the collective variables are specified, the problem is to calculate a path in collective variable space, ζ = Z(s), 0 ≤ s ≤ 1, connecting A_ξ to B_ξ where the transition paths are concentrated. Along with a parameterization of the path in collective variable coordinates, would be a realization of it in cartesian coordinates, so once the path is generated, structures can be studied as well. A drawback of this approach is the need to identify an appropriate set of collective variables. Indeed, defining suitable collective variables is an important research problem.²⁷

We want a minimal set of collective variables subject to two conditions: First, the coordinates ζ must suffice to describe states A_ξ, B_ξ in ζ-space corresponding to A, B. Second, coordinates ζ must also be rich enough to “express the mechanism of conformational change” along the transition path. To make the second condition more precise, we introduce the notion of “quasi-committor.”

To measure the progress of a transition, there is a natural reaction coordinate, known as the committor. This concept of a commitment probability was introduced by Onsager,²⁸ and the abbreviated term “committor” was introduced in Ref., ²⁹ which they defined as follows: For each point x in configuration space, consider a trajectory starting with X(0) = x and velocities drawn at random from a Maxwell distribution, and define the committor q(x) to be the probability of reaching B before A. Since it is the coordinates of the collective variables that are of interest, it is natural also to define a quasi-committor: For each point ζ, consider a trajectory starting with random initial values conditioned on ξ(x) = ζ and define the quasi-committor q̂(ζ) to be the probability of reaching B_ξ before A_ξ:

$$\widehat{q}(\zeta )=\text{Pr}(\xi (X(t))\text{reaches}{B}_{\xi }\text{before}{A}_{\xi }|\xi (X(0))=\zeta ).$$

We could say that the variables ζ = ξ(x) are rich enough to express the mechanism of conformational change if the quasi-committor q̂(ζ) has no local minima or maxima outside of A_ξ and B_ξ (except for regions of negligible probability). Otherwise, there is some unexpressed degree of freedom important to the transition. As an example, suppose that virtually all trajectories stay within a narrow tube having a geometry in full configuration space illustrated by Figure 1. Suppose that the free energy profile as a function of arc length along the transition tube is much higher in the backward section than it is in the two forward sections. Then most of the increase in the quasi-committor as a function of arc length occurs in the middle section of the tube. Consequently, the variation in the quasi-committor, as a function of the ill-chosen collective variable ζ corresponding to the horizontal axis, will be dominated by this middle section of the tube. This results in a graph of q̂(ζ) that increases at the beginning and end of its range but decreases in the middle part. In addition to q̂(ζ) having no local extrema, it is desirable that q̂(ξ(x)) ≈ q(x). The quality of the collective variables can be checked in principle by calculating quasi-committor values q̂(ζ) at points along the path from dynamics trajectories.

Figure 1.

A schematic illustration of a poor choice of collective variables. The horizontal axis is collective variables, and the vertical axis is unrepresented degrees of freedom. The collective variables fail to indicate the progress of the reaction.

Two approaches have been proposed for defining the center of a cluster of paths in ζ-space:

1. a most probable path, e.g., a swarm-of-trajectories string method¹² path, and

2. a path that intersects each isosurface of the quasi-committor at a center of the collection of points where reactive trajectories cross that isosurface, e.g., a finite temperature string method¹⁹ path and a maximum flux transition path.

An MFEP is a limiting case of both approaches. (The MFEP is obtained from these various approaches by letting β → ∞ in the path formula but not in the definition of the free energy profile.) Defining a representative path is a compromise between (i) best capturing the object of interest and (ii) simplicity.

One problem with seeking the most probable path is that it is unclear how to assign relative probabilities to paths. More importantly, the most probable path tends to be a path of minimum energy, and it is not clear—a priori—that this is a “representative” path. For Hamiltonian dynamics, it would seem that the probability that we attach to a path would be proportional to exp(−βE) where E is the energy. Hence, the most probable path is the one with just enough energy to surmount the potential energy barriers. For stochastic dynamics, the explanation of how to assign probability to paths is quite complicated—if paths of different durations are being compared. An explanation for Brownian dynamics is possible using Freidlin-Wentzell theory and the assumption of vanishingly small noise (see Appendix A of Ref. 9). It is reassuring though that the results of Freidlin-Wentzell theory agree with those of TPT in the zero-temperature limit (for F(ζ) held fixed).

For defining a path in terms of an intersecting point on each isosurface of a quasi-committor, one needs

1. a definition for the distribution of crossing points of reactive trajectories through a quasi-commitor isosurface and

2. a definition of centrality, e.g., mode, median, or mean.

We consider each of these in turn.

The finite-temperature string method defines the distribution of crossing points of reactive trajectories in a way that includes recrossings. A subsequent article¹⁰ illustrates the dramatic distortions that arise by including recrossings, and it emphasizes crossings of a surface by distinct reactive trajectories instead of all crossings by reactive trajectories. They define such a distribution in terms of the net crossings of reactive trajectories across each infinitesimal piece of a surface. It is not obvious, however, that this necessarily gives nonnegative values everywhere on the isosurface of a quasi-committor, so, instead, we use the density of last crossings by reactive trajectories, called last hitting points in Ref.8 For the Brownian dynamics approximation developed in the next section, these two measures are identical.

Consider now the question of defining the center. Let j(ζ) denote the density associated with a definition for the distribution of crossing points of reactive trajectories through a quasi-committor isosurface. One choice for the center is the point of highest probability, In other words, seek the path ζ = Z(s), 0 ≤ s ≤ 1, each of whose points Z(s) is a local maximum of the density j(ζ) on the quasi-committor isosurface Σ passing through Z(s). This is what we use for the MFTP. Another choice, associated with the finite-temperature string method, is to construct the path from the mean value ζ′ on each quasi-committor isosurface Σ: the point ζ′ that minimizes ∫_Σ|ζ′ – ζ|²j(ζ)dζ. Although this notion is a superior measure of centrality, it is more complicated to explain. In practice, methods for finding a maximum are designed only to find a local maximum, which is what we do for the MFTP. This is satisfactory if there is a choice of collective variables that produces a free energy landscape free of roughness at the scale of the thermal energy.²⁰ In any case, the equations defining a center-of-density path are intrinsically more expensive computationally to solve than those for the MFTP, because they require averaging on quasi-committor isosurfaces q̂(ζ) = constant (in addition to conditional averages on collective variable isosurfaces ξ(x) = ζ in full configuration space) rather than merely determining a (local) maximum.

These definitions for the center are flawed, however. “Collective variable space” is a set of points, each point ζ representing a manifold ξ(x) = ζ in configuration space of dimension 3N − ν. A change of variables within collective variable space, ξ(x) = χ(ξ′(x)), should not change the path, only its representation. This can be achieved by defining a metric tensor M(ζ) for measuring distances—the distance from ζ to ζ + dζ being given by (dζ^⊤M(ζ)dζ)^1/2—which somehow measures the distance between two infinitesimally close manifolds in configuration space. (Being a tensor means that M_ξ′(ζ′) = (∂χ/∂ζ′)^⊤M_ξ(χ(ζ′))∂χ/∂ζ′.) Appendix A derives a correction factor for hypersurface area, and accordingly, we define a corrected last hitting point density

$$j_{\mathrm{c}}(\zeta )=\frac{|\nabla \widehat{q}(\zeta )|}{|M{(\zeta )}^{-1/2}\nabla \widehat{q}(\zeta )|}(\text{det}M{(\zeta ))}^{-1/2}j(\zeta ).$$

A natural choice for M(ζ) arises during the course of deriving the hitting point density.

3 A method

As stated previously, computing q̂(ζ) is not feasible. Consequently, we derive a method, which employs three uncontrolled approximations—a controlled approximation being one that can be made arbitrarily accurate with sufficient computational effort. Section 3.1 approximates paths in collective variable space by those of Brownian dynamics; Section 3.4 assumes most paths lie in a tube where isocommittors are planar; and Section 3.5 assumes that on average the trajectories are parallel to the path. The basic ingredients of much of this development are present in the literature but scattered among several articles. Here they are combined to produce equations from which we derive the MFTP.

3.1 Brownian dynamics approximation of collective variable paths

The probability density function (p.d.f.) for ξ(x) is

$${\rho }_{\xi }(\zeta )=\langle \delta (\xi (x)-\zeta )\rangle ={\displaystyle \int {\displaystyle \int \delta (\xi (x)-\zeta )\rho (x,p)\mathrm{d}x\mathrm{d}p}}$$

where δ(ζ) = δ(ζ₁)δ(ζ₂)⋯δ(ζ_ν). Let 〈·〉_ζ be the expectation for the conditional density ρ(x, p|ξ(x) = ζ):

$$\langle O{(x)\rangle }_{\zeta }=\frac{\langle \delta (\xi (x)-\zeta )O(x)\rangle }{\langle \delta (\xi (x)-\zeta )\rangle }.$$

In Appendix B is an adaptation of an argument from Ref.9 (Sec. III, A and B) suggesting that as an approximation to q̂(ζ), we should seek a function q(ζ) that minimizes a certain functional I(q) that can be expressed in terms of collective variables ζ. Define the free energy F(ζ) for coordinates ζ = ξ(x) by

$${\mathit{\text{const}}}_{\xi }{\mathrm{e}}^{-\beta F(\zeta )}={\rho }_{\xi }(\zeta )=\langle \delta (\xi (x)-\zeta )\rangle .$$ (1)

Also define a proto-diffusion tensor D by

$$D(\zeta )=\frac{1}{2}{\beta }^{-1}\langle {\xi }_x(x)M^{-1}{\xi }_x{{(x)}^{\top }\rangle }_{\zeta }.$$

(There is freedom in the scaling of D. We use this freedom to make Eq. (4) below agree with an alternative derivation of the Brownian dynamics, in which one assumes instantaneous relaxation of the degrees of freedom not represented by the collective variables. The tensor D(ζ) fails to be a diffusion tensor because it is missing a time scale factor.) The functional is then

$$I(q)={\mathit{\text{const}}}_{\xi }{\displaystyle \int {\mathrm{e}}^{-\beta F(\zeta )}\nabla q{(\zeta )}^{\top }D(\zeta )\nabla q(\zeta )\mathrm{d}\zeta }$$ (2)

where the integral is over the transition region outside of A_ξ and B_ξ subject to q(ζ) = 0 on the boundary of A_ξ and q(ζ) = 1 on the boundary of B_ξ.

The corresponding Euler-Lagrange equation for q(ζ) is the Smoluchowski (backward Kolmogorov) equation:

$$-\nabla ·{\mathrm{e}}^{-\beta F(\zeta )}D(\zeta )\nabla q(\zeta )=0,$$ (3)

subject to q(ζ) = 0 on the boundary of A_ξ and q(ζ) = 1 on the boundary of B_ξ.

The function q that satisfies the Smoluchowski equation subject to the given boundary conditions can be shown to be the exact committor function for paths ζ = ζ(τ) in collective variable space generated by the Brownian dynamics

$$\frac{\mathrm{d}}{\mathrm{d}\tau }\zeta =-\beta D(\zeta )\nabla F(\zeta )+(\nabla ·D{(\zeta ))}^{\top }+\sqrt{2}{D}_{1/2}(\zeta )\eta (\tau )$$ (4)

where $D_{1/2}{D}_{1/2}^{\top }=D$ and η(τ) is a collection of standard white noise processes. The fact that τ is an artificial time does not affect the committor. In principle, the assumption q(ζ) ≈ q̂(ζ) can be checked a posteriori by comparing committor values of the Brownian dynamics to the quasi-committor values of actual dynamics.

Reference⁹ (Sec. III.C) appears to suggest that the Smoluchowski equation uniquely specifies dynamics except for scaling of time: If the Smoluchowski Eq. (3) is satisfied by committors q(ζ) for arbitrary sets $A_{\xi }^{\prime }$ and $B_{\xi }^{\prime }$ in collective variable space, then trajectories whose committor functions satisfy Eq. (3) must have paths that are those of the Brownian dynamics. Hence, paths in collective variable space can be generated with the proper probabilities from the system of stochastic differential equations.

3.2 Last hitting-point distribution

Appendix C considers the rate at which reactive trajectories cross an arbitrary surface Σ that separates collective variable space into two parts, one containing A_ξ and the other containing B_ξ. The result given there is that the rate of the last crossing of Σ by reactive trajectories is given by the integral

$${\displaystyle {\int }_{\sum }J(\zeta )·\widehat{n}(\zeta )d{S}_{\zeta },}$$

where n̂(ζ) points to the side containing B_ξ, and

$$J(\zeta )={\rho }_{\xi }(\zeta )D(\zeta )\nabla q(\zeta )$$

is the last hitting-point flux. The choice of the last hitting point to represent the point where a reactive trajectory crosses an isocommittor is somewhat arbitrary. Therefore, it is gratifying to know that the expression for J(ζ) also gives the net flux and the first hitting-point flux of reactive trajectories.

The normal to an isocommittor is given by n̂(ζ) = ∇q(ζ)/|∇q(ζ)|, so the distribution of last hitting points on an isocommittor is proportional to

$$j(\zeta )={\rho }_{\xi }(\zeta )\nabla q{(\zeta )}^{\top }D(\zeta )\nabla q(\zeta )/|\nabla q(\zeta )|.$$

In particular, of interest is the flow rate through a tiny disk at ζ. Thus, we consider here the corrected last hitting point density j_c(ζ). A natural choice for M(ζ) is D(ζ)⁻¹ because it simplifies the expression for j_c(ζ) and it can be shown to be a metric tensor. (D(ζ) is the “harmonic” Boltzmann-weighted average of $({\xi }_x{M}^{-1}{{\xi }_x^{\top })}^{-1}$, and $(\mathrm{\Delta }{\zeta }^{\top }({\xi }_x{M}^{-1}{{\xi }_x^{\top })}^{-1}{\mathrm{\Delta }\zeta )}^{1/2}$ is the distance from the hyperplane ξ(x) = ζ to the hyperplane ξ(x) = ζ + Δζ at the point x.) Hence, the corrected last hitting point density becomes

$$j_{\mathrm{c}}(\zeta )=|D{(\zeta )}^{1/2}\nabla q(\zeta )|(\text{det}D{(\zeta ))}^{1/2}{\rho }_{\xi }(\zeta ).$$

3.3 Defining the path

For computation it is convenient to label the isocommittors with the path parameter s. In particular, denote by Σ(s), 0 ≤ s ≤ 1, the isocommittor passing through ζ = Z(s). Write q̄(s) = q(Z(s)) and define σ(ζ) implicitly by

$$q(\zeta )=\overline{q}(\sigma (\zeta )).$$ (5)

In this way the committor q(ζ) is decomposed into two independent parts: one part σ(ζ) specifies the isocommittor label and the other part q̄(s) calibrates the isocommittors. Thus, ∇q(ζ) = q̄_s(σ(ζ))∇σ(ζ), and the corrected normal flux is

$$j_{\mathrm{c}}(\zeta )={\overline{q}}_s(\sigma (\zeta )){(\nabla \sigma {(\zeta )}^{\top }D(\zeta )\nabla \sigma (\zeta ))}^{1/2}(\text{det}D{(\zeta ))}^{1/2}{\rho }_{\xi }(\zeta )$$ (6)

(recalling that the subscript s denotes differentiation d/ds). Note that q̄_s(σ(ζ)) is constant on an isocommittor Σ(s), so it can be neglected when determining the center of intensity of j_c(ζ).

Each point Z(s) on the desired path maximizes the last hitting-point flux j_c(ζ) on the isocommittor q(ζ) = q(Z(s)). Hence, ∇j_c(Z(s)) ‖ ∇q(Z(s)). To keep the derivation independent of the calibration q̄(s), introduce a vector n(s), not necessarily normalized, such that n(s) ‖ ∇q(Z(s)). Hence,

$$\nabla j_{\mathrm{c}}(Z(s))\Vert n(s).$$ (7)

3.4 The localized tube assumption

Assume there exists a tube connecting A_ξ to B_ξ such that (i) on each isocommittor, regions of high j_c(ζ) are concentrated in the tube, (ii) each isocommittor is nearly planar in the tube. This scenario is illustrated in Figure 2 below.

Exploit the localized tube assumption by approximating the isocommittor through Z(s) as a plane Π(s) with normal n(s). Hence, the isocommittor surface Σ(s) : σ(ζ) = s has the simple description of a hyperplane,

$$\Pi (s):n(s)·(\zeta -Z(s))=0.$$ (8)

These approximations (see Ref.11 (Sec. 6.6.1)) are sufficient to define a practical method (see Ref.30 (Sec. 12)). The unknown direction vector n(s) is to be chosen to minimize the integral I(q)) of Eq. (2) restricted to some tube. For simplicity the boundary points Z(0) and Z(1) can be moved to points in A_ξ and B_ξ that locally minimize F(ζ). In this way the problem of solving for a committor of many variables is reduced to that of a one-dimensional calculation along the length of the tube.

It remains to derive the condition that determines Z(s). This is done in Appendix D, where it is shown that the condition is

$$-\beta \nabla F^{+}(Z)+\frac{{\nabla }_{\zeta }c(\zeta ,D(\zeta )n)}{c(\zeta ,D(\zeta )n)}{|}_{\zeta =Z}+\frac{n_s}{n^{\top }{Z}_s}\Vert n.$$

A further simplification is to assume (iii) D(ζ) is nearly constant on each isocommittor within the tube. More specifically, approximate D(ζ) by D(Z(σ(ζ))). Then, as shown in Appendix D, the above condition simplifies to

$$-\beta \nabla F(Z)+\frac{n_s}{n^{\top }{Z}_s}\Vert n.$$ (9)

3.5 The maximum flux transition path

Although the localized tube assumption is sufficient for defining a practical method, the method would not be simple, so we make an additional simplifying assumption: Assume the flux J(ζ) points in the direction of the path so that J(Z(s)) ‖ Z_s(s) or D(Z(s))∇q(Z(s)) ‖ Z_s(s), whence

$$n(s)\Vert D{(Z(s))}^{-1}{Z}_s(s).$$

As it can be shown, the result is a maximum flux transition path

$$-\beta \nabla F^{+}(Z)-\frac{{\nabla }_{\zeta }c(Z,Z_s)}{c(Z,Z_s)}+\frac{{(D{(Z)}^{-1}{Z}_s)}_s}{c{(Z,Z_s)}^2}\Vert D{(Z)}^{-1}{Z}_s.$$ (10)

(The simplifying assumption is justified, for example, if the probability is strongly peaked around the path, resulting in most of the probability contained in a narrow tube with a flux J(ζ) pointing in the direction of the tube and the path.) This assumption is also made for the FTS method, see Eq. (14) of Ref.19 and Sec. II.A. of Ref.20 Geometrically, this condition means that instead of having the free energy gradient vanish orthogonal to the path, it is balanced by a “centripetal” force, which reduces curvature and avoids cusps.

To express Eq. (10) as an equation, write it as −βc(Z, Z_s)²∇F⁺ − c(Z, Z_s)∇_ζc(Z, Z_s) + (D⁻¹Z_s)_s = λD(Z)⁻¹Z_s where λ is a scalar and premultiply by $Z_s^{\top }$ to obtain an expression for λ. After eliminating λ, the equation becomes

$$(I-\Pi )(c{(Z,Z_s)}^2\beta \nabla F^{+}(Z)+c(Z,Z_s){\nabla }_{\zeta }c(Z,Z_s)-(D{(Z)}^{-1}{Z_s)}_s)=0$$ (11)

where $\Pi =c^{-2}{D}^{-1}{Z}_s{Z}_s^{\top }$.

Note that, if D is constant, the limit β → 0 for Eq. (11) gives a geodesic Z_ss = 0, which is the desired result.

In the two-dimensional case with D = I, the Euclidean length of $(I-\Pi )D(D^{-1}{Z_s)}_s/(Z_s^{\top }{D}^{-1}{Z}_s)$ is exactly equal to the curvature, which is defined to be the reciprocal of the radius of curvature. To see this, note that this is true if we parameterize with (actual) arc length and note also that the curvature term is independent of parameterization (which can be checked analytically).

If we normalize the parameterization using (d/ds)c(Z,Z_s) = 0, this implies

$$\Pi ({\nabla }_{\zeta }c(Z,Z_s)-c{(Z,Z_s)}^{-1}(D{(Z)}^{-1}{Z_s)}_s)=0.$$

Combining with Eq. (11), we have

$$(I-\Pi )c{(Z,Z_s)}^2\beta \nabla F^{+}(Z)+c(Z,Z_s){\nabla }_{\zeta }c(Z,Z_s)-(D{(Z)}^{-1}{Z_s)}_s=0.$$

(If the normalization $(Z_s^{\top }{Z_s)}_s$ is used instead, the equation has the same form but with the projector $\Pi =(Z_s^{\top }{Z_s)}^{-1}{D}^{-1}{Z}_s{Z}_s^{\top }D$ .)

The presence of partial derivatives of D(ζ) can be awkward. From the simplified condition Eq. (9), we get the simplified maximum flux transition path (SMFTP)

$$-\beta \nabla F(Z)+\frac{{(D{(Z)}^{-1}{Z}_s)}_s}{c{(Z,Z_s)}^2}\Vert D{(Z)}^{-1}{Z}_s.$$ (12)

We will implement the SMFTP in the following section; a similar procedure can be devised for the MFTP.

Values obtained from constructing the path can be used to calculate the free energy F(Z(s)) along the path,

$$F(Z(s))-F(Z(0))={\displaystyle {\int }_0^s\nabla F(Z{(s\prime ))}^{\top }{Z}_s(s\prime )\mathrm{d}s\prime .}$$ (13)

However, F(Z(s)) is not a potential of mean force for the transition.

3.6 The minimum free energy path

The simplifying assumption of the preceding subsection, which is used to derive the MFTP, is valid in the limit β → ∞ in the Brownian dynamics approximation; see Ref. 11 (Sec. 6.6) and Ref.9 (App. A). A more systematic derivation might therefore neglect the curvature term. The result would be a minimum free energy path

$$Z_s\Vert -\beta D(Z)\nabla F(Z).$$

Each point ζ = Z(s) on the MFEP is a local minimum of F(ζ) in the hyper-plane orthogonal to D(Z(s))⁻¹Z_s(s).

One difference from an MFTP is that an MFEP can have a cusp at an intermediate local minimum. If the path passes sufficiently close to a local minimum ζ = ζ₀ of F(ζ), then for a short section of the path, ζ = Z(s), a ≤ s ≤ b, a quadratic approximation to F(ζ) is accurate. Assume D = constant and $F(\zeta )=\frac{1}{2}(\zeta -{{\zeta }_0)}^{\top }A(\zeta -{\zeta }_0)+$ constant, where A is symmetric positive definite. The MFEP is then defined by Z_s ‖ − βDA(Z − ζ₀). Perform a change of variables, $Y={\beta }^{-1/2}{Q}^{\top }{D}_{1/2}^{-1}(Z-{\zeta }_0)$ where QΛQ^⊤ is a diagonalization of $D_{1/2}^{\top }{\mathit{\text{AD}}}_{1/2}$. The MFEP for Y(s) is hence given by Y_s ‖ −ΛY. For simplicity, suppose that Y = [x, y]^⊤, that x(a) < 0 < x(b), and that Λ = diag(λ, µ) with λ > µ. The path is hence defined by y_s/(µy) = x_s/(λx), which can be integrated to yield the path

$$y=\{\begin{array}{ll}{(x/x(a))}^{\mu /\lambda }y(a),\hfill & x(a)\le x\le 0,\hfill \\ {(x/x(b))}^{\mu /\lambda }y(b),\hfill & 0\le x\le x(b),\hfill \end{array}$$

which has a cusp at x = 0.

The FTS method path is also likely to suffer from the presence of cusps, because for a harmonic potential, the average position is the same as the most probable position.

The presence of cusps undermines the localized tube assumption. In particular, the assumption of isocommittors being approximately planar breaks down at a cusp. This poses a difficulty when computing quantities that are averages on isocommittors. Additionally, cusps complicate the numerical approximation of paths.

4 An algorithm

An algorithm for calculating a transition path employs a progression of four controlled approximations: discretization of the path ζ = Z(s) and the equations that define it; a finite number of iterations for the solution of nonlinear discrete equations; use of restraints for constrained sampling; and finite sampling.

4.1 Discretization

The path Z(s), 0 ≤ s ≤ 1, is approximated as a piecewise polynomial with break points 0 = s₀ < s₁ < ⋯ < s_J = 1. Here we choose a uniform mesh s = 0, Δs, …, 1 and obtain the path by piecewise linear interpolation. Thus the problem is reduced to determining unknown nodal values Z_j ≈ Z(s_j), j = 0,1,…,J, each representing a replica of the system in a different configuration.

It is convenient for computation to use for the path parameter s the arc length along the path divided by the total length of the path. In such a case, |Z_s(s)| is constant. The arc length normalization becomes

$$|Z_{j+1}-Z_j|/\mathrm{\Delta }s=|Z_j-Z_{j-1}|/\mathrm{\Delta }s,j=1,2,\dots ,J-1.$$

Eq. (12) is written as

$$-\beta D\nabla F-\frac{1}{c^2}{D}_s{D}^{-1}{Z}_s+\frac{1}{c^2}{Z}_{\mathit{\text{ss}}}\Vert Z_s.$$

This is discretized by the finite difference scheme

$${(Z_s)}_j\Vert g_j,\text{where}{g}_j\stackrel{\text{def}}{=}-\beta D_j{(\nabla F)}_j-\frac{1}{c_j^2}{(D_s{D}^{-1}{Z}_s)}_j+\frac{1}{c_j^2}\frac{Z_{j+1}-2Z_j+Z_{j-1}}{\mathrm{\Delta }{s}^2}$$

and where

$$c_j^2=\frac{1}{2}\mathrm{\Delta }{s}^{-2}({\mathrm{\Delta }}_{-}{Z}_j^{\top }{D}_j^{-1}{\mathrm{\Delta }}_{-}{Z}_j+{\mathrm{\Delta }}_{+}{Z}_j^{\top }{D}_j^{-1}{\mathrm{\Delta }}_{+}{Z}_j),$$ (14)

$$(D_s{D}^{-1}{Z_s)}_j=\frac{1}{2}\mathrm{\Delta }{s}^{-2}({\mathrm{\Delta }}_{-}{D}_j{D}_j^{-1}{\mathrm{\Delta }}_{-}{Z}_j+{\mathrm{\Delta }}_{+}{D}_j{D}_j^{-1}{\mathrm{\Delta }}_{+}{Z}_j),$$ (15)

with

$${\mathrm{\Delta }}_{\pm }{D}_j=\mp (D_j-D_{j\pm 1}),\text{and}{\mathrm{\Delta }}_{\pm }{Z}_j=\mp (Z_j-Z_{j\pm 1}).$$

We choose upwinded differencing for (Z_s)_j based on the direction of the modified mean force g_j:

$${(Z_s)}_j=\{\begin{array}{ll}(Z_j-Z_{j-1})/\mathrm{\Delta }s\hfill & \text{if}{g}_j^{\top }(Z_j-Z_{j-1})>0,\hfill \\ (Z_{j+1}-Z_j)/\mathrm{\Delta }s\hfill & \text{if}{g}_j^{\top }(Z_j-Z_{j+1})>0.\hfill \end{array}$$ (16)

In the unlikely event that both conditions are satisfied, the choice is dictated by the arc length normalization step of the simplified string method to be discussed next.

Analogous to the development in Section 3.5, it is possible to use the parameterization normalization to get a nonsingular second order difference equation for the values Z_j, but this is omitted because the solution method uses the formulation given here.

For the MFEP, cusps can occur at some intermediate local minima, requiring an adaptive mesh to resolve.

4.2 Solution of nonlinear discrete equations

A second component of the algorithm is an iterative method for achieving rapid local convergence given a plausible initial guess.

Because of its simplicity and demonstrated effectiveness, we adopt the semi-implicit simplified string method used in Ref.22 (Eq. (11)). To determine a path, begin with an initial guess and generate successive improvements by alternating between moving the points of the curve Z_j in the direction g_j and reparameterizing.

The first step of each iteration is to solve the following equations for the $Z_j^{*}$:

$$\begin{array}{l}\frac{Z_j^{*}-Z_j}{{\tau }^2}=\frac{1}{c_j^2}\frac{Z_{j+1}^{*}-2Z_j^{*}+Z_{j-1}^{*}}{\mathrm{\Delta }{s}^2}-\frac{1}{c_j^2}{(D_s{D}^{-1}{Z}_s)}_j-\beta D_j{(\nabla F)}_j,j=1,2,\dots ,J-1,\hfill \\ \frac{Z_j^{*}-Z_j}{{\tau }^2}=-\beta D_j{(\nabla F)}_j,j=0,J,\hfill \end{array}$$

where $c_j^2$ and (D_sD⁻¹Z_s)_j are given in Eq. (14) and Eq. (15). (The extra factor τ provides the time scale factor missing from D.)

Then the normalization adjustment is to choose the {Z_j} to be equidistant along the resulting curve:

$$\begin{array}{ll}{s}_0^{*}\hfill & =0,s_j^{*}=s_{j-1}^{*}+|Z_j^{*}-Z_{j-1}^{*}|,\hfill \\ Z^{*}(s)\hfill & =\text{piecewise linear interpolation of}\{(s_j^{*}/s_J^{*},Z_j^{*})\},0\le s\le 1,\hfill \\ Z_j^{\text{new}}\hfill & =Z^{*}(j/J).\hfill \end{array}$$

It can be shown that if the semi-implicit simplified string method converges, the resulting points Z_j satisfy a nonstandard discretization of the differential equation containing τ as a parameter. In the limit τ → 0, the discretization becomes upwinded differencing.

For large systems, targeted molecular dynamics³¹ has been used to get an initial path.^2,32 Another potentially promising but quite different approach is rigidity analysis.³³

4.3 Conditional averages

Evaluation of ∇F and D at break points involves sampling on hyper-surfaces {x : ξ(x) = Z_j} of configuration space.

For calculating such conditional expectations, the Dirac delta function δ(s) can be approximated by the p.d.f. of a Gaussian δ_ε(s) = (2πε²)^−1/2exp(−s²/(2ε²)). Note

$${\delta }_{\epsilon }(\xi (x)-\zeta ){\mathrm{e}}^{-\beta U(x)}={(2\pi {\epsilon }^2)}^{-\nu /2}{\mathrm{e}}^{-\beta U(x;\zeta )}$$

where

$$U(x;\zeta )=U(x)+{\displaystyle \sum _{i=1}^{\nu }{u}_i(x,{\zeta }_i),\text{\hspace{1em}and }{u}_i(x,{\zeta }_i)=\frac{1}{2\beta {\epsilon }^2}{({\xi }_i(x)-{\zeta }_i)}^2.}$$ (17)

Then, 〈O(x)〉_ζ = 〈O(x)δ_ε(ξ(x) − ζ)〉/〈 δ_ε(ξ(x) − ζ)〉 is nothing but an average using U(x; ζ). The effect is that of using restraining potentials instead of constraints. These restraints should be as strong as possible without restricting the step size used in the sampling. From const_ξ exp(−βF(ζ)) = 〈δ_ε(ξ(x) − ζ)〉, we have

$$\nabla F(\zeta )=-\frac{1}{\beta {\epsilon }^2}\langle \xi {(x)-\zeta \rangle }_{\zeta }.$$

4.4 Sampling

We would like to estimate the statistical error of $Z_j^{*}$. Ideally, we want the standard deviation of the estimate smaller than some given tolerance. The major contribution to the sampling error of $Z_j^{*}$ comes from that of (∇F)_j, because of the cancelation and subsequent multiplication by ε⁻². Thus, we neglect the statistical error of D_j in estimating the error of g_j. So then, the statistical error of $Z_j^{*}$ comes from the sample average of ${\mathrm{\Delta }}_j=\beta D_j{(\nabla F)}_j^n$, n = 1,2,…,N, where N is the sample size. The statistical error is defined by (max_0≤j≤Jerror bar of Δ_j)τ², where an error bar is an estimate of 1 standard deviation. Such an estimate can be obtained using block averaging as in Ref.34 (Appendix D.3). In general, 32 blocks is a reasonable choice.

At each iteration, the configuration x from the previous iteration could be used to start the equilibration of the molecular dynamics. Thus, it is necessary that values of x be stored such that ξ(x) = Z_j, j = 0,1,…,J. It is reasonable to expect less equilibration time is needed in later iterations as the path converges.

5 Numerical tests

5.1 An artificial problem

As an example to illustrate our method, consider a problem finding the MFTP and MFEP for the potential energy function

$$\begin{array}{ll}U(x,y)=\hfill & -4\text{exp}(-4x^2-{(y-2.75)}^2)-5\text{exp}(-{(x-1)}^2-{(y-0.15)}^2)\hfill \\ \hfill & -5\text{exp}(-{(x+1)}^2-y^2)+8\text{exp}(-x^2-{(y+0.5)}^2)+0.001(x^4+y^4)\hfill \end{array}$$

where the energy unit is kcal/mol and the mass matrix M has identical diagonal entries. Unless specifically mentioned, the inverse temperature β⁻¹ = 0.59595 kcal/mol, corresponding to 300 K. In particularly, we take collective variables ζ = ξ(x,y) = (x,y). In this case, the MFEP becomes a minimum energy path (MEP). Alternatively, an MEP can be considered as an MFEP for which we have an accurate estimate of F(ζ).

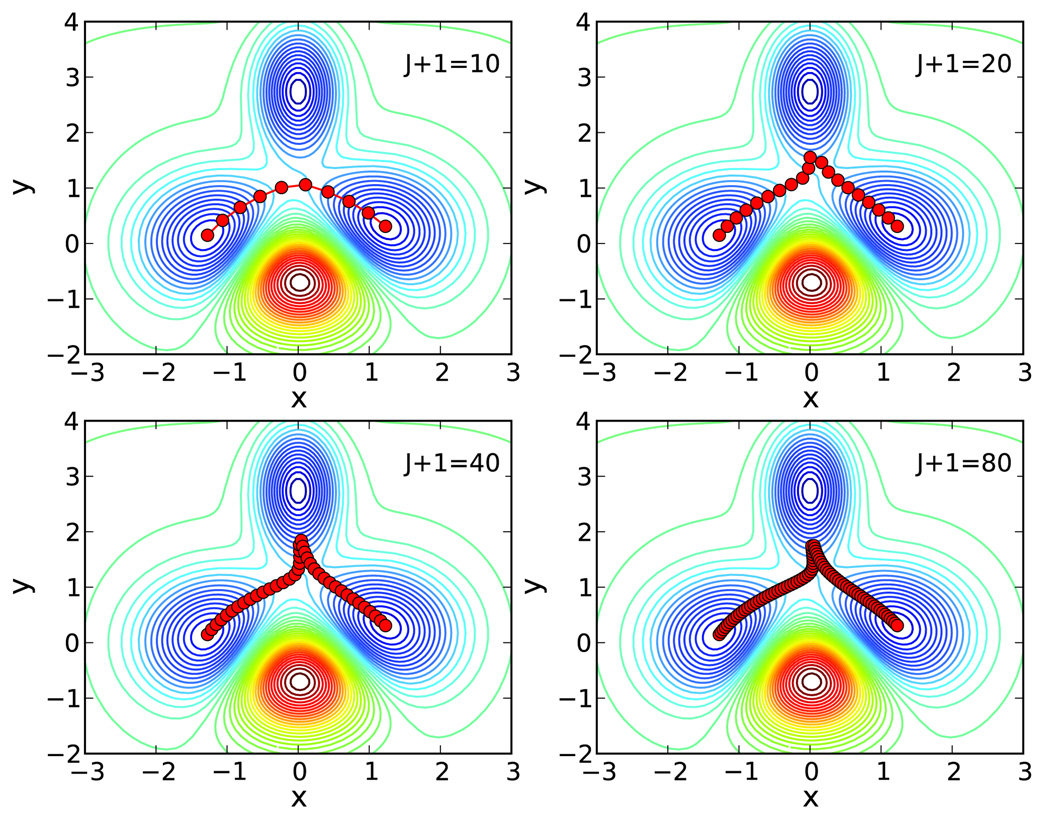
In Figure 3, we show an MEP connecting two local minima through the third local minimum. The MEP has a cusp at the intermediate minimum. The MEPs are computed using the simplified string method with piecewise linear interpolation and equal arc length normalization. The time step τ² = 0.01. The iteration is stopped if d < 0.00005, where $d={\text{max}}_{0\le j\le J}|Z_j^{\text{new}}-Z_j|$. From the figure, we can see that the cusp is missing if the number of images (J + 1 = 10) is too small. Also, the MEP does not go through the intermediate local minimum as it should, even with many images (J + 1 = 80).

Figure 3.

Minimum energy path obtained using the simplified string method. The initial path is the straight line between (−1,0) and (1,0). The path is discretized into J + 1 images. Four figures are generated using J + 1 = 10, 20, 40, 80 images, respectively.

A calculation (not shown here) similar to that for Figure 3 was done for the MFTP. The MFTP is calculated using the semi-implicit simplified string method described in Section 4. The MFTP can be resolved using a relatively small set of images, for example, the MFTP calculated by only 10 images (J = 9) is almost indistinguishable from the one calculated using 80 images (J = 79). The MFTP avoids the cusp problem.

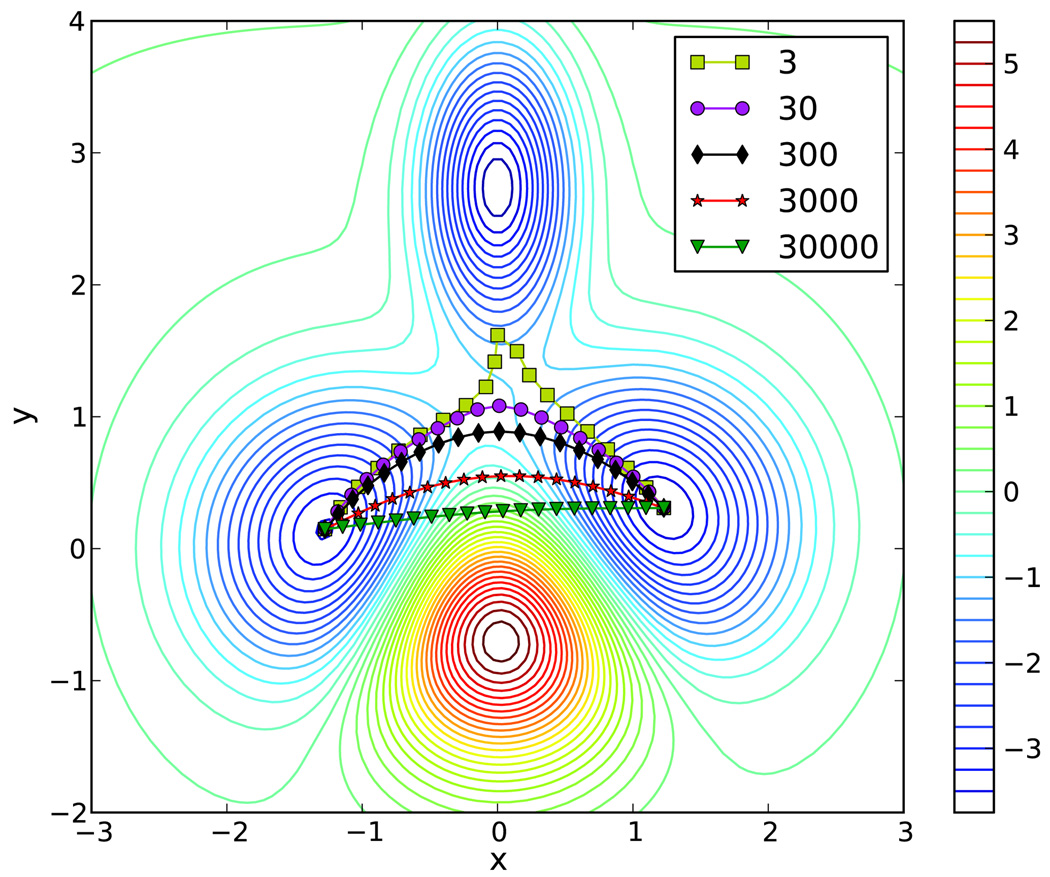
The MFTP generates different paths at different temperature. Figure 4 shows MFTPs at 3 K, 30 K, 300 K, 3000 K, 30000 K, respectively. It is clear that the MFTP is close to the MEP at low temperature (3 K) and is close to a straight line at high temperature (30000 K), which is what we expect.

Figure 4.

Maximum flux transition path obtained using the semi-implicit simplified string method. Here we used the same initial path and the same stopping criterion for convergence as for Figure 3. The MFTPs are generated using 20 images at 3 K, 30 K, 300 K, 3000 K, 30000 K, respectively (which roughly correspond to β⁻¹ = 0.006,0.06,0.6,6,60 kcal/mol.) The contour lines are separated by 0.25 kcal/mol.

An FTS method path is expected to be similar to an MFEP for this example.

5.2 Phi, psi for alanine dipeptide in vacuum

For comparison with the MFEP, we study alanine dipeptide at 300 K in vacuum.⁹ We compare the MFEP and the MFTP with two dihedral angles ϕ and ψ as collective variables. All simulations were performed using the CHARMM simulation program^25,35 and the full-atom representation of the molecule in the CHARMM force field.^36,37 Langevin dynamics with friction coefficient 10.0 ps⁻¹ and time step 1.0 fs was used. For the calculation of ∇F and D, harmonic potentials as in Eq. (17) were added involving the dihedral angles ϕ and ψ with force constant k = 2000 kcal/(mol rad²). (k = 1/βε² so ε = 1°.)

The initial path in collective variable space is a straight line between two points in (ϕ,ψ)-space. The path is discretized into J + 1 images. The configuration of alanine dipeptide at each image along the initial path is built using the IC module in CHARMM with dihedral angles fixed at the interpolated values. Then follow 1000 steps of minimization and 50,000 steps of heating before the iteration starts. Each iteration of the path involves 50,000 steps of equilibration and 500,000 steps of sampling (per image). The configuration at the final step of sampling in the previous iteration is used as the initial configuration for the equilibration in the next iteration.

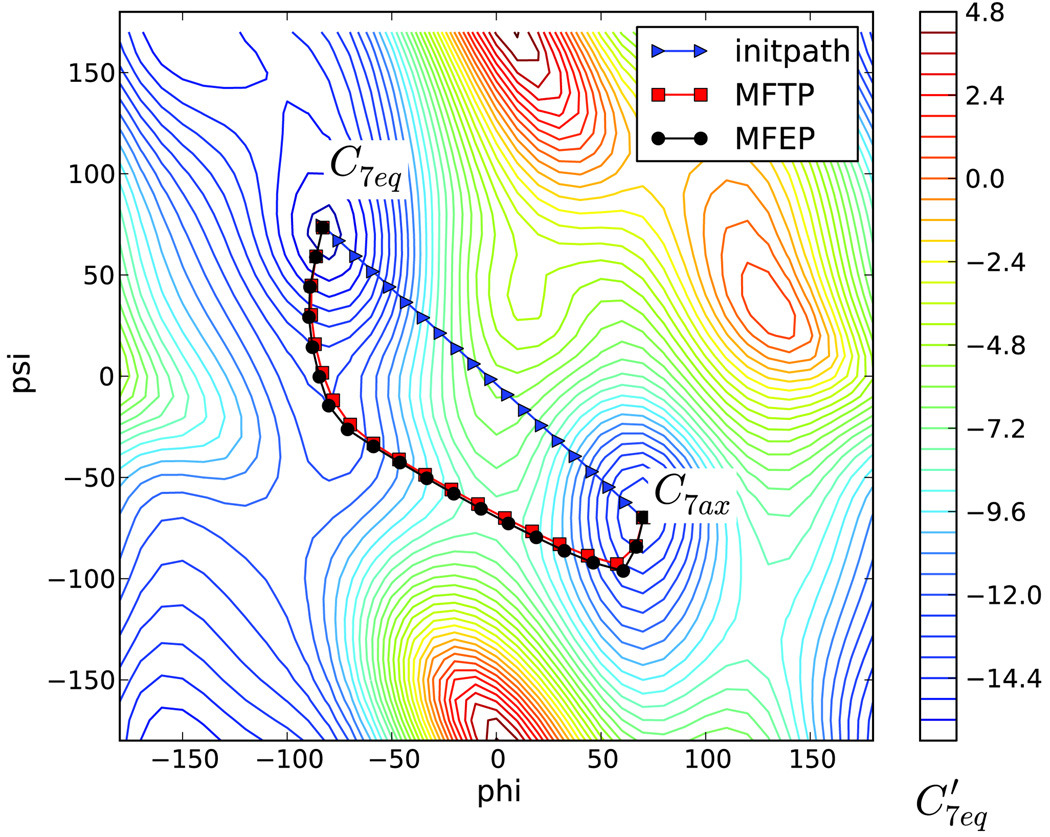
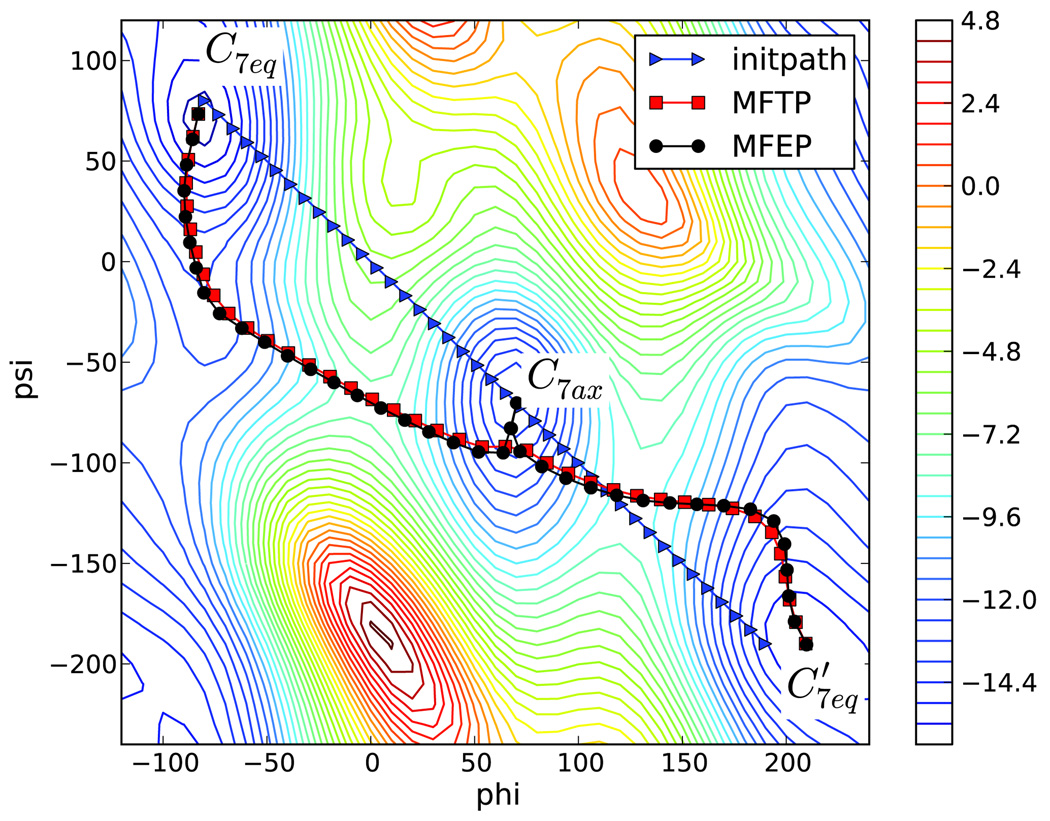
We begin by comparing the MFTP and MFEP from C_7eq to C_7ax. The MFEP is calculated using the simplified string method with linear interpolation between images and equal arc length normalization. The MFTP is calculated using the semi-implicit simplified string method. In Figure 5, the initial path is the straight line between (−83.2°,74.5°) and (70°, −70°), which were determined as C_7eq and C_7ax in Ref.9 The path is discretized into 20 images. The time step τ² = 0.16 in CHARMM time units squared, or τ² = (19.56fs)². The statistical error estimated by block averaging using 32 blocks is ±0.00577°. The iteration is stopped if d < 0.18°. (The tolerance value should be chosen properly since the statistical error will eventually dominate the other errors so that d fluctuates about a positive number.) It takes 34 and 31 iterations to converge for the MFTP and MFEP, respectively. The computational cost for two methods is comparable. The path calculated for this problem by the FTS method using the CHARMM force field is given in Figure 5 of Ref.19

Figure 5.

Maximum flux transition path and minimum free energy path from C_7eq to C_7ax for alanine dipeptide in vacuum at 300 K. Triangles are images of the initial path; rectangles are the images of the maximum flux transition path; and circles are the images of the minimum free energy path. The contours are those for the zero-temperature free energy (adiabatic energy). The contour lines are separated by 0.6 kcal/mol.

Next we compare the MFTP and MFEP from C_7eq to $C_{7\text{eq}}^{\prime }$. In particular, we calculate the transition path $C_{7\text{eq}}-C_{7\text{ax}}-C_{7\text{eq}}^{\prime }$, in which C_7ax serves as an intermediate metastable state. The initial path is taken to be the straight line between (−80°, 80°) and (190°, −190°). Figure 6 shows the MFTP and MFEP generated using 40 images. The time step τ² = 0.16 in CHARMM time units squared. The iteration is stopped if d < 0.18°. It takes 35 and 44 iterations for the MFTP and MFEP to converge, respectively. It is evident that the MFTP is more efficient than the MFEP in this case.

Figure 6.

Maximum flux transition path and minimum free energy path for alanine dipeptide from C_7eq to $C_{7\text{eq}}^{\prime }$ passing by C_7ax in vacuum at 300 K. The figure is generated using 40 images. Triangles are the images for the initial path; rectangles are the images of the maximum flux transition path; and circles are the images of the minimum free energy path. The contours are those for the zero-temperature free energy. The contour lines are separated by 0.6 kcal/mol.

5.3 Phi, psi for alanine dipeptide in solution

We also test our method for alanine dipeptide solvated in explicit water. Again, the backbone dihedrals ϕ and ψ are used as collective variables to describe the transition. The initial paths are straight lines connecting two points among (−77°, 138°), (55°, 48°), (60°, −72°), and (−77°, −39°) in (ϕ, ψ)-space.

For preparing the simulation, each starting structure for alanine dipeptide with constrained ϕ and ψ angels is solvated in a (20 × 18 × 15) ų box with 191 TIP3³⁸ water molecules and equilibrated for 50,000 ps. The molecular dynamics are carried out with the CHARMM program under the CHARMM22 force field. Periodic boundary conditions are used and the electrostatic interactions are treated with the particle–mesh Ewald method.³⁹ The system is simulated at a constant pressure of 1.0 atm and a constant temperature 300 K with the algorithm based on Hoover’s methods. We use a 1-fs time step with the SHAKE⁴⁰ algorithm to keep all bonds involving hydrogen atoms at fixed lengths.

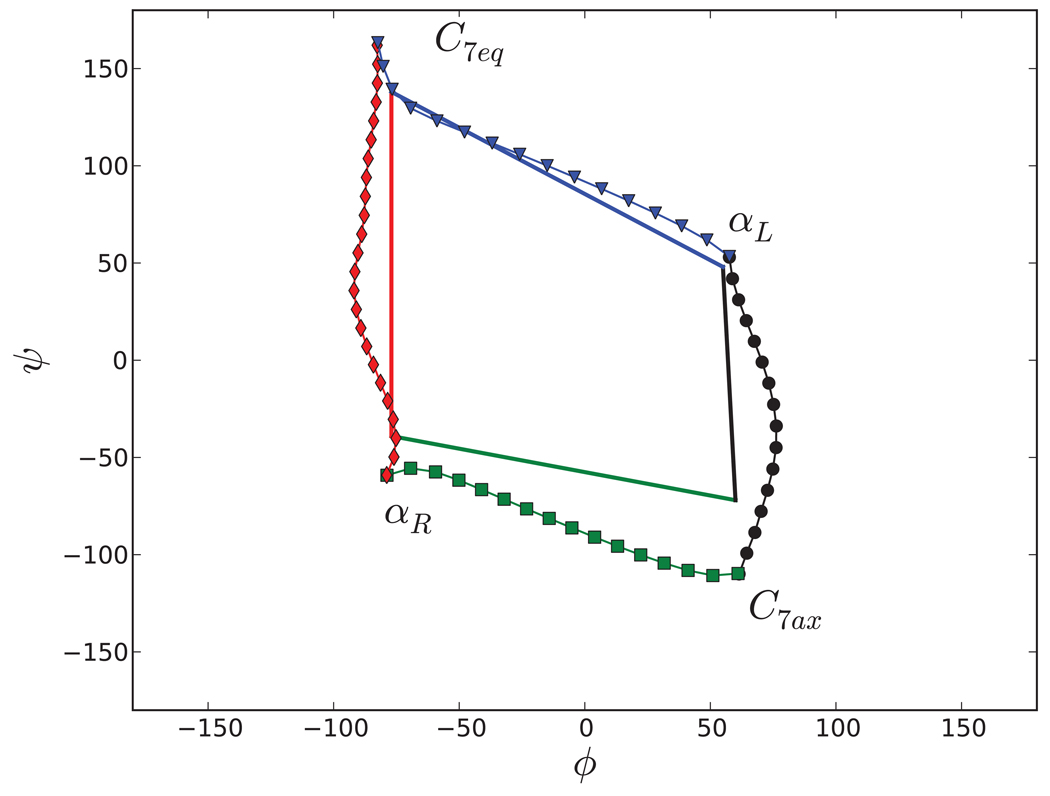
In Figure 7, four MFTPs are calculated using the semi-implicit simplified string method. Each iteration involves 50,000 steps of equilibration and 500,000 steps of sampling. The transition paths are the result of 50 iterations. The path C_7eq–α_R calculated for this problem by the FTP method using the CHARMM force field is given in Figure 12 of Ref.19 The MFTP is similar to the FTS method path.

Figure 7.

Maximum flux transition paths for alanine dipeptide in solution. The transition paths are calculated by the semi-implicit simplified string method with the nearby straight lines as initial paths.

5.4 Alpha carbon coordinates for alanine decapeptide in vacuum

In this example, conformational change of alanine decapeptide from a α-helical structure to a π helix is studied. Alanine decapeptide is a small molecule with 9 residues and 102 atoms, terminated with methyl groups.⁴¹ The transition from one state to another involves breaking and forming hydrogen bonds. In particular, the α helix forms hydrogen bonds between residues i and i + 4, and the π helix forms hydrogen bonds between residues i and i + 5.

In defining the reaction, the backbone atoms are more important than side chain atoms.⁴¹ In this study, we use the Cartesian coordinates of the 9 alpha carbon atoms as collective variables. The MFTP is calculated using the semi-implicit simplified string method, where the time step τ² = 0.2 in CHARMM time units squared and the iteration is stopped if d < 0.004 Å. The initial path is a straight line connecting coordinates of the α helix and π helix in collective variable space and it is discretized into 51 replicas. The molecular simulations are done using CHARMM program with CHARMM22 all-atom force field. The harmonic force constant is 200 kcal/mol/Ų (ε = 0.0547Å). At each iteration, samples are taken from a 500-ps simulation following 50-ps equilibration. It takes 234 iterations before the path converges. The more stringent stopping criterion requires more computational time, but it gives a better quality path.

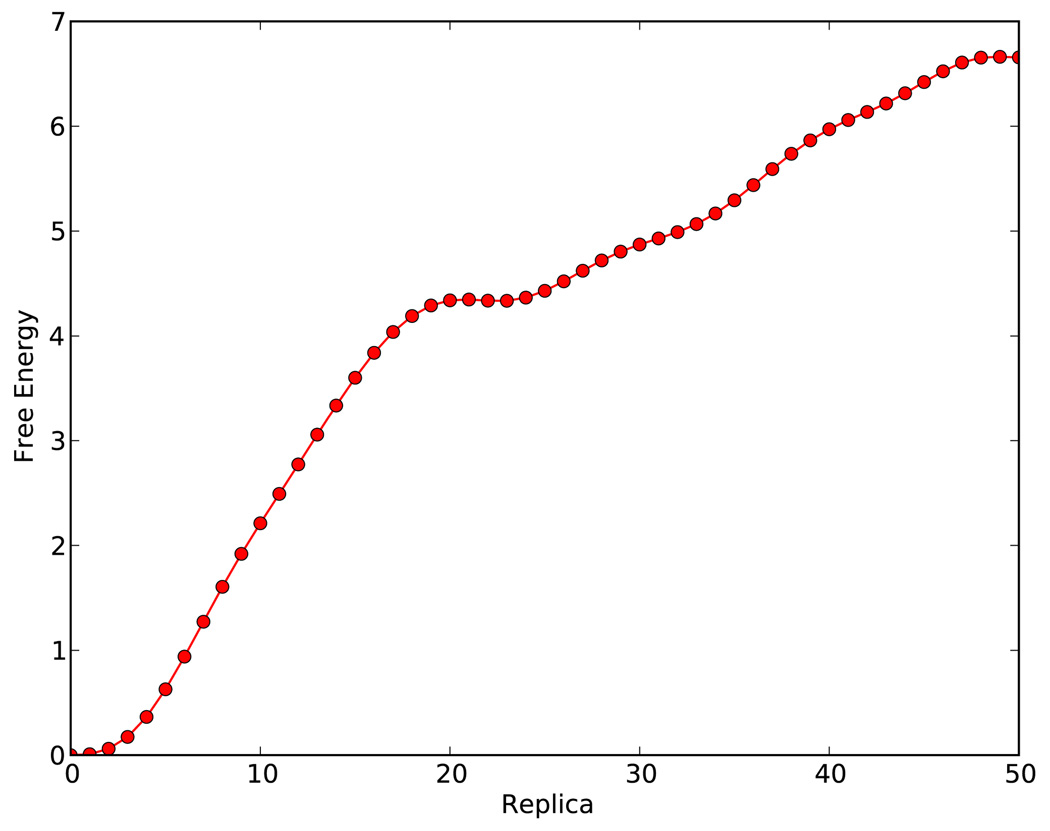
Figure 8 shows the free energy profile along the MFTP. The free energy is calculated using Eq. (13). Specifically, F₀ = 0, F_j = F_j−1 + (1/2)(∇F_j−1 + ∇F_j) · (Z_j−Z_j−1), j = 1,2,…,J. There might be transition states at replica 20 and 49 and a marginal intermediate metastable state at replica 23. Computation using backbone ϕ and ψ angels as collectiv variables yields a similar free energy plot. The free energy plot along the transition path is similar to one of the three MEPs in Ref.41 For the other two paths the transition takes place by passing through a higher energy barrier than the energy difference between the α helix and π helix. It appears that the transition from the α helix to π helix is not a barrier-crossing event.

Figure 8.

Free energy profile along the transition path.

A A correction factor for hypersurface area

The flow rate through a tiny disk at ζ is j(ζ) times the area of the disk. Let D(M;ε) be a disk of radius ε in the M(·)-metric on a quasi-committor isosurface at some point ζ. Then D(M;ε) is the intersection of the ball {ζ′ | (ζ′ − ζ)^⊤M(ζ)(ζ′ − ζ) ≤ ε²} with the surface {ζ′ | n̂ · (ζ′ − ζ) ≈ 0}, where n̂ = ∇q̂/|∇q̂|. Let 1_ε(u) = 1, 0 ≤ u ≤ ε, and 1_ε(u) = 0, u > ε. Then,

$$\text{area}={\displaystyle {\int }_{D(M;\epsilon )}\mathrm{d}{S}_{\zeta }={\displaystyle \int 1_{\epsilon }\left({(\zeta \prime -\zeta )}^{\top }M(\zeta )(\zeta \prime -\zeta )\right)}}\delta (\widehat{n}·(\zeta \prime -\zeta ))\mathrm{d}\zeta \prime .$$

After a change of variables ζ′ = ζ + M(ζ)^−1/2ζ″, we have

$$\begin{array}{ll}\text{area}\hfill & ={\displaystyle \int 1_{\epsilon }({(\zeta ″)}^{\top }\zeta ″})\delta (\widehat{n}·M^{-1/2}\zeta ″)\text{det}(M^{-1/2})\mathrm{d}\zeta ″\hfill \\ \hfill & =|M^{-1/2}\widehat{n}{|}^{-1}{(\text{det}M)}^{-1/2}{\displaystyle \int 1_{\epsilon }({(\zeta ″)}^{\top }\zeta ″)\delta (\zeta ″·\widehat{t})\mathrm{d}\zeta ″=|M^{-1/2}\widehat{n}{|}^{-1}{(\text{det}M)}^{-1/2}{\displaystyle {\int }_{D(I;\epsilon )}\mathrm{d}\zeta }}\hfill \end{array}$$

where t̂ = M^−1/2n̂/|M^−1/2n̂|. Accordingly, we obtain a correction factor

$$|M^{-1/2}\widehat{n}{|}^{-1}{(\text{det}M)}^{-1/2}=|\nabla \widehat{q}|{(\text{det}M)}^{-1/2}/|M^{-1/2}\nabla \widehat{q}|.$$

B Derivation of Brownian dynamics approximation

The quasi-committor is related to a full phase-space committor q* defined in Ref.11 (Sec. 6. 2) as follows:

$$q*(x,p)=\text{Pr}(X(t)\text{reaches}B\text{before}A|X(0)=x,P(0)=p).$$

Note that q*(x, p) = 0 or 1, because the dynamical equation is deterministic. By definition, the quasi-committor q̂(ζ) = 〈q*(x, p)〉_ζ.

It is not difficult to show that q̂(ξ(x)) approximates q*(x, p) in the sense that it minimizes 〈|q(ξ(x)) − q*(x, p)|²〉 over all q(ζ). However, this is not useful for determining q̂(ζ) because q*(x, p) is too costly to compute. On the other hand, it is possible to find a best approximation to q*(x, p) in another sense. Because q* is constant on a trajectory, we have

$$0=\frac{\mathrm{d}}{\mathrm{d}t}{q}^{*}(X(t),P(t))=({\mathit{\text{Lq}}}^{*})(X(t),P(t))\text{ where}L=(M^{-1}p)·{\nabla }_x-U_x·{\nabla }_p.$$

Consequently, q* satisfies the stationary Liouville equation

$$\begin{array}{ccc}{\mathit{\text{Lq}}}^{*}=0,& q^{*}=0\text{on}A,& q^{*}=1\text{on}B.\end{array}$$

Since we do know Lq* = 0, we seek instead an approximation q that minimizes I(q) = 〈|L(q(ξ(x)) − q*(x, p))|²〉, a standard tactic in numerical analysis. As shown in Sec. III.B of Ref.,⁹ this simplifies to

$$I(q)=\frac{1}{\beta }\langle |M^{-1/2}{\nabla }_{x}q(\xi (x)){|}^2\rangle ,$$

which is to be as small as possible. A low value for I(q) is attained by having q(ζ) increase monotonically from the value 0 on A_ξ to the value 1 on B_ξ, which is consistent with the prescription given earlier that ξ(x) be chosen so that the quasi-committor has no local minima or maxima outside of A_ξ and B_ξ.

The functional I(q) can be expressed in terms of collective variables ζ as given by Eq. (2) and shown in Eq. (15) of Ref.9

C Derivation of lasting hitting-point distribution

The proof of Proposition 5 in Ref.8 (p. 158) analyzes the flux of reactive trajectories. The flux J(ζ) gives the rate at which such trajectories cross an arbitrary surface Σ that divides collective variable space into two parts, one containing A_ξ and the other containing B_ξ, via the integral ∫_ΣJ(ζ) · n̂(ζ)dS_ζ where n̂(ζ) points to the side containing B_ξ. The proof actually examines not all crossings but only those occurring within a vanishingly small time interval before the last crossing—see Eq. (50) of Ref.8 Therefore, it considers the net flux only in this limiting sense. As the length of the time interval τ → 0, the positions of these crossings all converge to the position of the last crossing. So, indeed, one gets the flux of the last hitting point from Proposition 5 of Ref.8 The result given in Ref.8 (Eq. (39)), as well as in Ref.10 (Eq. (6), Eq. (A12)), and Ref.11 (Eq. (62)), is that the last hitting-point flux for reactive trajectories is J(ζ) = ρ_ξ(ζ)D(ζ)∇q(ζ). (Proposition 4 of Ref.8 does not apply to the infinitely damped case of Langevin dynamics.) The expression for J(ζ) also gives the net flux of reactive trajectories, see Eq. (32) of Ref.11 Also, the formula for j(ζ) in Section 3.2 agrees in the special case D = I with that for the first hitting point distribution given in Ref.42 (Appendix B). Last and first are the same for reversible dynamics like Brownian dynamics. Finally, there is an example in Metzner, Schütte, and Vanden-Eijnden (2006) section III.C, where it is suggested to use n̂ · J.

D Derivation of the maximum flux condition

We have from Eq. (1) and Eq. (6) that the normal flux is

$$j_{\mathrm{c}}(\zeta )=cons{t}_{\xi }\text{exp}(-\beta F(\zeta )){\overline{q}}_s(\sigma (\zeta )){(\nabla \sigma {(\zeta )}^{\top }D(\zeta )\nabla \sigma (\zeta ))}^{1/2}(\text{det}D{(\zeta ))}^{1/2}$$ (18)

where σ(ζ) is defined implicitly by q(ζ) = q̄(σ(ζ)). And for each point Z(s) on the desired path, the condition to be satisfied Eq. (7) is ∇j_c(Z(s)) ‖ n(s). Furthermore, the assumption Eq. (8) that isocommittors are planar implies

$$n(\sigma (\zeta ))·(\zeta -Z(\sigma (\zeta )))=0.$$ (19)

Differentiating Eq. (19) w.r.t. ζ, we get

$$(n_s(\sigma )·(\zeta -Z(\sigma ))-n(\sigma )·Z_s(\sigma ))\nabla \sigma +n(\sigma )=0,$$

where the argument ζ of σ has been omitted, whence

$$\nabla \sigma =(n(\sigma )·Z_s(\sigma )-n_s(\sigma )·(\zeta -Z{(\sigma )))}^{-1}n(\sigma ).$$ (20)

Substituting Eq. (20) into Eq. (18), the normal flux becomes

$$j_{\mathrm{c}}(\zeta )=\phi (\sigma (\zeta ),\zeta ),$$

where

$$\phi (s,\zeta )=cons{t}_{\xi }\text{exp}(-\beta F^{+}(\zeta )){\overline{q}}_s(s)(n(s)·Z_s(s)-n_s(s)·(\zeta -Z{(s))}^{-1}c(\zeta ,D(\zeta )n(s)).$$

Note that

$$\frac{{\nabla }_{\zeta }\phi }{\phi }=-\beta \nabla F^{+}+\frac{{\nabla }_{\zeta }c(\zeta ,D(\zeta )n)}{c(\zeta ,D(\zeta )n)}+\frac{n_s}{n·Z_s-n_s·(\zeta -Z)},$$

and

$${\frac{{\nabla }_{\zeta }\phi }{\phi }|}_{\zeta =Z}=-\beta \nabla F^{+}(Z)+\frac{{\nabla }_{\zeta }c(\zeta ,D(\zeta )n)}{c(\zeta ,D(\zeta )n)}{|}_{\zeta =Z}+\frac{n_s}{n^{\top }{Z}_s}.$$

Thus, we have

$$\frac{\nabla j}{j}=\frac{({\nabla }_{\zeta }\phi )(\sigma (\zeta ),\zeta )}{\phi (\sigma (\zeta ),\zeta )}+\frac{{\phi }_s(\sigma (\zeta ),\zeta )}{\phi (\sigma (\zeta ),\zeta )}\nabla \sigma (\zeta ),$$

and

$${\frac{\nabla j}{j}|}_{\zeta =Z}=-\beta \nabla F^{+}(Z)+\frac{{\nabla }_{\zeta }c(\zeta ,D(\zeta )n)}{c(\zeta ,D(\zeta )n)}{|}_{\zeta =Z}+\frac{n_s}{n^{\top }{Z}_s}+\frac{{\phi }_s(s,Z)n}{\phi (s,Z)n^{\top }{Z}_s}.$$

Hence, the maximum flux condition is that

$$-\beta \nabla F^{+}(Z)+\frac{{\nabla }_{\zeta }c(\zeta ,D(\zeta )n)}{c(\zeta ,D(\zeta )n)}{|}_{\zeta =Z}+\frac{n_s}{n^{\top }{Z}_s}\Vert n.$$

If we approximate D(ζ) by D̄(σ(ζ)) where $\overline{D}(s)\stackrel{\text{def}}{=}D(Z(s))$, then

$$\phi (s,\zeta )=cons{t}_{\xi }(\text{det}\overline{D}(s)n{(s)}^{\top }\overline{D}(s)n{(s))}^{1/2}\text{exp}(-\beta F(\zeta )){\overline{q}}_s(s)(n(s)·Z_s(s)-n_s(s)·(\zeta -Z{(s))}^{-1},$$

and

$${\frac{{\nabla }_{\zeta }\phi }{\phi }|}_{\zeta =Z}=-\beta \nabla F(Z)+\frac{n_s}{n^{\top }{Z}_s}.$$

Thus, the maximum flux condition simplifies to

$$-\beta \nabla F(Z)+\frac{n_s}{n^{\top }{Z}_s}\Vert n.$$