Inclusion of noise in iterated firing time maps based on the phase response curve

Abstract

The infinitesimal phase response curve (PRC) of a neural oscillator to a weak input is a powerful predictor of network dynamics; however, many networks have strong coupling and require direct measurement of the PRC for strong inputs under the assumption of pulsatile coupling. We incorporate measured noise levels in firing time maps constructed from PRCs to predict phase-locked modes of activity, phase difference, and locking strength in 78 heterogeneous hybrid networks of 2 neurons constructed using the dynamic clamp. We show that noise may either destroy or stabilize a phase-locked mode of activity.

The problem of synchronization and patterning of synchronization of oscillators is a problem that is of general interest in physics [1–6]. More specifically, the study of pulse-coupled oscillators has commanded substantial interest [7–14]. Networks of pulse-coupled oscillators are used to study many things [15]- e.g., plate tectonics [16], heart rhythms [17], and neural networks [18]. Synchrony is a dynamical feature of such networks [19–21]. These systems consist of oscillators coupled by discrete pulses. Phase response theory is often used to study network synchrony. The phase response curve (PRC) is tabulated as the shift in phase of an oscillator in response to a stereotyped input pulse [22]. When the pulse is sufficiently weak, interactions can be added linearly so the infinitesimal PRC (iPRC), or response to weak perturbations, which is the foundation for a powerful technique—the theory of weakly coupled oscillators—can be used to predict network activity [23], however, many real systems are coupled too strongly for weak coupling approaches [24, 25].

Phase response theory has a rich history in biological oscillators- especially in cardiac electrophysiology and neurophysiology. In the latter field, phenomena emerging from networks of two neurons are often used to help understand behaviors of networks containing large populations of neurons [18], however, this paradigm is limiting - the complexity seen in biology is far beyond that explained by existing models, which are largely limited to networks of identical neurons coupled identically and weakly with no noise included. Conversely, real neural systems often contain heterogeneous neural types coupled heterogeneously, strongly, and with noise. Several recent studies have pushed one or more these boundaries, e.g. showing noise-stabilized antiphase oscillations [26], synchronization in a network despite noise [27], optimal PRC shape for noise-driven synchrony (stochastic synchrony) [28], and bistability induced by shared noise [29]. Although noise has been included in maps of pulse-coupled neurons [30], no study has yet formalized the effects of noise in non-weakly coupled pulse-coupled networks. In [31] we briefly proposed a method to address these issues simultaneously, and we applied it in one example as a proof of concept.

Here, we present our method formally and apply it generally to describe 78 experimental networks from [31]. We explicitly incorporate noise measured during experimental determination of the PRC into the prediction method. In a hybrid network of two bursting neural oscillators coupled via synaptic excitation (τ_syn≈10ms with a network period of about a second), we found that this method could accurately predict phase locking in the presence of 10% variability in the intrinsic period. We have shown that networks including a biological oscillator may undergo noise-induced transitions, and that including measured noise in the firing time map may capture the effect of noise, giving results that are qualitatively and quantitatively similar to experiment [31].

Following the biological tradition [32, 33], in a two neuron network our phase response curves (PRCs, F_qi below) describe the effect of a stereotyped input from the partner neuron j on neuron i as a function of the timing of input, or phase ɸ_i. The qth order PRC is tabulated experimentally

$${\mathrm{F}}_{\text{qi}}({\mathrm{ɸ}}_{\mathrm{i}})=({\mathrm{P}}_{0\mathrm{i}}—{\mathrm{P}}_{\text{qi}})/{\mathrm{P}}_{0\mathrm{i}}$$

by measuring the qth cycle lengths P_qi and P_0i, where first order resetting q=1 measures response in the perturbed cycle, and second order resetting q=2 measures response in the next subsequent cycle. As such, F_1i measures the change of the cycle containing the start of input from neuron j

$${\mathrm{F}}_{1\mathrm{i}}({\mathrm{ɸ}}_{\mathrm{i}})=({\mathrm{P}}_{0\mathrm{i}}—{\mathrm{P}}_{1\mathrm{i}})/{\mathrm{P}}_{0\mathrm{i}}.$$

If the input is an infinitesimal voltage deflection, then our F_1i is equivalent to PRCs used in weak coupling theory [34, 35]. Second order resetting F_2i has been previously shown to be important in bursting neurons [24, 25, 31] and was recently modeled as leftover charge in dendrites resulting in partial reset [36].

We use these PRCs to construct a general model of pulse-coupled phase oscillators with no delays

$${\dot{ɸ}}_i=\frac{1}{P_{0i}}+{\displaystyle \sum _j{F}_{1i}({ɸ}_i)\delta (t-t_j^{*}),}$$ (1)

where ɸ_i ∈ [0,1) is the phase of neuron i modulo 1. A threshold event such as a spike or burst occurs when the phase reaches one, and the phase is immediately reset to zero afterwards. The coupling function is given by F_1i, δ is the Dirac delta function, and t_j^* is the time of a spike or burst initiation in neuron j. Because we use ideas from phase resetting theory, we constrain the behavior of our uncoupled oscillators to autonomous periodic activity, i.e., spiking or bursting, where for each neuron i there is an intrinsic period P_0i such that ɸ_i(t+P_0i)=ɸ_i(t). Note that the oscillators may be heterogeneous, each having its own intrinsic period P_0i≠P_0j.

The major drawback to using PRCs as coupling functions in our model is that we must assume the system returns to its limit cycle between pulses. In the phase space this means that when a relatively strong input moves the coupled oscillator far from its uncoupled trajectory, it must return before the next input arrives. In general, this is not a problem for weakly coupled oscillators. Returning to the limit cycle between inputs also implies that in the case of a neuron receiving multiple inputs in between two firing events, the second order effects F_2i must be zero for all inputs except the last one received before the 2^nd event. For two neurons, this is rarely a problem.

To expand (1) for non-weak inputs, we include F_2i by adding a second term, where ɸ_i^last is the value of ɸ_i at the last t_j^* if an input was received by neuron i in the previous cycle.

$$\begin{array}{c}{\dot{ɸ}}_i=\frac{1}{P_{0i}}-{\displaystyle \sum _j{F}_{1i}({ɸ}_i)\delta (t-t_j^{*})-A_i{F}_{2i}({{ɸ}_i}^{\mathit{\text{last}}})\delta (t-t_i^{*})}\hfill \\ {ɸ}_i\ge 1:A_i\to 0\hfill \\ {ɸ}_j\ge 1:A_i\to 1\hfill \end{array}$$ (2)

The switch A_i is one if an input was received in the previous cycle and zero otherwise. Additionally, each ɸ_i must now be defined for small negative values because if F_2i is a delay, ɸ_i will be reset to a negative value. A geometrical interpretation of the negative branch in ɸ_i is given in [37] − it “corresponds to an isochron that curls around the limit cycle, intersecting it at a position that is retrograde to the peak of the action potential.” For ɸ_i<0, F_qi are undefined, however, this is not a problem in our analysis, where we assume that for ɸ_i<0, F_qi(ɸ_i)=F_qi(0) because few inputs (if any) were received on this branch.

To account for noise in our experimentally measured PRC data, we simply include it directly in the PRCs,

$$\begin{array}{c}{F}_{1i}({\mathrm{ɸ}}_i)=F_{1i}^{\mathit{\text{fit}}}({\mathrm{ɸ}}_i)+{\mathrm{\xi }}_{1i}{\mathrm{\sigma }}_{1i}({\mathrm{ɸ}}_i),\\ F_{2i}({\mathrm{ɸ}}_i)=F_{2i}^{\mathit{\text{fit}}}({\mathrm{ɸ}}_i)+{\mathrm{\xi }}_{2i}{\mathrm{\sigma }}_{2i}({\mathrm{ɸ}}_i),\end{array}$$ (3)

where F_qi^fit is a piecewise polynomial fit to the experimental data, ξ_qi represents unitary Gaussian noise, and σ_qi is the standard deviation of the measured noise as a function of ɸ_i, found by binning the data and measuring in each bin. All PRCs used in this study are the same as in [31].

Consider a network of two heterogeneous coupled neural oscillators as in (2). To find modes of rhythmic network activity, we modify the iterative pulse coupled map with no predetermined firing order from [38] to include noise in the PRCs as in (3). We iterate the map as follows, where φ_i[m] is the phase of neuron i after all effects of the previous pulse event m are added, S[m] is the set of neurons that emit a pulse m, and R[m] is the set that receives a pulse.

We initialize each neuron with a phase φ_i[0] and a memory of second order resetting F_2i(φ_i^last[0]). Then, we poll for which neuron(s) will fire next: if P_0i (1 - φ_i[m]) = min { P_0i (1 - φ_i[m]) } over all i, then i ∈ S[m], else i ∉ S[m]. If i sends a pulse then j receives one: for i ∈ S[m], j ∈ R[m] else j ∉ R[m], where i ≠ j. Now update each neuron according to whether it fires a pulse and whether it receives a pulse: If i ∈ S[m], i ∉ R[m], then reset φ_i to zero plus F_2i from previous cycle: φ_i[m+1]= 0 – A_iF_2i (φ_i^last[m]), and reset the switch A_i to zero. If i ∈ S[m], i ∈ R[m], then set φ_i[m+1] = 0 – A_iF_2i(φ_i^last[m]) - F_1i(φ_i[m] + (t[m+1] - t[m])/ P_0i), and reset the switch A_i to zero‥ If i ∉ S[m], i ∈ R[m], then advance phase by elapsed time plus 1st order resetting from current cycle: φ_i[m+1] = φ_i[m] + (t[m+1]-t[m])/P_0i – F_1i(φ_i[m]+(t[m+1]-t[m])/P_0i). Update the memory of 2nd order resetting: for i ∈ R[m], φ_i^last[m+1]= φ_i[m] + (t[m+1] - t[m])/ P_0i, and set the switch A_i to one. Now start again - poll for which neuron(s) will fire next, etc.

To summarize:

• For i ∈ S[m], i ∉ R[m], φ_i[m+1]= 0 – A_i F_2i (φ_i^last[m]), A_i =0

• For i ∈ S[m], i ∈ R[m], φ_i[m+1] = 0 – A_i F_2i(φ_i^last[m]) - F_1i(φ_i[m] + (t[m+1] - t[m])/ P_0i), A_i =0

• For i ∉ S[m], i ∈ R[m], φ_i[m+1] = φ_i[m] + (t[m+1]-t[m])/P_0i – F_1i(φ_i[m]+(t[m+1]-t[m])/P_0i), φ_i^last[m+1]=φ_i[m] + (t[m+1] - t[m])/ P_0i, A_i =1

This map is difficult to analyze because of the discontinuities introduced by the min function. First, there is no assumption of firing order. It is even possible that the neurons will fire synchronously or that one neuron will not fire at all. Next, a neuron’s phase is updated differently depending on whether it fires a pulse, receives a pulse, or does both simultaneously. Note that the phase is updated each time that an input is received, in contrast to the weak coupling assumption where phase is not updated when each pulse is received based on resetting that occurs earlier in the cycle.

We have ignored conduction delays here, although they may be added to the map [39]. In our experimental system consisting of bursting neurons, we defined an event as the start of a burst in the presynaptic neuron. Using the map, we can iterate a number of cycles N_map roughly matching the number of observed cycles N_obs and compare results using circular statistics as in [31]. The inclusion of noise in the firing time map is similar to [30]; the major difference is the use of F₂ in addition to F₁ in our method. Further, we explicitly restrict the tails of ξ_i according to their causal limits. In [31], these limits translate to recovery interval t_r≥0 and stimulus interval t_s≥0 as defined below.

Comparison of map to experimental data and noise-free method

To evaluate our methods on experimental networks, we applied them to an existing dataset of 78 coupled networks [31]. These networks are constructed from one biological neuron and one model neuron by using the dynamic clamp [40, 41] to implement artificial synapses. The biological neuron used (N=5) was the AB/PD complex from the pyloric network in the Stomatogastric ganglion of Homarus Americanus, which is a regularly bursting group of 3 electrically coupled neurons that act as a single oscillator. This group was isolated pharmacologically using standard methods [31]. The model neurons used were from a heterogeneous set of four regularly bursting pyloric model neurons from a database [42].

We compared experimental observations to predictions made using a noise-free method of pulsatile coupling [25, 31] and to the predictions of our iterated map using steady state stimulus intervals t_s for each neuron in the network, where t_s is the interval between the time of an event in one neuron and the time of the next input it receives from its partner neuron (Figure 1). For the case of 1:1 locking this is equivalent to t[M] above, where M is the set of odd or even whole numbers. Using both methods, we predicted qualitative behavior — whether a mode of 1:1 phase-locking would be observed — and quantitative behavior — the stable phase difference and strength of phase-locking. We quantify the strength of phase-locking using the circular statistic R². When each n of N phase differences $\mathrm{\Phi }[\mathrm{n}]=2\pi *{\mathrm{t}}_{\mathrm{s}1}[\mathrm{n}]/{\mathrm{P}}_{\text{net}}\in [0,1),{\mathrm{P}}_{\text{net}}=\frac{1}{N}{\displaystyle \sum _{n=1}^N({\mathrm{t}}_{\mathrm{s}1}[\mathrm{n}]+{\mathrm{t}}_{\mathrm{s}2}[\mathrm{n}])}$ is plotted on the unit circle, then R² ∈ [0,1] is the length of the vector from the origin to the average position of the plotted points [43, 44]. We used a threshold R²>0.7 to define phase-locking as in [31].

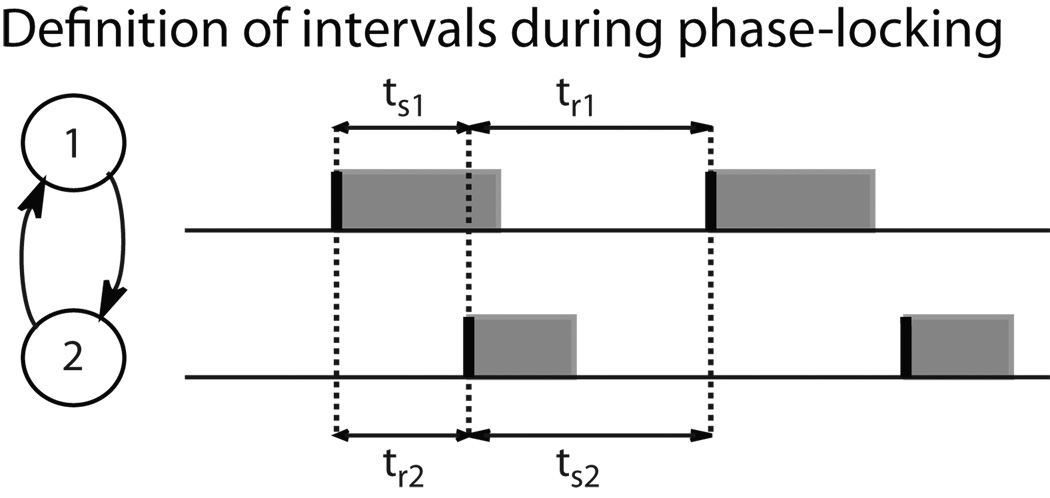
Figure 1.

Definition of terms, A: stimulus time (t_s) and response time (t_r) during 1:1 phase locking are shown for bursting neurons 1 and 2. The shaded regions correspond to the burst duration, which can be a substantial fraction of the cycle period.

In the 78 networks tested, the noise-free method was qualitatively incorrect 16 times and the iterative map was able to make the correct prediction for 8 of those networks (see [31] for full analysis of the noise-free method in these networks) as well as 61 that were correctly predicted by the noise-free methods, for a total success rate of 69 out of 78, an improvement of 10%. We excluded eight networks that exhibited continuous spiking due to positive excitatory feedback as a result of the coupling, breaking the assumption of a limit cycle burster under which the PRCs were generated [31]. Five failures of the map were due to overestimation of noise. Over the course of hours, noise levels in the biological neuron varied. In all cases, removing noise from the firing time map by setting σ=0 in (3) produced a match to the predictions of the noise-free method.

To best compare predictions made using our firing time map to those made using the noise-free methods, we focus on networks that were experimentally observed to phase-lock. In Figure 2, we compare methods for 28 such networks by showing steady state t_s intervals for each neuron in the network. Each network is represented by an ordered group of symbols separated by vertical dotted lines, showing t_s values obtained for each of the methods used. Where a phase-locked mode was not observed or predicted by a method, the appropriate symbol is plotted in red below.

Figure 2.

(color) Map with noise. Comparison of observed behavior from [31] to analytical and firing time map predictions including F₂ in the firing time map. Empirical observation (o and error bars), analytical prediction (x), and prediction using the firing time map (square and error bars) are shown for mdl (model neuron, blue) and bio (biological neuron, green) neurons in each hybrid network, separated by dotted lines and sorted by qualitative match for clarity. Modes that were not observed or predicted to exist are marked by a red symbol (o, x, or square) in the row labeled DNE. For clarity, error bars are shown only in one direction. Analytical predictions are noise-free so they do not have error bars. The × axis is the arbitrary experimental network number. A. For networks observed to phase-lock, the noisy map produced results that were generally in agreement with observations. In one case (red x) the noisy map succeeded where the noise free method failed, but in five cases (red squares) the noisy map failed presumably due to overestimation of noise. (B) In cases where noise was previously shown to cause the analytical prediction to fail, the noisy map correctly predicted the failure to lock in seven cases, and the noise-induced ability to lock, albeit with some error, in one case.

When F₂ was removed from the firing time map (not shown), F_2i=0 in (2), prediction accuracy dropped from 85% to 45%, as we would expect from [24, 25, 31]. In B, we compare prediction methods in 8 networks previously shown to exhibit noise-induced transitions [31]. The analytical method, which is noise-free, was qualitatively incorrect in each of these cases, and the map was correct in each case. Out of the 8 networks with such behavior, only 1 was observed to phase-lock and the map method was qualitatively accurate (network 8, shaded). Note that in this network, the analytical methods did not predict a phase-locked mode, so adding noise to the PRCs caused a new stable fixed point to appear, showing that in the firing time map, noise can both generate and destroy modes of phase-locking.

We have verified that variability in a PRC does modulate the strength of phase-locking in a network of 2 neurons. When noise was added to the map, the differential effects of noise on structurally stable and unstable systems was captured qualitatively and quantitatively using circular statistics. This simple idea is a powerful tool for understanding the predictive utility of PRCs because it simulates the measured variability of the biological neuron and gives outputs that are readily compared to experimental data.

Bendels and Leibold [27] note a threshold in noise level above which “low-synchrony” phase-locking occurs but is not predicted by their mean-field approximation method due to occasional slipping. This threshold can be explained by the noise level at which the envelope of phase-dependent noise around the PRC disrupts the basin of attraction of the noise-free fixed point. We do not analyze this threshold here, but our data give examples where a stable fixed point in the noise-free system transitions to a quasi-stable fixed point when noise is added, seen as stable phase-locking with occasional slipping.

An input can never advance the event time to a time before the input was applied: this is the causal limit. If no input is given at phase ɸ, then the next event is expected to follow at a time interval of P₀(1-ɸ), the remaining interval. Therefore the observed phase resetting can never drop below the line (F_1i(ɸ)=ɸ-1), which biases the noise observed in first order PRCs. For example, in Tsubo et al. [45] the authors note that they could fit the distributions of the fluctuations in the phase responses at phases less than 0.5 with Gaussian distributions with a variance that was nearly constant. However, at phases greater than 0.5, the variance decreased. Fig. 2E of that paper makes it clear that the causal limit is responsible, but the role of the causal limit was not addressed. Phoka et al. show that noise in Purkinje cells introduces a bias in the mean measured PRC due to the causal limit [46]. To correct for the bias, they use all spikes in a train as reference, one at a time, rather than using only the spike before and after. Polhamus et al. proposed a different solution, which was to average only ISIs longer than the stimulus interval to determine the average period to use to calculate the phase. Our method accounts for the missing variance in the first order resetting by treating second order resetting separately.

Netoff et al. [30] also observed PRCs in which the noise was limited by causality. In their studies of excitatory inputs, the scatter decreased inversely proportional to the square root of the phase, but for inhibitory inputs causality is not an issue and variance was independent of phase. Netoff et al. [30] also incorporated noise into a PRC-based map. They chose firing times for each cell by adding the spike time response curve (STRC) value (mean + normally distributed random component scaled by the time-dependent SD, each measured from the STRC) to the unperturbed firing period of the cell in question [30].

Since our map is different from that of Netoff et al. [30] only in that that we used second order resetting, it is interesting that our maps perform more poorly if F₂ is ignored. This is likely because the neurons in [30] are spiking, rather than the bursting neurons that we used, and spiking neurons tend to have small F₂ amplitudes. The new method incorporates the true variance rather than underestimating it at late phases. To our knowledge, this point has not been made previously. For example, after commenting on the phase dependence of the variance observed by Netoff et al., Ermentrout and Sanders state that "An adequate theory of this dependence remains to be resolved" [26]. In our method, the variance in F₂ in the subsequent cycle compensates for reduction in variance at late phases in F₁.