Concurrent Musculoskeletal Dynamics and Finite Element Analysis Predicts Altered Gait Patterns to Reduce Foot Tissue Loading

Abstract

Current computational methods for simulating locomotion have primarily used muscle-driven multibody dynamics, in which neuromuscular control is optimized. Such simulations generally represent joints and soft tissue as simple kinematic or elastic elements for computational efficiency. These assumptions limit application in studies such as ligament injury or osteoarthritis, where local tissue loading must be predicted. Conversely, tissue can be simulated using the finite element method with assumed or measured boundary conditions, but this does not represent the effects of whole body dynamics and neuromuscular control. Coupling the two domains would overcome these limitations and allow prediction of movement strategies guided by tissue stresses. Here we demonstrate this concept in a gait simulation where a musculoskeletal model is coupled to a finite element representation of the foot. Predictive simulations incorporated peak plantar tissue deformation into the objective of the movement optimization, as well as terms to track normative gait data and minimize fatigue. Two optimizations were performed, first without the strain minimization term and second with the term. Convergence to realistic gait patterns was achieved, with the second optimization realizing a 44% reduction in peak tissue strain energy density. The study demonstrated that it is possible to alter computationally predicted neuromuscular control to minimize tissue strain while including desired kinematic and muscular behavior. Future work should include experimental validation, before application of the methodology to patient care.

Introduction

In musculoskeletal biomechanics, computational modeling often represents a cost-effective approach to iterate design variables of interest as well as estimate otherwise unmeasurable metrics, e.g. tissue loading. Current computational methods for simulating human movement have primarily consisted of muscle-driven movement simulations (Neptune, 2000; Zajac et al., 2003; Anderson & Pandy, 2001; Erdemir et al., 2007; van den Bogert, 1994). Due to computational expense, such simulations generally include assumptions which simplify joint or soft tissue behavior. Joints are typically modeled as hinge or spherical and soft tissue effects are included as spring-dashpot systems. These limiting assumptions are serious obstacles to applications such as ligament injury or osteoarthritis, where local tissue loading must be predicted (McLean et al., 2003; Lin et al., 2009). Conversely, continuum soft tissue deformation models, generally performed using the finite element (FE) method, can provide information on local tissue loading but require assumed or measured boundary conditions (Huiskes & Hollister, 1993; Zhang et al., 1998; Jones & Wilcox, 2008). Coupling detailed deformable soft tissue and musculoskeletal models would help overcome the limitations of each modeling domain by combining their strengths.

Previously, multidomain studies have been performed but until recently these were generally non-concurrent, in which tissue deformations were analyzed by post-processing of a given musculoskeletal loading state (Besier et al., 2005; Cattaneo et al., 2005; El-Rich & Shirazi-Adl, 2005; Fernandez & Pandy, 2006; Hopkins et al., 2005). These studies lacked the coupled nature of soft tissue deformation and muscular loading. Of notable exception, Koolstra and van Eijden (Koolstra & van Eijden, 2005) used an explicit FE approach to estimate mandible stresses during a forward dynamic simulation. However, computational expense of such an approach limits the framework for use in iterative analyses, i.e. optimization or probabilistic studies. More recently, we demonstrated direct coupling between a musculoskeletal lower extremity model and FE foot model to solve a maximum height jumping objective (Halloran et al., 2009). To reduce the computational cost of FE foot simulations, an adaptive surrogate modeling method was adopted, based on locally weighted regression to estimate ankle reaction loads. The study showed that it would be possible to simultaneously predict movement and tissue deformations in a coupled iterative analysis. Nonetheless, the study has limited clinical relevance, and the potential of tissue level mechanical variables to influence predicted movement was not employed.

The capability to predict adaptations in movement due to mechanical changes in tissues, or as a function of desired unloading of the tissue, has important implications for design of surgical, therapeutic and rehabilitative interventions. For example, this would provide a scientific basis for design of neuromuscular strategies to prevent anterior cruciate ligament injury (Shimokochi et al., 2009; Boden et al., 2000; Markolf et al., 2004; McLean et al., 2004). Rehabilitation programs for tissue relief could be developed for the prevention of lower back pain, osteoarthritis, or plantar tissue pressure, thought to be a contributor to diabetic foot ulceration (Veves et al., 1992). With continuum models of tissue behavior, internal conditions, such as strain, shear, and stress, could not only be quantified but utilized in the formulation of the movement objective.

The goal of the current study was twofold: first, develop a predictive neuromuscular controlled simulation of gait by coupling a finite element (FE) model of the foot with a lower limb musculoskeletal model; and second, incorporate the minimization of a peak plantar tissue deformation metric into the objective of a predictive movement optimization. The successful demonstration of this capability establishes a framework to develop future clinical applications.

Methods

Musculoskeletal Model

Details of the musculoskeletal model have been described previously (Gerritsen et al., 1998). Briefly, the model was two-dimensional and contained seven body segments: trunk, thighs, shanks, and feet. Joints were ideal hinges, and there were no kinematic constraints between the feet and ground, resulting in a total of nine kinematic degrees of freedom. Eight muscle groups were included in each lower extremity: Iliopsoas, Glutei, Hamstrings, Rectus Femoris, Vasti, Gastrocnemius, Soleus, and Tibialis Anterior. Each muscle was represented by a 3-element Hill model, as described in McLean et al. (2003), with muscle properties from Gerritsen et al. (1998), and simulated with custom C code. The model had 50 state variables in x: 9 generalized coordinates in q̇, 9 generalized velocities in q̇, 16 l_ce, and 16 muscle activations in a. Equations of motion were muscle contractile element lengths in generated by SD/Fast (Parametric Technology Corp., Needham, MA):

$$M(q)\ddot{q}+C(q,\stackrel{.}{q})+{RF}_{MT}+G(q)+Q_{fr}(q,\stackrel{.}{q})+Q_{\mathit{FEA}}(q_{\mathit{FEA}}(q))=0,$$ (1)

where M is the mass matrix, C are centrifugal and Coriolis effects, G contains gravity terms, F_MT are the muscle forces, applied via a matrix of moment arms R, and Q_fr is the friction term (described below). The final term represents reaction loads applied to the calcaneus by the finite element model of the foot, which is introduced below. These loads are only dependent on kinematic boundary conditions q_FEA which are a known function of skeleton pose q.

Finite Element Model of the Foot

A plane strain foot model was implemented in Abaqus (Simulia, Providence, RI) (Halloran et al., 2009). A sagittal plane cross-section along the second ray of the foot was used to represent the bone and tissue geometry. Bones were modeled as rigid and the soft tissue as an Ogden material model with material properties based on heel pad indentation tests (Erdemir et al., 2006). Bones other than the phalanges were combined into one rigid segment, which was controlled by prescribing the vertical position and the orientation of the talus relative to the ground. These were the kinematic boundary conditions for the finite element analyses. As a result, the ankle is modeled as a hinge joint with the FE model of the foot and the musculoskeletal model sharing rigid body boundary conditions at the calcaneus. Ankle joint coordinates, q_FEA, were directly coupled between the FE and musculoskeletal models. The phalanges were represented as another rigid segment, which was free to move during simulations. Soft tissue surrounding the metatarsophalangeal (MTP) joint served to restrain the movements of this segment during passive toe flexion. Elements between the metatarsal head and the proximal phalanx also contributed to passive MTP joint stiffness and were modeled as linearly elastic (E=1e6 Pa, v=0.3). Contact between foot and ground was modeled as frictionless in the finite element analysis, but an approximate friction model was included in the musculoskeletal simulations to represent the overall shear loading on the foot, as described below. Each time the vertical position of the talus and its orientation was passed to the finite element model, the FE model was solved and vertical reaction force and moment at the calcaneus were returned to the musculoskeletal model. As friction was not included in the FE contact definition, the need to prescribe the horizontal position of the talus was unnecessary. Stress-strain distribution within the soft tissue and plantar pressures were available as additional outputs from the finite element analysis.

Friction Model

Friction between feet and ground was not included in the FE model, but is required for normal gait. The horizontal contact force Q_fr was modeled by an approximation of the Coulomb friction defined as a function of the net vertical (normal) ground reaction force f_y generated by the FE foot model and an estimation of the horizontal, sliding velocity of the contact points v_cx as

$$Q_{fr}=-\frac{1-exp(-v_{cx}/v_c)}{1+exp(-v_{cx}/v_c)}\mu f_z,$$ (2)

where v_c is a scaling factor set to v_c = 0.05 m s⁻¹ and μ is the friction coefficient set to μ = 1.0 (Ackermann and van den Bogert, in press). Sliding velocity of the contact points, v_cx was defined as a function of ankle vertical position z, ankle horizontal velocity v_x, and rotational velocity of the foot, ω_z, as

$$v_{cx}=v_x+{\omega }_{z}z.$$ (3)

Movement Prediction

The predictive gait simulation was formulated as an optimal control problem that searches for time histories of states x(t) and neural excitations u(t) that are periodic, have a specified walking speed (here set at 1.1 m/s), satisfy the system dynamics and minimize a cost function (Ackermann and van den Bogert, in press). The following cost function was used:

$$J={\omega }_1{J}_{tr}+{\omega }_2{J}_{\mathit{ftg}}+{\omega }_3{J}_{\mathit{str}},$$ (4)

where J_tr is a “tracking” term containing the deviation from normative gait kinematics and ground reaction data in Winter (1991), J_ftg is a term quantifying muscle “fatigue”, and J_str is a term expressing maximal strain energy density in the foot tissue. Weights ω _n were included for each term. The “tracking” was computed as

$$J_{tr}=\frac{1}{T}\frac{1}{n_{tr}}\sum _{j=1}^{n_{tr}}\underset{0}{\overset{T}{\int }}{\left(\frac{y_j(t)-{\overline{y}}_j(t)}{{\sigma }_j(t)}\right)}^{2}dt,$$ (5)

where n_tr is the number of tracked variables, y_j is the simulated variable, y¯_j is the mean measured value of the variable, σ _j is the standard deviation of the measurements. Knee, hip, ankle angles, and vertical and horizontal ground reaction forces were tracked using published inter-subject mean and standard deviation data, and this term was included to approximate the simulated gait to normal patterns (Winter, 1991). The “fatigue” term was defined as

$$J_{\mathit{ftg}}={\left(\sum _{i=1}^m{\mathrm{\Phi }}_i^{10}\right)}^{\frac{1}{10}}\approx {\mathit{minmax}}_i{\mathrm{\Phi }}_i,$$ (6)

where m is the number of muscle groups and Φ is a measure of muscle fatigue related to the cube of muscle activation a (Crowninshield and Brand, 1981):

$${\mathrm{\Phi }}_i=\underset{0}{\overset{T}{\int }}{a}_i^3(t)dt.$$ (7)

The exponent in Eq. (6) provides a continuous approximation to the minmax problem of minimizing the maximal muscle fatigue, i.e. maximizing endurance (Rasmussen et al., 2001). This term is necessary because muscle force sharing is not uniquely determined by the tracking term in the cost function. The third term in Eq. (4) quantifies the tissue mechanical state over the gait cycle through a continuous function of the maximal strain energy density as

$$J_{\mathit{str}}={\left(\frac{1}{T}\underset{0}{\overset{T}{\int }}\sum _{k=1}^{n_{FE}}{\varphi }_k^6(t)dt\right)}^{\frac{1}{6}},$$ (8)

where n_FE is the number of FE nodes including both feet and ϕ is the strain energy density at each node in the FE foot model tissue in N/mm². The exponent of six in Eq. (8) was selected because it strongly penalizes large strain energy densities while avoiding the strong nonlinearities associated with even higher exponents.

Direct collocation was used to transform the optimal control problem into a Nonlinear Programming Problem (NLP) which was solved in Matlab (The Mathworks, Inc., Natick, MA) using the optimization package SNOPT (Tomlab Optimization, Pullman, WA), interacting with Abaqus (Simulia, Providence, RI) for finite element analysis and custom C code for musculoskeletal dynamics. Details are provided in Ackermann and van den Bogert (in press).

As per the objectives of the study, two simulations were performed. The first incorporated just the tracking and fatigue terms (ω₃ = 0) with ω₁ = 1 and ω₂ = 10, both set to bring the terms to the same order of magnitude. In the results, this solution is referred to as “tracking”. In the second simulation, the ω₁ and ω₂ weights were retained and ω₃ was set to 500, resulting in approximately equal contributions of all terms. This solution is referred to as the “strain” simulation.

Results

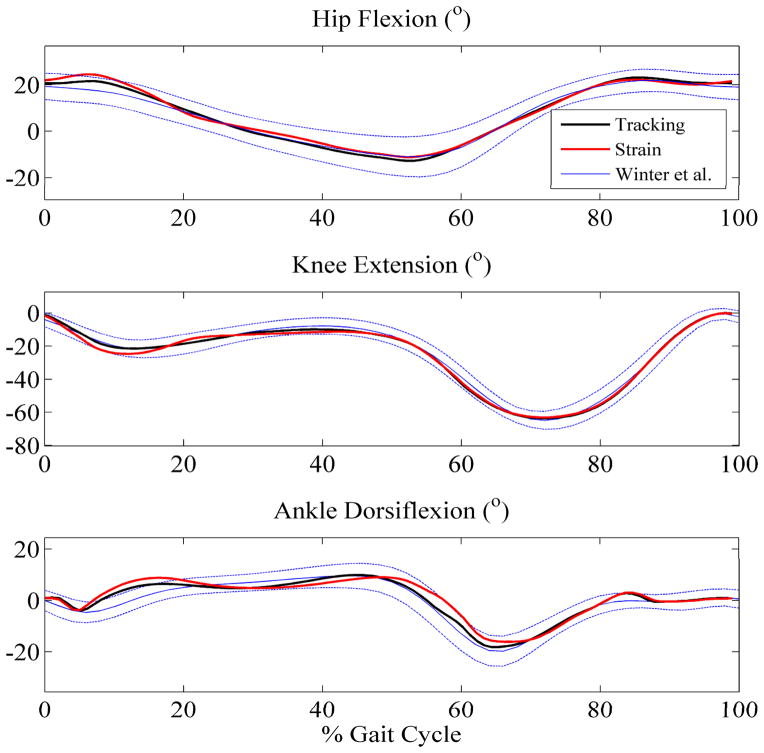
The optimization successfully converged for both objective functions (Figure 1). Dynamic equilibrium and periodicity were satisfied throughout the simulations. The “tracking” solution matched desired kinematics with root mean square (RMS) values of 1.5°, 1.5°, and 1.9° for hip, knee, and ankle angles, respectively (Figure 2). The physical location of peak strain energy density occurred at progressive locations in the plantar tissue throughout the cycle, from the heel to the toe throughout the cycle. Incorporating the minmax approximation of peak strain energy density into the objective function led to a 44% reduction in its maximum value during the gait cycle. This reduction was realized near toe-off (just under 60% of the cycle) and occurred in the plantar tissue directly under the metatarsal heads (Figure 3). As might be expected, the “strain” optimization caused the RMS values for kinematic tracking to increase slightly to 2.3°, 2.1°, and 3.3° for hip, knee, and ankle angles due to the incorporation of the additional term in the objective (Figure 2). Muscle activation patterns displayed important differences between the two objectives. In order to reduce the peak strain near toe-off, the “strain” solution altered the magnitudes of the soleus, gastrocnemius, and tibialis anterior muscles (Figure 4), possibly to restrict ankle plantarflexion, to reduce the internal forefoot deformation at about 60% of the gait cycle (Figure 3). This difference, while leading to a significant drop in peak strain energy, reduced the peak contact pressure by only 7% and ground reaction force by 26%, at the same point in the cycle (Figure 5). Of note, the temporal location of peak strain energy did not coincide with the maximum GRF and contact pressure locations, which occurred at either ~15% or ~50% of the cycle, depending on the solution (Figure 5). This result is due to the relatively thin layer of plantar tissue in the toes and forefoot where internal tissue deformations can be high even for lower external loads.

Figure 1.

Stick figure results for the “tracking” (top) and “strain” (bottom) solutions. An outline of the deformable finite element foot is shown with closeup von Mises stress distribution for heel-strike, mid-stance, and toe-off (left to right) below each stick figure. The mid-stance stress contours demonstrate how the “strain” solution modified the tissue loading during minimization of the peak strain energy density. The legend is consistent for all simulations and is in MPa.

Figure 2.

Hip, knee, and ankle angles as a function of gait cycle. Experimental data (Winter 1991) includes one standard deviation from the mean, represented by the dashed lines.

Figure 3.

Peak strain energy density as a function of percent gait cycle. 0% represents heel-strike while toe-off occurs at approximately 60% of the cycle. The physical location of peak strain energy density occurred at progressive locations in the plantar tissue throughout the cycle, from the heel to the toe. The maximum value during the cycle occurred just before toe-off and in the plantar tissue directly under the metatarsal heads.

Figure 4.

Normalized muscle activation patterns throughout the gait cycle. From top to bottom individual muscles are labeled as follows: Ilio = iliopsas, Glu = gluteus, Ham = hamstrings, RF = rectus femoris, Vas = vasti, Gas = gastrocnemius, Sol = soleus, and TA = tibialis anterior. The vertical, dashed line represents the temporal location of maximum strain energy density for the “tracking” solution (Figure 3).

Figure 5.

Ground reaction force (GRF) and peak contact pressure as a function of percent gait cycle. 0% represents heel-strike while toe-off occurs at approximately 60% of the cycle.

Computation time ranged from 14 days for the “tracking” solution to 10 days for the “strain” solution using a single processor 2 GHz Pentium Xeon desktop machine. For both solutions, more than 99.5% of the computation time was spent solving the FE model.

Discussion

This study demonstrated that model-based prediction of gait adaptations to accommodate localized tissue relief is computationally feasible. Within an optimal control framework, direct collocation allowed coupled simulations of movement and tissue mechanics. Novelty was not only achieved by including a continuum model of tissue deformation in simulation of gait but also by incorporating an internal tissue deformation metric into the movement optimization objective. By simulating an entire gait cycle and requiring periodicity at a specified velocity, we avoided the trivial solutions which reduce tissue loading simply by reducing muscle activations and ground reaction forces. Any reduction in ground reaction force must be compensated by an increase elsewhere in the gait cycle, to maintain the specified velocity and periodic movement. These constraints in the tissue loading optimization could only be achieved because a dynamic musculoskeletal model with optimal control was coupled to the finite element model.

The results specifically showed that relatively small changes in neuromuscular control for the “strain” solution resulted in minor kinematic changes but substantial reduction in peak strain energy density experienced by the plantar tissue by unloading the metatarsal heads. Sensitivity of the solution to the chosen objective function weight values (Eq. 4) is recognized as well as the currently unknown method the nervous system uses to prioritize tissue strain or tracking, if it uses these metrics at all. We emphasize that such predictions still require validation with human experiments, both at the tissue level and the neuromuscular level.

Strain energy density, a local internal tissue deformation metric, reflects the amount of strain in a localized area and, for that optimization, results were only weakly corroborated by external contact pressures. Even with this simple FE foot model, internal tissue conditions did not reflect external loading or plantar pressure distribution. This discrepancy, due to the material response of soft tissue and the anatomical detail of foot structures, is highly relevant to the study of loading and contact conditions which could potentially lead to diabetic foot ulceration. Loads and pressures as typically measured in a gait lab may not necessarily reflect the extent of underlying tissue deformation. The preliminary findings and their clinical implications will be further explored after future model validation.

After this demonstration of methods and their feasibility, ongoing development and validation is necessary to produce accurate and valid 3D models from extensive data sets (Erdemir et al., 2009). A noteworthy limitation in the present work is the incorporation of friction. Due to the added complexity, friction was not defined explicitly in the FE contact but rather in the musculoskeletal system as a global measure. Also of note in the friction model, an approximation of Coulomb behavior was chosen (Eq. 2) to ensure continuity of the underlying model, a necessary characteristic to facilitate convergence when using gradient based optimization and direct collocation. Future work will include implementing a more realistic and local friction model.

Computational expense may still be a concern, even for this relatively simple planar model. It should be noted that the same optimization with a simple spring-damper ground contact model, required less than one hour to solve (Ackermann & van den Bogert, in press), pointing towards FE simulations as the computational bottleneck. This issue will be confounded with increased complexity and will be addressed in future work through the use of a previously developed surrogate modeling method (Halloran et al., 2009). With this method, interpolation is performed on previous results to reduce the need for computationally expensive FE simulations. Computation time may still dependent on many other factors but given the temporal setup of the direct collocation method, parallel processing with multiple CPU cores is possible.

Previous studies have demonstrated the importance of a reasonable initial guess when using direct collocation (Ackermann & van den Bogert, in press). The initial guess for the “tracking” solution found in this study was adopted from the work by Ackermann and van den Bogert (in press). To minimize the number of iterations, the “strain” optimization used the “tracking” simulation as its initial guess. The computation times show that the “strain” optimization indeed required fewer iterations to arrive at convergence. Sensitivity of the results to the initial guess and formulation of the objective should be evaluated but results remain encouraging and robustness was demonstrated through the successful implementation of multiple objectives. Solutions were able to predict different motor control patterns while providing the underlying tissue, joint, and muscular loading. It is worth noting that the problem could have also been framed without including a tracking term in the objective. Alternative gait patterns could thus be explored in future studies.

After sufficient validation, multidomain simulations such as these have many potential clinical applications. The minimization of peak tissue strain is relevant for mechanically induced foot complications such as diabetic ulcers, but the methodology is not limited to the foot. A coupling of a musculoskeletal movement simulation with a knee joint model could lend insight into the mechanical and neuromuscular mechanisms that contribute to osteoarthritis. The complex interaction between muscular loading and soft tissue restraint present in the spinal column would also be a worthwhile framework to develop, to provide a scientific basis for the relationship between neuromuscular control and back pain. The approach may also be extended to include coupling tissue level loading with cell mechanics to predict biological responses to cell deformation. Obviously the possibilities are numerous and the methods are being developed as general modeling tools, to be applied as the need arises.

The presented modeling framework represents a worthwhile advancement in modeling capabilities. This is the first study to model gait with a concurrent coupled simulation of musculoskeletal and tissue deformation models. This study was also the first to successfully incorporate a local tissue deformation metric into the objective of a movement optimization. This advancement opens the door to explore the interactions between tissue deformation, muscle forces and control, kinematics, and external loading. This type of work is necessary to help advance the capability and clinical relevance of predictive movement simulations and it is the hope of the authors the methods will be adopted and expanded on by the research community.

Nomenclature

FE

finite element

MTP

metatarsophalangeal

NLP

nonlinear programming

RMS

root mean square

q

skeleton pose

q_FEA

finite element ankle position

M

mass matrix

C

centrifugal and coriolis terms

G

gravity terms

F_MT

muscle forces

R

muscle moment arms

Q _fr

friction term

Q_FEA

finite element reaction loads

f_z

net vertical (normal) ground reaction force

v_cx

horizontal sliding velocity of the contact points

v_c

friction term scaling factor

μ

friction coefficient

z

ankle vertical position

v_x

ankle horizontal velocity

ω _z

foot rotational velocity

T

gait cycle period

x(t)

musculoskeletal time histories of model states

u(t)

time histories of muscle neural excitations

J_tr

kinematics tracking term

J_ftg

muscle fatigue term

J_str

maximal strain energy density in the plantar tissue

ω _n

cost function weight values

n_tr

number of tracked variables in tracking term

y_j

simulated kinematics variable

ȳ_j

mean measured kinematics

σ_j,

standard deviation of kinematics measurements

m

number of muscle groups

Φ

muscle fatigue function

a

muscle activations

ϕ

function describing stress-strain distribution within plantar tissue

n_FE

number of finite element nodes