The Genetics of Pain and Analgesia in Laboratory Animals

Abstract

Pain and analgesia traits are heritable in humans and in mice. To better understand the mechanisms of heritability, animal models that provide greater control than is possible in humans over genotype, previous history, environment, and stimulus parameters are available. This chapter will highlight several common methods to study the genetic mechanisms of heritable sensitivity to pain and pain-related traits in rodents. Methods to demonstrate and estimate the heritability of a trait are discussed, as are genetic correlation analysis and linkage mapping. Practical concerns are highlighted throughout this chapter. Due to limitations on the use of humans for similarly powered experiments, these and other animal models remain an essential component in the study of heritable mechanisms of pain and analgesia.

1. Introduction

The study of the genetics of heritable pain sensitivity in rodent models of pain has proven to be a valid and productive endeavor. Novel genetic relationships among types of pain models have been detected (1–3), and novel genes identified via mapping studies have been convincingly demonstrated to be responsible for variability in several pain traits (4–6). Moreover, findings from mouse genetic studies have been translated to humans (5, 7, 8). One can study the role of single genes in pain and analgesia with transgenic knockout mice, or with oligonucleotides or small-interfering RNA (siRNA) that inhibits the function of specific genes. However, these methods do not directly examine heritable variability. This chapter will concentrate on common methods used to study the genetic mechanisms of heritable sensitivity to pain and pain-related traits in rodents.

2. Heritability of Pain Traits

The heritability of a trait is the proportion of the overall variability observed in that trait that is due to inherited genetic factors. Determining the heritability of a trait is the first step in examining the genetic factors that contribute to trait variability. Heritability estimates provide a gauge of the value of subsequent genetic mapping studies. Only if a significant proportion of the variability can be ascribed to genetic factors will it be of value to pursue the identification of those genes. To quantify the heritability of a trait, the “narrow-sense heritability” (h²) can be calculated by comparing the between-strain (or allelic) variance (V_A) with the total variance comprised of the between-strain variance and the within-strain (or environmental) variance (V_E): h² = V_A/(V_A+V_E) (9). Narrow- sense heritability can be easily calculated based on the results of a one-way analysis of variance (ANOVA) of an inbred strain survey as described below. “Broad-sense heritability” can also be estimated, but is significantly more complex especially if little is known about the genetic mechanisms of variability in the trait. Broad-sense heritability includes allelic (or additive) variance in the numerator in addition to other genetic sources of variance including allelic dominance and gene–gene interactions (called epistasis), which are mostly unknown at present.

Several methods and animal models exist that one can use to determine whether a trait is heritable. The careful choice of the appropriate model can maximize the yield and impact of the results. Some models have greater long-term utility of the results, allowing for further comparisons with previous and additional experiments, and justifying their increased costs. In many cases, the matching of short-term and long-term goals and the available and expected budget for the overall research program is critical.

2.1. Selective Breeding

Selective breeding, or artificial selection, of rats or mice is one method to demonstrate that genetic factors contribute to a pain trait. In a population of outbred rodents, trait variability will exist within the strain. If the trait is heritable, successive breeding of highly sensitive members of the strain with other highly sensitive members will result in progeny that are more sensitive overall than progeny of highly resistant members of the strain. With successive generations, the distribution of sensitivity will be forced toward the extremes of the range seen prior to selective breeding due to the additive effects of fixation of alleles (i.e., gene variants) segregating in the population. Successful selection is prima facie evidence of heritability. Selective breeding for highly heritable traits largely controlled by one (monogenic) or a few genes (oligogenic) requires fewer generations of breeding to produce progeny with extreme sensitivities when compared with traits that are less heritable or more polygenic. Several examples of selective breeding of pain traits exist in the literature, including programs for neuropathic pain, and drug- and stress-induced analgesia (10–13).

2.2. Inbred Strain Differences

Strain comparisons can also be used to demonstrate and quantify the influence of heritable factors on pain sensitivity. With this method, the type, number, and selection of strains is critical. Numerous comparisons have been performed between two out-bred or inbred strains of rats or mice. Comparing outbred strains is problematic because they are not isogenic; trait (phenotypic) differences might be due to genotype and might also be due to chance selection of individuals in the sample. Two-strain comparisons have serious limitations that should dissuade one from picking such a limited comparison to reveal genetic mechanisms. For instance, although the genetic background is known to differ between the Lewis and Fisher 344 inbred rat strains, the two strains also have known differences in hormonal responsivity to stressors and stressor-induced behavioral patterns (14, 15). As such, it becomes exceedingly difficult to ascribe strain differences in a pain trait to any of the numerous alleles that differ between the strains. It is much preferable to use larger panels of inbred strains with known genomic differences (16).

2.3. Genetic Reference Populations: Standard Inbred (SI) and Recombinant Inbred (RI) Strains

SI and RI mouse strains are genetic reference populations in which alleles of genes throughout the genome have been forced into homozygosity by inbreeding for over 20 generations. RI strains are derived by crossing two SI strains and fully inbreeding the F2 progeny (see Fig. 4 for an illustration). For both SI and RI strains, the genotype of each inbred strain is fixed over time. Another way of saying this, of course, is that within-strain, individual SI and RI mice are clones of each other. A panel of SI or RI mouse strains can be used to estimate the narrow-sense heritability (h²) of a pain trait by comparing the between-strain variance ( V_A) with the total variance based on the results of a one-way analysis of variance (ANOVA) by dividing the between-strain sum of squares (SS) term by the sum of the between-strain and within-strain SS terms.

Fig. 4.

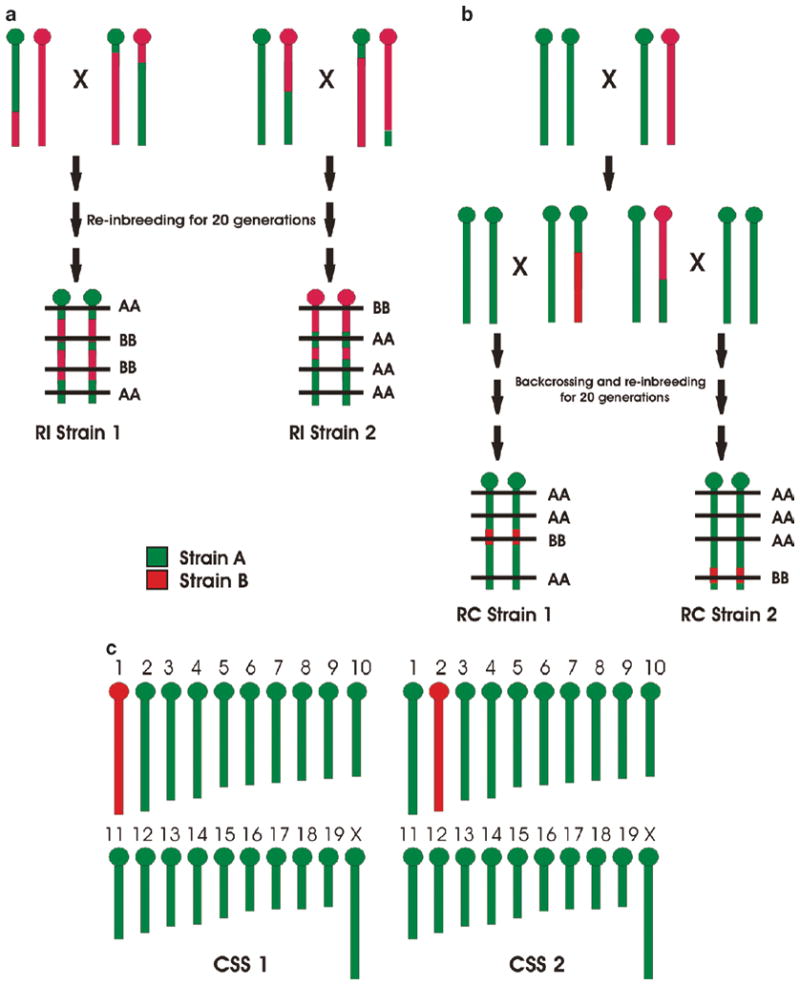
Advanced QTL mapping populations. Graph A shows the construction of recombinant inbred (RI) strains. Only one chromosome is illustrated for simplicity. F2 hybrids constructed from two strains, Strain A (green) and Strain B (red), are reinbred for 20 generations. Eventually all loci become fixed in a homozygous state, but the pattern of homozygosity differs from one strain (e.g., RI Strain 1) to another (e.g., RI Strain 2). QTL mapping proceeds by identifying a genomic location (horizontal line) in which genotype correlates with the phenotype among a large set of RI strains. Graph B shows the partial construction of recombinant congenic (RC) strains. Again, only one chromosome is illustrated for simplicity. A backcross is first constructed by breeding an F1 hybrid back to one parental strain (in this case, Strain A). The offspring are further backcrossed and then reinbred to homozygosity. Unlike RI strains that are 50% Strain A, 50% Strain B (albeit in different patterns), RC strains are constructed so that they have a minority of “donor” genome (in this case, Strain B) placed on a majority “recipient” background (in this case, Strain A). The location of the donor genome differs from one strain (e.g., RC Strain 1) to another (e.g., RC Strain 2). Commonly, a reciprocal RC set is created where the donor and recipient genome is swapped. Again, QTL mapping proceeds by identifying a genomic location (horizontal line) in which genotype correlates with the phenotype among relevant RC strains. Graph C illustrates (the construction process is beyond the scope of this chapter) chromosome substitution strains (CSSs). In these, the donor segment represents an entire chromosome (e.g., chromosome 1 in CSS1 and chromosome 2 in CSS2). The statistically significant phenotypic divergence of a CSS from its background strain is prima facie evidence of a QTL on that chromosome

One should be cautious not to over interpret heritability estimates since they are specific to the particular conditions of the experiment. These include the dose or intensity of the pain producing stimulus, the experimenter, the rodent strains chosen, and known and unknown environmental factors. Optimization of these parameters using one or a limited number of outbred strains can greatly increase the heritability obtained in a panel of inbred strains, providing heritability estimates that can be much larger in rodent models than those obtained in human subjects, and in turn, facilitating subsequent studies. The mosaicity of inbred strains is an important factor to consider when selecting strains in order to maximize the genetic diversity among strains being tested. Several articles examining the mosaicity of inbred rodents using a range of methods can be referred to for the phylogenetic placement of inbred strains of mice or rats in their respective evolutionary trees (17–19).

Paying careful heed to environmental factors can also increase heritability estimates. For most pain traits in humans and in many rodent pain models, genetic factors account for a minority (<50%) of the total variability in the trait (20) although a median of approximately ~50% heritability has been demonstrated over numerous pain-related traits in SI mice (1, 3, 21, 22). Thus, to minimize environmental noise, strict control is necessary of environmental factors including experimenter, season, cage density, time of day, humidity, diet, housing, social factors (including proximity to other mice during testing) genetic background of cagemates, habituation to the testing room and apparatus, and state of arousal during testing, all of which can affect pain traits and may interact with genotype (23–29).

3. Genetic Correlations

Once heritability of the trait has been determined and quantified, the same genetic resources can be used to perform a genetic correlation analysis. Genetic correlation analysis is a method that allows for the understanding of the biological basis of a trait prior to determination of the responsible genes (30–32). Given a particular strain distribution pattern (SDP) of means for a trait determined in an inbred strain survey, for example, strong positive correlation with the strain means for a second trait indicates that similar genetic mechanisms underlie heritable variability in both traits (see Fig. 1). If the genetic correlation between the strain means for the two traits is close to zero, it indicates that independent genetic mechanisms underlie variability in each of the traits. If a strong negative correlation exists between two traits, the same genetic mechanisms may increase one trait and decrease the second trait. Note that genetic similarities or dissimilarities suggest biological similarities or dissimilarities, respectively, and this suggestion can be quite heuristic.

Fig. 1.

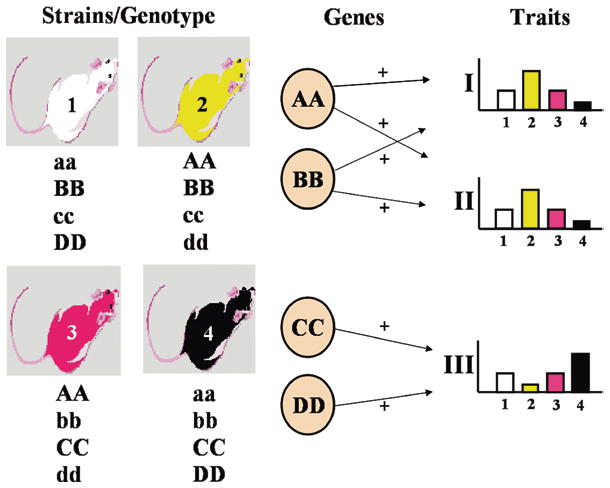
Genetic correlation analysis. A genetic correlation analysis examines whether the heritable variability in two traits (or phenotypes) is due to the same underlying genetic mechanisms. Inbred strains of mice or rats are tested for their responsiveness or sensitivity to determine the strain distribution pattern (SDP) of means for the traits. Pearson’s correlation coefficient or a Spearman rank correlation is then calculated between the means of each trait. If the SDPs are similar and a sufficient number of strains have been tested, the traits are “genetically correlated”, and the correlation can be ascribed to common genetic mechanisms. The figure demonstrates the logic behind this inference. Fully inbred strains have alleles forced into homozygosity throughout the genome as demonstrated in the figure (e.g., AA). Pain traits are considered to be polygenic with several genes contributing to increases or decreases of the traits. For this example, we will assume that the capital letter alleles of A and B genes contribute to increases in traits I and II, but not trait III, and C and D genes contribute positively to trait III, but not to traits I and II. Phenotyping the mice produces similar SDPs for traits I and II. Since trait III is mediated by different genes, C and D, the SDP for the same strains is different from those of traits I and II. By adding up the gene effects for each contributing gene, one can see the relationship between genotype of each inbred strain and the phenotype value (e.g., strain 2 has two positively contributing alleles to traits I and II). Therefore, even prior to determining the precise mechanisms of heritability, one can make the inference regarding shared genetic mechanisms based on similar SDPs for two or more traits. Note that use of this method requires a significant number of inbred strains (preferred minimum of 11; absolute minimum of 8) be simultaneously phenotyped, and environmental factors must be strictly controlled throughout the experiment

Calculation of a genetic correlation is performed with a Pearson correlation coefficient or a Spearman rank correlation coefficient, with the distribution of the strain means determining the most appropriate method (30). Note that the correlation is calculated using strain mean values and not using values from individual mice, which would contain environmental variability as well. As a general rule, a minimum of eight strains should be used in order for the correlations to indicate common or distinct mechanisms and to be able to detect statistically significant correlations. It is ideal to have a wide range of strain means that are continuously distributed, as comparisons with or between bimodally distributed traits or traits exhibiting a poor spread of means are not as valid or informative with respect to indicating common genetic mechanisms.

3.1. Genetic Correlations Among Multiple Traits

When a sufficient number of traits have been tested in the same inbred strains, the genetic relationships among the traits can be determined and a genetic framework developed using multivariate statistical methods. A growing literature of SI and RI “strain surveys” exists, with online resources to search these data and to directly compare previous and new strain surveys (e.g., http://www.jax.org/phenome, http://www.genenetwork.org). Provided enough common strains were selected in each strain survey, multivariate analyses can be used to visualize the genetic relationships among a group of pain traits simultaneously (2, 3). Using the multivariate methods of multidimensional scaling (MDS) and principal components analysis (PCA), clustering of genetically similar traits in a two- (or three-) dimensional representation of the genetic correlations can be easily illustrated, as can informative genetic relationships among groups of traits, and even potentially meaningful dimensions or factors that distinguish the traits. One can also determine the relative similarity of inbred strains for a set of related traits to identify outlier strains, for instance (33).

In both MDS and PCA methods, a set of points representing each trait is plotted with the distance between points fitting as closely as possible a matrix of measured similarities between the traits such as correlations. In the two-dimensional MDS plot, points representing highly positively correlated traits will have the smallest distances between them, highly negatively correlated traits will have the largest inter-point distances, and uncorrelated traits will have intermediate distances between their points. In a two-dimensional PCA graph, points at the end of vectors emanating from the center are plotted. Angles between vectors that are close to zero indicate highly positively correlated traits, angles close to 180° indicate highly negatively correlated traits, and angles close to 90° indicate uncorrelated traits. The MDS and PCA plots are usually complementary, each providing additional information. Note that each trait in the multivariate analysis has an influence on the relative position of every other trait. Thus, adding a new trait that is differentially correlated with two positively correlated traits can change the relative position of the two moderately positively correlated traits. Incomplete data sets (with few strains in common between traits) can also have profound effects on the overall 2-D representation, as can bimodally distributed traits or strain means with a small range of values.

These multivariate methods have been used to identify genetically fundamental types of pain (as clusters of assays), and to determine the genetic relationships among hypersensitivity measures and their relation to baseline nociceptive measures (2, 3) (see Fig. 2). We observed, for example, that mechanical hypersensitivity is distinct from thermal hypersensitivity, even when induced in the same nerve injury model, and that thermal hypersensitivity models differ in their genetic relatedness to baseline nociception models.

Fig. 2.

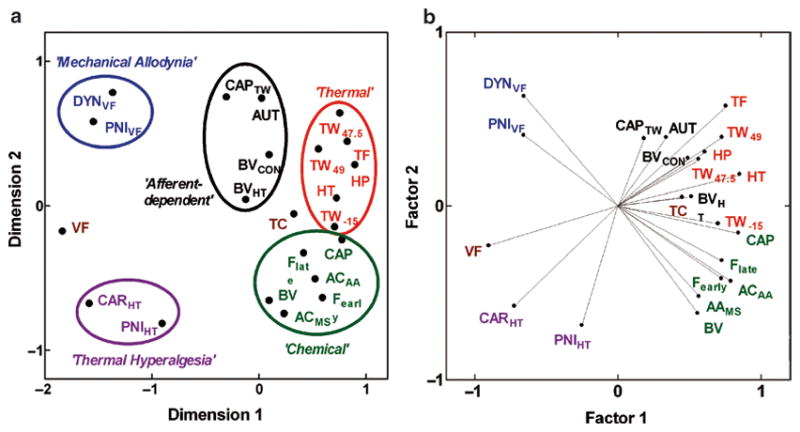
Multivariate statistics methods for genetic correlation analysis of several traits simultaneously. Multidimensional scaling (MDS) and principal components analysis (PCA) plots facilitate visualization of the genetic relationships among a group of pain traits simultaneously. Clustering of genetically similar traits in a two-dimensional representation of the matrix of pairwise trait correlations can be easily determined, as can informative genetic relationships among groups of traits and meaningful dimensions or factors that distinguish the traits. (a) With MDS, points representing highly positively correlated traits will be closest, highly negatively correlated traits will be furthest apart, and uncorrelated traits will have intermediate distances between their points. (b) With a PCA, traits are represented as points at the end of vectors. Highly positively correlated traits have angles between their vectors close to zero, highly negatively correlated traits have angles close to 180°, and uncorrelated traits have between-vector angles close to 90°. Each method can provide complementary information. For example, from the PCA plot in (b) it is apparent that the “Afferent-dependent” hypersensitivity traits represented with black points and font are genetically related to the “Thermal” nociception traits with red points and font, but this is not obvious from only the MDS plot in (a). See refs. 2, 3 for full description of assays represented in the figure. Figure reprinted from (3) with permission from the International Association for the Study of Pain^® (IASP^®)

The methods can also be effectively used to compare pain traits to traits of another biological domain that are hypothesized to be genetically related (e.g., locomotion, anxiety, neurotrans-mitter release in specific brain areas, hormone release). Numerous traits from several domains have been examined in SI and RI mouse strains and have been placed in online databases for perusal and analysis by the interested investigator (http://www.jax.org/phenome, http://www.genenetwork.org). These resources should be consulted during selection of strains to include in a new strain survey. Data sets of baseline mRNA transcript expression in specific brain areas and other tissues, obtained by microarray gene expression profiling, are also available online for particular RI strains, permitting direct comparisons of pain traits with transcript expression profiles.

4. Linkage Mapping Studies of Pain and Analgesia

Of course, the main reason to employ genetic animal models is because they allow a relatively inexpensive path to the identification of the responsible genes. Using linkage mapping, one is lead to those genes by their genomic position alone, and thus no prior assumptions are necessary. This allows for the discovery of entirely novel determinants of pain sensitivity.

4.1. Techniques

4.1.1. Theory of Linkage

Linkage mapping, including QTL mapping, exploits the phenomenon of homologous recombination (also called crossing-over) to estimate the distance between genomic loci (34). Recall that during meiosis, DNA strands can physically break, switch places, and reattach to one another such that the resulting haploid chromosome (to be packaged in a gamete) is recombinant, containing, for example, paternal alleles proximal to the breakpoint and maternal alleles distally. Homologous recombination occurs quite naturally as a way to produce new genotypic combinations. Because crossing-over occurs commonly (approximately once per 100 Mb per meiosis) and randomly (with the exception of so-called recombination “hot spots” and “dead spots”), the probability of any two loci on a chromosome being separated from each other (i.e., independently assorted) by a cross-over event is directly related to their physical distance on that chromosome. (Note that the independent assortment of loci on different chromosomes is assured, and known even by Mendel.) As a practical matter, then, the genetic distance between two loci can be defined as the number of offspring who are recombinant for those two loci (i.e., a cross-over occurred between the loci) out of the total number of offspring; this ratio provides the recombination frequency, θ, which ranges from 0–50%. Loci with θ < 50% are thus “linked”. In experimental organisms like mice, where matings can be constructed so that the divergent parental genotypes are known and the genotypes and phenotypes of offspring can be easily typed (called “genotyping” and “phenotyping,” respectively), calculation of θ is trivial. Somewhat more computationally intensive (and beyond the scope of this chapter) are the inferential statistics used to determine whether linkage at any θ is statistically reliable. These include the logarithm of the odds (LOD) score, the χ² statistic, and, increasingly, p-values estimated by iterative permutation of the actual data set.

It is important to understand that linkage can be demonstrated between any two loci on a chromosome, regardless of what those loci are. One can talk about linkage between two genes, between a gene and a genomic “marker”, between two markers, or, importantly, between a marker and a phenotype itself (because the phenotype is being affected by a DNA sequence with a particular location). Genomic markers used in linkage mapping have evolved from restriction fragment length polymorphisms (RFLPs) to microsatellites (simple sequence repeat polymorphisms; SSRPs), to single-nucleotide polymorphisms (SNPs), with the more modern markers exhibiting higher frequencies in the genome (thus ensuring fuller coverage). Linkage mapping of a trait is in fact the demonstration of linkage between the phenotype and a genomic marker, followed by an inference of linkage between the genomic marker and the responsible DNA variant. Transitive logic ties the phenotype with the DNA variant, which is of course the point of the exercise. See Fig. 3 for an illustration of the principles underlying linkage mapping.

Fig. 3.

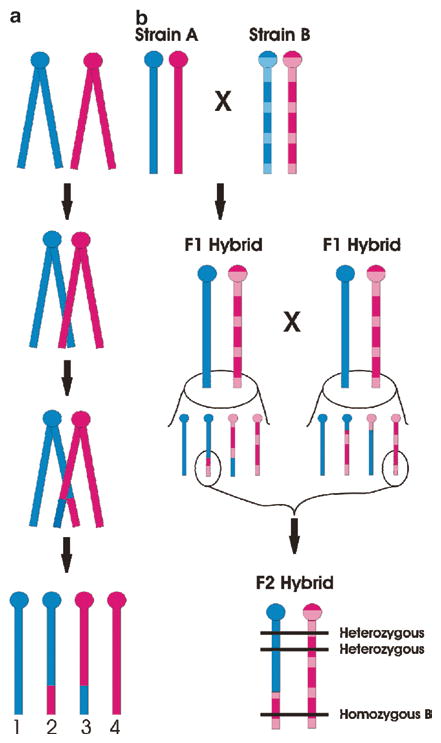
Linkage mapping theory. Note that murine chromosomes are telocentric, with the centromere (ball) located at the proximal end of the chromosome. Blue and pink colors represent the paternally and maternally derived chromosomes, respectively. For simplicity only one chromosome is illustrated. Graph A shows homologous recombination (crossing-over) in a chromosome during meiosis. During prophase I, the two paired chromosomes (i.e., four chromatids) are found very close to one another, and homologous sites on two chromatids can mesh and exchange places. As a result, four gametes are possible: two nonrecombinant (gametes 1 and 4), inherited unchanged from the parental form, and two recombinant (gametes 2 and 3), in which both paternal and maternal genetic information is represented. Graph B illustrates how homologous recombination produces “linkage” of intra-chromosomal genetic locations in an F2 hybrid mouse. Inbred Strain A (solid) and Strain B (hatched) when mated will produce identically heterozygous F1 hybrid animals. In the F1 hybrids, however, the effects of homologous recombination can be seen, and both nonrecombinant and recombinant gametes are created. Assuming the highlighted gametes result in the conception of an F2 hybrid, shown, genomic locations (horizontal lines) near each other physically will tend to have the same genotype (in this case, heterozygous), whereas genomic locations far away physically will tend to have a different genotype (in this case, homozygous for Strain B alleles). Thus, physical locations of unknown genetic factors can be estimated (see text)

4.1.2. Implementation of Linkage Mapping in Segregating Populations

The most straightforward way to implement linkage mapping in an experimental organism like the mouse is to create a segregating population (i.e., F2 hybrid or backcross) from inbred parental genotypes displaying a large phenotypic strain difference. By doing this, one maximizes the number of trait-relevant genes that can be found (since only genes with variant alleles in the two parental strains are “visible” to linkage mapping), and guarantees that only two genotypes are possible in the backcross (one homozygous, one heterozygous) and three genotypes are possible in the F2 hybrid (two homozygous, one heterozygous) at the responsible variant and all strongly linked markers. One great advantage of using experimental organisms rather than human pedigrees for linkage mapping is that it is perfectly feasible to create segregating populations numbering the hundreds or even thousands (in lower organisms like Drosophila and in plants even much higher numbers are routine), providing as much statistical power as is necessary to detect QTLs, which often account for only a small percentage of the genetic variance. As microsatellite and/or SNP genotyping has become quite affordable, the limiting factor is phenotyping cost and effort. Typically, all subjects of the segregating population are phenotyped, and genomic DNA obtained from any tissue is then genotyped at approximately 100 microsatellites spanning the genome. Interval mapping can then be performed on the data to detect linkage by interpolating between the markers (e.g., ref. 35). It is important to note that due to the large distance of linkage disequilibrium (LD) around microsatellite markers (κ100 kb), QTL mapping typically provides only a very rough estimate of the location of the responsible variant, usually no better than 10 Mb (36) although new and evolving models may significantly increase the resolution (37).

Proceeding from QTL detection to identification of the responsible gene (the quantitative trait gene; QTG) and responsible variant in or near that gene is known as positional cloning, and often proceeds via the construction and testing of congenic strains, in which donor genome from one strain is placed (“introgressed”) onto the background of another via repeated backcrossing (see ref. 38). The process of congenic strain construction can be speeded up by the use of marker-assisted breeding strategies (“speed congenics”) (39), but positional cloning remains laborious and time-consuming (40). Of course, at any point in the process, one is free to entertain and test candidate gene hypotheses of any gene known to reside in the genomic confidence interval containing the QTL.

4.1.3. Advanced Mapping Populations

One weakness of performing linkage mapping using segregating populations is that they are one-shot experiments; the population disappears forever as soon as the subjects are tested and euthanized. More useful might be genetic reference populations, whereby segregation is reinbred so that it is stable, able to be propagated intact through multiple generations so that new phenotypes can be tested at will (see ref. 41). The oldest of these are RI strain sets (42), in which individual members of an F2 hybrid cross are used as progenitors of new inbred strains, each one representing a discrete and unchanging “shuffling” of the progenitor alleles. Other examples of inbred mapping populations include recombinant congenic (RC) strain sets, in which small portions (different in each strain) of “donor” genome are placed on a recipient background (43) and chromosomal substitution strain (CSS; consomic) sets, in which entire donor chromosomes are placed on a recipient background (see ref. 44). See Fig. 4 for an illustration of the construction and use of these models.

The advantage of using stable mapping populations over de novo segregating populations is that the mapping populations have already been genotyped by their developers. To use them, therefore, one only needs to obtain and phenotype the set of strains, and correlate the phenotypic data with databased genotyping data in order to detect linkages. The disadvantage is that for practical reasons, the size of these strain sets is too small to provide statistical power to detect any but the largest linkages; typically, a provisional QTL detection in RI, RC or CSS panels is followed by confirmation in an F2 intercross or backcross (45). In other cases, advanced mapping populations can be used to confirm a linkage and/or reduce the size of the genomic interval containing the QTL (see ref. 41). A new, very powerful (46) advanced mapping population, the Collaborative Cross (37, 47) represents an attempt to combine the advantages of a genetically stable mapping population with the statistical power afforded by the sheer number of strains (500–1,000). The Cross has yet to be completed and used, however, and haplotype mapping of large sets of inbred strains (see below) provides some of the same advantages.

4.1.4. In silico H aplotype Mapping

A significant disadvantage of both segregating populations and advanced mapping populations derived from them is that only gene variants divergent in the two progenitor strains can be detected; variation contained in the >450 other inbred mouse strains (16), for example, is not brought to bear. A notable exception is the population of mice in the Collaborative Cross, which is derived from an 8-way cross of standard inbred strains (47). Following the sequencing of the (C57BL/6) mouse genome (48) and the re-sequencing of the genomes of many other strains to identify SNPs among them, it has been revealed that variation among inbred laboratory mouse strains is best explained as a mosaic of three founder subspecies: Mus musculus (M. m.) domesticus, M. m. musculus, and M. m. molossinus (18). In fact, SNPs are not inherited independently, but in so-called haplotype blocks (with high LD of SNPs within the block) of varying sizes (but averaging κ30 kb, approximately the size of a single gene), and only a small number of (typically no more than four) observed haplotypes among large sets of strains. Thus, simply by phenotyping a large (>15) set of strains and comparing the distribution of those phenotypes to the distribution of haplotype blocks across the genome in those same strains (49), one can detect QTLs, and with gene-level (or even subgenic) resolution (see ref. 50). See Fig. 5 for an illustration of haplotype mapping.

Fig. 5.

Haplotype mapping theory. Along the stretch of DNA illustrated (center), sequencing reveals only five nucleotide bases showing polymorphisms (i.e., single-nucleotide polymorphisms; SNPs) across a set of 11 strains. Although 5⁴ = 625 permutations are possible, in fact only three sequences of these five SNPs (haplotypes) are observed: A-T-G-A-A, C-G-A-C-T, and C-C-G-A-T. This is because these SNPs are inherited together in a haplotype block, and population bottlenecks in the species’ history has limited the number of extant haplotypes. We can label the haplotypes in this block in order of their frequency: 1, 2 and 3. QTL mapping proceeds by identifying haplotypes that correlate with the phenotype among a large set of inbred strains

Note that haplotype mapping is fundamentally different from standard linkage mapping in that it relies on patterns of LD between strains rather than detecting linkage per se. The limitation of the technique is that its statistical power is limited in the same manner as for advanced mapping populations; only a finite number of strains have been genotyped at SNPs blanketing the genome.

4.2. Findings

Although murine linkage mapping studies of pain and analgesia have been conducted for almost 15 years, the practical challenges surrounding its use have ensured only a small number of published findings. For details of these findings, consult any one of a number of reviews on the topic (20, 51–53). A listing of significant QTLs and the genes possibly (and in some cases, likely) responsible for them is provided in Table 1.

Table 1.

Statistically significant QTLs of relevance to pain and analgesia in laboratory mice

Phenotype	Chromosome	LODa	Locationb	Candidate gene(s)	Reference
Acute/tonic pain
Capsaicin	2	5.9	30		(55)
	7	4.8	10		(55)
	7	5.8	50		(55)
	8	4.4	30		(55)
Formalin	9	5.2	60	Atp1b3 (51 cM)	(56)
	10	4.3	70	Avpr1a (68 cM)	(56)
Hot-plate	4	3.8 (♂ only)	71	Oprd1 (65 cM)	(57)
Paw withdrawal	7	6.3	50	Calca (54 cM)	(4)
Tail-withdrawal	4	3.6 (♂ only)	56	Oprd1 (65 cM)	(6)
	7	12.6	33	Trpv1 (44 cM)	(6)
	11	7.8	46
Analgesia
Clonidine	1	4.7	100	Kcnj9 (94 cM)	(6)
Morphine	1	4.7 (♀ only)	10	Oprk1 (6 cM)	(58)
	1	3.2	91	Htr1b (46 cM)	(6)
	9	5.2 (♀ only)	20	Oprm1 (8 cM)	(58)
	9	4.5	42		(59)
	10	7.5	9		(60)
Stress-induced	8	6.1 (♀ only)	56	Mc1r (68 cm)	(57)
U50,488	8	2.7 (♀ only)	67	Mc1r (68 cM)	(5)
WIN55,212-2	1	4.4	100	Kcnj9 (94 cM)	(6)
	7	4.8	40	Trpv1 (44 cM)	(6)
Opioid hyperalgesia
Chronic morphine	5	p = 0.000083 *	1	Abcb1b (1 cM)	(61)
	18	p = 0.00037 *	34	Adrb2 (34 cM)	(62)

^aLOD logarithm of the odds score

^bLocation of peak LOD score in centiMorgans (cM), a unit of genetic distance. Note that confidence intervals in QTL mapping projects are generally very large

5. Conclusions

Pain genetics does not need to be conducted in laboratory animals. Genes responsible for monogenic pain disorders like congenital insensitivities to pain and primary erythermalgia can be identified by linkage mapping, and genetic association studies have provisionally implicated a handful of genes in more common pain pathologies (53). The latter technique has suffered from lack of replication (53), however, and so far the powerful methodology of the whole-genome association study (WGAS) remains too expensive to be applied to pain (54). It seems likely, however, that pain genetics in laboratory rodents will continue to play an important role, both in the discovery of novel genes and in the characterization of how their allelic variants produce variable sensitivity to pain and analgesics.