Abstract
To survive changes in climate, successful species shift their geographic ranges to remain in suitable habitats. For parasites and other highly specialized species, distributional changes not only are dictated by climate but can also be engineered by their hosts. The extent of host control on parasite range expansion is revealed through comparisons of host and parasite migration and demographic histories. However, understanding the codistributional history of entire forest communities is complicated by challenges in synthesizing datasets from multiple interacting species of differing datatypes. Here we integrate genetic and fossil pollen datasets from a host–parasite pair; specifically, the population structure of the parasitic plant (Epifagus virginiana) was compared with both its host (Fagus grandifolia) genetic patterns and abundance data from the paleopollen record of the last 21,000 y. Through tests of phylogeographic structure and spatial linear regression models we find, surprisingly, host range changes had little effect on the parasite's range expansion and instead host density is the main driver of parasite spread. Unlike other symbionts that have been used as proxies to track their host's movements, this parasite's migration routes are incongruent with the host and instead reflect the greater importance of host density in this community's assembly. Furthermore, these results confirm predictions of disease ecological models regarding the role of host density in the spread of pathogens. Due to host density constraints, highly specialized species may have low migration capacities and long lag times before colonization of new areas.
Keywords: comparative phylogeography, host–parasite interactions, eastern North America, Orobanchaceae, Fagus
Because of species-specific interactions and obligate host–parasite relationships, many parasites are thought to closely track their hosts during range expansions. With their shorter generation times and more quickly evolving genomes, parasites can make attractive proxies for understanding host migration patterns (1, 2). However, parasite and host phylogeographic histories may be incongruent, and that conflict reflects processes that have limited the spread of the parasite relative to the host. In particular, host density has been implicated in disease systems as a constraint on parasite spread (3, 4). We take a historical approach to investigate the effects of host density on both population differentiation and postglacial migration in the assembly of a tree–herb, host–parasite system. The influence of changes in host range and host density on a parasite's migration history is examined by comparing the parasite phylogeography with both the host phylogeography (5) and host abundance data (6) over the last 21,000 y. Postglacial migration is approximately analogous to present-day range shifts due to climate change (7), so our approach can help to understand current factors controlling community assembly at different trophic levels.
The eastern North American study system consists of the parasitic plant, Epifagus virginiana (beechdrop; Orobanchaceae), and its host tree, Fagus grandifolia (American beech; Fagaceae). E. virginiana is an annual, self-fertilizing root parasite that grows obligately on the single species, F. grandifolia. The migration and demographic history of F. grandifolia has been extensively studied with both molecular (5, 8) and paleopollen tools (6, 9 –11). Along with other eastern North American species, F. grandifolia has contributed to a long-held paradigm concerning the capacity of temperate forests to successfully track climate change. On the basis of fossil pollen data of these species, rapid migration rates have been estimated for trees confined in southern refuges during glacial periods that expanded their ranges quickly northward to their current distributional limits (9, 11). These migration rates are orders of magnitude faster than estimates based on life history and seed trap data (12). However, the pollen data are prone to false negatives, especially when population densities are low (13), and accurately tracking range margins is very challenging (14). We reinterpret the fossil pollen datasets as reflecting changes in abundance rather than documenting changes in range limits. This interpretation is similar to assumptions in other paleoecological studies that use changes in fossil pollen abundances to understand shifts in tree densities and community structure (e.g., ref. 6). In contrast, molecular datasets are more likely to show the initial migration pathways, because they are sensitive to small population sizes and founder events likely to occur at the range margins (5, 15). Molecular phylogeographies have since uncovered more northerly refuges at midlatitudes closer to the ice margin for several plant species (5, 16, 17), which produce lower estimates of migration rates (18). Together, molecular and paleopollen datasets provide insights into the two host factors most likely to influence broad-scale parasite migration patterns: changes in host range and host density.
The availability of such detailed host information allows us to generate hypotheses to test against parasite migration patterns. If host susceptibility rates are high and density independent and parasite dispersal is high, then the appearance of new host habitat is the major constraint on parasite range expansion. In this case, the host and parasite phylogeographies should show evidence of comigration and have similar population structures. However, many disease systems are additionally sensitive to fluctuations in host density, and successful establishment of a parasite may be limited by these effects (3, 4). In this scenario, the parasite phylogeography should be correlated with changes in host density seen in the fossil pollen record. Due to the extensive sampling of parasite and host data, we have the opportunity to use powerful analytical tools to answer the question: Did the parasite, E. virginiana, primarily respond to changes in the host range or to changes in host density as it colonized the postglacial landscape? We implemented comparisons between the host and parasite migration histories using (a) Monmonier's algorithm (19), which describes the geographic locations of genetic boundaries, (b) Bayesian coalescent methods that estimate population demographic parameters (20), and (c) a newly developed method that utilizes spatial linear models to test relationships between the genetic and fossil datasets.
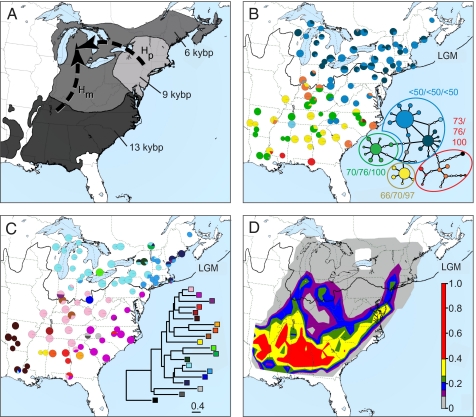
The initial migration of F. grandifolia into newly unglaciated territory was largely accompanied by rapid increases in abundance except in the colonization of the midwest. The fossil pollen data show beech to be broadly distributed in the south at 13,000 y before present (kyBP), followed by density increases in the northeast at 9 kyBP, and then a steadily westward increase in density into the midwest by 6 kyBP (H p in Figs. 1A and 2C) (6). In contrast, the host molecular data (Fig. S1) suggest a refuge near the glacial boundary from which colonists dispersed directly northward (H m in Fig. 1A) (5, 8). The initial dispersal of the host into the Midwest must have occurred at low density, so that the pattern was not captured in the pollen record. If the parasite was able to colonize these marginal, low-density populations, then the parasite should show similar migration routes to H m. Alternatively, if the parasite was limited by host density, then the parasite's range should track the development of high-density beech forests (H p). The results have implications for the parasite's migration capacity. Even if host species can rapidly equilibrate with global change, additional factors may cause parasite and other specialized species to lag behind. This lag would result in the disassembly of the community and creation of systems with no past analogs (21), making forecasting future range expansions problematic.
Fig. 1.
Genetic structure of Epifagus virginiana. (A) Range map with competing migration route hypotheses based on host fossil pollen (H p) or host cpDNA (H m). Regions (shaded) were defined by the distribution of host fossil pollen at 13, 9, and 6 kyBP. (B) Distribution of cpDNA haplotypes and haplotype network (Inset). Numbers are the parsimony and likelihood bootstraps and Bayesian posterior probability values. (C) Distribution of microsatellite clusters and cluster phenogram (Inset). (D) Areas of high genetic differentiation. Colors correspond to the average number of genetic breaks found at that location over 1,000 cross-validation subsamples. Color assignments were based on the 50th–90th percentiles: red, 90+%; yellow, 80–89%; green, 70–79%; blue, 60–69%; purple, 50–59%. LGM, ice margin at the last glacial maximum. Maps were drawn in Google Earth (copyright 2010 Google).
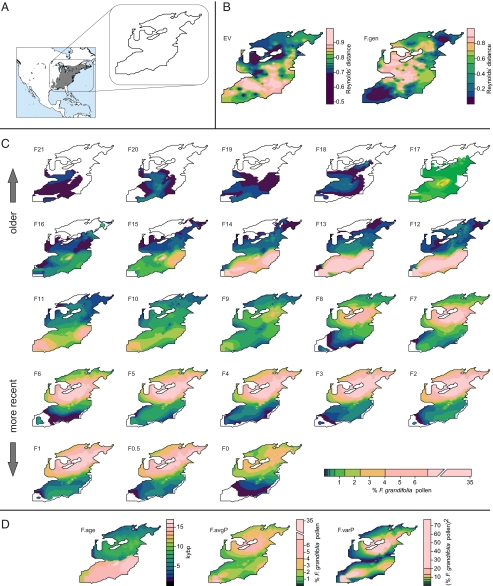
Fig. 2.
Genetic and fossil map layers of Epifagus virginiana and Fagus grandifolia. (A) Geographic range of both species. Outline shows extent of interpolated data layers. (B) Genetic distance maps for E. virginiana (EV) and F. grandifolia (F.gen). F. grandifolia genetic data are redrawn from McLachlan et al. (5). (C) Fossil pollen layers for F. grandifolia from 21 kyBP (F21) to present (F0) in 1,000-y increments. A pollen layer for 500 ybp (F0.5) is also shown. Pollen layers are redrawn from Williams et al. (6). (D) Summary pollen layers (F.age, F.avgP, and F.varP) of F. grandifolia as described in text. Warmer colors correspond with higher values in all maps. Maps were visualized using a 10-quantile color ramp.
Results and Discussion
To elucidate the migration history of E. virginiana 467 samples from 88 localities across the range of the host were sequenced at two chloroplast DNA (cpDNA) loci and genotyped using nine presumably nuclear microsatellite markers (Fig. 1 B and C). The Northeast (regions defined below) contained lower allelic richness than the South and the Midwest in both cpDNA (4.9 versus 12.6 and 11.2 haplotypes after rarefaction to 50) and microsatellite datasets (4.3 versus 5.8 and 6.6 alleles after rarefaction to 100 averaged over all loci). Also, population differentiation was highest in the South with F ST’s largest there (averaged over all loci: F ST-South = 0.78, F ST-Northeast = 0.49, F ST-Midwest = 0.53). Whereas these results suggest more isolation between the southern populations, they stop short of providing the geographic locations of the boundaries segregating the genetic variation. To locate these barriers we used Monmonier's algorithm, a method that identifies the spatial boundaries that maximize genetic differences between localities (19) (see SI Materials and Methods for a full description of the method). To explore the robustness of the inferred patterns, the data were cross-validated by reconstructing genetic boundaries in 1,000 subsampled datasets. Subsampling occurred at the locality level with 50% of localities sampled with replacement.
The results of the cross-validated Monmonier analyses show genetic breaks concentrated in the South, with almost no genetic breaks north of the ice margin and none between the Northeast and the Midwest (Fig. 1D). The highest proportion of breaks separate the orange/red/pink microsatellite clusters in Alabama and Georgia and the brown cluster from the rest of the landscape (Fig. 1D). The breaks are broad because barriers can shift depending on what populations were included in the subsample. The northernmost barrier generally corresponds with the blue allele distributions with a peak separating the lower and upper Midwest (between Indiana/Ohio and Michigan) (Fig. 1 B–D). Multiple runs with different levels of subsampling (50–90%) and numbers of barriers recorded per subsample (1 –5) confirm the general pattern of high differentiation in the South and barriers separating the lower Midwest from the upper Midwest (Fig. S2).
The location of additional barriers between the upper and lower Midwest suggests a suture zone in this area between colonists from different sources, so even if there was some migration northward (H m), southern populations did not contribute significantly to diversity farther north. This result is consistent with the interpretation that E. virginiana survived the glaciation in isolated, low-density host populations across the southern range. In the North, the few genetic barriers and low population differentiation are consistent with uninterrupted range expansion from the Northeast coincident with host density increases (H p; Fig. 1A).
The lack of northward migration into the Midwest is further supported by migration rates and divergence times among regions estimated through Bayesian coalescent-based analyses (Table 1) (20). Localities were grouped into geographic regions defined by the range of host fossil pollen at 13, 9, and 6 kyBP, hereafter referred to as regions 13, 9, and 6 (Fig. 1A). Migration rates from the South into region 6, which encompasses the Midwest, were significantly lower than those along East-to-West routes [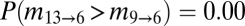 , Table 1 and Table S1], reflecting the extensive sharing of alleles between the Midwest and the Northeast versus the restricted southern distributions of the other allelic groups. These results were robust to other regional definitions where borderline localities were swapped among regions (see SI Materials and Methods, Fig. S3, and Table S2 for alternate regional definitions and results). For instance, even if the area south of the ice margin in region 6 is included within region 13 (forming region 13+ and 6−), migration rates from the expanded southern region were still significantly less than from the Northeast [
, Table 1 and Table S1], reflecting the extensive sharing of alleles between the Midwest and the Northeast versus the restricted southern distributions of the other allelic groups. These results were robust to other regional definitions where borderline localities were swapped among regions (see SI Materials and Methods, Fig. S3, and Table S2 for alternate regional definitions and results). For instance, even if the area south of the ice margin in region 6 is included within region 13 (forming region 13+ and 6−), migration rates from the expanded southern region were still significantly less than from the Northeast [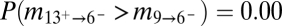 , Table S2]. The Midwest's divergence time from the South was older than from the Northeast [
, Table S2]. The Midwest's divergence time from the South was older than from the Northeast [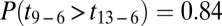 , Table 1 and Table S3], adding further evidence to the Northeast being the colonization source for the Midwest.
, Table 1 and Table S3], adding further evidence to the Northeast being the colonization source for the Midwest.
Table 1.
Population demographic parameters of Epifagus virginiana
| r1 | r2 | θ1 (4N1μ) | θ2 (4N2μ) | θA (4NAμ) |
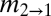 (m2→1/μ) (m2→1/μ) |
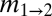 (m1→2/μ) (m1→2/μ) |
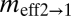 (2N1m2→1) (2N1m2→1) |
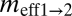 (2N2m1→2) (2N2m1→2) |
t (tμ) |
| 13 | 9 | 0.73 | 0.25 | 9.76 | 0.59 | 5.05 | 0.22 | 0.64 | 0.06 |
| (0.2–1.7) | (0.08–0.59) | (4.95–26.72) | (0.11–5.90) | (0.62–13.75) | (0.02–0.37) | ||||
| 13 | 6 | 1.94 | 12.93 | 5.04 | 1.03 | 0.04 | 1.00 | 0.24 | 0.36 |
| (1.27–3.02) | (10.03–21.15) | (3.42–21.15) | (0.38–2.23) | (0.01–2.02) | (0.30–3.90) | ||||
| 9 | 6 | 0.42 | 239.49 | 8.59 | 6.34 | 8.17 | 1.33 | 978.02 | 0.28 |
| (0.08–0.59) | (47.80–236.38) | (5.39–46.12) | (3.11–11.20) | (6.28–11.63) | (0.18–1.28) |
Regions (r1 and r2) are defined in Fig. 1A and in text. θ1, θ2, and θA refer to the scaled effective population sizes of r1, r2, and the ancestral population, respectively. 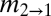 and
and 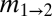 are the scaled migration rates forward in time from r2 to r1 and vice versa.
are the scaled migration rates forward in time from r2 to r1 and vice versa. 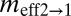 and
and 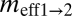 are the effective migration rates (taking into account population size). t is the scaled divergence time between the regions. All values (except
are the effective migration rates (taking into account population size). t is the scaled divergence time between the regions. All values (except 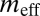 ) are scaled by the unknown per gene per generation mutation rate, μ. m, migration rate per gene per generation; n, effective population size; t, time in generations. The 95% credible interval is given below each estimate. Because
) are scaled by the unknown per gene per generation mutation rate, μ. m, migration rate per gene per generation; n, effective population size; t, time in generations. The 95% credible interval is given below each estimate. Because 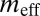 is a point estimate, no credible interval is given.
is a point estimate, no credible interval is given.
Whereas the results of the Monmonier and coalescent analyses suggest that E. virginiana may be broadly tracking changes in host density, these findings are consistent with many hypothetical migration routes within regions 9 and 6 that may not agree with more detailed host patterns. To better assess the relationships between parasite genetic patterns, host genetic patterns, and host density, a method was developed to analyze these spatial data within a geographic information system (GIS) framework using spatial linear regression models. First, genetic and fossil datasets were transformed into comparable raster map layers. Genetic patterns were summarized by calculating Reynolds’ distances (22) averaged across all loci (cpDNA and microsatellite) between neighboring locality pairs. Neighboring localities were determined via Delaunay triangulation. The genetic distances were assigned to coordinates halfway between locality pairs. The distances were interpolated to form a map layer (23) of the same grid cell size (50 × 50 km) and extent as available host fossil pollen layers (Fig. 2A). The parasite map layer was consistent with the Monmonier results that indicated high levels of differentiation among localities in the southern part of the range [E. virginiana (EV), Fig. 2B]. For the host, the locations of strongest genetic differentiation are in the midwestern and central parts of the range (F.gen, Fig. 2B), and host density grew from the South, to the Northeast, and at present is highest in the North (Fig. 2C). Because the focus of this project was understanding the influence of host variables on parasite patterns instead of other topological or environmental barriers, spatial linear models were restricted to predicting the parasite genetic map layer (EV) on the basis of (a) host genetics (F.gen), (b) any one of the host pollen density layers from a particular time (F0–F21), or (c) summaries of the host pollen layers, such as pollen averaged across times (F.avgP), variance in pollen (F.varP), and date of arrival of >2% pollen at a location (F.age) (Fig. 2). A spatial lag term (ρ) was included to account for spatial nonindependence within the data layers (24). Because of the inherent relationships between layers based on host pollen (F0–F21, F.avgP), univariate models with these explanatory variables were competed via Akaike's information criterion (AIC) scores (25) to select the best pollen density layer that was then used in multivariate analyses.
In the univariate pollen density models predicting parasite genetic distances, the younger host pollen layers outperformed the older ones, where models using layers younger than 2 kyBP (F0–F2) were 91% probable to be the best model compared with models based on older time slices (Table S4). The most probable model was based on the 500 yBP time slice [F0.5, weighted (w)AIC = 0.52, Table S4], which was then used in multivariate parasite models. Models with one, two, three, or four explanatory variables were constructed on the basis of the host layers F0.5 or F.avgP, F.gen, F.age, and F.varP. Univariate models and the one multivariate model with significant coefficients are described in Table 2. Models that included the host genetic data were universally poor, without significant coefficients, and outcompeted (wAIC = 0, Table 2), strongly indicating that host genetic structure has no influence on parasite patterns. Increasing levels of parasite genetic distance were related to lower host pollen densities (F0.5 and F.avgP) (Table 2). This finding agrees with the interpretation that higher host densities support larger parasite populations, and high levels of gene flow connect areas of high density. Similarly, models dependent on host establishment ages (F.age) showed that older parts of the range harbored higher parasite genetic distances (Table 2). Interestingly, models including the temporal variance in pollen density (F.varP) were not informative (Table 2). Layers with density data averaged across time (F.avgP, F.age, and F.varP) were worse predictors of parasite patterns than the most recent host density layer, suggesting that recent patterns in host density had the most influence on present-day parasite population structure. Alternatively, because many of the recent (<7 kyBP) host density time-slice layers performed similarly (Table S4), the overall genetic patterns may have been established earlier, although were still amenable to small recent changes in density. Older time-slice layers have most of their data in the unglaciated South, so parasite populations could be older than 21 kyBP and structured by numerous compounding glacial cycles. If host density effects are most prominent at the time of initial population establishment, then we would expect southern populations to be influenced by even older host density changes not considered here and less sensitive to recent postglacial host demographic changes.
Table 2.
Best spatial regression models of host variables predicting Epifagus virginiana genetic distances
| Model (EV ∼) | Intercept | Coefficient | Z-value | ρ | AIC | ΔAIC | wAIC |
| F.gen | 0.03307 | −0.00301 | 0.214 | 0.960 | −5347.7 | 12.7 | 0.00 |
| F0.5 | 0.04669 | −0.00109 | 0.000 | 0.945 | −5360.4 | 0.0 | 0.59 |
| F.age | 0.03417 | 0.00061 | 0.002 | 0.949 | −5355.9 | 4.5 | 0.06 |
| F.avgP | 0.03670 | −0.00103 | 0.034 | 0.957 | −5350.6 | 9.8 | 0.00 |
| F.varP | 0.03123 | −0.00005 | 0.389 | 0.961 | −5346.9 | 13.5 | 0.00 |
| F.avgP + | 0.04195 | −0.00116 | 0.020 | 0.943 | −5359.3 | 1.1 | 0.35 |
| F.age | 0.00065 | 0.001 |
Fagus grandifolia and E. virginiana variables are shown in Fig. 2. Coefficients and their corresponding Z-values refer to host data layer coefficients, whereas ρ is the spatial lag coefficient. All values of ρ were significant (P < 0.01). AIC, ΔAIC, and weighted (w)AIC values are reported following Wagenmakers and Farell (25). The best model is in boldface type.
The comparisons of the demographic histories of the host and the parasite strongly suggest that host density was the primary determinant in the parasite's range expansion and population genetics—not the host's own genetic patterns and migration routes. Because of this dependence on host density, this parasite should not be used as a direct indicator of host range expansion even though its life history (obligate, host-specific parasitism and mostly vertical transmission) suggests its utility as a proxy (1). In this case, the parasite was unable to keep up with the range margin of its host, perhaps indicating that the host's initial range expansion occurred at low density and thus limited the establishment of the parasite in new populations. Meanwhile, the parasite differentiated within isolated refuges in the South. Once the threshold host density level was reached in contiguous northern populations, parasites from the opportune source population then quickly colonized. More generally, it seems likely that herbs and other highly specialized species may lag behind because the habitats they require are distributed in a more complex fashion across the landscape (26). For instance, other parasitic plants have shown high levels of population differentiation typical of long periods of isolation, small population sizes, and patchy habitats (27, 28), and patterns of genetic diversity in the mistletoe, Arceuthobium americanum, and its host, Pinus contorta var. latifolia, have supported a lag between host and parasite colonization of formerly glaciated territory (29). Nonplant parasites, such as lungworms, have also shown this lagged migration pattern controlled by low-density host populations at the migration front (4). The slower movement of herbs and parasites suggests that forest assemblages may partially disassociate while species react separately to climate change, and it is unclear if the migration capacity of highly specialized species is sufficient to outrun extirpation from their current ranges.
Materials and Methods
Epifagus virginiana Datasets.
Specimens were collected from 88 localities spread across the range of E. virginiana during 2003–2007. Standard procedures were followed in extracting DNA, performing PCR, cycle sequencing, scoring markers, calculating diversity measures, and estimating phylogenetic relationships (see SI Materials and Methods for detailed information).
PCR was performed on 467 samples to amplify two cpDNA regions: pseudogenes rbcL + atpB and the second intron of clpP (primers given in Table S5). Indel regions were excluded from analyses, leaving 1,016 bp that defined 41 unique cpDNA haplotypes (Dataset S1).
In addition to the two cpDNA loci, genotypic data were generated from nine presumably nuclear microsatellite loci of 113–362 bp (primers given in Table S5). In total, 455 samples were genotyped, 350 (77%) of which were from all nine loci and 403 (89%) from six or more (Dataset S1).
The microsatellite data were categorized into clusters using the Bayesian spatial clustering method implemented in BAPS v.5.2 (30). This method utilizes biallelic genotypic data (only the microsatellite genetic data were used, and the cpDNA data were excluded) and assigns individuals to clusters that have restricted gene flow between them. In addition to the genetic data, this method incorporates spatial information within the prior distribution for the clusters (30) (details given in SI Materials and Methods).
F. grandifolia Datasets.
A total of 1,901 bp of cpDNA data from 121 samples from 97 localities was obtained from McLachlan et al. (5).
Fossil pollen data for the host, F. grandifolia, were obtained from Williams et al. (6). The data are interpolated pollen percentages at 1,000-y time slices since 21 kyBP and a layer at 500 yBP. Absent data were assigned zero values (see SI Materials and Methods for details). The F.avgP layer was calculated excluding zero values.
Monmonier Analysis with Cross-Validation.
Pairwise genetic distances between neighboring populations were calculated using several summary statistics such as Nei's distances and Reynolds’ distances averaged across all cpDNA and microsatellite data. Results were similar across distance methods, so only results using Reynolds’ distances are discussed. See SI Materials and Methods for specific input parameters. Cross-validation analyses were performed by randomly subsampling with replacement the original data by 50, 75, or 90% of the localities at a time. One to five Monmonier barriers were then recomputed for each replicate. To summarize results, paths from all replicates were binned into a 2D 38 × 23-cell histogram; each cell was 0.75° × 0.75°. The average number of paths to intersect each grid cell is reported in Fig. 1D and Fig. S2.
Estimating Migration Rates and Other Population Demographic Parameters Using IMa (20).
Because eastern North America has few clear biogeographic boundaries to separate regions, we tried multiple regional definitions. In addition to the three geographic regions described above, we ran models with three to four geographic regions on the basis of a combination of fossil evidence, the location of the last glacial maximum, and the boundary of the prairie peninsula (31) (SI Materials and Methods and Fig. S3). Results were similar across regional definitions (Table 1 and Table S2). Because we were interested in relative migration rates among regions, parameters were left scaled to an unknown mutation rate and not converted to per generation values. Also, because population sizes varied among regions, the effective migration rates that account for population size were also reported. Specific prior values and program parameters are given in SI Materials and Methods.
Spatial Linear Regression Models.
The genetic map layers, EV and F.gen, were based on interpolated genetic distances between localities of E. virginiana and F. grandifolia, respectively, as described in the text. Interpolations proceeded according to a modified quadratic Shepard's inverse weighting method (32). Only points within the present-day distribution of F. grandifolia were assigned nonzero values.
To determine which F. grandifolia layer(s) best predicted the parasite's genetic population structure, multiple spatial autoregressive lag models were compared. These models are linear regressions that include an additional spatial lag term as an explanatory variable, thereby accounting for spatial nonindependence in the E. virginiana genetic data layer (24). Lagrange multiplier tests were performed on all models to check for any further residual autocorrelation; none were detected (P > 0.05 in all cases). Models without significant regression coefficients were discarded. To evaluate the remaining multivariate models an AIC was also used, where Akaike weights represent the probability that a model is the best of the set (25).
Supplementary Material
Acknowledgments
We thank our specimen collectors, especially Y. C. Tsai, and C. W. Cunningham, A. J. Shaw, W. F. Morris, J. S. Clark, and two anonymous reviewers for helpful comments on the manuscript. This material is based upon work supported by the National Science Foundation under Grant 0608310, the Mellon Foundation, Sigma Xi, Duke University Graduate School, Duke University Department of Biology, the Association for Women in Science, Sigma Delta Epsilon/Graduate Women in Science, and the American Society of Plant Taxonomists.
Footnotes
The authors declare no conflict of interest.
Data deposition: The sequences reported in this paper have been deposited in the GenBank database (accession nos. HQ197795–HQ197859).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1006225107/-/DCSupplemental.
References
- 1.Nieberding CM, Olivieri I. Parasites: Proxies for host genealogy and ecology? Trends Ecol Evol. 2007;22:156–165. doi: 10.1016/j.tree.2006.11.012. [DOI] [PubMed] [Google Scholar]
- 2.Wirth T, Meyer A, Achtman M. Deciphering host migrations and origins by means of their microbes. Mol Ecol. 2005;14:3289–3306. doi: 10.1111/j.1365-294X.2005.02687.x. [DOI] [PubMed] [Google Scholar]
- 3.Arneberg P, Skorping A, Grenfell B, Read AF. Host densities as determinants of abundance in parasite communities. Proc Biol Sci. 1998;265:1283–1289. [Google Scholar]
- 4.Phillips BL, et al. Parasites and pathogens lag behind their host during periods of host range advance. Ecology. 2010;91:872–881. doi: 10.1890/09-0530.1. [DOI] [PubMed] [Google Scholar]
- 5.McLachlan JS, Clark JS, Manos PS. Molecular indicators of tree migration capacity under rapid climate change. Ecology. 2005;86:2088–2098. [Google Scholar]
- 6.Williams JW, Shuman BN, Webb T, Bartlein PJ, Leduc PL. Late-quaternary vegetation dynamics in North America: Scaling from taxa to biomes. Ecol Monogr. 2004;74:309–334. [Google Scholar]
- 7.Petit RJ, Hu FS, Dick CW. Forests of the past: A window to future changes. Science. 2008;320:1450–1452. doi: 10.1126/science.1155457. [DOI] [PubMed] [Google Scholar]
- 8.Morris AB, Graham CH, Soltis DE, Soltis PS. Reassessment of phylogeographical structure in an eastern North American tree using Monmonier's algorithm and ecological niche modelling. J Biogeogr. 2010;37:1657–1667. [Google Scholar]
- 9.Davis MB. Quaternary history of deciduous forests of eastern North-America and Europe. Ann Mo Bot Gard. 1983;70:550–563. [Google Scholar]
- 10.Bennett KD. The spread of Fagus grandifolia across eastern North America during the last 18000 years. J Biogeogr. 1985;12:147–164. [Google Scholar]
- 11.Delcourt PA, Delcourt HR. Long Term Forest Dynamics of the Temperate Zone: A Case Study of Late-Quaternary Forests in Eastern North America. New York: Springer; 1987. [Google Scholar]
- 12.Clark JS, et al. Reid's paradox of rapid plant migration. Bioscience. 1998;48:13–24. [Google Scholar]
- 13.McLachlan JS, Clark JS. Reconstructing historical ranges with fossil data at continental scales. For Ecol Manage. 2004;197:139–147. [Google Scholar]
- 14.Davis MB, Schwartz MW, Woods K. Detecting a species limit from pollen in sediments. J Biogeogr. 1991;18:653–668. [Google Scholar]
- 15.Vucetich JA, Waite TA. Spatial patterns of demography and genetic processes across the species’ range: Null hypotheses for landscape conservation genetics. Conserv Genet. 2003;4:639–645. [Google Scholar]
- 16.Gonzales E, Hamrick JL, Chang S-M. Identification of glacial refugia in south-eastern North America by phylogeographical analyses of a forest understory plant, Trillium cuneatum . J Biogeogr. 2008;35:844–852. [Google Scholar]
- 17.Pyhäjärvi T, Salmela M, Savolainen O. Colonization routes of Pinus sylvestris inferred from distribution of mitochondrial DNA variation. Tree Genet Genomes. 2008;4:247–254. [Google Scholar]
- 18.Provan J, Bennett KD. Phylogeographic insights into cryptic glacial refugia. Trends Ecol Evol. 2008;23:564–571. doi: 10.1016/j.tree.2008.06.010. [DOI] [PubMed] [Google Scholar]
- 19.Manni F, Guérard E, Heyer E. Geographic patterns of (genetic, morphologic, linguistic) variation: How barriers can be detected by using Monmonier's algorithm. Hum Biol. 2004;76:173–190. doi: 10.1353/hub.2004.0034. [DOI] [PubMed] [Google Scholar]
- 20.Hey J, Nielsen R. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci USA. 2007;104:2785–2790. doi: 10.1073/pnas.0611164104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Williams JW, Jackson ST. Novel climates, no-analog communities, and ecological surprises. Front Ecol Environ. 2007;5:475–482. [Google Scholar]
- 22.Reynolds J, Weir BS, Cockerham CC. Estimation of the coancestry coefficient: Basis for a short-term genetic distance. Genetics. 1983;105:767–779. doi: 10.1093/genetics/105.3.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Miller MP. Alleles in space (AIS): Computer software for the joint analysis of interindividual spatial and genetic information. J Hered. 2005;96:722–724. doi: 10.1093/jhered/esi119. [DOI] [PubMed] [Google Scholar]
- 24.Ward MD, Gleditsch KS. Spatial Regression Models. Thousand Oaks: Sage; 2008. [Google Scholar]
- 25.Wagenmakers E-J, Farrell S. AIC model selection using Akaike weights. Psychon Bull Rev. 2004;11:192–196. doi: 10.3758/bf03206482. [DOI] [PubMed] [Google Scholar]
- 26.Pakeman RJ. Plant migration rates and seed dispersal mechanisms. J Biogeogr. 2001;28:795–800. [Google Scholar]
- 27.Schmidt K, Jensen K. Genetic structure and AFLP variation of remnant populations in the rare plant Pedicularis palustris (Scrophulariaceae) and its relation to population size and reproductive components. Am J Bot. 2000;87:678–689. [PubMed] [Google Scholar]
- 28.Zuber D, Widmer A. Phylogeography and host race differentiation in the European mistletoe (Viscum album L.) Mol Ecol. 2009;18:1946–1962. doi: 10.1111/j.1365-294x.2009.04168.x. [DOI] [PubMed] [Google Scholar]
- 29.Jerome CA, Ford BA. Comparative population structure and genetic diversity of Arceuthobium americanum (Viscaceae) and its Pinus host species: Insight into host-parasite evolution in parasitic angiosperms. Mol Ecol. 2002;11:407–420. doi: 10.1046/j.0962-1083.2002.01462.x. [DOI] [PubMed] [Google Scholar]
- 30.Corander J, Siren J, Arjas E. Bayesian spatial modeling of genetic population structure. Comput Stat. 2008;23:111–129. [Google Scholar]
- 31.Transeau EN. The prairie peninsula. Ecology. 1935;16:423–437. [Google Scholar]
- 32.Franke R. Scattered data interpolation: Tests of some methods. Math Comput. 1982;38:181–200. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.