Incorporating Individual-level Distributions of Exposure Error in Epidemiologic Analyses: An Example Using Arsenic in Drinking Water and Bladder Cancer

Abstract

Purpose

Epidemiologic analyses traditionally rely on point estimates of exposure for assessing risk despite exposure error. We present a strategy that produces a range of risk estimates reflecting distributions of individual-level exposure.

Methods

Quantitative estimates of exposure and its associated error are used to create for each individual a normal distribution of exposure estimates which is then sampled using Monte Carlo simulation. After the exposure estimate is sampled, the relationship between exposure and disease is evaluated; this process is repeated 99 times generating a distribution of risk estimates and confidence intervals. This is demonstrated in a bladder cancer case-control study using individual-level distributions of exposure to arsenic in drinking water.

Results

Sensitivity analyses indicate similar performance for categorical or continuous exposure estimates, and that increases in exposure error translate into a wider range of risk estimates. Bladder cancer analyses yield a wide range of possible risk estimates, allowing quantification of exposure error in the association between arsenic and bladder cancer, typically ignored in conventional analyses.

Conclusions

Incorporating distributions of individual-level exposure error results in a more nuanced depiction of epidemiologic findings. This approach can be readily adopted by epidemiologists assuming distributions of individual-level exposure.

Introduction

Error in estimates of exposure is pervasive but seldom receives substantive consideration in epidemiologic investigations. For decades, researchers called for suitable and easy to implement methods to incorporate exposure error in calculating risk measures (1-3). In practice, investigators almost uniformly continue to assume that so long as misclassification is nondifferential it will bias estimates toward the null, despite several instances where this assumption was shown to be flawed (4-8).

Before proceeding further, we wish to clarify our nomenclature. The terms “measurement error”, “misclassification”, “noise”, “exposure error”, and “uncertainty” are used virtually interchangeably to describe the discrepancy between the true value of a variable, and its estimate (9). In this report, we use “exposure error” or “error in exposure” to characterize this difference between true exposure and its estimate.

Several researchers have developed approaches for addressing exposure error in epidemiologic analyses yet these techniques are rarely adopted by epidemiologists (9,10). Broadly conceptualized, one set of techniques evaluates how a range of rates for sensitivity and specificity of exposure classification influence effect measures (e.g., odds ratios, relative risks) (11-17). How to derive this range of rates remains however a major stumbling block for epidemiologists. Another set of techniques corrects for exposure error using an exposure validation dataset (or estimates of true exposure) to produce new point estimates of exposure for each participant; this approach relies on regression calibration, SIMEX, Bayesian, or maximum likelihood-based methods (18-26). These techniques have begun to receive attention in the epidemiologic literature (27), however, exposure validation datasets required for their implementation are seldom available, and may increase bias if they are small (28). A related set of techniques uses probabilistic sensitivity or Bayesian analyses to incorporate error distributions (29-31) but their implementation is not straightforward. Here we describe and provide relevant SAS code for a variation on probabilistic sensitivity analysis that is easy to implement.

The strategy we put forth, rather than correcting for exposure error, produces a range of possible epidemiologic risk estimates reflecting the underlying range of approximate exposure error. This method does not rely on a separate validation dataset. Ranges of exposure error are increasingly calculated alongside exposure estimates for each study participant (32-34), which allows researchers to calculate a distribution of possible exposure estimates for each individual, a considerable improvement over single point estimates of exposure. Adopting a probabilistic sensitivity analysis for exposure error, Monte Carlo simulation allows one to draw estimates from these exposure distributions which can then be used to generate a range of possible effect measures and confidence intervals (35-37). This approach is described and demonstrated using data from a case-control study investigating lifetime exposure to arsenic in drinking water and bladder cancer in Michigan.

Methods

Arsenic exposure and bladder cancer dataset

Exposure assessment and epidemiologic study design of the relationship between arsenic exposure and bladder cancer have previously been described (38). Briefly, a population-based bladder cancer case-control study was conducted in southeastern Michigan; 411 cases were enrolled with the assistance of the Michigan State Cancer Registry and 566 controls were enrolled using random digit dialing of age-weighted lists. Conventional analyses that ignored exposure error produced an OR=1.17 (95% CI: 0.94, 1.44) per 5 μg/L arsenic. These results will be compared with results from probabilistic sensitivity analysis presented in this paper. Research was approved by the University of Michigan IRB-Health Committee and participants provided written informed consent.

Exposure distributions

Arsenic concentration in drinking water and its associated error terms were estimated at each residence over the life-course (Table 1). Arsenic was measured in drinking water at each participant's current residence and modeled at past residences. Error terms were estimated to be 20% of the measured value at the current residence based on measurement error and limited temporal variability (39). Five situations were considered for past residences: 1) private well in the study area, estimates of arsenic and standard deviations were generated from a geostatistical model (40, 41), 2) private wells outside the study area, arsenic was estimated using local averages and standard deviations from a US Geological Survey (USGS) database of well water arsenic levels (42), 3) public supplies within the study area, average arsenic concentrations and standard deviations were derived from a State database and public water supply histories, 4) public supplies outside the study area served by Detroit City water, arsenic estimates and error terms were generated from measurements and measurement error, respectively (39), and 5) other public supplies outside the study area, arsenic estimates and standard deviations were generated from arsenic data compiled for public water supplies in the US (43). Standard deviations generated from these statistical models were treated as estimates of error terms. Point values of exposure and corresponding error terms were estimated for each residence accounting for 98% of person-years over the lifetime. Some individual-level estimates were associated with little error (e.g., ±10%) due to greater certainty in the statistical models at some locations, while other individual-level estimates displayed much larger errors (e.g., ±200%).

Table 1.

Estimates of Error in Exposure to Arsenic in Drinking Water

	Case Person-Years	Control Person-Years	Source of Error	Error Term Estimatea
Source of Drinking Water
Measurements at Current Residence	27.9%	27.4%	Measurement Error and Temporal Variability	±20% Median=0.20
Past Residencesb in Study Area
Private Well	16.4%	16.0%	SD from Geostatistical Model	±10-200%c Median=8.87
Public Supply	23.0%	21.8%	SD from Historical DBd	±10-200%c Median=3.00
Past Residencesb Outside of Study Area
Private Wells	5.7%	4.8%	SD from National Private Well DBe	±10-200%c Median=6.55
Detroit City Water	12.8%	13.8%	Measurement Error	±20% Median=0.10
Public Supply	12.0%	14.7%	SD from National DBf	±10-100%c Median=0.30
No Estimates	2.2%	1.5%

Abbreviations: SD, Standard Deviation; DB, Database

^aEstimate of error term above or below the exposure prediction. Estimate is specific to each individual's residence. For example, one residence may have measured arsenic in drinking water and an error term =20%; another residence may have arsenic predicted from the geostatistical model and error term =35%; a third residence may also be predicted from the geostatistical model but with an error term=75%.

^bBottled water not reported at past residences.

^cEstimates of error terms determined for each individual based on confidence in exposure prediction as expressed by error terms (e.g., SDs) in statistical models and databases. Some individual-level estimates are associated with little error (e.g., 10%) while others have large ranges of error (e.g., 200%).

^dEstimates from Michigan Department of Environmental Quality database, and water supplier history.

^eEstimates from United States Geological Survey database of arsenic in groundwater.

^fEstimates from Natural Resources Defense Council database of arsenic in public water supplies.

Time-weighted average (TWA) point estimates of exposure and corresponding error terms were constructed for arsenic concentration (μg/L) over each participant's life-course. Summary statistics for these two quantities are presented in Table 2. Under a Gaussian model, exposure estimates and error terms are used to generate approximate distributions of exposure, as will be described in step 1 of the simulation framework.

Table 2.

Ranges of Estimates of Exposure and Error Terms Among Bladder Cancer Cases and Controls

	TWA Exposure Estimate (μg/L)			TWA Error Term Estimate (μg/L)
	5th %ile	50th %ile	95th %ile	5th %ile	50th %ile	95th %ile
Cases	0.30	1.16	14.00	0.04	2.10	11.14
Controls	0.30	1.13	11.59	0.04	1.54	10.89

Monte Carlo simulation

The following simulation framework is used for incorporating a range of exposure error into epidemiologic analyses (a flow chart is provided in Appendix 1):

1. For each individual, a point estimate of exposure and its associated error term are constructed. For example, participant 1 could have drinking water arsenic equal to 5 μg/L and error term equal to 2 μg/L, participant 2 arsenic equal to 25 μg/L and error term equal to 12 μg/L, and so on. It is important to emphasize that these error terms are not generated from a validation dataset and are uncertain. A distribution of possible exposure estimates is then defined according to a normal model with mean and standard deviation equal to the point estimate of exposure and the error term. We assumed a normal distribution for our arsenic analyses because our error terms generally correspond to a standard deviation generated by geostatistical analyses and summary statistics.

2. An exposure estimate is generated for each participant by sampling randomly the exposure distribution. Exposure estimates below the detection limit (0.06 μg/L) were assigned a value equal to detection limit / √2 = 0.04 μg/L. For sake of simplicity all errors were assumed uncorrelated among participants, hence the sampling of exposure probability distribution was conducted independently for each individual. Although errors might be correlated in some circumstances (e.g., among individuals served by public water supply), we chose to model all errors uncorrelated because we are most concerned about exposure estimates for arsenic in past private wells where we do not expect correlated error between nearby wells because of substantial short-range spatial variability (40).

3. Exposure estimates are used to calculate an effect measure using procedures conducted in a typical epidemiologic study. In this example, unconditional logistic regression analyses are conducted to compute odds ratios and 95% confidence intervals.

4. Steps 2 and 3 are repeated (generally 99-4999 times) to generate a range of odds ratios and confidence intervals reflecting the impact of the range of error in the exposure estimate.

SAS code for implementing this simulation framework can be found in Appendix 2.

Characterizing behavior of the simulation

Before using individual-level estimates of error terms in the Monte Carlo simulation procedure, we investigated performance of the simulation procedure under more controlled scenarios. Using our arsenic exposure data, three scenarios were developed in which we created error terms for all study participants equal to 10%, 25%, and 50%, of the TWA exposure estimate. For example, if an individual had a point estimate exposure equal to 5 μg/L, they would be assigned an error estimate equal to 0.5, 1.25, 2.5 μg/L, respectively, under the three scenarios. Therefore, each individual's exposure error term was calculated as a percentage of its exposure estimate in the scenarios. We then created a distribution of possible exposure estimates using the simulation framework and conducted logistic regression analyses.

Analyses of drinking water arsenic and bladder cancer

Using estimates of exposure and error terms, odds ratios (OR) and 95% confidence intervals (CI) were calculated using unconditional logistic regression analyses embedded in the Monte Carlo simulation framework, run in SAS (Cary, NC). Arsenic was treated both as a continuous variable (modeled linearly per 5 μg/L increment), and categorized a priori into three classes: <1 μg/L, 1-10 μg/L, and >10 μg/L. This categorization permitted examination of risk in the low-to-moderate exposure range above the current maximum contaminant level (MCL) (10 μg/L), where little information currently exists (38). Analyses were adjusted for factors shown to be associated with bladder cancer in univariate models or otherwise deemed important: age, race (white, black, other), sex, smoking (never smoker, former < 20 pack-years, former ≥ 20 pack-years, current < 20 pack-years, current ≥ 20 pack-years), education (highest level attained), history of urinary bladder cancer in an immediate relative (parent, sibling, or child), and at least five years of employment in a high risk occupation (dye workers and users, aromatic amine manufacturing, leather workers, painting, driving trucks or other motor vehicles, aluminum workers, machinists, and automobile assemblers) (44, 45). Our previous results suggested a possible association between arsenic exposure and bladder cancer among individuals consuming above average amounts of water from home (38); analyses presented here were limited to the strata of above average home water consumption (> 1 L/day). Analyses were conducted using TWA lifetime exposure distributions. In the conventional analysis using categorical arsenic estimates, there were 79 cases and 123 controls in the low exposure category, 104 cases and 124 controls in the medium exposure category, and 19 cases and 15 controls in the high exposure category. In the probabilistic sensitivity analysis, different combinations of cases and controls appear in these different exposure categories reflecting error in the exposure estimates. A preliminary analysis found little difference in results using 4999, 999, and 99 simulations, therefore 99 simulations were conducted.

We also re-examined our previous exploratory analyses of timing of exposure which suggested that exposures during ages 45-52 were most associated with risk of bladder cancer (38). Five-year moving averages were calculated from yearly estimates of arsenic exposure and associated errors available over each participant's life; these averages were assigned to the middle year of each five-year window, and called yearly estimates of exposure and error terms. A distribution of possible exposure estimates was created for each year using the simulation framework and logistic regression was conducted each year for each of the 99 simulations.

Results

For controlled scenarios, Table 3 indicates that the use of error terms equal to 10% of the exposure estimate results in a narrow range of ORs and 95% CI consistent with those from conventional analyses. As the size of the error term increases, the range of the OR and 95% CI grows, indicating greater uncertainty in the risk estimate. Results are similar using continuous and categorical measures of exposure.

Table 3.

Impact from Incorporating Fixed Exposure Error Terms in Estimates of Risk: Example of Arsenic in Drinking Water and Bladder Cancer

	Conventional Approach		Simulations Incorporating Distributions of Exposure Error
	OR	95% CI	Rangea of ORs	Rangea of Lower 95% CI	Rangea of Upper 95% CI	% of Simulations Significantly Positiveb	% of Simulations Significantly Negativeb
TWA Arsenic Concentration
Continuous (per 5 μg/L increase)
Conventional Approach:	1.17	0.94, 1.44
Single Exposure Estimate
Simulations Incorporating
Distributions of Exposure Errorc
±10% Error Term			1.12 – 1.22	0.90 – 0.98	1.39 – 1.52	0%	0%
±25% Error Term			1.05 – 1.28	0.84 – 1.02	1.30 – 1.61	2%	0%
±50% Error Term			0.94 – 1.35	0.76 – 1.08	1.15 – 1.69	5%	0%
Categorical
Conventional Approach:
Single Exposure Estimate
< 1 μg/L	1.00
1-10 μg/L	1.05	0.69, 1.59
> 10 μg/L	1.62	0.72, 3.64
Simulations Incorporating
Distributions of Exposure Errorc
±10% Error Term
< 1 μg/L			1.00
1-10 μg/L			0.92 – 1.44	0.61 – 0.95	1.41 – 2.19	0%	0%
> 10 μg/L			1.23 – 2.14	0.55 – 0.93	2.77 – 5.08	0%	0%
±25% Error Term
< 1 μg/L			1.00
1-10 μg/L			0.85 – 1.44	0.55 – 0.95	1.29 – 2.19	0%	0%
> 10 μg/L			0.83 – 2.63	0.33 – 1.12	2.08 – 6.15	5%	0%
±50% Error Term
< 1 μg/L			1.00
1-10 μg/L			0.65 – 1.45	0.43 – 0.96	1.00 – 2.20	0%	0%
> 10 μg/L			0.55 – 2.85	0.22 – 1.25	1.42 – 6.91	8%	0%

Abbreviations: OR, odds ratio; CI, confidence interval; TWA, time-weighted average.

^aRange of values (middle 95%) generated from 99 simulations.

^bSignificance determined by whether or not 95% CI of the OR intersects 1.0.

^cFixed error term above or below the exposure prediction applied to all participants. Normal distributions used in the simulations, with exposure estimate defined as the mean, and the error term specified as the standard deviation in the distribution.

In analyses using exposure estimates and estimated error terms (as opposed to the relative 10%, 25%, and 50% error terms in the controlled scenarios), a wide range of possible ORs and 95% CIs is generated for assessing the risk of bladder cancer associated with arsenic exposure, indicating uncertainty in the risk estimates (Table 4). The range of risk estimates encompasses those generated from conventional analyses, with a few statistically significant results. The figure illustrates the range of risk estimates that can be observed over the 99 simulations.

Table 4.

Multivariate-Adjusted^a Odds Ratios and 95% Confidence Intervals for Time-Weighted Average Arsenic in Drinking Water and Bladder Cancer, Among Those who Consume Above 1 L/day Water from Home, Southeastern Michigan, Enrolled 2002-2006.

	Conventional Approach		Simulations Incorporating Distributions of Exposure Error
	OR	95% CI	Rangeb of ORs	Rangeb of Lower 95% CI	Rangeb of Upper 95% CI	% of Simulations Significantly Positivec	% of Simulations Significantly Negativec
TWA Arsenic Concentration
Continuous (per 5 μg/L increase)
Conventional Approach:	1.17	0.94, 1.44
Single Exposure Estimate
Simulations Incorporating
Distributions of Exposure Error			0.95 – 1.30	0.76 – 1.05	1.19 – 1.61	6%	0%
Categorical
Conventional Approach:
Single Exposure Estimate
< 1 μg/L	1.00
1-10 μg/L	1.05	0.69, 1.59
> 10 μg/L	1.62	0.72, 3.64
Simulations Incorporating
Distributions of Exposure Error
< 1 μg/L			1.00
1-10 μg/L			0.63 – 1.30	0.41 – 0.85	0.97 – 1.99	0%	5%
> 10 μg/L			0.79 – 2.31	0.38 – 1.11	1.59 – 4.80	8%	0%

Abbreviations: OR, odds ratio; CI, confidence interval; TWA, time-weighted average.

^aAdjusted for cigarette smoking history, education, history of employment in high-risk occupation, family history of bladder cancer, age, race, and sex.

^bRange of values (middle 95%) generated from 99 simulations.

^cSignificance determined by whether or not 95% CI of the OR intersects 1.0.

A similar procedure was used to investigate the impact of timing of exposure on risk estimates. Previous exploratory analyses suggested that risk from arsenic exposure was increased between ages 45-52 among individuals consuming above average amounts of water from home (38). Accounting for the exposure error reveals a wide range of possible risk estimates, with significantly positive results (95% CI > 1.0) in 38% of simulations using continuous exposure estimates (Table 5). Categorical exposure estimates result in significantly positive risk estimates in 31% of simulations for exposures in the 1-10 μg/L range and none for exposures above 10 μg/L. The wide range of risk estimates, especially for the above 10 μg/L arsenic group, reflects high degree of uncertainty in the exposure estimates.

Table 5.

Multivariate-Adjusted^a odds ratios and 95% confidence intervals for arsenic in drinking water and bladder cancer, among those who consume >1 L/day of water from home, ages 45-52^b; southeastern Michigan, enrolled 2002-2006.

	Conventional Approach		Simulations Incorporating Distributions of Exposure Error
	Medianc OR	Medianc 95% CI	Ranged of ORs	Ranged of Lower 95% CI	Ranged of Upper 95% CI	% of Simulations Significantly Positivee	% of Simulations Significantly Negativee
Yearly Arsenic Concentration for Ages 45-52
Continuous (per 5 μg/L increase)
Conventional Approach:	1.18	1.01, 1.36
Single Exposure Estimate
Simulations Incorporating
Distributions of Exposure Error			1.02 – 1.20	0.91 – 1.07	1.14 – 1.37	38%	0%
Categorical
Conventional Approach:
Single Exposure Estimate
< 1 μg/L	1.00
1-10 μg/L	1.52	1.00, 2.32
> 10 μg/L	2.15	1.12, 4.12
Simulations Incorporating
Distributions of Exposure Error
< 1 μg/L			1.00
1-10 μg/L			1.00 – 2.08	0.63 – 1.30	1.61 – 3.47	31%	0%
> 10 μg/L			0.30 – ∞	0.00 – 0.48	9.90 – ∞	0%	0%

Abbreviations: OR, odds ratio; CI, confidence interval; TWA, time-weighted average.

^aAdjusted for cigarette smoking history, education, history of employment in high-risk occupation, family history of bladder cancer, age, race, and sex.

^bSignificantly higher risks reported for ages 45-52 in prior exploratory analyses of risk from timing of exposure, reported here under “Conventional Approach”.

^cMedian value from analyses of yearly exposure, calculated for ages 45-52.

^dRange of values (middle 95%) generated from 99 simulations.

^eSignificance determined by whether or not 95% CI of the OR intersects 1.0.

Discussion

This paper introduces a simulation-based probabilistic sensitivity analysis for propagating uncertainty about individual-level estimates of exposure through logistic regression analyses. The basic idea is to generate a distribution of possible exposure estimates, which reflects the underlying range of possible exposure errors, and then to use each estimate as input to a logistic regression, yielding a range of possible odds ratios and confidence intervals. Individuals assigned higher exposure levels in one run of the simulation, may have lower exposure levels in another run of the simulation; this individual-level variability in exposure assignment is reflected in the distribution of odds ratios generated by this probabilistic analysis (Figure). Importantly, this procedure is not a correction for exposure error since we do not have true error estimates. Rather, this method uses a probability distribution of exposure values to generate a range of possible risk estimates, both above or below those found in a conventional analysis.

Figure.

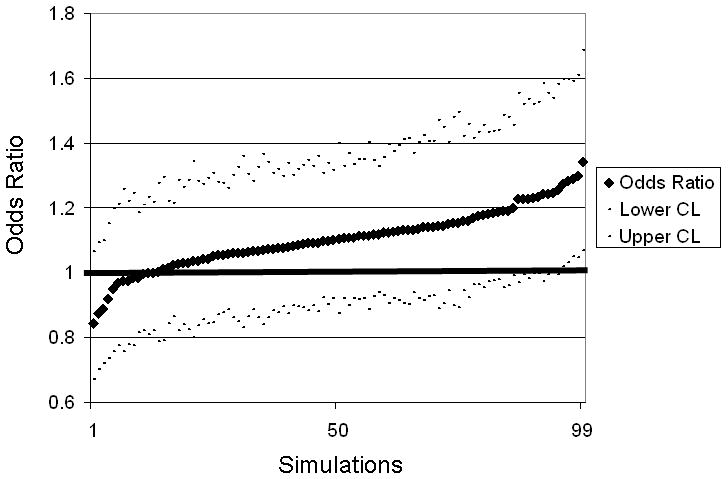
Results from simulations that incorporate distributions of exposure error to produce multivariate-adjusted odds ratios and 95% confidence intervals for arsenic in drinking water and bladder cancer, among those who consume >1 L/day of water from home; southeastern Michigan, enrolled 2002-2006. Adjusted for cigarette smoking history, education, history of employment in high-risk occupation, family history of bladder cancer, age, race, and sex. Risk per 5 μg/L increase in time-weighted average arsenic concentrations. Simulations are presented in sequence from low to high odds ratios.

We illustrate this approach using estimates of exposure and associated error terms in a case-control study investigating the link between arsenic in drinking water and bladder cancer. Following common practice in epidemiologic research, the initial study (38) relied on a single estimate of exposure, thereby ignoring exposure error. These previous results suggested a possible association between arsenic exposure and bladder cancer among individuals consuming above average amounts of water from home. When a distribution of individual-level exposure error is incorporated alongside measures of TWA lifetime arsenic exposure, odds ratios are generally still above the null, although statistical significance is seldom achieved. Results are consistent for both categorical and continuous exposure metrics.

Performance of the simulation procedure was investigated for controlled scenarios where the error term was set to 10%, 25%, and 50%, respectively, of the exposure estimate. As the size of the error term increases, the distribution of the risk estimate widens, indicating greater uncertainty in these estimates. Results did not display strong evidence of bias and suggested that our implementation of Monte Carlo simulation is a reasonable approach for propagating exposure error and producing a range of possible risk estimates. The Bayesian framework provides an alternative approach to be investigated in the future. The main challenge is to reduce bias while keeping the approach accessible to epidemiologists.

Given potential for long latency and sensitive periods of exposure in cancer development, measures such as life-course TWA may not be sensitive enough to highlight significant trends resulting from low-level exposure (46). Lacking a suitable a priori temporal hypothesis, we previously investigated yearly averages of arsenic exposure under a highly exploratory framework. Exposures during ages 45-52 appeared most correlated with bladder cancer in this study population (38), and risk during these years was re-examined here accounting for exposure error distributions. As with life-course TWA measures, odds ratios remained elevated but statistical significance was not compelling when incorporating exposure error distributions. Fewer than half of the simulations produced significant results for exposures during ages 45-52; risk estimates from categorical exposures > 10 μg/L were particularly uncertain. Given the exploratory nature of these temporal analyses, this dampens our confidence that these ages of exposure may be important for subsequent development of bladder cancer. Methods for investigating timing of exposure and risk are an important area of research, along with efforts to incorporate exposure error.

One objection to our approach might be concerns about our estimates of exposure error terms, specifically our rough estimates of measurement error, temporal variability, and our reliance on standard deviations from statistical models. In response to this concern, we stress, like others (29), that conventional analysis that fails to incorporate quantitative estimates of exposure error (a common practice) implicitly assumes that exposure error is zero, a rather unrealistic assumption. Quantitative estimates of exposure error terms, even if imperfect, should be more informative than an assumption that they do not exist. To keep the simulation-based method easy to implement by epidemiologists, correlation among errors was ignored. This simplification is reasonable for the present case-study since arsenic in past private wells is known to exhibit high degrees of spatial variability and therefore uncorrelated estimation error among residences. If necessary, both correlated and uncorrelated error could be incorporated, yet it would require the challenging joint modeling of correlated and uncorrelated error (33, 47).

In the probabilistic sensitivity analyses presented here, we assumed a Gaussian shape for the distribution of possible exposure for each individual. Other distributions (e.g. triangular, lognormal) could easily have been chosen, even with other types of data. For example, categorical questionnaire data using a 1-5 rating scale could be assigned an exposure estimate from the questionnaire, while the researcher would select an error term and a distribution (e.g., ±1 category in the scale and truncated at the high and low end of the scale to maintain the same maximum=5 and minimum=1 in the scale).

The proposed approach does not provide insight as to which is the most likely risk estimate within the distribution. As such, determining how best to present the findings is another area of future inquiry. In this manuscript, we presented a figure of a distribution of ORs and CIs, as well as tables displaying ranges of ORs and CIs; we do not yet know which method is most effective for communicating uncertainty in the risk estimates when accounting for error in exposure.

The common practice of using a single effect measure and confidence interval, corresponding to a single estimate of exposure, is overly simplistic and ignores the underlying error in the exposure estimate. Results of a Monte Carlo simulation that incorporate distributions of exposure error present a more nuanced depiction of the data. While propagating exposure errors does not help us quantitatively address unmeasured confounding, selection bias, or recall bias in our epidemiologic results, it allows us to present our results accounting for some of the error inherent in the analysis. Given the ease of implementation, this Monte Carlo simulation approach can be readily adopted by epidemiologists who possess quantitative measures of exposure and its associated error terms.

List of Abbreviations and Acronyms

CI

confidence interval

MCL

maximum contaminant level

OR

odds ratio

TWA

time-weighted average

USGS

United States Geological Survey