PROSTATE INTRAFRACTION MOTION ASSESSED BY SIMULTANEOUS KV FLUOROSCOPY AT MV DELIVERY II: ADAPTIVE STRATEGIES

Abstract

Purpose

To investigate potential benefits of adaptive strategies for managing prostate intrafractional uncertainties when interfraction motion is corrected online.

Methods and Materials

Prostate intrafraction motion was measured using kV fluoroscopy during MV delivery for 571 fractions from 30 hypofractionated radiotherapy patients. We evaluated trending over treatment course using ANOVA statistics, and we evaluated the ability to correct patient specific systematic error and apply patient specific statistical margins after 2–15 fractions to compensate 90% of motion. We also evaluated the ability to classify patients into small and large motion subgroups based on the first 2–20 fractions using discriminant analysis.

Results

No time trend was observed over treatment course and intra-fraction motion was patient specific (p<0.0001). Systematic error in the first week correlated well with subsequent weeks with correlation coefficients of 0.53, 0.50, and 0.41 in right-left (RL), anterior-posterior (AP), and superior-inferior (SI), respectively. After 5 fractions, the adaptive strategy resulted in an average margin reduction of 0.3, 0.7, and 0.7mm in RL, AP, and SI, respectively, with margins ranging from 1–3.2mm in RL, 2–7.0mm in AP, and 2–6.6mm in SI. In contrast, population margins to include the same percentage of motion were 1.7, 4.0, and 4.1mm. After 2 and 5 fractions, patients were classified into small and large motion groups with ~77% and ~83% accuracy.

Conclusions

Adaptive strategies are feasible and beneficial for intrafraction motion management in prostate cancer online image-guidance. Patients may be classified into large and small motion groups in early fractions using discriminant analysis.

Introduction

Before the development of image guidance in external beam radiotherapy, target motion could only be compensated by large margins designed to account for day-to-day changes in target position (interfraction motion), and internal organ motion during treatment (intrafraction motion). The incorporation of image guidance technologies with medical linear accelerators has allowed for more sophisticated motion management strategies. For prostate cancer radiotherapy, interfraction motion management strategies fall into two categories: online corrections and offline adaptive strategies. Daily online corrections can be performed using x-ray imaging (1, 2), localization using implanted electromagnetic transponders (3), or ultrasound (4). Adaptive strategies use imaging information collected during initial fractions to create a modified treatment plan for future fractions that accounts for patient specific organ motion (5).

When interfractional motion is managed by online correction, remaining target uncertainty includes residual setup error and intrafraction motion (6, 7). In most cases this is now accounted for through margins. However, similar to interfractional motion, intrafractional uncertainties may in principle be managed through online corrections or adaptive strategies. Online correction techniques include tracking and gating, the implementation of which may be possible using technologies capable of target localization during radiotherapy such as MV imaging (8), kV fluoroscopy (2), combined MV-kV imaging (9), and electromagnetic transponders (3). Adaptive strategies would make use of motion measurements during initial fractions to account for intrafractional uncertainties of future fractions on a patient specific basis. However there has been little research investigating adaptive strategies for prostate intrafraction motion.

Some studies have qualitatively observed that prostate intrafraction motion is patient specific (3). In a companion paper, we found the motion probability to vary considerably per patient (10). Under adaptive strategies, patients with relatively little intrafractional uncertainty would not be penalized by a population wide approach that includes patients with large motion. Furthermore, while tracking and gating require real-time localization, synchronization, and analysis, adaptive strategies may be implemented offline using retrospective measurements.

While a patient specific approach to dealing with prostate intrafraction motion has clear benefits, it remains to be shown that the motion can be characterized with reasonable accuracy in initial fractions. We have available at our clinic measurements of prostate intrafraction motion made during MV delivery using a gantry mounted kV imager for 30 hypofractionated radiotherapy patients, and in this study we use this data to investigate the feasibility of adaptive strategies for intrafraction uncertainties when interfraction motion is corrected online.

Methods and Materials

Treatment Protocol and Data Set

We utilize positional measurements at treatment delivery of implanted fiducial markers (Visicoil, IBA, Bartlett TN) acquired using a gantry mounted kV imager. Patients enrolled in a hypofractionated prostate radiotherapy protocol approved by an internal review board underwent 20 fractions of 3.2 Gy per fraction. At each fraction the patient was aligned to skin marks and an online couch translation was performed based on CBCT image guidance. Radiotherapy was delivered at 5–7 gantry angles with kV fluoroscopy being acquired during MV delivery to evaluate intrafraction motion, followed by a second CBCT after treatment delivery. The intrafraction motion evaluation and the accuracy thereof have been described in detail previously; in summary, the error in estimating the 3D position is typically less than ~1.5mm for 95% of localizations (11, 12). The analysis resulted in one prostate localization per beam, for a total of 3112 localizations from 571 fractions and 30 patients (10).

Motion Characteristics

Adaptive strategies for intrafractional uncertainties rely on motion characterization during early fractions and assume they remain unchanged or predictable throughout treatment course. We wish to quantify the relationship between patient specific motion in early and late fractions.

In our analysis, for each patient we define µ_i,j as the mean and σ_i,j as the standard deviation of all positional measurements in each axis acquired by kV fluoroscopy between fractions i and j, with positive displacements corresponding to the right, posterior, and superior directions. To evaluate trending, we performed a multiway Analysis of Variance (ANOVA) testing if µ_i,i and σ_i,i calculated for each fraction i varied significantly between patients and fractions. We also evaluated correlation between the mean, standard deviation, and mean vector displacement per patient calculated for the first week and each subsequent week (µ_1,5 vs. µ_6,10, etc.). Finally, we evaluated correlation of fraction number with the population mean displacement from the plan in each axis.

Adaptive Strategy

We investigate the feasibility of an adaptive strategy to compensate for intrafraction motion and residual setup error similar to adaptive strategies for interfraction motion (5). In particular, we evaluate the ability to (1) perform an additional correction of patient specific systematic intrafractional error at each fraction, and (2) apply a patient specific geometric margin to account for the random intrafractional error.

The patient specific systematic error in each axis is µ_1,F, where F is the total number of fractions for the patient. This error can have significant dosimetric consequences because it causes shifting of the dose distribution. For the adaptive strategy, we estimate µ_1,F at the current fraction c as µ_1,c-1, which is essentially a cumulative estimate of µ_1,F. This error can be managed by either a margin of |µ_1,c-1|, or by shifting the patient by -µ_1,c-1. For this study, we choose to evaluate shifting the patient rather than increasing the margin. In other words, the patient translation at each fraction is not only corrected according to a registration of pre-treatment CBCT to planning CT, but also by an additional -µ_1,c-1, in anticipation of intrafractional drift. If trending occurs over treatment course, a moving average can be used instead, which is calculated as µ_c-v,c-1, where v is the number of fractions used in the average. Both methods require intrafractional measurements at all fractions; we also investigated the effectiveness of the adaptive strategy when intrafractional localizations are acquired only in initial fractions and µ_1,F is estimated as µ_1,k, where k is the fraction after which the adaptive strategy is applied, i.e., correction of -µ_1,k is applied for all fractions after k.

For the adaptive strategy we compensate patient specific random error (σ_1,F) by applying a patient specific margin. While daily estimation and correction of µ_1,F is feasible, applying patient specific margins requires re-planning, therefore we apply the margins only once after a few fractions. The margin must also account for residual error that occurs because only a limited number of fractions are available for margin calculation. As described by Yan et al. (5), when k fractions are used in estimating the systematic and random error, the upper bound of the residual in predicting µ_1,F can be calculated with Student’s t distribution, and the upper bound of the random error can be calculated using the χ² distribution with k-1 degrees of freedom. We can use this to calculate the required margin in each axis that will contain a proportion p of remaining treatments when adaptive radiotherapy is applied after k fractions:

$$m_k(p)={\mathit{\text{norm}}}^{-1}(p)\cdot {\sigma }_{1,k}\sqrt{\frac{k-1}{{\chi }_{1-\alpha ,k-1}^2}}+\frac{{\sigma }_{1,k}\cdot t_{\alpha /2,k-1}}{\sqrt{k}}$$ (1)

where norm⁻¹ is the inverse of normal distribution, ${\chi }_{1-\alpha ,k-1}^2$ is the χ² distribution with k-1 degrees of freedom, t_α/2,k-1 is Student’s t distribution with k-1 degrees of freedom, and the expected proportion within all three margins is ~p³. Equation 1 takes into account the upper bound of uncertainty due to limited data in estimating σ_1,F and µ_1,F, based on the 1-α confidence interval, and is applicable when µ_1,F is estimated once after k fractions or when a moving average is applied using k fractions. However, when intrafraction motion is measured at each fraction and a cumulative estimate is used for the correction, the residual error in predicting µ_1,F decreases with each fraction. In this case we may use the root-mean-square of the residual of µ_1,F over the remaining treatment course:

$$m_k(p)={\mathit{\text{norm}}}^{-1}(p)\cdot {\sigma }_{1,k}\sqrt{\frac{k-1}{{\chi }_{1-\alpha ,k-1}^2}}+\sqrt{\frac{1}{(N-k+1)}{\displaystyle \sum _{i=k}^N{\left(\frac{{\sigma }_{1,k}\cdot t_{\alpha /2,i-1}}{\sqrt{i}}\right)}^2}}$$ (2)

We simulated applying an adaptive strategy after 2–15 fractions using patient specific margins from Equation 2 with the systematic error corrected using a cumulative estimate at each fraction, using p=0.9 and α=0.1. To avoid underestimating margins, we enforced minimum margins of 1mm in RL, and 2mm in AP and SI. We calculated the percentage of remaining treatment for which the prostate was within each margin, as well as the percentage within all three margins. For comparison, we evaluated the reduction in effectiveness when systematic error was not corrected, and we evaluated using margins from Equation 1 while correcting systematic error with a moving average and with a single estimate after k fractions.

Hybrid Strategy

While adaptive management of intrafraction motion may have potential benefits, it requires added workload to calculate and apply mean corrections and patient specific margins. Because of this, we also propose and investigate a novel strategy for compensating intrafraction motion, which is essentially a hybrid of the adaptive strategy and a population margin. The strategy has two parts: (1) identification of population subgroups, and (2) discriminant analysis to predict a new patient’s subgroup after a few fractions. Margins are calculated and applied separately for each subgroup.

The purpose of identifying subgroups is so that patients with high target stability are not penalized with large margins due to patients with greater motion. Therefore we desire to identify subpopulations with distinct motion characteristics and margins. We used k-means clustering to divide patients into two groups, with input being the expected 90^th percentile of measured vector displacement from the plan during treatment delivery for each patient. The expected 90^th percentile assuming a normal distribution was used because it is calculated using all motion measurements and may be a less noisy measure than the actual 90^th percentile. It should be noted that choice of subpopulations is arbitrary; any method could be used for their identification including manual selection to conform to pre-defined margins or protocols.

The purpose of the classification is to predict a patient’s proper subpopulation in initial fractions. In clinical application the subpopulations would be defined using motion measurements from patients who have previously completed therapy. The classification algorithm would then be constructed using these measurements as input (training) data, and would be used to predict the proper subpopulation for each new patient. In this study for each patient we constructed a classification algorithm using motion measurements from all patients except the one to be classified, after which and we tested the ability of the algorithm to correctly classify the patient based on information from initial fractions.

To avoid over-fitting we desire to limit input to a few meaningful variables. For each axis, we used as input to the classifier the expected 90^th percentile of motion per patient assuming a normal distribution. Also, as studies have shown correlation between rectal filling and prostate intrafraction motion (13, 14), we also evaluated including as input to the classifier the mean of a log transformation of pre-treatment gas volumes. The gas volume within the patient was calculated from the daily CBCT images by summing voxels below an automatically chosen threshold within the patient interior (including ±6cm SI from treatment isocenter) as was described previously (14). Gas volume was not measured for 2 patients due to CBCT artifacts from hip prosthesis; therefore they were omitted from the analysis when gas volume was incorporated.

For the classification algorithm we used a linear discriminant function defined using the Perceptron algorithm. A linear discriminant function was chosen because it is intuitive and consists of a single boundary separating the subgroups (a line for 2D data and a plane for 3D data) (15). Finally, we evaluated the accuracy of the classifier in predicting group membership of each patient using the initial 2–20 fractions, with and without incorporating gas volume.

Comparison of Motion Compensation Strategies

To compare the various strategies for compensating intrafraction motion we calculated descriptive statistics for the entire population, the population with µ_1,F corrected for each patient, and the patient subpopulations defined in the hybrid strategy. We also calculated geometric margins for the population and subgroups that contain 90% of motion, and we compared them to patient specific margins from the adaptive strategy applied after 5 fractions.

Results

Motion Characteristics

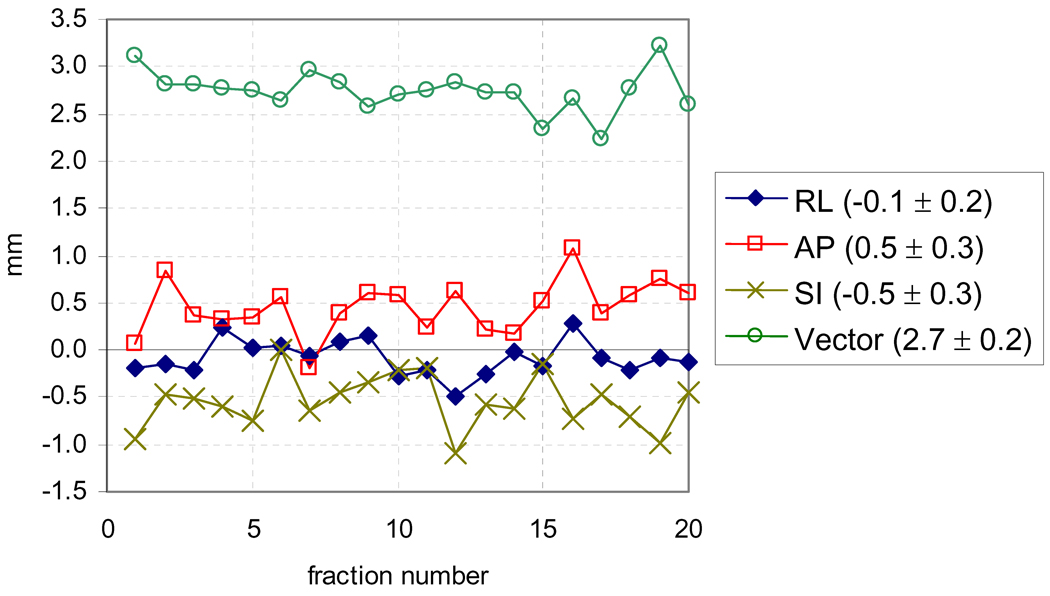
The population mean displacement is plotted verses fraction in Figure 1 and shows no trend over treatment course. The ANOVA test confirmed this, with the null hypothesis that no difference exists between samples of µ_i,i and σ_i,i from separate patients being rejected for each axis with high statistical power (p<0.0001), while the null hypothesis that no difference exists between samples from separate fractions could not be rejected at α=0.05, with p≥0.14 for each axis. These results indicate that intrafraction motion is highly patient specific with no detectable trend over treatment course.

Figure 1.

Population mean displacement per fraction. The mean ± standard deviation of each line is given in the legend.

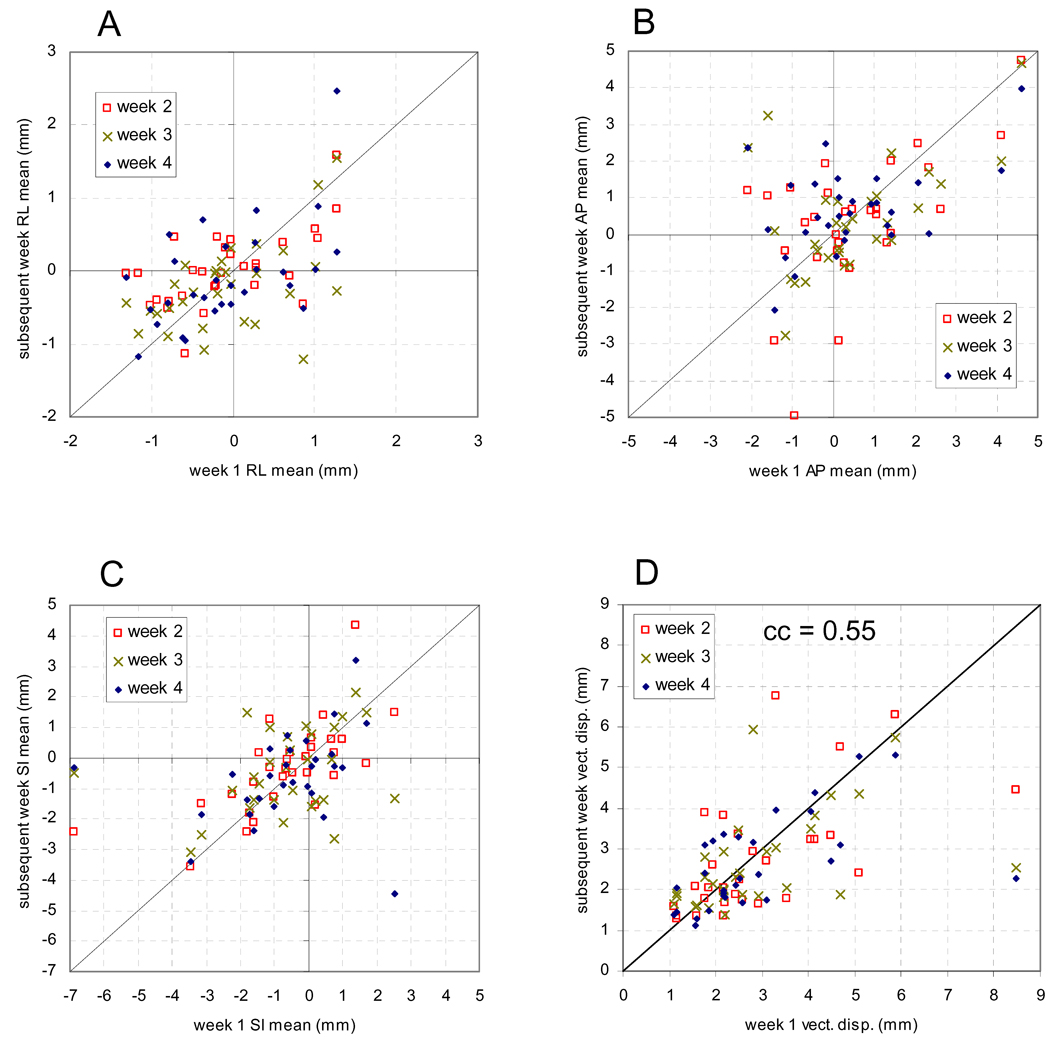
In Figure 2, the systematic error per patient in RL (2A), AP (2B), SI (2C), and the mean vector displacement (2D) calculated for the 1^st week of treatment is plotted versus the value calculated for each subsequent week. The correlation coefficients (cc) and their statistical significance (p) of the systematic and random errors per week are given in Table 1. The random error was slightly less correlated in AP and SI, with little correlation in RL.

Figure 2.

Systematic displacement from the plan for each patient calculated for the first week versus the systematic displacement for each subsequent week in RL (A), AP (B), SI (C), and vector displacement (D).

Table 1.

Correlation coefficient (cc) and statistical significance (p) between first and each subsequent week of treatment course for the patient specific mean (µ_i,j) and standard deviation (σ_i,j).

	Axis	cc	p
µi,j	Right-Left	0.53	<0.0001
	Anterior-Posterior	0.50	<0.0001
	Superior-Inferior	0.41	0.0001
σi,j	Right-Left	0.37	0.0004
	Anterior-Posterior	0.42	<0.0001
	Superior-Inferior	0.37	0.0004

Adaptive Strategy

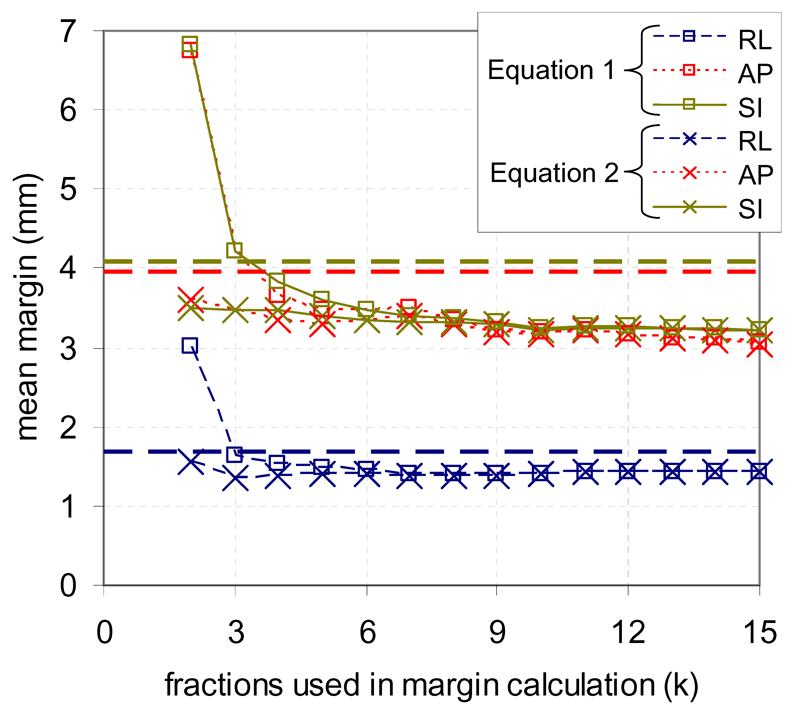
Figure 3 shows the mean of all patient specific margins for each axis using Equation 1–Equation 2 vs. number of fractions used in the calculation. Also shown as horizontal dashed lines are population margins containing 90% of motion. Patient specific margins decreased as more fractions data were available for estimating margins. When more than three fractions were used to estimate the margins, the mean margins over all patients was smaller than population data due to reduced error from correcting for µ_1,F.

Figure 3.

Mean of all patient specific margins calculated for each axis after 2–15 fractions for an adaptive strategy using a single estimate of systematic error (Equation 1) and using a cumulative estimate (Equation 2), as well as population margins to contain 90% of motion in each axis (horizontal lines).

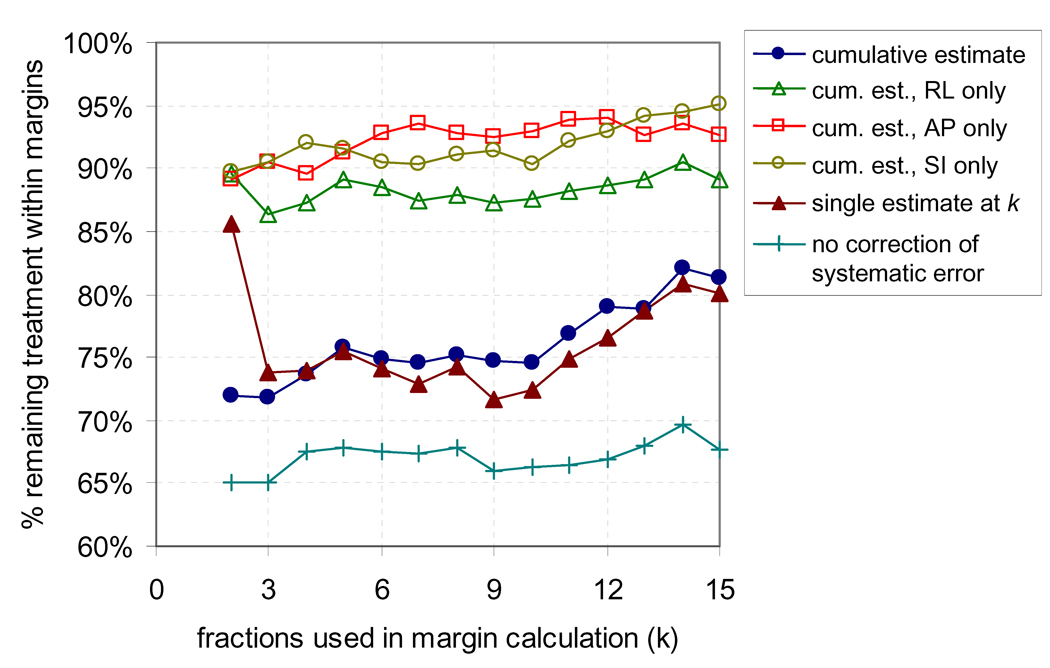
Figure 4 shows the percentage of remaining treatment for which the prostate was within the margins versus number of fractions used in margin calculation. When the adaptive strategy was used with a cumulative estimate of µ_1,F, the proportion of remaining treatment within each margin was ~p, while the proportion within all margins was ~p³, as expected. The percentage within the RL-axis margin was slightly lower than for AP and SI. Using a single estimate of µ_1,F at fraction k rather than a cumulative estimate had similar coverage, however at the cost of increased margins for smaller k as shown in Figure 3. When the systematic error was not corrected the coverage decreased, with the percentage within all margins decreasing from 76% (with correction) to 68% (without correction) at fraction 5. The cumulative estimate of µ_1,F resulted in marginally better results than a moving average (not shown), which confirmed that no trending occurred over treatment course.

Figure 4.

Percentage of remaining treatment for which the prostate is within all three margins when adaptive radiotherapy is applied after 2–15 fractions when systematic error is corrected using a cumulative estimate, a single estimate from initial fractions, and when no correction is performed. Also shown is the percentage of remaining treatment within each individual margin for the adaptive strategy with the cumulative estimate.

Hybrid Strategy

The subpopulations defined by k-means clustering divided the population into two groups. Group 1 had relatively little motion and consisted of 19/30 patients, while group 2 had relatively large motion and consisted of the remaining 11 patients. Motion magnitude was similar for both groups in RL, while there were pronounced differences in AP and SI. Because of this, RL-axis motion was omitted from the classification algorithm.

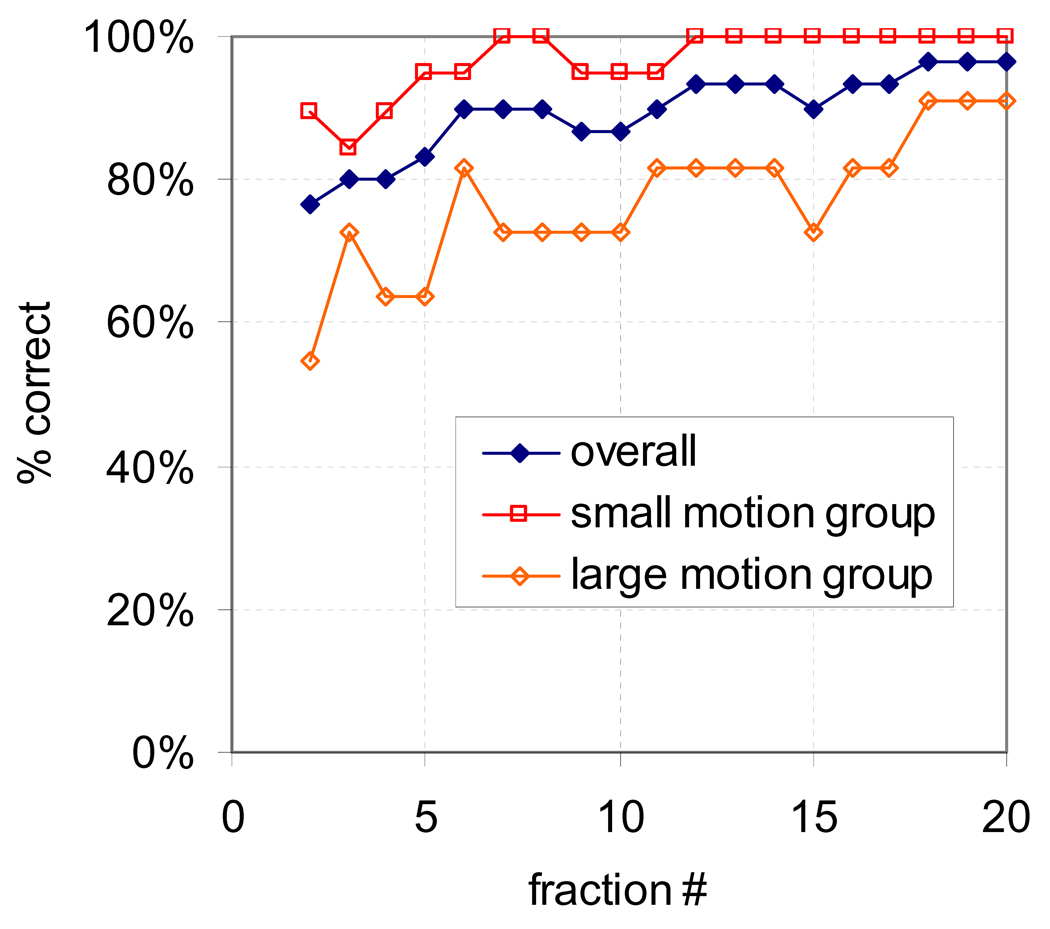
The percentage of patients whose subpopulation was accurately predicted after 2–20 fractions is shown in Figure 5 for all patients and for both subgroups. After 2 fractions, 77% (23/30) patients were classified correctly, rising to 83% (25/30) after 5 fractions. The classification was more accurate for patients in the small motion group than the large motion group. Although not shown, incorporating gas volume did not improve prediction accuracy.

Figure 5.

Percentage of patients classified correctly versus number of fractions used in the classification for all patients, and for the small and large motion subgroups.

Comparison of Strategies

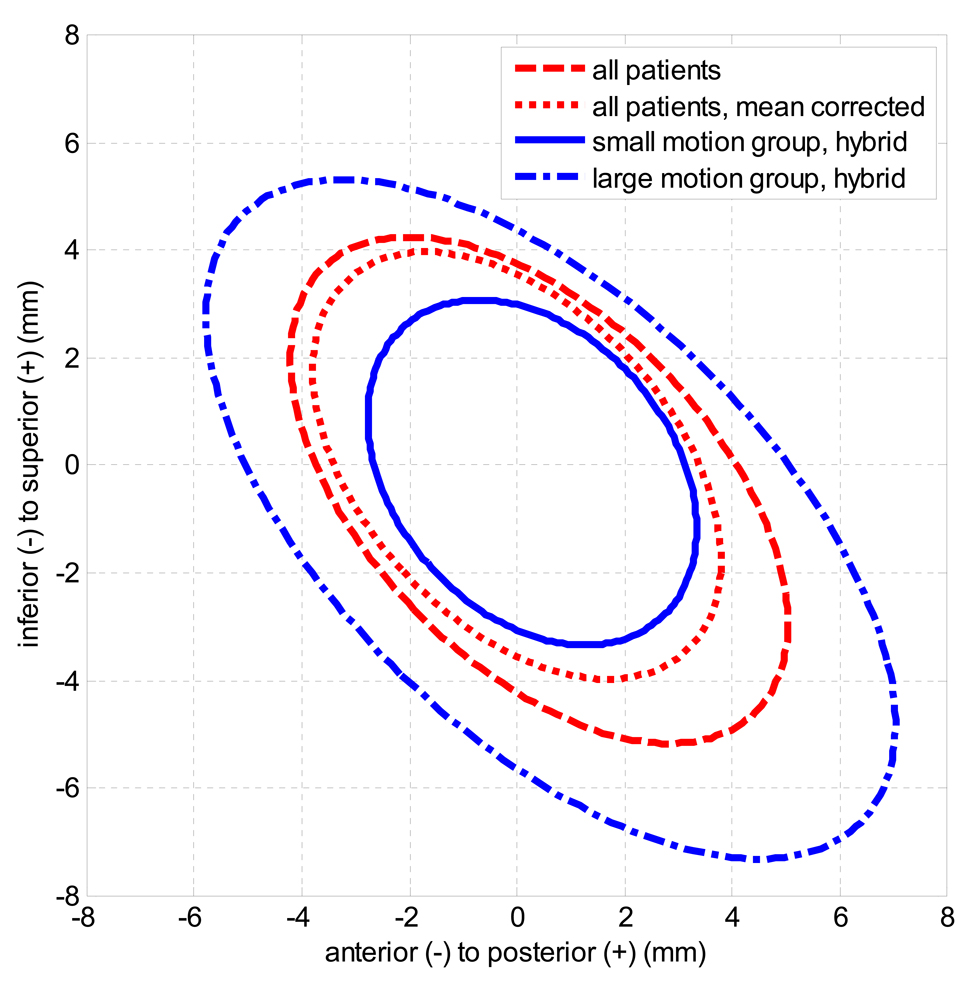
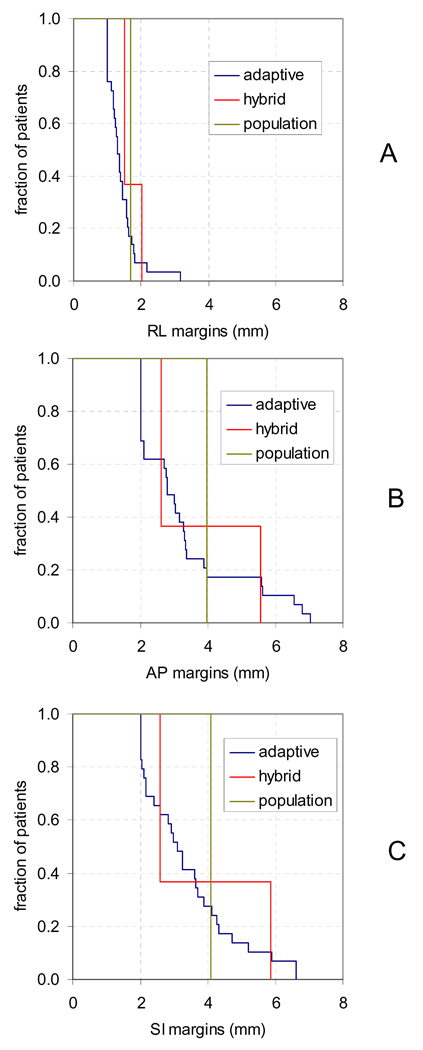
The mean and standard deviation of all measured intrafraction motion is shown in Table 2 for the entire population with and without correcting µ_1,F, and for each subpopulation defined for hybrid strategy. Figure 6 shows the ellipses containing 90% of measurements for each group assuming a bivariate normal distribution in AP and SI. These results show that correcting patient specific systematic error moderately decreased population target uncertainty in all axes, that the two subgroups defined by the hybrid technique had very different motion characteristics in AP and SI, and that posterior and inferior motion were correlated for all groups. Figure 7 is the cumulative distribution of margins over all patients in RL (A), AP (B), and SI (C) for adaptive, hybrid, and population margins to contain 90% of motion.

Table 2.

Mean ± standard deviation of all motion measurements from kV fluoroscopy for entire population with no adaptive technique and when patient specific systematic error (µ_1,F) is corrected, and for the subpopulations defined for the hybrid technique.

adaptive technique	patient group	# patients	population mean ± standard deviation (mm)
			RL	AP	SI
none	all	30	−0.1±1.0	0.4±2.2	−0.5±2.2
µ1,F corrected	all	30	0.0±0.8	0.0±1.8	0.0±1.9
hybrid	small motion	19	−0.2±0.8	0.3±1.4	−0.1±1.5
hybrid	large motion	11	0.1±1.2	0.6±3.0	−1.0±2.9

Figure 6.

Ellipses containing 90% of measured displacements from the plan in the AP and SI-axes, for the entire population with and without the patient specific systematic error corrected, and for the small and large motion groups defined using the hybrid strategy. A bivariate normal probability distribution was assumed for each ellipse.

Figure 7.

Cumulative distribution of RL (A), AP (B), and SI (C) margins for adaptive, hybrid, and population strategies. Margins were calculated to contain 90% of motion.

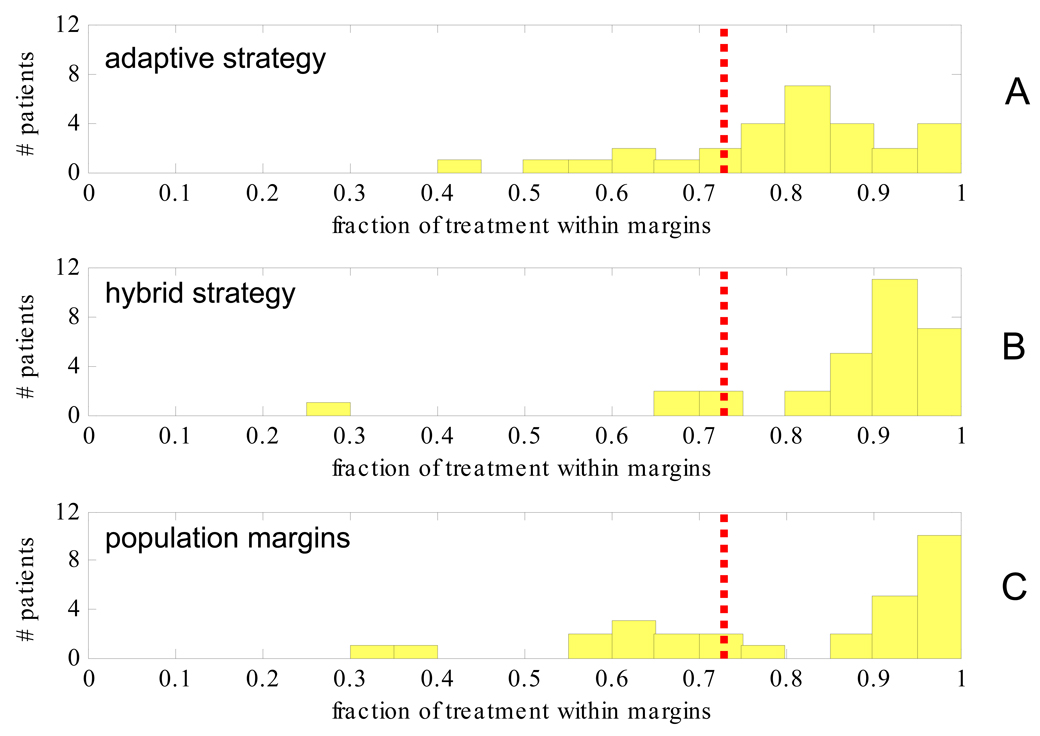
Figure 8 is the histogram of the percentage of intrafraction motion per patient within all three margins for the remaining treatment fractions as measured by kV fluoroscopy when motion is managed after 5 fractions using the adaptive strategy (A), the hybrid strategy (B), and population margins (C). For the adaptive strategy, population margins were used in the RL-axis. If the systematic and random errors had been predicted perfectly then the adaptive strategy would result in all patients having ≥73% (0.90³) of remaining treatments within all three margins (shown as red dashed vertical lines), while variation from this indicates prediction error. It should be noted that the comparison in Figure 8 is compounded by the fact that adaptive margins are on average smaller than population margins (Figure 7).

Figure 8.

Histogram of the fraction per patient of treatment within all three margins for adaptive (A) hybrid (B) and population (C) strategies applied after 5 fractions. Margins were calculated to contain 0.90³ of motion (red dashed line).

Discussion

We did not observe any trending over treatment course, which may be because we utilize hypofractionation and effects of radiotherapy may not occur until treatment is completed. However Kotte et al. evaluated prostate intrafraction motion with 35 fractions and also found no correlation (16).

Our results indicate that adaptive strategy in the RL-axis is less effective than in other axes. Figure 1 shows the RL-axis global mean is near zero, while the percentage of treatment within RL-margins in Figure 4 was slightly less than the other axes. Also Figure 7A showed very little variation between RL margins for adaptive, hybrid and population strategies. Because of this, we recommend that adaptive strategies in the RL-axis be limited to a correction of systematic error with a population margin, or that no adaptive strategy be implemented for RL-axis motion.

The results presented here indicate that adaptive strategy for prostate intrafraction motion is feasible, even when initiated after only a few fractions. Figure 7 shows that the range of patient specific margins is large in AP (2–7mm) and SI (2–6.6mm), however Figure 3 shows that the maximum average decrease in AP and SI margins is only ~1mm. Figure 3 indicates a tradeoff between starting the adaptive strategy early and calculating patient specific statistics with sufficient accuracy. For example, it is possible to begin the adaptive strategy after only 2 fractions; however the required margins will be detrimentally large if patient specific systematic error is not corrected using a cumulative estimate at each fraction. In contrast, when adaptive strategy is applied after 5 fractions there is little difference whether µ_1,F is estimated cumulatively or only at k=5.

As opposed to the adaptive strategy, the uncertainty in the margin calculation is nearly eliminated in the hybrid strategy because margins are calculated for each subgroup using previously completed patients. However, there is a probability that patients may be incorrectly classified. We evaluated the hybrid strategy using initial fractions for 30 patients and found the accuracy to be ~83% after 5 fractions. It is also possible that the accuracy found here may be improved when a larger data set and more sophisticated classification algorithm are incorporated. One benefit of the hybrid strategy is that it can account for new motion measurements and continual accrual of patients, therefore improving over time. Also while the adaptive strategy requires re-planning and re-evaluation after initial fractions, the hybrid strategy can be performed by creating one plan for each subpopulation before treatment initialization. The correct plan would then be decided by the classification algorithm.

Correcting µ_1,F eliminated the population and patient specific systematic error and reduced the population standard deviation. The difference between these two distributions, rows 1–2 in Table 2, represents the maximum attainable benefit from correcting systematic error since µ_1,F cannot be corrected perfectly. Also the large difference in motion characteristics between the population subgroups underscores the patient specific nature of the intrafraction motion. While adaptive strategies for intrafractional uncertainties may be beneficial, one concern is the increased workload they require. One option is to use the hybrid strategy to identify patients for which adaptive strategies will be of most benefit, and to use a population approach for the remaining patients.

One limitation of our study is the limit in number of patients in the population and in the subgroups defined for the hybrid management strategy. However the hybrid strategy is not necessarily limited to our arbitrary choice of subgroups. Our main purpose was to demonstrate feasibility of predicting motion characteristics from initial fractions rather than to use k-means clustering to describe inherent subgroups of a population.

The potential benefits of adaptive strategies that we investigated here must still be verified dosimetrically. Equation 1 – Equation 2 are useful for determining margins to achieve a desired probability of coverage during treatment delivery, but do not necessarily guarantee a specific target dose. Determining optimal patient specific margins requires a dosimetric evaluation, which will be the focus of future studies.

We investigated adaptive strategies to manage intrafractional prostate translation when interfraction motion is corrected online by CBCT. One disadvantage is that our online image guidance correction was limited to translation; interfractional rotations and deformations were not corrected and therefore these uncertainties were compensated by the planning margins. Alternatively, an adaptive strategy could incorporate interfractional rotation and deformation (5), However one challenge of doing this is the added workload required for accurate contouring on CBCT images in order to quantify deformation. While intrafractional rotation and deformation also occur; intrafractional rotations have been shown to be small (typically ≤1.8°) (7), and most intrafractional localization techniques are fiducial based, providing limited information about rotation and deformation.

In summary, we have shown that adaptive strategies may be used to manage AP and SI prostate intrafractional motion after an online correction for interfraction motion, and that patients may be classified into large and small motion groups using motion measurements from initial fractions.