Detecting ‘Wrong Blood in Tube’ Errors: Evaluation of a Bayesian Network Approach

Abstract

Objective

In an effort to address the problem of laboratory errors, we develop and evaluate a method to detect mismatched specimens from nationally collected blood laboratory data in two experiments.

Methods

In Experiment 1 and 2 using blood labs from National Health and Nutrition Examination Survey (NHANES) and values derived from the Diabetes Prevention Program (DPP) respectively, a proportion of glucose and HbA1c specimens were randomly mismatched. A Bayesian network that encoded probabilistic relationships among analytes was used to predict mismatches. In Experiment 1 the performance of the network was compared against existing error detection software. In Experiment 2 the network was compared against 11 human experts recruited from the American Academy of Clinical Chemists. Results were compared via area under the receiver-operating characteristics curves (AUCs) and with agreement statistics.

Results

In Experiment 1 the network was most predictive of mismatches that produced clinically significant discrepancies between true and mismatched scores ((AUC of 0.87 (±0.04) for HbA1c and 0.83 (±0.02) for glucose), performed well in identifying errors among those self-reporting diabetes (N = 329) (AUC = 0.79 (± 0.02)) and performed significantly better than the established approach it was tested against (in all cases p < .0.05). In Experiment 2 it performed better (and in no case worse) than 7 of the 11 human experts. Average percent agreement was 0.79. and Kappa (κ) was 0.59, between experts and the Bayesian network.

Conclusions

Bayesian network can accurately identify mismatched specimens. The algorithm is best at identifying mismatches that result in a clinically significant magnitude of error.

1. Introduction

Medical errors are a significant problem in the United States. They kill more Americans each year than motor vehicle accidents, breast cancer, and AIDS combined [1]. In laboratory medicine, of particular concern are patient identification errors. Proper patient identification is essential to reducing errors and improving patient safety. The Joint Commission on Accreditation of Healthcare Organizations (JCAHO) recognizes this and has included “Improve the accuracy of patient identification” as one of its “National Patient Safety Goals” [2]. Patient identification and other laboratory errors have received increased attention in the research literature both inside [3] and outside [4,5] the United States. In this paper we propose a method that can be used to screen for an error that is particularly difficult to identify in the laboratory, the mislabeled specimen or “wrong blood in tube” error. This type of error refers to a specimen of blood collected on Patient A, but for which the accompanying requisition and label is for Patient B [3].

A wrong blood in tube error is more pernicious than many other blood laboratory errors. If a patient’s results are like most others in the lab, then a mismatched sample will often yield a result that is similar to that of the patient’s true result. Further, for any set of values for which a proportion of specimens are switched statistical characteristics (e.g., mean and standard deviation) will be the same as if they were not switched. In sum, to identify such mismatched specimens, more sophisticated methods are needed than simple comparisons of values to a norm. In this paper, we develop, train and test a network for detecting wrong blood in tube errors when glucose and HbA1c analytes are analyzed in separate vials. We report on two experiments. Experiment 1 evaluates the network against an established method for automatic detection of errors, LabRespond [5], using the National Health and Nutrition Examination Survey (NHANES) data set. Experiment 2 compares the performance of a Bayesian network to expert lab reviewers when values are derived from a pre-diabetic population.

1.1. Bayesian Networks

We approach the problem of detecting wrong blood in tube errors by implementing a Bayesian Network [6]. A Bayesian network is a graphical representation of a joint probability distribution over a set of random variables. A Bayesian Network B = ⟨G, P⟩ consists of a representing graph, G, and an associated joint probability distribution, P. The graph, G, in the network is described by a finite set of nodes V and a binary relation, R on V. A binary relation on a set of nodes V is a subset of ordered pairs (v_i, v_j) in V × V. The relation R characterizes edges in the graph, where R = {(v_i, v_j) ∈ V × V: v_i is a parent of v_j}. Let v_iRv_j denote v_i is a parent of v_j. The relation R is irreflexive (for every v_i ∈ V, not v_iRv_i) and acyclic (for any finite sequence of distinct elements v₁,v₂,…,v_k ∈ V such that k > 1 and v_jRv_j+1 for all j ∈ {1, 2, …, k-1} , not v_kRv₁). An irreflexive graph is called a directed graph, its edges are directed edges, and thus, graphs in Bayesian networks are referred to as directed and acyclic graphs (DAGs). The DAG, G, in the Bayesian network, B = ⟨G, P⟩, represents the probability distribution, P, where nodes in V characterize random variables and directed edges describe stochastic dependence. If v_i is a variable in the graph then the graph specifies conditional probability distributions P(v_i|π(v_i)), where π(v_i) are parents of v_i. While each variable v_i is dependent on its parents, it is also conditionally independent of any of its non-descendants given its parents. Hence, given a directed acyclic graph G with a set of nodes V = {v₁, …, v_n} the joint probability distribution of the network may be factored as follows:

$$\mathrm{P}({\mathrm{v}}_1,\dots ,{\mathrm{v}}_{\mathrm{n}})=\prod \mathrm{P}({\mathrm{v}}_{\mathrm{i}}\mid \pi ({\mathrm{v}}_{\mathrm{i}}\left)\right)$$ (1)

1.2. Bayesian Networks and Blood Laboratory Errors

Bayesian Networks provide a graphical means for representing uncertain relationships between and among variables and allow us to model what might influence belief in why a particular analytic value is observed. In the case of Bayesian networks for detecting blood laboratory errors, we must consider both continuous variables (e.g., analyte values) and discrete variables (e.g., wrong blood in tube: true or false). To guarantee exact computation, we impose on the DAG the condition that discrete variables are not allowed to have continuous parents [7].

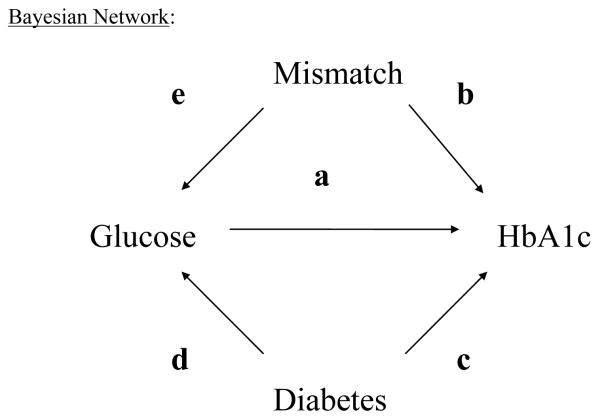
From a network, we may infer a probability that there is wrong blood in the tube given empirical information about observed analyte values and the structure of the network. To understand our approach, consider the following model: The graph in Figure 1 encodes knowledge about what influences our belief in analyte values, mismatch and diabetes status. For example, we know of three factors which would influence belief in an (unobserved) HbA1c score:

1. Observed glucose score (directed edge “a”), because HbA1c is formed in the patient via a non-enzymatic pathway by hemoglobin’s normal exposure to glucose,

2. Knowledge of a mismatch (directed edge “b”), because this, too, may cause one to observe a particular HbA1c score, and

3. Diagnosis of diabetes (directed edge “c”), because HbA1c scores are in general higher for these patients.

Figure 1.

Bayesian Network

Also, disease status (Diabetes = (‘yes’ or ‘no’)) affects our belief in an (unobserved) glucose score (directed edge “d”). In practice, given both a purported glucose and HbA1c score on a patient, we cannot uniquely identify whether a mismatch was due to a glucose vial switch or an HbA1c vial switch, only that a mismatch in at least one of the two vials may have occurred. Therefore, we draw an arrow from “Mismatch” to “Glucose” as well (directed edge “e”).

Notice in Figure 1, that absence of arrows communicates important information. For example, our model presented above does not have an arrow from “diabetes” to “mismatch”. This is because these events are probabilistically independent. A lab technician handling vials is not more prone to mismatch a diabetic patient’s vial as s/he is to mishandle a nondiabetic patient’s vial and there is no clear way to justify such an arrow. Therefore, the model we use imposes that one’s disease status does not influence belief in a mismatch, but does influence belief in observed fasting glucose and HbA1c score. We note also that to implement the model does not require that diabetes status be known. Belief in diabetes status, however, will be influenced by glucose and HbA1c score. This is an important point, because in a clinical laboratory patient diagnosis is often unknown. The graph in Figure 1 then constrains the relationships among conditional probabilities among the variables and this network is the basis for our analysis of NHANES data because it incorporates many of the basic facts about glucose and HbA1c analytic results and variables that may influence glucose and HbA1c score.

2. Experiments

2.1 Experiment 1

2.1.1 Overview

This experiment compares the performance of the network against a validated benchmark method of error detection, LabRespond.

2.1.2 Methods

2.1.2.1 Data source

The current study utilized data from the National Health and Nutrition Examination Survey (NHANES). The National Health and Nutrition Examination Survey is an ongoing survey and examination of the civilian, non-institutionalized U.S. population. The study is characterized by a complex stratified multistage probability survey design [8]. Mobile examination centers are used for a majority of the health examinations and specimen collections for subsequent analysis at a clinical laboratory. Data from the 2003-2004 survey years were utilized in this analysis with glucose from the biochemistry profile, included 6492 results, and glycohemoglobin from the glycohemoglobin profile, included 6601 results. We excluded patients with missing glucose or glycohemoglobin results, leaving a total 6486 patients. Each patient’s self-reported diabetic status was incorporated from the medical conditions questionnaire.

2.1.2.2 Specimen Collection

In order to measure glycohemoglobin, a whole blood sample was collected from the patient by the mobile examination center staff, which then shipped the sample to the University of Missouri-Columbia for analysis using a Primus instrument [8]. To measure glucose, 800ul of serum was aliquoted from pooled serum obtained from red top tubes, shipped to Collaborative Laboratory Services, and analyzed on an LX20 [8].

2.1.2.3 Training and Test Sets

Participants were randomly assigned to either the training (N = 2,000) or testing (N = 4,486) data sets; once assigned, wrong blood in tube errors were introduced. This was achieved as follows: 1) Subjects were randomly paired with another participant in their data set to form potential “switching pairs”, 2) the chance of a switch was decided randomly with probability, p, 3) if a switch obtained in Step 2 then glucose values were switched within the pair of participants with probability ½, otherwise HbA1c values were switched. The probability p gives the probability of a mismatch between glucose and HbA1c for any switching pair. We implemented this switching process to create three mismatch scenarios: 1) 50% of specimens mismatched (i.e., p = ½), 2) 10% of specimens mismatched (i.e., p = ¹/₁₀), and 3) 3% of specimens mismatched (i.e., p = ³/₁₀₀). Note that by the aforementioned process there is an equal probability of an analytic value being switched with any other. In a sub-analysis, we made a switch contingent on the size of the error it would produce (small, medium or large).

The classifier results presented here may be susceptible to bias if the chance of mismatch in observational studies is associated strongly with analyte score. Such a relationship would attenuate classification performance, because switches would occur more often among like results. This effect would be mediated through a third variable that affects both probability of switch and analyte score.

There are at least two potential mechanisms by which sample switching may occur. Here we discuss how these mechanisms might or might not affect mismatch probability as a function of analyte score. The first is through incorrect labeling after samples reach the laboratory. Because laboratories label a large number of samples arriving from different locations, collected at different times and the arrival and labeling occur in a nonsystematic manner (i.e., clinical sites and laboratories do not coordinate when blood is sent or labeled), there is no discernible pathway by which analyte score may be associated with increased probability of a switch. A second mechanism for switching is at collection and processing by the phlebotomist. With this mechanism a relationship between analyte score and switch could be mediated through time-of-draw. It is plausible that, due to fatigue of the phlebotomist, later draws may occasion more switching errors. Further, other variables that affect analyte score, like health-status of the patient, might also relate to time-of-draw. Because this stands as a potential threat to the current analysis, we evaluate the effect of time-of-draw in explaining analyte score variance. If time-of-draw is a poor predictor of analyte score then we are less concerned that time-of-draw may influence the probability of a switch.

2.1.2.4 Benchmark Method

In order to evaluate the validity of our approach, we compared our results to those of an established method, or “benchmark”. We chose to a validated and published method for error detection call “LabRespond” [5]. LabRespond is an automated patient validation system, or “autoverification” system, which uses statistical methods to estimate the plausibility of observed clinical laboratory results on patient demographics and other analytes that are thought to covary with the analyte of interest.

A summary of the LabRespond algorithm is as follows and may also be found elsewhere [5]:

1. For each target analyte, look up the predictive test combinations using reference table. For example, glucose is predicted by previous glucose (if collected within 7 days), potassium, and sodium. HbA1c is predicted by previous HbA1c (if collected within 90 days) and glucose. There are no historical results for patients within the NHANES dataset. Therefore, HbA1c is predicted by only glucose and glucose is predicted by potassium and sodium.

2. For each target analyte the LabRespond algorithm determine the gender-specific pre-test plausibility by computing the percentage of results in the value’s class. The class of each value is determined by segmenting the range of analytical values at the 5^th, 15^th, 35^th, 65^th, 85^th, and 95^thpercentiles. For example, if the value is in the 25^th percentile, then it is in the class containing entries between the 15^th and 35^th percentiles, which should contain about 20% of the data, and would, therefore, have a pre-test plausibility of 20%.

3. For each pair of analytes, such as glucose/sodium and glucose/potassium, compute a 7 × 7 observed frequency matrix containing the frequency with which each pair of classes is observed together. This matrix is then smoothed using a neighborhood average algorithm.

4. For each pair of analytes, compute a 7 × 7 expected frequency matrix where the value in each cell is the product of each analyte’s expected class frequency. For example, an HbA1c in the range of the 5^th – 15^th percentile and a glucose in the 35^th-65^th percentile would have an expected frequency of 3% (10% × 30%).

5. For a patient’s results, the post-test plausibility is computed as the pre-test plausibility times the ratio of the observed pair frequency to the expected observed frequency. For example, if the pre-test plausibility is 10%, the expected pair-wise class frequency is 3%, and the observed pair-wise class frequency is 9%, then the post-test plausibility of 30% ((10% × 9% )/ 3%). When a target analyte, such as sodium, has more than one dependent analyte, the post-test plausibility is taken as the product of the pre-test plausibility and the appropriate ratios.

6. Extreme values less than then 1^st percentile or greater than the 99^th percentile are not autoverified in addition to values below some pre-defined criteria, such as 5%.

The LabRespond algorithm is capable of pair-wise modeling of complex relationships by making discrete continous data. However, the effect of making the data discrete limits the sensitivity of the LabRespond method to detect smaller errors as only errors resulting in class changes may be detected.

2.1.2.5 Statistical Analysis

The Bayesian network (Model 3) was constructed in Hugin Researcher version 6.8. We used the Survey package for R version 2.5.1 [9] to perform the parameter learning on the training sets for the model. This package accommodates representative sampling design sampling weights. The effect of time of day of blood draw on analyte score was evaluated using a general linear model in R [9].

2.1.3 Results

The average representatively weighted participant was 42.3 years of age, female (51.2%), Caucasian and had more than a high school education. Average (± S.D.) glucose scores and HbA1c scores were 5.017 mmol/L (± 0.694 mmol/L) and 5.32% (± 0.21) respectively, for those not reporting diabetes (92.22%) and were 7.931 mmol/L (± 4.179 mmol/L) and 7.20 (± 2.94), respectively, for those reporting diabetes (6.65%).

Table 1 illustrates performance of the network for the entire NHANES sample (“overall”), for identifying switching errors among persons with diabetes and for persons without diabetes. For overall switches

Table 1.

Area under the receiver-operator characteristic curve (AUC) for Bayesian network versus LabRespond and z-test results for entire sample, persons with diabetes and persons without diabetes

	Bayes Net	LabRespond
	Mean (± S.D.)	Mean (± S.D.)	Z*
Overall	0.65 (± 0.003)	0.55 (± 0.01)	29.77
Diabetics	0.79 (± 0.020)	0.50 (± 0.04)	13.66
Non-Diabetics	0.63 (± 0.001)	0.56 (± 0.01)	25.33

^*all Z-values p < 0.0001

Understanding under what conditions the Bayesian network and LabRespond each do and do not perform well is important for recommendation of model use. One way to understand this is to examine error classification of these two approches in Glucose X HbA1c space. Figure 2 illustrates the decision boundaries for the Bayesian network and LabRespond among non-diabetic females when predicting sample switching errors.

Figure 2.

Detectability of HbA1c Sample-Switching Errors In Non-Diabetic Females

Switching error rates are over represented in Figure 2 (50% switched analytes) to provide large enough error frequencies in small regions of the space. The relative performance of the two algorithms was not affected by error rate. Further, although decision boundary rules varied by diabetes status and gender, the graph in Figure 2 is prototypical of what we observe under various conditions. The specificity (true negatives/ [true negatives + false positives]) of the two algorithms is set at 95% (standard for LabRespond) in Figure 2. Such specificity is realistic for real-world applications of these methods because false positive results are expensive to investigate. In Figure 2, the dashed diagonal lines represent the decision boundary for the Bayesian network, the interior space between these lines indicates a decision to classify as “no error”, the exterior space indicates decision to classify as “error”. The solid lines represent the decision boundary for LabRespond, the interior spaces between and exterior spaces outside of these lines also represent classification as “no error” and “error” respectively. The dotted ellipse shows where 95% of error free blood lab pairs are located. Areas A – H are regions of the space defined by intersection of boundary rules for the different algorithms. The companion table to Figure 2, Table 2, indicates decision rules for each algorithm within areas A-H and the number of errors per total cases within region.

Table 2.

(Companion to figure 2)

	Bayesian Network (BN)
	LabRespond (LR)
	95% of true Non-Errors
	A B C D E F G H
Error? BN:	Y Y N Y N N Y Y
(Y/N) LR:	Y N Y Y N Y N Y

Areas A, D and H indicate where the Bayesian network and LabRespond jointly agree in classification as “error” and in these regions the algorithms generally do well in detecting actual errors. In area E the algorithms agree in a “no error” classification, but are often wrong. This is because small changes in analyte value are very difficult to detect when patterns of these values are used as predictors. Though prediction in this region is desirable, it is of low clinical value because clinical decisions within this region remain the same regardless of error status. Areas B, C, F and G indicate where the algorithms disagree on classification. Areas B and G indicate where the Bayesian network classifies cases as “error”, but LabRespond indicates “no error”. Here the Bayesian network is fairly efficient at identifying errors. Conversely, areas C and F indicate where LabRespond classifies cases as “error”, but the Bayesian network indicates “no error”. In these regions, there is inefficiency in error detection. In general, the Bayesian network was generally more sensitive than LabRespond. And, in cases where LabRespond utilized a more liberal error classification rule (area C), the payoff was low (1 error out of 5 cases). Notably, when error is defined as a 1.11 mmol/L glucose and 1 point HbA1c analyte change after switch most of the 591 cases are not considered as error, both algorithms perform better, but the Bayesian network remains somewhat superior. In summary, the Bayesian network cutoff was sensitive to high frequency high glucose and low HbA1c switched pairs whereas LabRespond was not. And, LabRespond was sensitive to high HbA1c and high Glucose pairs which were uncommon and rarely erroneous. Both algorithms performed much better when detecting errors entailed identifying significant changes in analyte value after switching.

In terms of pitfalls of these algorithms, both the Bayesian network and LabRespond each fail to properly classify many errors that do not result in a significant change in blood lab value. Further, LabRespond tends to classify high valued pairs as errors, when often these scores are not errors. Further it treats high glucose and normal HbA1c as a non-error, but often such values are switched. The Bayesian network does better with respect to classification of the aforementioned pairs, but is not perfect.

Because the majority of NHANES participants did not have diabetes, persons with diabetes (i.e., with high analyte values) were likely to have their blood switched with a person without diabetes (i.e., normal analyte values). Such errors were easier for the network to detect. Table 3 presents a different type of comparison. Rather than grouping patients into categories, in Table 3, we group error magnitude resulting from a switch into categories. In Table 3 switches were contingent on size of the difference between true and switched score: small, medium and large HbA1c and glucose errors. Thus, a switch occurred only if it met some criterion for magnitude of error. As is clear the network performed better than the benchmark LabRespond in all cases. Like LabRespond, the Bayesian network was better at detecting clinically significant errors (i.e., those of higher magnitude). The network also performed well in predicting lab errors among diabetic patients.

Table 3.

Area under the receiver-operator characteristic curve (AUC) for Bayesian network versus LabRespond and z-test results when switching errors were made contingent on magnitude of discrepancy between true and switched value.

	Bayes Net	LabRespond
	Mean (± S.D.)	Mean (± S.D.)	Z*
Small (≥ 0.50 units) HbA1c error	0.76 (± 0.010)	0.69 (± 0.01)	9.12
Medium (≥ 0.75 units) HbA1c error	0.83 (± 0.010)	0.79 (± 0.02)	3.58
Large (≥ 1.00 unit) HbA1c error	0.87 (± 0.010)	0.84 (± 0.02)	3.08
Small (≥ 0.278 mmol/L) Glucose error	0.68 (± 0.004)	0.59 (± 0.01)	16.08
Medium (≥ 0.555 mmol/L) Glucose error	0.73 (± 0.005)	0.65 (± 0.01)	17.00
Large (≥ 1.11 mmol/L) Glucose error	0.83 (± 0.020)	0.78 (± 0.01)	5.12

^*all Z-values p < 0.0001

While area under the receiver-operator characteristic curve is a useful approach to evaluating overall performance, it is useful to examine the receiver-operator characteristic curves to evaluate the performance of the network over different error thresholds. Figures 2a and 2b illustrate the performance of the Bayesian Network and LabRespond for Glucose error (1.11 mmol/L) and HbA1c error (1 unit) respectively.

As is clear from Figures 3a and 3b, the Bayesian network performs better than LabRespond for low and moderate false positive rates, but performs worse when high false positive rates are allowed. In clinical practice such high false positive rates would not be acceptable because they would result in the frequent re-analysis of correct results. Thus, we can conclude for acceptable levels of false positive the Bayesian Network performs better than LabRespond.

Figure 3a. Glucose Error Detection.

The x-axis is true positive rate (TRP). The y-axis is the false positive rate (FPR)

Figure 3b. HbA1c Error Detection.

The x-axis is true positive rate (TRP). The y-axis is the false positive rate (FPR)

Analysis of NHANES data to determine if time-of-draw affects glucose and HbA1c score indicated that only 1% of additional variance was explained by time-of-draw. Table 4 illustrates means and standard deviations for gluose and HbA1c as a function of time-of-draw.

Table 4.

NHANES Mean (± S.D.) glucose (mmol/L) and HbA1c by time-of-draw^†

Time-of-draw	Glucose	HbA1c
Morning	1.10 (± 0.01)	5.44 (± 0.02)
Afternoon	1.05 (± 0.01)	5.49 (± 0.03.)
Evening	1.02 (± 0.01)	5.38 (± 0.04)

^†Ordinary least squares analysis indicated an additional incremental R² of 1% variance explained in Glucose (and HbA1c) variance.

2.2 Experiment 2

2.2.1 Overview

This experiment compares the performance of the Bayesian network against 11 human experts recruited from the American Academy of Clinical Chemists.

2.2.2 Methods

2.2.2.1 Data Source

The training and testing datasets were generated using a model of a pre-diabetic population in order to provide a clean dataset known to be free from errors and one with sufficient variability for a meaningful evaluation. Based on data reduction of the Diabetes Control and Complications Trial (DCCT) lab values, we assumed a linear relationship, between glucose and glycosylated hemoglobin such that: HbA1c = 4.22 + 0.1604 × glucose [10]. This equation was determined from an analysis of glucose and glycosylated hemoglobin (HbA1c) results in a pre-diabetic population and are similar to published data for a pre-diabetic group [11].

2.2.2.2 Specimen Collection

Samples were collected from patients, self-reported to be fasting, at one of 26 study-sites across the United States. Samples for glycohemglobin were collected into 5ml purple-top vacutainers and shipped fresh and uncentrifuged to the Central Biochemistry Laboratory at the University of Washington. Samples for glucose were collected into 5ml gray-top vacutainers containing sodium fluoride with glycolytic inhibitor and were processed per the laboratory’s Manual of Operation to yield 1ml plasma, which was shipped frozen on dry ice to the Central Biochemistry Laboratory. Glucose was on a chemistry autoanalyzer by the glucokinase method and glycohemoglobin was measured by a Biorad Variant ion-exchange high-performance liquid chromatography instrument. While actual samples were not used as data, samples were used to obtain summary data from which clinical samples were simulated.

2.2.2.3 Participants

Members of the American Association for Clinical Chemistry’s Laboratory Information Systems and Medical Informatics Division were contacted by email and asked to participate in a web-based survey. The laboratory error detection task described here was a sub-portion of this larger survey. There were 28 survey participants. Of these, 11 reported that they were qualified to evaluate glucose and HbA1c errors. These 11 persons were recruited for the lab error detection task.

2.2.2.4 Design and Measures

One hundred and twenty glucose values were randomly selected from a normal distribution and HbA1c was computed from the aforementioned equation (see section labeled “Data Source” above). Because a lengthy exercise on the human evaluation for errors could lead to participant fatigue, the 120 pairs were split into two test sets each comprised of 60 items. In the two tests, 37% of the HbA1c samples were switched to generate errors. Because the test sets were small, we wanted to guarantee a meaningful proportion of clinically significant error. Therefore, we imposed that in order for a random HbA1c switch to hold, it must result in a difference of 0.5 units. Participants were randomized to one of the two test sets. The 60 test set items were further divided into two groups of thirty and each group began with “Consider a pre-diabetic population where the average glucose is 103 mgl/dL (standard deviation 11 mg/dL) and the average glycosylated hemoglobin (HbA1c) is 5.9 (standard deviation 0.2). For each of the 30 sets below, what is your belief that the HbA1c value is in error given the fasting glucose value? ”. For each of the 60 questions respondents selected one of Definitely Not an Error, Probably Not an Error, Neutral, Probably an Error, Definitely an Error.

2.2.2.5 Statistical Analysis

By varying the classification threshold between 0% and 100%, we produce an ROC curve for the Bayesian network’s performance for each of the two comparisons. The laboratory experts, however, did not provide a probability for use in creating an ROC curve, since the rating system is ordinal. We, therefore, created an ROC curve for each expert by computing their sensitivity (true positive rate) and specificity (1 – false positive rate) as the classification threshold is varied from “definitely an error” to “definitely not an error”. We computed an average ROC curve by averaging the true positive rate over the false positive rate dimension. In order to ensure a fair comparison of ROC curves between experts and the Bayesian network, we fit 1-parameter convex ROC curve to the data in order to smooth the curves. Without this smoothing, experts would be at a disadvantage because expert raw ROC curves were comprised of the 5-point response scale.

2.2.3. Results

Table 5 illustrates the results of the comparison between experts and the Bayesian Network (Figure 1). The first column gives expert number, 1 through 11. The second column gives the test set (described in the “Methods” section), test set 1 or test set 2. The third column gives, performance of the expert, the fourth column the performance of the network and the fifth column the z-test comparing, statistically, the performance of the expert to that of the network. As is clear, the network always performed at least as well as the experts. Further, in 7 of 11 cases the network performed significantly better in detecting errors. Expert performance was overall satisfactory ranging between 0.67 and 0.85 AUC, and suggesting the experts were capable evaluators of errors and non-errors.

Table 5.

Comparison of experts with a Bayesian network in two test sets.

Expert Number	Test Set	AUC (± S.E.)		Z-test (p-value)
		Expert	Bayes Net
1	1	0.68 (± 0.08)	0.93 (± 0.04)	2.83 (p < 0.05)
2	1	0.79 (± 0.07)	0.93 (± 0.04)	1.99 (p < 0.05)
3	1	0.74 (± 0.07)	0.93 (± 0.04)	2.33 (p < 0.05)
4	1	0.84 (± 0.06)	0.93 (± 0.04)	1.55 (p = n.s.)
5	1	0.76 (± 0.07)	0.93 (± 0.04)	2.37 (p < 0.05)
6	2	0.78 (± 0.06)	0.86 (± 0.05)	1.20 (p = n.s.)
7	2	0.70 (± 0.07)	0.86 (± 0.05)	2.25 (p < 0.05)
8	2	0.71 (± 0.07)	0.86 (± 0.05)	2.07 (p < 0.05)
9	2	0.85 (± 0.05)	0.86 (± 0.05)	0.17 (p = n.s.)
10	2	0.67 (± 0.07)	0.86 (± 0.05)	2.97 (p < 0.05)
11	2	0.76 (± 0.07)	0.86 (± 0.05)	1.48 (p = n.s.)

In addition to evaluation of an AUC, we examined percent agreement of the Bayesian network with experts and with LabRespond. Table 6 illustrates these agreement statistics. In Table 6, the probability of error threshold for the Bayesian network equal to 0.68, to give a 95% specificity. Percent agreement with experts ranged between 0.65 and 0.93 for the Bayesian network and 0.53 and 0.96 for LabRespond. Average Kappa (κ), a statistic that corrects for chance agreement, was 0.59 for the Bayesian network and 0.53 for LabRespond. Generally, agreement was satisfactory for all comparisons. However, Labrespond’s agreement with experts was more variable than was the Bayesian network’s. Even correcting for chance agreement (Kappa) both LabRespond and the Bayesian network had satisfactory agreement with experts.

Table 6.

Bayesian network and LabRespond agreement with experts Agreement

	Bayesian Network†	LabRespond
Expert 1	0.83	0.96
Expert 2	0.75	0.58
Expert 3	0.83	0.90
Expert 4	0.87	0.80
Expert 5	0.93	0.76
Expert 6	0.85	0.72
Expert 7	0.65	0.52
Expert 8	0.73	0.63
Expert 9	0.68	0.75
Expert 10	0.80	0.87
Expert 11	0.80	0.93
Average	0.79	0.77
Kappa (κ)	0.59	0.53

^†Probability of error threshold ( equal to 0.68) is set to give specificity (95%) equivalent to LabRespond.

3. Discussion

The findings of this study suggest that a Bayesian Network for detecting errors in HbA1c and Glucose blood analytes performs better than benchmark statistical approach to mismatched sample detection. The network also performed significantly better than 64% of human lab experts studied and performed at least as well as the other 36% of experts. Together these findings indicate that Bayesian networks maybe a promising approach for detecting wrong blood in tube errors. LabRespond did very poorly overall in detecting switching errors, performing near chance (see Table 1), but performed better when switches resulted in minimal size errors. This is likely due to the generally conservative decision boundaries for errors under LabResond relative to the Bayesian network (see for example Figure 2).

There are several limitations to the current study that need to be mentioned. First, the Bayesian network is incapable of reliably detecting wrong blood in tube errors when sample switching is done between patients with identical lab values. Of course such switches have no clinical impact as the same clinical decision would result from such a switch. However, for the purposes of quality control, such switching would go unnoticed under the Bayesian approach. Second, while the Bayesian network performed better at detecting wrong blood in tube errors than either most human experts or the benchmark statistical approach (LabRespond), it is unclear if such networks would outperform these other approaches if other types of error were the focus of study (e.g., instrumentation error). However, because the hallmark characteristic of most (if not all) other types of errors is a deviation of the analyte value from its true value, it is likely that a well-constructed Bayesian network would identify such errors. Third, while great care was taken in collecting the NHANES data set, however, some clinical data sets may not involve such rigorous and careful procedures for collecting data and thus may have more ‘noise’ which could diminish the sensitivity of the error detection approach we evaluated. Fourth, our switching procedure assumed random switching. It is plausible that switches could occur later in the day (when phlebotomists are fatigued). This would affect network performance if analyte values vary strongly by time-of-draw. We evaluated whether there were differences by examining how time-of-draw partitioned variance in analyte score and found only very small score differences, by time. Fifth, the findings of this study are limited to errors relating to analytes associated with the disease diabetes and may or may not generalize to networks developed on other analytic tests.

Bayesian networks have the advantage of being able to represent beliefs while faithfully adhering to the laws of probability. In doing so, they represent a rational form of decision-making that captures both our human understanding of the world, but with mathematical rigor. This computational approach to detecting errors is likely most suited to integration within an auto verification system.