Abstract
In time-series studies of ambient air pollution and health in large urban areas, measurement errors associated with instrument precision and spatial variability vary widely across pollutants. In this paper, we characterize these errors for selected air pollutants and estimate their impacts on epidemiologic results from an ongoing study of air pollution and emergency department visits in Atlanta. Error was modeled for daily measures of 12 air pollutants using collocated monitor data to characterize instrument precision and data from multiple study area monitors to estimate population-weighted spatial variance. Time-series simulations of instrument and spatial error were generated for each pollutant, added to a reference pollutant time-series, and used in a Poisson generalized linear model of air pollution and cardiovascular emergency department visits. Reductions in risk ratio due to instrument precision error were less than 6%. Error due to spatial variability resulted in average risk ratio reductions of less than 16% for secondary pollutants (O3, PM2.5 sulfate, nitrate and ammonium) and between 43% and 68% for primary pollutants (NOx, NO2, SO2, CO, PM2.5 elemental carbon); pollutants of mixed origin (PM10, PM2.5, PM2.5 organic carbon) had intermediate impacts. Quantifying impacts of measurement error on health effect estimates improves interpretation across ambient pollutants.
Introduction
Exposure measurement error is inherent to time-series studies of ambient air pollution and health in large populations and its assessment has been cited as a research priority [1-4]. Zeger et al. [5] describe three components of measurement error: (1) differences between individual exposures and average personal exposure, (2) differences between average personal exposure and ambient levels, and (3) differences between measured and true ambient concentrations. In this paper, we investigate this third component of measurement error, which can be divided into two subcategories [6]: (a) instrument error, which results from inaccuracy and imprecision in the ambient monitor observations, and (b) spatial error, which results from the inability of a single time-series to accurately represent the ambient levels throughout the study area.
Instrument error can be examined through analysis of measurements from collocated monitors. Discrepancy between independent measurements at the same location may be due to instrument calibration and drift as well as errors in sample preparation, collection, analysis, data acquisition, and data processing. Uncertainty estimates based on laboratory tests often underestimate error associated with actual use of the instrument when assessed from collocated instrument data [7-8].
A second source of error addressed here is that resulting from the use of a single measure (e.g., central monitor data or spatial average estimates using data from multiple monitors) to characterize ambient pollutant levels over a study area. Both micro- and macro-scale variations in ambient air pollution have been observed in metropolitan areas [9]. Spatial variation, if not independent of ambient concentration, can bias effect estimates in time-series health studies. Sheppard et al. [10] found that measurement error resulting from spatial variability led to an attenuation of acute health effect estimates of 7.7% for PM2.5 mass when exposure was estimated from a single monitor. Wilson et al. [11] observed associations between ambient PM2.5 and cardiovascular mortality to be lower in geographical subpopulations farther from a central monitoring site compared with populations close to the central site in a daily time-series study. While investigating three spatial models in a study of airborne particles and respiratory emergency hospital admissions, Chen et al. [12] found that effect estimates of PM10 were underestimated when a nonspatial approach was used. In a recent study of ambient air pollution and emergency department visits, effect estimates for spatially heterogeneous pollutants (CO and NO2) were dependent on which monitor was used, whereas observed associations for spatially homogeneous pollutants (O3 and PM2.5) were similar regardless of the monitoring site [13]. These results suggest that there may be greater attenuation of health risk estimates for spatially heterogeneous primary pollutants than for spatially homogeneous secondary pollutants, as one might expect.
In this paper, we address the need for a comprehensive examination of measurement error impacts on health risk estimates in a study of air pollution and emergency department (ED) visits for cardiovascular disease (CVD) in Atlanta. Our objectives were, first, to characterize and model measurement error using ambient air monitoring data, and, second, to assess the impact of measurement error by rerunning epidemiologic models using reference pollutant data with modeled error added. For selected ambient air pollutants in the metropolitan Atlanta region, we provide a detailed characterization of both instrument precision error and error due to spatial variability as these errors have been previously demonstrated to be the relevant sources of potential bias in regression coefficients in time-series studies [14]. This study is limited to variability in ambient air pollution as assessed from regulatory and regional study monitors at fixed locations throughout the area of interest; microscale variability, such as that associated with near-roadway concentrations, is not addressed; nor is temporal microscale variability addressed, such as that associated with meteorological events on subhour time scales. Microscale spatial and temporal variability in pollutant levels may be sources of error in etiologic investigations of acute health effects from air pollution, but this study examines the impact of error on health risk estimates for ambient levels of pollutants measured in accordance with regulatory specifications. Finally, this study addresses the effects of instrument imprecision and spatial variability, not the effects of instrument inaccuracy and spatial heterogeneity (e.g., urban-rural differences in primary air pollutant concentrations). The former result in day-to-day lack of correlation between air pollutant measurements at either the same location with different instruments or at different locations; the latter reflect systematic differences in pollutant concentration measurements between instruments or over space.
Methods
Our approach for characterizing measurement error and assessing its impact in a time-series health study involves five steps: (1) collection of ambient air pollutant data; (2) characterization of instrument precision by analyzing collocated instrument data; (3) characterization of spatial variability using geostatistical methods; (4) generation of simulations by adding modeled error to reference pollutant data; and (5) use of the simulations in epidemiologic models and comparison of results with those obtained using the reference time-series data. Methods used in each of these steps follow.
Ambient Air Pollutant Data
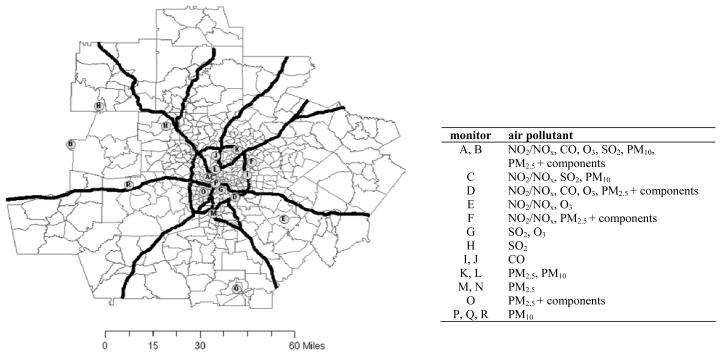
Twelve pollutants were assessed: NO2, NOx, O3, SO2, CO, PM10 mass, PM2.5 mass, and PM2.5 components sulfate (SO4), nitrate (NO3), ammonium (NH4), elemental carbon (EC), and organic carbon (OC). Metropolitan Atlanta area monitors are shown in Figure 1. Air pollution measurements from three sources were utilized: the US EPA's Air Quality System (AQS), including State and Local Air Monitoring System and Speciation Trends Network for PM2.5 component measurements; the Southeastern Aerosol Research and Characterization Study (SEARCH) network [15], including the Atlanta EPA supersite at Jefferson Street [16]; and the Assessment of Spatial Aerosol Composition in Atlanta (ASACA) network [17]. To assess measurement error due to instrument imprecision and spatial variability, 1999-2004 data sets were used, except where noted.
FIGURE 1.
Map of 20-county metropolitan Atlanta study area. Census tracts, interstate highways, and ambient air pollutant monitoring sites are shown.
For several pollutants, different measurement methods were used. SEARCH monitors (sites A and B) independently measure NO and NO2, whereas the AQS NOx measurement may include additional oxides of nitrogen. For SO2 measurement, less SO2 is lost by water condensation in the SEARCH sampling system than in the AQS measurement. For PM2.5 mass measurements, both Federal Reference Method (FRM) instruments, which provide 24-h average filter-based measurements, and Tapered Element Oscillating Microbalance (TEOM) instruments, which provide 1-h semicontinuous data, were used. The TEOM analyzers were operated to minimize loss of semivolatiles [18]. For PM2.5 components, data were obtained from particle composition monitors (PCM) providing 24-h filter samples, except for collocated data which were obtained using continuous methods. Ions (SO4, NO3, NH4) were detected by chromatographic analysis; for carbon data, SEARCH uses the thermal optical reflectance method for differentiating EC and OC, whereas AQS uses the thermal optical transmittance method. The EC-OC split differs between these methods [19]; however, the measures are highly correlated [20]. The differences between measurement methods are expected to have little impact on the assessment of instrument error in this study because error here is based on the correlation, not the bias, between measurements.
Instrument Precision
Collocated instrument data during 1999-2004 were available for NO2, NOx, and O3 at Yorkville (Figure 1, site B) from AQS and SEARCH monitors. For PM2.5 total mass and major components, collocated filter-based measurements and unadjusted continuous data [18] at the Jefferson Street SEARCH site (Figure 1, site A) were used over the six-year period 2002-2007. For SO2, CO, and PM10, collocated instrument data were not available.
Continuous PM2.5 ion measurements tend to underestimate concentrations[21-22], which has been attributed to excess water in the instrument and reductions in flash volatilization efficiency at high concentrations [21, 23]. For carbon fractions, the filter-based EC and OC measurements were compared with aethalometer measurement of black carbon and a semicontinuous total carbon measurement with the aethalometer black carbon subtracted, respectively. Compounded error in the continuous OC estimates is expected to result in conservatively high estimates of instrument error for this pollutant.
Spatial Variability
The semivariogram provides information on the spatial correlation of data and has been used previously for air pollutant data [24-25]. In this study, modified semivariograms were used to assess spatial variability error over the entire six-year study period. In the raw semivariogram, γ(h), defined here as one-half of the variance of the differences between observations (Cj and Ck) at two locations (j and k) located a distance h apart over all days, is plotted versus h. Here, the semivariance is normalized by the temporal variance of the average of two observations to yield a scaled semivariance, γ′.
| (1) |
Thus, γ′ represents the spatial semivariance scaled to a quantity indicative of the range of exposures over which health risk is being assessed; it is unitless and allows for comparison across pollutants. It can be shown that this scaled semivariance is related to the Pearson correlation coefficient (R) between observations at two sites as follows [25].
| (2) |
Thus, a scaled semivariance value of 0 corresponds to perfectly correlated observations (R = 1) and a value of 1 corresponds to perfectly uncorrelated observations (R = 0). The scaled semivariance as defined by eqs 1 and 2 is, therefore, a measure of spatial variability for the entire study period that can be compared across pollutants. Since the power to observe an association in a time-series health study depends on the temporal variability of pollutant concentrations, the impact of error due to spatial variability will depend on how large the spatial variance is relative to the temporal variance, evaluated for the entire study population over the entire study period.
Assuming the spatial variation of air pollutants to be isotropic, the scaled semivariance was modeled as a function of the distance between observations, h, as follows.
| (3) |
Here, , called the nugget, is the semivariance when monitors are collocated and, therefore, represents instrument precision error scaled by the temporal variance. Collocated monitor data were analyzed to determine the nugget semivariance and, thus, characterize instrument precision error. The sill, , is the asymptote of the semivariance, and the range, 3ae, is the distance at which 95% of the sill is reached. The exponential model above provided a reasonable fit to the data, as will be shown.
We used the theoretical semivariogram to compute an average scaled semivariance relative to the urban center for the entire study population for each pollutant. Data from the 2000 census for 660 tracts in the metropolitan Atlanta study area were used to develop the following relationship between population density, P(r), and distance from the urban center, r (Supporting Information, Figure S1).
| (4) |
Parameters A and B are regression coefficients. This relationship (eq 4) was used with the modeled semivariogram (eq 3) to calculate an integrated population-weighted semivariance, , for each pollutant.
| (5) |
Here, the radius of the Atlanta study area, R, is 80 km, B is 0.052 km−1, and the nugget , partial sill and range (3ae ) are determined for each pollutant (Supporting Information, Table S1). Since a nonzero nugget is included in the integration, the population-weighted semivariance includes instrument imprecision effects. We hypothesize that this integrated scaled semivariance can be used to predict the impact of error due to spatial variability on health risk estimation.
Simulations
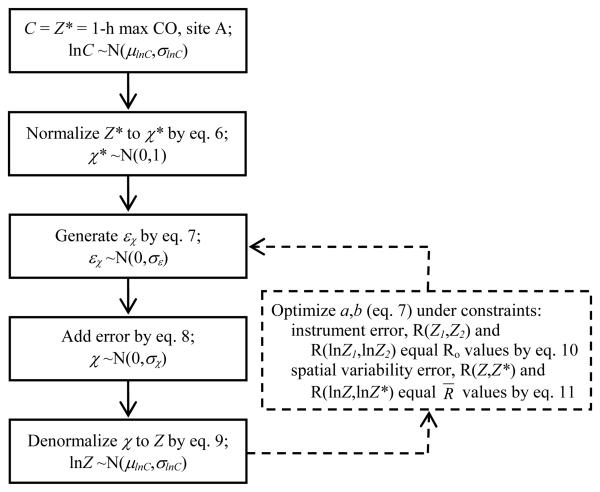
To develop simulated data sets with modeled instrument and spatial error added to measurements, the steps shown in Figure 2 were taken. First, a reference time-series was chosen so that impacts on health effect estimates of adding error for each pollutant could be compared to the same base case. Based on preliminary epidemiologic model results, we chose the 1-h maximum CO time-series at a central monitor (site A) as our base case because of its significant positive association with ED visits for CVD. Site A was chosen as the base case because it is a former EPA supersite and is heavily used in epidemiologic studies in Atlanta. Second, the log-normally distributed CO concentrations were normalized to avoid negative concentrations and preserve log-normality after error is added.
| (6) |
Here, is the normalized concentration on day i and μlnC and σlnC are the mean and standard deviation, respectively, of the log concentrations over all days; thus, the mean and standard deviation of are 0 and 1, respectively. Third, error in the normalized concentration was modeled as a function of concentration based on the observed dependence of error on pollutant concentration.
| (7) |
Here, εχi is the modeled error in for day i, Ni is a random number with distribution ~ N(0,1) and inclusive of short-term temporal autocorrelation, and a and b are constants obtained by optimization under the constraints described below. Fourth, the simulated error was introduced to normalized data (eq 8), and, fifth, to provide simulations of CO data with error added that have similar distributions to the original CO data, these were denormalized (eq 9).
| (8) |
| (9) |
Here, σχis the standard deviation of χi , which is slightly larger than 1 due to the error added to . Thus, the simulations with error added (Zi) have the same log mean and standard deviation as the central monitor CO data. These simulations represent alternative time-series derived from the same base case (i.e., the “true” time-series, Z*) with error added and with similar distributions as the base case.
FIGURE 2.
Time-series simulation flow chart. For each error type and each pollutant, the procedure was repeated 20 times to obtain average of a and b and then repeated without optimization (dashed lines) to generate 1000 simulated time-series.
For each pollutant, two semivariograms were constructed, one using log-concentration data and the other using concentration data directly. The corresponding two semivariogram nuggets and two population-weighted semivariances provide constraints for optimizing a and b for instrument imprecision and spatial variability, respectively. These constraints are calculated from the semivariogram nuggets and population-weighted semivariances by inverting eq 2, as shown in eq 10 and eq 11, respectively.
| (10) |
| (11) |
For instrument error, since the relationship between measurements is known but the relationship between measurement and truth is not, simulated time-series datasets are constrained to have inter-correlations, R(lnZ1,lnZ2) and R(Z1,Z2), that equal those from collocated instruments (Ro). It was found that these constraints yielded error of the same magnitude and concentration dependence as observed in the data (Supporting Information, Figure S2). For spatial error, defined here as the error that results from extrapolating central site exposures to locations removed from the central site, simulated time-series datasets are constrained to have correlations with the base case, R(lnZ,lnZ*) and R(Z,Z*), that equal the average of correlations of ambient pollution time-series datasets at residences of all people in the study area with a central ambient pollutant time-series (R̄). This optimization procedure was repeated 20 times to obtain average a and b values for use in 1000 Monte Carlo simulations.
Three measurement error models were developed for each of 12 pollutants in order to simulate three scenarios: (1) instrument error with semivariogram nuggets constrained and temporal autocorrelation of error included; (2) spatial error with population-weighted semivariances constrained and temporal autocorrelation of error included; (3) spatial error simulations with population-weighted semivariances constrained but without temporal autocorrelation of error included. Thus, 36 sets of 1000 simulated time-series for the six-year period 1999-2004 of central monitor (site A) CO data with error added were produced.
Epidemiologic Model
Relationships between daily measures of ambient air pollution and daily counts of ED visits for CVD (including ischemic heart disease, dysrhythmia, congestive heart failure, and peripheral/cerebrovascular disease) were assessed using methods described elsewhere [26] and briefly summarized here. There were 166,950 ED visits for CVD in the 20-county metropolitan Atlanta area during 1999-2004. Lag 0 associations between daily pollutant concentration and the daily count of ED visits were assessed using Poisson generalized linear models that accounted for overdispersion. The general form of the epidemiologic model is
| (12) |
where Yi is the count of emergency department visits on day i, Zi is the pollutant concentration on day i at a central monitor, and confoundersi is the vector of potential confounders on day i. The specific potential confounders included in the model were indicator variables for day-of-week, season, and when a hospital entered or left the study; cubic terms for maximum temperature and dew point; and a cubic spline with monthly knots for day of follow-up. The parameter α is the intercept, β is the log of the rate ratio for a change in pollutant concentration, and γ is the vector of regression coefficients for the suspected confounders included in the model. The risk ratio (RR) is given by eq 13.
| (13) |
Using data from the central monitor (site A), preliminary epidemiologic assessments were performed for all air pollutants and ED visits for CVD. Consistent with previous findings [26], significant positive associations were found for several traffic-related pollutants, including 1-h maximum NOx, 1-h maximum CO, and 24-h average EC. To compare the impacts of adding error across all pollutants, we selected 1-h maximum CO for our base case time-series. Monte Carlo simulations of instrument and spatial error added for each pollutant to the base case were used to test the impact of measurement error on epidemiologic analyses. With this approach, the actual central monitor CO observations are considered the “true” values (Z*), and the simulated data sets with error added are the “measured” values (Z). A total of 36,000 epidemiologic analyses were performed using simulated time-series.
Results and Discussion
Ambient Air Quality Data
Daily metrics for 12 ambient air pollutants were calculated: 1-h maximum NO2, NOx, SO2 and CO, 8-h maximum O3, and 24-h average PM10, PM2.5, and PM2.5 components NO3, SO4, NH4, EC, and OC. These measures were found to be best described by lognormal distributions. Lognormal distribution properties (geometric mean, μg, and standard deviation, σg) for all 12 pollutants measured at the central SEARCH monitor (site A) and at the rural SEARCH monitor (site B) are listed in Table 1. Data completeness for 1999-2004 (2192 days) ranged from 82% to 97% across the pollutants. Levels of primary pollutants (NO2, NOx, SO2, CO, and EC) are much higher at the urban monitor and much less spatially correlated (urban-rural R ranging from 0.10 to 0.43). For pollutants of largely secondary origin (O3, NO3, SO4, and NH4), the average levels are similar at urban and rural sites and the spatial correlation is much higher (urban-rural R ranging from 0.72 to 0.92). Pollutants of mixed origin (PM2.5, PM10, and OC) have an intermediate level of spatial heterogeneity and spatial correlation.
TABLE 1.
Lognormal distribution properties of urban (site A) and rural (site B) SEARCH monitors, 1999-2004, and collocated instrument and urban-rural spatial Pearson correlation coefficients.
| urban (site A) | rural (site B) | collocated | urban-rural | |||
|---|---|---|---|---|---|---|
| μ g | σ g | μ g | σ g | R | R | |
| 1-h max NO2 | 38.1 ppb | 1.51 | 7.74 ppb | 2.47 | 0.92 a | 0.10 |
| 1-h max NOx | 86.8 ppb | 2.23 | 8.39 ppb | 2.56 | 0.94 a | 0.21 |
| 8-h max O3 | 35.8 ppb | 1.92 | 45.2 ppb | 1.54 | 0.99 a | 0.89 |
| 1-h max SO2 | 11.4 ppb | 2.58 | 6.32 ppb | 2.40 | N/A | 0.10 |
| 1-h max CO | 0.89 ppm | 2.11 | 0.24 ppm | 1.39 | N/A | 0.18 |
| 24-h PM10 | 23.8 μg/m3 | 1.55 | 17.2 μg/m3 | 1.68 | N/A | 0.78 |
| 24-h PM2.5 | 15.2 μg/m3 | 1.62 | 11.5 μg/m3 | 1.73 | 0.97 b (0.991) c | 0.85 |
| 24-h PM2.5-SO4 | 3.85 μg/m3 | 1.95 | 3.71 μg/m3 | 2.07 | 0.96 b (0.998) d | 0.92 |
| 24-h PM2.5-NO3 | 0.74 μg/m3 | 2.13 | 0.63 μg/m3 | 2.20 | 0.94 b (0.993) d | 0.80 |
| 24-h PM2.5-NH4 | 2.02 μg/m3 | 1.79 | 1.97 μg/m3 | 1.95 | 0.91 b (0.994) d | 0.72 |
| 24-h PM2.5-EC | 1.28 μg/m3 | 1.87 | 0.57 μg/m3 | 1.81 | 0.92 b (0.903) d | 0.43 |
| 24-h PM2.5-OC | 3.79 μg/m3 | 1.65 | 2.70 μg/m3 | 1.71 | 0.85 b (0.979) d | 0.59 |
Yorkville (site B), SEARCH and AQS monitors, 1999-2004.
Jefferson St (site A), filter-based and continuous monitors, 2002-2007.
Yorkville (site B), two filter-based FRM instruments, 2002-2008.
Centreville, Alabama, two filter-based instruments, 2001-2008.
Instrument Precision Error
The collocated instrument correlations in Table 1 are indicative of the amount of instrument error for each pollutant. For PM2.5 total mass and major constituents, the correlations between filter-based measurements and measurements using continuous methods are lower than correlations between collocated data from a Centreville, Alabama site using identical filter-based instruments (shown in parentheses). Thus, our instrument error estimations are conservative in that they include some variability due to different instruments or analytical methods. The collocated OC observations were least correlated, likely due to compounded error in the continuous OC measurement involving taking the difference between total carbon and black carbon observations.
Collocated instrument time-series were used to calculate nugget semivariance values on a concentration basis and a log-concentration basis, which characterize instrument precision in the error simulation model. In the case of CO, SO2, and PM10 for which we did not have collocated instrument data, a value fitted by the semivariogram was used. All nugget semivariance values are listed in Supplemental Information, Table S1.
In general, instrument error was observed to increase with increasing concentration; this concentration dependence was modeled via eq 7. Short-term temporal autocorrelation of error was also observed, with correlation coefficients averaged across all pollutants of 0.59 ± 0.13 (standard deviation) and 0.33 ± 0.17 for one-day and two-day lags, respectively; this was modeled by using a three-day running average of random numbers for Ni (eq 7). The desired level of error autocorrelation was verified in all models, as was the concentration dependence of the magnitude of error. The most extreme outliers in the observed error were not captured, however (Supporting Information, Figure S2).
Spatial Variability Error
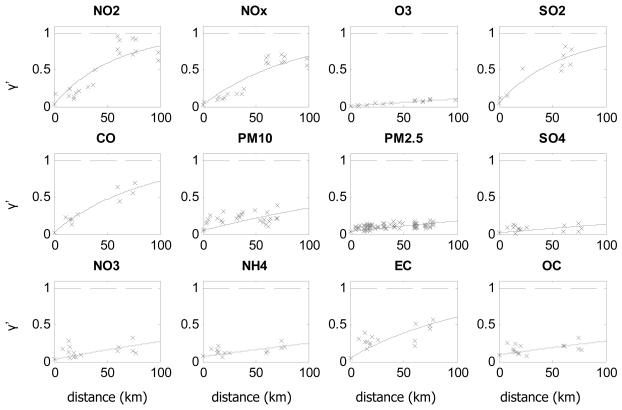
Correlations between observations from all pairs of monitors measuring the same pollutant during 1999-2004 were calculated on a concentration basis and log concentration basis. As shown in Figure 1, there were six NO2 and NOx monitoring sites, five sites each for SO2, CO, and O3 (with three O3 sites providing only March-November data), eight PM10 sites (with five providing data only every 6 days), nine PM2.5 mass sites (with four providing data only every 3 days), and five sites with PM2.5 composition monitors. Scaled semivariograms were constructed for both concentrations and log concentrations, using eq 2, and plotted as a function of distance between monitors. In Figure 3, log concentration semivariograms are shown for all pollutants. Exponential theoretical semivariograms were fit to the data (eq 3) by using least-squares regression to determine the range, assuming a sill of 1 and using a nugget derived from the instrument precision analysis.
FIGURE 3.
Semivariograms for the log normalized pollutant concentrations. Exponential curves are fitted to the data. Similar semivariograms were constructed for normalized pollutant concentrations.
Secondary pollutants (O3, NO3, SO4, and NH4) have large range values (from 1100 km to 3000 km), indicating their greater spatial autocorrelation. Primary pollutants (NO2, NOx, SO2, CO, and EC), conversely, have lower range values (from 100 to 330 km), demonstrating greater spatial variability of these pollutants. Scatter in the raw semivariogram suggests a degree of anisotropic behavior (i.e., directional dependence) in the data in addition to observational error.
Population-weighted semivariances were derived from both the concentration and log concentration semivariograms (Supporting Information, Table S1). While nuggets were all small (<0.1), indicative of low levels of instrument error, population-weighted semivariograms suggest much larger error due to spatial variability. As mentioned previously, secondary pollutants exhibit much less spatial variability than primary pollutants. Ozone exhibits the least spatial variability, and SO2 the most. Moreover, SO2 spatial variability is likely underestimated due to an insufficient number of monitors for this pollutant whose emissions are dominated by a few point sources.
Simulations with Modeled Error Added
Optimization yielded values of parameters a and b that were very similar across the 20 trials (Supporting Information, Table S2) for each error type and each pollutant, indicative of a relatively stable solution to the error model optimization routine. After optimization of model parameters a and b, 1000 simulations were generated for each pollutant by adding instrument precision error and error due to spatial variability, both with and without temporal autocorrelation, to the reference time-series via the procedure outlined in Figure 2. Average correlation coefficients between simulations agreed with expected values, with wider ranges of results from spatial error models of primary pollutants (Supporting Information, Figure S3). The range of simulation results is consistent with the observed variability in yearly intermonitor covariance.
Error Impact on Health Risk Assessment
For the base case of 1-h maximum CO exposures (Z*) and CVD outcomes, a risk ratio of 1.0139 was observed, with p-value of 0.000009. Differences between this result and results from the regression of the same health outcome data against the simulations with error added instead of the CO data reflect the impact of error. Results of 1000 epidemiologic models for 12 air pollutants and three error scenarios are summarized in Table 2. The degree to which the risk ratio observed using the simulations is decreased toward one (the null hypothesis) from the risk ratio observed using the base case data can be expressed as a percent bias-to-null in the risk ratio.
| (14) |
Here, β* is the effect estimator when CO central monitor data (Z*) were used in the epidemiologic model, and β is the effect estimator when simulations with error added (Z) were used.
TABLE 2.
Average risk ratios and median p-values for 1000 trials with error added to base case.a
| instrument error | spatial error |
spatial error (no autocorrelation) |
||||
|---|---|---|---|---|---|---|
| RR per ppm |
p-value | RR per ppm | p-value | RR per ppm |
p-value | |
| 1-h max NO2 | 1.0133 | 0.000021 | 1.0046 (1.0026 - 1.0065) |
0.1038 (0.0236 - 0.362) |
1.0044 | 0.1196 |
| 1-h max NOx | 1.0132 | 0.000018 | 1.0079 (1.0057 - 1.0100) |
0.0263 (0.0053 - 0.119) |
1.0074 | 0.0321 |
| 8-h max O3 | 1.0139 | 0.000010 | 1.0128 (1.0118 - 1.0139) |
0.000050 (0.000011 - 0.00018) |
1.0126 | 0.000059 |
| 1-h max SO2 | 1.0132 | 0.000026 | 1.0045 (1.0023 - 1.0065) |
0.1411 (0.0355 - 0.425) |
1.0042 | 0.1695 |
| 1-h max CO | 1.0131 | 0.000020 | 1.0059 (1.0039 - 1.0077) |
0.0392 (0.0073 - 0.172) |
1.0049 | 0.0465 |
| 24-h PM10 | 1.0131 | 0.000027 | 1.0103 (1.0085 - 1.012) |
0.0017 (0.00025 - 0.0089) |
1.0099 | 0.0021 |
| 24-h PM2.5 | 1.0138 | 0.000016 | 1.0126 (1.0113 - 1.0139) |
0.00015 (0.000027 - 0.00070) |
1.0123 | 0.00019 |
| 24-h PM2.5-SO4 | 1.0134 | 0.000015 | 1.0121 (1.0109 - 1.0133) |
0.00011 (0.000019 - 0.00047) |
1.0118 | 0.00012 |
| 24-h PM2.5-NO3 | 1.0143 | 0.000011 | 1.0145 (1.0128 - 1.016) |
0.00015 (0.000032 - 0.00081) |
1.0141 | 0.00020 |
| 24-h PM2.5-NH4 | 1.0141 | 0.000020 | 1.0117 (1.0101 - 1.0134) |
0.00057 (0.000091 - 0.0032) |
1.0113 | 0.00076 |
| 24-h PM2.5-EC | 1.0134 | 0.000022 | 1.0079 (1.0050 - 1.0107) |
0.0440 (0.0071 - 0.192) |
1.0078 | 0.0420 |
| 24-h PM2.5-OC | 1.0132 | 0.000045 | 1.0101 (1.0084 - 1.0118) |
0.0017 (0.00024 - 0.0092) |
1.0097 | 0.0021 |
Base case results: RR = 1.0139, p-value = 0.000009. For spatial error, interquartile ranges are shown in parentheses.
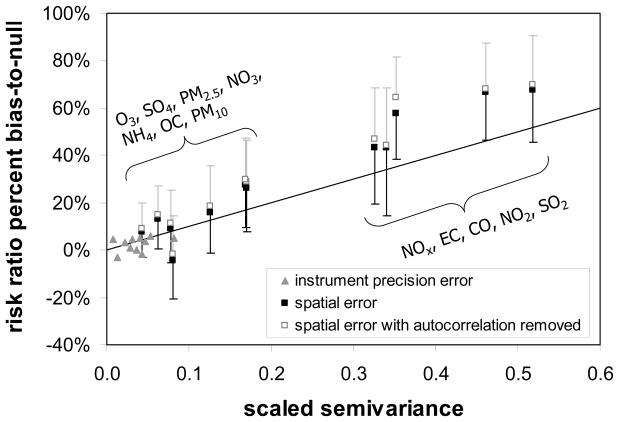
The addition of instrument precision error to monitor data was found to have little impact on risk ratio and significance estimates. Average risk ratios ranged from 1.0131 to 1.0143 (compared to 1.0139), and median p-values ranged from 0.000010 to 0.000045 (compared to 0.000009). In comparison, the impact of error due to spatial variability was much larger. Loss of significance of association at the 95% level was observed for SO2 and NO2. For primary pollutants, risk ratios on average ranged from 1.0045 for SO2 to 1.0079 for NOx, corresponding to average bias-to-null estimates of 68 to 43%, respectively. For pollutants largely of secondary origin, the results exhibited less bias-to-null, with risk ratios on average ranging from 1.0117 for NH4 to 1.0145 for NO3; these correspond to average bias-to-null estimates of less than 16%. For pollutants of mixed origin, intermediate levels of bias-to-null were observed. The presence of temporal autocorrelation in spatial error slightly decreased the bias-to-null and increased significance, likely due to the fact that the air pollution data themselves have temporal autocorrelation.
In Figure 4, average values of the bias-to-null from all models are shown as a function of the integrated scaled semivariance, which is a measure of the magnitude of error added. These results support our hypothesis that the impact of error due to spatial variability depends on how large the spatial variance is relative to the temporal variance, evaluated for the entire study population over the entire study period.
FIGURE 4.
Percent reduction in risk ratio due to instrument precision error and spatial variability error versus semivariogram nugget (γo) and integrated population-weighted semivariance (), respectively, on concentration basis with one-sided error bars indicating the standard deviation of the 1000 simulations. Spatial variability error points are labeled in order of increasing . For reference, a one-to-one line is shown.
This investigation was limited to error associated with the lack of correlation between exposure measurements. Results are limited to single pollutant analyses. Our results can be used directly to reinterpret results from single pollutant models across multiple pollutants, with health effect estimator attenuation varying across pollutants. Our modeling framework could be extended for use in multipollutant models as well by including joint variance effects in the semivariogram analysis.
In this paper, we have shown the relative impacts of measurement error on health risk assessment using simulated time-series of ambient levels. The amount of error was derived from observations; however, bias in the health response estimate is dependent on both the amount and type of measurement error. In terms of the latter, two extremes in the conceptual framework for error type have been proposed: classical error and Berkson error [5, 10]. The type of error simulated in this work is neither classical nor Berkson (Supporting Information, Figures S4 and S5). In ongoing work, we are exploring the impact of varying error type, while keeping the amount of error constant, on health effect estimation by relaxing the assumption that the simulations with error added have the same distribution as the true values.
Brief.
Ambient air pollutant measurement error due to instrument imprecision and spatial variability is characterized and its impacts on health risk estimates are assessed.
Supplementary Material
Acknowledgements
The authors acknowledge financial support from the following grants: NIEHS R01ES012967, EPA STAR R89291301, EPRI EP-P277231/C13172, NIEHS R01ES11199, EPA STAR R83362601, and EPA STAR R83386601.
Footnotes
Additional figures and tables detailing the measurement error model can be found in Supporting Information.
Literature Cited
- 1.Integrated Science Assessment for Particulate Matter (Final Report) US Environmental Protection Agency; Washington, DC: 2009. [PubMed] [Google Scholar]
- 2.Brauer M, Hoek G, van Vliet P, Meliefste K, Fischer P, et al. Estimating long-term average particulate air pollution concentrations: Application of traffic indicators and geographic information systems. Epidemiology. 2003;14(2):228–239. doi: 10.1097/01.EDE.0000041910.49046.9B. [DOI] [PubMed] [Google Scholar]
- 3.Brunekreef B, Holgate ST. Air pollution and health. Lancet. 2002;360(9341):1233–1242. doi: 10.1016/S0140-6736(02)11274-8. [DOI] [PubMed] [Google Scholar]
- 4.Jerrett M, Arain A, Kanaroglou P, Beckerman B, Potoglou D, et al. A review and evaluation of intraurban air pollution exposure models. J. Exp. Anal. Environ.Epidemiol. 2005;15(2):185–204. doi: 10.1038/sj.jea.7500388. [DOI] [PubMed] [Google Scholar]
- 5.Zeger SL, Thomas D, Dominici F, Samet JM, Schwartz J, et al. Exposure measurement error in time-series studies of air pollution: concepts and consequences. Environ. Health Perspect. 2000;108(5):419–426. doi: 10.1289/ehp.00108419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Research priorities for airborne particulate matter. National Academy Press; 1998. [Google Scholar]
- 7.Hyslop NP, White WH. An evaluation of interagency monitoring of protected visual environments (IMPROVE) collocated precision and uncertainty estimates. Atmos. Environ. 2008;42(11):2691–2705. [Google Scholar]
- 8.White WH, Ashbaugh LL, Hyslop NP, McDade CE. Estimating measurement uncertainty in an ambient sulfate trend. Atmos. Environ. 2005;39(36):6857–6867. [Google Scholar]
- 9.Hewitt CN. Spatial Variations in Nitrogen-Dioxide Concentrations in an Urban Area. Atmos. Environ. B Urban Atmos. 1991;25(3):429–434. [Google Scholar]
- 10.Sheppard L, Slaughter JC, Schildcrout J, Liu LJS, Lumley T. Exposure and measurement contributions to estimates of acute air pollution effects. Exp. Anal. Environ. Epidemiol. 2005;15(4):366–376. doi: 10.1038/sj.jea.7500413. [DOI] [PubMed] [Google Scholar]
- 11.Wilson WE, Mar TF, Koenig JQ. Influence of exposure error and effect modification by socioeconomic status on the association of acute cardiovascular mortality with particulate matter in Phoenix. J. Exp. Sci. Environ. Epidemiol. 2007;17(Suppl 2):S11–S19. doi: 10.1038/sj.jes.7500620. [DOI] [PubMed] [Google Scholar]
- 12.Chen LP, Mengersen K, Tong SL. Spatiotemporal relationship between particle air pollution and respiratory emergency hospital admissions in Brisbane, Australia. Sci. Total Environ. 2007;373(1):57–67. doi: 10.1016/j.scitotenv.2006.10.050. [DOI] [PubMed] [Google Scholar]
- 13.Sarnat SE, Klein M, Sarnat JA, Flanders WD, Waller LA, et al. An examination of exposure measurement error from air pollutant spatial variability in time-series studies. J. Exp. Sci. Environ. Epidemiol. 2010;20(2):135–146. doi: 10.1038/jes.2009.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Carrothers TJ, Evans JS. Assessing the impact of differential measurement error on estimates of fine particle mortality. J. Air & Waste Manage. Assoc. 2000;50(1):65–74. doi: 10.1080/10473289.2000.10463988. [DOI] [PubMed] [Google Scholar]
- 15.Hansen DA, Edgerton ES, Hartsell BE, Jansen JJ, Kandasamy N, et al. The southeastern aerosol research and characterization study: Part 1-overview. J. Air & Waste Manage. Assoc. 2003;53(12):1460–1471. doi: 10.1080/10473289.2003.10466318. [DOI] [PubMed] [Google Scholar]
- 16.Solomon PA, Chameides W, Weber R, Middlebrook A, Kiang CS, et al. Overview of the 1999 Atlanta Supersite Project. J. Geophys. Res. Atmos. 2003;108(D7) [Google Scholar]
- 17.Butler AJ, Andrew MS, Russell AG. Daily sampling of PM2.5 in Atlanta: results of the first year of the assessment of spatial aerosol composition in Atlanta study. J.Geophys. Res. Atmos. 2003;108(D1) [Google Scholar]
- 18.Edgerton ES, Hartsell BE, Saylor RD, Jansen JJ, Hansen DA, Hidy GM. The Southeastern Aerosol Research and Characterization Study, part 3: Continuous measurements of fine particulate matter mass and composition. J. Air & Waste Manage. Assoc. 2006;56(9):1325–1341. doi: 10.1080/10473289.2006.10464585. [DOI] [PubMed] [Google Scholar]
- 19.Chow JC, Watson JG, Crow D, Lowenthal DH, Merrifield T. Comparison of IMPROVE and NIOSH carbon measurements. Aerosol Sci. Technol. 2001;34(1):23–34. [Google Scholar]
- 20.Solomon P, Baumann K, Edgerton E, Tanner R, Eatough D, et al. Comparison of integrated samplers for mass and composition during the 1999 Atlanta Supersites project. J. Geophys. Res. Atmos. 2003;108(D7) [Google Scholar]
- 21.Chow JC, Watson JG, Lowenthal DH, Park K, Doraiswamy P, et al. Continuous and filter-based measurements of PM2.5 nitrate and sulfate at the Fresno Supersite. Environ. Monitoring Assess. 2008;144(1-3):179–189. doi: 10.1007/s10661-007-9987-5. [DOI] [PubMed] [Google Scholar]
- 22.Hogrefe O, Schwab JJ, Drewnick F, Lala GG, Peters S, et al. Semicontinuous PM2.5 sulfate and nitrate measurements at an urban and a rural location in New York: PMTACS-NY summer 2001 and 2002 campaigns. J. Air & Waste Manage. Assoc. 2004;54(9):1040–1060. doi: 10.1080/10473289.2004.10470972. [DOI] [PubMed] [Google Scholar]
- 23.Long RW, McClenny WA. Laboratory and field evaluation of instrumentation for the semicontinuous determination of particulate nitrate (and other water-soluble particulate components) J. Air & Waste Manage. Assoc. 2006;56(3):294–305. doi: 10.1080/10473289.2006.10464462. [DOI] [PubMed] [Google Scholar]
- 24.Casado LS, Rouhani S, Cardelino CA, Ferrier AJ. Geostatistical Analysis and Visualization of Hourly Ozone Data. Atmos. Environ. 1994;28(12):2105–2118. [Google Scholar]
- 25.Wade KS, Mulholland JA, Marmur A, Russell AG, Hartsell B, et al. Effects of instrument precision and spatial variability on the assessment of the temporal variation of ambient air pollution in Atlanta, Georgia. J. Air & Waste Manage. Assoc. 2006;56(6):876–888. doi: 10.1080/10473289.2006.10464499. [DOI] [PubMed] [Google Scholar]
- 26.Metzger KB, Tolbert PE, Klein M, Peel JL, Flanders WD, et al. Ambient air pollution and cardiovascular emergency department visits. Epidemiology. 2004;15(1):46–56. doi: 10.1097/01.EDE.0000101748.28283.97. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.