The sensitivity of memory consolidation and reconsolidation to inhibitors of protein synthesis and kinases: Computational analysis

Abstract

Memory consolidation and reconsolidation require kinase activation and protein synthesis. Blocking either process during or shortly after training or recall disrupts memory stabilization, which suggests the existence of a critical time window during which these processes are necessary. Using a computational model of kinase synthesis and activation, we investigated the ways in which the dynamics of molecular positive-feedback loops may contribute to the time window for memory stabilization and memory maintenance. In the models, training triggered a transition in the amount of kinase between two stable states, which represented consolidation. Simulating protein synthesis inhibition (PSI) from before to 40 min after training blocked or delayed consolidation. Beyond 40 min, substantial (>95%) PSI had little effect despite the fact that the elevated amount of kinase was maintained by increased protein synthesis. However, PSI made established memories labile to perturbations. Simulations of kinase inhibition produced similar results. In addition, similar properties were found in several other models that also included positive-feedback loops. Even though our models are based on simplifications of the actual mechanisms of molecular consolidation, they illustrate the practical difficulty of empirically measuring “time windows” for consolidation. This is particularly true when consolidation and reconsolidation of memory depends, in part, on the dynamics of molecular positive-feedback loops.

Activation of kinases and altered protein synthesis is essential for consolidation of new memories and reconsolidation of established memories (for reviews, see Abel and Lattal 2001; Kandel 2001; Alberini 2005, 2008; Alberini et al. 2006; Moore and Roche 2007; Abraham and Williams 2008; Hernandez and Abel 2008; Klann and Sweatt 2008; Miyashita et al. 2008). Moreover, it appears that memory formation depends on a temporally limited phase of protein synthesis (a critical time window), which exists from before to shortly after training. During this window, protein synthesis inhibition (PSI), which blocks ≥95% of protein synthesis (Barondes and Cohen 1968), disrupts consolidation (for an early review, see Davis and Squire 1984). Similar windows exist for long-term synaptic plasticity. For example, in sensorimotor neuron co-cultures from the mollusk Aplysia, the window during which PSI blocks consolidation of serotonin (5-HT)-induced long-term synaptic facilitation (LTF) a correlate of long-term memory (LTM), ends ∼30 min after application of 5-HT (Montarolo et al. 1986). Similarly, consolidation of late long-term potentiation (L-LTP) occurs with an analogous time window (Krug et al. 1984; Stanton and Sarvey 1984; Otani et al. 1989; Fonseca et al. 2006; Frey and Frey 2008), and for the consolidation of both LTF and L-LTP, a temporally limited phase of kinase activation is also required, constituting a second time window of similar duration (English and Sweatt 1997; Sharma et al. 2003). These results imply that within a few hours of training, LTM transits from being dependent on kinase activation and protein synthesis to being relatively independent of these processes. Recent studies also imply that when an established memory is reactivated, a critical time window exists during which the memory is labile (for reviews, see Alberini 2005; Nader and Hardt 2009; Wang and Morris 2010). PSI immediately after reactivation disrupts memory, but PSI 2, 4, or 6 h after reactivation does not (Nader et al. 2000; Rose and Rankin 2006; Artinian et al. 2008). These results suggest that the molecular mechanisms for consolidation and reconsolidation may have some common features.

A ubiquitous molecular motif that may contribute to learning and memory is a positive-feedback loop of enzymatic reactions (Bhalla and Iyengar 1999; Pettigrew et al. 2005; Song et al. 2006, 2007; Cheng et al. 2008; Klann and Sweatt 2008; Pi and Lisman 2008; Smolen et al. 2008; Tanaka and Augustine 2008; Aslam et al. 2009; Ogasawara and Kawato 2009; Burrill and Silver 2010). Such feedback loops can be bistable and a brief, transient stimulus can trigger changes in protein levels, kinase activities, or levels of protein phosphorylation that far outlast the initial triggering stimulus (e.g., Ferrell 2002; Xiong and Ferrell 2003; Kobayashi et al. 2004; Kramer et al. 2004; Ajo-Franklin et al. 2007; Greber and Fussenegger 2007; Chatterjee et al. 2008; Mitrophanov and Groisman 2008; Pomerening 2008; Tanaka and Augustine 2008). Empirical data suggest that many molecular processes implicated in learning and memory may be regulated by positive-feedback loops. For example, calcium/calmodulin kinase II (CaMKII) and protein kinase M (PKM) may, when active, increase their own synthesis and such positive feedback may contribute to LTP (Atkins et al. 2005; Pastalkova et al. 2006). Bistability in a CaMKII signaling pathway may also play a role in spike-timing dependent plasticity (STDP) (Graupner and Brunel 2007), and positive feedback between protein kinase C (PKC) and mitogen-activated protein kinase (MAP kinase) may play a role in cerebellar long-term depression (Tanaka and Augustine 2008). In Aplysia, the promoter region of the creb1 gene has binding sites for its own gene product, the transcription activator CREB1 (Mohamed et al. 2005). A positive-feedback loop is thus formed, which is important for the consolidation of LTF (Liu et al. 2008). Thus, understanding the dynamical properties of molecular positive-feedback loops may provide insights into memory processes, such as the temporal properties of consolidation and reconsolidation.

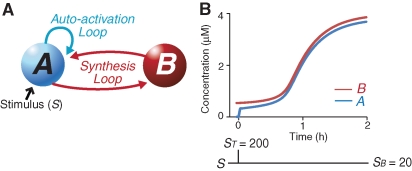
To study the dynamical properties of positive-feedback loops, Smolen et al. (2009) proposed a biologically inspired computational model describing biochemical processes that may be involved in LTM. This model consists of two positive-feedback loops (Fig. 1A). The first loop represents autoactivation of a kinase. In the second, slower loop, active kinase feeds back to induce further kinase synthesis. This model has both lower and upper stable steady states in the amount of kinase, and thus is bistable. The model develops a resistance to perturbations ∼1 h after switching the activated kinase, A, to its upper state. This resistance relies on the slow positive-feedback loop of protein synthesis.

Figure 1.

Two-loop model. (A) Schematic of feedback loops. A denotes activated kinase. B denotes total kinase. The blue loop represents fast positive feedback in which A directly or indirectly activates itself. The red loop represents slow positive feedback in which A directly or indirectly enhances the synthesis of B. (B) In the two-loop model, S_T was increased from 0 to 200 for 10 sec at t = 0. In the absence of PSI, this “training” stimulus induced a transition of A and B to an upper stable state. The transition required ∼2 h to complete.

In the present study, we used a modified version of the Smolen et al. (2009) model to examine how positive-feedback loops with kinase autoactivation and protein synthesis may contribute to the temporal sensitivity of memory consolidation to PSI and kinase inhibition (Fig. 1A). We heuristically equated an increase to a stable upper state of kinase activity, A, and total amount of kinase, B, with consolidation of a new memory. This two-loop model was used to examine whether positive-feedback loops were responsible for the empirically obtained time windows for sensitivity of memory consolidation and reconsolidation to PSI with physiological “dosages” (e.g., 95% ∼ 98% PSI) (Squire and Davis 1975; Milekic and Alberini 2002). We also examined whether the two-loop model reproduced a time window for sensitivity of memory consolidation to kinase inhibition. To examine whether these time windows require both fast and slow feedback loops, we eliminated kinase autoactivation to generate a one-loop model that had only slow feedback. We used this one-loop model to investigate whether a single feedback loop involving protein synthesis suffices to generate resistance of memory consolidation to PSI (≥95%).

Results

To simulate training, the value of the training stimulus, S_T, was increased from 0 to 200 for 10 sec to switch A from the lower stable state (0.03 µM) (Fig. 1B) to the upper state (≥0.3 µM). In the two-loop model (Equation 1a,b), A switched to the upper stable state rapidly (Fig. 1B) due to the fast positive-feedback loop (Fig. 1A). To obtain a bistable switch that responds to brief stimuli, it is essential that the fast feedback loop (Equation 1a) exhibits bistability. Hill functions with a coefficient (power) ≥3 are commonly used in mathematical models to produce bistable responses to brief stimuli (Burrill and Silver 2010). The Hill functions on the right-hand sides of Equation 1a,b used a coefficient of 4. After A switched, B increased due to the slow positive-feedback loop (Fig. 1B). Increased B leads, via mass action, to a further increase in A. A and B reached upper stable values close to the upper bound for B, B_MAX (Equation 1b), ∼2 h after training (A = 3.8 µM, B = 4 µM) (Fig. 1B).

Bifurcation analyses reveal dynamical properties of the positive-feedback loops that underlie the stability of A and B

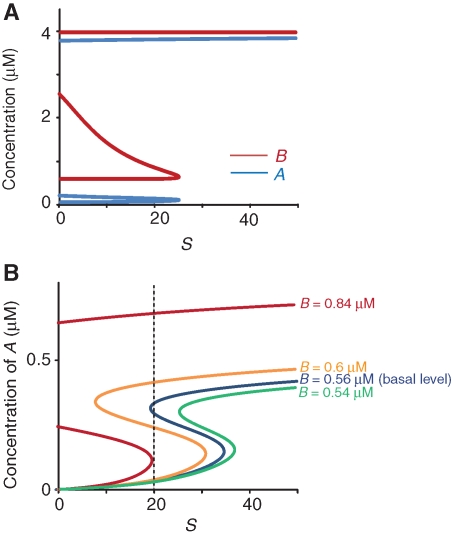
Bifurcation analyses were performed to define the time window governing the sensitivity of A and B to perturbations. In the first analysis, both A and B were treated as variables (Fig. 2A). A and B have both upper and lower stable steady states for S ranging from 0 to ∼25 (Fig. 2A). This analysis demonstrates that the full model, variables A and B, are bistable for a range of stimulus values that includes the basal value S_B=20.

Figure 2.

Bifurcation diagrams for A as a function of stimulus S in the two-loop model when B is treated as a variable (A) or B is treated as a fixed parameter (B). (A) Both A and B are bistable at S = 20. (B) A has both upper and lower stable steady states when S = 20 and B = 0.56 µM. A only has an upper steady state when B ≥ 0.84 µM and S = 20. A only has a lower steady state when B ≤ 0.54 µM and S = 20. A “consolidated state” was defined as one in which A remains ≥0.3 µM and B remains ≥0.84 µM.

In the second bifurcation analysis, the slow variable B was treated as a parameter in determining the steady states of the fast variable A as a function of stimulus S. A has both upper and lower stable steady states when S = 20 and B = 0.56 µM (i.e., basal level) or B = 0.60 µM (blue and orange traces, respectively, in Fig. 2B). A brief stimulation will switch A from the lower to the upper steady state. Due to the hysteretic effect, A will remain at its upper steady state after S returns to 20. B increases due to the slow positive feedback, and A in turn increases due to mass action. Thus, the bifurcation curve of A shifts to the left (i.e., from blue to orange traces in Fig. 2B). A loses its lower steady state when B increases past 0.84 µM (for S = 20) (red trace in Fig. 2B). Without a lower state, a brief perturbation will only transiently decrease A. After the perturbation, A will return to its upper state. Therefore, the increase of B makes A progressively resistant to brief perturbations. In contrast, when B decreases to 0.54 µM (Fig. 2B, green trace), the bifurcation curve of A shifts to the right and A loses its upper steady state. Therefore, a decrease in B makes A progressively resistant to brief stimuli that would otherwise switch A to its upper steady state.

As a heuristic, we considered consolidation of LTM to be initiated by the switch of A from 0.03 to 0.3 µM. These represented the two steady states of A at S = 20 for the value of B at its basal level (blue trace in Fig. 2B). The level of the upper steady state of A at S = 20 substantially increased with B. For example, the upper state of A increased from 0.3 to 0.41 µM when B increased from its basal level of 0.56 to 0.6 µM (from blue to orange traces in Fig. 2B). The lower steady state of A at S = 20, on the contrary, remained ∼0.03 µM until B reached 0.84 µM (Fig. 2B).

Based on the above bifurcation analysis, we considered consolidation to occur when A has only an upper steady state when S is at its basal value (S_B = 20). Following a stimulus that increases B, A has only an upper state when B increases past 0.84 µM, at which time we consider consolidation to be complete. In the absence of any inhibitors, B increased past 0.84 µM ∼40 min after training (Fig. 1B). Therefore, we considered consolidation was “delayed” if A switched to its upper state but B increased past 0.84 µM later than 40 min after training. We considered consolidation was “blocked” if B remained <0.84 µM for more than seven simulated days or if A was reverted to the lower state (e.g., by a strong kinase inhibitor) even if B ≥ 0.84 µM.

The sensitivity of memory consolidation to PSI has a time window

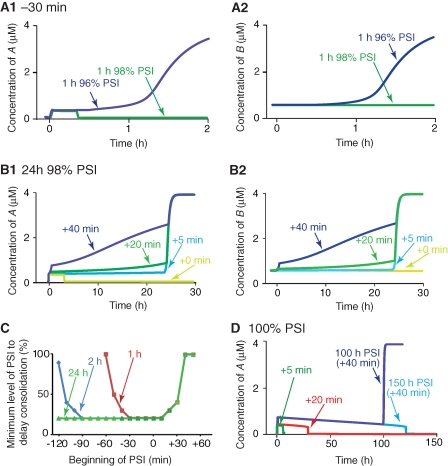
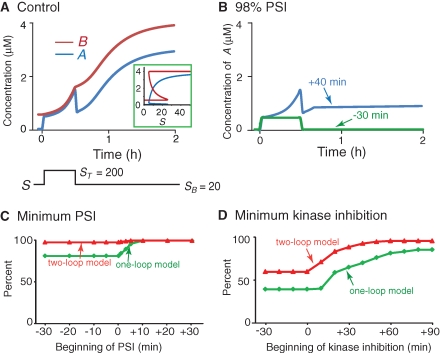
Although in vitro, protein synthesis inhibitors can be as effective as ∼99% (Grollman 1967), the best estimates from in vivo behavioral studies are 96%–98% effective block (Squire and Davis 1975). For example, subcutaneously administering 30 mg/kg anisomycin to mice was estimated to produce 96% PSI (Squire and Davis 1975). Administering this dose of anisomycin 30 min before discrimination training produced a significant deficit in LTM assessed 24 h later. In addition, a substantially greater deficit was seen with mice given 210 mg/kg anisomycin (estimated to produce 98% PSI) 30 min before training (Squire and Davis 1975). To simulate PSI, we increased ANI in Equation 1b. Similar to empirical studies, the effect of ANI on protein synthesis rate was first tested before training, when A and B were in the lower state (i.e., A = 0.03 µM and B = 0.56 µM). When ANI = 0.96, the synthesis rate of B reduced to 4% of control. When 1 h 96% PSI began 30 min prior to training (Fig. 3A1,A2, blue traces), consolidation was initiated by the increase of A from 0.03 to 0.3 µM, but B did not increase to 0.84 µM until ∼1 h after training (i.e., consolidation was delayed) (Fig. 3A2). However, the consolidation was blocked when 1 h 98% PSI began 30 min before training. In this case, A returned to the lower state after a transient increase and B never increased (Fig. 3A1,A2, green traces). The return of A to the lower state occurred because 98% PSI, but not 96%, sufficed to decrease B to 0.54 µM, thus A lost the upper state. Similarly, 24 h 96% PSI (started 30 min before stimulus) only delayed consolidation whereas 24 h 98% PSI blocked consolidation (not shown).

Figure 3.

State transitions in the presence of PSI. (A) One hour PSI either 96% or 98% was imposed 30 min before (−30 min) the 10-sec stimulus. The 1-h treatment with 96% PSI delayed the increase of A (A1) and B (A2) (blue traces). B increased past 0.84 µM later than 40 min after training. In contrast, the 1-h treatment with 98% PSI blocked the increase of A (A1) and B (A2) (green traces). (B) The increase of A (B1) and B (B2) was blocked when 24 h, 98% PSI started immediately after training (+0 min, yellow traces). In contrast, 24 h 98% PSI only delayed the increase when the treatment began +5 min (light blue traces in B1 and B2), +20 min (green traces in B1 and B2), or +40 min after training (dark blue traces in B1 and B2). Both A and B rapidly increased, completing consolidation, once the PSI was removed after 24 h. (C) For different start times, with 1 h (red trace), 2 h (blue trace), and 24 h (green trace) treatments with PSI, the minimum percentages of PSI required to delay the consolidation were compared. For example, a 1-h treatment was relatively ineffective when begun −60 min before training because >98% PSI was required to delay the consolidation. In contrast, the 1-h treatment was much more effective when it began at times −30 min before training. For all the treatments, >98% PSI was required to delay the consolidation when PSI began +40 min after training. (D) The increase of A was transient and A eventually returned to its lower state with continuous 100% PSI beginning +5 min (green trace), +20 min (red trace), or +40 min (light and dark blue traces) after training. Although all treatments appeared to revert A to its lower state, this was not always the case. A rapidly switched to its upper state when 100% PSI began +40 min after training and was removed after 100 h. However, A did not switch back to its upper steady state if PSI was removed after 150 h, which indicated that the sensitivity of consolidation to PSI depends on the duration of PSI.

We also simulated 24 h 98% PSI after training. In the two-loop model, consolidation was blocked when 24 h 98% PSI started immediately after training (Fig. 3B1,B2, +0 min traces). In contrast, consolidation occurred with a delay if 24 h 98% PSI began 5 min or later after training (Fig. 3B1,B2, +5 min traces). A switched to a reduced upper state (Fig. 3B1); however, B did not reach 0.84 µM until PSI was removed (Fig. 3B2). B did not increase to 0.84 until ∼20 h after training with 98% PSI beginning 20 min after training (Fig. 3B2). However, B remained higher than 0.84 µM with 98% PSI beginning 40 min after training (Fig. 3B2). These results indicate that the two-loop model develops a progressive resistance of memory consolidation to PSI after training.

We next examined whether the model can reproduce the empirically obtained time window for sensitivity of memory consolidation to PSI. We measured the minimum levels of PSI required to delay consolidation, i.e., to keep B below 0.84 µM >40 min after training, when PSI had different durations, 1, 2, and 24 h, and began at different time points (Fig. 3C). The results delineated the critical time window for the sensitivity of simulated memory consolidation to PSI. The shape and extent of the time window before training depended strongly on the duration of PSI (Fig. 3C). However, the time windows for all PSI durations ended ∼40 min after training (Fig. 3C) in that 40 min or more after training, >98% PSI was always required to disrupt the consolidation. Forty minutes was also the time required for B to increase to 0.84 µM so that A only had the upper steady state. Thus, our model qualitatively reproduced the extent of the empirical time window.

We also examined whether the model produces the same time window for sensitivity of memory consolidation to continuous 100% PSI beginning at various times after training (Fig. 3D). B never increased to 0.84 µM (not shown) and A transited to the lower state ∼6 or ∼29 h after training with 100% PSI beginning 5 or 20 min after training (Fig. 3D, green and red traces, respectively). With 100% PSI applied 40 min after training, A underwent a long decline and did not drop abruptly to the lower state until B decreased to 0.54 µM and A lost the upper state ∼130 h after training (Fig. 3D, blue trace). A recovered to the upper state if 100% PSI was removed prior to 130 h (Fig. 3D, purple trace). Thus, 100% PSI applied 40 min after training required ∼5 d to revert A to the lower state, whereas 100% PSI applied 20 min after training only required ∼1 d. These results further indicated that memory was more sensitive to PSI within the time window that ended ∼40 min after training.

LTM is “maintained” by increased protein synthesis

The synthesis rate of B was measured at different time points after training when PSI was added (Table 1). Before training, the basal synthesis rate was 6.56 × 10⁻⁷ μM/sec. The synthesis rate increased to 4.89 × 10⁻⁴ μM/sec 40 min after training, due to the slow positive-feedback loop. When 98% PSI was applied after training, at times that failed to block consolidation, the synthesis rate of B decreased by 98%, but nevertheless remained higher than the basal synthesis rate before training (Table 1). The maintained synthesis was due to the increase of A⁴/(A⁴ + K_B−1⁴) in Equation 1b that compensated for the decrease of (1 – ANI) in Equation 1b. This result indicates that even with 98% PSI, LTM was still being “maintained” by increased protein synthesis. The resistance of memory consolidation to PSI results from the increased protein synthesis produced by the positive-feedback loop.

Table 1.

Protein synthesis rate of B (μM/sec) at different time points after training with and without PSI

	30 min before training	0 min after training	5 min after training	20 min after training	40 min after training
The two-loop model (half-life of B ∼6 d)
Without PSI	6.56 × 10−7	3.46 × 10−5	4.25 × 10−5	9.53 × 10−5	4.89 × 10−4
98% PSI	1.31 × 10−8	5.70 × 10−7	8.53 × 10−7	1.91 × 10−6	9.85 × 10−6
The model without BMAX (half-life of B ∼7 h)
Without PSI	1.55 × 10−5	3.61 × 10−4	4.18 × 10−4	4.68 × 10−4	4.73 × 10−4
95% PSI	7.73 × 10−7	7.73 × 10−7	2.09 × 10−5	2.34 × 10−5	2.36 × 10−5
The model without BMAX (half-life of B ∼1 h)
Without PSI	1.09 × 10−4	4.57 × 10−4	5.12 × 10−4	5.61 × 10−4	5.66 × 10−4
70% PSI	3.28 × 10−5	1.06 × 10−4	1.54 × 10−4	1.68 × 10−4	1.70 × 10−4

The treatments that blocked consolidation are underlined.

LTM is sensitive to transient degradation

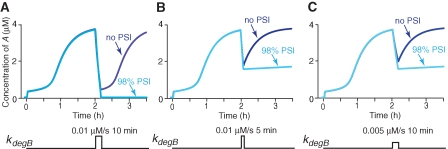
Recent results suggest that memory recall is associated with a transient increase in protein degradation (Artinian et al. 2008; Lee et al. 2008; for review, see Kaang et al. 2009). Consequently, the recall process itself could destabilize previously established memory, and the extent to which recall destabilizes LTM could be dependent on the intensity and duration of increase in protein degradation that might be related to the duration of the retrieval stimulus (Lee et al. 2008). Figure 4 illustrates the consequences of increasing the maximal degradation rate for B, k_{deg B} in Equation 1b, to different intensities and for different durations. Without PSI, increasing k_{deg B} to 0.01 µM/sec for 10 min at 2 h after training only produced a transient decrease in A and B (Fig. 4A). The recovery process was dependent on new protein synthesis to “reconsolidate” the memory and return B to the upper steady state. In contrast, the same amount and duration of k_{deg B} increase drove A and B to their basal levels when 98% PSI began immediately after (or 30 min before) the k_{deg B} increase (Fig. 4A). A and B did not recover to their original upper states after PSI was removed (simulation not shown). However, A remained well above 0.3 µM, albeit at a reduced upper state, and B remained higher than 0.84 µM, even with 98% PSI applied immediately after (or 30 min before) the k_{deg B} increase, if k_{deg B} was increased to ∼0.01 µM/sec for 5 min (Fig. 4B) or ∼0.005 µM/sec for 10 min (Fig. 4C). A and B recovered to their original upper states after PSI was removed (simulation not shown). These results indicate that, although 98% PSI applied after the time window did not block consolidation (Fig. 3B), it did make LTM sensitive to perturbations such as transient increases in degradation rates. In addition, the ability of PSI to disrupt reconsolidation depends on the duration and intensity of increased degradation (Fig. 4). Moreover, A remained well above 0.3 µM, albeit at a reduced upper state, and B remained at an upper state above 0.84 µM if k_{deg B} was increased as in Figure 4A and 98% PSI was applied 30 min or later after the increase of k_{deg B}. These results indicate that in our model, the sensitivity of memory reconsolidation to PSI also has a time window, with a duration similar to the consolidation window.

Figure 4.

Responses to transient increases of k_{deg B}. Two hours after training, k_{deg B} in Equation 1b was increased to 0.01 µM/sec for 10 min (A), 0.01 µM/sec for 5 min (B), 0.005 µM/sec for 10 min (C). (A) Without PSI, the increase of k_{deg B} to 0.01 µM/sec for 10 min failed to revert A to the lower state (dark blue trace). In contrast, A was reverted when continuous 98% PSI began immediately after k_{deg B} increased (light blue trace). Shorter (B) or weaker (C) k_{deg B} failed to revert A to the lower state. A remained >0.3 µM, albeit reduced from the level with no PSI (from dark blue traces to light blue traces in B and C), despite the continued presence of PSI.

The sensitivity of memory consolidation to kinase inhibition has a time window

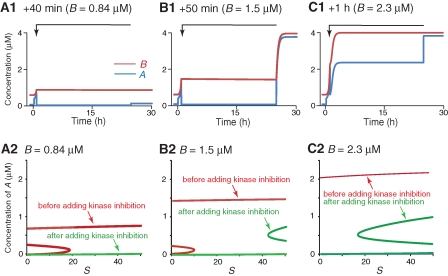
We next simulated the effects of blocking kinase activity. Because potent inhibitors can inhibit ≥90% of kinase activity (English and Sweatt 1997), we increased PKI in Equation 1a to 0.9 for 24 h starting during and at different times (40, 50, and 60 min) after training. Inhibition that started during or 40 min (when B = 0.84 µM) after training decreased A irreversibly to the lower state (Fig. 5A1). Inhibition that started 50 min after training, at which time slow positive feedback had increased B to 1.5 µM, greatly decreased A, but only transiently. A recovered to the upper state after the removal of inhibition (Fig. 5B1). When the inhibition started 1 h after training at which time B = 2.3 µM (Fig. 5C1), its only effect was to reduce the upper state of A during the time of the kinase inhibition. A remained well above 0.3 µM and B remained higher than 0.84 µM. These simulations characterized a time window (∼1 h) for the sensitivity of memory consolidation to kinase inhibition, which is somewhat longer than the time window for PSI (∼40 min). The longer kinase window is explained by bifurcation analysis. Unlike PSI, kinase inhibition affects the fast feedback loop (Equation 1a) and alters the bifurcation curves of A (Fig. 5A2,B2,C2). A only has an upper stable state when S = 20 and B ≥ 0.84 µM in the absence of kinase inhibition (Fig. 5A2,B2,C2, red traces), whereas A only has a lower stable state at S = 20 if 90% kinase inhibition is present when B = 0.84 µM or B = 1.5 µM (Fig. 5A2,B2, green traces). Therefore, kinase inhibition can revert A to the lower state when B = 0.84 µM or 1.5 µM. In contrast, A has an upper stable state at S = 20 if kinase inhibition does not start until B = 2.3 µM (green trace in Fig. 5C2). Therefore, A becomes resistant to kinase inhibition 1 h after training with B ≥ 2.3 µM. In all cases, A resumed the bifurcation curves in the absence of kinase inhibition (e.g., Fig. 5A2–C2, red traces). Therefore, A recovered to its upper state after the removal of inhibition if B ≥ 0.84 µM (Fig. 5B1). Note that 24 h 90% kinase inhibition slightly decreased B. B was reduced from 0.84 to ∼0.83 µM with kinase inhibition beginning 40 min after training in Figure 5A1. This small decrease gave rise to a stable lower state of A for S = 20. Therefore, A did not recover to its upper state (Fig. 5A1). These results indicate that positive-feedback loops sustain the progressive development of resistance of memory consolidation to kinase inhibition, as was found above for PSI.

Figure 5.

State transitions in the presence of 24 h 90% inhibition of kinase activation. S_T was increased to 200 for 10 sec at t = 0. The transition of A to the upper state was reverted with kinase inhibition beginning either +40 min after training (A1) at which time B = 0.84 µM, or +50 min after training (B1) at which time B = 1.5 µM. A remained >0.3 µM and B remained >0.84 µM when kinase inhibition started +1 h after training (C1). Both A and B rapidly switched to their upper states in (B1) and (C1) once the PSI was removed after 24 h, but not in (A1). (A2–C2) Bifurcation diagrams for A as a function of stimulus S in the absence/presence of 90% kinase inhibition when B is 0.84 µM (A2), 1.5 µM (B2), or 2.3 µM (C2). In the presence of 90% kinase inhibition, A has both upper and lower stable steady states when S = 20 and B = 2.3 µM (C2); A only has a lower steady state when B < 2.3 µM and S = 20 (A2, B2).

Alternative models support the hypothesis that positive feedback can account for the resistance of memory consolidation to PSI

We used three alternative models to further investigate the contribution of the positive-feedback loops to the resistance of memory consolidation to inhibitors. The first two models were derived from the two-loop model, whereas the third model was from Pettigrew et al. (2005). In the first alternative model, we considered the possibility that resistance of the upper state to ≥95% PSI applied after training might result from the upper bound B_MAX imposed on B in the model of Equation 1a and b, and not from the positive-feedback loop per se. Therefore, we tested the sensitivity of memory consolidation to PSI in a model variant without B_MAX (Equation 2). In this model, the degradation term for B was modified by increasing the degradation Michaelis constant, K_B−2, and maximal degradation rate, k_{deg B}. This was done because without B_MAX, this model is susceptible to an instability in which B increases without bound, which can only be eliminated by modifying the degradation kinetics. Bistability was restored by this modification. The parameters governing the synthesis of B were also adjusted to maintain the basal level of B at 0.56 µM as above. S_T was again increased from 0 to 200 for 10 sec to represent training. Because the differential equation and parameter values for A (Equation 1a) were not changed, consolidation was still equated as the transition of A to the upper state followed by the increase of B from 0.56 to 0.84 µM. Two sets of parameters were used in this model to examine the possible effect of degradation on the resistance of memory consolidation to PSI. In the first set, the degradation rate of B was 1.55 × 10⁻⁵ μM/sec. The half-life of B was ∼7 h and the upper bound of B was ∼68 µM (Materials and Methods; parameter set 1 below Equation 2). In the second set, the degradation rate of B was 1.09 × 10⁻⁴ μM/sec. The half-life of B was ∼1 h and the upper bound of B was ∼5 µM (Materials and Methods; parameter set 2 below Equation 2). A was bistable at S_B = 20 in both sets, and B increased to 0.84 µM ∼20 min after training.

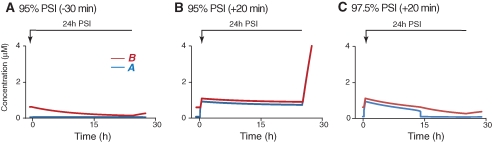
With the first set of parameters, the upper state of A was destabilized with 24 h 95% PSI applied before or immediately after training (Fig. 6A). However, it was not destabilized if 24 h 95% PSI was begun 20 min after training and B always remained higher than 0.84 µM (Fig. 6B). Therefore, this model also exhibited a time window for the sensitivity of memory consolidation to PSI. With the second set of parameters, consolidation was blocked with 24 h 70% PSI applied before or immediately after training (simulation not shown). However, consolidation was not blocked with 24 h 70% PSI 20 min after training. Both parameter sets had higher degradation rates of B than did the original two-loop model (Equation 1a,b) (6.56 × 10⁻⁷ µM/sec), making the new model more sensitive to high levels of PSI, so A was reverted to the lower state when 97.5% (Fig. 6C) or 76% PSI was applied 20 min after training (simulation not shown). Therefore, positive-feedback loops were responsible for bistability and consequent resistance of memory consolidation to PSI, whereas the time window for the sensitivity of memory consolidation to PSI was affected by various factors (e.g., degradation rates, and inhibitor duration and concentrations).

Figure 6.

State transitions in the presence of PSI in the model without B_MAX. In a model with parameters that yield a relatively long half-life of B (∼7 h), the increase of A and B was blocked by 24 h 95% PSI imposed −30 min before training (A) whereas A was maintained >0.3 µM and B > 0.84 µM in the presence of 95% PSI imposed +20 min after training (B). Therefore, memory remained in the consolidated state. Similar to Figure 3B, A and B increased further after 24 h 95% PSI ended. (C) 97.5% PSI imposed +20 min after training reverted A and B to their lower states.

With this model without B_MAX, the synthesis rate of B was again higher in the upper state of B than in the lower state, irrespective of the presence of PSI (Table 1). Thus, LTM, in the absence and presence of PSI, was being “maintained” by a protein synthesis rate higher than the rate before training and in the absence of PSI. In both models (Equations 1a,b and Equations 1a, 2) positive feedback sufficed to maintain an increased level of protein synthesis, an upper state of A and B, and LTM, irrespective of >95% PSI.

In the second alternative model, we turned off the fast loop in the two-loop model (Equation 3) to further explore the contributions of individual feedback loops to LTM. Due to the loss of the autoactivation loop, A did not increase as rapidly after stimuli, so a brief stimulus could not induce a state transition. The duration needed to be increased to ∼30 min (S_T = 200). The consolidation (Fig. 7A) was blocked by 98% PSI started 30 min before training (Fig. 7B, green trace). In contrast, the upper state of A was not destabilized, albeit it was reduced (Fig. 7B, blue trace), and B (not shown) remained higher than 1.8 µM when 98% PSI started 40 min after training onset (i.e., 10 min after stimulus offset). As with the two-loop model (Equation 1a,b), the time window during which PSI disrupted LTM was relatively brief. We compared the minimum levels of 24 h PSI required to block the switch of A to its upper state at different time points for both models, with a 30-min induction stimulus (Fig. 7C). The minimum PSI required to block the switch was 80.9% in the one-loop model and 98.1% in the two-loop model when PSI began 30 min prior to training. The difference between models decreased as PSI began later. Ten minutes or later after training, ∼100% PSI was required for both models. Thus, the one-loop model had weaker resistance of memory consolidation when PSI was imposed before training, but after training a single feedback loop involving protein synthesis (increase of B) sufficed to render LTM resistant to PSI.

Figure 7.

Comparison of two-loop and one-loop models for LTM consolidation. (A) At t = 0, S_T was increased from 0 to 200 for 30 min. Without PSI, the stimulus induced a transition of A and B to an upper stable state. (Insert) Bifurcation diagram for A and B as a function of S. (B) The increase of A was blocked with 24 h 98% PSI beginning −30 min before training. A remained >0.3 µM when this PSI began +40 min after training. (C,D) For different start times, the minimum percentages of continuous PSI or kinase inhibition required to block the increase of A were compared in two models. (C) PSI had a greater effect on the one-loop model when applied before training, whereas after training the minimum PSI in the one-loop model approached the minimum PSI in the two-loop model. (D) Compared with the two-loop model, the single feedback loop had lower minimum levels for kinase inhibition applied before or after training.

We also compared the minimum levels of 24 h kinase inhibition required to block the switch of A to upper state (Fig. 7D). Forty percent inhibition was required in the one-loop model and 60% in the two-loop model when inhibition began 30 min before training, whereas 85% inhibition was required in the one-loop model and 95% in the two-loop model when inhibition began 90 min after training. Therefore, the one-loop model retained considerable resistance of memory consolidation to kinase inhibition after training. However, the fast autoactivation loop in the two-loop model always enhanced resistance to kinase inhibition.

With both models, we also carried out simulations in which the slow feedback loop was removed (i.e., B was held constant). The fast autoactivation loop alone was sufficient to generate bistability, and A switched from the lower state to the upper state following a brief stimulus. However, the upper state was much more sensitive to perturbations without the consolidating increase of B. For example, the upper state was destabilized by <10% kinase inhibition with parameters near standard values for Equation 1a,b. Therefore, the slow loop is essential to generate a robust LTM.

To test further whether a slow feedback loop involving protein synthesis generates resistance of memory consolidation to PSI, PSI was applied to a model developed by Pettigrew et al. (2005), which describes more specifically aspects of the formation of LTM in Aplysia. In Aplysia (Dash and Moore 1996), and in vertebrates (Huang et al. 1994; Impey et al. 1996), protein kinase A (PKA) activation is necessary for LTF and L-LTP. The Pettigrew model simulates the dynamics of Aplysia PKA activation following five pulses of 5-HT (Müller and Carew 1998). Long-term PKA activation (for >20 h) is heuristically equated to LTF and the establishment of LTM. The Pettigrew model has a positive-feedback loop between PKA activity and protein synthesis, in which PKA activates synthesis of an immediate-early gene product Ap-Uch. Ap-Uch in turn contributes to long-term PKA activation (Hegde et al. 1997), closing the loop. To simulate the effects of PSI, the protein synthesis rates of both PKA and Ap-Uch were reduced by 99% for 24 h. The effects on the time course of long-term PKA activation were observed.

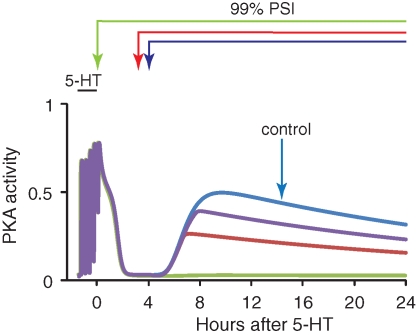
Figure 8 illustrates responses of PKA to five pulses of 5-HT in the presence and absence of PSI. The normal late increase in PKA activity was blocked with 24 h 99% PSI started immediately after 5-HT. However, PKA activity measured 24 h after stimulus was only reduced to ∼50% of control with 99% PSI started 3 h after 5-HT, and PKA activity was ∼70% of control with 99% PSI started 4 h after 5-HT. These results indicate that the Pettigrew model also has a critical time window within which long-term PKA activity was sensitive to PSI. It appears plausible that the maintenance of LTM in the presence of substantial (≥95%) PSI may be due, at least in part, to one or more positive-feedback loops.

Figure 8.

PSI dependency for long-term PKA activation in the Pettigrew model. For these simulations, the parameters V_syn, k_ApSyn, and k_ApSynBasal (Pettigrew et al. 2005) were reduced by 99% to simulate the effects of a 99% inhibition of protein synthesis (other model parameters as in Pettigrew et al. [2005]). Five pulses of 5-HT were applied to induce PKA activation (blue trace, control with no PSI). PKA activity (measured at 24 h) failed to increase (green trace) when 24 h 99% PSI began immediately after 5-HT. PKA activity at 24 h was, respectively, ∼50% (red trace) and ∼70% (purple trace) of the control when this PSI began 3 or 4 h after 5-HT.

Noise affects the sensitivity to PSI

Noise, due to environmental perturbations, is ubiquitous in biological systems, and a plausible model for the consolidation of LTM should be relatively insensitive to noise. We examined the sensitivity of the first two-loop model (Equation 1a,b) to noise in the stimulus by incorporating Gaussian noise S_N (σ = 3%∼20% of S_B, see Materials and Methods). Both lower (A = 0.03 µM and B = 0.56 µM) and upper states (A ≥ 0.3 µM and B ≥ 0.84 µM) remained stable in the presence of noise with σ = 20% of S_B. However, noise did affect the ability of the model to transit between stable states. We monitored the fraction of 1000 simulations that transited from the lower to the upper state within 7 dafter training and observed a moderate, but not extreme, sensitivity to stimulus noise. Without PSI and with σ = 10% S_B, no transition was blocked in 1000 simulations. With σ = 20% S_B, transitions were blocked in ∼27% of 1000 simulations.

The transition without noise was only delayed with 1 h of 96% PSI started 30 min before stimulus (Fig. 3A1,A2), whereas, the transition was blocked in >99% of 1000 simulations with noise of σ = 10% S_B. Thus, consolidation was not blocked by 96% PSI applied before training without noise, whereas consolidation was blocked when the same PSI treatment was applied with noise. However, all 1000 simulations remained at the upper state with 98% PSI beginning 40 min after training and stimulus noise of σ = 20% S_B. Similarly, 993 of 1000 simulations remained at the upper state with 90% kinase inhibition beginning 1 h after training and stimulus noise of σ = 20% S_B. Therefore PSI substantially increased the sensitivity of the model to noise by delaying the increase of B to 0.84 µM.

Discussion

A common method for investigating the temporal requirements for kinase activation and protein synthesis in stabilizing memory is to pharmacologically block kinases and protein synthesis. The results can be difficult to interpret, in part, because inhibitors of kinase and protein synthesis, even at high concentrations, do not completely block these processes (Barondes and Cohen 1968; Milekic and Alberini 2002). Thus, the possibility remains that with inhibition, decreased capacities for kinase activation and protein synthesis contribute to the maintenance of the LTM beyond the empirically determined windows for disruption. This question is difficult to address empirically because practically a 100% block of synthesis or activity cannot be attained due, for example, to toxicity of high inhibitor concentrations (for review, see Rudy et al. 2006). An alternative approach is to use computational models of putative molecular mechanisms for LTM and simulate inhibition of protein synthesis or kinase activity to examine the time window for the effects of these processes on consolidation.

Our approach was to build reduced models to examine general properties that may govern the time windows for the sensitivity of memory consolidation to PSI and kinase inhibition. Therefore, our models were not detailed representations of biochemical pathways. In our models, the two variables A and B represent the levels of activated kinase and total kinase, respectively. Our simulations suggested that a single slow feedback loop involving protein synthesis suffices to develop the resistance of memory consolidation to PSI (Fig. 7), a suggestion further supported by the Pettigrew model (Fig. 8). A fast autoactivation loop alone can sustain a bistable switch (Smolen et al. 2009) and might therefore store LTM, but previous models have suggested this LTM would be vulnerable to disruption by brief perturbations or noise (Smolen et al. 2009; see also Brandman et al. 2005; Zhang et al. 2007). Simulations confirmed such vulnerability. With B unable to increase, <10% kinase inhibition abolished the upper state of A. Without elevation of the slow variable B, there is not a sufficient restoring force to sustain a recovery of A or an upper state.

In our models, the kinase A up-regulates its own synthesis. Empirical evidence suggests that at least two kinases implicated in LTP—CAMKII and PKM—can up-regulate their own synthesis. The induction of hippocampal L-LTP requires the activation of CaMKII (Malenka et al. 1989; Malinow et al. 1989; Fukunaga and Miyamoto 2000). Persistent activation of CAMKII has been hypothesized to play an important role in the maintenance of LTP (Sanhueza et al. 2007), and in addition, the amount of CAMKII in individual spines correlates with the strength of synapses onto those spines (Asrican et al. 2007). Autoactivated CaMKII phosphorylates a translation regulator, cytoplasmic polyadenylation element binding protein (CPEB), which stabilizes LTF in Aplysia (Si et al. 2003) and can bind regulatory elements in CaMKII mRNA to regulate translation (Wu et al. 1998; Atkins et al. 2004, 2005). In this manner, CaMKII may act to increase its own translation. Therefore, it is plausible that an increase in the amount of both total and active CAMKII, mediated by positive feedback involving translation, could constitute one mechanism for the maintenance of LTM. Aslam et al. (2009) developed a bistable model based on this putative positive feedback, and simulated the sensitivity of L-LTP induction and maintenance to PSI and kinase inhibition. In addition, the maintenance of L-LTP requires the persistent activity of PKM (Pastalkova et al. 2006). Empirical studies of PKM in hippocampal neurons indicate that PKM activity is required for the synthesis of new PKM (Kelly et al. 2007). These data suggest that a positive-feedback loop involving protein synthesis of PKM may contribute to its persistent activity. Empirical data also suggest that a positive-feedback loop involving the transcriptional up-regulation of the transcriptional activator CREB1 is important for the consolidation of synaptic LTF in Aplysia (Liu et al. 2008). In our models, kinase A can also autoactivate itself in a fast positive-feedback loop. For CAMKII, this type of positive feedback, in which CAMKII maintains its own activity by autophosphorylation, has been hypothesized to be important for LTP (Pi and Lisman 2008), although empirical confirmation has not yet been obtained.

Small differences in PSI can lead to large differences in memory consolidation

Empirically, LTM is significantly impaired in mice given a dose of anisomycin estimated to produce ∼96% PSI 30 min before training, and greater impairment is seen with a higher dose (∼98% PSI) (Squire and Davis 1975). In the two-loop model, blocking consolidation by 98% PSI (Fig. 3A) could represent the effect of a higher dose. Blocking consolidation prevented A and B from increasing even if 98% PSI was removed after training (Fig. 3A1,A2). In contrast, consolidation was initiated but delayed with 96% PSI (Fig. 3A). Although A and B reached their upper states, the delay made the model sensitive to disturbances, which we simulated as stimulus noise. In the presence of noise and 96% PSI, A and B only sometimes switched to the upper state. Therefore, either input (stimulus) noise or other environmental disturbances might block the consolidation of LTM for a subpopulation of neurons and/or synapses. Because the consolidation of a physiological memory presumably involves multiple synapses and neurons, such a result might be expressed behaviorally as an impairment, but not complete block, of LTM. Hence, with our model 96% PSI may represent the consolidation of impaired LTM, whereas 98% PSI represents a complete failure to establish LTM.

Reconsolidation

Nader et al. (2000) gave rats a retrieval test 24 h after long-term fear conditioning, in the absence or presence of anisomycin. When retested again 48 h after training rats that had first been tested in the presence of anisomycin exhibited memory impairment, whereas rats in the control group retained the memory. Rats given anisomycin in the absence of the 24-h test, or 6 h after the 24-h test, did not exhibit memory impairment on the 48-h test. Together with other studies (Alberini 2005; Rossato et al. 2006), these results illustrate that during a critical time window after reactivation, memory retention is labile to disruption by PSI. During this time, memory undergoes another phase of protein synthesis-dependent consolidation, which has been termed reconsolidation.

Empirical studies indicate that despite potential significant differences, consolidation and reconsolidation may share some molecular mechanisms (Alberini 2005). Due to this putative similarity of mechanism, the positive-feedback models presented here may provide insights into understanding reconsolidation. For example, a memory retrieval may lead to destabilization through a transient increase in protein degradation (Artinian et al. 2008; Lee 2008; Lee et al. 2008; for review, see Kaang et al. 2009). If so, reconsolidation is required after a retrieval test. As with consolidation, the time window during which PSI can disrupt reconsolidation appears to be brief (Nader et al. 2000; Rossato et al. 2006; Artinian et al. 2008). However, the existence of the time window depends on the duration of retrieval. Suzuki et al. (2004) found that PSI did not disrupt reconsolidation if the duration of the retrieval stimulus was as short as 1 min. This finding was supported by Lee et al. (2008), suggesting that a 1-min retrieval stimulus is not sufficient to significantly increase protein degradation.

In the two-loop model, a retrieval test would be equivalent to a transient increase in k_{deg B} (Fig. 4). For model parameters as in Figure 4A, the increase in k_{deg B} to 0.01 µM for 10 min did not disrupt established LTM. However, with 98% PSI, this increase in k_{deg B} did disrupt LTM, forcing A and B to the lower state. These simulations may represent aspects of successful reconsolidation (without PSI) and failure of reconsolidation (with PSI). The upper state was not destabilized, if 98% PSI was applied later, e.g., 30 min after the increase of k_{deg B}. This simulation predicts that empirically, the time window during which PSI can disrupt reconsolidation will be brief, like that for consolidation, and will be dependent on intensity and duration of destabilization, because a shorter or weaker increase of k_{deg B} failed to force A and B to the lower state in the presence of 98% PSI (Fig. 4B,C). Artinian et al. (2008) reported that anisomycin injected immediately after a retrieval stimulus blocked reconsolidation, whereas injection 2 h after retrieval failed to block. Thus, the empirical time window appears to be <2 h. Our modeling results suggest that the duration of the time window of the sensitivity of memory reconsolidation to PSI is similar to the time window of consolidation to PSI. Experiments have not yet defined this window at a higher resolution.

Bifurcation analysis may help to explain the time window of reconsolidation. In Figure 2A, A loses its upper steady state when S = 20 and B decreases to 0.54 µM (green trace). A retrieval test, if it is equated to a transient increase in k_{deg B}, decreases B. The transient increase in k_{deg B} in Figure 4A in the absence of PSI did not suffice to decrease B to 0.54 µM. Similarly, a shorter or weaker increase of k_{deg B} in the presence of PSI (Fig. 4B,C) was not sufficient to decrease B to 0.54 µM. Thus, B recovered to the upper state after k_{deg B} returned to its basal level. However, this transient increase in k_{deg B} made B decrease to <0.54 µM when 98% PSI was present in Figure 4A. The upper steady state of A was destabilized. A and B returned to the lower state and stayed there after k_{deg B} returned to its basal level.

Empirical and computational limitations of PSI study

The analyses of our models indicate that protein synthesis remains important after consolidation (Table 1). Empirical studies of PSI may not detect this aspect, not only because of empirical limitations for applying PSI, but also because the synthesis rate of a specific protein can remain elevated even in the presence of PSI if one or more positive-feedback loops are up-regulating this synthesis. A conclusion of apparent independence of LTM from PSI based on empirical observations should, therefore, be made with caution.

In the simulation of Figure 3B2 with 98% PSI, B will remain >0.84 µM, corresponding heuristically to continued preservation of a stable LTM. However, this relatively simple model, with only one protein, does not represent the effect on cell viability of blockage of constitutive protein synthesis by 98% PSI. Clearly, this strong inhibition of constitutive protein synthesis would eventually damage neurons and eliminate LTM. However, based on the previously referenced empirical studies in which LTF was retained for ∼24 h with high levels of PSI (Montarolo et al. 1986), we suggest our models represent some of the essential dynamic elements, such as bistability of kinase activity, which may maintain LTM for ∼1 d. Our model does not represent other processes known to be important for the consolidation of LTP and LTM, such as increased insertion of glutamate receptors of the α-amino-3-hydroxy-5-methyl-4-isoxazole propionate (AMPA) subtype (AMPARs) into the postsynaptic membrane. However, some of these processes may be downstream from, or modulated by, persistent kinase activation. For example, phosphorylation of AMPARs increases membrane insertion, supporting LTP (Esteban et al. 2003). Phosphorylation of the GluR1 AMPAR subunit at either the CaM kinase II site (Ser 831) or the protein kinase A site (Ser 845) appears sufficient to support LTP (Lee et al. 2010).

In our model, the time window within which PSI blocks LTM assessed 24 h after training is relatively short (<1 h). Although this brief time window is consistent with a substantial amount of empirical data, there are some exceptions. In mice, 24 h spatial memory has been reported to also require a second wave of protein synthesis at ∼4 h (Artinian et al. 2008). Several hippocampal proteins implicated in LTM are up-regulated 24 h after training, but not 3 h after (Igaz et al. 2004). In Aplysia, 5-HT also induces temporally distinct changes in the synthesis of individual proteins, some of which are involved in LTF (Barzilai et al. 1989; Noel et al. 1993; Liu et al. 2008). In particular, Barzilai et al. (1989) found that the synthesis of four proteins was elevated at 3 h after 5-HT, but not at 1 h after 5-HT. To simulate these dynamics, our model would need to incorporate a second phase of protein synthesis, which could correspond, at least in part, to activation of transcription by proteins synthesized in the first phase.

Protein synthesis at times well after training, outside the time window of our model, has been shown to be necessary for the maintenance of LTM over ∼1 wk. Bekinschtein et al. (2007, 2008) found that PSI applied 12 h after training blocked persistence of hippocampal LTM at 7 d after training, although not at 2 d. Similarly, inhibition of transcription 24 h after training blocks persistence of hippocampal LTM at 7 d, although not at 2 d (Katche et al. 2010). Therefore, a model describing LTM maintenance, and PSI effects, over such long periods would need additional equations describing the synthesis and turnover of proteins with long half-lives, and/or the assembly and degradation of structural elements such as the postsynaptic density.

In our model, reconsolidation relies on synthesis of protein B that is sufficient to overcome the effect of temporarily enhanced degradation of B. PSI, by blocking synthesis, would thus irreversibly inhibit LTM. However, recent data indicate that block of hippocampal reconsolidation by PSI is sometimes less persistent than block of consolidation (Stafford and Lattal 2009). This difference in persistence of consolidation versus reconsolidation suggests our model may not represent all mechanistic differences between these processes.

Determining the time window of consolidation

Even though our models are based on simplifications of the actual mechanisms of molecular consolidation, they illustrate the practical difficulty of empirically measuring “time windows” for consolidation. The consolidation period in this study was defined as the time during which protein synthesis was required for B to increase to a level such that A only has an upper steady state (for basal stimulus strength). Simulations indicated this was also the time window during which ≥95% PSI was able to block or delay consolidation. However, the results from alternative models indicated that the time window for the sensitivity of memory consolidation to PSI was dependent on several factors including the concentration and duration of PSI, and the parameters governing protein degradation rates. Moreover, the time window for the sensitivity of memory consolidation to kinase inhibition was longer than the time window for the sensitivity of memory consolidation to PSI. These results illustrate that empirically determined temporal windows of consolidation are dependent on the type, strength, and duration of amnesic treatments and the underlying molecular mechanism of the memory. The effects of varying the parameters of amnesic treatments can be particularly nonlinear if the mechanism for LTM consolidation involves one or more positive-feedback loops.

Materials and Methods

The two-loop model was derived primarily from the model of Smolen et al. (2009) (Fig. 1A; see also Brandman et al. 2005; Zhang et al. 2007) and was used to characterize the time windows for the sensitivity of memory consolidation to inhibitions. Two alternative models were derived from this model to further investigate the contributions of the feedback loops to the resistance of memory consolidation to PSI and kinase inhibition. The importance of slow positive feedback involving protein synthesis was also supported by a fourth model (Pettigrew et al. 2005).

Two-loop model

The two-loop model has two variables (Equation 1a,b). Variable A represents the amount of activated kinase. A enhances its own activation though a fast positive-feedback loop. Variable B represents the total amount of kinase. A increases B via a slow positive-feedback loop, which might represent transcription or translation. B determines the upper bound of A. An increase in B acts to increase A via mass action. In the two-loop model, an upper bound B_MAX was imposed on B:

$$\begin{array}{cc}\multicolumn{1}{c}{\frac{\mathit{dA}}{\mathit{dt}}=}& \{(k_{1}S+k_2\frac{A^4}{A^4+K_{A-1}^4})(B-A)+k_{\text{min}A}\}\hfill \\ \multicolumn{1}{c}{}& \times (1-\mathit{PKI})-k_{\mathrm{deg}A}\frac{A}{A+K_{A-2}},\hfill \end{array}$$ 1a

$$\begin{array}{cc}\multicolumn{1}{c}{\frac{\mathit{dB}}{\mathit{dt}}=}& \{k_3\frac{A^4}{A^4+K_{B-1}^4}(B_{\mathrm{MAX}}-B)+k_{\text{min}B}\}\hfill \\ \multicolumn{1}{c}{}& \times (1-\mathit{ANI})-k_{\mathrm{deg}B}\frac{B}{B+K_{B-2}}.\hfill \end{array}$$ 1b

Standard parameter values were S_B = 20, k₁ = 1×10⁻² sec⁻¹, k₂ = 1.0 sec⁻¹, K_A−1 = 0.3 µM, k_minA = 3×10⁻³ µM/sec, k_degA = 0.2 µM/sec, K_A−2 = 2.6×10⁻² µM, k₃ = 7.2×10⁻⁴ sec⁻¹, K_B−1 = 1 µM, B_MAX=4 µM, k_minB = 6.54×10⁻⁷ µM/sec, k_degB = 1.83×10⁻⁶ µM/sec, K_B−2 = 1 µM. Stimulus S = S_T + S_B. S_T represents the training stimulus. During training, S_T was increased from 0 to 200. S_T returned to 0 after training. Basal stimulus S_B was set to 20, i.e., 10% of maximal S_T. Except during training, S = S_B = 20. The parameters (Equation 1a,b) were chosen to support bistability of activated kinase A and total kinase B at S_B (Fig. 2A). Models of interconnected positive-feedback loops can exhibit either mono- or bistable behaviors in different regions of their parameter space. We selected parameters that supported bistability, consistent with theoretical work that suggests bistable, switch-like behaviors in signaling cascades may play a role in long-term cellular changes such as differentiation, the cell cycle, and memory (Zhang et al. 2007; Guantes and Poyates 2008; Kapuy et al. 2009; Smolen et al. 2009).

The timescale of the slow positive-feedback loop, which increases B, depends most strongly on the parameter k_degB, the rate constant for the degradation of B in Equation 1b. k_degB is small (1.83×10⁻⁶ µM/sec), making this feedback loop slow. The time constant of the fast “autoactivation” positive-feedback loop, which increases A, depends most strongly on k_degA, the rate constant for the degradation of A. k_degA is much larger (0.2 µM/sec). The slow feedback loop alone can sustain bistability. However, the strength of bistability (i.e., the size of the region in parameter space that supports two stable solutions for A and B) is increased by strengthening the fast positive-feedback loop. Fast positive feedback, in turn, is stronger for larger values of either the rate constant k₂ or the coefficient of the Hill function (i.e., 4 in Equation 1a).

In neurons, data suggest that two kinases, CAMKII and PKM, may, when active, regulate their own synthesis (Wu et al. 1998; Atkins et al. 2004, 2005; Pastalkova et al. 2006). In the model, the expression A⁴/(A⁴ + K_B−1⁴) in Equation 1b represents the strength of feedback in which active kinase A up-regulates the synthesis of total kinase B. In Smolen et al. (2009), this feedback term used only a first power of A. The modification to fourth power increases the nonlinearity of feedback from A to B.

Protein synthesis and kinase inhibition were simulated by square pulses of ANI and PKI. ANI represents the effect of PSIs (e.g., anisomycin). ANI = %synthesis inhibition/100. PKI represents the effect of kinase inhibitors. PKI = %kinase inhibition/100. In Equation 1a,b, the degradation functions of A and B are Michaelis-Menten equations, whereas they were linear functions in Smolen et al. (2009). With the modified degradation functions, the half-life of total kinase B is increased to ∼6 d, which is within the biological range (Waelsch and Lajtha 1961).

The alternative models derived from the two-loop model

Model without B_MAX

In this model, we removed B_MAX in Equation 1b. The equation describing fast positive feedback remained unchanged. Equation 1b was modified to Equation 2, yielding:

$$\frac{\mathit{dB}}{\mathit{dt}}=\{k_3\frac{A^4}{A^4+K_{B-1}^4}+k_{\text{min}B}\}(1-\mathit{ANI})-k_{\mathrm{deg}B}\frac{B}{B+K_{B-2}}.$$ 2

For this model, two sets of parameter values were used:

1. k₃ = 4.6 × 10⁻⁴ µM/sec, K_B−1 = 0.3 µM, k_minB = 1.54 × 10⁻⁵ µM/sec, k_degB = 6.25 × 10⁻⁴ µM/sec, K_B−2 = 22 µM. The half-life of total kinase B is ∼7 h.

2. k₃ = 4.6 × 10⁻⁴ µM/sec, K_B−1 = 0.3 µM, k_minB = 1.09 × 10⁻⁴ μM/sec, k_degB = 1.25 × 10⁻³ μM/sec, K_B−2 = 5.85 µM. The half-life of total kinase B is ∼1 h.

These changes in values from those used for the first model (Equation 1b) were required to

1. Maintain the bistability of activated kinase A and total kinase B at basal stimulus level, S_B.

2. Maintain the basal level of B at 0.56 µM, same as the two-loop model.

3. Keep the increased synthesis rate of B after training similar to that in the two-loop model.

Therefore, the results from both the models were comparable.

One-loop model

In this model, the fast autoactivation feedback loop was eliminated and Equation 1a reduced to:

$$\frac{\mathit{dA}}{\mathit{dt}}=\{\left(k_{1}S\right)(B-A)+k_{\text{min}A}\}(1-\mathit{PKI})-k_{\mathrm{deg}A}\frac{A}{A+K_{A-2}}.$$ 3

Equation 1b, describing slow positive feedback, remained unchanged.

Standard parameter values are as for Equation 1a,b. This model also exhibited bistability of activated kinase A and total kinase B at S_B (Fig. 7A).

Numerical methods

To check the consistency of results, the integrations of differential equations in all the simulations were calculated by two methods, forward Euler and Runge-Kutta (Hairer et al. 1993). No significant differences were observed in the results. The time step was 10 ms. No significant improvements in accuracy were found upon further reduction of the time step. Prior to any training stimulation, the steady state levels of variables were determined after at least two simulated days. The models were programmed in Java and XPP. Bifurcation analysis examined the ways in which steady-state levels of A and B depend on the strength of the stimulus S. The bifurcation software AUTO was used (Doedel 1981).

Simulation of stimulus noise

Stimulus noise was simulated by adding a white Gaussian noise term with mean zero to the stimulus S (variable S_N) (see also Smolen et al. 2009). The noise term had the form S_N = σ × sqrt[−2 ln(U₁)] × cos(2πU₂) where U₁ and U₂ were random numbers uniformly distributed on (0,1). The standard deviation (σ) was 3%–20% of S_B. Thus, S = S_T + S_B + S_N. Fluctuations that took S to negative values were reset to S = 0. The noise time step was 1 sec. Programs are available upon request.