Abstract
Whether human infants spontaneously represent number remains contentious. Clearfield & Mix (1999) and Feigenson, Carey & Spelke (2002) put forth evidence that when presented with small sets of 1–3 items infants may preferentially attend to continuous properties of stimuli rather than to number, and these results have been interpreted as evidence that infants may not have numerical competence. Here we present three experiments that test the hypothesis that infants prefer to represent continuous variables over number. In Experiment 1, we attempt to replicate the Clearfield & Mix study with a larger sample of infants. Although we replicated their finding that infants attend to changes in contour length, infants in our study attended to number and perimeter/area simultaneously. In Experiments 2 and 3, we pit number against continuous extent for exclusively large sets (Experiment 2) and for small and large sets combined (Experiment 3). In all three experiments, infants noticed the change in number, suggesting that representing discrete quantity is not a last resort for human infants. These results should temper the conclusion that infants find continuous properties more salient than number and instead suggest that number is spontaneously represented by young infants, even when other cues are available.
Although a handful of studies from the early 1980s suggested that infants could discriminate small numerosities, such as 2 and 3 (e.g. Antell & Keating, 1983; Starkey & Cooper, 1980; Starkey, Spelke & Gelman, 1983; Strauss & Curtis, 1981), more recent research has challenged this claim. In the early studies, infants were habituated to dot arrays or slides of household objects that contained a common number of elements (e.g. 2 or 3) and then shown new stimuli that contained the same number and a new number of elements (e.g. 2 and 3). Infants looked preferentially at the novel numerosity, suggesting that infants could discriminate the numerosities from each other. Continuous variables such as area, contour length and density, however, were not carefully controlled and tended to co-vary with number. This made it impossible to determine exactly which quantity infants used as the basis for their discriminations.
In a widely cited and influential study, Clearfield & Mix (1999) found that infants preferentially attended to continuous variables over number. In this study, 6–8-month-old infants were habituated to arrays of 2 (or 3) squares that had an unvarying total contour length. The infants were then tested with arrays that had the same number of squares but were novel in total contour length, and with arrays that were novel in number but had the same total contour length as the habituation displays. Infants looked longer at the arrays that contained the novel contour length/familiar number compared with the last three habituation trials, but did not dishabituate to arrays with a novel number/familiar contour length. These results, along with similar findings from studies pitting cumulative area against number (Clearfield & Mix, 2001; Feigenson, Carey & Spelke, 2002), have challenged the idea that infants represent number. Based on these results, it has been argued that (1) infants preferentially attend to continuous properties of sets rather than to number and, more strongly, (2) infants may not be capable of tracking number at all (e.g. Gao, Levine & Huttenlocher, 2000; Mix, Huttenlocher & Levine, 2002; Mix, Levine & Huttenlocher, 1997; Newcombe, 2002).
The Clearfield & Mix (1999) results have had an important impact on the field – they emphasized the critical importance of controlling for continuous variables when attempting to study numerical competence in infancy (see also Feigenson, Carey & Spelke, 2002). This was a welcome contribution to the field and has raised the bar for stimulus controls, allowing for more systematic and rigorous tests of infant numerical abilities. Consequently, there have been a number of published studies involving strenuous manipulations of continuous variables reporting strong evidence for numerical sensitivity in infants. It is now known that when continuous variables are controlled, 6-month-old infants discriminate sets with more than 3 items when numerosity changes by at least a 1:2 ratio. That is, 6-month-old infants discriminate sets of 4 from 8, 8 from 16, 16 from 32, and 7 from 21 (Brannon, Abbot & Lutz, 2004; Cordes & Brannon, 2008; Lipton & Spelke, 2003; Wood & Spelke, 2005; Xu, 2003; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005). When sets are small (3 items or fewer), infants also detect changes based on number without the cues of continuous extent (Feigenson, 2005; Feigenson & Carey, 2003). Thus, contrary to Clearfield & Mix's claims, without the influence of continuous variables, infants are capable of discriminating sets based upon numerosity cues. However, the question remains whether infants continue to represent number when other (non-numerical) cues for discrimination are available, or if it is instead a last-resort strategy for discrimination.
The question brought about by Clearfield & Mix's central thesis is pre-dated by research in the animal literature concerning the ‘Last-Resort’ hypothesis (Davis, 1993; Davis & Memmott, 1983). According to this hypothesis, animals are capable of tracking number, yet they fail to do so when other, more salient, cues (i.e. continuous variables such as time or amount) are available. Thus, the experiments reported here were designed to address a human infant analogue of the Last-Resort hypothesis. Using Clearfield & Mix's original design that pits number against continuous dimensions, the current study investigates the relative salience of number and continuous variables in human infants and thus tests whether number is a last resort for human infants.
In Experiment 1, we replicate the original Clearfield & Mix (1999) design, pitting number against continuous extent for small sets (2 and 3), using computer-generated images presented on a monitor and with a larger sample of infants (24 versus 16) than in the original study. Our findings differ from those of Clearfield & Mix in one important way – infants were found to attend to number as well as to continuous extent.
Experiments 2 and 3 examine the relative salience of number and continuous variables for exclusively large sets (8 and 16 elements – Experiment 2) and for small sets contrasted with large sets (2 and 8 elements – Experiment 3). The distinction between small and large sets is an important one when it comes to infant numerical competences (Feigenson, Dehaene & Spelke, 2004). Data from three distinct paradigms have led researchers to theorize that infants use distinct cognitive mechanisms for representing the numerosities of small sets and of large sets. Small sets (< 4) are putatively represented via object files, an exact representation system used for tracking objects. Owing to limitations of the visual attention system, infants appear to only have three available object files, thus limiting the number of items that can be represented by this system (Feigenson & Carey, 2003; Uller, Carey, Huntley-Fenner & Klatt, 1999). Large sets (> 3), on the other hand, are represented in an accumulator system via continuous (analogue) mental magnitudes with inherent noise (variability) in the representation. Although there is no obvious limit to the values that this system can represent, noise in the representations makes discriminability dependent upon the ratio of the two values in question (Cordes & Brannon, 2008; Wood & Spelke, 2005; Xu & Spelke, 2000). The idea of multiple mechanisms is further supported by the fact that discriminations of small sets from large and vice versa (e.g. 2 vs. 4, 2 vs. 8) are markedly less precise than discriminations of small sets from small and large sets from large (they fail unless number changes by at least a 1:4 ratio; Cordes & Brannon, submitted). That is, when discriminating exclusively large sets or exclusively small sets, infants can discriminate at least a two-fold change in number. However, once the discrimination involves a small set (< 4) and a large set (> 3), infants fail to notice a two-fold change in number. Only when the values change four-fold (e.g. 2 versus 8) do infants detect numerical disparity. This phenomenon is well explained under the assumption of distinct representational systems for small and large values. Thus, the process of comparing the representation of a small numerosity (i.e. object files) with the representation of a large one (i.e. an analogue magnitude) is particularly difficult for the infant because it is like comparing apples with oranges. The fact that infants do in fact succeed at discriminating small from large sets given dramatic (four-fold) changes in number suggests that infants have some way of getting around this problem (Cordes & Brannon, submitted). Perhaps the infant converts the representations into a common currency – for example, infants may use analogue magnitudes to ‘count’ the number of open object files (representing the small set) in order to be able to compare a magnitude with a magnitude (representing the large set). Whatever the process may be, it clearly results in a compromise in representational precision. Regardless, this interesting finding again supports the hypothesis that infants use distinct systems to represent small and large numerosities.
If it is the case that small sets are represented via a different mechanism than large sets, number may be more or less salient depending on the mechanism(s) involved. This possibility is explored in Experiments 2 and 3, in which infants are presented with exclusively large sets (Experiment 2), and with a combination of small and large sets (Experiment 3). Contrary to the findings of Mix, Huttenlocher & Levine (2002), in all three experiments infants attend to changes in number even when continuous variable cues are available, indicating that representations of number are not a last-resort strategy for infants.
Experiment 1
In our first experiment, we replicated the design of Clearfield & Mix (1999), in which number and continuous extent variables are pitted against each other for small sets (2 versus 3 items).
Method
Participants
Participants were 24 healthy full-term 7-month-old infants (mean age = 7 months 3 days, range: 6 months 13 days–7 months 18 days). Ten of the infants were female. Data from an additional 19 babies were discarded because of failure to reach the habituation criterion (n = 11), fussiness resulting in failure to complete at least four test trials (n = 4), and parental interference (n = 4). Although many studies include infants who fail to meet the habituation criterion (e.g. Xu, 2003; Wood & Spelke, 2005), we thought it was important to have a full sample of habituated infants because Clearfield & Mix reported that all their infants habituated. In addition, the number of infants who failed to meet the habituation criterion is typical of many other studies (e.g. Brannon, Abbott & Lutz, 2004; Clearfield & Mix, 2001; Xu, 2003).
Design
The design was a replication of that of Clearfield & Mix (1999). Infants were habituated to stimuli that were composed of 2 squares or 3 squares and tested with arrays of 2 and 3 squares that were familiar in contour length and novel in number or novel in contour length and familiar in number. Half of the infants were randomly assigned to the 2-square condition and half to the 3-square condition.
Stimuli
Stimuli were created with Canvas software and displayed in the centre of the computer monitor (see Figure 1 for example stimuli). Each square was black and had a contour length of 16 cm; therefore, the 2-square displays had a total contour length of 32 cm and the 3-square displays had a total contour length of 48 cm.1 There were six 2-square and six 3-square habituation stimuli in which the spatial configuration of the dots varied. Following habituation, infants were presented with six test trials that alternated between 2- and 3-square displays. The individual contour length in the 2-square displays was 24 cm (i.e. the total contour length was 48 cm), and the individual contour length in the 3-square displays was 10.67 cm (i.e. the total contour length was 32 cm).
Figure 1.
Schematic representation of the stimuli used in Experiment 1, in which number and contour are pitted against each other for exclusively small sets.
Apparatus
Infants were seated in a high-chair (or on a parent's lap) 60 cm from a computer monitor resting on a stage surrounded by blue fabric. Parents were seated next to their infants and instructed to keep their eyes closed and to refrain from talking to, touching, or otherwise interacting with their infant for the duration of the experiment. If an infant became fussy, the experimenter initiated a short break and then resumed the experiment. For an infant to remain in the final sample, the break must have been less than 1 minute in duration and could not occur between a pair of test trials. A microcamera monitoring the infant's face and a feed directly from the stimulus presentation computer were multiplexed onto a TV monitor and VCR. One or two experienced experimenters blind to the experimental condition recorded the infants' looking behaviour while viewing the live video with the display occluded. Looking behaviour was recorded by holding a button down when the infant was looking at the computer monitor and letting go when the infant looked away. The button input was fed into a Visual Basic program, which automatically advanced the stimulus and automatically moved onto the test phase when the criterion was met. The Visual Basic program recorded infants as looking or not looking for each 100-ms interval and calculated inter-observer reliability. Reliability between the two observers who coded 75% of the data live (as conservatively computed based on agreement or disagreement at each 100-ms interval for each trial, averaged across trials, and then across subjects) was on average 90%.
Procedure
Informed consent was obtained from a parent of each participant before testing. The experimenter initiated trials when the infant looked in the direction of the computer monitor. Each trial continued until the infant looked for a minimum of .5 s, and ended after the infant looked for a total of 60 s or looked away for a continuous 2 s. The six different habituation stimuli were presented in a pseudo-random order until the infant met the habituation criterion (a 50% reduction in looking time over three consecutive trials, relative to the first three trials in which the infant looked for a total of at least 12 s) or until 16 trials were completed. After habituation the infants were tested with six test trials according to the same procedure and alternated between familiar and novel cumulative contour lengths.
Results
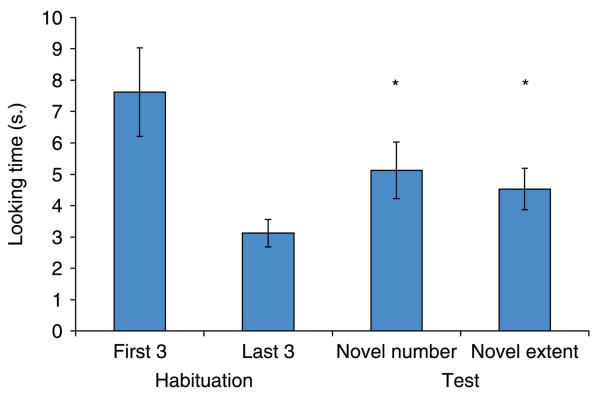
Figure 2 shows the mean looking time for the first three and last three habituation trials, the three novel number test trials and the three novel contour-length test trials. Not surprisingly, given that all infants included in the sample habituated, a paired t-test revealed a significant reduction in looking time from the first three habituation trials (M = 7.62 s) to the last three habituation trials (M = 3.12; t(23) = 4.4, p < .001). The average number of trials to habituation was 8.4.
Figure 2.
Average looking times for infants in Experiment 1 for the first three and last three habituation trials and for the novel contour length/familiar number and novel number/familiar contour length test trials.
A 2 × 2 × 2 mixed-factor analysis of variance (ANOVA) testing the between-subjects factors of habituation condition (2 or 3 squares) and test trial order (novel number or novel contour length first) and the within-subjects factor of test trial type (novel number or novel contour length) on infants' looking time revealed a significant habituation – test trial order interaction (F(1, 20) = 4.6, p = .044), revealing that those infants habituated to the 3-item display looked longer overall in tests when first presented with the novel contour display than when presented with the novel number.2 No other main effects or interactions were revealed by the ANOVA.3
Paired t-tests revealed that infants looked longer at the change in number (M = 5.13) and at the change in contour length (M = 4.53) compared with the last three habituation trials (t(23) = 2.2, p = .04 and t(23) = 2.2, p = .04, respectively). A significant number of infants looked longer at the change in number as compared with the last three habituation trials (17/24, binomial, p < .05), whereas the number of infants looking longer at the change in extent only approached significance (16/24, binomial, p = .08). Infants, however, did not show a preference to either the change in number or the change in contour length (t(23) = .72, p > .4) – slightly more than half the infants (15/24) looked longer at the change in number compared with the change in contour length (binomial, p > .05). In other words, contrary to Clearfield & Mix's (1999) findings, infants dishabituated to both types of test stimuli and showed no additional preference to the change in contour length or the change in number. It is important to note that the absolute values of the looking times in habituation and test in our study look roughly similar to those of Clearfield & Mix's study, the main difference being the elevated amount of time spent looking at the novel number condition in our sample compared with theirs.
Experiment 2
The results of Experiment 1 suggest that, contrary to previous findings by Clearfield & Mix (1999), infants notice changes in both number and continuous extent when the two are pitted against each other. However, most experiments with strict stimulus controls that have shown infants' ability to represent number independently of continuous variables have employed large sets (e.g. Brannon et al., 2004; Cordes & Brannon, 2008; Lipton & Spelke, 2003; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005). A possibility that has been raised previously is that infants may preferentially attend to different variables for small and large sets (Feigenson, 2005; Xu, 2003). Thus in Experiment 2 we used the Clearfield & Mix design to assess the relative salience of number and cumulative area for large sets.
Method
Participants
Participants were 16 healthy full-term 7-month-old infants (mean age = 7 months 3 days, range: 6 months 15 days–7 months 18 days). Six of the infants were female. Data from an additional 10 babies were discarded because of failure to reach the habituation criterion (n = 5), fussiness resulting in failure to complete at least four test trials (n = 4), and experimenter error (n = 1).
Design
Infants were habituated to stimuli that were composed of 8 or 16 elements and tested with arrays of 8 and 16 squares that were familiar in continuous extent but novel in number or novel in continuous extent but familiar in number. Half of the infants were randomly assigned to the contour test condition, in which stimuli were squares and the continuous extent variable of interest was cumulative contour. The other eight infants were in the area test condition, in which stimuli were circles and the cumulative area of the stimuli was the continuous extent variable of interest.
Stimuli
Stimuli were created with Canvas software and displayed in the centre of the computer monitor (see Figure 3 for example stimuli).
Figure 3.
Schematic representation of the stimuli used in Experiment 2 in the (A) contour control condition and the (B) area control condition, in which continuous extent is pitted against number for exclusively large sets.
Contour condition
To mirror the design of Experiment 1 and of Clearfield & Mix (1999), half of the infants were presented square stimuli in which number was pitted against cumulative contour. In these habituation displays, each square was black and had a contour length of 12 cm; therefore, the 8-square displays had a total contour length of 96 cm, and the 16-square displays had a total contour length of 192 cm. There were six 8-square and six 16-square habituation stimuli in which the spatial configuration of the squares varied. Following habituation, infants were presented with six test trials that alternated between 8- and 16-square displays. The individual contour length in the 8-square test displays was 24 cm (i.e. the total contour length was 192 cm), and the individual contour length in the 16-square displays was 6 cm (i.e. the total contour length was 96 cm).
Area condition
The other half of the infants were presented with an identical design, except that they were shown circle stimuli in which number was pitted against cumulative area, instead of against cumulative contour. In habituation, each dot was black and had a surface area of 10 cm2; therefore, the 8-dot displays had a cumulative surface area of 80 cm2 (and a cumulative contour of 89.7 cm), and the 16-dot displays had a cumulative surface area of 160 cm2 (and a cumulative contour of 179.4 cm). There were six 8-dot and six 16-dot habituation stimuli for which the spatial configuration of the dots varied. Following habituation, infants were presented with six test trials that alternated between 8- and 16-dot displays. The individual dot size in the 8-dot displays was 20 cm2 (the cumulative surface area was 160 cm2), and the individual dot size in the 16-dot displays was 5 cm2 (the cumulative surface area was 80 cm2), thus making the cumulative contour in both test conditions 126.8 cm (the geometric mean of the contour parameters from the habituation stimuli). Thus in test, when number was equal to that of habituation, the cumulative surface area varied 2-fold. Similarly, when cumulative area was equal to that of habituation, number varied 2-fold.
The area-control condition was included for a number of reasons. First, because this experiment involved a greater number of elements, when controlling for contour, the change in cumulative area from habituation to test was markedly greater in Experiment 2 than in Experiment 1. Whereas in Experiment 1 infants saw as much as a 2.2-fold change in cumulative area from habituation to test (a ratio known to not be discriminable to infants in this age range; Brannon, Abbot & Lutz, 2004; Cordes & Brannon, 2008), in the contour-control design of Experiment 2, the novel contour would also entail a 4-fold change in cumulative area (as compared with only a 2-fold change for the novel number), a discrepancy known to be dis-criminable to infants (Cordes & Brannon, 2008). Thus, we were concerned that significantly greater changes in area, not contour, may play a part in infant discriminations observed in this task. As can be seen, in the area-control condition, contour is completely controlled for such that it cannot be used as a basis for discrimination. In addition, the majority of studies investigating infant representations of continuous extent have focused on area, not contour (e.g. Brannon, Abbot & Lutz, 2004; Brannon, Lutz & Cordes, 2006; Cordes & Brannon, 2008; Feigenson, Carey & Spelke, 2002; Feigenson, Carey & Hauser, 2002; Clearfield & Mix, 2001), and thus this variable may be more relevant to the current literature. Finally, Clearfield & Mix (2001) found infants to be more sensitive to changes in area than to those in number, suggesting that continuous extent variables in general (be it contour or area) may be more salient to the infant.
Apparatus and procedure
Apparatus and procedure were identical to those of Experiment 1, with the exception that RealBasic software was used to present the stimuli on the computer screen. Reliability between the two observers who coded 75% of the data live was on average 93%.
Results
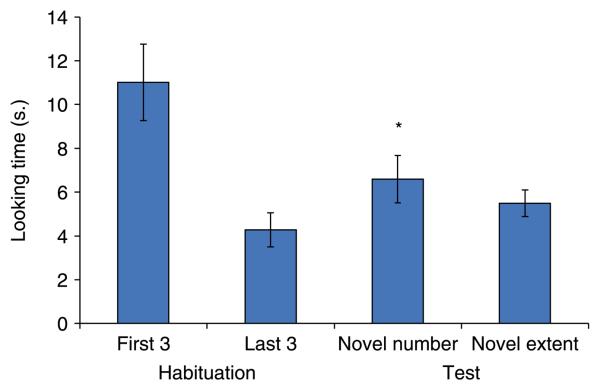
Figure 4 shows the mean looking time for the first three and last three habituation trials, the three novel numerosity test trials and the three novel continuous extent test trials. Again, not surprisingly given that only habituated infants were included in the final sample, a paired t-test revealed a significant reduction in looking time from the first three habituation trials (M = 11.0 s) to the last three habituation trials (M = 4.3; t(15) = 6.2, p < .001). The average number of trials to habituation was 8.6.
Figure 4.
Average looking times for infants in Experiment 2 for the first three and last three habituation trials and for the novel number/familiar extent and novel extent/familiar number test trials.
A 2 × 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of control condition (contour or area), habituation condition (8 or 16 squares), and test trial order (novel number or novel extent first) and the within-subjects factor of test trial type (novel number or novel extent) on infants' looking time revealed no significant main effects or interactions. Importantly, the controlled extent variable was not a factor in our results, suggesting that manipulations of cumulative area did not yield different effects from manipulations of contour length. Given that control condition was not a significant factor affecting results, a second 2 × 2 × 2 ANOVA was conducted (similar to the first, but excluding control condition), again revealing no main effects or interactions.
Paired t-tests revealed that infants looked longer at the change in number (M = 6.6) but not at the change in extent (M = 5.5) compared with the last three habituation trials (t(15) = 2.5, p = .03 and t(15) = 1.4, p = .17, respectively). This finding was echoed by the number of infants exhibiting this pattern; that is, 13 of 16 infants (binomial, p < .05) looked longer at the novel number as compared with their last three habituation trials, whereas only 11 (p > .05) looked longer at the novel extent. Although there was a greater preference to the change in number, infants did not look significantly longer at the change in number over the change in extent (t(15) = 1.2, p > .24). Approximately half the infants looked longer at the change in number compared with the change in extent (9/16; binomial, p > .05). In sum, when number was pitted against continuous extent in large sets, there was evidence that infants detected the change in number relative to habituation but no evidence that they detected the change in continuous extent.
Experiment 3
The findings of Experiment 2 suggest that infants detect numerical changes even when continuous extent is held constant for large sets and further provide no evidence that continuous extent is more salient than number for large sets. In Experiment 3, we provide the first test of the last-resort hypothesis for contrasts between small and large sets. Although a number of studies have reported infant failures to discriminate small from large sets when number changes 2-fold (e.g. 2 vs. 4; Xu, Spelke & Goddard, 2005; Feigenson, Carey & Hauser, 2002), Cordes & Brannon (submitted) have recently reported that infants succeed when presented with sets that vary 4-fold (e.g. 1 vs. 4, 2 vs. 8). Thus, to ensure that number changes were at the least discriminable in this experiment, number and cumulative surface area varied 4-fold in test.
Method
Participants
Participants were 16 healthy full-term 7-month-old infants (mean age = 7 months 1 day, range: 6 months 13 days–7 months 16 days). Eight of the infants were female. Data from an additional seven babies were discarded because of failure to meet habituation criterion (n = 4) and fussiness resulting in failure to complete at least four test trials (n = 3).
Design
Because control condition did not play a part in the data in Experiment 2 and there were a number of reasons to prefer the area control condition over the contour control condition (see above), the design of Experiment 3 was similar to that of the area control condition of Experiment 2. Infants were habituated to stimuli that contained 2 or 8 circles of constant size and tested with arrays of 2 and 8 circles that were novel in number but familiar in area or familiar in number but novel in area. Half of the infants were habituated to 2 dots and half to 8 dots.
Stimuli
Stimuli were black circles created with Canvas software and displayed in the centre of a computer monitor (see Figure 5 for example stimuli). In habituation, each circle had a surface area of 15 cm2; therefore, the 2-dot displays had a cumulative surface area of 30 cm2 (and a cumulative contour of 27.5 cm) and the 8-dot displays had a cumulative surface area of 120 cm2 (and a cumulative contour of 109.83 cm). There were six 2-dot and six 8-dot habituation stimuli for which the spatial configuration of the dots varied. Following habituation, infants were presented with six test trials that alternated between 2- and 8-dot displays. The individual dot size in the 2-dot displays was 60 cm2 (cumulative surface area 120 cm2), and the individual dot size in the 8-dot displays was 3.75 cm2 (cumulative surface area 30 cm2), thus making the cumulative contour in both test conditions 54.9 cm (the geometric mean of the contour parameters from the habituation stimuli). Thus in test, when number was equal to that of habituation, cumulative surface area varied 4-fold, and similarly, when cumulative area was equal to that of habituation, number varied 4-fold.
Figure 5.
Schematic representation of the stimuli used in Experiment 3, in which number and continuous extent are pitted against each other for small and large sets.
Apparatus and procedure
Apparatus and procedure were identical to those of Experiment 2. Reliability between the two observers who coded 75% of the data live was on average 92%.
Results
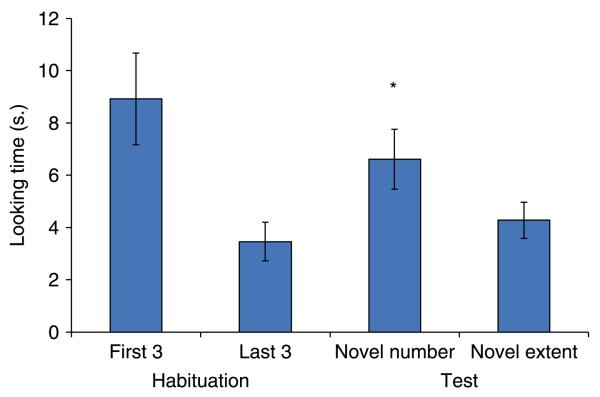
Figure 6 shows the mean looking times for the first three and last three habituation trials and the novel number/familiar extent and novel extent/familiar number test trials. Again not surprisingly, given that only habituated babies were included in the final sample, a paired t-test revealed a significant reduction in looking time from the first three habituation trials to the last three habituation trials (t(15) = 5.1, p < .001).
Figure 6.
Average looking times for infants in Experiment 3 for the first three and last three habituation trials and for the novel number/familiar extent and novel extent/familiar number test trials.
A 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of habituation condition (2 or 8 dots) and test trial order (novel number or novel extent first) and the within-subjects factor of test trial type (novel number or novel extent) on looking times during test revealed a main effect of test trial type (F(1, 12) = 6.1, p = .03), indicating that infants looked longer at displays that were novel in number compared with those that were novel in area. There were no other significant main effects or interactions.
Three distinct analyses demonstrate that infants were sensitive to the change in number but not to the change in extent. First, a paired-samples t-test revealed that infants looked longer at the novel number/familiar extent (M = 6.6 s) than at the novel extent/familiar number (M = 4.3 s) test trials (t(15) = 2.6, p = .02). Second, 14 of 16 infants looked longer at the change in number compared with the change in area (binomial, p < .05). Third, a paired-samples t-test revealed that infants looked significantly longer at the novel number test trials compared with the last three habituation trials (t(15) = 3.7, p < .005) but did not look longer at the novel area test trials compared with the last three habituation trials (t(15) = 1.0, p > .05). Finally, 15 of the 16 babies looked longer at the novel number test trials than at the last three habituation trials (p < .05), whereas only nine infants looked longer at the novel area test trials compared with habituation (p > .05). This pattern was consistent across habituation conditions, in that all 8 infants (p < .05) habituated to 2 dots looked longer at novel number trials (M = 7.4 s) as compared with the last three habituation trials (M = 4.1 s), and 7 of the 8 infants (p < .05) habituated to 8 dots looked longer at the novel number trials (M = 5.1 s) as compared with habituation (M = 2.8 s). In contrast, only 4 of the infants habituated to 2 dots (p > .05) and 5 of the infants habituated to 8 dots (p > .05) looked longer at the novel area test trials as compared with habituation. These findings are notable not only because they corroborate the findings of Experiments 1 and 2 but also in that this is one of a handful of studies reporting that infants successfully discriminated set sizes across the small–large boundary (see also Cordes & Brannon, submitted; Wynn, Bloom & Chiang, 2002).
General Discussion
Results from three experiments support the conclusion that infants do not use number as a last-resort strategy for discriminating sets. Even when continuous extent variables are viable cues for set representation, infants continue to represent the number of items in the set. This pattern of results held for small and large sets alike and even for comparisons between small and large sets, suggesting that, regardless of set size, number is an important and salient variable to human infants.
These results are consistent with recent findings indicating that infant representations of cumulative area (continuous extent) are significantly less precise than numerical representations (Brannon, Abbot & Lutz, 2004; Cordes & Brannon, 2008). That is, in studies where continuous extent varies but number remains constant, infants are capable of discriminating a 2-fold change in set size. In contrast, when number varies but continuous extent remains constant, infants fail to discriminate a 2-fold (or even 3-fold) change in continuous extent (Brannon, Abbot & Lutz, 2004; Cordes & Brannon, 2008), only succeeding when cumulative area changes 4-fold across sets. Thus, it makes sense that infants would attend to number even when other cues are available, given that representations of number are more precise, and therefore more reliable, than representations of other quantitative variables.
The results of Experiment 1 replicate Clearfield & Mix's finding in that infants did detect a change in continuous extent when number remained unchanged from that of habituation; however, infants also detected a change in number and showed no preference for one change or the other. Although the present results differ from those of Clearfield & Mix (1999, 2001), the results are remarkably similar to those reported by Suriyakham, Ehrlich & Levine (submitted). In Experiment 2 of their report, 8-month-old infants dishabituated to both a change in contour length and a change in number of elements regardless of whether simple or complex geometric shapes were used.
Previous research has implicated a double dissociation in infants' ability to attend to number and continuous properties of small sets (Feigenson, Carey & Spelke, 2002; Feigenson, 2005). Feigenson, Carey & Spelke (2002) demonstrated that infants were unable to track number and instead tracked area in a 1 vs. 2 condition when the objects were homogeneous in their individual properties. In contrast, Feigenson (2005) recently showed that infants tracked number and not area in the same 1 vs. 2 contrast when objects were heterogeneous in their individual properties. She concluded that infants may track only number or area but not both for small sets. In contrast, our results suggest that infants can in some circumstances attend to continuous variables and number simultaneously. Additional research will be needed to determine why infants track only one variable in some cases and two variables in others.
Our results should not undermine the importance of the need to control continuous variables carefully when attempting to study numerical abilities in infancy. The Clearfield & Mix (1999) and Feigenson, Carey & Spelke (2002) papers did much to make this argument and raise experimental rigour in the field. However, our results suggest that the implication that infants do not represent discrete number of small sets should be reconsidered. Although there are many circumstances, such as food choice contexts, in which it would make sense for infants to attend to continuous variables over number (e.g. Feigenson, Carey & Hauser, 2002, Experiment 3a) there are other circumstances in which it would be important for infants to attend to number regardless of continuous variables (e.g. Feigenson & Carey, 2003). Our results suggest that infants may in fact track both in habituation studies involving small sets.
An alternative explanation for these results, however, is that infants in Experiment 1 dishabituated to a change in the size (surface area) of the individual elements, as opposed to number or overall contour. From habituation to test, element size changed more than 2-fold (2.25:1) for both types of test stimuli (the 2-element display and the 3-element display). Given that previous research has revealed that 6-month-old infants can detect a 2-fold change in the surface area of a single element (Brannon et al., 2006), infants in this experiment may simply have noticed the change in the size of the individual elements. It should be noted that this aspect of the stimuli was inherent to the Clearfield & Mix experimental design and was simply replicated here. However, we have reason to believe that this was not a factor in our results. Individual element size varied 2-fold between habituation and test in the area control condition of Experiment 2, and varied as much as 4-fold in the contour control condition of Experiment 2 and in Experiment 3. These 4-fold changes are presumably much more salient to the infant than the 2.25-fold change in Experiment 1 or the 2-fold change in the area control condition of Experiment 2. If element size were driving infant looking times, we should find the greatest novelty effects between habituation and both types of test trials in Experiment 2 (contour control condition) and Experiment 3. Yet results of those experiments do not support the hypothesis that infants attended to individual element size – that is, there was no difference in looking times between the two control conditions of Experiment 2, and, furthermore, infants in both Experiment 2 and Experiment 3 did not dishabituate to both types of test trials and instead only dishabituated to the change in number. Thus, our results are inconsistent with the conclusion that infants attended to changes in individual element size.
Why do the results of Experiment 1 differ from those of the original Clearfield & Mix paper? Despite efforts to replicate their design, our experiment did differ from the original in a few minor ways. First, the original experiment was conducted using computer-generated drawings of black squares mounted on white foam board, whereas our design involved computer-generated images presented on computer monitors. Our decision to present images on a computer screen rather than on foam board was motivated by a desire for an increase in precision and control in the timing of stimulus presentation. Throughout the literature, results obtained using three-dimensional objects as stimuli and those obtained using computer-generated stimuli are treated as equivalent in discussions of infant cognition. Currently, there is no evidence to suggest that the employment of varying stimulus types should differentially affect infant quantity representations. Thus, although we had no a priori reason to suspect that this factor would affect results, it is possible that the difference in stimuli led to our different findings. Our study also included a larger sample of infants (24 as opposed to 16 in the original Clearfield & Mix paper), but this change in sample size should not have affected the pattern of results obtained, only increasing the strength of the impact of the results. Finally, Clearfield & Mix limited looking time on each trial to a maximum of 10 seconds and they only analysed looking times obtained from the first two test trials. In contrast, looking time in our experiment was limited to a maximum of 60 seconds per trial, and looking times in all three pairs of test trials were included in the analyses (as is commonly done throughout the infant literature – Brannon, 2002; Feigenson & Carey, 2003; McCrink & Wynn, 2005; Xu, Spelke & Goddard, 2005). Although it is quite likely that these differences in data collection and analysis led to the discrepancy in result patterns, we argue that, in order to allow a reasonable comparison with other findings in the literature, data collection and treatment should be identical to that of other laboratories. Thus, these changes in data collection and analysis were necessary prerequisites for generalizing these results.
On the other hand, there has been very little prior research, if any, investigating the relative salience of number and continuous variables for set sizes larger than 3. Prior to the current study, there have only been two studies investigating continuous extent representations of large sets (Cordes & Brannon, 2008; Brannon, Abbott & Lutz, 2004), both suggesting that these representations are significantly less precise than those of number for large sets. Results of Experiments 2 and 3 indicate that infants preferentially attend to number over continuous extent variables, a finding that is consistent with these previous studies.
Experiment 3 is also notable in that it is one of the first data sets revealing successful numerical discriminations of sets crossing the small–large boundary in young infants (see also Cordes & Brannon, submitted). Although infants are capable of discriminating a 2-fold change in number across large sets and even smaller ratios for small sets, they consistently fail to detect a similar change in number when one set is small and the other is large (Xu, Spelke & Goddard, 2005; Feigenson, Carey & Spelke, 2002; Feigenson & Carey, 2005; Cordes & Brannon, submitted). Recently, however, Cordes & Brannon (submitted) found that 7-month-old infants require a 4-fold change in number to discriminate small from large sets successfully, suggesting the comparison of small sets with large sets is a significantly noisier process than that for exclusively large or exclusively small sets. The results of Experiment 3 corroborate and extend these findings by revealing that, given a sufficient ratio of change, infants attend only to changes in number and do not look longer to a comparable change in continuous extent when comparing small and large sets.
In conclusion, the results of our three experiments, in conjunction with similar findings by Suriyakham, Ehrlich & Levine (submitted), challenge the notion that continuous variables are more salient than number for human infants. Regardless of whether infants were presented with small sets, large sets, or both small and large sets, continuous summary set representations did not trump number. It is important to note that only our final experiment, in which a comparison of small and large sets was made, provided any evidence that number was more salient than extent for infants. In all three studies, however, there was evidence that infants attended to numerical changes even when continuous variables were held constant. Much like recent findings indicating that monkeys represent number even when continuous variable cues are available (Cantlon & Brannon, 2007), human infants spontaneously attend to number despite the availability of other cues for discrimination. Thus, contrary to previous claims by Clearfield & Mix (1999; Mix, Huttenlocher & Levine, 2002), our results suggest that, when encountering sets, representing the number of items in the set is not a last-resort strategy for infants.
Acknowledgements
We thank Donna Lutz for conducting Experiment 1. We thank the members of the Brannon Cognitive Development Laboratory – as well as Susan Levine – for comments on a draft of this paper. We also thank the parents and infants who donated their time to participate in the research. This material is based on work supported by the National Science Foundation (Grant No. 0448250 and an NSF ROLE/DLS research grant to EMB), the National Institute for Mental Health (RO1 MH066154 to EMB), and an NIH NRSA Post-Doctoral Fellowship (to SC).
Footnotes
The absolute sizes of the elements were doubled from the Clearfield & Mix (1999) study, because the infants in this study were seated twice as far from the displays as in the original study (60 cm rather than 30 cm). This was necessary because stimuli were presented on a computer screen rather than as paper slides on a poster board – a minor difference between our design and that of the original Clearfield & Mix design.
Throughout the experiments reported in this paper, all looking times that exceeded 3 standard deviations of the mean of looking times for all test trials in that experiment were treated as outliers and were replaced with the next longest looking time (that was within 3 standard deviations of the mean). This resulted in a total of two looking times in Experiment 1, three in Experiment 2 and one in Experiment 3 being replaced. The original Clearfield & Mix (1999) paper did not exclude outliers, but each trial was limited to a maximum of 10 s, thus preventing the problem of outliers.
Clearfield & Mix (1999) did not conduct an ANOVA on their data. Their analyses involved only looking times measured during the first pair of test trials, relative to looking during the last three habituation trials. In this study, we use the results of all three pairs of test trials, a much more common practice in the infancy literature (e.g. Brannon, 2002; Feigenson, 2005; Xu & Spelke, 2000).
References
- Antell SE, Keating DP. Perception of numerical invariance in neonates. Child Development. 1983;54:695–701. [PubMed] [Google Scholar]
- Brannon EM. The development of ordinal numerical knowledge in infancy. Cognition. 2002;83:223–240. doi: 10.1016/s0010-0277(02)00005-7. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Abbott S, Lutz DJ. Number bias for the discrimination of large visual sets in infancy. Cognition. 2004;93:B59–B68. doi: 10.1016/j.cognition.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Lutz DJ, Cordes S. The development of area discrimination and its implications for numerical abilities in infancy. Developmental Science. 2006;9(6):F59–F64. doi: 10.1111/j.1467-7687.2006.00530.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. How much does number matter to a monkey (Macaca mulatta)? Journal of Experimental Psychology – Animal Behavior Processes. 2007;33(1):32–41. doi: 10.1037/0097-7403.33.1.32. [DOI] [PubMed] [Google Scholar]
- Clearfield MW, Mix KS. Number versus contour length in infants' discrimination of small visual sets. Psychological Science. 1999;10:408–411. [Google Scholar]
- Clearfield MW, Mix KS. Amount versus number: iInfants' use of area and contour length to discriminate small sets. Journal of Cognition and Development. 2001;2:243–260. [Google Scholar]
- Cordes S, Brannon EM. Discrimination of continuous quantities in 6-month old infants: using number is just easier. Child Development. 2008;79(2):476–489. doi: 10.1111/j.1467-8624.2007.01137.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. Discrimination of small from large numbers in 7-month old infants. (submitted) [Google Scholar]
- Davis H. Numerical competence in animals: life beyond Clever Hans. In: Boysen ST, Capaldi EJ, editors. The development of numerical competence: Animal and human models. Erlbaum; Hillsdale, NJ: 1993. pp. 109–125. [Google Scholar]
- Davis H, Memmott J. Autocontingencies: Rats count to three to predict safety from shock. Animal Learning and Behavior. 1983;11:95–100. [Google Scholar]
- Feigenson L. A double-dissociation in infants' representations of object arrays. Cognition. 2005;95:B37–B48. doi: 10.1016/j.cognition.2004.07.006. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S. Tracking individuals via object-files: evidence from infants' manual search. Developmental Science. 2003;6:568–584. [Google Scholar]
- Feigenson L, Carey S. On the limits of infants' quantification of small object arrays. Cognition. 2005;97(3):295–313. doi: 10.1016/j.cognition.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser M. The representations underlying infants' choice of more: object files versus analog magnitudes. Psychological Science. 2002;13:150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Spelke ES. Infants' discrimination of number vs. continuous extent. Cognitive Psychology. 2002;44:33–66. doi: 10.1006/cogp.2001.0760. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Gao F, Levine SC, Huttenlocher J. What do infants know about continuous quantity? Journal of Experimental Child Psychology. 2000;77:20–29. doi: 10.1006/jecp.1999.2556. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: large-number discrimination in human infants. Psychological Science. 2003;14:396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Ratio abstraction by 6-month-old infants. Psychological Science. 2007;18(8):740–745. doi: 10.1111/j.1467-9280.2007.01969.x. [DOI] [PubMed] [Google Scholar]
- Mix KS, Levine SC, Huttenlocher J. Numerical abstraction in infants: another look. Developmental Psychology. 1997;33:423–428. doi: 10.1037//0012-1649.33.3.423. [DOI] [PubMed] [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Multiple cues for quantification in infancy: is number one of them? Psychological Bulletin. 2002;128:278–294. doi: 10.1037/0033-2909.128.2.278. [DOI] [PubMed] [Google Scholar]
- Newcombe N. The nativist–empiricist controversy in the context of recent research on spatial and quantitative development. Psychological Science. 2002;13:395–401. doi: 10.1111/1467-9280.00471. [DOI] [PubMed] [Google Scholar]
- Starkey P, Cooper RG. Perception of numbers by human infants. Science. 1980;210:1033–1035. doi: 10.1126/science.7434014. [DOI] [PubMed] [Google Scholar]
- Starkey P, Spelke ES, Gelman R. Detection of intermodal numerical correspondences by human infants. Science. 1983;222:179–181. doi: 10.1126/science.6623069. [DOI] [PubMed] [Google Scholar]
- Starkey P, Spelke ES, Gelman R. Numerical abstraction by human infants. Cognition. 1990;36:97–127. doi: 10.1016/0010-0277(90)90001-z. [DOI] [PubMed] [Google Scholar]
- Strauss MS, Curtis LE. Infant perception of numerosity. Child Development. 1981;52:1146–1152. [PubMed] [Google Scholar]
- Suriyakham LW, Ehrlich SB, Levine SC. Infants' sensitivity to quantity: number, continuous extent, or both? (submitted) [Google Scholar]
- Uller C, Carey S, Huntley-Fenner G, Klatt L. What representations might underlie infant numerical knowledge? Cognitive Development. 1999;14:1–36. [Google Scholar]
- Wood JN, Spelke ES. Infants' enumeration of actions: numerical discrimination and its signature limits. Developmental Science. 2005;8:173–181. doi: 10.1111/j.1467-7687.2005.00404.x. [DOI] [PubMed] [Google Scholar]
- Wynn K, Bloom P, Chiang W. Enumeration of collective entities by 5-month-old infants. Cognition. 2002;83(3):B55–B62. doi: 10.1016/s0010-0277(02)00008-2. [DOI] [PubMed] [Google Scholar]
- Xu F. Numerosity discrimination in infants: evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES, Goddard S. Number sense in human infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]