Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2010 Apr 21;30(9):1598–1607. doi: 10.1038/jcbfm.2010.49

MRI estimation of global brain oxygen consumption rate

Varsha Jain 1, Michael C Langham 1, Felix W Wehrli 1,*
PMCID: PMC2949253  PMID: 20407465

Abstract

Measuring the global cerebral metabolic rate of oxygen (CMRO2) is a valuable tool for assessing brain vitality and function. Measurement of blood oxygen saturation (HbO2) and flow in the major cerebral outflow and inflow vessels can provide a global estimate of CMRO2. We demonstrate a rapid noninvasive method for quantifying CMRO2 by simultaneously measuring venous oxygen saturation in the superior sagittal sinus with magnetic resonance susceptometry-based oximetry, a technique that exploits the intrinsic susceptibility of deoxygenated hemoglobin, and the average blood inflow rate with phase-contrast magnetic resonance imaging. The average venous HbO2, cerebral blood flow, and global CMRO2 values in eight healthy, normal study subjects were 64%±4%, 45.2±3.2 mL per 100 g per minute, and 127±7 μmol per 100 g per minute, respectively. These values are in good agreement with those reported in literature. The technique described is noninvasive, robust, and reproducible for in vivo applications, making it ideal for use in clinical settings for assessing the pathologies associated with dysregulation of cerebral metabolism. In addition, the short acquisition time (∼30 seconds) makes the technique suitable for studying the temporal variations in CMRO2 in response to physiologic challenges.

Keywords: cerebral blood flow measurement, cerebral oxygen metabolism, MR susceptometry, oxygen saturation, phase-contrast MRI

Introduction

Under normal physiologic conditions, aerobic metabolism of glucose is the primary metabolic fuel for energy production in the human brain (Greene et al, 2003; Lowry et al, 1964). Although the brain represents only 2% of the body weight, it receives 15% of the cardiac output and consumes 20% of the total body oxygen (Magistretti and Pellerin, 1996; Quastel and Wheatley, 1932). The above highlights the critical dependence of brain function on continuous, efficient usage of oxygen, and the organ's heightened vulnerability and sensitivity to alterations in oxygen supply. There is a considerable body of research exploring the dysregulation of glucose oxidative metabolism in diseases of the brain. Many of the most common disorders of the brain, such as Alzheimer's, Parkinson's, Huntington's, multiple system disorder, progressive supranuclear palsy, mitochondrial encephalomyopathy, and others, have been found to be associated with alterations in cerebral oxygen metabolism (Ishii et al, 1996; Leenders et al, 1986; Santens et al, 1997; Shishido et al, 1996; Tanaka et al, 1997). In addition, a measure for assessing the cerebral metabolic rate of oxygen (CMRO2) consumption will further enhance our understanding of normal cerebral physiology during rest, sleep, anesthesia, aging, functional brain tasks, and physiologic challenges, as well as be useful for evaluating the effect of systemic disease processes such as hypertension and diabetes on cerebral oxygen metabolism. Thus, a robust and reliable measure for quantifying CMRO2 would serve as an important tool for exploring the neuro-metabolic–hemodynamic relationships during cerebral activation and pathophysiologic conditions.

Currently, CMRO2 is not routinely measured clinically, in that several practical limitations have prevented its widespread application. Positron emission tomography provides the most direct measurement of CMRO2 through imaging of the accumulated inhaled 15O-labeled radiotracers in the brain, which, after distribution into the tissue, are converted into 15O-labeled water (Ito et al, 2005; Mintun et al, 1984). Positron emission tomography is, however, restrictive in terms of its utility because of the high radiation dose, relatively complex setup required for the constant delivery of radio-labeled gases, high associated expenses, and long scan times, during which it is assumed that no change in physiologic state occurs.

Other methods for quantifying CMRO2 have relied on estimating venous oxygen saturation levels using jugular vein oximetry involving catheterization and measuring flow through optical measurements or Doppler ultrasound (Mayberg and Lam, 1996). However, because of the invasiveness of the technique, it is prone to complications such as carotid artery puncture (incidence 1% to 4.5%), hematoma formation, jugular vein occlusion, thrombosis, risk of bacteremia, and other infections (Coplin et al, 1997). In addition, the accuracy of the method is highly dependent on personnel skill and experience.

In a recent paper, a magnetic resonance imaging (MRI) approach for quantifying CMRO2, based on the measurement of transverse relaxation time T2 (Wright et al, 1991), has been described (Xu et al, 2009). The method, termed T2-relaxation-under-spin-tagging (Lu and Ge, 2008), allows noninvasive estimates of venous oxygen saturation in vivo. However, T2-based methods rely on an in vitro calibration curve to translate T2 measurements to venous oxygen saturation levels (Wright et al, 1991). In addition, an acquisition time of over 4 minutes limits the utility of this technique for obtaining time-resolved CMRO2 measurements, as would be desirable to study the effect of physiologic challenges and functional tasks on the global rate of oxygen consumption.

In this study, we present a rapid noninvasive method for quantifying CMRO2. The method comprises simultaneous estimation of oxygen saturation and cerebral blood flow (CBF) in the major vessels draining and feeding the brain. Specifically, venous blood oxygen saturation is estimated using susceptometry-based oximetry (Fernandez-Seara et al, 2006; Haacke et al, 1997), which quantifies the intravascular bulk magnetic susceptibility relative to the surrounding tissue by exploiting the inherent paramagnetism of deoxyhemoglobin in erythrocytes. The blood flow is quantified in the major inflow vessels (internal carotid arteries and vertebral arteries) using phase-contrast MRI (Bryant et al, 1984; Dumoulin and Hart, 1986).

Materials and Methods

Estimation of the Cerebral Metabolic Rate of Oxygen Consumption

The cerebral metabolic rate of oxygen can be estimated by combining venous and arterial oxygen saturation and CBF measurements using Fick's principle (Kety and Schmidt, 1948),

graphic file with name jcbfm201049e1.jpg

where CMRO2 is the cerebral metabolic rate of oxygen consumption in μmol/minute per 100 g, CBF is the total cerebral blood inflow to the brain in mL per 100 g per minute, SaO2 and SvO2 represent the arterial and venous oxygen saturation levels, respectively, Ca is the oxygen concentration in moles of O2 per 100 mL of blood. On the basis of a typical hemoglobin level of 14.7 g/dL (at a hematocrit (Hct) of 0.42) and an O2 carrying capacity of 1.39 mL of O2 per gram of hemoglobin (West, 2007), using the ideal gas law, Ca was calculated to be 836 μmol O2 per 100 mL blood. For our CMRO2 measurements, an arterial oxygen saturation value of 98% was assumed. This is a valid assumption for normal healthy adults under resting conditions, in whom arterial blood is almost fully oxygenated (West, 2007). SvO2 was estimated by magnetic resonance blood oximetry. We note that, in principle, blood oximetry can be used to estimate SaO2 as well. However, this measurement of cerebral arterial supply is challenging as the presence of the oropharynx or trachea in the neck causes severe susceptibility-induced magnetic field perturbations, making the SaO2 measurement in the internal carotid and vertebral arteries difficult. The measurement in the distal cerebral arterial vasculature (such as the middle cerebral artery) is hampered by constraints such as vessel tortuosity, orientation with respect to Bo field, and small-vessel diameter (∼2 mm). The flow rate was quantified with a nongated phase-contrast MRI technique (Bryant et al, 1984; Dumoulin and Hart, 1986; see below).

Principles of Magnetic Resonance Blood Oximetry

Magnetic resonance susceptometry-based oximetry (Fernandez-Seara et al, 2006; Haacke et al, 1997) relies on the magnetic susceptibility difference Δχ between intravascular blood and surrounding tissue. By modeling the blood vessel as a long paramagnetic cylinder, an exact expression for the incremental field ΔB can be derived as (Schenck, 1996)

graphic file with name jcbfm201049e2.jpg

ΔB is measured from a phase difference image that yields φ(TE1)−φ(TE2)=γΔBΔTE, where ΔTE is the interecho spacing between two gradient-recalled echoes. For whole blood

graphic file with name jcbfm201049e3.jpg

where Δχdo=4π·0.27 p.p.m. (Spees et al, 2001) is the susceptibility difference in SI units between fully deoxygenated and fully oxygenated erythrocytes, HbO2 is the fraction of the oxygenated hemoglobin, Hct is the volume fraction of the packed erythrocytes in whole blood, and θ is the tilt angle of the vessel with respect to the main field Bo. It is noted that various values of Δχdo (Thulbourn et al, 1982; Weisskoff et al, 1992; Plyavin et al, 1983) have been reported earlier. We have particular confidence in the value reported by Spees et al based on their thorough work, agreement with two different approaches, and a semitheoretical analysis. Thus, HbO2 can be determined by combining equations (2) and (3) as

graphic file with name jcbfm201049e4.jpg

where Δφ is the average phase difference between intravascular blood and the surrounding tissue.

Magnetic Resonance Flow Quantification

The flow rate was quantified with a phase-contrast technique (Bryant et al, 1984; Dumoulin and Hart, 1986). In the implementation used, the imaging pulse sequence is played out twice in an interleaved manner. In both the acquisitions, the zeroth gradient moment for the slice-selection gradient (i.e., the gradient parallel to the direction of flow) is 0, as usual; thus, the signal from stationary tissue protons is nulled on subtraction of the two datasets. The first gradient moment (M1=∫G(t)t dt) of the two interleaves, which determines the sensitivity of the measured phase difference, Δϕ, accrued by the flowing spins, is given as

graphic file with name jcbfm201049e5.jpg

where ΔM1 is the difference in first moment between the two interleaves. It is convenient to introduce the parameter VENC (Velocity ENCoding) (Pelc et al, 1994), which is the velocity causing a phase shift of π radians. In this manner, equation (5) can be rewritten as

graphic file with name jcbfm201049e6.jpg

from which the blood flow velocity is determined pixel by pixel. It should be noted that the maximum velocity measured should not exceed the user-defined parameter VENC to avoid phase aliasing.

Magnetic Resonance Imaging Protocol

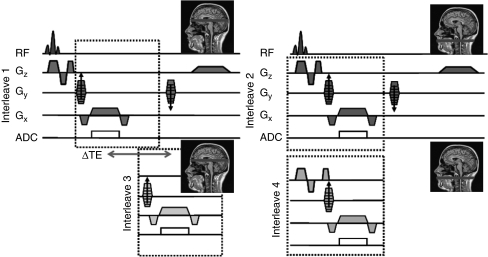
Magnetic resonance experiments were performed on a 3-T Siemens TIM Trio system using vendor-supplied head and neck coils. An interleaved 2D gradient-recalled echo sequence programmed in SequenceTree (Magland and Wehrli, 2006), shown in Figure 1, was used to obtain simultaneous oxygen saturation and CBF measurements. The sequence consisted of four interleaves (Figure 1). All but the fourth interleave (VENC=60 cm/s) were flow compensated (i.e., the slice-selection gradient structure was chosen such that M1=0) and the interleaves alternated between making the acquisition at the level of the superior sagittal sinus (SSS) and mouth orifice to measure oxygen saturation and total cerebral inflow, respectively. The first and the third interleaves with an echo time (TE) of 7.025 and (7.025+2.5) milliseconds (interecho time, ΔTE=2.5 milliseconds), respectively, were acquired at the level of SSS in the occipital region for blood oxygenation quantification. This interleaved acquisition scheme allowed us to attain short interecho times, thereby avoiding phase wrapping. The second and fourth interleaves were acquired with the same echo time (7.025 milliseconds) at the level of the mouth orifice and were used to quantify the average velocity. For the static phantom experiments, all interleaves were acquired at the same axial location and the data from the first and third interleaves were used for estimation of susceptibility relative to distilled water.

Figure 1.

Figure 1

Open in a new tab

Interleaved 2D gradient-recalled echo sequence alternating between the two anatomic locations (Gx=frequency-encoding gradient, Gy=phase-encoding gradient, Gz=slice-selection gradient). All but the fourth interleave are flow compensated along the slice-select direction. The fourth interleave is flow encoded with a Velocity ENCoding (VENC)=60 cm/second. The echo time difference (ΔTE) between the first and third interleaves is 2.5 milliseconds (TE=7.025 milliseconds). The dashed boxes represent sequence parameters that changed between the interleaves.

The scan parameters used were as follows: FOV=208 × 208 × 5 mm3, voxel size=1 × 1 × 5 mm3, dwell time=15 μs, flip angle=25°, VENC=60 cm/second, repetition time (TR)=30 milliseconds, yielding a total scan time of 28 seconds. In addition, a high-resolution scan at the level of the mouth orifice over the same slice as chosen above (voxel size=0.5 × 0.5 × 5 mm3, FOV=208 × 208 × 5 mm3) was obtained to improve the accuracy of estimation of the vessel cross-sectional area.

The location of the SSS was prescribed based on a sagittal image (Figure 4A). A multislice axial localizer was used to choose a slice with a relatively straight section of SSS based on the observation of a relatively constant spatial position and cross-section of the vessel. The imaging slice was oriented axially, intersecting the SSS at about 1 to 2 cm above the confluence of sinuses (location at which the inferior sagittal, straight, and transverse sinuses join the SSS). For the prescription of an appropriate slice for flow imaging, it is noted that the anatomic courses of the internal carotid and vertebral arteries before the second cervical vertebra are both nearly parallel to the scanner's z axis. This parallel linear segment is variable in length because of individual differences in the location of the common carotid bifurcation, but is generally a few centimeters in length. A multislice axial localizer was used to identify this segment in the region of the oropharynx, based on the observation of a relatively constant in-plane position and cross-section of the vessel, as it is at the same axial location as the second and third cervical vertebrae.

In addition, we acquired a T1-weighted 3D magnetization-prepared rapid gradient-echo (MPRAGE; Mugler and Brookeman, 1990) image dataset (voxel size=1 × 1 × 1 mm3) to estimate the intracranial volume in each subject, so that the CMRO2 levels could be calculated per 100 g of brain mass. An average brain density of 1.05 g/mL was used for the above calculation (Kretschmann et al, 1986).

The times taken for various scans were 1:12 minutes for the multislice localizer, 28 seconds for the 2D gradient-recalled echo for simultaneous oxygen saturation and flow measurements, 1:37 minutes for T1-MPRAGE, summing to a total scan duration of 3:17 minutes for whole brain global CMRO2 estimation.

Rationale for Cerebral Metabolic Rate of Oxygen Measurement Locations

The SSS was preferred over the internal jugular vein (another major draining vein) in light of the often severe susceptibility artifacts caused by the proximity of air spaces such as the oral cavity and trachea. In addition, Xu et al (2009) have previously shown that the oxygen saturation levels in the SSS are comparable to those in the internal jugular vein. Phase measurement in the SSS is convenient and robust in the absence of major tissue interfaces with markedly different susceptibilities.

Blood flow rates were measured at the neck level in the four feeding vessels, the left and right internal carotid, and vertebral arteries. These vessels run parallel to the neck and the spine, respectively, and the chosen axial slice was perpendicular to the vessels and Bo. Total CBF was quantified by measuring inflow instead of outflow, as besides the internal jugular vein, certain secondary vessels such as the vertebral venous plexi also drain the brain (Cooper, 1960); the flow measurement in these vessels is challenging.

Phantom Experiments

The blood vessel of interest (SSS) was modeled as a long circular cylinder (Fernandez-Seara et al, 2006; Haacke et al, 1997). The SSS runs in the sagittal grove from the anterior to posterior head, tucked between the two cerebral cortices. As a result, the vessel has a triangular (rather than a circular) cross-section. To ensure the applicability of the previously validated model, a phantom was constructed. It consisted of two 12-cm-long tubes, with a circular and triangular cross-section, filled with paramagnetic gadolinium-doped distilled water. The tubes were immersed in the center of a cylindrical plastic container filled with distilled water, with the tubes oriented parallel to the container's long axis. The concentrations of Gd-DTPA in the solutions were 1, 1.25, 1.5, and 1.75 mmol/L so as to cover a range of relative magnetic susceptibilities matching the expected range of susceptibility differences found between partially deoxygenated blood and tissue. The concentrations chosen corresponded to oxygen saturation values between 58% and 76% (assuming an Hct of 0.42).

In Vivo Estimation of Cerebral Metabolic Rate of Oxygen

The human subject studies were approved by the Institutional Review Board of the University of Pennsylvania and informed written consent was obtained from each volunteer. Eight healthy male volunteers participated in the study (mean age 25 years; s.d. 5 years). The CMRO2 measurement was repeated three times in each volunteer at intervals of 5 to 10 minutes. In each session, three consecutive measurements were obtained to estimate the mean and standard deviation of each parameter for each session. The subject was asked to rise from the scanner table between each of the three scanning sessions. A cushioned head stabilizer was used to minimize motion and the subject was instructed to stay alert during the course of the scans as CMRO2 measurements are known to be affected by degree of mental alertness.

Data Analysis

For HbO2 quantification phase maps were obtained, computed as the phase difference between echoes through

graphic file with name jcbfm201049e7.jpg

where Z1 and Z2 represent complex values of a particular pixel in the images of two echoes, respectively; the asterisk denotes complex conjugate. The susceptibility difference between air and tissue compartments causes field inhomogeneity, resulting in low spatial-frequency modulation of the phase signal. To reduce its effect, a retrospective correction method was implemented, which approximates the field inhomogeneity with a second-order polynomial, after appropriately masking and weighting the phase image with the corresponding masked magnitude image (Langham et al, 2009a). To estimate the susceptibility values, the average phase difference between the region of interest and the neighboring area (adjacent water in the phantom experiments and tissue for in vivo studies) was calculated. It should be noted that at the investigated field strength, the phase difference images acquired at relatively short TEs are not sensitive to the white and gray matter boundaries (Abduljalil et al, 2003) as shown in Figure 4D. The background brain parenchyma was also used as reference tissue in a study using a similar method for quantifying oxygen saturation in pial veins (Haacke et al, 1997).

For the quantification of total cerebral blood flow, a signal intensity threshold was applied to the high-resolution magnitude image to obtain a mask for each of the four vessels of interest (internal carotid and vertebral arteries) for measuring the cross-sectional area. The mask was then downscaled to match the resolution of the phase-contrast image and applied to the velocity maps to obtain the whole-brain cerebral blood velocity in mL/minute. Total brain volume was estimated using a semiautomated region growing algorithm in ITKSnap (Yushkevich et al, 2006). Analysis of variance was used to test intersubject variability of various test parameters. Within-subject coefficient of variation and intraclass correlation coefficient were used to test technique reproducibility. In addition, the correlation between the arterio-venous oxygen saturation difference (AVO2D=SaO2−SvO2) and global CBF was analyzed. The above were performed using JMP Statistical Software Package 7.0 (SAS, Cary, NC, USA).

Results

Phantom Experiments

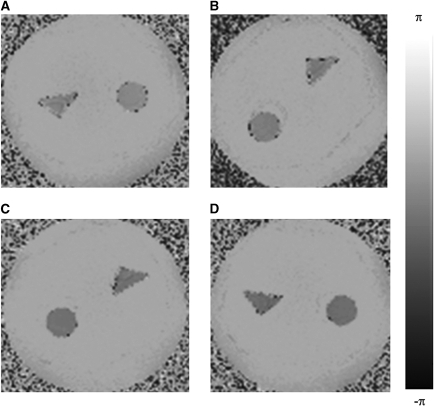
Figure 2 shows the phase difference images of the four phantom experiments. The relative mean difference between the susceptibility values derived from the phase measurements in the circular and triangular cross-section phantoms was 2.6%, which would correspond to an average absolute difference in oxygen saturation of 0.8% at a Hct of 0.42 (Table 1).

Figure 2.

Figure 2

Open in a new tab

Phase-difference images of the cross-sectional area of the phantoms containing (A) 1 mmol/L, (B) 1.25 mmol/L, (C) 1.5 mmol/L, and (D) 1.75 mmol/L Gd-DTPA in distilled water.

Table 1. The difference in oxygen saturation between the circular and triangular phantom tubes for various concentrations of Gd (assuming Hct=0.42).

[Gd] (mmol/L) ΔOx-Sat (%)
1 1.08
1.25 0.08
1.5 0.75
1.75 1.19
Open in a new tab

Gd, Gadolinium; Hct, hematocrit; Ox-Sat, Oxygen Saturation.

Summary data from the triangular phantom study.

In Vivo Studies

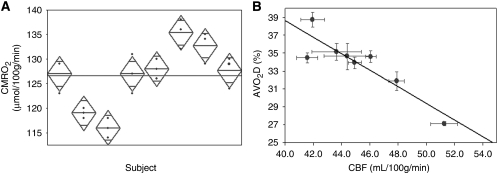
Magnitude and velocity images for the estimation of the whole-brain CBF are showed in Figure 3. Figure 4 shows the magnitude and phase difference images acquired at the level of the SSS used for the estimation of oxygen saturation. The average values of venous oxygen saturation and CBF for the group of eight subjects were 64%±4% and 45.2±3.2 mL per 100 g per minute, respectively. The mean CMRO2 value found was 127±7 μmol per 100 g per minute. The results of the reproducibility test performed in eight subjects are summarized in Table 2. The oxygen saturation and flow measurements in the three sessions varied maximally by 2% HbO2 and 2.3 mL per 100 g per minute, respectively. The maximal variation in CMRO2 over the three sessions for the group was 8 μmol per 100 g per minute. Figure 5A shows a scatter plot of the mean CMRO2 values computed for each subject for the three scanning sessions. The coefficients of variation for CMRO2, venous oxygen saturation, and CBF measurements were 3.2%, 2.3%, and 3.1%, and the intraclass coefficients were 0.94, 0.98, and 0.97, respectively. The AVO2D was found to be negatively correlated with global CBF across the subjects (R2=0.74, P<0.006), with large AVO2D corresponding to low global CBF values (Figure 5B).

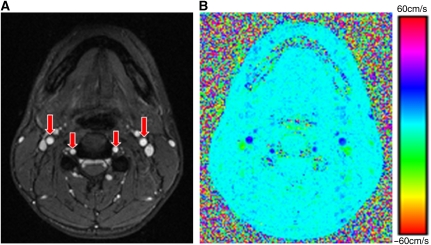
Figure 3.

Figure 3

Open in a new tab

(A) Axial magnitude image of mouth orifice highlighting the major inflow vessels (internal carotid and vertebral arteries; red arrows); (B) corresponding velocity map used for the calculation of total cerebral blood flow rate.

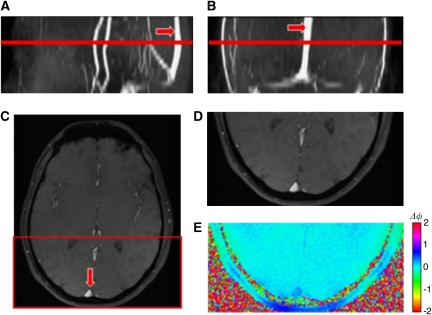
Figure 4.

Figure 4

Open in a new tab

(A) Sagittal, (B) coronal, and (C) axial magnitude images of the brain highlighting the superior sagittal sinus (red arrow). Note that the sinus is fairly straight; the highlighted red line represents the imaging slice location. Zoomed in axial (D) magnitude and (E) phase image of the superior sagittal sinus.

Table 2. Estimated total cerebral blood flow (CBF), venous oxygen saturation in superior sagittal sinus (SvO2), and cerebral metabolic rate of oxygen (CMRO2) levels in eight subjects evaluated in three successive sessions to show short-term reproducibility.

  Session 1 Session 2 Session 3
  CBF SvO2 CMRO2 CBF SvO2 CMRO2 CBF SvO2 CMRO2
Subject (mL per 100 g per minute) (%) (μmol per 100 g per minute) (mL per 100 g per minute) (%) (μmol per 100 g per minute) (mL per 100 g per minute) (%) (μmol per 100 g per minute)
1 44.4±1.2 65±1 123±4 45.1±1.0 64±1 129±5 45.4±0.7 64±1 129±4
2 42.4±1.7 64±2 119±5 41.0±1.3 63±2 118±2 41.4±0.7 63±1 120±3
3 52.4±1.1 71±1 118±4 50.8±1.1 71±2 114±4 50.7±1.3 70±1 116±3
4 47.3±1.3 66±2 127±6 48.2±0.6 65±1 131±7 48.3±1.3 67±2 123±5
5 46.3±1.2 65±2 128±3 43.6±1.4 63±2 126±3 43.3±1.7 62±2 130±3
6 41.3±2.0 57±2 136±3 42.9±0.4 58±0 138±2 41.7±1.2 59±1 132±2
7 45.7±1.3 63±1 129±5 46.5±2.3 62±2 134±2 46.1±1.6 62±2 135±2
8 45.2±1.2 63±1 130±1 42.5±0.5 62±1 124±3 42.8±1.5 61±0 129±4
Average 45.7±3.8 64±4 126±6 45.1±3.3 64±4 127±8 45.0±3.3 64±4 127±6
Open in a new tab

Summary of the reproducibility data. Global averages are given in the last row.

Figure 5.

Figure 5

Open in a new tab

(A) Scatter plot of the cerebral metabolic rate of oxygen (CMRO2) for each subject over three scanning sessions illustrating reproducibility. The vertical span of each diamond represents the 95% confidence interval (CI) for each group. (B) Correlation between AVO2D and total cerebral blood flow (CBF) in the eight subjects (R2=0.74, P<0.006). Note that subjects with higher CBF values tend to have lower AVO2D.

Discussion and Conclusion

We have introduced an MRI-based technique for quantifying absolute CMRO2 in humans in vivo. The method is robust, reproducible, and allows for simultaneous measurement of oxygen saturation and flow rate. Our protocol takes around 3 minutes for whole-brain CMRO2 quantification (including localizers), where the physiologically relevant SvO2 and blood flow estimation takes less than 30 seconds. The short acquisition times afforded by the technique make it suited for monitoring changes in CMRO2 in response to physiologic challenges. The measured whole-brain CMRO2 level averaged across the eight study subjects was 127±7 μmol per 100 g per minute, which is in good agreement with the values reported in literature (Hattori et al, 2004; Ibaraki et al, 2008; Xu et al, 2009). Our results illustrate that the technique can estimate CMRO2 with a high degree of precision and reliability (average coefficient of variation and intraclass correlation coefficient of 3.2% and 0.94, respectively). This level of precision is comparable to that reported using more invasive techniques. The strong correlation observed between the AVO2D and global CBF is expected and has been reported earlier (Xu et al, 2009; Figure 5B). The intersubject variations in venous oxygen saturation, CBF, and CMRO2 measurements were found to be statistically significant as compared with the intrasubject variations in these parameters (two-tailed analysis of variance, P<0.003). These intersubject differences observed are physiologic and represent normal differences between subjects; the range seen is consistent with literature reports that have evaluated oxygen saturation and CMRO2 levels using invasive methods such as jugular vein catheterization and positron emission tomography (Coles et al, 2002; Hattori et al, 2004; Nagdyman et al, 2005; Powers et al, 1985).

Other MRI-based approaches for the noninvasive quantification of blood oxygenation have resorted to measurements of the transverse relaxation times, T2 and T2*, which are also related to the deoxyhemoglobin concentration in erythrocytes (Chien et al, 1994; Li et al, 1998; Wright et al, 1991). Unlike susceptometry-based oximetry, the sensitivity of T2 and T2*-based measurements varies with the level of hemoglobin oxygen saturation (both depend quadratically on HbO2, although the relationship is piece-wise linear over a small range of HbO2 values; Chien et al, 1994; Li et al, 1998; Wright et al, 1991). The in vivo estimation of these parameters in the major blood vessels is complicated by body motion (requiring suspended respiration), pulsatile blood flow (necessitating cardiac gating), and the need for long pulse repetition times, leading to prolonged acquisition times (Li et al, 1998; Stainsby and Wright, 1998). The above factors make these methods less suited for measuring physiologic variations in CMRO2 over experimental time frames as well as for clinical evaluations. Alternative approaches using positron emission tomography or Single Positron Emission Tomography (SPECT) (Frackowiak et al, 1980; Mintun et al, 1984) rely on contrast agents, are invasive (generally requiring arterial/venous lines for the administration of contrast agents), lengthy, and expensive.

Owing to the thin medial layer and lower distending pressure in veins, the SSS does not have a circular (or elliptic) cross-section as shown in Figure 4C. However, as ∣χ∣≪1, the induced field inside the vessel is parallel to the applied field (Schenck, 1996), and more importantly, the effect of cross-sectional geometry is negligible as long as the vessel is parallel to the applied field. In our study, the SSS, used for SvO2 measurement, was essentially parallel to Bo (average tilt angle across subjects <6°) and has negligible curvature at the measurement site (Figures 4A and 4B). The above predictions are supported by our phantom experiments (Figure 2; Table 1), consisting of test tubes with triangular and circular cross-section filled with varying Gd-DTPA-doped water concentrations positioned parallel to Bo. The uniform phase accumulation inside the triangular tubes, the clear phase separation from the surrounding distilled water, and strong agreement with the susceptibility measurement in the circular tubes lend strong support to the validity of the model adopted in this work. The largest relative difference in measured susceptibility between tubes of circular and triangular cross-section was less than 5%, which translates to a difference of less than 2% HbO2. In keeping with the requirements for applicability of the model, the SSS also complies with the long cylinder approximation. Previous work has shown that a length to diameter ratio of ∼ 6 is sufficient to apply the long cylinder model (Langham et al, 2009b). Posteriorly, the typical sagittal sinus segment has length to diameter ratios of >6 (typical vessel diameter ∼5 to 6 mm; vessel segment length ∼4 cm; Figures 4A and 4B).

Finally, a few constants prone to intersubject variability and used in the estimation of CMRO2 can be additional sources of error. A typical Hct value of 42% was used for all our measurements. We expect that the variation in hematocrit within our study cohort is minimal (all males, age: 25±5 years) and could be obtained by blood draws. A typical SaO2 value of 98% was used for all the calculations. Although this value is widely accepted in literature, an accurate measurement of SaO2 can easily be obtained at a different site where an artery is present.

The present technique estimates global CMRO2 but not regional. All previously explored methods for regional CMRO2 quantification are model based and are still in their developmental stages. One such approach relies on the estimation of the contribution to the effective transverse relaxation rate from regional magnetic field inhomogeneity (T2′) resulting from partially desaturated blood in the capillary bed. From this quantity, along with a measurement of capillary volume, the oxygen extraction fraction is derived (An and Lin, 2003; He and Yablonskiy, 2007). Nonetheless, the importance of a global measure to estimate absolute cerebral metabolism is of interest in its own right.

In conclusion, we have shown a noninvasive MRI-based approach for the estimation of global whole-brain CMRO2 based on simultaneous measurement of average blood flow rate and oxygen saturation in major inflow and outflow vessels to the brain. The noninvasive nature of the technique, its robustness, and straightforward implementation make it suitable for applications in clinical settings for the assessment of pathologies associated with disorders of brain metabolism. Rapid acquisition afforded by the technique makes it specially suited for studying temporal variations in CMRO2 under physiologic challenges such as hypercapnia, hyperoxia, caffeine stimulation, and sedation, as well as under functional brain paradigms.

The authors declare no conflict of interest.

References

  1. Abduljalil AM, Schmalbrock P, Novak V, Chakeres DW. Enhanced gray and white matter contrast of phase susceptibility-weighted images in ultra-high-field magnetic resonance imaging. J Magn Reson Imaging. 2003;18:284–290. doi: 10.1002/jmri.10362. [DOI] [PubMed] [Google Scholar]
  2. An H, Lin W. Impact of intravascular signal on quantitative measures of cerebral oxygen extraction and blood volume under normo- and hypercapnic conditions using an asymmetric spin echo approach. Magn Reson Med. 2003;50:708–716. doi: 10.1002/mrm.10576. [DOI] [PubMed] [Google Scholar]
  3. Bryant DJ, Payne JA, Firmin DN, Longmore DB. Measurement of flow with NMR imaging using a gradient pulse and phase difference technique. J Comput Assist Tomogr. 1984;8:588–593. doi: 10.1097/00004728-198408000-00002. [DOI] [PubMed] [Google Scholar]
  4. Chien D, Levin DL, Anderson CM. MR gradient echo imaging of intravascular blood oxygenation: T2* determination in the presence of flow. Magn Reson Med. 1994;32:540–545. doi: 10.1002/mrm.1910320419. [DOI] [PubMed] [Google Scholar]
  5. Coles JP, Minhas PS, Fryer TD, Smielewski P, Aigbirihio F, Donovan T, Downey SP, Williams G, Chatfield D, Matthews JC, Gupta AK, Carpenter TA, Clark JC, Pickard JD, Menon DK. Effect of hyperventilation on cerebral blood flow in traumatic head injury: clinical relevance and monitoring correlates. Crit Care Med. 2002;30:1950–1959. doi: 10.1097/00003246-200209000-00002. [DOI] [PubMed] [Google Scholar]
  6. Cooper ER. The vertebral venous plexus. Acta Anat (Basel) 1960;42:333–351. doi: 10.1159/000141669. [DOI] [PubMed] [Google Scholar]
  7. Coplin WM, O'Keefe GE, Grady MS, Grant GA, March KS, Winn HR, Lam AM.1997Thrombotic, infectious, and procedural complications of the jugular bulb catheter in the intensive care unit Neurosurgery 41101–107.discussion 107–9 [DOI] [PubMed] [Google Scholar]
  8. Dumoulin CL, Hart HR., Jr Magnetic resonance angiography. Radiology. 1986;161:717–720. doi: 10.1148/radiology.161.3.3786721. [DOI] [PubMed] [Google Scholar]
  9. Fernandez-Seara MA, Techawiboonwong A, Detre JA, Wehrli FW. MR susceptometry for measuring global brain oxygen extraction. Magn Reson Med. 2006;55:967–973. doi: 10.1002/mrm.20892. [DOI] [PubMed] [Google Scholar]
  10. Frackowiak RS, Lenzi GL, Jones T, Heather JD. Quantitative measurement of regional cerebral blood flow and oxygen metabolism in man using 15O and positron emission tomography: theory, procedure, and normal values. J Comput Assist Tomogr. 1980;4:727–736. doi: 10.1097/00004728-198012000-00001. [DOI] [PubMed] [Google Scholar]
  11. Greene AE, Todorova MT, Seyfried TN. Perspectives on the metabolic management of epilepsy through dietary reduction of glucose and elevation of ketone bodies. J Neurochem. 2003;86:529–537. doi: 10.1046/j.1471-4159.2003.01862.x. [DOI] [PubMed] [Google Scholar]
  12. Haacke EM, Lai S, Reichenbach JR, Kuppusamy K, Hoogenraad FGC, Takeichi H, Lin W. In vivo measurement of blood oxygen saturation using magnetic resonance imaging: a direct validation of the blood oxygen level-dependent concept in functional brain imaging. Hum Brain Mapp. 1997;5:341–346. doi: 10.1002/(SICI)1097-0193(1997)5:5<341::AID-HBM2>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
  13. Hattori N, Bergsneider M, Wu HM, Glenn TC, Vespa PM, Hovda DA, Phelps ME, Huang SC. Accuracy of a method using short inhalation of (15)O-O(2) for measuring cerebral oxygen extraction fraction with PET in healthy humans. J Nucl Med. 2004;45:765–770. [PubMed] [Google Scholar]
  14. He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn Reson Med. 2007;57:115–126. doi: 10.1002/mrm.21108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ibaraki M, Miura S, Shimosegawa E, Sugawara S, Mizuta T, Ishikawa A, Amano M. Quantification of cerebral blood flow and oxygen metabolism with 3-dimensional PET and 15O: validation by comparison with 2-dimensional PET. J Nucl Med. 2008;49:50–59. doi: 10.2967/jnumed.107.044008. [DOI] [PubMed] [Google Scholar]
  16. Ishii K, Kitagaki H, Kono M, Mori E. Decreased medial temporal oxygen metabolism in Alzheimer's disease shown by PET. J Nucl Med. 1996;37:1159–1165. [PubMed] [Google Scholar]
  17. Ito H, Ibaraki M, Kanno I, Fukuda H, Miura S. Changes in cerebral blood flow and cerebral oxygen metabolism during neural activation measured by positron emission tomography: comparison with blood oxygenation level-dependent contrast measured by functional magnetic resonance imaging. J Cereb Blood Flow Metab. 2005;25:371–377. doi: 10.1038/sj.jcbfm.9600030. [DOI] [PubMed] [Google Scholar]
  18. Kety SS, Schmidt CF. The effects of altered arterial tensions of carbon dioxide and oxygen on cerebral blood flow and cerebral oxygen consumption of normal young men. J Clin Invest. 1948;27:484–492. doi: 10.1172/JCI101995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kretschmann HJ, Kammradt G, Krauthausen I, Sauer B, Wingert F. Brain growth in man. Bibl Anat. 1986;28:1–26. [PubMed] [Google Scholar]
  20. Langham MC, Magland JF, Epstein CL, Floyd TF, Wehrli FW. Accuracy and precision of MR blood oximetry based on the long paramagnetic cylinder approximation of large vessels. Magn Reson Med. 2009b;62:333–340. doi: 10.1002/mrm.21981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Langham MC, Magland JF, Floyd TF, Wehrli FW. Retrospective correction for induced magnetic field inhomogeneity in measurements of large-vessel hemoglobin oxygen saturation by MR susceptometry. Magn Reson Med. 2009a;61:626–633. doi: 10.1002/mrm.21499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Leenders KL, Frackowiak RS, Quinn N, Marsden CD. Brain energy metabolism and dopaminergic function in Huntington's disease measured in vivo using positron emission tomography. Mov Disord. 1986;1:69–77. doi: 10.1002/mds.870010110. [DOI] [PubMed] [Google Scholar]
  23. Li D, Wang Y, Waight DJ. Blood oxygen saturation assessment in vivo using T2* estimation. Magn Reson Med. 1998;39:685–690. doi: 10.1002/mrm.1910390503. [DOI] [PubMed] [Google Scholar]
  24. Lowry OH, Passonneau JV, Hasselberger FX, Schulz DW. Effect of ischemia on known substrates and cofactors of the glycolytic pathway in brain. J Biol Chem. 1964;239:18–30. [PubMed] [Google Scholar]
  25. Lu H, Ge Y. Quantitative evaluation of oxygenation in venous vessels using T2-relaxation-under-spin-tagging MRI. Magn Reson Med. 2008;60:357–363. doi: 10.1002/mrm.21627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Magistretti PJ, Pellerin L. Cellular mechanisms of brain energy metabolism. Relevance to functional brain imaging and to neurodegenerative disorders. Ann N Y Acad Sci. 1996;777:380–387. doi: 10.1111/j.1749-6632.1996.tb34449.x. [DOI] [PubMed] [Google Scholar]
  27. Magland J, Wehrli F.2006Pulse sequence programming in a dynamic visual environment Proceedings of the 14th Annual Meeting of ISMRMSeattle, WA (Abstract 578)
  28. Mayberg TS, Lam AM. Jugular bulb oximetry for the monitoring of cerebral blood flow and metabolism. Neurosurg Clin N Am. 1996;7:755–765. [PubMed] [Google Scholar]
  29. Mintun MA, Raichle ME, Martin WR, Herscovitch P. Brain oxygen utilization measured with O-15 radiotracers and positron emission tomography. J Nucl Med. 1984;25:177–187. [PubMed] [Google Scholar]
  30. Mugler JP, III, Brookeman JR. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE) Magn Reson Med. 1990;15:152–157. doi: 10.1002/mrm.1910150117. [DOI] [PubMed] [Google Scholar]
  31. Nagdyman N, Fleck T, Schubert S, Ewert P, Peters B, Lange PE, Abdul-Khaliq H. Comparison between cerebral tissue oxygenation index measured by near-infrared spectroscopy and venous jugular bulb saturation in children. Intensive Care Med. 2005;31:846–850. doi: 10.1007/s00134-005-2618-0. [DOI] [PubMed] [Google Scholar]
  32. Pelc NJ, Sommer FG, Li KC, Brosnan TJ, Herfkens RJ, Enzmann DR. Quantitative magnetic resonance flow imaging. Magn Reson Q. 1994;10:125–147. [PubMed] [Google Scholar]
  33. Playvin YA, Blum EY. Magnetic parameters of blood cells and high gradient paramagnetic and diamagnetic phoresis. Magnitnaya Gidrodinamika. 1983;19:3–15. [Google Scholar]
  34. Powers WJ, Grubb RL, Jr, Darriet D, Raichle ME. Cerebral blood flow and cerebral metabolic rate of oxygen requirements for cerebral function and viability in humans. J Cereb Blood Flow Metab. 1985;5:600–608. doi: 10.1038/jcbfm.1985.89. [DOI] [PubMed] [Google Scholar]
  35. Quastel JH, Wheatley AH. Oxidations by the brain. Biochem J. 1932;26:725–744. doi: 10.1042/bj0260725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Santens P, De Reuck J, Crevits L, Decoo D, Lemahieu I, Strijckmans K, Goethals P. Cerebral oxygen metabolism in patients with progressive supranuclear palsy: a positron emission tomography study. Eur Neurol. 1997;37:18–22. doi: 10.1159/000117398. [DOI] [PubMed] [Google Scholar]
  37. Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23:815–850. doi: 10.1118/1.597854. [DOI] [PubMed] [Google Scholar]
  38. Shishido F, Uemura K, Inugami A, Tomura N, Higano S, Fujita H, Sasaki H, Kanno I, Murakami M, Watahiki Y, Nagata K. Cerebral oxygen and glucose metabolism and blood flow in mitochondrial encephalomyopathy: a PET study. Neuroradiology. 1996;38:102–107. doi: 10.1007/BF00604789. [DOI] [PubMed] [Google Scholar]
  39. Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJ. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T(1), T(2), T*(2), and non-Lorentzian signal behavior. Magn Reson Med. 2001;45:533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
  40. Stainsby JA, Wright GA. Partial volume effects on vascular T2 measurements. Magn Reson Med. 1998;40:494–499. doi: 10.1002/mrm.1910400322. [DOI] [PubMed] [Google Scholar]
  41. Tanaka M, Kondo S, Okamoto K, Hirai S. Cerebral perfusion and oxygen metabolism in Parkinson's disease: positron emission tomographic study using oxygen-15-labeled CO2 and O2. Nippon Rinsho. 1997;55:218–221. [PubMed] [Google Scholar]
  42. Thulborn KR, Waterton JC, Matthews PM, Radda GK. Oxygenation dependence of the transverse relaxation time of water protons in whole blood at high field. Biochim Biophys Acta. 1982;714:265–270. doi: 10.1016/0304-4165(82)90333-6. [DOI] [PubMed] [Google Scholar]
  43. Weisskoff RM, Kiihne S. MRI susceptometry: image-based measurement of absolute susceptibility of MR contrast agents and human blood. Magn Reson Med. 1992;24:375–383. doi: 10.1002/mrm.1910240219. [DOI] [PubMed] [Google Scholar]
  44. West JB.2007Pulmonary physiology and pathophysiology: an integrated, case-based approach2nd ed.Philadelphia, PA: Lippincott Williams & Wilkins [Google Scholar]
  45. Wright GA, Hu BS, Macovski A. 1991 I.I. Rabi Award. Estimating oxygen saturation of blood in vivo with MR imaging at 1.5 T. J Magn Reson Imaging. 1991;1:275–283. doi: 10.1002/jmri.1880010303. [DOI] [PubMed] [Google Scholar]
  46. Xu F, Ge Y, Lu H. Noninvasive quantification of whole-brain cerebral metabolic rate of oxygen (CMRO2) by MRI. Magn Reson Med. 2009;62:141–148. doi: 10.1002/mrm.21994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Cerebral Blood Flow and Metabolism: Official Journal of the International Society of Cerebral Blood Flow and Metabolism are provided here courtesy of SAGE Publications

RESOURCES