Statistics in experimental cerebrovascular research: comparison of more than two groups with a continuous outcome variable

Abstract

A common setting in experimental cerebrovascular research is the comparison of more than two experimental groups. Often, continuous measures such as infarct volume, cerebral blood flow, or vessel diameter are the primary variables of interest. This article presents the principles of the statistical analysis of comparing more than two groups using analysis of variance (ANOVA). We will also explain post hoc comparisons, which are required to show which groups significantly differ once ANOVA has rejected the null hypothesis. Although statistical packages perform ANOVA and post hoc contrast at a key stroke, in this study, we use examples from experimental stroke research to reveal the simple math behind the calculations and the basic principles. This will enable the reader to understand and correctly interpret the readout of statistical packages and to help prevent common errors in the comparison of multiple means.

In part I of this series, we used a simple two-group comparison of a continuous outcome variable to introduce the basic concepts of statistical testing: a priori formulation of hypotheses and planned statistical analysis, error considerations, and power analysis (Schlattmann and Dirnagl, 2010). We are thus prepared to move one step further and explain another cornerstone of statistical testing in experimental and clinical biomedicine: comparing more than two groups with a continuous outcome variable. This would seem to be a trivial task. However, a review of the research literature shows that although multiple comparisons are among the most frequently used statistical approaches (Kilkenny et al, 2009), failure to adjust for multiple comparisons is highly prevalent in many fields (Williams et al, 1997; Murphy, 2004). Already in 1983, Ian Ford observed that errors in multiple comparisons were common in the first two volumes of the Journal of Cerebral Blood Flow and Metabolism (Ford, 1983). In a recent systematic analysis of all papers published in 2008 in this journal, we found that this lamentable situation remains unchanged (Deister et al, in preparation).

Therefore, we believe that it is justified to revisit a time-honored approach which provides an overall global test, which is the analysis of variance (ANOVA). Although all statistical packages and even simple spreadsheet programs deliver such tests on the press of a button, we opt to explain the simple math behind them using the published results of a typical experiment from experimental stroke research. Only by understanding the basics of a statistical test will the researcher be able to use it properly and interpret results given by computer programs.

Example I

Our first example is from a study which asked the question whether treatment with compound X is protective in a mouse model of middle cerebral artery occlusion (MCAO). The end point of the study was infarct volume measured from serial brain sections and staining with hematoxylin–eosin. Compound X was compared with vehicle treatment (‘negative' control) and with an established neuroprotectant (compound Y) as a ‘positive' control.

The study design allows us to answer the following questions: (1) Is there an effect of compound X on infarct volume after MCAO in comparison with vehicle (i.e., is it a neuroprotectant?); (2) Is there an effect of compound Y in comparison with vehicle? (i.e., was it possible to protect the brain in this experimental series?); and (3) How does compound X compare with a known ‘standard' (compound Y).

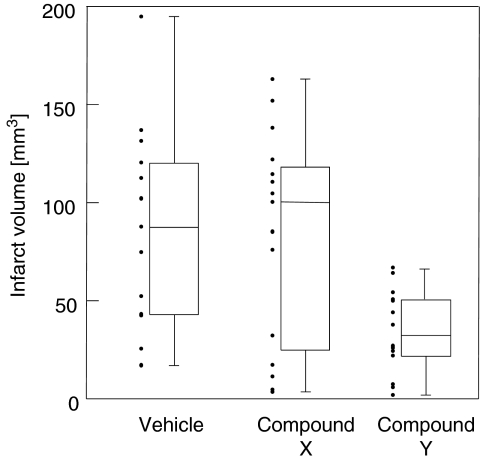
Figure 1 shows box and scatter plots of the data. Visual inspection already suggests that compound Y, the established neuroprotectant, indeed protected the brain. However, the other questions can only be addressed by a more formal analysis.

Figure 1.

Infarct volume after MCAO. Box plot: median, first and third quartile; whiskers: range; dots: data. MCAO, middle cerebral artery occlusion.

Multiple Hypothesis Tests

An intuitive approach to this set of data would be to perform several t-tests, as described for two-group comparisons in our recent article (Schlattmann and Dirnagl, 2010). For example, using t-tests we might want to compare the vehicle and compound X groups, as well as the vehicle and compound Y groups. However, the multiple comparisons involved will inflate the probability of declaring a significant difference when it is not in fact present. Thus, it is necessary to control the type I error, which is the probability of falsely rejecting the null hypothesis.

If we test a null hypothesis which is true (i.e., there is no difference between the groups) and perform a statistical test at the 5% significance level, the probability of coming to the correct conclusion of no difference between groups is 95%. If we perform two tests (and both null hypotheses are true) without correction, the probability that no test turns out with a statistically significant difference is 0.95 × 0.95=0.90. In other words, the probability that at least one test rejects the null hypothesis at the 5% level is ∼10%, given by 1−(0.95 × 0.95). If we perform four tests without correction, the probability of obtaining no significantly different comparison turns out be 0.95⁴=0.82, and the probability of at least one erroneously significantly different comparison is given by 1−0.82=0.18. Hence, type I error increases rapidly with the number of comparisons. In general, if the null hypothesis is true, the probability of obtaining no statistically significantly different comparison when performing k independent tests at a significance level of α is rendered by (1−α)^k. Accordingly, the probability of observing at least one significantly different comparison is given by 1−(1−α)^k.

One way to control the overall type I error is to perform a Bonferroni correction: α is divided by the number of tests performed (α/k) and used as the new, corrected significance level. However, this simple and straightforward procedure comes at the price of losing statistical power.

Analysis of Variance

A common approach to compare several groups of continuous data without losing power is ANOVA, which provides a single overall test of whether there are differences between groups or treatments. The procedure relies on the same assumptions as the t-test. That is, we need continuous, normally distributed, and independent data with a common variance in each group.

One might ask why the procedure is known as ANOVA, as we compare groups to investigate whether the population means differ. The term ‘ANOVA' becomes clear if we understand that this test is based on partitioning the total variation of the data into components of within- and between-group variance. Between-group variability depends on the size of the difference between group means. This leads to the so-called variance of means. Obviously, if all group means are equal, the between-group variability is zero.

For the data in Table 1, the overall mean equals 67.87; thus, the squared contribution of the first group to the variance of means is given by (87.57−67.87)². As we have made 14 observations, the total contribution is 14 × (87.57−67.87)². Consequently, the variance of means for the three groups is given by

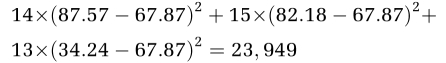Table 1. Infarct volumes measured histologically after experimental middle cerebral artery occlusion in the mouse.

	Vehicle (n=13)	Compound X (n=15)	Compound Y (n=14)
	120.07	114.48	50.54
	87.43	100.19	26.74
	194.72	104.61	66.58
	101.88	121.73	25.68
	74.64	85.03	63.81
	52.14	110.31	5.64
	42.19	151.75	7.33
	42.89	75.63	37.69
	112.29	162.72	1.79
	131.27	32.03	53.94
	16.94	137.94	21.81
	136.71	11.21	43.74
	25.30	3.36	49.77
		17.20	24.34
		4.48
Mean	87.57	82.18	34.24
s.d.	51.66	55.25	21.30

Analysis of variance quantifies whether the between-group variance is larger than expected by chance than the within-group variance. Under the null hypothesis, the between-group variance and the within-group (residual) variance will be the same, and thus their expected ratio will be equal to one. The test statistic (F-value) is the ratio of the between- and within-variance estimates. The larger the F-value, the more evidence is available against the null hypothesis that the population group means are equal.

As we are using two different variance estimates, we need to consider different degrees of freedom (d.f.). Therefore, the F-value must be compared with tables based on the denominator and numerator d.f.. The numerator d.f. depends on the number of groups k and is given by k−1. The denominator d.f. depends on the total number of observations n and the number of groups k. They are calculated as n−k.

The first column of Table 2 shows the source of variation, the second column shows the d.f., and the third the corresponding sum of squares. The next column gives the mean square error, which is the variance estimate of the between- and within-group variance. The variance ratio (F-value) is then given by 11,975/2,068=5.79. This value of the test statistic can be compared with tables of the F-distribution with 2 and 39 d.f. For the data in Table 2, an F-value >3.24 would be significant with a P-value <0.05. The last column of Table 2 shows the probability of observing a value >5.79 when the null hypothesis is true (Pr(>F)). Thus, we reject the null hypothesis that the animal populations are equal. At present, all of this is performed conveniently by software. Many packages provide most of the parameters explained above (e.g., F-values) in their output.

Table 2. Analysis of variance table for the data in Table 1.

Source of variation	Degrees of freedom (d.f.)	Sum of squares	Mean square	Variance ratio (F-value)	Pr (>F)
Between groups	2	23,949	11,975	5.79	0.0063
Within groups	39	80,654	2,068

The last column of Table 4 shows the probability to observe a value >6.75 when the null hypothesis is true (Pr(>F)).

Multiple Comparisons

When a significant F-ratio has been found using ANOVA, we still do not know which means differ significantly. Therefore, it is necessary to conduct post hoc comparisons between pairs of treatments. There are many procedures for pairwise comparison. The performance of one or several of these pairwise comparisons requires a procedure that takes the full range of potential comparisons into account. For example, Bonferroni's correction, Scheffé's method, or Tukey's method could be used. An overview may be found, e.g., in the book by Armitage et al (2002) or in the articles by Jaccard et al (1984), Godfrey (1985), or Seaman et al (1991). See also the list of web resources following the reference list.

Statistical procedures need to be defined a priori (Schlattmann and Dirnagl, 2010), i.e., between formulating the research hypothesis and performing the experiments. If ANOVA is the test of choice, post hoc procedures and contrasts need to be set in case the null hypothesis is rejected. The choice of post hoc comparisons depends on the investigator's needs and the study design. If confidence intervals are desirable or the design is unbalanced (i.e., unequal group sizes) but with equal variances, then the Tukey procedure is recommended (Stoline, 1981; Bender and Lange, 2001).

Thus, in the following, we will apply Tukey's method to our data in Table 1 to test the null hypothesis that all possible pairs of treatment means are equal.

Tukey's test is one of several methods of ensuring that the chance of finding a significant difference in any comparison (under a null hypothesis) is maintained at the α-level of the test. In other words, it preserves ‘family-wise type I error.'

Tukey's test is often referred to as the HSD (honestly significant difference) test, and makes use of a single value against which all differences are compared. To test all pairwise comparisons among means using Tukey's HSD, one computes the test statistic t_i for each pair of means. The test statistic t_i depends on the difference of means, the root mean square error (within-group mean square error), and the harmonic mean of the respective sample sizes.

The critical value t_critical is determined from the distribution of the studentized test statistics. The number of means in the experiment is used in the determination of the critical value, and this critical value is used for all comparisons among means.

Table 3 shows that compound Y is significantly different from the vehicle and compound X group, whereas the null hypothesis that compound X is equal to vehicle after MCAO was not rejected.

Table 3. Multiple comparisons based on Tukey's procedure with simultaneous 95% confidence limits.

Group comparison	Difference between means	Simultaneous 95% confidence limits		Adjusted P-value
Compound X-vehicle	−5.40	−47.40	36.59	0.947
Compound Y-vehicle	−53.33	−96.01	−10.66	0.011
Compound Y-Compound X	−47.94	−89.11	−6.76	0.019

As noted above, as an alternative procedure, the Bonferroni method could have been applied. This implies simply dividing the selected significance level by the number of comparisons. In our case, three comparisons are performed for all pairwise comparisons, which lead to a corrected significance level of 0.05/3=0.0166. This procedure often lacks power and as a result other post hoc comparison methods such as Tukey's method are preferred.

Two-way Analysis of Variance

Example II

In example I, we used ANOVA to analyze data from a study with one independent variable (‘treatment'). We will now address how to analyze data from a study with two independent variables using two-way ANOVA.

Royl et al (2009) investigated the hypotheses that treatment with the inhibitor of phosphodiesterase type 5, vardenafil, increases cerebral blood flow and improves functional recovery after temporary focal cerebral ischemia in mice. Thus, the effects of vardenafil on survival, functional outcome, lesion size, and cerebral blood flow after cerebral ischemia were investigated. Mice were subjected to MCAO for 45 minutes or to a sham procedure. In either group, mice received vardenafil or alternatively vehicle 3 hours after MCAO. The summary data for the pole test (time in seconds a mouse needs to turn and to reach the floor after being placed head up on pole), a measure of motor coordination, are shown in Table 4.

Table 4. Functional recovery after cerebral ischemia.

	Sham		MCAO
	Vehicle (n=8)	Vardenafil (n=10)	Vehicle (n=11)	Vardenafil (n=11)
	5.74	5.31	9.01	7.41
	5.26	4.84	6.92	6.58
	4.78	6.23	7.96	5.32
	5.03	5.57	7.97	6.29
	4.64	8.14	6.60	5.97
	4.68	5.15	8.67	8.06
	5.38	5.09	8.02	10.38
	5.97	3.77	8.21	5.84
		5.18	5.58	6.09
		4.90	5.78	6.01
			4.79	6.51
Mean	5.18	5.42	7.23	6.77
s.d.	0.50	1.14	1.38	1.42

MCAO, middle cerebral artery occlusion.

Pole test (performed on day 22 after MCAO): time mouse needs to turn and to reach the floor after being placed head up on pole.

This experiment represents a typical 2 × 2 factorial design (type of surgery (sham, MCAO) × treatment (vehicle, vardenafil)). In factorial designs, a factor is a major independent variable. In this example, we have two factors: type of treatment and surgery.

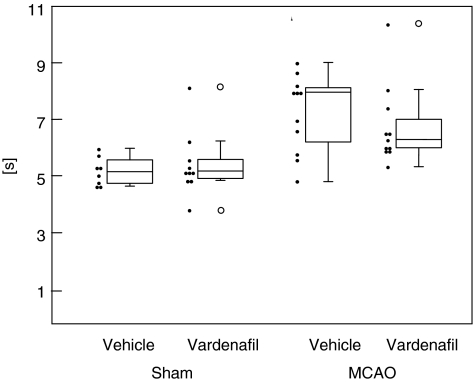
This study design allows us to answer the following questions: Is there an effect of MCAO on motor outcome at day 22? Does vardenafil have an effect on sham animals, and most importantly, can it improve functional outcome after experimental stroke? Figure 2 shows box and scatter plots of the data. Visual inspection already suggests that MCAO does seem to have an impact on outcome.

Figure 2.

Functional recovery after MCAO. Pole test (performed on day 22 after MCAO): the time the mouse needs to turn and to reach the floor after being placed head up on pole. Box plot: median, first and third quartile; whiskers: range; dots: data. MCAO, middle cerebral artery occlusion.

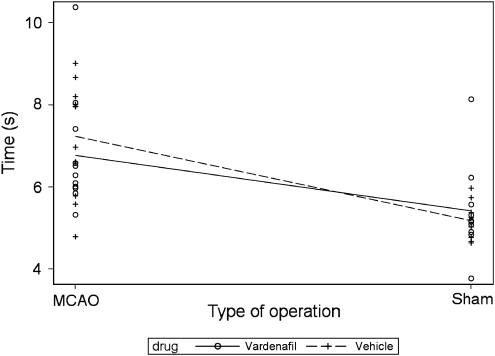
A standard plot in a two-factor experiment is known an interaction plot and may be given by the predicted response at each combination of the factors. Figure 3 shows an interaction plot with no strong suggestion that vardenafil acts differently in sham- and MCAO-operated animals, although the predicted response lines cross.

Figure 3.

Interaction plot for the 2 × 2 factorial design: predicted time to recovery at each combination of the factors of surgery and drug.

However, our questions (see above) can only be addressed properly by a formal analysis. Two-way ANOVA is the appropriate method for this purpose.

Two-way ANOVA partitions the total variability of the data into a maximum of four sources. The first source of variation is the variability due the type of surgery (sham, MCAO), and the second source is the variability due the type of drug (vehicle, vardenafil). The third source of variation denotes the interaction between the type of surgery and drug. This implies that vardenafil acts differently in operated or sham-operated animals. In addition, as in one-way ANOVA, the within-group (residual) variance needs to be considered.

Results

Now, for each of the first three sources of variability an F-test is performed. Looking at the F-test for the type of surgery, the sum of squares is equal to 28.19, with 1 d.f. The residual mean square error is given by 52.62 on 36 d.f. Thus, the mean square error is given by 52.62/36=1.46. Consequently, the F-test for the type of surgery is given by 28.19/1.46=19.29. This turns out to be significant at the 5% level, with a corresponding P-value of 0.0001.

The other sources of variance are treated in the same manner. For example, the F-test for the effect of drug is given by 0.23/1.46=0.16, P-value=0.69. Similarly, looking at the results of the two-way ANOVA in Table 5, there is no evidence for a significant interaction.

Table 5. Analysis of variance table for the data in Table 4.

Source of variation	Degrees of freedom (df)	Sum of squares	Mean square	Variance ratio (F-value)	Pr(>F)
MCAO	1	28.19	28.19	19.38	0.0001
Drug	1	0.23	0.23	0.16	0.69
MCAO × drug	1	1.19	1.19	0.81	0.37
Within groups	36	52.62	1.46

MCAO, middle cerebral artery occlusion.

The last column of Table 5 shows the probability to observe a value >6.75 when the null hypothesis is true (Pr(>F)).

Table 6, in which Tukey's procedure as post hoc comparison method has been applied, only reveals an effect of surgery (animals with sham surgery perform better than animals after MCAO). The null hypotheses that vardenafil provides an equal outcome in comparison with vehicle after MCAO or sham operation could not be rejected.

Table 6. Multiple comparisons based on Tukey's procedure with simultaneous 95% confidence limits (CLs).

Group comparison	Difference between means	Simultaneous 95% confidence limits		Adjusted P-value
MCAO−sham	1.69	0.91	2.47	0.0001
Vardenafil−vehicle	−0.15	−0.93	0.62	0.69
MCAO+vehicle−sham+vehicle	2.05	0.54	3.56	0.004
MCAO+vardenafil−sham+vehicle	1.59	0.07	3.10	0.03
MCAO+vardenafil−MCAO+vehicle	−0.46	−1.85	0.93	0.81
MCAO+vardenafil−sham+vardenafil	1.35	−0.07	2.77	0.07
Sham+vardenafil−sham+vehicle	0.23	−1.31	1.77	0.97
Sham+vardenafil−MCAO+vehicle	−1.81	−3.23	−0.39	0.008

MCAO, middle cerebral artery occlusion.

Conclusions

Analysis of variance overcomes the problem that multiple two-sample t-tests inflate the chance of committing a type I error by performing a global hypothesis test comparing three or more means. Having found a significant group difference in ANOVA (and only then), we proceed to perform pairwise comparisons between groups to find significant differences between individual groups.

Analysis of variance is a special type of the general linear model, which can also be applied to more complex settings. A future article of this series will show the proper use of a linear model in the analysis of experimental data.

The authors declare no conflict of interest.