Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Nov 1.
Published in final edited form as: Clin Biomech (Bristol). 2010 Jul 23;25(9):853–858. doi: 10.1016/j.clinbiomech.2010.06.010

A Biomechanical Model for Estimating Loads on Thoracic and Lumbar Vertebrae

Sravisht Iyer 1,2, Blaine A Christiansen 2,3, Benjamin J Roberts 2, Michael J Valentine 2, Rajaram K Manoharan 2, Mary L Bouxsein 2,3
PMCID: PMC2949493  NIHMSID: NIHMS217386  PMID: 20655634

Abstract

Background

Biomechanical models are commonly used to estimate loads on the spine. Current models have focused on understanding the etiology of low back pain and have not included thoracic vertebral levels. Using experimental data on the stiffness of the thoracic spine, ribcage, and sternum, we developed a new quasi-static stiffness-based biomechanical model to calculate loads on the thoracic and lumbar spine during bending or lifting tasks.

Methods

To assess the sensitivity of the model to our key assumptions, we determined the effect of varying ribcage and sternal stiffness, maximum muscle stress, and objective function on predicted spinal loads. We compared estimates of spinal loading obtained with our model to previously reported in vivo intradiscal pressures and muscle activation patterns.

Findings

Inclusion of the ribs and sternum caused an average decrease in vertebral compressive force of 33% for forward flexion and 18% in a lateral moment task. The impact of maximum muscle stress on vertebral force was limited to a narrow range of values. Compressive forces predicted by our model were strongly correlated to in vivo intradiscal pressure measurements in the thoracic (r=0.95) and lumbar (r=1) spine. Predicted trunk muscle activity was also strongly correlated (r=0.95) with previously published EMG data from the lumbar spine.

Interpretation

The consistency and accuracy of the model predictions appear to be sufficient to justify the use of this model for investigating the relationships between applied loads and injury to the thoracic spine during quasi-static loading activities.

Keywords: Spine, biomechanical model, back injury, muscle activation

Introduction

Biomechanical models are commonly used to estimate loads on the spine during occupational bending and lifting tasks, as well as during common activities of daily life. Current models have focused on low back pain, and as a result have dealt almost exclusively with forces in the lumbar and sacrolumbar regions.

Acute pain in the upper back and shoulders is a commonly occurring injury among industrial and service workers (Andersen et al., 2007). Furthermore, vertebral fractures are most common at the mid-thoracic and thoracolumbar regions (Delmas et al., 2005, Melton et al., 1993). Despite these injury patterns, little progress has been made toward understanding the loads applied to the thoracic spine during common activities. Existing biomechanical models of the thoracic spine have studied respiratory mechanics, scoliosis, and ribcage deformities (Andriacchi et al., 1974, Closkey et al., 1992, Kong and Goel, 2003, Loring, 1991), rather than forces applied to the thoracic vertebrae. Thus, a biomechanical model capable of estimating forces applied to thoracic vertebrae and exerted by surrounding trunk musculature may provide insights into the etiology of musculoskeletal disorders in this region.

Accurately modeling the thoracic spine requires developing a new approach to incorporate the mechanical contribution of the ribcage and sternum. Clinical observations and experimental studies provide evidence that the ribcage and sternum add stiffness to the thorax and serve to reinforce the thoracic spine during compression and bending (Andriacchi et al., 1974, Berg, 1993, Oda et al., 2002, Oda et al., 1996, Watkins et al., 2005).

Thus, our objective was to use experimental observations regarding ribcage and sternum stiffness to develop a quasi-static biomechanical model capable of estimating trunk muscle forces and loads on the vertebral bodies in the thoracic and lumbar regions during various tasks. To examine the soundness of assumptions used in the model, we conducted sensitivity analyses of ribcage and sternum stiffness and maximum muscle stress to examine their effect on predicted forces in the spine. Finally, we compared the estimates of spinal loading obtained with our model to previously reported in vivo intradiscal pressures and muscle activation patterns for various activities.

Methods

Our model uses principles that are similar to previously published quasi-static models of the lumbar spine (Bean et al., 1988, Brown and Potvin, 2005, Rasmussen et al., 2001). Briefly, each movement or task was divided into a series of body positions encompassing the entire movement. For each body position, muscle forces and loads on the vertebral body were determined separately for each individual vertebral cross-section (T6-L5) and were calculated independent of the forces in the cross-sections above or below. These forces were calculated using a two-step process assuming static equilibrium (forces due to motion were not considered). First, for a given body position, external forces and moments were calculated at each vertebral level using subject height, weight, and anthropometric data for body-segment lengths and masses (Contini, 1972, Liu et al., 1971, Winter, 1990). External forces and moment acting on each cross section were calculated using the weight of the body above the level of interest. The body superior to the lumbo-sacral joint was modeled by seven segments: the head and neck, the thorax, the abdomen, the upper arms, the forearms, and hands. For each body position and segment, the axial rotation and angles from vertical and horizontal were used as inputs. The segment-specific distribution of weight was determined using anthropologic data for body segment length and trunk mass (Contini, 1972, Liu et al., 1971). Second, muscle forces and compressive forces on the vertebral body were determined by minimizing the sum of cubed muscle intensities required to balance the external moments and forces (Crowninshield and Brand, 1981, Hughes, 2000).

Trunk muscle, ribcage, and sternum morphology

Morphologies of trunk muscles, ribs, and the sternum at each vertebral cross section were measured from quantitative computed tomography (QCT) scans of subjects enrolled in the Framingham Heart Study Multidetector CT Study, a community-based study of vascular calcification (Hoffmann et al., 2008). Subjects included 14 men with a mean age of 56.8 yrs (SD 4.1 yrs), height of 180 cm (SD 6 cm), and weight of 91.4 kg (SD 12.8 kg). The QCT scans had a nominal in-plane pixel size of 0.68 × 0.68 mm and a slice thickness of 2.5 mm. Muscle cross-sectional area (CSA), centroid location and line of action were measured at each vertebral level (T6 – L5) for each trunk muscle of interest (Table 1). A single operator manually outlined each muscle or structure, followed by calculation of CSA and centroid location using custom software. Moment arm lengths (MAL) in the medial-lateral and anterior-posterior direction were calculated as the distance from the centroid of the muscle or structure to the centroid of the vertebral body.

Table 1.

Muscles and bony structures measured from QCT scans and included in the biomechanical model, by vertebral level.

T6 T7 T8 T9 T10 T11 T12 L1 L2 L3 L4 L5
Pectoralis Major X X X X
Rectus Abdominus X X X X X X X X
Serratus Anterior X X X X X X
Latissimus Dorsi X X X X X X X X X X
Trapezius X X X X X X
External Oblique X X X X X X X X
Internal Oblique X X X X
Erector Spinaea X X X X X X X X X X X X
Transversospinalisb X X X X X X X X X X X X
Psoas Major X X X X X
Quadratus Lumborum X X X X
Rib Cage X X X X X X X
Sternum X X X X X
Open in a new tab

General optimization scheme to determine muscle forces at each vertebral level

Minimization of the sum of cubed muscle intensities was performed using the Matlab function ga found in the Genetic Algorithm and Direct Search Toolbox 2.4 (The Mathworks, Natick, MA). The Genetic Algorithm uses a stochastic method and the principles of natural selection to optimize muscle activation. This algorithm allows for small variations in predicted compressive force for a given task. To characterize this variation, the optimization algorithm was performed ten times for a single task (30 degree trunk flexion), and the resulting vertebral body compressive forces were computed. Muscle forces were assumed to be ≥0, with a maximum muscle stress (MMS, force/area) of 0.9 MPa based on the physiologic cross-sectional area, calculated as previously described (Narici, 1999).

Inclusion of the Ribcage and Sternum

At thoracic levels (T6–T10), the ribcage and sternum were included in the model as load-bearing elements, with their individual mechanical contribution determined based on experimental data of the stiffness contributions of the sternum and ribcage to the thoracic spine (Watkins et al., 2005). The ratios of ribcage and sternum force to compressive force on the vertebral body were determined as though the four elements (i.e., the R rib, L rib, sternum and vertebral body) were parallel springs in a mechanical circuit (Fig 1). The total stiffness of the ribcage-sternum-spine complex was calculated as:

ktotal=kleft_ribcage+kright_ribcage+ksternum+kvertebra (1)

Using this relationship, the portion of the total external force (Ftotal) that is distributed to the ribs and sternum was:

Fsternum=Ftotal(ksternumktotal) (2)
Fright_ribcage=Ftotal(kright_ribcagektotal) (3)
Fleft_ribcage=Ftotal(kleft_ribcagektotal) (4)

Using the moment arm of the ribcage and the sternum at each cross-section, we calculated the proportion of the external moment acting about the vertebral body that was not being supported by the sternum and ribcage:

Mvertebralbody=Mtotal−FsternumMALsternum−Fright_ribcageMALright_ribcage−Fleft_ribcageMALleft_ribcage (5)

where Mtotal was the total external moment calculated based on body position and anthropometric data, and MALsternum, MALright_ribcage, MALleft_ribcage were the sternal, right, and left ribcage moment arm lengths. Note that moment arm lengths were measured from the centroid of the vertebral body, therefore Fvertebrae was not considered in this calculation.

Figure 1.

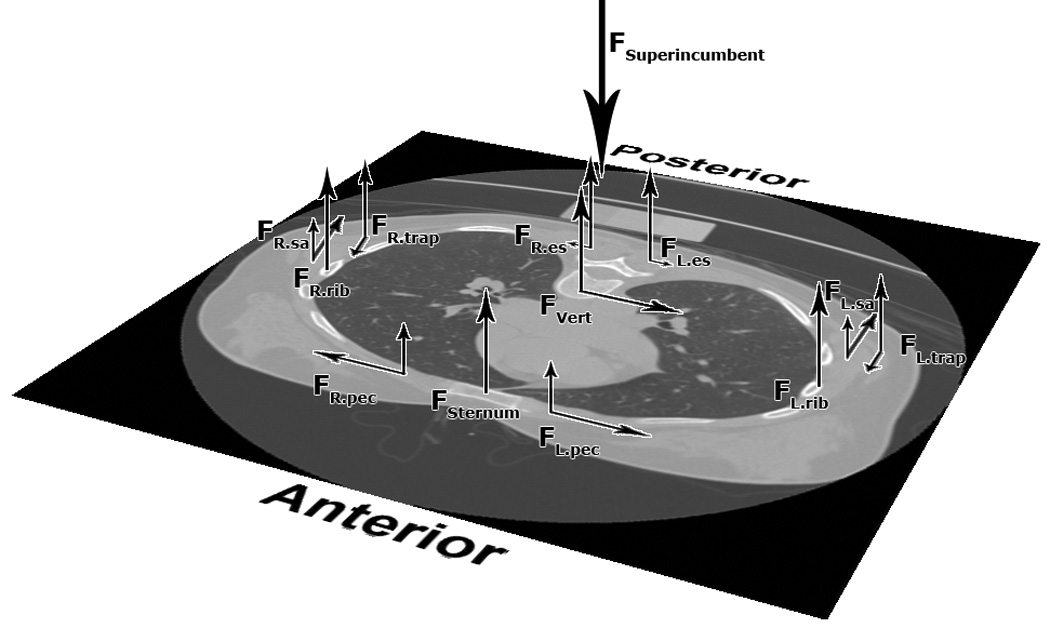
Figure 1

Open in a new tab

At each vertebral level, the superincumbent force and the subsequent moment about the vertebral body are balanced by forces in the sternum and ribcage and muscle forces. The relative mechanical contributions of the spine, ribcage, and sternum in each vertebral cross-section were calculated based on the relationship between parallel springs, using experimentally determined stiffness data (Watkins et al., 2005)

The external moment calculated by the biomechanical model was divided into components acting around the anteroposterior, mediolateral and superoinferior axes. The remaining moment acting about the vertebral body, Mvertebralbody, was balanced by muscle forces in the cross-section.

Our model does not include deformation of the spine per se, but rather models flexion and extension as an inclination of the upper body; therefore, we used experimental stiffness values determined for axial compression (Watkins et al., 2005) for all simulated tasks. However, future models could include task-dependent stiffness values, since the stiffness contributions of the sternum and ribcage were found to be different for axial compression, axial torque, lateral bending, and flexion/extension (Watkins et al., 2005).

Using data from Watkins and colleagues (2005), sternal stiffness was assumed to be 29.4% of ktotal and was included at each level from T6 to T10. Ribcage stiffness was assumed to be 10.4% of ktotal (Watkins et al., 2005) and was evenly distributed to each half of the ribcage. The stiffness of the floating ribs at T11 and T12 was neglected, as they are not part of the sternum-ribcage complex. Finally, the stiffness contribution of each rib was presumed to be distributed through each cross section in which they were visible. Whereas cross-sectional images of levels T6–T10 typically had three ribs visible on each side, T11 and T12 typically had two and one rib visible, respectively. The stiffness of the ribcage at T11 and T12 was therefore assumed to be 2/3 and 1/3 of the stiffness at other levels, respectively.

Sensitivity Analyses

We conducted three sensitivity analyses to characterize the sensitivity of the model to our key assumptions. First, the stiffness of the ribcage and sternum were varied from 0 (no weight bearing by the ribs and sternum) to 200% of baseline stiffness (Watkins et al., 2005) for two tasks: 30 degree flexion and lateral moment. Second, the maximum muscle stress was varied from 0.5 to 1.0 MPa. Third, we determined the influence of the objective function on predicted vertebral compressive forces by comparing the min/max objective function to the sum of cubed intensities algorithm. In the min/max method, the optimization function attempts to minimize the maximum muscle stress at any given level (Bean et al., 1988).

Model Validation

To assess the accuracy of the model, we compared predicted vertebral compressive forces and muscle activation patterns to published experimental data. Vertebral compressive forces were compared to in vivo intradiscal pressures in the thoracic (Polga et al., 2004) and lumbar (Wilke et al., 1999) spine. The tasks validated included relaxed standing, lateral moment, trunk flexion of 30 degrees, trunk extension of 15 degrees, 10 kg load with elbows flexed to 90 degrees, and a 10 kg load with 30 degrees of trunk flexion and arms at the sides. For trunk flexion/extension tasks, the model was inclined at the hip; flexion of the spine itself was not considered. For all tasks except for “elbows flexed”, the load was assumed to be held at the sides (0 degrees from vertical).

Muscle activation patterns predicted by the model were compared to EMG data from the lumbar spine (Schultz et al., 1982). Specifically, we compared the activation of the obliques and the muscles in the back (erector spinae, multifudus and latissimus dorsi) to myoelectric signal amplitude for 5 different tasks: 1) relaxed standing, 2) standing with arms extended to 90 degrees 3) 8 kg load held at sides, 4) trunk flexion of 30 degrees with arms extended, and 5) trunk flexion of 30 degrees with arms extended, holding 8 kg.

Results

Forces on the vertebral bodies depended on the simulated task (Figure 2). Among the tasks examined, compressive forces on the thoracic spine were highest for holding a 10 kg load in the hands with elbows bent to 90 degrees (mean 1552 N, SD 119 N), an increase of 448% compared to relaxed standing. Mean lumbar compressive force for the same task was 1693 N, a 252% increase compared to standing. This task also produced a higher compressive force in the thoracic spine compared to forward flexion (1552 N vs. 593 N), even though these tasks produced similar forces in the lumbar spine (1693 N vs. 1721 N).

Figure 2.

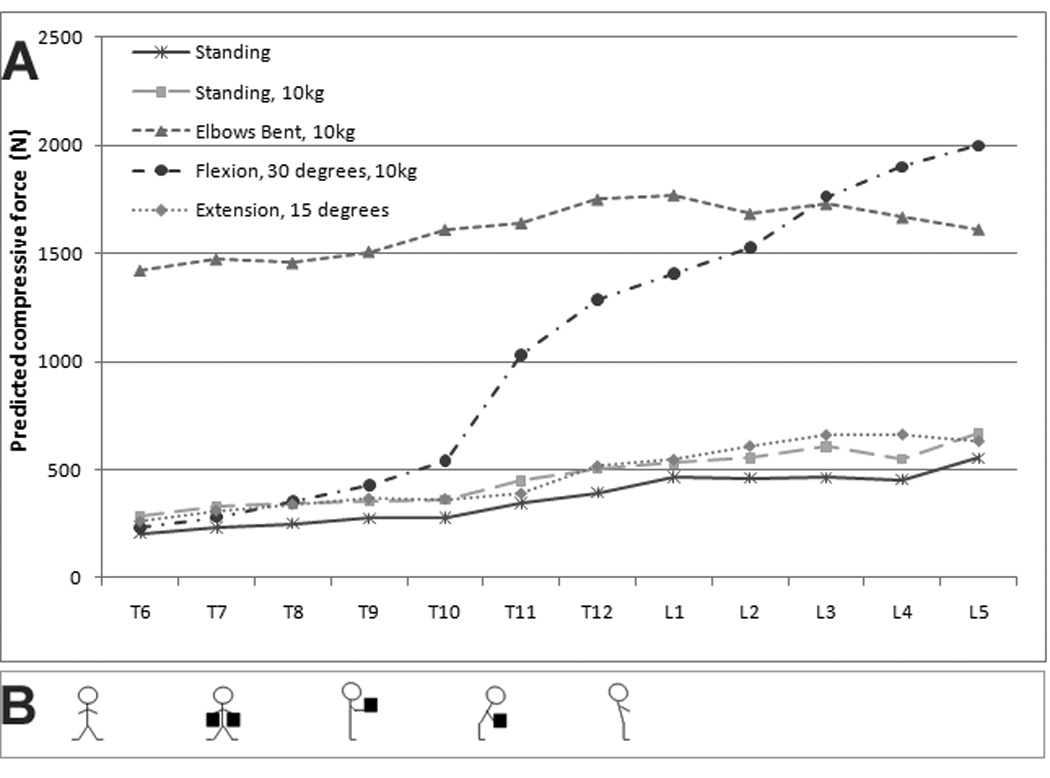
Figure 2

Open in a new tab

Model compressive forces depended strongly on the predicted task. The figure above depicts task-dependent changes in compressive force (A). The tasks modeled in this figure are also shown (B). From left to right, these are: standing, standing with 10kg (5 kg on each arm), lifting 10 kg with elbows bent, 30 degrees flexion with 10kg, and 15 degrees of extension.

Characterizing the optimization algorithm

Using the sum of cubed intensities objective function, the ga optimization algorithm produced consistent results. The range of the vertebral compressive forces for 10 repeated trials was less than 6 N, or less than 0.8% of the mean force for all vertebral levels. Because the variation of predicted compressive forces was so small, multiple optimization analyses were not performed in subsequent simulations.

Sensitivity Analyses

(i) Ribcage and Sternal Stiffness

As expected, varying the ribcage-sternal stiffness influenced the predicted vertebral compressive force in the thoracic spine (Figure 3). In the forward flexion task, with ribcage stiffness set to 0 (i.e., no load bearing by the ribcage), the average compressive force on thoracic vertebral bodies was 752 N, ranging from 521 N at T6 to 1038 N at T12. Addition of the ribs/sternum caused an average decrease in vertebral compressive force in the thoracic spine of 222 N (33%). Increasing ribcage stiffness to 200% of baseline caused on average a 51% decline in mean compressive force compared to baseline.

Figure 3.

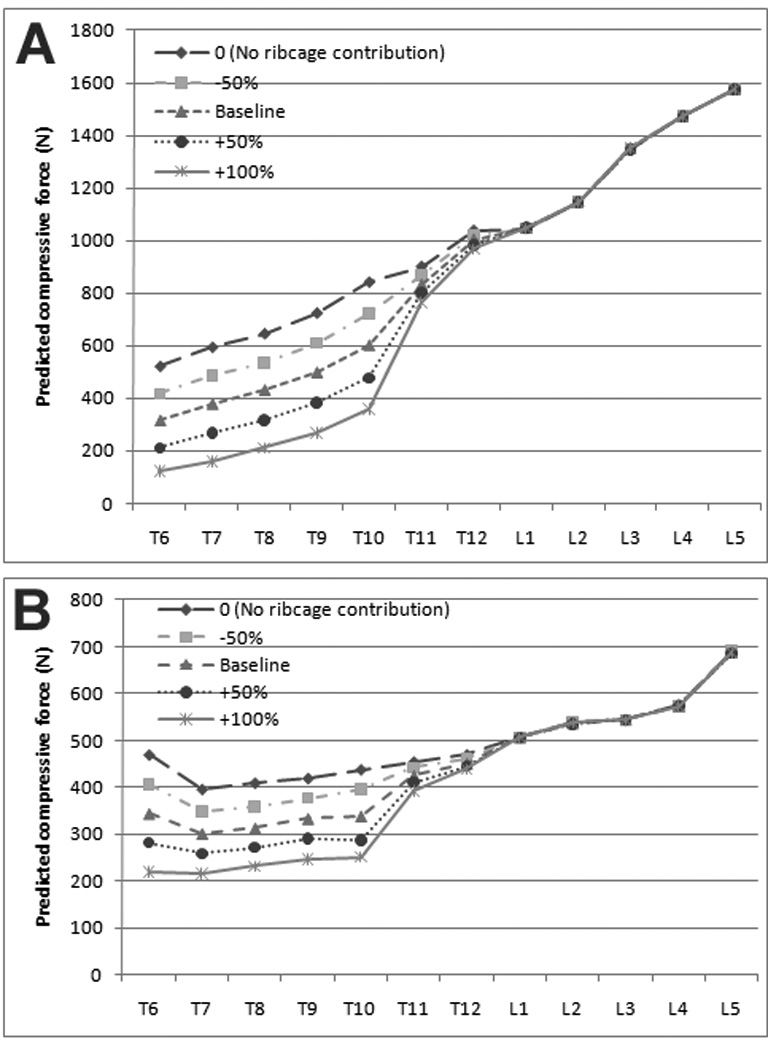
Figure 3

Open in a new tab

Compressive forces during forward flexion and lateral moment tasks. Predicted compressive forces are shown for 30 degrees of flexion (A) and for a lateral moment with 5 kg in the right hand (B). For both panels, ribcage-sternal stiffness, the load bearing contribution of the ribcage, was varied from 0 (no loadbearing by the ribs) to 200% of the baseline value. Compressive force on the vertebral body were strongly dependent on the mechanical contributions of the sternum and ribcage at thoracic levels.

Whereas compressive forces associated with forward flexion showed large changes with the inclusion of the sternum/ribcage construct, predicted vertebral forces due to a lateral moment were not as sensitive to changes in the ribcage stiffness (Figures 3A and 3B). With no load bearing by the ribcage, average compressive forces in the thoracic spine were 438 N during the lateral moment task. Addition of the ribcage caused the average vertebral compressive force to fall by 78 N (18 %). Increasing rib cage stiffness to 200% of baseline values resulted in a further 21% decline in the average compressive force on the thoracic vertebral bodies.

(ii) Maximum Muscle Stress

Varying maximum muscle stress (MMS) caused task-dependent changes in compressive forces (Supplemental Data, Table 1). In general, changing MMS had little effect on vertebral force predictions but tended to grow larger with more demanding tasks. When lifting a 20 kg load with elbow flexion, for example, a larger minimum MMS was required in order for the algorithm to find a feasible solution (Supplemental Data, Figure 1). For this task, the effect of varying MMS was largest at T8 and T9; the differences at these levels were as high as 29% with a 0.01 MPa change in MMS. The force generated by the latissimus dorsi decreased from 450 N to 45 N as MMS was increased from 0.82 MPa to 0.85 MPa.

(iii) Optimization Objective Function

Using an alternate min/max optimization objective function caused changes in predicted compressive force that varied as a function of the task and vertebral level analyzed (Supplemental Data, Table 2). When standing, the difference in compressive force for the sum of cubes objective function compared to the min/max objective function averaged 2.8% (range: 0.2% –6.5% ). The difference between the two approaches increased with the task severity (e.g., addition of weight and flexion). In a flexion task carrying a 10 kg load, the difference between predicted compressive forces was as high as 29% at T10. However, for the remainder of the vertebral levels, the difference in predicted compressive force with the objective function ranged from 3.5% to 17.0%

Model Validation

Vertebral compressive forces calculated by the biomechanical model were strongly correlated with in vivo intradiscal pressures measured in the thoracic (r2 = 0. 95, Figure 4) and lumbar (r2 = 1.0, Supplemental Data, Figure 2 and Supplemental Data, Table 4) spine. Increases in predicted vertebral compressive force during forward flexion were much lower in the thoracic than in the lumbar spine. Absolute values for predicted compressive force in the lumbar spine for forward flexion with and without weight in hands were within 5% of previously reported values (Schultz et al., 1982): 1) 30% forward flexion: 1400 N (Schultz et al) vs 1349 N (current model), and 2) 30% forward flexion with 8 kg in hands: 1620 N (Schultz et al) vs 1685 N (current model).

Figure 4.

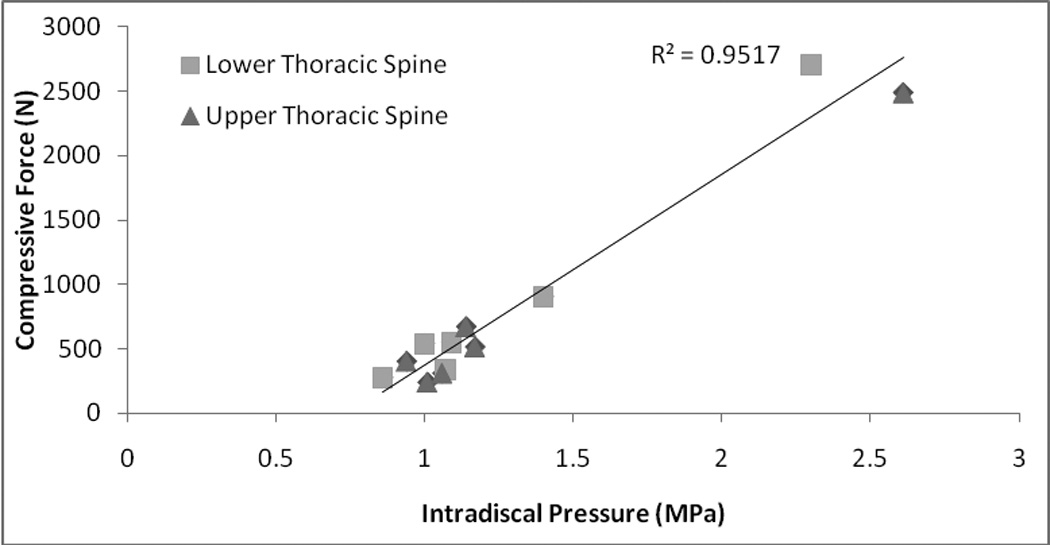
Figure 4

Open in a new tab

Vertebral compressive force at T9 and T10 predicted by the biomechanical model showed strong correlation to reported intradiscal pressures at T9/T10 and T10/T11 in the thoracic spine for various tasks (Polga et al., 2004).

Predicted muscle activation patterns were also strongly correlated to previously reported EMG recordings of the erector muscles at L3 (r2 = 0.95, Supplemental Data, Figure 3). Muscle activity increased 5-fold for flexion compared to standing, similar to previous EMG recordings (Schultz et al., 1982). During flexion, muscles of the anterior abdominal wall (rectus abdominus) were not activated, whereas these muscles played an important role when the subject was standing with arms out (Supplemental Data, Table 3).

Discussion

We developed a biomechanical model of the spine that includes stiffness-based contributions of the sternum and ribcage for prediction of vertebral compressive forces in the thoracic spine. The mechanical contribution of the ribcage and sternum were based on previously published stiffness values (Watkins et al., 2005). Predictions made by our model were strongly correlated to in vivo thoracic intradiscal pressures (Polga et al., 2004) and EMG data from the lumbar spine (Schultz et al., 1982). Altogether, the consistency of the model predictions are sufficient to justify the use of this model for investigating applied loads and injury to the thoracic spine during quasi-static loading activities.

Incorporating the mechanical contribution of the ribcage and sternum substantially reduced predicted compressive forces on the thoracic vertebral bodies for flexion and load-carrying tasks. However, in other tasks (relaxed standing and lateral moment) there was a smaller decrease in compressive force with the addition of the ribcage. This result seems physiologically intuitive. During tasks such as standing the ribcage cannot contribute a large moment since it is acting to support a relatively small load. In comparison, for tasks such as forward flexion, when the moment applied to the spine is considerably larger, the ribcage-sternum complex acts to generate a moment that counters loading and prevents the drastic increase in compressive force observed in the lumbar spine for the same task. Our model predicted that a change from standing to 30 degrees flexion would cause a 185% increase in vertebral compressive force in the lumbar spine but only a 57% increase in the thoracic spine. Flexion tasks have been reported to increase intradiscal pressure in the lumbar spine between 120–220% (Sato et al., 1999, Schultz et al., 1982, Wilke et al., 1999) but only increase intradiscal pressure in the thoracic spine by 26% (Polga et al., 2004). This observation invites future study as it suggests that tasks that cause injury to the thoracic spine might be fundamentally different from tasks that cause injury to the lumbar spine.

In addition to characterizing the effect of ribcage stiffness, we sought to examine how changing the maximum muscle stress affects prediction of compressive forces. Previously published models used MMS values from 0.2 – 1.0 MPa (Hansen et al., 2006). Varying MMS had minimal effect on vertebral force predictions unless the MMS approached the minimum required MMS to find a feasible solution. Certain tasks required higher MMS to find a feasible solution at a given vertebral level, e.g., 0.82 MPa was required at T8 for 20kg load with elbow flexion. Around these minimum MMS points, any increase in MMS resulted in a significant decrease in compressive force as more muscles were recruited to balance the superincumbent force.

We also examined the effect of the optimization function on the predicted compressive force. Whereas predicted forces were similar for the sum of cubed intensities and min/max functions, the difference in predicted compressive force increased with more demanding tasks (Rohlmann et al., 2006). The sum of cubed muscle intensity algorithms we used also predicted small amounts of co-contraction in the muscles of the anterior abdominal wall during demanding tasks (e.g. lifting weights with arms out). This is similar to previously published data (Hughes, 2000, Stokes and Gardner-Morse, 2001). Nonetheless, it is likely that our model still underestimates in vivo antagonist muscle activity given the nature of our optimization function. A lack of co-contraction is a limitation of many current models of the spine (Brown and Potvin, 2005).

Stiffness-based models have been used extensively to characterize motion (Farley et al., 1993, Schmitt and Holmes, 2000), load distribution (Liu and Nigg, 2000, Zadpoor et al., 2007) and stability (Obusek et al., 1995) during walking. Spring-like stiffness properties have been assigned to passive elements along the spine (Kiefer et al., 1998, Muri et al., 2008) and used to study the effects of intra-abdominal pressures on stability (Cholewicki et al., 1999). There is evidence to suggest that a similar stiffness-based approach might also accurately model the mechanical contributions of the ribcage and sternum. First, the sternum and ribcage significantly increase the load-bearing capacity of the spine (Andriacchi et al., 1974). Second, injury to the sternum is associated with an increased risk of progressive, degenerative injury to the thoracic spine due to a loss of the stability and weight bearing contributions of the sternum (Berg, 1993). Finally, removal of the costovertebral joints causes significant increases in the flexibility of the thoracic spine (Oda et al., 2002, Oda et al., 1996). Watkins, et al. (2005) tested a human thoracic spine with ribcage and sternum attached, reporting a 12% increase in axial compression and 20–40% increase in flexion-extension and lateral-bending following a displaced sternal fracture and 50–60% increase in flexion extension and lateral-bending flexibility when the sternum and ribcage complex were removed.

For our model, we had to make assumptions about how loads are distributed across the ribs and sternum. Watkins et al. (2005) and Oda et al. (1996, 2002) found comparable increases in range of motion following removal of the ribcage from the thoracic spine. This suggests that the ribcage has the same stiffness at each level that it does as a construct. For this reason, we used a single value for ribcage stiffness based on the experimental findings of Watkins et al. (2005). Whether the same is true for the sternum, however, has not been verified by in vitro tests. In the current model, we assumed full sternal stiffness across the vertebral levels in which it was present. More in vitro testing is needed to determine whether this assumption is borne out empirically.

We chose not to include the attachments of trunk muscles to the ribcage in our model. Previous models that have included muscle attachments to the ribcage (Kiefer et al., 1998, Shirazi-Adl et al., 2005) have not examined the effect of these attachments on predicted compressive force in the thoracic vertebrae. In addition to muscle attachments, it was necessary to simplify our consideration of the costovertebral and costotransverse joints. Changes in the costovertebral joint may have a significant functional consequence during breathing tasks; Polga, et al. (2004) have shown that regular breathing causes a significant oscillation (up to 0.14 MPa, ~10–15%) of measured intradiscal pressure in the thoracic spine. Intervertebral joints may also be considered in future models. Translation and rotation of individual vertebrae and the ribcage-sternum construct would not only allow for more realistic modeling of the tasks described within this manuscript, but might also have an important contribution to a stiffness based model, since rotational deformation would invalidate Equation (1) above. In this manuscript, we have only considered the ribs at T6–T10. Future work that includes higher and lower thoracic levels could explore possible changes in stiffness and mechanical properties at different levels of the spine.

The paucity of experimental data from the thoracic spine limits our ability to validate our predicted compressive forces at T6–T12. While we achieved good correlation with in vivo intradiscal pressures (Polga et al., 2004), our model may over- or under-estimate actual compressive forces. Though we believe our prediction of thoracic compressive forces is accurate, this assertion is based primarily on validation of our model against in existing models of the lumbar spine (Hughes, 2000, Schultz et al., 1982, Stokes and Gardner-Morse, 2001, van Dieen et al., 2003). We hope this paper stimulates additional research in this area, including in vivo, ex vivo and modeling studies, which would allow further refinement of the current model.

With regards to validation of our model for the lumbar spine, the data presented here closely approximates previously presented data for muscle activation and axial compression (Hughes, 2000, Schultz et al., 1982, Stokes and Gardner-Morse, 2001, van Dieen et al., 2003). A comparison with literature values shows that the current model predictions agree with data reported for in vivo intradiscal pressures as well (Sato et al., 1999, Wilke et al., 1999).

Finally, while we have validated the compressive forces predicted by this model, we have chosen to reserve the discussion of shear for future work. While the presented model does calculate shear forces, it does not yet incorporate concepts of the follower load (Patwardhan et al., 1999). Recent work has shown that inclusion of the follower load more closely approximates shear forces measured in vivo (Kim and Kim, 2008, Rohlmann et al., 2009).

In conclusion, using a stiffness-based mechanical spring model for the ribcage, spine and sternum, we have developed a new biomechanical model for estimating forces applied to thoracic and lumbar vertebral bodies during various activities. This model builds on currently available biomechanical models of the spine, and represents an important step toward accurately predicting spinal forces at thoracic vertebral levels, and thereby may provide insights into the biomechanical contributions to vertebral fractures and back pain in the thoracic spine.

Supplementary Material

01
02
03
04
05. Supplemental Data, Figure 1.

The effect of MMS on predicted compressive force was greatest near the minimum MMS required to find a feasible solution. For this task, lifting a 20kg load with elbows flexed, no feasible solutions were found when the MMS was under 0.82. The percent change in was calculated using 2471N, the compressive force with MMS = 1.20, as a baseline.

06. Supplemental Data, Figure 2.

Average predicted compressive force at L4 compared to intradiscal pressures in the spine lumbar spine measured at L4–L5 (Wilke et al., 1999). The three tasks modeled in this figure are standing, 30 degrees of flexion and lifting a 20kg load with elbows bent.

07. Supplemental Data, Figure 3.

Muscle activity of the muscles of the back (erector spinae, multifidus, and latissimus dorsi) at L3 predicted by the biomechanical model were strongly correlated to measured myoelectric signal amplitude, as previously reported by Schultz and colleagues (Schultz et al., 1982).

Acknowledgements

We thank Dr. Thomas Lang (UCSF Department of Radiology) for development of the muscle analysis software. This work was supported by NIH R01AR053986, R01AR/AG041398, T32 AG023480, the National Heart, Lung, and Blood Institute (NHLBI) Framingham Heart Study (NIH/NHLBI Contract N01-HC-25195), the Harvard-MIT Division of Health Sciences and Technology Research Assistantship, and the HMS/HSDM Office of Enrichment Programs / Division of Service Learning.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

REFERENCES

  1. Andersen JH, Haahr JP, Frost P. Risk factors for more severe regional musculoskeletal symptoms: a two-year prospective study of a general working population. Arthritis Rheum. 2007;56:1355–1364. doi: 10.1002/art.22513. [DOI] [PubMed] [Google Scholar]
  2. Andriacchi T, Schultz A, Belytschko T, Galante J. A model for studies of mechanical interactions between the human spine and rib cage. J Biomech. 1974;7:497–507. doi: 10.1016/0021-9290(74)90084-0. [DOI] [PubMed] [Google Scholar]
  3. Bean JC, Chaffin DB, Schultz AB. Biomechanical model calculation of muscle contraction forces: a double linear programming method. J Biomech. 1988;21:59–66. doi: 10.1016/0021-9290(88)90192-3. [DOI] [PubMed] [Google Scholar]
  4. Berg EE. The sternal-rib complex. A possible fourth column in thoracic spine fractures. Spine (Phila Pa 1976) 1993;18:1916–1919. [PubMed] [Google Scholar]
  5. Brown SH, Potvin JR. Constraining spine stability levels in an optimization model leads to the prediction of trunk muscle cocontraction and improved spine compression force estimates. J Biomech. 2005;38:745–754. doi: 10.1016/j.jbiomech.2004.05.011. [DOI] [PubMed] [Google Scholar]
  6. Cholewicki J, Juluru K, Mcgill SM. Intra-abdominal pressure mechanism for stabilizing the lumbar spine. J Biomech. 1999;32:13–17. doi: 10.1016/s0021-9290(98)00129-8. [DOI] [PubMed] [Google Scholar]
  7. Closkey RF, Schultz AB, Luchies CW. A model for studies of the deformable rib cage. J Biomech. 1992;25:529–539. doi: 10.1016/0021-9290(92)90093-g. [DOI] [PubMed] [Google Scholar]
  8. Contini R. Body segment parameters. II. Artif Limbs. 1972;16:1–19. [PubMed] [Google Scholar]
  9. Crowninshield RD, Brand RA. A physiologically based criterion of muscle force prediction in locomotion. J Biomech. 1981;14:793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
  10. Delmas PD, Van De Langerijt L, Watts NB, Eastell R, Genant H, Grauer A, Cahall DL. Underdiagnosis of vertebral fractures is a worldwide problem: the IMPACT study. Journal of Bone and Mineral Research. 2005;20:557–563. doi: 10.1359/JBMR.041214. [DOI] [PubMed] [Google Scholar]
  11. Farley CT, Glasheen J, Mcmahon TA. Running springs: speed and animal size. Journal of Experimental Biology. 1993;185:71–86. doi: 10.1242/jeb.185.1.71. [DOI] [PubMed] [Google Scholar]
  12. Hansen L, De Zee M, Rasmussen J, Andersen TB, Wong C, Simonsen EB. Anatomy and biomechanics of the back muscles in the lumbar spine with reference to biomechanical modeling. Spine. 2006;31:1888–1899. doi: 10.1097/01.brs.0000229232.66090.58. [DOI] [PubMed] [Google Scholar]
  13. Hoffmann U, Massaro JM, Fox CS, Manders E, O'donnell CJ from the Framingham Heart Study. Defining normal distributions of coronary artery calcium in women and men. American Journal of Cardiology. 2008;102:1136–1141. doi: 10.1016/j.amjcard.2008.06.038. 1141 e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hughes RE. Effect of optimization criterion on spinal force estimates during asymmetric lifting. J Biomech. 2000;33:225–229. doi: 10.1016/s0021-9290(99)00153-0. [DOI] [PubMed] [Google Scholar]
  15. Kiefer A, Shirazi-Adl A, Parnianpour M. Synergy of the human spine in neutral postures. European Spine Journal. 1998;7:471–479. doi: 10.1007/s005860050110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kim K, Kim YH. Role of trunk muscles in generating follower load in the lumbar spine of neutral standing posture. J Biomech Eng. 2008;130:041005. doi: 10.1115/1.2907739. [DOI] [PubMed] [Google Scholar]
  17. Kong WZ, Goel VK. Ability of the finite element models to predict response of the human spine to sinusoidal vertical vibration. Spine. 2003;28:1961–1967. doi: 10.1097/01.BRS.0000083236.33361.C5. [DOI] [PubMed] [Google Scholar]
  18. Liu W, Nigg BM. A mechanical model to determine the influence of masses and mass distribution on the impact force during running. J Biomech. 2000;33:219–224. doi: 10.1016/s0021-9290(99)00151-7. [DOI] [PubMed] [Google Scholar]
  19. Liu YK, Laborde JM, Van Buskirk WC. Inertial properties of a segmented cadaver trunk: their implications in acceleration injuries. Aerosp Med. 1971;42:650–657. [PubMed] [Google Scholar]
  20. Loring SH. Coordination of respiratory muscles in respiratory efforts. Nihon Kyobu Shikkan Gakkai Zasshi. 1991;29:312–315. [PubMed] [Google Scholar]
  21. Melton LJ, 3rd, Lane AW, Cooper C, Eastell R, O'fallon WM, Riggs BL. Prevalence and incidence of vertebral deformities. Osteoporosis International. 1993;3:113–119. doi: 10.1007/BF01623271. [DOI] [PubMed] [Google Scholar]
  22. Muri J, Winter SL, Challis JH. Changes in segmental inertial properties with age. J Biomech. 2008;41:1809–1812. doi: 10.1016/j.jbiomech.2008.03.002. [DOI] [PubMed] [Google Scholar]
  23. Narici M. Human skeletal muscle architecture studied in vivo by non-invasive imaging techniques: functional significance and applications. J Electromyogr Kinesiol. 1999;9:97–103. doi: 10.1016/s1050-6411(98)00041-8. [DOI] [PubMed] [Google Scholar]
  24. Obusek JP, Holt KG, Rosenstein RM. The hybrid mass-spring pendulum model of human leg swinging: stiffness in the control of cycle period. Biol Cybern. 1995;73:139–147. doi: 10.1007/BF00204052. [DOI] [PubMed] [Google Scholar]
  25. Oda I, Abumi K, Cunningham BW, Kaneda K, Mcafee PC. An in vitro human cadaveric study investigating the biomechanical properties of the thoracic spine. Spine (Phila Pa 1976) 2002;27:E64–E70. doi: 10.1097/00007632-200202010-00007. [DOI] [PubMed] [Google Scholar]
  26. Oda I, Abumi K, Lu D, Shono Y, Kaneda K. Biomechanical role of the posterior elements, costovertebral joints, and rib cage in the stability of the thoracic spine. Spine (Phila Pa 1976) 1996;21:1423–1429. doi: 10.1097/00007632-199606150-00005. [DOI] [PubMed] [Google Scholar]
  27. Patwardhan AG, Havey RM, Meade KP, Lee B, Dunlap B. A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine (Phila Pa 1976) 1999;24:1003–1009. doi: 10.1097/00007632-199905150-00014. [DOI] [PubMed] [Google Scholar]
  28. Polga DJ, Beaubien BP, Kallemeier PM, Schellhas KP, Lew WD, Buttermann GR, Wood KB. Measurement of in vivo intradiscal pressure in healthy thoracic intervertebral discs. Spine. 2004;29:1320–1324. doi: 10.1097/01.brs.0000127179.13271.78. [DOI] [PubMed] [Google Scholar]
  29. Rasmussen J, Damsgaard M, Voigt M. Muscle recruitment by the min/max criterion -- a comparative numerical study. J Biomech. 2001;34:409–415. doi: 10.1016/s0021-9290(00)00191-3. [DOI] [PubMed] [Google Scholar]
  30. Rohlmann A, Bauer L, Zander T, Bergmann G, Wilke HJ. Determination of trunk muscle forces for flexion and extension by using a validated finite element model of the lumbar spine and measured in vivo data. J Biomech. 2006;39:981–989. doi: 10.1016/j.jbiomech.2005.02.019. [DOI] [PubMed] [Google Scholar]
  31. Rohlmann A, Zander T, Rao M, Bergmann G. Realistic loading conditions for upper body bending. J Biomech. 2009;42:884–890. doi: 10.1016/j.jbiomech.2009.01.017. [DOI] [PubMed] [Google Scholar]
  32. Sato K, Kikuchi S, Yonezawa T. In vivo intradiscal pressure measurement in healthy individuals and in patients with ongoing back problems. Spine. 1999;24:2468–2474. doi: 10.1097/00007632-199912010-00008. [DOI] [PubMed] [Google Scholar]
  33. Schmitt J, Holmes P. Mechanical models for insect locomotion: dynamics and stability in the horizontal plane I. Theory. Biol Cybern. 2000;83:501–515. doi: 10.1007/s004220000181. [DOI] [PubMed] [Google Scholar]
  34. Schultz A, Andersson G, Ortengren R, Haderspeck K, Nachemson A. Loads on the lumbar spine. Validation of a biomechanical analysis by measurements of intradiscal pressures and myoelectric signals. J Bone Joint Surg Am. 1982;64:713–720. [PubMed] [Google Scholar]
  35. Shirazi-Adl A, El-Rich M, Pop DG, Parnianpour M. Spinal muscle forces, internal loads and stability in standing under various postures and loads--application of kinematics-based algorithm. European Spine Journal. 2005;14:381–392. doi: 10.1007/s00586-004-0779-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Stokes IA, Gardner-Morse M. Lumbar spinal muscle activation synergies predicted by multi-criteria cost function. J Biomech. 2001;34:733–740. doi: 10.1016/s0021-9290(01)00034-3. [DOI] [PubMed] [Google Scholar]
  37. Van Dieen JH, Cholewicki J, Radebold A. Trunk muscle recruitment patterns in patients with low back pain enhance the stability of the lumbar spine. Spine. 2003;28:834–841. [PubMed] [Google Scholar]
  38. Watkins RT, Watkins R, 3rd, Williams L, Ahlbrand S, Garcia R, Karamanian A, Sharp L, Vo C, Hedman T. Stability provided by the sternum and rib cage in the thoracic spine. Spine. 2005;30:1283–1286. doi: 10.1097/01.brs.0000164257.69354.bb. [DOI] [PubMed] [Google Scholar]
  39. Wilke HJ, Neef P, Caimi M, Hoogland T, Claes LE. New in vivo measurements of pressures in the intervertebral disc in daily life. Spine. 1999;24:755–762. doi: 10.1097/00007632-199904150-00005. [DOI] [PubMed] [Google Scholar]
  40. Winter DA. Biomechanics and Motor Control of Human Movement. New York: Wiley Interscience, John Wiley & Sons; 1990. [Google Scholar]
  41. Zadpoor AA, Nikooyan AA, Arshi AR. A model-based parametric study of impact force during running. J Biomech. 2007;40:2012–2021. doi: 10.1016/j.jbiomech.2006.09.016. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS217386-supplement-01.doc (84KB, doc)
02
NIHMS217386-supplement-02.doc (39.5KB, doc)
03
NIHMS217386-supplement-03.doc (35.5KB, doc)
04
NIHMS217386-supplement-04.doc (29.5KB, doc)
05. Supplemental Data, Figure 1.

The effect of MMS on predicted compressive force was greatest near the minimum MMS required to find a feasible solution. For this task, lifting a 20kg load with elbows flexed, no feasible solutions were found when the MMS was under 0.82. The percent change in was calculated using 2471N, the compressive force with MMS = 1.20, as a baseline.

NIHMS217386-supplement-05.tif (42.1KB, tif)
06. Supplemental Data, Figure 2.

Average predicted compressive force at L4 compared to intradiscal pressures in the spine lumbar spine measured at L4–L5 (Wilke et al., 1999). The three tasks modeled in this figure are standing, 30 degrees of flexion and lifting a 20kg load with elbows bent.

NIHMS217386-supplement-06.tif (18.8KB, tif)
07. Supplemental Data, Figure 3.

Muscle activity of the muscles of the back (erector spinae, multifidus, and latissimus dorsi) at L3 predicted by the biomechanical model were strongly correlated to measured myoelectric signal amplitude, as previously reported by Schultz and colleagues (Schultz et al., 1982).

NIHMS217386-supplement-07.tif (42KB, tif)

RESOURCES