Abstract
A novel assay employing D-enantiomers of phospholipids as diluents for characterizing surface kinetics of lipid hydrolysis by phospholipases is introduced. The rationale of the method are: (i) D-enantiomers resist hydrolysis because of the stereoselectivity of the enzymes toward L-enantiomers and (ii) mixtures of L+D-lipids at various L:D ratios but constant L+D-lipid concentrations yield a surface dilution series of variable L-lipid concentration with constant medium properties. Kinetic characterization of bee-venom phospholipase A2 activity at bile salt + phospholipid aggregate-water interfaces was performed using the mixed L+D-lipid surface dilution assay and interface kinetic parameters were obtained. The assay applies to bio-membrane models as well. Activity was measured by pH-Stat methods. Aggregation numbers and interface hydration/microviscosity measured by time resolved fluorescence quenching and electron spin resonance respectively confirmed that interface properties were indeed invariant in a surface dilution series, supporting rationale (ii) and were used to calculate substrate concentrations. Activity data show excellent agreement with a kinetic model derived with D-enantiomers as diluents and also that D-phospholipids bind to the enzyme but resist hydrolysis; underscoring rationale (i). The assay is significant to enabling determination of interface specific kinetic parameters for the first time and thereby characterization of interface specificity of lipolytic enzymes.
Keywords: phospholipase, lipid hydrolysis, interface, kinetics, surface dilution
Introduction
Phospholipase A2 (PLA2) catalyzes hydrolysis of the fatty-acid-ester linkage at the sn-2 position of phospholipids [1]. Enzymatic activity is most significant when lipid substrates are in aggregated forms[2–5]. The activity occurs at the aggregate-water interface[6]. Kinetic investigation is a useful approach to elucidate the mechanistic role of the interface in the rate of membrane lipid hydrolysis which is as yet not fully understood. The basic requirement for testing any kinetic model is that the medium properties not change as the substrate concentration is varied. Otherwise the concentration effects and medium effects become inextricably linked and it is not possible to test kinetic schemes. Designing a surface dilution series with invariable medium properties to test models of interfacial enzymatic kinetics has been a long standing problem in interfacial enzymology. The problem in the case of lipid substrates solubilized in detergent micelles is that, the interface properties change as the lipid concentration or lipid to detergent ratio is varied because aggregation numbers, micellar shape, surface charge, interface hydration, and microviscosity are quite sensitive to the lipid/detergent ratio as well as the total lipid + detergent concentration. In the case of membrane models, such as vesicle bilayers, the surface concentration cannot even be varied because the only component in the medium is the substrate lipid.
A new approach to designing a variable concentration interface, without drastically affecting interface properties, for characterizing kinetics of surface active enzymes is much needed. We propose the mixed L+D lipid assay as a novel solution to this long standing problem in surface enzymology. In this assay, the total L+D-lipid concentration is kept constant while the L:D ratio is varied. The enzyme is stereoselective for the L-lipid substrate [7, 8]. Therefore the substrate is the L-lipid and the D-lipid is the diluent together with any other diluents that may be used such as detergents in the case of micellar aggregates. In traditional methods surface-dilution of substrate L-lipid concentration was achieved by addition of detergents as diluents [3, 4, 9–12]. In contrast, substrate concentration in the present system is diluted within the lipid portion of the kinetic medium with a neutral diluent in the form of the respective D-phospholipid enantiomer that has been found to resist hydrolysis and also to preserve the integrity of the medium when substituted for the L-phospholipid in the act of dilution. A surface dilution series is achieved by decreasing the L:D ratio. The advantage of such a series is that medium properties remain constant as substrate concentration is varied, because the total lipid concentration and detergent concentration (in the case of micellar interfaces) remain constant. This allows direct determination of the concentration dependence of the enzyme activity with respect to a specific target substrate without having to adjust for medium property variations. In existing methods, presence of medium property variations and their impact on kinetic parameters have always been recognized to be a source of problem in data analyses and interpretation[3, 12–14]. The present method should therefore offer significantly better grounds for investigating kinetic schemes and deriving interface-enzyme and lipid-enzyme interaction parameters.
We use this assay to characterize the kinetics of enzymatic activity of bee-venom phospholipase A2 (PLA2) at the bile salt sodium taurocholate (NaTC) + (L+D-DPPC) aggregate–water interface. The power of the assay is most effectively demonstrated with these aggregates but applies to bio-membrane models as well. Activity was measured by pH-stat methods. Biophysical characterization of the mixed bile salt + phospholipid aggregates was performed to obtain the interface substrate concentration; which also confirmed that properties of aggregation number, interface hydration (polarity), and microviscosity do not change with change in L:D-lipid ratio, as long as the total lipid (L+D-lipid) and total bile salt concentrations are each kept constant. Thus, the series satisfies basic requirements for testing kinetic models namely that, medium properties remain invariable while the substrate concentration is varied. This would not be possible with use of just the L-lipid alone because varying the lipid to bile salt ratio to vary substrate concentration significantly affects aggregate properties; that is, the parameters defining the kinetic medium are not constant. Using the mixed lipid surface dilution series as the new assay, interface kinetic parameters are obtained for the activity of bee-venom PLA2. Excellent agreement of the measured enzymatic activity with an interface kinetic model that includes the presence of the D-enantiomers shows that both of the L and D-lipids bind to the enzyme but the D-enantiomer is not hydrolyzed. The present assay allows mapping of the functional dependence of the kinetic parameters on interface microstructure and thus a paradigm that the role of the interface is expressed through the kinetic parameters.
Materials and Methods
Materials
The lipids, L-α-phosphatidylcholine, dipalmitoyl (L-DPPC; Avanti polar lipids, 100%) and D-α-phosphatidylcholine, dipalmitoyl (D-DPPC; Sigma, >99%) were obtained as lyophilized powders. The bile salt, sodium taurocholate (NaTC, >95%) was obtained from Sigma and used as received.
Phospholipase A2 (PLA2) from honey bee venom was obtained from Sigma as a lyophilized powder. The enzyme was dialysed against 0.05M sodium phosphate buffer at pH 8.0 for three days, changing the buffer every 8 hours. Protein concentration was determined by the method of Lowry et al. [15] using bovine serum albumin (BSA) as standard and also by the extinction coefficient method [16, 17]. Both of these methods gave results consistent to within ±5%. The dialyzed enzyme was stored at pH 8.0 in 0.05M sodium phosphate buffer at 4°C.
Fluorescence probe pyrene (optical grade, 99%, Aldrich) and quencher 3,4-dimethyl benzophenone (DMBP, 99%, Aldrich) were used for biophysical characterization of the aggregate by time resolved fluorescence quenching (TRFQ). 5-doxyl stearic acid methyl ester (5DSE) obtained from Sigma was used as spin probe in the ESR experiments. Double distilled water was used to prepare all the solutions.
Kinetic Model
The kinetic scheme comprises of three key sequential steps: 1) enzyme-interface binding, with association and dissociation rate constants k1 and k−1 respectively, and equilibrium dissociation constant denoted by , to form the bound enzyme E*; 2) enzyme-substrate lipid binding at the active site to form the interfacial complex E*L with association and dissociation rate constants k2s and k-2s respectively; and 3) substrate lipid hydrolysis with rate constant k3[3]. When another entity that also binds to the enzyme active site but resists hydrolysis is included in the interface, the scheme gives for initial reaction velocity per mole of enzyme referred to as activity, A[18]
| (1) |
where [micelles] is the concentration of bile salt + lipid aggregates in solution; n is the number of binding sites per aggregate. The subscript s on the concentrations refers to interface or surface concentrations; thus: [L]s and [D]s are respectively the interface concentrations of substrate and the hydrolysis resistant D-enantiomer, KDs is the interfacial equilibrium D-enantiomer-enzyme dissociation constant, and
| (2) |
is the interface Michaelis-Menten parameter defined by the interface reaction rate constants k3, k2s and k−2s. When vesicles are used as membrane models, [micelles] is to be replaced with [vesicles]. Eq. 1 is the generalized result that includes the special cases: (i) D-enantiomers or the other binding entity is absent, [D]s = 0 and we get back the classic equation of Deems et al. [3, 9]; (ii) the second entity is hydrolysis resistant and much stronger binding than substrate (like an inhibitor), then eq. 1 is the same as the one derived by Berg et al., in the presence of inhibitors (also eq. 1 in the reference cited) [18]; (iii) the D-enantiomer does not bind, then it would be a neutral diluent just like the detergent. The activity would then be given by eq. 1 with KDs → ∞ and expected to exhibit the well-known saturation behavior with increase in [L]s. The assay method does not require that the D-enantiomers bind to the enzyme. The function of the D-enantiomers is to facilitate variation of the substrate concentration without compromising the underlying structure.
If the total surface lipid concentration, [L]s+[D]s = [Total Lipid]s is constant, then eq. 1 may be rewritten as,
| (3) |
| (4) |
| (5) |
The consequence of the presence of a competitively binding but hydrolysis resistant component is the negative sign in the denominator in eq. 3 which leads to a continuous non-saturating increase in activity with [L]s.
The two variables for testing the model for activity in eq. 1 or 3 are [L]s and [micelles]. The micelle concentration is given by,
| (6) |
where [NaTC], [L-DPPC] and [D-DPPC] are the solution concentrations of sodium taurocholate, L-DPPC and D-DPPC respectively, Nagg is the number of molecules forming the aggregate and [free NaTC] is the unassociated free NaTC monomer concentration in the aqueous phase. The concentrations of unassociated monomeric lipids can quite reasonably be taken to be negligible.
Problems with using only the L-enantiomers
If only the L-enantiomers are present as in the usual assays, varying the concentration of the lipid while keeping the detergent concentration constant, or varying the lipid to detergent ratio while keeping the total lipid + detergent constant causes the aggregation number, micelle concentration, and interface properties of hydration (polarity) and microviscosity to change quite significantly [10]. The parameters KS, KM, and k3 that define the kinetic medium are sensitive to interface properties and are not constant anymore. Properties of ionic as well as non-ionic micelles are also sensitive to the total detergent + lipid concentration even if the lipid to detergent ratio is held constant [10, 19–21]. So the idea of varying [micelles] while keeping the lipid to detergent ratio constant does not achieve a reliable kinetic medium either. Furthermore [L]s and [micelles] cannot be varied independently of each other.
Mixed L+D-lipid assembly
The ability to vary [L]s without varying [micelles] or any of the interface properties is possible if the [Detergent] and [L+D-lipids] are each constant and the L:D-lipid ratio is varied. This is the surface dilution series and eq. 3 applies. The aggregation number, and hence [micelles], hydration and microviscosity are constant for this series, as shown in this work (Appendix Fig. A1). It is reasonable therefore to expect that the kinetic parameters would be invariant. Thus the mixed lipid assay is close to being an ideal kinetic medium to investigate kinetic models. [L]s and [micelles] can be varied independently of each other.
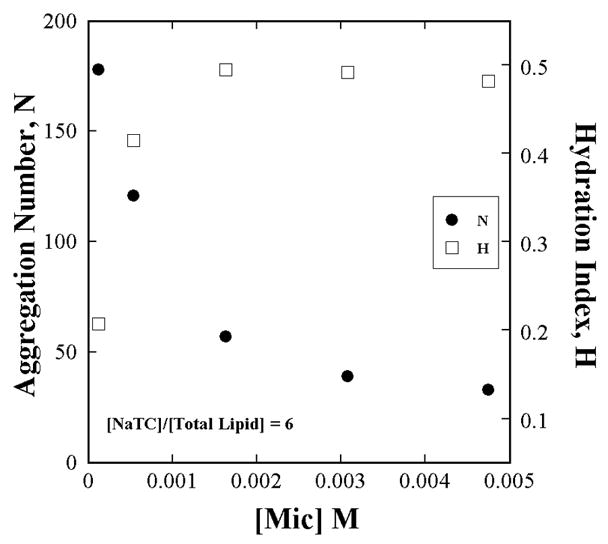
Figure A1.
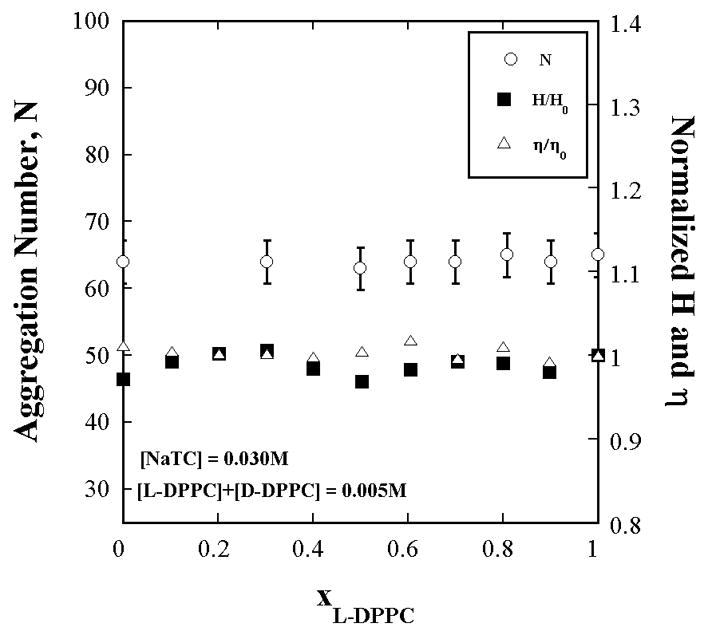
The aggregation number (by TRFQ), hydration index, H (by ESR) and microviscosity, η (by ESR) of NaTC+L-DPPC+D-DPPC aggregates do not change with the L-DPPC fraction in the lipid portion. Aggregate properties remain invariant with substrate concentration. The NaTC and total L+D-DPPC concentrations are each [L - DPPC] constant. The L-DPPC to D-DPPC ratio is varied. H and η are referred to their values H0 (=0.43) and η0 (= 0.17 cP) at xL-DPPC = 0 (xD-DPPC = 1).
Mixed micelle solution preparation
The ratio of [NaTC] to [Total Lipid] (i.e. [L-DPPC]+[D-DPPC]) was kept constant at 6 in all the samples. The composition of the samples was expressed in molar fraction of L-DPPC (XL-DPPC), defined by,
| (7) |
For enzyme activity measurements, five different series’ of samples were prepared each with [Total Lipid] = 2, 5, 10, 15, and 20mM. In each of the surface dilution series the fraction of L-DPPC in the lipid portion ranged from 0.1 to 1.0. For each series, stock solutions of NaTC+L-DPPC and NaTC+D-DPPC were prepared by mixing appropriate amount of lipid powder with few drops of ethanol. The resulting mixture was vortexed thoroughly to produce a clear solution which was then dried under dry N2 flux to produce a film of lipid. Thereafter, the required amounts of the NaTC and water were added to the dry film to achieve the final concentrations. The solution was stirred overnight to ensure the complete solubilization of phospholipid. Then appropriate volumes of two stock solutions were mixed to achieve the final XL-DPPC. Finally, CaCl2 was added to a concentration of 10mM to all the samples, as calcium ion is a required cofactor for hydrolysis by PLA2.
In the samples for TRFQ characterizations, pyrene as the probe and DMBP as quencher, were included. The concentration of pyrene was kept at about one hundredth the concentration of micelles to ensure that the fraction of micelles with two or more pyrene is negligible. The quencher (DMBP) concentration was kept at about 1.3[micelles]. The samples for ESR were similarly prepared with 5DSE as the spin probe at a concentration of 0.003[total surfactant].
Enzyme activity
The activity of enzyme was measured as the μmol of fatty acid released per milligram of enzyme per unit time. The enzyme activity measurements were conducted employing standard pH-stat methods [9]. Deprotonation of the fatty acid released by the chemical reaction causes the pH to drop and the amount of NaOH needed to bring the pH back to a preset value is a measure of enzyme activity. PLA2 activity in NaTC/DPPC aggregates was measured by addition of 30 μL of enzyme (≈7 μg) into 5 mL of aggregate solutions, and monitoring the amount of 0.01 M NaOH required per minute to maintain a constant pH of 8.00 using a Radiometer pH-stat assembly consisting of a titrator, an auto burette, and a pH meter, Model TIM 854 electrode, interfaced to a computer for recording data. The reaction was followed for about 6 min. The initial rate of activity was determined from the first 1 to 4 min of data. The yield increases linearly with time and the slope of the line divided by the mass of the enzyme in mg gives the activity, in units of μmol/min/mg. The error in the fitted slopes was < 1%. All activity measurements were conducted at 37 °C.
To account for possible batch to batch or temporal variations in enzymatic activity, hydrolytic activity towards standard assay systems was used as reference to obtain normalization factors. Two different reference assay mixtures used in this study were (i) standard egg yolk emulsion as described by Nieuwenhuizen et. al. [22] and (ii) an internal standard mixture of a zwitterionic surfactant 3-Dodecyldimethylammoniopropanesulfonate (DPS) and DMPC as explained in our previous work [9]. The composition of the DPS+DMPC mixture used as standard was [DMPC] = 4mM and [DPS] = 8mM. The observed activity in DPS+DMPC assay mixture was 2200 (±10%) μmol/min/mg. The stock solution of PLA2 showed no loss of enzymatic activity over the time period of study. All the experiments were conducted with the same batch of enzymes to avoid batch to batch variations in enzymatic activity. The precision error in the activity was determined from several repeated measurements on a few samples, with the same batch of enzyme under the same experimental conditions, over the course of the entire set of experiments, and was found to be ±5%. Care was taken to maintain identical experimental conditions (instrument warm up time, sample preparation and equilibration times). These cautionary measures are believed to have minimized scatter in the data so that reliable conclusions could be drawn.
Results and Discussion
The dependence of the activity of bee-venom PLA2 on interfacial substrate concentration is shown in Fig. 1 for five surface dilution series’, differing in total [NaTC] + [Total Lipid] concentration but with the same detergent to total lipid ratio. Each of the curves therefore refers to some constant micelle concentration that is different from the others. [L]s was determined from the measured aggregation number, interface hydration and model calculations as described in the Appendix.
Figure 1.
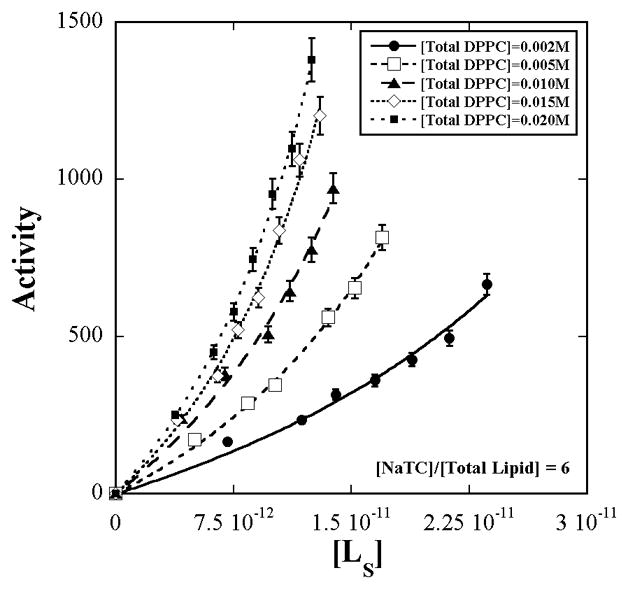
Enzymatic activity of bee-venom PLA2 (±5%) on L-DPPC in mixed aggregates of sodium taurocholate + L-DPPC +D-DPPC as a function of the interface substrate concentration, [L]s for five surface dilution series’. The concentration ratio of bile salt to total DPPC is constant at six. The total DPPC concentration varies from 0.002 to 0.020 M. Within each of the series, variation in [L]s is achieved by varying the L-DPPC to D-DPPC ratio. [L]s was calculated from measured values of aggregation number and interface hydration according to the methods in the Appendix. The lines are fits to eq. 3.
The initial slow increase in activity with [L]s followed by a rapid rise with no saturation agrees with the prediction of eq. 3 confirming that the D-enantiomer binds but resists hydrolysis.
The constant α1 extracted by fitting of eq. 3 to each of the curves varies with [micelles] as shown in Fig. 2. Examination of the behavior of α1 as a function of [micelles] must take into account the dependence of [Total Lipid]s on [micelles]. This is because aggregation number varies with NaTC + lipid concentration. The lipid surface concentration, therefore, is not constant even though the lipid to detergent ratio in solution is constant. Fit of eq. 4 to α1 vs. [micelles] after including the empirical dependence of [Total Lipid]s on [micelles] given by eq. A6 in the Appendix, yields
Figure 2.
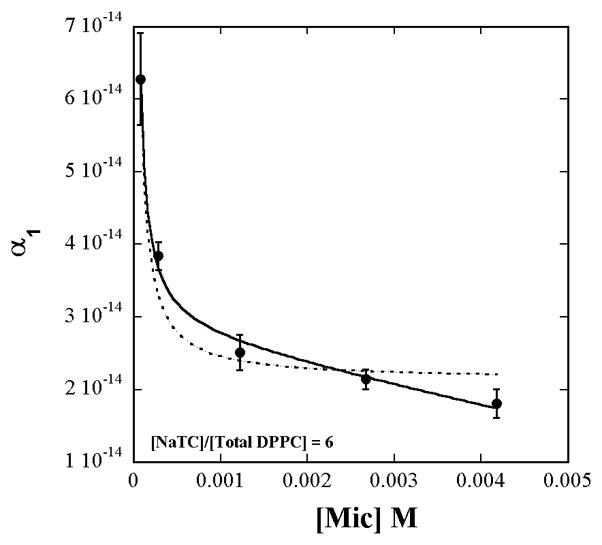
The value of α1 from the fit of eq. 3 to the data in Fig. 1 viewed as a function of the measured concentration of [micelles]. The solid and dashed lines are respectively the fits obtained to eq. 4 with and without inclusion of the observed [Total Lipid]s dependence on [micelles] according to eq. A6 and Fig. A4 (Appendix).
| (8) |
| (9) |
| (10) |
The values of α2 from each of the fits in Fig. 1 have a larger precision error and the average value is:
| (11) |
The individual kinetic parameters were then calculated as solutions to the fitting results in eq. 8–11 and the values are reported in Table 1.
Table 1.
| n | KC/10−12(Mcm−2) | Ks/10−3(M) | Km/10−12(Mcm−2) | k3(μmol/min/mg) |
|---|---|---|---|---|
| 4 | 6.05 | 1.12 | 2.2 | 2658 |
The fits in Fig. 1 and Fig. 2 show the appropriateness of expressing the lipid concentration as surface concentrations rather than mole fractions. If the lipid surface concentrations were expressed as mole fractions, then [Total Lipid]s in eq. 4 would be replaced by a constant (= 1/7 in this work) and would appear to not contribute to the variation of α1 with [micelles]. The dashed line is the fit obtained when only the inverse variation of α1 with [micelles] through just the first term alone in eq. 4, is considered and the [Total Lipid]s variation with [micelles] is ignored. However the surface concentration does vary because of the variations of the aggregation number, aggregate shape, and hydration with total lipid + detergent concentration (Fig. A4 in Appendix).
Figure A4.
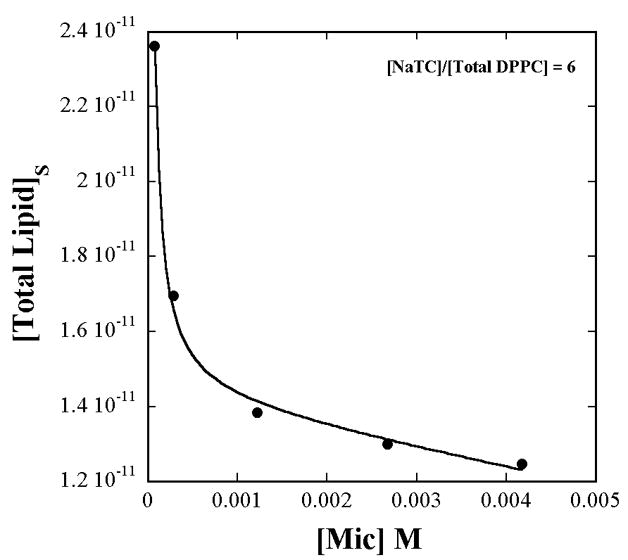
The total lipid (all L-DPPC in this measurement) interface concentration in units of Mcm−2 varies with micelle concentration due to the dependence of the aggregation number and hydration on the total NaTC+lipid concentration (as shown in Fig. A2), even when the lipid mole fraction is constant at 1/7. The solid line is the empirical fit given in eq. A6.
Biophysical characterization of aggregates thus allows determination of surface concentrations and verification of not only the appropriateness of the interface medium for kinetic characterization, but also the effects on the substrate concentration due to changes in size and shape.
Data presented in Fig. A1 confirm that aggregate properties do not vary with L:D lipid ratio and therefore it is possible to realize a true surface dilution series; one with constant medium properties. On the other hand a micelle dilution series is not dependable as Fig. A2 an A4 clearly show that aggregate properties and substrate concentration vary with micelle concentration although the lipid mole fraction is constant.
Figure A2.
The aggregation number (by TRFQ) and hydration index (by ESR) of NaTC+L-DPPC aggregates change with total NaTC+L-DPPC concentration even when the NaTC to Lipid ratio is constant.
The three step kinetic scheme and the resulting model for activity in eq. 1 (with [D]s = 0) was originally proposed and tested by Deems at al. with cobra venom PLA2 acting on phospholipids in Triton X-100 micelles. Activity vs. total detergent + lipid concentration was measured for each of several different constant lipid to detergent ratio. The data of Deems et al. and subsequent experiments along the same lines, by other researchers, exhibit saturation kinetics and general viability of the surface dilution kinetic model [4, 5, 11–14]. However the scatter in the data and lack of agreement of the model with the observed activity dependence on lipid mole fraction have led the same authors to question the validity of their assumptions on lipid mole fraction effects on micellar structure [3, 12]. The micelle physicochemical characterization data in the appendix indeed show that the aggregation number, interface polarity and microviscosity not only vary with lipid mole fraction but also with total concentration (Fig. A2 and A4). Therefore series’ of varying L-lipid mole fraction or varying [micelles] using mixed micelles of detergent and only L-lipid are not ideal systems for testing kinetic schemes and deriving kinetic parameters [13]. Nevertheless, mixed micelle kinetic media continue to be in use and have yielded useful information on kinetic parameters, schemes, and protein-lipid interactions, notwithstanding problems due to non-invariable interface characteristics within a series that can lead to scatter in the data [11, 12]. This type of information can be reliably obtained and substantially improved with the platform of mixed lipid systems here presented because the mixed lipid surface dilution series’ are an innovative way to vary the substrate lipid concentration while keeping the total L+D-lipid mole fraction, and hence medium properties, constant.
Detailed kinetic analysis and kinetic parameters are potentially keys to understanding the differences between different forms of enzymes. A significant point about the present mixed lipid surface dilution is that it is capable of addressing specificity of the kinetic parameters to the type of interface, substrate lipid, and enzyme individually, precisely because the interface properties can be held constant and interaction parameters of a specific lipid-specific enzyme at a specific interface can be determined. In this context, for example, the activity of two forms of phosphatidylinositol 4-kinases at phosphatidylinositol +Triton X-100 micellar interfaces were shown to exhibit significantly different interfacial enzymological characteristics and kinetic parameters [11, 12]. These experiments clearly make the case for the presence of specificity of kinetic parameters to not only the lipid and enzyme but also to the interface. Kinetic characterization with the present mixed lipid assay system would advance the approach to better elucidate protein-lipid interactions at interfaces through derivation and comparisons of kinetic parameters of mutant enzymes and different isoforms [14, 23].
The application presented here shows how kinetic parameters specific to an interface, lipid, and enzyme can be derived. It is part of a broader approach toward interfacial enzymology because the mixed lipid assay and proposed surface kinetic schemes apply to all types of lipid interfaces including mixed micelles, and lipid bilayer membrane models like vesicles and liposomes [14]. In the case of membrane models one would use mixtures of L+D-lipids in various proportions to prepare vesicles or liposomes. Our initial investigations using electron spin resonance of spin probes incorporated into mixed L and D-DPPC vesicles to measure the temperature dependence of the micropolarity (hyperfine coupling constant) and microviscosity of the bilayer medium [24, 25] showed that these properties not only are independent of the proportion in the mixture but also show a sudden change at 41°C, for all mixtures, which corresponds to the gel-liquid phase transition temperature of DPPC. Phase transition temperatures are quite sensitive to intermolecular interactions. The observation that each of L-DPPC, D-DPPC and their mixtures exhibits the same phase transition temperature is indicative that any complexation between L and D-lipids is either absent or does not affect physicochemical properties. The other chiral molecule in the sample solution is the enzyme. Possibility of complexation of the D-phospholipids with the enzyme is taken into account through the inclusion of the interfacial enzyme-lipid dissociation constant KDs in the kinetic scheme (eq. 1).
Conclusions
The new surface dilution assay using the D-enantiomers of the phospholipid substrate as diluents represents a significant advance in interface enzymology, because the surface substrate concentration can be varied without affecting the underlying kinetic medium. The results show that the D-enantiomers bind to enzyme, resist hydrolysis and do not change medium properties when substituted for the substrate L-enantiomers. In this sense they are neutral diluents. The medium effects can be disentangled from the substrate concentration effects and kinetic parameters specific to the interface medium can be determined. The assay permits separation and characterization of the individual steps of hydrolysis.
As an illustration, the assay was employed to determine the kinetic parameters for the interfacial activity of bee-venom PLA2 in sodium taurocholate+phospholipid aggregates for a particular lipid mole fraction of 0.14. Conducting the assay on surface dilution series’ at different mole fractions would allow the investigation of the dependence of the kinetic parameters on interface structure.
The idea of using enantiomeric mixtures should be applicable to kinetic characterization of other stereoselective surface acting enzymes. The assay is also applicable to membrane models and should open the door to characterize the kinetics of membrane lipolysis and the role of the membrane interface in it. There have been no studies of activity dependence on interface substrate concentration in membranes presumably due to lack of a method to vary this concentration. Mixed L+D-lipid bilayers can be a platform for investigating enzymatic kinetics in membranes and it is the future course of the present project.
Acknowledgments
The authors thank the NIH for their support of this project through grant S06 GM048680.
Appendix
a. Characterization of Sodium Taurocholate + DPPC aggregates
The methods used to characterize micellar aggregates and obtain the substrate concentration have been described in some detail in our previous publications [20, 26–28]. Only a brief outline and data are presented here.
Aggregation numbers were determined by time resolved fluorescence quenching (TRFQ). DMBP quenched decay of the fluorescence from pyrene solubilized in the aggregates was measured [29–31]. TRFQ measurements were carried out on several NaTC/L+D-DPPC solutions of various compositions. The aggregate concentrations and the aggregation numbers were determined from fits of the decay curves to the Infelta-Tachiya micellar quenching model [32].
The decay curves indicated small globular (spherical, ellipsoidal or small cylinders with length to diameter ratios of about six or less) polydisperse aggregates. The weight averaged aggregation numbers, Nagg, were determined from the quencher concentration dependence of the decay fit values [10, 33, 34]. The unassociated NaTC monomer concentration is expected to be less than 10 % of the [NaTC]+[Total lipid] (> 12 mM in this work) and is neglected in the calculation of Nagg and [micelles] [10].
The aggregation number does not vary with L to D-DPPC ratio for the surface dilution series where the NaTC and total L+D-DPPC are each kept constant as confirmed by Fig. A1. However the aggregation number does vary with the total concentration of NaTC and Lipid as shown in Fig. A2. The data in Fig. A2 are obtained with all L-DPPC in the lipid portion of the mixture because Nagg does not depend anyway on the proportions of the enantiomers (Fig. A1).
Also shown in Fig. A1 and A2 are the hydration index, H, and microviscosity, η, measured by electron spin resonance (ESR) using the spin probe 5-DSE incorporated in the aggregate [10, 26, 35]. The hydration index is the polarity of the environment of the spin probe and is given by the volume fraction of OH dipoles (including those from water as well as NaTC) in that environment [35, 36]. The precision errors in H and η are < 1%. b. Model calculations of [L]s. Taking the entire lipid population to be solubilized in the aggregates, the surface substrate concentration is,
| A1 |
where Amic is the aggregate surface area. The following procedure is used to calculate Amic.
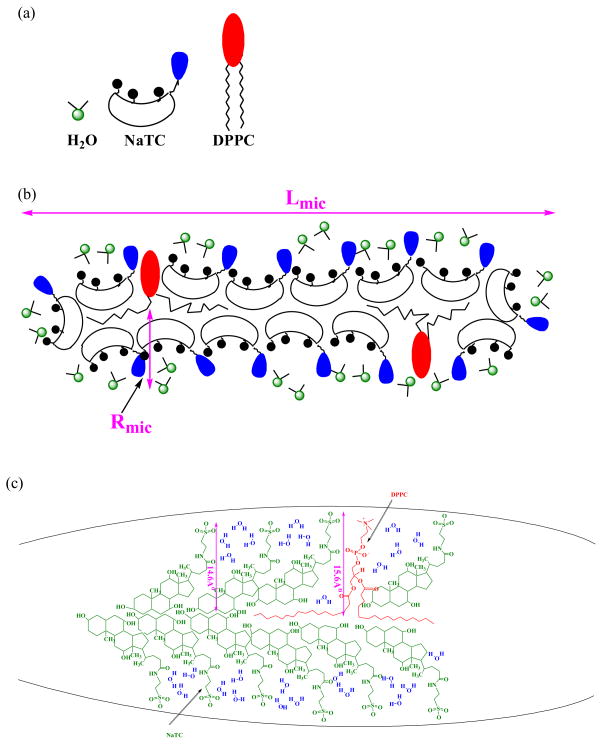
Mixed aggregates of bile salts and phospholipids are generally known to form cylindrical aggregates [10]. The aggregate and its components are shown in Fig. A3. In the present calculation the aggregate form is represented as a cylinder whose volume, Vmic (with radius and length denoted respectively by Rmic and Lmic) is
Figure A3.
(a) Components of the aggregate. (b) NaTC+DPPC cylindrical aggregate. (c) Structural formulae and arrangement of NaTC, DPPC and water molecules in a cylindrical aggregate. The dimensions shown are the local radii, estimated by Chemdraw 3D ultra 5.0, from which the average radius was derived as in eq. A3.
| A2 |
Hydration index data (Fig. A1 or A2) show that the OH dipoles from NaTC and the associated water occupy 43 % of the volume in the spin probe environment and therefore water is an important micelle component. The volume VOH in eq. A2 includes the volume of aggregate associated water and the volume of the OH portion of the NaTC. VTC-OH is the volume of the taurocholate excluding the OH (≅496 Å3) and VL is the volume of a phospholipid molecule (≅ 797 Å3) [10, 37]. NDPPC and NTC are the numbers of the phospholipid and taurocholate molecules in the aggregate. The counterion (sodium) volume is not included because it is negligible in comparison to volumes of the phospholipid and taurocholate headgroups. The arrangement of the molecules in the aggregate is visualized in Fig. A3. Such an organization is attributed to the non-linear boat-like architecture of the bile salt molecule resulting from the differences in the planes of the headgroup and each of the steroid rings and to the flexibility of the lipid chains[10]. The surface of the cylinder is nonuniform because of the heterogeneity in the sizes and shapes of the molecules in the aggregate. The occurrence of the largest radius of the aggregate is due to the (taurocholate headgroup + the steroid rings) (14.6 Å) + the cylindrical radius of lipid chain (~1 Å). The smallest radius occurs in the bile salt rich region and is about 14.6 Å. The compositionally averaged radius is thus;
| A3 |
where and are the mole fractions of DPPC and NaTC in the aggregate respectively and are taken to be equal to their solution concentrations because the free monomer concentrations are insignificant compared to the total concentrations, particularly for the lipids. For the same reason the NDPPC and NTC are also taken as their molar concentration fraction of the total aggregation number.
The volume of the spin probe environment is taken to be the total micelle volume, so that,
| A4 |
In micelles of conventional linear surfactants, the ESR signal from the spin probe is due to the polar nitroxide moiety which points in to the polar interface of micelles and in this case the spin probe environment is the interface [26]. On the other hand in bile salt assemblies containing lipids, the majority of the steroid ring volume is part of the aggregate surface as a result of the boat shape of the bile salt molecule (Fig. A3). The contribution of the NaTC headgroup to the aggregate radius is much greater than that of the steroid rings. Therefore there is no clear subdivision of the aggregate volume into an interface volume and hydrophobic core volume as in micelles of conventional linear surfactants. (For this reason bile salt assemblies are often described as aggregates rather than micelles).
Applying eq. A4, VOH in eq. A2 is replaced by . Eq. A2 can then be solved for Lmic using the numerical value of Rmic given by eq. A3. Amic is then calculated using,
| A5 |
Substitution in eq. A1 yields [L]s.
The importance of the calculation of the interface substrate concentration is illustrated in Fig. A4, which shows that it is not constant, although XDPPC is constant. The lipid surface concentration dependence on [micelles] is an outcome of the aggregation number dependence on the total solute concentrations of bile salts and lipids. The data are described empirically by the fit;
| A6 |
This dependence is of consequence in treating the data of α1 vs. [micelles] in Fig. 4 because of its presence in eq. 4.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Dennis EA. The growing phospholipase A2 superfamily of signal transduction enzymes. Trends Biochem Sci. 1997;22:1–2. doi: 10.1016/s0968-0004(96)20031-3. [DOI] [PubMed] [Google Scholar]
- 2.Pieterson WA, Vidal JC, Volwerk JJ, de Haas GH. Zymogen-catalyzed hydrolysis of monomeric substrates and the presence of a recognition site for lipid-water interfaces in phospholipase A2. Biochemistry. 1974;13:1455–1460. doi: 10.1021/bi00704a021. [DOI] [PubMed] [Google Scholar]
- 3.Deems RA, Eaton BR, Dennis EA. Kinetic Analysis of Phospholipase A2 Activity toward Mixed Micelles and Its Implications for the Study of Lipolytic Enzymes. J Biol Chem. 1975;250(23):9013–9020. [PubMed] [Google Scholar]
- 4.Hoffman WJ, Vahey M, Hajdu J. Pancreatic Porcine Phospholipase A2 Catalyzed Hydrolysis of Phosphatidycholine in Lecithin-Bile Salt Mixed Micelles: Kinetic Studies in a Lecithin-Sodium Cholate System. Arch Biochem and Biophys. 1983;221(2):361–370. doi: 10.1016/0003-9861(83)90155-8. [DOI] [PubMed] [Google Scholar]
- 5.Jain MK, Berg O. The kinetics of interfacial catalysis by phospholipase A2 and regulation of interfacial activation: hopping versus scooting. Biochim Biophys Acta. 1989;1002:127–156. doi: 10.1016/0005-2760(89)90281-6. [DOI] [PubMed] [Google Scholar]
- 6.Berg OG, Gelb MH, Tsai MD, Jain MK. Interfacial Enzymology: The Secreted Phospholipase A2-Paradigm. Chem Rev. 2001;101(9):2613–2653. doi: 10.1021/cr990139w. [DOI] [PubMed] [Google Scholar]
- 7.Pattus F, Slotboom AJ, De Haas GH. Regulation of the interaction of pancreatic phospholipase A2 with lipid-water interfaces by calcium(2+) ions: a monolayer study. Biochemistry. 1979;18:2698–2702. doi: 10.1021/bi00580a002. [DOI] [PubMed] [Google Scholar]
- 8.Gudmand M, Rocha S, Hatzakis NS, Peneva K, Müllen K, Stamou D, Uji-I H, Hofkens J, Bjørnholm T, Heimburg T. Influence of Lipid Heterogeneity and Phase Behavior on Phospholipase A2 Action at the Single Molecule Level. Biophys J. 2010;98:1873–1882. doi: 10.1016/j.bpj.2010.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Singh J, Ranganathan R, Hajdu J. Kinetics of Bacterial Phospholipase C Activity at Micellar Interfaces: Effect of Substrate Aggregate Microstructure and a Model for the Kinetic Parameters. J Phys Chem B. 2008;112(51):16741–16751. doi: 10.1021/jp807067g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Singh J, Unlu Z, Ranganathan R, Griffiths PC. Aggregate properties of sodium deoxycholate and dimyristoylphosphatidylcholine mixed micelles. J Phys Chem B. 2008;112(13):3997–4008. doi: 10.1021/jp077380w. [DOI] [PubMed] [Google Scholar]
- 11.Nickels JT, Buxeda RJ, Carman GM. Purification, characterization, and kinetic analysis of a 55-kDa form of phosphatidylinositol 4-kinase from Saccharomyces cerevisiae. J Biol Chem. 1992;267:16297–16304. [PubMed] [Google Scholar]
- 12.Buxeda RJ, Nickels JT, Belunis CJ, Carman GM. Phosphatidylinositol 4-kinase from Saccharomyces cerevisiae. Kinetic analysis using Triton X-100/phosphatidylinositol-mixed micelles. J Biol Chem. 1991;266:13859–13865. [PubMed] [Google Scholar]
- 13.Roberts MF. Assays of Phospholipases on Short-Chain Phospholipids. Methods Enzymol. 1991;197:95–113. doi: 10.1016/0076-6879(91)97137-n. [DOI] [PubMed] [Google Scholar]
- 14.Carman GM, Deems RA, Dennis EA. Lipid Signaling Enzymes and Surface Dilution Kinetics. J Biol Chem. 1995;270:18711–18714. doi: 10.1074/jbc.270.32.18711. [DOI] [PubMed] [Google Scholar]
- 15.Lowry OH, Rosebrough NJ, Lewis Farr A, Randall RJ. Protein Measurement with the Folin Phenol Reagent. J Biol Chem. 1951;193:265–275. [PubMed] [Google Scholar]
- 16.Scopes RK. Measurement of protein by spectrophotometry at 205 nm. Anal Biochem. 1974;59:277–282. doi: 10.1016/0003-2697(74)90034-7. [DOI] [PubMed] [Google Scholar]
- 17.Stoscheck CM. Quantitation of Protein. Methods Enzymol. 1990;182:50–69. doi: 10.1016/0076-6879(90)82008-p. [DOI] [PubMed] [Google Scholar]
- 18.Berg OG, Yu BZ, Rogers J, Jain MK. Interfacial catalysis by phospholipase A2: determination of the interfacial kinetic rate constants. Biochemistry. 1991;30:7283–7297. doi: 10.1021/bi00243a034. [DOI] [PubMed] [Google Scholar]
- 19.Quina FH, Nassar PM, Bonilha JBS, Bales BL. Growth of Sodium Dodecyl Sulfate Micelles with Detergent Concentration. J Phys Chem. 1995;99:17028–17031. [Google Scholar]
- 20.Ranganathan R, Tran L, Bales BL. Surfactant and Salt Induced Growth of Normal Alkyl Sodium Sulfate Micelles Well above Their CMC. J Phys Chem B. 2000;104:2260–2264. [Google Scholar]
- 21.Ranganathan R, Okano LT, Yihwa C, Quina FH. Growth of Cetyltrimethylammonium Chloride and Acetate Micelles with Counterion Concentration. J Coll Int Sci. 1999;214:238–242. doi: 10.1006/jcis.1999.6217. [DOI] [PubMed] [Google Scholar]
- 22.Nieuwenhuizen W, Kunze H, De Haas GH. Phospholipase A2 (phosphatide acylhydrolase, EC 3.1.1.4) from porcine pancreas. Methods Enzymol. 1974;32B:147–154. doi: 10.1016/0076-6879(74)32018-6. [DOI] [PubMed] [Google Scholar]
- 23.Aloulou A, Rodriguez JA, Fernandez S, van Oosterhout D, Puccinelli D, Carrière F. Exploring the specific features of interfacial enzymology based on lipase studies. Biochimica et Biophysica Acta (BBA) - Molecular and Cell Biology of Lipids. 2006;1761:995–1013. doi: 10.1016/j.bbalip.2006.06.009. [DOI] [PubMed] [Google Scholar]
- 24.Alves M, Peric M. An EPR study of the interfacial properties of phosphatidylcholine vesicles with different lipid chain lengths. Biophys Chem. 2006;122:66–73. doi: 10.1016/j.bpc.2006.02.003. [DOI] [PubMed] [Google Scholar]
- 25.Alves M, Bales BL, Peric M. Effect of lysophosphatidylcholine on the surface hydration of phospholipid vesicles. Biochim Biophys Acta (BBA) - Biomembranes. 2008;1778:414–422. doi: 10.1016/j.bbamem.2007.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Singh JS, Miller J, Ranganathan R. Physicochemical characterization of phospholipid solubilized mixed micelles and a hydrodynamic model of interfacial fluorescence quenching. J Phys Chem B. 2007;111:9317–9324. doi: 10.1021/jp0720340. [DOI] [PubMed] [Google Scholar]
- 27.Bales BL, Ranganathan R, Griffiths PC. Characterization of Mixed Micelles of SDS and a Sugar Based Nonionic Surfactant as a Variable Reaction Medium. J Phys Chem B. 2001;105:7465–7473. [Google Scholar]
- 28.Ranganathan R, Giongo C, Bakshi MS, Bales BL, Hajdu J. Phospholipid containing mixed micelles: Characterization of diheptanoylphosphatidylcholine (DHPC) and sodium dodecyl sulfate and DHPC and dodecyl trimethylammonium bromide. Chem Phys Lipids. 2005;135:93–104. doi: 10.1016/j.chemphyslip.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 29.Gehlen MH, De Schryver FC. Time-Resolved Fluorescence Quenching in Micellar Assemblies. Chem Rev. 1993;93(1):199–221. [Google Scholar]
- 30.Almgren M, Löfroth JE. Determination of Micelle Aggregation Numbers and Micelle Fluidities by Time-Resolved Fluorescence Quenching Studies. J Coll Int Sci. 1981;81:486–499. [Google Scholar]
- 31.Almgren M. In: Kinetics and Catalysis in Microheterogeneous Systems. Grätzel M, Kalyanasundaram K, editors. Marcel Dekker, Inc; New York: 1991. pp. 63–113. [Google Scholar]
- 32.Tachiya M. Application of a generating function to reaction kinetics in micelles. Kinetics of quenching of luminescent probes in micelles. Chem Phys Lett. 1975;33:289–292. [Google Scholar]
- 33.Almgren M, Swarup S. Size of Sodium Docecyl Sulfate Micelles in the Presence of Additives. 2. Aromatic and Saturated Hydrocarbons. J Phys Chem. 1982;86:4212. [Google Scholar]
- 34.Reekmans S, Bernik D, Gehlen M, Van Stam J, Van der Auweraer M, De Schryver FC. Change in the Micellar Aggregation Number or in the Size Distribution? A Dynamic Fluorescence Quenching Study of Aqueous Cetyltrimethylammonium Chloride. Langmuir. 1993;9:2289–2296. [Google Scholar]
- 35.Bales BL, Messina L, Vidal A, Peric M, Nascimento OR. Precision Relative Aggregation Number Determinations of SDS Micelles Using a Spin Probe. A Model of Micelle Surface Hydration. J Phys Chem. 1998;102:10347–10358. [Google Scholar]
- 36.Mukerjee P, Ramachandran C, Pyter RA. Solvent Effects on the Visible Spectra of Nitroxides and Relation to Nitrogen hyperfine Coupling Constants. Nonempirical Polarity Scales for Aprotic and Hydroxylic Solvents. J Phys Chem. 1982;86:3189–3197. [Google Scholar]
- 37.Zhao YH, Abraham MH, Zissimos AM. Fast Calculation of van der Waals Volume as a Sum of Atomic and Bond Contributions and its Application to Drug Compounds. J Org Chem. 2003;68:7368–7373. doi: 10.1021/jo034808o. [DOI] [PubMed] [Google Scholar]