Numerical Investigation of the Performance of Three Hinge Designs of Bileaflet Mechanical Heart Valves

Abstract

Thromboembolic complications (TECs) of bileaflet mechanical heart valves (BMHVs) are believed to be due to the nonphysiologic mechanical stresses imposed on blood elements by the hinge flows. Relating hinge flow features to design features is, therefore, essential to ultimately design BMHVs with lower TEC rates. This study aims at simulating the pulsatile three-dimensional hinge flows of three BMHVs and estimating the TEC potential associated with each hinge design. Hinge geometries are constructed from micro-computed tomography scans of BMHVs. Simulations are conducted using a Cartesian sharp-interface immersed-boundary methodology combined with a second-order accurate fractional-step method. Leaflet motion and flow boundary conditions are extracted from fluid–structure-interaction simulations of BMHV bulk flow. The numerical results are analyzed using a particle-tracking approach coupled with existing blood damage models. The gap width and, more importantly, the shape of the recess and leaflet are found to impact the flow distribution and TEC potential. Smooth, streamlined surfaces appear to be more favorable than sharp corners or sudden shape transitions. The developed framework will enable pragmatic and cost-efficient preclinical evaluation of BMHV prototypes prior to valve manufacturing. Application to a wide range of hinges with varying design parameters will eventually help in determining the optimal hinge design.

Introduction

Native heart valves with compromised function due to congenital birth defects or disease are commonly replaced by prostheses. Several prosthetic heart valves are currently available, but the prosthesis of choice remains the bileaflet mechanical heart valve (BMHV) with more than 130,000 implants every year worldwide. Nonetheless, implantation of BMHV is known to cause major complications. Despite changes and improvements in BMHV designs over the years and the development of new drug therapies, the problems of thromboembolism still persist. Clinical reports and recent in vitro experiments suggest that these problems are associated with the hemodynamic environment experienced by the blood elements flowing in the complex, nonphysiologic flow of the BMHV hinge region.

The importance of the flow fields through the hinge region of a BMHV was first brought forward by the unsuccessful clinical trials of the Medtronic Parallel (MP) BMHV. During the trials, the MP valve was found to induce unacceptably high rates of thrombosis. MP explants showed the presence of thrombi in the hinge regions. Ensuing in vitro studies of the MP hinge region indicated that the angulated sudden expansion and contraction zones of the MP hinge give rise to rotating flows, stagnation regions, and elevated shear stresses.6 Indeed, elevated fluid shear stress levels are likely to induce hemolysis and platelet activation, while flow stasis and regions of recirculating flow are believed to inhibit proper hinge wash out and favor thrombus formation by promoting cell-to-cell contact.

In vitro and clinical investigations of the hinge have provided the first and essential clues to establish a relationship between hinge design, characteristic flow features, and thromboembolic potential. However, to date most hinge studies relied on experimental measurement techniques. Because of the small dimensions of the hinge region, the opacity and the motion of the leaflets, these experimental studies could only provide limited information on the flow field, such as two-dimensional velocity fields at selected locations.6–8,16,18,20,24 In order to gain a thorough understanding of the flow-induced thromboembolic potential of the hinge, it is essential to capture the three-dimensionality of the flow at all locations within the hinge recess and to estimate the forces, in particular the viscous shear stresses, experienced by the blood elements crossing the hinge.10

Consequently, researchers have sought to develop numerical solvers capable of capturing the complex 3D pulsatile hinge flow fields. However, in order to reach clinically relevant conclusions, it is of critical importance that the simulated hinge flows reproduce the in vivo flow conditions as closely as possible, including: (1) simulating the entire cardiac cycle9,16,21 and not only considering steady conditions or parts of the cycle2,17,26; (2) capturing the full-three-dimensional hinge flow fields rather than using a 2D model14; and (3) employing highly resolved numerical meshes to accurately capture the unsteady hinge flow structures. Moreover, the simulated hinge flow fields should be related to the potential for hemolysis and platelet activation14 to gain a better insight into flow-related complications. To date and to the best knowledge of the authors, no studies have successfully met most of the above requirements and attempted to numerically assess the effect of hinge design on both the hinge flow fields and the thromboembolic potential.

This study makes use of a well-validated and extensively tested, state-of-the-art immersed-boundary approach in conjunction with a one-way coupling between large- and small-scale flow solvers, to efficiently resolve the 3D flow structures within the hinge region over the cardiac cycle. Furthermore, analysis of the flow using a Lagrangian particle-tracking algorithm combined with existing blood damage models2,4,12,27,28 provides the means for estimating the environment experienced by blood elements along their trajectories and compute a surrogate measure of the hinge thromboembolic potential. Assuming Newtonian blood flow, the proposed methodology, applied to hinges with varying design parameters, can be used to perform parametric studies where the relative hemodynamics of different hinge designs can be computed and compared within the limitations of the model. In this study, we investigate the effect of hinge curvature and hinge gap width on the hinge flow fields and the associated thromboembolic potential. Three hinge models are explored and the 3D pulsatile flow in the hinge region of each of these models is simulated under physiologic aortic flow conditions. The hemodynamic performance of the three hinges is compared and their thromboembolic potential estimated. We first present the numerical method to solve the governing equations and the boundary conditions. We describe thoroughly the three selected hinge models, then present the Eulerian and Lagrangian results for each of the three hinges, and finally compare their flow performance and blood damage potential.

Methods

Flow Solver

The present numerical solver is an extension of the fully validated methodology developed by Sotiropoulos and coworkers3,5,11,13 and is briefly presented herein. Details on the selected schemes are available in the literature.11,13 The Navier–Stokes equations that govern the flow are solved on a non-uniform Cartesian grid using a hybrid staggered/non-staggered control-volume method. In this method, the convective terms are approximated using a second-order accurate upwind QUICK scheme, while the divergence operator in the continuity equation, the pressure gradient, and the viscous terms are discretized using a three-point central scheme. The governing equations are integrated in time using an efficient, second-order accurate two-step fractional method. In the first step, the momentum equations, discretized using a second-order backward Euler scheme for the temporal term, are solved using the restarted Generalized Minimal Residual Method (GMRES) solver with a block Jacobi preconditioner. In the second step, the pressure Poisson equation is solved using a GMRES solver enhanced with a multigrid approach as a preconditioner.

This flow solver is coupled with a hybrid Cartesian sharp-interface immersed-boundary approach.13 The walls of the numerical model (which comprises the leaflet, valve housing, and valve chamber) are discretized using an unstructured, triangular mesh. This mesh is then immersed into the background Cartesian fluid grid domain and treated as a sharp-interface. The governing equations are solved at all Cartesian fluid nodes with all nodes interior to the body excluded from the computational domain. The flow variables at the nodes in the immediate vicinity of the immersed surface are reconstructed via second-order accurate interpolation along the local normal direction to the body surface, to guarantee that the effect of the moving leaflet on the surrounding fluid is appropriately represented.13

It should be noted that the hinge Reynolds number, based on a hinge gap width of 150 μm and a maximum hinge velocity of 3.5 m/s (from previously published experimental hinge data) does not exceed 150. This low Reynolds number indicates that the flow in the hinge region is far from the transitional and turbulent regimes, and consequently no turbulence modeling is here included.

Hinge Geometries and Flow Domain

The numerical model corresponds to a section of a BMHV inserted into a simplified aorta chamber composed of a straight pipe with an axisymmetric expansion representing the sinus region. Only one of the four hinges is modeled (Fig. 1). This numerical model is immersed into a Cartesian grid of approximately 5.9 million grid nodes. This number of grid nodes reaches the limit of the computational resources currently available and, therefore, a grid or time increment refinement study could not be performed. Nonetheless, the grid is selectively stretched to ensure a fine spatial resolution within the hinge recess and to capture all details of the hinge flow structures: the spatial resolution within the hinge recess is approximately 8 μm yielding a minimum of 80,000 grid nodes within the recess itself.

FIGURE 1.

Hinge numerical model. In the large-scale numerical model, a BMHV model is inserted into a simplified aorta consisting of a straight tube with an axisymmetric expansion representing the sinus region. As shown in this figure, the hinge model corresponds to a section of this large-scale model. The butterfly recess characteristic of the hinge region is clearly visible in the zoom-in panel. The positions of the boundary planes defining the Cartesian grid are also included

Three hinge configurations are investigated in order to determine the effect of hinge design on the flow fields and thromboembolic potential. The effect of wall curvature is assessed by comparing the hinge performance of the two currently most implanted BMHVs: the CarboMedics (CM) and the St Jude Medical (SJM) valves (Fig. 2). The hinge and leaflet designs are obtained from micro-computed tomography (CT) scan of actual SJM and CM clinical valves. RainDrop Geomagic (Geomagic Studio 10 SR2) is used to extract and smoothen the hinge recess and leaflet ear surfaces from the micro-CT scan. These surfaces are then extended to include the chamber using Pro|Engineer (Pro|Engineer Wildfire 3.0 M020). In both models, the leaflet ear is positioned within the hinge recess such that the hinge gap width (Fig. 1) is approximately that seen in clinical valves (150 μm). The final unstructured triangular mesh is generated using Gambit (Gambit 2.4.6, Fluent Inc.) software. The grid is selectively stretched to preserve as best as possible the geometry curvature without generating an excessively high number of triangular elements. In the hinge recess, the dimension of the triangular cells is on the order of 130 μm.

FIGURE 2.

Top and side views of the investigated hinge designs. The hinges of the two most commonly implanted bileaflet mechanical heart valves are studied: the St Jude Medical (SJM) valve and the CarboMedics (CM) valve. In order to assess the effect of the hinge gap width on the flow, two configurations of the SJM hinge are investigated: a SJM hinge with a regular hinge gap width (SJM regular hinge) and a SJM hinge with a larger than regular hinge gap width (SJM large hinge, not shown). The terminology used to describe the hinge recess is included. Note that the images are to scale and that the leaflet is in its fully closed position

The effect of the hinge gap width is investigated by comparing the performance of two SJM hinge designs with distinct hinge gap widths. The aforementioned SJM model constitutes the model of reference. The same leaflet and hinge recess geometries are then used to generate a hinge model with a larger hinge gap width: the leaflet is shifted out of the hinge recess by 100 μm so as to have a larger hinge gap width of approximately 250 μm.

Boundary Conditions

In this study, the following normal aortic physiologic flow conditions are imposed: peak valvular flow rate of approximately 25 L/min, systolic duration of one-third of the cardiac cycle, a cardiac cycle of 860 ms, and a heart rate of 70 beats/min. Inflow conditions and leaflet motion are obtained from the validated large-scale FSI simulation of the bulk flow through an aortic BMHV with no detailed hinge geometry.3 During the forward flow phase, velocity profiles are extracted from the large-scale simulation and used as boundary flow conditions for the ventricular plane of the hinge domain. However, during the leakage flow phase, the leaflets are closed and the flow features and magnitude are mainly dictated by the dimensions of the gaps offered to the flow. In the large-scale model, the periphery gap (the gap between the closed leaflets and the valve housing) is larger than in actual clinical valves, thereby limiting the relevance of the computed large-scale diastolic flow fields. A plug flow profile is therefore applied at the aortic plane of the hinge domain and the magnitude of this plug flow is set so as to reach a physiologic cross-valvular pressure drop of approximately 80 mmHg at mid-diastole. Transition between the systolic and diastolic boundary conditions is performed when the cross-valvular flow rate is zero, just before valve closure. The magnitude of the imposed diastolic plug flow is then linearly increased from 0 to its diastolic value during the leaflet closing phase.

The flow velocity at the outlet plane (i.e., the downstream/upstream plane during systole/diastole, respectively) is scaled in order to ensure mass conservation throughout the domain. Zero-transverse flux is enforced across the top and b-datum planes.

Finally, a no-slip condition is enforced along all body surfaces, including the non-moving housing and the rotating leaflet. During the forward flow phase, the leaflet motion is prescribed based on the large-scale FSI model.3 The leaflet is assumed to have only one degree of freedom: any translation motion is neglected and only a rotation motion around a fixed hinge axis is modeled. The leaflet position spans from 0° in the fully closed position to 54.2° in the fully open position in 85 ms. During systole, the leaflet remains in its fully open position for about 255 ms before starting to close. The leaflet closing phase lasts about 43 ms. After valve closure, the leaflet rebound is neglected and the leaflet is kept in a static closed position. It should be noted that the fully open leaflet makes an angle of 4.8° with the main stream flow direction. More details on the leaflet motion can be found in the literature.3,23

Lagrangian Flow Analysis

A particle-tracking algorithm is used to estimate, from the precomputed flow fields, the representative trajectories of blood elements crossing the hinge. The blood elements are modeled by weightless point particles and are assumed to be passively advected by the velocity field. Approximately, 300 particles are released within the hinge recess every 15 ms and their trajectory is computed. The principal shear stress is computed along each trajectory and used to assess the shear stress history for each particle. The most simplistic approach in assessing blood damage is defined by a linear stress-exposure time model. However, blood studies have shown that the dependency on time and stress is far more complex. Using experimental data from Wurzinger et al.,27,28 Giersiepen et al. 12 established a power law model to specifically quantify the amount of cytoplasm enzyme (LDH) released by platelets (proportional to the level of platelet activation), and the amount of hemoglobin (Hb) released by red blood cells (representative of the amount of hemolysis). Assuming that blood damage is linearly accumulated,2,4 the models proposed by Giersiepen et al. may be rewritten to compute surrogate measures of platelet activation and hemolysis levels as follows:

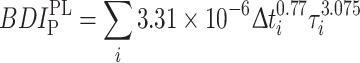1

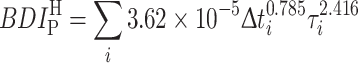2

where τ is the principal shear stress (N/m²) and Δt is the exposure time (s). BDI ^PL is the blood damage index corresponding to platelet activation, while BDI ^H refers to hemolysis and i denotes successive time points along the trajectory of particle P. The cardiac cycle is divided into 10,000 time steps, and the position of the particle tracking is updated every 40 time steps, leading to an exposure time of approximately 3 ms. Moreover, because of computational resource limitations, the Lagrangian analysis of the flow is focused on the first part of the cardiac cycle, more precisely from early systole to after valve closure (from 0 to 520 ms).

Results

The terminology used to describe the hinge recess geometry is provided in Figs. 1 and 2. The plane of reference is chosen as the flat level, which is the level flushed with the valve housing. The results for the SJM hinge with a regular hinge gap width (called SJM regular hinge) are presented in detail, whereas the presentation of the SJM hinge with a large hinge gap width (called SJM large hinge) and CM hinge focuses on their differences with respect to the SJM regular hinge.

Visualization of the full 3D and time-varying flow structures constitutes a challenge in itself. For each hinge, two sets of images are thus provided that depict the hinge flow structures at selected key instances of the cardiac cycle: first qualitatively, using 3D instantaneous streamtraces (Fig. 3); and then more quantitatively, using 2D velocity vectors superimposed on the out-of-plane velocity component contours (Figs. 4–6). The main systolic and diastolic flow features in each of the three hinge designs are shown in Fig. 9. Table 1 provides the maximum velocity magnitude and the range of each individual velocity component at peak systole and mid-diastole. These two instances are representative of the overall maximum observed throughout the forward and leakage flow phases, respectively. To help assess the shear stress distribution, Figs. 7 and 8 display the iso-surfaces of the principal shear stress at peak systole and mid-diastole. Table 1 also includes the maximum principal shear stress values during the forward and leakage flow phases.

FIGURE 3.

Three-dimensional instantaneous streamtraces at peak systole and mid-diastole for all three hinge configurations. At peak systole, the streamtraces entering the hinge first through the ventricular side of the hinge are shown in blue, those entering the hinge through the aortic side of the hinge in red. At mid-diastole, the streamtraces are colored to help the identification of the three main leakage jets

FIGURE 4.

Two-dimensional in-plane velocity vectors superimposed on the out-of-plane velocity (V ^o-p) contours at four instances of the cardiac cycle for the SJM regular hinge. The flow fields are shown at the flat level (level flush with the valve housing) and at the 195 μm level (level located 195 μm within the hinge recess, away from the flat level)

FIGURE 6.

Two-dimensional in-plane velocity vectors superimposed on the out-of-plane velocity (V ^o-p) contours at four instances of the cardiac cycle for the CM hinge. The flow fields are shown at the flat level (level flush with the valve housing) and at the 195 μm level (level located 195 μm within the hinge recess, away from the flat level)

FIGURE 9.

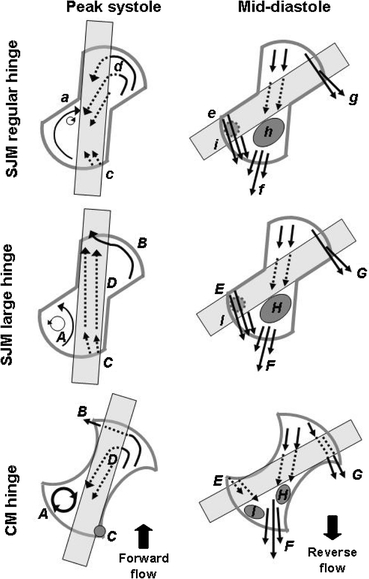
Characteristic flow features observed at peak systole and mid-diastole in all three hinge designs. Labels are used to identify each flow structure and are explained in the text in the discussion section

TABLE 1.

Velocity and shear stress at peak systole (PS) and mid-diastole (MD) for all three hinge configurations

	SJM regular hinge		SJM large hinge		CM regular hinge
	PS	MD	PS	MD	PS	MD
Velocity range
u	[−0.71; 0.71]	[−2.40; 2.40]	[−0.81; 0.80]	[−2.90; 2.97]	[−0.42; 0.67]	[−3.01; 3.34]
v	[−0.51; 0.72]	[−2.20; 2.96]	[−0.58; 0.30]	[−2.87; 2.96]	[−0.80; 0.63]	[−1.82; 3.49]
w	[−0.29; 1.53]	[−4.57; 0.70]	[−0.14; 1.65]	[−4.91; 1.55]	[−0.36; 1.45]	[−4.60; 0.13]
Max. vmag	1.54	4.75	1.66	5.26	1.46	4.61
SSmax (hinge)	1310	6515	1460	5445	1060	5910
SSmax (vicinity)	2080	8535	1730	6320	1800	8985

The table lists the range of velocity components and maximum velocity magnitude (vmag in m/s) across the hinge recess and also includes the maximum principal shear stress (SS_max in dyn/cm²) in the hinge and in the hinge vicinity (defined as the hinge region and up to 500 μm above the flat level)

FIGURE 7.

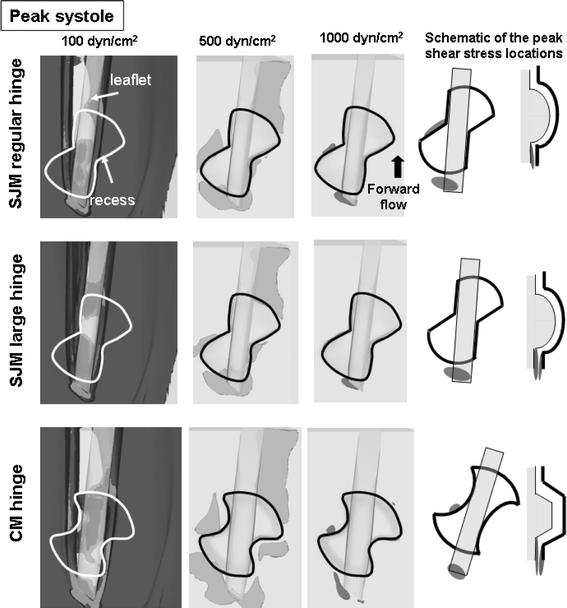
Iso-surfaces of shear stress levels at peak systole for all three hinge designs. Iso-surfaces of three shear stress levels (100, 500, and 1,000 dyn/cm²) are displayed in the near-hinge region. Top- and side-view schematics of the hinge are provided on the right side to illustrate the location of the shear stress iso-surfaces with respect to the hinge geometry

FIGURE 8.

Iso-surfaces of shear stress levels at mid-diastole for all three hinge designs. Iso-surfaces of three shear stress levels (100, 500, and 1,000 dyn/cm²) are displayed in the near-hinge region. Top- and side-view schematics of the hinge are provided on the right side to illustrate the location of the shear stress iso-surfaces with respect to the hinge geometry

SJM Hinge with a Regular Hinge Gap Width

During systole, the instantaneous flow paths strongly depend upon the point of entry of the fluid into the hinge. This is best visualized in Fig. 3 where the streamtraces entering the hinge through the ventricular side are color-coded in blue while those entering through the aortic corner are color-coded in red. The flow entering through the ventricular side (blue streamtraces) impinges against the upstream edge of the leaflet, then dives inside the hinge recess before flowing toward the adjacent corner. The flow then collides with the wall of the adjacent corner and exits the recess through the downstream-most tip of the adjacent corner with a strong out-of-plane motion. The impingement of the flow on the recess wall induces a clockwise rotating flow pattern, which appears at the end of the opening phase and persists throughout the fully open leaflet phase (Fig. 4). A drastically different path is followed by the flow entering from the aortic side (red streamtraces). Despite the forward flow outside of the hinge recess, a local flow reversal with a parabolic-like profile is observed at the bottom of the hinge recess throughout the forward flow phase. These red streamtraces are observed to mix with the blue streams coming from the ventricular corner, further increasing the portion of the blood flow exiting through the adjacent hinge corner. All of the above observations, including the presence of flow recirculation in the adjacent corner and flow reversal at the bottom of the hinge, correlate well with the experimental observations of Simon et al.22 The observed flow patterns are persistent throughout systole but vary in intensity with the magnitude of the incoming flow rate, the velocity magnitude being the largest at peak systole when the bulk valvular flow rate is at its peak (Table 1).

Accordingly, the shear stress structures at peak systole (Fig. 7) are similar to those at mid-acceleration and mid-deceleration (not shown), but with higher magnitudes due to the overall larger bulk valvular flow rate at this instant. Throughout systole, the elevated shear stress levels are observed in two main locations: (1) near the downstream edge of the adjacent corner, immediately downstream of the region of flow impingement identified in Figs. 3 and 4; and (2) immediately upstream of the hinge ventricular pocket, where the flow is squeezed between the surface of the flat level and the leaflet surface.

Systole ends with the leaflet closing phase during which the leaflet moves from its fully open to its fully closed position. During this closing phase, the flow field is strongly dominated by the clockwise rotating leaflet inducing a clockwise flow pattern throughout the hinge recess (not shown). The flow patterns present throughout the leakage flow phase start to form. Diastole is characterized by highly 3D leakage flows throughout the hinge. Three independent flow structures are identified: adjacent, ventricular, and lateral jets, named after the corner through which they exit the hinge. These jets are color-coded in Fig. 3 in green, blue, and red, respectively. The ventricular jet enters the hinge through the aortic corner, flows underneath the leaflet ear, and exits the hinge recess through the ventricular corner. The adjacent and lateral jets flow on either side of the leaflet ear. Both the ventricular and lateral jets show a streamlined pattern (Fig. 3) as they exit the hinge recess. The orientation of these leakage jets is consistent with previously published data.22 All three leakage jets exit the hinge recess with a strong out-of-plane motion, as indicated by the u-velocity contours in Fig. 4. Detachment of these fast-moving jets from the leaflet surface and the valve housing creates a complex combination of fast flowing fluid jets and regions of near stagnant flow. After flowing under the leaflet ear, the ventricular jet detaches from the leaflet surface and induces a large region of low flow along the ventricular surface of the leaflet. The adjacent jet (in green in Fig. 3), on the other hand, appears to detach from the valve housing at the edge of the recess, leading to the formation of a region of low flow at deep levels in the tip of the adjacent corner (feature i in Fig. 9).

Considering the hinge flow structures throughout the cardiac cycle, it is during the leakage flow phase that the velocity magnitudes within the hinge recess are the highest and that the flow three-dimensionality is the most pronounced (Table 1). Furthermore, the presence of localized jets and regions of flow separation yields elevated shear stresses. This is well illustrated by the large shear stress iso-surfaces shown in Fig. 8. As expected, the maximum shear stresses are seen in the wake of the leakage jets: two regions on either side of the leaflet ear corresponding to the adjacent and lateral leakage jets, as well as the flow through the peripheral gap (leaflet-housing gap); and a large iso-surface at the center of the hinge corresponding to the ventricular jet. Contrary to systole, elevated shear stresses (above 1,000 dyn/cm²) are computed not only outside of the recess, but also within the hinge. Furthermore, it is during diastole that the overall highest shear stresses are computed (Table 1). This suggests that, within the hinge recess, the leakage phase might be more detrimental to blood elements than the forward flow phase and consequently that the propensity for hemolysis and platelet activation might be higher during diastole.

SJM Hinge with a Large Hinge Gap Width

The overall flow features of the SJM large hinge are similar to those seen in the SJM regular hinge during the forward flow phase, with highly 3D and unsteady flow features (Fig. 5). The most notable differences occur at peak systole. While flow reversal is present at the bottom of the SJM regular hinge throughout systole, such a flow reversal is seen in the SJM large hinge only at mid-acceleration and mid-deceleration. At peak systole, the reverse flow is replaced by a forward flow pattern (blue streamtraces in Fig. 3). This change in flow direction impacts the flow in the other corners of the hinge, in particular in the adjacent corner where a large counter-clockwise recirculating flow pattern, not seen in the SJM regular hinge, forms (Figs. 3–5).

FIGURE 5.

Two-dimensional in-plane velocity vectors superimposed on the out-of-plane velocity (V ^o-p) contours at four instances of the cardiac cycle for the SJM large hinge. The flow fields are shown at the flat level (level flush with the valve housing) and at the 195 μm level (level located 195 μm within the hinge recess, away from the flat level)

During the leakage flow phase, the flow distribution in the SJM large hinge is similar to that of the SJM regular hinge with the presence of three main leakage jets, and regions of low flow along the ventricular leaflet surface. The overall direction of the leakage jets is similar to that seen in the SJM regular hinge, but the velocity magnitudes are larger (Table 1).

Comparison of the shear stress iso-surfaces shows similar global distribution between the SJM large and regular hinges (Figs. 7 and 8). The only major difference is seen at mid-diastole when the iso-surfaces in the SJM large hinge are seen to extend further toward the ventricular side of the hinge compared to the SJM regular hinge.

CM Hinge with a Regular Hinge Gap Width

The flow features are similar between the SJM regular and CM hinges during systole (Figs. 3, 4, and 6), except in the adjacent corner where the most striking difference is seen. Because of the confined geometry of the CM hinge, the adjacent corner is characterized by a well-defined clockwise rotating flow that spans the entire corner while in the SJM regular hinge a small localized rotating flow pattern is observed. Differences are also seen in the aortic corner. In the CM hinge, part of the fluid is seen to dive into the lateral corner and follow the curved downstream hinge wall before exiting the recess from the left-most tip of the aortic corner. This pattern corresponds to the region of elevated velocity magnitude and large out-of-plane u-velocity component seen in the aortic corner tip (Fig. 6). This localized flow pattern is not seen in the SJM regular hinge (Fig. 4).

The diastolic flow patterns of the CM hinge are similar to those of the SJM regular hinge, with three main leakage jets. However, the overall position and direction of these jets differ, as the fluid in the CM hinge is able to flow through the un-swept corner tips (Figs. 3 and 6). Moreover, it is clear that, in the CM hinge, both the ventricular and adjacent fast-paced flow jets are associated with flow separation, while in the SJM regular hinge, only the ventricular leakage jet is seen to detach from the leaflet surface. This leads to a different distribution of the regions of low flow in the ventricular side of the hinge.

The overall shear stress distribution is similar to that seen with the SJM regular hinge (Figs. 7 and 8). Nonetheless, it is worth noting that the region of elevated shear stress located in the center of the hinge recess (identified by the 1,000 dyn/cm² iso-surface) occupies nearly the entire recess of the CM hinge.

Discussion

In this study, 3D time-accurate simulations are carried out to model the flow through the hinge recess of three BMHV hinge models under physiologic aortic flow conditions. The flow features computed for the SJM regular hinge were compared to the flow structures qualitatively assessed using hydrogen bubble flow visualization techniques (courtesy Medtronic Inc), and to the Laser Doppler Velocimetry measurements reported by Simon et al.24 Comparison of the numerical and experimental results, provided in the accompanying article of this publication,23 demonstrated that the current numerical solver could accurately capture the intricacies of the hinge flow fields. Furthermore, the observed flow structures highlight the need for performing full 3D hinge simulations rather than 2D simulations.

The objective of this study is to assess the impact of different design parameters on BMHV thromboembolic potential associated with the hinge flow fields. The result section depicts the details of each hinge flow field, whereas in the following discussion section we focus on their comparison. To that end, Figs. 10 and 11 illustrate the performance of the three investigated hinge designs from a blood cell standpoint. Figure 10 shows the cumulative distribution of the maximum shear stress experienced by all the particles seeded within these three hinges along their trajectories. This figure provides the percentage of particles experiencing a maximum shear stress level larger than a set value. For example, 14% of the particles crossing the SJM large hinge are subjected to a maximum shear stress level greater than 1,000 dyn/cm². In the SJM regular hinge, the corresponding percentage is only 8%. Figure 11 uses the same display to show the cumulative distribution of blood damage index (BDI) for both hemolysis and platelet activation. Relating the differences in thromboembolic performance of the three investigated hinges to the differences in flow structures and local design parameters provides some general implications on the optimal hinge design.

FIGURE 10.

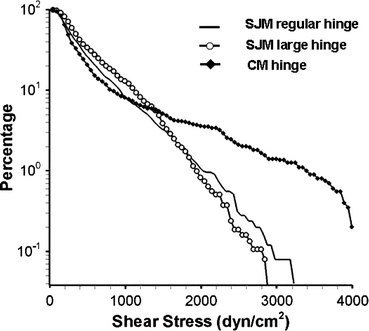
Cumulative distribution of the maximum shear stress experienced along the particle trajectories for the SJM regular, the SJM large, and the CM hinges

FIGURE 11.

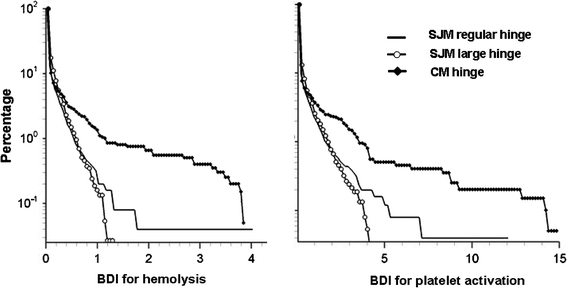
Cumulative distribution of the blood damage indices for hemolysis (left) and platelet activation (right) as a function of the particle percentage for all three hinge designs

Effect of Hinge Gap Width

The effect of the hinge gap width is evaluated using two SJM hinge models whose only difference in design stems from the prescribed dimension of the hinge gap width.

During systole, the effect of the hinge gap width on the flow features is best noted at peak systole at the bottom of the hinge recess (Fig. 9). In the SJM regular hinge, the observed flow reversal (feature d in Fig. 9) may be attributed to a region of low pressure located in the aortic (left) surface of the leaflet due to the detachment of the main stream in this region. This region of low pressure results in a negative pressure gradient between the lateral and adjacent corners of the hinge, thereby inducing the flow reversal observed at the bottom of the recess, with fluid going from the lateral to the adjacent corner. In the SJM large hinge, on the other hand, this flow reversal is replaced at peak systole by a forward flow pattern (feature D in Fig. 9). The larger hinge gap width offers lower resistance to the flow than the regular hinge gap width. This lower resistance, combined with the large valvular flow rate at peak systole, explains the change of flow direction and the formation of a forward flow pattern. The hinge gap width thus alters the flow at the bottom of the hinge recess, and in turn, in the adjacent corner. Indeed, the reverse flow pattern in the SJM regular hinge leads to the formation of a clockwise rotating flow in the adjacent corner (feature a in Fig. 9); whereas, in the SJM large hinge, the forward flow pattern present at the hinge bottom yields a counter-clockwise rotating flow structure (feature A in Fig. 9). Finally, the lateral corner of the SJM regular hinge is characterized by a smooth streamlined flow; whereas, in the SJM large hinge, a more complex flow pattern is noted. Shear stress levels computed within either hinge model during systole were of similar magnitude, suggesting a similar propensity of blood cell damage. However, the observed differences in flow structures throughout the hinge recess are expected to yield variations in the residence time of blood elements within the hinge recess and, thus, on the potential for thrombus formation between the two SJM hinge designs.

During diastole, the hinge gap width has a minor effect of the hinge flow structures, but the reported velocity values are higher in the SJM large hinge compared to the SJM regular hinge. This observation corroborates the earlier experimental findings19 which reported larger peak velocities in the SJM large hinge than in the SJM regular hinge under mitral flow conditions. The two SJM valves experience a similar trans-valvular diastolic pressure gradient and the SJM large hinge model offers a lower resistance to flow than the SJM regular hinge due to its larger gap dimensions. As a result, the diastolic flow rate is larger in the SJM large hinge than in the SJM regular hinge. This ultimately translates into faster and more three-dimensional diastolic flow in the SJM large hinge compared to the SJM regular hinge. The larger shear stress iso-surfaces observed at mid-diastole in the SJM large hinge compared to the SJM regular hinge suggest a higher thromboembolic potential in the SJM large hinge during diastole. This is in agreement with previously published blood studies by Travis et al.,25 who concluded that the hinge gap width had a significant effect on platelet damage initiated by leakage flow, the large hinge gap width being more detrimental than the regular hinge gap width.

From Fig. 10, it is evident that, up to 1,500 dyn/cm², the curve corresponding to the SJM large hinge is slightly above that of the SJM regular hinge. At larger shear stress levels, the percentage of particles is low (<1%) and the distribution is similar for both SJM hinges. Overall, Fig. 10 shows that a larger portion of the particles seeded in the SJM large hinge experience more detrimental conditions compared to the SJM regular hinge. As a result, this suggests a larger propensity for shear-induced platelet activation in the SJM large hinge. Comparison of the cumulative BDI distribution indicates that the majority of the particles seeded in the SJM large hinge experienced higher BDI than those in the SJM regular hinge. Exception should be noted for the high BDI values, for which the trend is inverted. However, these probabilities represent only very few of the seeded particles and conclusions drawn from few individual particles are to be taken cautiously.

Overall, the thromboembolic performances of the two SJM hinges appear to be similar, suggesting that the hinge gap width plays a minor role on the hinge performance. However, it should be pointed out that only one cardiac cycle is here considered. The differences in washout, flow stagnation, and shear stresses, though small, may accumulate over repeated number of passes, thereby exacerbating the influence of the hinge gap width on the flow and blood damage performance of the hinge.

Effect of the Recess and Leaflet Wall Curvature

In order to assess how wall curvature impacts the flow structures and associated thromboembolic potential, the fluid dynamic performance of the SJM regular and CM hinges are here compared.

During systole, the curvature of the wall is seen to strongly affect the flow features in the adjacent corner of the hinge, where a large rotating flow structure is seen to encompass the entire CM corner while a more localized rotating flow is seen in the SJM regular hinge (see features a and A in Fig. 9). Rotating flows are known to promote platelet aggregation and thrombus formation by trapping cells and favoring cell-to-cell contact. This, in turn, suggests a longer blood cell residence time and consequently a greater thrombogenic risk profile for the CM hinge compared to the SJM regular hinge. The variation in the curvature of the hinge corner tip is also seen to alter the systolic flow features. For instance, the CM hinge corners are not entirely swept by the leaflet ear. When the leaflet is in its fully open position, an “unswept” area exits at the tip of the aortic corner through which fluid can flow and accelerate leading to the formation of an isolated jet. Such a jet is clearly seen in the aortic corner of the CM hinge (feature B in Fig. 9) but is not present in the SJM regular hinge. The difference in wall design also alters the propensity for regions of low flow to form during systole. Abrupt changes in the geometry, such as those in the CM hinge design, disrupt the flow, leading to flow separation and the formation of low flow regions. For instance, an isolated region of low flow persists at the tip of the ventricular corner throughout the fully open leaflet phase in the CM hinge (feature c in Fig. 9). This is not seen in the SJM hinge (feature C in Fig. 9). This region of low flow is thought to play an important role in the overall thromboembolic potential of the CM hinge design by favoring cell-to-cell contact, platelet aggregation, and thrombosis. This is further emphasized by the velocity magnitude distribution during systole, where the slower velocities in the CM hinge suggest longer residence times while the larger velocities in the SJM regular hinge indicate a better washout and consequently reduced potential for thrombosis.

During diastole, similarly to what was observed during the forward flow phase, the design differences, in particular in the hinge corners, lead to differences in flow structures. The design of the CM hinge corner tips leads to the formation of bounded localized leakage jets, associated with elevated velocities and large shear stress levels. In addition, the sharp angulated surface of the CM leaflet ear promotes flow separation and the formation of a region of low flow. This is illustrated in Figs. 4 and 6, where the two hinge recesses exhibit distinct regions of low flow (feature h for the SJM regular and features I and H for the CM hinge in Fig. 9). The larger regions of low flow seen during diastole in the CM hinge suggest a greater propensity for cell-to-cell contact and thrombus formation.

Overall, the smooth streamlined SJM hinge profile, with a gradual change in geometry reduces the propensity for flow separation. In contrast, the angulated CM hinge features sharp corners that disrupt the flow and lead to large regions of elevated shear stress levels (Fig. 8). This clearly suggests that blood elements passing through the CM hinge may experience more severe flow conditions than those passing through the SJM hinge, and consequently that the CM hinge may have a higher potential for platelet activation during diastole than the SJM regular hinge. This finding correlates well with previously published experimental studies, which concluded based on a purely fluid dynamics assessment that, under mitral18 and aortic24 conditions, the thromboembolic potential might be larger in the CM hinge compared to the SJM regular hinge.

This is further confirmed by the Lagrangian analysis of the flow. Figure 10 clearly shows that a larger portion of the particles seeded in the CM hinge experience elevated shear stresses, and thus detrimental conditions, compared to the SJM regular hinge. It is noteworthy mentioning that the maximum shear stresses experienced by the particles along their trajectory are lower than those reported in the Eulerian analysis of the flow. This is not surprising since the particles are not required to travel to regions of high shear stresses. A particle seeding density closer to the actual blood cell concentration levels, yet unachievable with current computer resources, would provide a better sampling of the hinge flow features and deeper insight into the influence of the hinge design. Nonetheless, comparison of the BDI also shows that a larger percentage of particles crossing through the CM hinge experience higher BDI than those traversing through the SJM hinge (Fig. 11). Hence, this suggests a larger propensity for shear-induced red blood cell damage and platelet activation in the CM hinge. This correlates well with previous in vitro and clinical studies, which suggest that the CM hinge induces more detrimental flow conditions18,24 and higher clinical complication rates1 than the SJM hinge.

General Observations

During systole, independent of the hinge gap width and design, the largest shear stresses are not seen within the recess but immediately upstream of the recess, at the edge of the gap formed by the leaflet and the flat level surfaces. This suggests that efforts to reduce systolic shear stresses should focus on the design of the immediate hinge vicinity. On the other hand, the design of the hinge was seen to impact the flow structures within the hinge and the extent of the flow stagnation regions.

During diastole, the shear stress distribution in both SJM hinges reveals four main regions of elevated shear stresses, namely: (1) along the wall of the ventricular corner; (2) in the tip of the lateral corner; (3) along the wall of the adjacent corner; and finally (4) at the bottom of the hinge recess. The locations of these high shear stresses suggest that the curvature of the recess wall along with that of the leaflet ear play a key role in the shear stress distribution. Differences observed between the SJM and CM hinges confirm this inference and strongly suggest that angulated design and sharp corners should be avoided in favor of smooth streamlined transitions. Nonetheless, evaluating different smooth hinge designs with varying wall curvature would be of interest to determine a possible optimum curvature to minimize shear stress levels. Finally, in all three designs, close inspection of the flow fields underscores the presence of regions of low flow induced by fast flowing jets detaching from the leaflet surface and valve housing. To minimize flow separation, one may therefore envision altering the leaflet ear design as well as the hinge geometry at the edge of the recess. Sharp edges would lead to immediate flow separation while rounded edges would tend to reduce it. Changes in the curvature of the hinge edges and leaflet ear curvature should therefore reduce the propensity for platelet aggregation and thrombus formation.

Finally, it should be noted that the overall size of the leaflet is large compared to the dimensions of the hinge recess and leaflet ear. Consequently, the leaflet motion is expected to be predominantly dominated by the large-scale flow features. This is further confirmed by previous studies where the hinge recess was modeled as a simple pivot point, and yet the computed leaflet kinematics and overall fluid dynamics were in good agreement with in vitro data.3,15 In this study, only small variations in the hinge design are included. Accordingly, solely the local hinge flow features are expected to be affected, while the bulk flow dynamics and global leaflet motion should remain unaltered. However, such a hypothesis would no longer hold if the modifications to the hinge design modified the fully closed/open leaflet angles or the leaflet span. Such variations would have to be taken into account in the simulations of both the bulk flow and the detailed hinge flow fields to accurately capture the physics of the blood flow near the valve.

Limitations

In this study, the physiologic conditions are reproduced as closely as possible. However, the instant of valve closure, with the associated sudden increase in velocity magnitude and cross-valvular pressure gradient, is not accurately captured by the current modeling approach. Valve closure is here modeled such that pressure and flow smoothly transition toward their diastolic value. Such a smoothing likely leads to an underestimation of the shear stresses experienced by the blood elements. Accurate numerical modeling of the instant of valve closure would require a full two-way coupling between the large-scale and the hinge solvers and would exceed currently available computational resources. Nonetheless, all investigated hinge designs suffer from the same limitation and the design implications drawn here are expected to be comparable to those that would have been drawn with the inclusion of the exact valve closure instant modeling.

Additionally, the blood is here modeled as an incompressible single-phase Newtonian fluid. In reality, blood is a particulate fluid that exhibits non-Newtonian properties. Because of the small dimension of the hinge, large cell-to-cell interactions are expected, and these interactions would likely influence the overall trajectory and behavior of the particles. As a result, the validity of the Newtonian single-phase flow assumption used to describe the flow in the hinge recess is limited. Nevertheless, in this study, all three hinge designs have been compared within the same computational framework and the observed differences indicate the potential for significant differences in hemodynamic performance under more realistic in vivo conditions. Finally, it should be acknowledged that even the most advanced blood damage models to date only provide a rough estimate of the actual blood damage. Nonetheless, these models provide useful insights, in particular in terms of relative performance comparison across different hinge designs. An area of interest might thus be to refine the existing BDI models, thereby increasing the accuracy of fluid-based optimization frameworks such as the one described herein.

In this study, a selectively stretched grid of about 6 million nodes was used to discretize the fluid domain. Due to computational limitations, further refinement in the grid and time increment could not be performed. Nonetheless, the numerical results were found to capture the essential hinge flow structures seen experimentally, and thus, could be used to estimate the overall relative blood damage induced by the three hinges. However, in order to accurately compute the blood damage at the cell level, spatial and temporal refinement studies of particulate simulations would need to be completed to ensure (1) accurate modeling of the path of each blood cell and (2) accurate estimation of the instantaneous fluctuations of the viscous shear stresses experienced by each blood cell. Such complex and thorough refinement studies would become possible as computer cluster capabilities increase.

Conclusions

This study provides a detailed insight into the 3D flow structures within three different hinge recesses and in their vicinity while subjected to physiological aortic conditions. The findings highlight the complexity and three-dimensionality of the hinge flow fields throughout the cardiac cycle. The diastolic phase is found to be associated with the highest shear stress levels. The bottom of the hinge recess and the wake of the leakage jets are identified as the most harmful regions from a blood cell standpoint. During the forward flow phase, the shear stress levels are lower than during the leakage flow phase; however, a region of elevated shear stress is identified immediately upstream of the hinge recess at peak systole. Moreover, the velocities are also lower during systole compared to diastole. The systolic phase is thus more prone to thrombosis than diastole while the diastolic phase is plagued by an elevated risk for platelet activation.

As expected, the comparative assessment of the three hinge designs shows that the geometrical design of the hinge recess and leaflet ear has a large impact on the flow features and the associated shear stress levels. In particular, avoiding sharp corners or sudden shape transitions appears as a key geometrical design parameter. Smooth streamlined geometries, with gradual changes, should be favored to abrupt and angulated geometries to optimize hinge flow fields and minimize flow-induced complication rates. Specific studies on smooth streamlined geometries could help determine the optimal curvature of the recess and leaflet ear that will concurrently minimize blood damage and ensure that the leaflet is securely entrapped within the hinge recess and cannot be dislodged. More importantly, this study shows for the first time that the housing region immediately upstream of the hinge and the edge of the leaflet are two critically important regions to optimize in order to reduce detrimental flow conditions during the forward flow phase. Finally, in contrast to the shape of the hinge and near-hinge regions, the width of the hinge gap was found to have a minimal influence on the levels of shear stresses. Nonetheless, this parameter should not be overlooked as it could help in reducing the overall valvular thromboembolic potential.

The implications of this study are twofold. First, the computed flow fields underscore the need to perform full 3D pulsatile simulations throughout the cardiac cycle in order to fully capture the complexity and unsteadiness of hinge flows. Second, the developed framework enables rapid and cost-efficient preclinical evaluation of prototype BMHV designs prior to valve manufacturing. Application to a wide range of hinges with varying design parameters will help in determining optimal hinge design criteria. Such a study, combined with parametric studies investigating the different leaflet designs and their effect on global flow features (for instance15) is essential to optimize the overall valve design and reduce the valvular thromboembolic potential.