Only signaling modules that discriminate sharply between stimulatory and nonstimulatory inputs require basal signaling for fast cellular responses

Abstract

In many types of cells, binding of molecules to their receptors enables cascades of intracellular chemical reactions to take place (signaling). However, a low level of signaling also occurs in most unstimulated cells. Such basal signaling in resting cells can have many functions, one of which is that it is thought to be required for fast cellular responses to external stimuli. A mechanistic understanding of why this is true and which features of cellular signaling networks make basal signaling necessary for fast responses is unknown. We address this issue by obtaining the time required for activation of common types of cell signaling modules with and without basal signaling. Our results show that the absence of basal signaling does not have any dramatic effects on the response time for signaling modules that exhibit a graded response to increasing stimulus levels. In sharp contrast, signaling modules that exhibit sharp dose-response curves which discriminate sensitively between stimuli to which the cell needs to respond and low-grade inputs (or stochastic noise) require basal signaling for fast cellular responses. In such cases, we find that an optimal level of basal signaling balances the requirements for fast cellular responses while minimizing spurious activation without appropriate stimulation.

INTRODUCTION

Sufficiently strong binding of appropriate molecules (ligands) to receptors on cell surfaces can stimulate the onset of intracellular biochemical reactions (signaling), which can ultimately result in new gene transcription programs and functional responses. Low basal levels of signaling occur in unstimulated cells and can be important for many reasons. For example, it is commonly believed that a low level of basal signaling in resting cells results in fast responses when cell surface receptors are stimulated by binding of the appropriate cognate ligand. Indeed, basal signaling is sometimes referred to as “tonic” signaling to indicate that it performs a function analogous to toning one’s muscles to keep in shape and respond faster to external stimuli. While intuitively appealing, a mechanistic understanding of whether, why, and for which types of signaling networks, basal signaling required for fast responses is not available.

To remedy this situation, we studied how the time required for activation of common types of signaling modules depends upon basal signaling levels. Our results show that basal signaling is required for fast responses to external stimuli only if the signaling module exhibits a sharp dose-response curve, a feature necessary for sensitive discrimination between stochastic noise (or low-grade signals) and stimulatory doses or types of ligands. For such cases, we find that an optimal level of basal signaling balances the requirements of fast responses and avoiding spurious noise-induced activation.

MODEL DEVELOPMENT AND THEORY

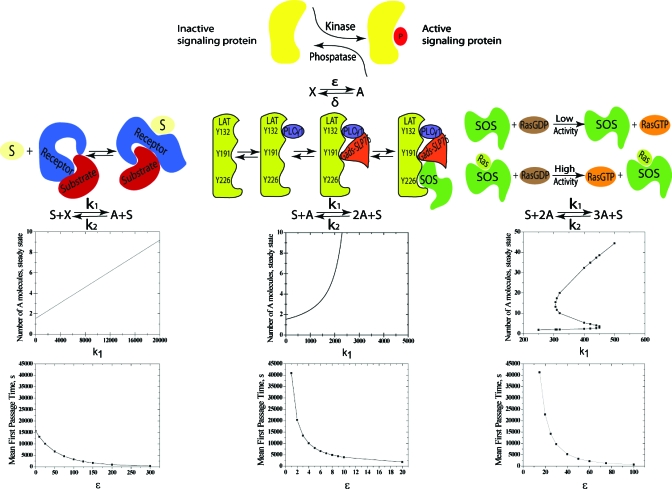
We constructed the simplest representations of common cell signaling modules because they can be analyzed exactly to reveal whether and why basal signaling determines the speed of cellular responses. Basal signaling is often established by a balance between the actions of kinases and phosphatases which activate and deactivate signaling components, respectively. For example, basal activity of the earliest signaling event in T lymphocytes is maintained by the phosphorylation of the immune receptor tyrosine activation motifs (ITAMs) of the T cell receptor by the Src kinase, Lck, and dephosphorylation of the same residues by phosphatases.¹ The simplest representation of such basal signaling is to consider a protein (X) which is converted to its active state (A) at rate ε and deactivated at another rate δ (Fig. 1, top row). The effects of basal signaling level can then be studied by varying a single parameter ε (ε=0 implies no basal signaling).

Figure 1.

The importance of basal signaling for different types of signaling modules. The first row shows the simplest model for basal signaling; active proteins (A) are produced from inactive ones (X) and deactivated. ε and δ are rates of the forward and reverse steps, respectively. The second row depicts three examples of signaling modules that exhibit graded or sharp dose-response curves (see text) and their simplest representations. The third row shows that these simple models exhibit graded, sharp, and bistable dose-response curves (see text) since the parameter k₁ represents the strength of the stimulus. The results in this row are for ε=4000, δ=2600, k₂=10, and N=6. The fourth row shows the mean time to activation as a function of the level of basal signaling (ε) for each of the modules that we studied (with k₁=320, δ=2600, k₂=10, and N=6). Parameter sensitivity studies show that these qualitative results are independent of the choice of the few parameters in these models (Figs. S2–S7) (Ref. ¹⁵).

Complex signaling modules have evolved to regulate cellular behavior.² We focus on commonly found modules that regulate membrane-proximal signaling upon receptor stimulation because the influence of basal signaling on speed of signal propagation should be relevant for the earliest events. Cellular responses to dose or type of external stimuli can be graded or sharp.² Signaling modules that exhibit graded dose-response curves do not require cooperative interactions between participating signaling components. Ligand sensing modules wherein the receptor undergoes a conformational change upon ligand binding, thereby making a substrate (e.g., ITAMs) more easily accessible for downstream action by other signaling molecules (e.g., kinases), are examples of such a situation.³ The simplest representation of such a signaling module is to consider a stimulus S, which leads to a much faster rate of activation of X than that due to basal signaling (Fig. 1, second row, left column). We calculated the steady-state dose-response curve for this model and it is graded (Fig. 1, third row, first column).

Signaling modules that exhibit sharp dose-response curves involve cooperative interactions between signaling components. We consider two types of such signaling modules. The first type results in a sharp dose-response curve characterized by a large Hill coefficient.⁴ An example drawn from T cell signaling is shown in Fig. 1 (second column). A protein called ZAP70,⁵ which is recruited and activated upon phosphorylation of the T cell receptor, phosphorylates multiple tyrosines on the linker for activation of T cells (LAT). Many proteins bind to phosphorylated LAT to assemble a key signaling complex. LAT phosphorylation and binding of these proteins to LAT involve a number of cooperative interactions,^{6, 7, 8} which can make signal propagation past the LAT signaling complex exhibit a sharp dose-response curve.⁹ We caricature this type of signaling module with a biochemical reaction which exhibits a steady-state dose response curve with a large Hill coefficient (Fig. 1, second and third rows, second column).

Positive feedback regulation of signaling components is ubiquitous and can lead to bistability.¹⁰ Bistability implies that in a range of stimulus levels, two cellular states are possible: one with a very high level of signaling activity and the other is not. Thus, as stimulus level is increased past a threshold, due to stochastic effects, some cells exhibit high signaling levels (activated or “on”) and others maintain basal signaling (not activated or “off”). Such “digital” responses often mediate sharp discrimination between stimulatory and nonstimulatory ligand type or dose.² One example is provided by the activation of Ras proteins by the guanine exchange factor Son of Sevenless (SOS). Active Ras bound to an allosteric site in SOS increases SOS’ catalytic activity by a factor of 75,¹¹ and it has been suggested that this positive feedback regulation influences digital signaling in lymphocytes.¹² We studied a simple signaling reaction that exhibits bistability in its steady-state response (Fig. 1, third column, rows two and three).

Activation usually corresponds to the production of a sufficiently large number of active signaling components. We used the framework of Master equations in statistical physics,¹³ which accounts for stochastic cell-to-cell variations, to obtain an exact formula for the mean time (τ_m) required for a population of cells to be activated (i.e., N activated proteins, A, are produced given that m active proteins were present initially) for the signaling modules shown in Fig. 1.

Consider an activated signaling protein A created at a small rate ε and decaying at a rate δ, i.e., the basic processes are

$$\text{X}\underset{\delta }{\overset{\epsilon }{\rightleftarrows }}\text{A}.$$

Starting with m copies of A at time t=0, the probability p_n(t|m) to find n copies of A at time t then evolves according to the forward Master equation

$$\frac{d}{dt}{p}_n\left(t|m\right)=-\left(\epsilon +n\delta \right)p_n\left(t|m\right)+\epsilon p_{n-1}\left(t|m\right)+\left(n+1\right)\delta p_{n+1}\left(t|m\right).$$ (1)

For ε=0 there will be no “basal expression,” and m=0. With finite ε the steady state probability distribution is

$$p_n^{*}=\frac{1}{n!}{\left(\frac{\epsilon }{\delta }\right)}^n{e}^{-\epsilon ∕\delta }.$$ (2)

At time t=0, stimulation results in the production of more A molecules. We would like to know how much time it takes for the system to produce a sufficient number of active signaling proteins (A) required for activation, given different levels of basal expression (encoded in the parameter ε). We will assume that activation corresponds to the production of a threshold number N of A molecules. This is equivalent to placing an absorbing boundary condition at n=N (achieved via having zero rates for transitions out of N).

The mean first passage time to a state with N molecules of A can be computed by integrating the forward Master equation

$$\frac{d}{dt}{p}_N\left(t|m\right)=-\left(\epsilon +m\delta \right)p_N\left(t|m\right)+\epsilon p_N\left(t|m+1\right)+m\delta p_N\left(t|m-1\right)$$ (3)

from 0 to ∞, and using integration by parts, as

$${\int }_0^{\infty }dt{p}_N\left(t|m\right)=t{p}_N\left(t|m\right){|}_0^{\infty }-{\int }_0^{\infty }dtt\frac{d{p}_N\left(t|m\right)}{dt}.$$ (4)

Since dp_N(t|m)∕dt is the absorption probability at time t, the last factor is the mean absorption time τ_m, which thus satisfies

$$1=\left(\epsilon +m\delta \right)\tau \left(m\right)-\epsilon \tau \left(m+1\right)-m\delta \tau \left(m-1\right)=\epsilon \left(\tau \left(m\right)-\tau \left(m+1\right)\right)-m\delta \left(\tau \left(m-1\right)-\tau \left(m\right)\right).$$ (5)

In terms of general forward and backward rates [r⁺(m) and r⁻(m)], Eq. 5 can be recast as a recursion relation for the time differences

$${\Delta }_m\equiv \left(\tau \left(m\right)-\tau \left(m+1\right)\right)=\frac{1}{r^{+}\left(m\right)}+\frac{r^{-}\left(m\right)}{r^{+}\left(m\right)}{\Delta }_{m-1}.$$ (6)

The absence of a backward rate for m=0 implies Δ₀=1∕r⁺(0) for the starting point of the recursion, leading to

$${\Delta }_m=\frac{1}{r^{+}\left(m\right)}+\sum _{z=1}^m\frac{1}{r^{+}\left(z-1\right)}\prod _{x=z}^m\frac{r^{-}\left(x\right)}{r^{+}\left(x\right)}.$$ (7)

Finally, starting from τ(N)=0, and working backward with the above differences yields

$$\tau \left(m\right)=\sum _{y=m}^{N-1}\left(\frac{1}{r^{+}\left(y\right)}+\sum _{z=1}^y\frac{1}{r^{+}\left(z-1\right)}\prod _{x=z}^y\frac{r^{-}\left(x\right)}{r^{+}\left(x\right)}\right).$$ (8)

To make the formula correct for m=0 we add and subtract the next term of the first sum

$$\tau \left(m\right)=\sum _{y=m}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{r^{+}\left(z-1\right)}\left(\prod _{x=z}^{y+1}\frac{r^{-}\left(x\right)}{r^{+}\left(x\right)}\right)\frac{r^{+}\left(y+1\right)}{r^{-}\left(y+1\right)}\right).$$ (9)

Note again that r⁺(x) and r⁻(x) are the rates at which an additional activated protein is produced and deactivated, respectively, given a state with x activated proteins, and these rates are different for each signaling module in Fig. 1. We used Eq. 9 to obtain (see below) how the mean time to activation is influenced by different levels of basal signaling (values of ε) for each type of module shown in Fig. 1.

Model 1

$$\text{X}\underset{\delta }{\overset{\epsilon }{\rightleftarrows }}\text{A},$$

$$\text{S}+\text{X}\underset{k_2}{\overset{k_1}{\rightleftarrows }}\text{A}+\text{S},$$

Noting that concentrations of X and S species always remain constant and are included in the reactions rate values, for model 1, and Eq. 9 becomes

$$\tau =\sum _{y=m}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\left(\delta +k_2\right)\left(y+1\right)}\left(\prod _{x=z}^{y+1}\frac{\left(\delta +k_2\right)x}{\epsilon +k_1}\right)\right).$$ (10)

For the situation where there is no basal signaling (i.e., ε=0), Eq. 10 becomes

$$\tau \left(\epsilon =0\right)=\sum _{y=0}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\left(\delta +k_2\right)\left(y+1\right)}\left(\prod _{x=z}^{y+1}\frac{\left(\delta +k_2\right)x}{k_1}\right)\right).$$ (11)

So the mean first passage time will have some finite value even when there is no basal signaling.

Model 2

$$\text{X}\underset{\delta }{\overset{\epsilon }{\rightleftarrows }}\text{A},$$

$$\text{S}+\text{A}\underset{k_2}{\overset{k_1}{\rightleftarrows }}2\text{A}+\text{S},$$

For model 2, Eq. 9 becomes

$$\tau =\sum _{y=m}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\epsilon +k_1\left(z-1\right)}\left(\prod _{x=z}^{y+1}\frac{\delta x+k_{2}x\left(x-1\right)∕2}{\epsilon +k_{1}x}\right)\frac{\epsilon +k_1\left(y+1\right)}{\delta \left(y+1\right)+k_{2}y\left(y+1\right)∕2}\right).$$ (12)

For the case when there is no basal signaling, we set ε→0 to obtain

$$\tau =\sum _{y=0}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\epsilon +k_1\left(z-1\right)}\left(\prod _{x=z}^{y+1}\frac{\delta x+k_{2}x\left(x-1\right)∕2}{\epsilon +k_{1}x}\right)\frac{\epsilon +k_1\left(y+1\right)}{\delta \left(y+1\right)+k_{2}y\left(y+1\right)∕2}\right).$$ (13)

Consider two cases because the system must contain at least one molecule of A to start an autocatalytic reaction

• (1)
  N=1, then it is obvious

  $$\tau \left(\epsilon \to 0\right)=\frac{1}{\epsilon }.$$ (14)
• (2)
  N>1, then Eq. 13 becomes

  $$\tau \left(\epsilon \to 0\right)=\frac{1}{\epsilon }\left(1+\sum _{y=1}^{N-1}\prod _{x=1}^y\frac{\delta +k_2\left(x-1\right)∕2}{k_1}\right)+\sum _{y=1}^{N-1}\sum _{z=2}^{y+1}\frac{1}{k_1\left(z-1\right)}\prod _{x=z}^y\frac{\delta +k_2\left(x-1\right)∕2}{k_1}.$$ (15)

  So for the second model mean first passage time diverges as 1∕ε as ε→0.

Model 3

$$\text{X}\underset{\delta }{\overset{\epsilon }{\rightleftarrows }}\text{A},$$

$$\text{S}+2\text{A}\underset{k_2}{\overset{k_1}{\rightleftarrows }}3\text{A}+\text{S}.$$

For the third model Eq. 9 becomes

$$\tau =\sum _{y=m}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\epsilon +k_1\left(z-1\right)\left(z-2\right)∕2}\left(\prod _{x=z}^{y+1}\frac{\delta x+k_{2}x\left(x-1\right)\left(x-2\right)∕6}{\epsilon +k_{1}x\left(x-1\right)∕2}\right)\frac{\epsilon +k_{1}y\left(y+1\right)∕2}{\delta \left(y+1\right)+k_{2}y\left(y+1\right)\left(y-1\right)∕6}\right).$$ (16)

For the case where there is no basal signaling, we set ε→0 to obtain

$$\tau =\sum _{y=0}^{N-1}\sum _{z=1}^{y+1}\left(\frac{1}{\epsilon +k_1\left(z-1\right)\left(z-2\right)∕2}\left(\prod _{x=z}^{y+1}\frac{\delta x+k_{2}x\left(x-1\right)\left(x-2\right)∕6}{\epsilon +k_{1}x\left(x-1\right)∕2}\right)\frac{\epsilon +k_{1}y\left(y+1\right)∕2}{\delta \left(y+1\right)+k_{2}y\left(y+1\right)\left(y-1\right)∕6}\right).$$ (17)

Now we should consider three cases, because to start an autocatalytic reaction the system must contain at least two molecules of A

• (1)
  N=1

  $$\tau \left(\epsilon \to 0\right)=\frac{1}{\epsilon }.$$ (18)
• (2)
  N=2, then Eq. 17 becomes

  $$\tau \left(\epsilon \to 0\right)=\frac{\delta }{{\epsilon }^2}+\frac{2}{\epsilon }.$$ (19)
• (3)
  N>2, then Eq. 17 becomes

  $$\tau \left(\epsilon \to 0\right)=\frac{\delta }{{\epsilon }^2}\left(1+\sum _{y=2}^{N-1}\prod _{x=2}^y\frac{\delta +k_2\left(x-1\right)\left(x-2\right)∕6}{k_1\left(x-1\right)∕2}\right)+\frac{1}{\epsilon }\left(2+\sum _{y=2}^{N-1}\prod _{x=2}^y\frac{\delta +k_2\left(x-1\right)\left(x-2\right)∕6}{k_1\left(x-1\right)∕2}\right)+\sum _{y=2}^{N-1}\sum _{z=3}^{y+1}\frac{1}{k_1\left(z-1\right)\left(z-2\right)∕2}\prod _{x=z}^y\frac{\delta +k_2\left(x-1\right)\left(x-2\right)∕6}{k_1\left(x-1\right)∕2}.$$ (20)

  For the third model the mean first passage time diverges as 1∕ε² as ε→0.

RESULTS AND DISCUSSION

We used Eqs. 10, 12, 16 (and the software package, MATHEMATICA¹⁴) to calculate the mean first passage time for various levels of basal signaling (i.e., values of ε). Our qualitative results are independent of the choice of the parameters k₁, k₂, and δ (Figs. S2–S7).¹⁵ We also used the Gillespie algorithm¹⁶ to compute the entire distribution of times required for activation, and these calculations showed that the mean value obtained from Eqs. 10, 12, 16 is representative of the entire distribution (Fig. S1).¹⁵

Our results are shown in Fig. 1 (last row). For signaling modules that do not involve cooperative interactions and exhibit a graded dose-response curve, the absence of basal signaling does not lead to any dramatic consequences as the mean time to activation is finite for ε=0 [as also predicted by the limiting result in Eq. 11]. In contrast, for both types of cooperative signaling modules, the mean time to activation increases sharply as the basal signaling level becomes small. For the models we studied, the mean activation time becomes infinitely long when there is no basal signaling (diverging as 1∕ε and 1∕ε² for the models shown in the second and third columns in Fig. 1, respectively; see limiting results in Eqs. 14, 15, 18, 19, 20.

The second and third types of signaling modules that we consider exhibit dose-response curves that discriminate sharply between ligands (type or dose) that are stimulatory and those that are not (see steady-state responses in Fig. 1); the first type of model does not. Our results for the time to activation suggest that basal signaling is essential for fast cellular responses if the signaling module discriminates sharply between cognate ligands and inappropriate ones that bind to the receptor weakly. One “price” for sensitive discrimination between appropriate stimuli to which the cell needs to respond fast, and irrelevant stimulation, is to maintain basal signaling.

Why is basal signaling necessary for fast responses when the signaling module discriminates sharply between stimulatory and nonstimulatory ligands? Signaling modules that result in sharp dose-response curves require cooperative interactions between proteins to assemble a moiety whose creation potentiates efficient signal propagation. For example, Ras activation by SOS (Fig. 1, second row, third column) is much faster after a sufficient number of SOS molecules have active Ras proteins bound to the allosteric site of SOS.^{11, 12} In the two simple cooperative signaling modules we studied, this effect is modeled by the requirement that two or three molecules of active A proteins are needed for efficient production of more active molecules (Fig. 1, second row, second and third columns). Basal signaling allows one to reach the threshold number of A molecules required for efficient signal propagation more rapidly. More generally, for signaling modules that discriminate sharply between stimulatory and nonstimulatory ligands, a “critical nucleus” of signaling components must be formed after which signals propagate quickly. The threshold stimulus required for activation is also that required to assemble the critical nucleus. Upon appropriate stimulation, this critical nucleus is assembled more rapidly when there is basal signaling. For example, if there is some basal Ras activity, it is easier to form a threshold number of SOS molecules with active Ras bound to the allosteric site (the critical nucleus) than if there were no active Ras proteins prior to stimulation.

An analogy can be made with the requirement that for a chemical reaction to proceed, the reactants must come together with sufficient free energy to overcome a threshold (that of the transition state¹³). Higher temperatures increase the chance (or rate) of occurrence of such an event, with zero temperature resulting in a zero rate of reaction. Basal signaling enhances the speed of activation of cooperative signaling modules in a manner analogous to how higher temperature increases the speed of a chemical reaction.

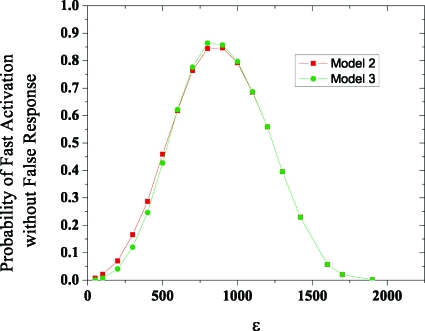
Too high a level of basal signaling would result in frequent spurious responses because the critical nucleus could be readily created even if the appropriate stimulus was absent. For the two cooperative signaling modules shown in Fig. 1, using Gillespie-based simulations,¹⁶ we calculated the probability of spurious activation (P₁) within an observation time when there is no stimulus (just basal signaling). We also calculated the probability of activation (P₂) within the same time when the appropriate stimulus (S) is present. The observation time is the typical time that the cell is in contact with a medium that could have stimulatory ligands. For example, in lymphoid tissues, T lymphocytes scan antigen presenting cells for 3 min at a time.¹⁷ The desired behavior is to be activated within this contact time if the appropriate ligand is present and not be stimulated by irrelevant ligands. A measure of how well a signaling module achieves this goal is the product, (1–P₁)×P₂, as it is the probability that, during the observation time, the cell is activated by cognate ligands but not spuriously activated. This quantity is graphed as a function of ε in Fig. 2 and the results show that there is an optimal level of basal signaling which results in fast responses to cognate ligands without frequent spurious activation. Modest levels of tonic signaling in cells with signaling networks that discriminate sharply between ligands of different quality serve this purpose.

Figure 2.

An optimal level of basal signaling results in fast responses to appropriate stimuli without spurious “noise-induced” activation. The product of the probability of activation when cognate ligand is present and the probability of not being activated without ligand (within an observation time) is graphed as a function of basal signaling level. The parameters are k₁=320, δ=2600, k₂=10, N=6, and the observation time is 5 s. Figs. S8–S9 (Ref. ¹⁵) show that this qualitative result is robust to changes in these parameters.