Contributions of Efference Copy to Limb Localization: Evidence from Deafferentation

Abstract

Previous research with deafferented subjects suggests that efference copy can be used to update limb position. However, the contributions of efference copy to limb localization are currently unclear. We examined the performance of JDY, a woman with severe, longstanding proprioceptive deficits from a sensory peripheral neuropathy, on a reaching task to explore the contribution of efference copy to trajectory control. JDY and eight healthy controls reached without visual feedback to a target that either remained stationary or jumped to a second location after movement initiation. JDY consistently made hypermetric movements to the final target, exhibiting significant problems with amplitude control. Despite this amplitude control deficit, JDY’s performance on jump trials showed that the angle of movement correction (angle between pre- and post-correction movement segments) was significantly correlated with the distance (but not time) of movement from start to turn point. These data suggest that despite an absence of proprioceptive and visual information regarding hand location, JDY derived information about movement distance that informed her movement correction on jump trials. The same type of information that permitted her to correct movement direction on-line, however, was not available for control of final arm position. We propose that efference copy can provide a consistent estimate of limb position that becomes less informative over the course of the movement. We discuss the implications of these data for current models of motor control.

1. Introduction

Current accounts of motor control posit that estimates of the position of the limb during movement are derived from both sensory feedback (primarily from vision and proprioception) and predicted from efference copy using a “forward model” (Desmurget and Grafton, 2000; Gritsenko et al., 2009). Support for the latter comes from a study by Wolpert and colleagues (1995); these investigators instructed subjects to localize hand position without vision at the end of a movement while being subjected to a null, assistive, or resistive force field. Subjects consistently overestimated limb position in the direction of the movement; this overestimation bias was increased by assistive forces and decreased by resistive forces, demonstrating that the difference in the motor plan required to compensate for the force field influenced the perception of hand location. Wolpert and colleagues modeled this localization by incorporating input from sensory inflow as well as motor outflow. More specifically, a copy of the motor plan (efference copy) was found to contribute to a forward model of limb position during a movement, such that when the limb was stopped, the subject sensed that the limb was farther along the planned movement path. Furthermore, TMS studies have provided evidence for independent contributions of sensory feedback and predictive models. For example, Miall and others (2007) induced specific disruption of sensory information whereas Desmurget and colleagues (1999) perturbed the forward model in reaching tasks.

The relative contributions of these sources of information can be difficult to determine. Although visual feedback can be eliminated, neither proprioception nor motor outflow can be easily removed experimentally with normal subjects. The performance of subjects lacking proprioception because of peripheral deafferentation may be revealing in this respect because when reaching without vision, any limb state estimate must be based solely on motor outflow.

Past studies have examined reaching with and without visual feedback in deafferented subjects to examine the contributions that proprioceptive input and efference copy make to movement execution. Gordon and colleagues (1995) instructed three deafferented subjects to make single, uncorrected two-dimensional movements, without visual feedback, to targets presented at various lengths and angles from the subject. Deafferented subjects were inaccurate in a variety of ways, making larger directional and extent errors than controls. Specifically, these errors reflected an inability to compensate for the inertial properties of the arm (i.e., intersegmental dynamics), as deafferented subjects made hypermetric movements along the axis of least inertia. These results provide evidence that proprioceptive input is necessary for movement correction and for updating internal models (see also Ghez et al., 1990; Ghez et al., 1995b).

Later, Bard and colleagues (1999) further examined the capacity of internal models to guide action in a study of a deafferented subject (GL) using an unconscious double step task. GL was instructed to move her hand through a visually-defined target location without visual feedback of the hand; on some trials the target shifted imperceptibly (6°) during a saccade. The authors found that GL could accurately (as judged by being within the range of normal controls) modify her movement after the target shift, providing evidence that deafferented subjects are able to correct movements without perceptual feedback regarding hand position. This supports claims that movement correction can be based on an on-line estimate of hand position derived from efference copy. However, in this study subjects were tested on small, unconscious shifts with relatively quick (250–350ms) movements. These small, unconscious trajectory adjustments are thought to involve automatic motor processes (Prablanc and Martin, 1992); and it is not clear whether efference copy can be used to accurately update conscious changes in movement.

Sarlegna and colleagues (2006) presented GL with a conscious double step task. GL’s movements to visual targets were made in a stair-step manner; she first moved to the initial target, made a second corrective movement, and then a final straight movement to the target. The authors argued that if GL had accurate knowledge of hand position during the movement, there should be a correlation between the hand direction when the first trajectory adjustment occurred and the amplitude of the second corrective movement segment. However, a poor correlation was observed, suggesting that GL did not take current hand position into account in order to make corrective movements. Thus, the results of Sarlegna et al (2006) suggest that efference copy was not sufficient to accurately localize hand position (see also Fourneret et al., 2002; Vercher et al., 1996).

As demonstrated in previous studies, the analysis of movement correction in deafferented subjects has contributed to our understanding of the role of efference copy to the on-line control of movement. Although previous studies have shown that efference copy can be used to update estimates of limb position, the accuracy of efference copy alone is still unclear. As previous work with GL suggested that conscious double step tasks provide a greater challenge to deafferented patients than smaller, unconscious jumps we presented a deafferented subject (JDY) and controls with a conscious target double step task. Subjects were instructed to reach, without vision of the hand, to targets presented 20 cm distal and either 30° left or right (with straight ahead being 0°) of a start circle. On no jump trials, the target maintained its position during the entire movement. During jump trials, the target jumped 60° shortly after movement onset, and the subject was required to adjust their movement in order to make accurate movements to the final target. With this task, we explored the degree to which efference copy accurately informs hand position estimates during both the initial and terminal phases of movement. If efference copy information can be used to localize the limb during the initial stage of movement, one would expect to see a correlation between the distance of the pre-turn movement segment and the angle taken towards the final target. Furthermore, because Sarlegna et al. (2006) did not require GL to end her movements in the target, we required JDY to try to produce accurate movement amplitudes to specifically examine whether any mid-movement limb position misestimations (as expected from the results of Sarlegna and colleagues) would affect endpoint accuracy as well. If efference copy information can be used to localize limb position at the end of her movement, one would expect that JDY would stop near the location of the final target. Conversely, if JDY is unable to utilize efference copy information during the end of her movements, one would predict substantial endpoint inaccuracy.

2. Results

Movement paths (Figure 1) and velocity profiles (Figure 2) are shown for a selected control and JDY. Table 1 shows the performance of controls and JDY on jump and no jump trials for selected variables. Examining temporal variables, JDY’s reaction time did not significantly different from controls (t(7) = .05, p = .961). However, JDY did differ from controls in that her total movement time on both no jump (t(7) = 4.57, p = .003) and jump trials (t(7) = 2.56, p = .037) was longer than controls. On jump trials, it is clear that this difference in total movement time is due to the post-correction segment of the movement. JDY’s time from movement onset to turn was well within the range of normal controls (t(7) = .44, p = .673), along with her time from the jump point to turn (t(7) = .13, p = .895). However, her movement time from turn to final target was substantially longer than controls (t(7) = 3.35, p = .012).

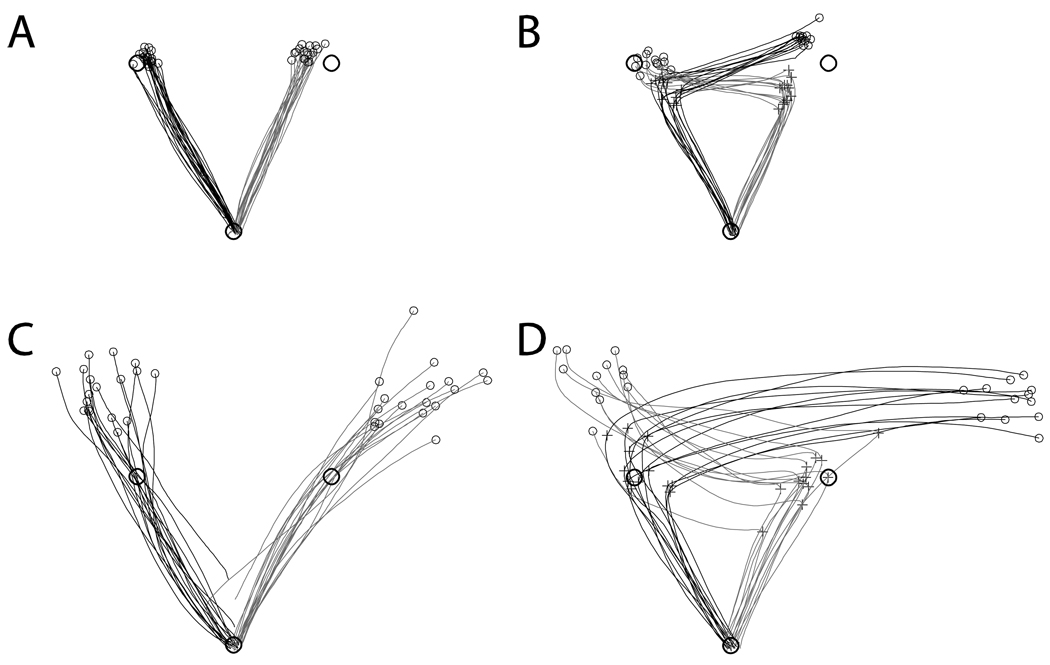
Figure 1. Movement paths.

Movement paths, turn points (+ symbol) and end points (small circles) for no jump (a) and jump (b) trials for a selected control, and no jump (c) and jump (d) trials for JDY. Start and target circles are represented by large circles. Initial movements to the left target are in black, with initial movements to the right target in grey.

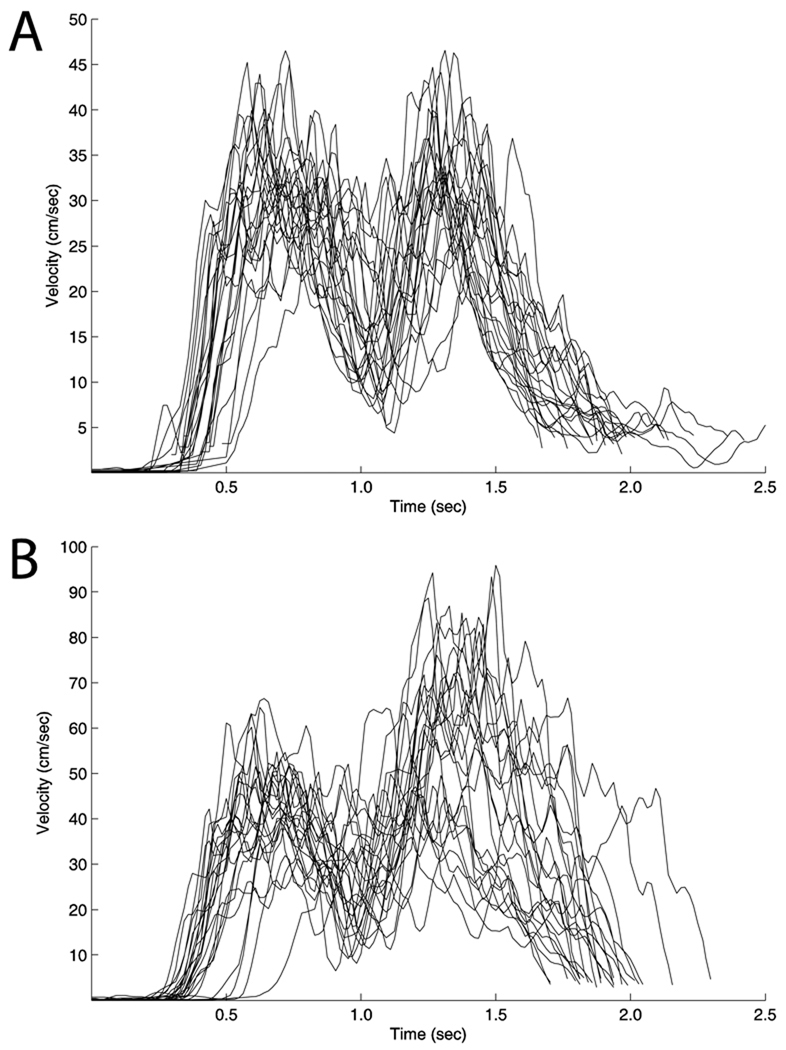
Figure 2. Velocity profiles.

Velocity profiles for all trials in a session are shown for a selected control (a) and JDY (b).

Table 1.

Performance of JDY and controls on selected measures for each target.

	Left target		Right target
	Controls	JDY	Controls	JDY
Reaction time (ms)	429 (96)	453	446 (126)	410
Time from movement onset to movement endpoint - no jump (ms)	848 (194)	1806 **	813 (207)	1765 **
Time from movement onset to turn - jump (ms)	649 (150)	603	671 (122)	841
Time from target jump to turn (ms)	445 (125)	401	444 (89)	516
Time from turn to movement endpoint - jump (ms)	794 (189)	1318 *	792 (132)	1375 *
Movement length, onset to movement endpoint - no jump (cm)	19.8 (2.3)	31.4 **	21.2 (3.0)	39.9 **
Movement length, onset to turn - jump (cm)	19.3 (3.6)	17.7	17.5 (2.7)	16.1
Movement length, turn to endpoint - jump (cm)	21.2 (2.9)	33.2 **	22.7 (2.0)	46.1 **
Movement length variability, onset to movement endpoint - no jump (cm)	0.81 (0.27)	6.50 **	0.96 (0.23)	8.00 **
Movement length variability, onset to turn - jump (cm)	1.43 (0.42)	4.24 **	1.20 (0.39)	3.09 **
Movement length variability, turn to endpoint - jump (cm)	1.24 (0.55)	8.30 **	1.37 (0.24)	9.83 **
Final target error - no jump (cm)	2.6 (1.2)	12.5 **	3.2 (1.5)	20.9 **
Final target error - jump (cm)	2.6 (1.3)	11.6 *	3.1 (1.5)	20.6 **
Movement direction error - no jump (deg)	4.54 (2.28)	4.80	3.57 (2.75)	5.75
Movement direction error - jump (deg)	4.03 (2.84)	7.82	4.82 (2.55)	7.6
Movement direction variability - no jump (deg)	1.71 (.63)	4.74 **	1.38 (.67)	4.77 **
Movement direction variability - jump (deg)	1.63 (.77)	3.63 *	2.13 (.62)	4.01 *

Asterisks and bolding denote a significant difference between JDY and controls (* p < .05; ** − p < .01). Parentheses for controls denote one standard deviation from control mean.

These differences are likely due to the substantially longer movement paths for JDY, as suggested by her significantly greater final target error compared to controls on both no jump (t(7) = 11.84, p < .001) and jump (t(7) = 11.46, p < .001) trials. JDY consistently made hypermetric movements on both jump and no jump trials (see Figures 1c and 1d). On no jump trials, JDY’s movements were on average 15.2 cm longer than controls (t(7) = 5.57, p = .001). Specifically examining jump trials, JDY’s movement distances from movement onset to turn point (t(7) = −.46, p = .657) were not significantly different from controls, whereas she made significantly longer movements from the turn point to the final target stop (t(7) = 6.822, p < .001). Separating trials by target, JDY did make substantially more hypermetric movements towards the right target on both no jump trials (39.9 cm vs. 31.4 cm, p = .002) and during the turn to final target segment of jump trials (46.1 cm vs. 33.2 cm, p < .001). However, we also found that control subjects demonstrated the same pattern of performance, making significantly longer movements towards the right target on no jump trials (19.8 cm vs. 21.8 cm, p = .028) and during the turn to final target segment of jump trials (22.7 cm vs. 21.2 cm, p = .007).

Although she consistently overshot the target on both no jump and jump trials, JDY performed relatively well on other kinematic measures. For example, although she was significantly more variable than controls on both no jump (t(7) = 6.64, p > .001) and jump (t(7) = 3.17, p = .016) trials in movement direction error, JDY was not significantly different from controls in overall movement direction error on no jump trials (t(7) = .63, p = .550) or for the start to turn segment of jump trials (t(7) = 1.52, p = .173). Furthermore, as noted before, the length of her start to turn segment on jump trials (i.e. where she made the turn) was similar to where controls turned.

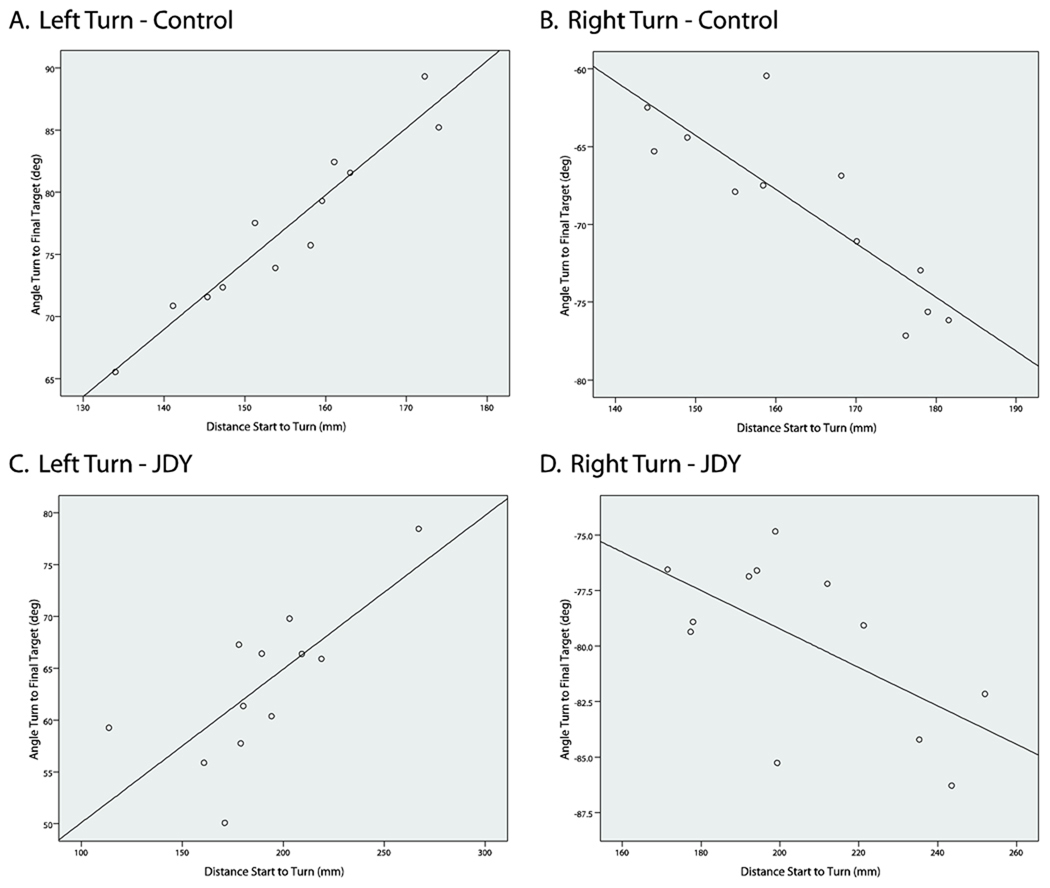
These results clearly demonstrate that JDY was deficient at moving the correct distance to a final target. Analyses suggest that JDY was relatively accurate during the initial start to turn movement segment on jump trials, but then made grossly hypermetric movements from the turn point to the final target. In order to further examine JDY’s knowledge of limb position during the initial phase of jump trials, we examined the relationship between the distance traveled during the pre-correction movement segment and the magnitude of the change in direction in the post-correction segment. If JDY had information regarding her hand position at the turn point on jump trials, one would predict a strong correlation between the distance covered during the onset to turn movement segment and the movement direction from the turn point to the final target stop. However, if distance information during the ballistic phase was not maintained, one would expect little or no correlation between pre-correction distance and post-correction direction. As shown in Figures 3a and 3b, JDY exhibited a strong correlation between movement distance and the angle from turn to final target stop (left turn, r = .535, p < .027; right turn, r = .743, p < .002). The magnitude of these correlations were similar to the average correlation for controls (left turn, r = .631, right turn, r = .736), and there was no difference in correlation between JDY and controls (left turn, t(7) = .27, p = .79; right turn, t(7) = .02, p = .98).

Figure 3. Correlations of pre-turn distance and turn angle.

Correlations of movement angle from turn to final target stop with movement distance from movement onset to turn for a selected control (left turn, a; right turn, b) and JDY (left turn, c; right turn, d).

An alternative explanation of this finding is that JDY used information about the time, rather than distance covered, during the pre-correction segment to determine turn angle. However, a similar correlational analysis between movement time during the pre-correction segment and angle of turn to final target stop showed no significant correlation for JDY (left turn, r = −.422, p = .092; right turn, r = −.307, p = .266). Furthermore, these correlations were similar to controls (left turn, r = −.383, right turn, r = −.339) with no significant difference in correlations between JDY and controls (left turn, t(7) = .10, p = .93; right turn, t(7) = −.06, p = .96). These results suggest that JDY’s motor system is primarily using distance information, and not time, to make appropriate turns to the final target.

Although JDY showed a strong correlation between the distance of her first movement segment and the angle of the turn to the second movement segment, her turns were not accurate in the sense that her post-turn movements did not pass through the target. Instead, JDY’s movement direction error from turn to final target stop was on average 14.5° wider than the correct turn angle given her turn point, such that she frequently moved farther in the radial dimension from the target. In comparison, controls movement direction error from turn to final target was on average only 1.6° wider than the optimal turn angle at their turn point; this was true for both left and right turns (left turn, t(7) = 2.4, p = .047; right turn, t(7) = 2.5, p = 0.41).

3. Discussion

The major finding of the current investigation is that JDY derives at least relatively precise information regarding her hand location in the early stages of reaching despite the fact that she is unable to see her hand or determine its location on the basis of proprioceptive feedback. JDY demonstrates a significant correlation between the distance of the initial movement segment and the turn angle, suggesting a relatively detailed representation of limb position at the point of turn. These data indicate that efference copy can provide a relatively accurate representation of arm position during the initial stages of reaching.

We note that other investigators have also provided evidence that deafferented subjects can modify trajectory based on information from efference copy (Bard et al., 1999; Sarlegna et al., 2006), allowing for on-line corrections of movement in the absence of sensory feedback about hand position. Our results add to these findings, providing novel evidence regarding the contributions of efference copy to motor correction. First, we found that JDY’s turns on a double step paradigm were informed by on-line information about arm position; in this respect, JDY differs from patient GL as reported by Sarlegna et al (2006). One possible explanation appeals to differences in movement velocity that may reflect discrepancies in the strategies employed by JDY and GL. The typical peak velocity of the first segment of GL’s movements in Sarlegna et al (2006) were substantially greater (approximately 90 cm/sec) than those of JDY and controls (30–50 cm/sec). Furthermore, GL’s movements on turn trials consisted of stair-like movements with an initial movement towards the initial target, a second perpendicular movement in the direction of the final target, and a final movement to the target (see Figure 4b, Sarlegna et al., 2006). In light of her substantially faster movement velocity, GL may not have been able to adjust her movement towards the displaced target in only one step. At that point, the optimal control strategy may have been to decelerate before the target and initiate a second movement. In contrast, JDY’s more moderate movement velocities may have afforded her greater ability to modify her trajectory mid-movement, making it easier to incorporate information from efference copy regarding limb position into the next segment of the movement.

Second, our results provide novel evidence that JDY’s movement corrections were based specifically on efference copy and not simply movement time. One might speculate that when making adjustments to consciously presented targets, subjects make a movement correction on the basis of time rather than limb position. Against this possibility, we found a significant correlation between turn angle and movement distance, but not movement time. This finding suggests that the location of her turns is determined by the distance travelled by the effector rather than simply time elapsed since movement initiation.

We also found that JDY consistently made hypermetric movements causing her to overshoot the final target location, similar to prior reports of deafferented subjects (Ghez et al., 1990; Ghez et al., 1995a; Ghez et al., 1995b; Gordon et al., 1995; Sainburg et al., 1995). Hypermetric errors in deafferented subjects have been explained as an inability to take into account the limb’s inertial properties when programming a movement. Consistent with this hypothesis, deafferented subjects were substantially more likely to make hypermetric movements along the axis of least inertia (for right-handed subjects, this corresponds to a right, no-jump trial in our experiment) compared to a movement perpendicular to that axis (e.g., Figure 5a, Gordon et al., 1995). We also find evidence that inertial factors do influence movement lengths, as both JDY and controls (all right-handed) make longer movements towards the right target compared to the left target.

Furthermore, JDY’s turn angles were typically wider than optimal and she consistently ended movements distal to the target in the radial dimension. Thus, JDY’s turn bias without visual feedback suggests that she consistently misjudged her hand position to lag behind its true position. This pattern of performance is likely an early manifestation of her inability to compensate for limb inertia, which is more clearly observed in her highly hypermetric movements to final targets. Although there is evidence that her estimate of arm position is being informed by efference copy (as demonstrated by the significant correlation between initial movement segment length and turn angle), it is possible that her inability to compensate for limb inertia results in a slight underestimation of limb position, even during the initial movement segment. If so, this would result in an estimate of limb position that would slightly lag behind her actual limb position, thus lead to wider turns than necessary to the final target.

Although inertial factors may provide at least a partial explanation for the hypermetric movements exhibited by JDY and other deafferented subjects, it is not clear why the information provided by efference copy in the early portions of her movements does not permit greater accuracy at the terminal stages of movement. There are at least two potential hypotheses to explain these results. First, efference copy information, along with information regarding the expected sensory consequences of movement, contributes to an internal model of movement. As JDY does not have inputs from proprioception to her internal model, information from efference copy may more strongly contribute to her internal model compared to controls. Although efference copy may be used during the entire movement to localize limb position, its accuracy may decrease as the movement unfolds. Along with her clear impairment in integrating proprioceptive information into localizing limb position, this would result in a more inaccurate estimate of limb position as the movement progresses. At the point of the turn, it is possible that the detrimental effects of this inaccurate estimate are minimal, and that they increase as the movement reaches its conclusion, thereby leading to her severely hypermetric movements. A second possibility appeals to a distinction between the initial transport phase and subsequent terminal corrective phase of movement (Elliott et al., 2001; Jeannerod, 1988; Keele, 1986; Woodworth, 1899). During the initial transport phase, limb movements are thought to be adjusted both on the basis of contributions from efference copy (Cooke and Diggles, 1984; Higgins and Angel, 1970) and sensory feedback. During the terminal stage of movement, in contrast, corrections are guided primarily via sensory inflow from vision and proprioception (Carlton, 1981; Redon et al., 1991). One possibility is that, due to the reliance on sensory feedback during the terminal stage of movement, the contributions of efference copy are minimized during this stage of movement. Unfortunately, it is difficult to differentiate between these two models in deafferented subjects, as poor final target accuracy could be explained by either hypothesis. Future research is necessary to differentiate between these two possibilities.

4. Experimental Procedure

4.1 Subjects

JDY is a 45-year-old female physician with a 21 year history of severe sensory loss from the sensory form of chronic inflammatory demyelinating polyneuropathy. She works full time and is fully independent in all of her activities of daily living. She performs in most settings when visual input is available. For example, when staying in a hotel room she did well until the lights were unexpectedly turned off, causing her to fall to the ground. She has reports repeatedly falling out of a chair when lights were extinguished. She has suffered a number of minor injuries; in one instance, she reported putting her hand through a glass storm door. The patient states that she has been neurologically stable for 21 years; she has been followed by a neurologist with expertise in neuro-muscular disease for approximately 20 years during which time her examination and clinical electrophysiologic studies have remained stable.

Neurological exam at the time of testing revealed relatively preserved cutaneous sensation. Using the Rivermead Test of Somatosensory Function (Winward et al., 2002), proprioception was assessed by the examiner generating movements across single joints while the subject sat with her eyes closed. She failed to detect large amplitude movements of the fingers, wrists, or ankles. She detected large amplitude movements at the elbows but performed at chance (6/10 at both elbows) when asked to determine if movements of approximately 25° were flexion or extension. Similarly, she detected large amplitude movements at her shoulder but could not reliably indicate the direction of the movements. On tests of tactile perception, she discriminated sharp from dull perfectly on her right and left cheeks and almost perfectly in her extremities (5/6 right palm; 6/6 left palm). She reliably discriminated light touch with a brush from no touch on her left and right cheeks (16/16) as well as left or right index fingers (16/16 left; 15/16 right). She performed at chance on a two-point discrimination task in which either one or two stimuli (5 mm separation) were presented to the palmar surface of the tip of the right or left index finger. Vibration detection threshold (512 Hz tuning fork) was normal on the skull but she could not detect maximal amplitude vibration in the forearms or legs. She noted a faint sensation of vibration with maximal amplitude stimulation at the right and left olecranon (elbow) and the right and left lateral clavicle. She was areflexic but muscle power and bulk were normal.

Eight neurologically intact right-handed controls (3 males; mean age 46.2 ± 15.1) were also tested. All research was carried out in compliance with institutional guidelines and was approved by the Institutional Review Board of the University of Pennsylvania.

4.2. Apparatus

Subjects sat upright in a height-adjustable chair in front of a target display apparatus. A 48” × 36” (121.9 × 91.4 cm) horizontal digitizing tablet (GTCO Calcomp DrawingBoard IV; 60 Hz, spatial accuracy .25 mm) was centered in front of the subject. Stimuli were projected via a video projector onto a screen, which was viewed by the participants on a half-silvered mirror located 25 cm above the digitizing board. The room was darkened such that subjects only saw the reflected stimuli on the half-silvered mirror and importantly, not their arms below the mirror. With this setup, stimuli appeared to be in the same horizontal plane as the digitizing tablet. During each trial, subjects held a digitizing pen that tracked hand position. The pen was centered and encased inside a light hollow plastic cylinder (4.75 cm tall, 3 cm diameter) with a felt base in order to make it easier for JDY to move and grasp.

4.3. Experimental Task

At the beginning of the trial, the subject moved his/her right hand into a 12 mm radius start circle using pen-position feedback from a small (3 mm radius) circular cursor. The start circle was positioned approximately 15 cm from the subject’s trunk, and aligned with the subject’s trunk midline. In this position, the subject’s right forearm was approximately 30° extended from the subject’s trunk midline. Once in the start circle for 1000 ms, a set of crosshairs located 20 cm distal to the start circle and aligned with the subject’s trunk midline, appeared for 500 ms. Subjects were instructed to fixate on these crosshairs upon presentation. Two hundred milliseconds after crosshair offset, a target circle (12 mm radius) appeared either 30° to the left or right of the start circle, 20 cm distal to the start circle. The subject was instructed to move his/her hand quickly but accurately to the target circle, stop, and then return to the start circle. After the cursor was 2.4 cm from the start circle, visual feedback regarding hand location was extinguished. The cursor reappeared as the subject returned within 2.4 cm of the start circle. No feedback regarding performance was provided at the end of the trial.

Each 10 trial block included two trial types. On the six no jump trials, the target’s location remained fixed during the entire trial. On the four jump trials, the target “jumped” to the other target location when the pen had been moved 2.4 cm from the start circle. On these trials the subject was instructed to quickly adjust his/her movement trajectory to reach the new target. Jump and no jump trials were presented to each side of space with equal frequency. Testing was completed in one session of seven blocks. The first block was regarded as practice and was not analyzed.

4.4. Data Analyses

After testing, several kinematic variables were calculated using MATLAB 2007. Movement onset was calculated as the first sample where the hand’s velocity was greater than 3 cm/sec. Movement endpoint was calculated as the first point at which the hand’s velocity was less than 3 cm/sec for 50 ms. Reaction time was defined as the time from presentation of the initial target to movement onset. Movement time was the time from movement onset to movement endpoint. Final target error was the distance between the movement endpoint and the center of the target. Movement direction from onset was calculated as the direction of movement from movement onset to either the movement endpoint (no jump trials) or movement turn point (jump trials). Movement direction error was calculated as the absolute difference between movement direction and a straight-line movement to the target. Movement direction variability was the standard deviation of movement direction error for each subject.

Additional kinematic measures were derived for the jump trials. Jump trial analysis began by identifying the turn point, which was the location of the hand after target jump at which the hand path first deviated by at least 20° over 50 ms from the direction of the pre-correction movement segment. Movement direction from turn to movement endpoint was calculated by measuring the angle from the turn point to movement endpoint (0° turn being a continuation from the original movement direction and 90° turn would generate a movement perpendicular to the original movement direction). Time from jump point to turn was the time from when the target jumped to the time at the movement turn point. Finally, we defined the optimal turn angle as the movement angle from the turn point to the location of the final target.

All statistical comparisons between JDY and controls utilized modified two-tailed t-tests for comparing performance of an individual against a control sample (Crawford and Garthwaite, 2002). Comparisons are collapsed across targets, except for variables where there was a significant effect of target for either controls or JDY.