Abstract
We present a simple method, ARTSY, for extracting 1JNH couplings and 1H-15N RDCs from an interleaved set of two-dimensional 1H-15N TROSY-HSQC spectra, based on the principle of quantitative J correlation. The primary advantage of the ARTSY method over other methods is the ability to measure couplings without scaling peak positions or altering the narrow line widths characteristic of TROSY spectra. Accuracy of the method is demonstrated for the model system GB3. Application to the catalytic core domain of HIV integrase, a 36 kDa homodimer with unfavorable spectral characteristics, demonstrates its practical utility. Precision of the RDC measurement is limited by the signal-to-noise ratio, S/N, achievable in the 2D TROSY-HSQC spectrum, and is approximately given by 30/(S/N) Hz.
Keywords: ARTSY, catalytic core domain, HIV integrase, quantitative J correlation, TROSY, RDC
Residual dipolar couplings (RDCs) in proteins, as measured by solution state NMR, constitute an important source of both structural and dynamic information (Prestegard et al. 2000; Bax and Grishaev 2005; Tolman and Ruan 2006). Although a wide range of different types of RDCs can be measured, including 1H-1H, 1H-13C, 1H-15N, 15N-13C, and 13C-13C (Tjandra and Bax 1997; Yang et al. 1999; Permi et al. 2000; Boisbouvier et al. 2003; Vijayan and Zweckstetter 2005), in larger, slowly tumbling proteins measurements are often restricted to the backbone amide 1H-15N RDC, 1DNH. With assignment of the backbone amide signals being a prerequisite for any detailed analysis of protein structure and dynamics, the additional effort needed to collect such couplings for modest size proteins is limited, and they can readily be obtained from the 15N-{1H} splittings in 2D or 3D NMR spectra, recorded in the absence of 1H decoupling during 15N evolution (Tolman et al. 1995). Increased spectral overlap associated with the doubling of the number of resonances in such spectra can be mitigated by separating the two doublet components by the IPAP method (Ottiger et al. 1998; Yao et al. 2009), or by separately recording spectra for each multiplet component using the principle of spin-state selective polarization transfer (Lerche et al. 1999).
For larger proteins, a problem associated with the frequency domain measurements is caused by the very different intrinsic line widths of the two 15N-{1H} doublet components. The downfield component benefits from favorable relaxation interference between the 15N-1H dipolar coupling and 15N chemical shift anisotropy (CSA) mechanisms, resulting in very narrow 15N line widths, a property utilized in the original TROSY-HSQC method for obtaining spectral resolution enhancement in larger proteins (Pervushin et al. 1997). In contrast, the upfield doublet component has increased 15N line widths relative to a 1H-decoupled 15N resonance, and can become vanishingly weak in larger proteins, making it difficult or impossible to measure the 1JNH or 1JNH + 1DNH splittings. The adverse impact of relaxation interference broadening of the upfield 15N-{1H} doublet component on the accuracy of the measured splitting can be mitigated by instead measuring halved couplings as the splitting between the TROSY component and the peak position in a conventional decoupled 1H-15N HSQC spectrum (Kontaxis et al. 2000). More generally, by limiting the time during which the broad upfield component evolves in the transverse plane, a scaled 1JNH + 1DNH splitting can be measured at a relative accuracy that significantly exceeds that of the unscaled splitting (Yang et al. 1999; Bhattacharya et al. 2010; Mantylahti et al. 2010). An elegant implementation of this principle distributes the relaxation losses equally over the two doublet components, and appears to offer the highest accuracy at which 1JNH + 1DNH splittings can be obtained from frequency domain measurements in larger proteins (Arbogast et al. 2010).
The size of the 1JNH (or 1JNH + 1DNH) splitting may also be extracted from the relative intensities observed in two or more spectra recorded with pulse schemes where 1JNH dephasing or rephasing is active for different durations, τ. Typically, the amplitude of a correlation in the corresponding spectra is a function of sin(πJNHτ), and the coupling is extracted from these intensities using the principle of “quantitative J correlation” (Bax et al. 1994). Although intrinsically very precise values can be obtained from such measurements (Tjandra et al. 1996; Tolman and Prestegard 1996), the rapid transverse relaxation of the upfield 15N-{1H} doublet component during the τ period, caused by relaxation interference between 15N-1H dipolar and 15N CSA relaxation mechanisms, adversely impacts sensitivity of this approach, in particular for larger proteins.
Here, we introduce an alternate quantitative J-correlation method for 1JNH measurement, where 1JNH dephasing is active while 1H magnetization is in the transverse plane, and it is the smaller relaxation interference between 1HN CSA and 15N-1H dipolar coupling which afflicts the measurement. Our new method for measuring amide RDCs by TROSY Spectroscopy is dubbed ARTSY. By limiting the time during which 1HN CSA/15N-1H dipolar coupling relaxation interference is active to (1JNH)−1≈ 10.7 ms, relaxation losses are kept at a minimum, in particular when considering that half of this period already is utilized as part of the standard INEPT transfer (Morris and Freeman 1979) in the regular TROSY-HSQC experiment (Pervushin et al. 1997). By carrying out the measurement on a perdeuterated sample with back-exchanged amide protons, such as often used for NMR studies of larger proteins, such experiments based on 1H-dephasing are shown to be remarkably effective for measurement of 1DNH RDCs. We demonstrate the accuracy of ARTSY for the small model protein GB3, and its applicability to larger systems for the catalytic core domain of HIV integrase, a 36 kDa homodimer with rather unfavorable spectral characteristics (Fitzkee et al. 2010).
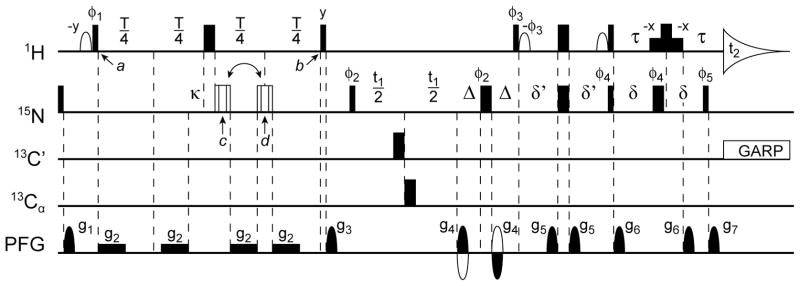
The ARTSY pulse scheme is very similar to the standard TROSY-HSQC experiment (Figure 1). The primary differences are that the initial 1H dephasing duration of the first INEPT transfer module (between time points a and b) is set to T = (|1JNH|)−1≈10.7 ms, instead of the usual (2|1JNH|)−1≈5.35 ms value. The experiment is carried out twice, in an interleaved manner: once with 1H 1JNH dephasing active during half the T interval (reference experiment), and once with 1JNH dephasing active during the full interval (attenuated experiment). The value of the coupling is then extracted from the intensity ratio, Q, of the attenuated over the reference intensity:
| (1) |
Figure 1.
The ARTSY pulse scheme used to measure 1H-15N RDCs. Narrow and wide pulses correspond to 90° and 180° flip angles, respectively. Unless marked, RF phases of all pulses are x. The 1H carrier frequency is set to the water frequency, and 15N, 13C′, and 13Cα carriers are set to 117, 176, and 56 ppm, respectively. Open 1H pulses are 90°, with a shape corresponding to the center lobe of a sinc(x) function. The last non-selective 180° 1H pulse is flanked by two low power 1.2-ms rectangular pulses (90° each) which aid in H2O signal suppression (Piotto et al. 1992). The 180° proton pulse during this element is offset slightly (by ~150 μs) relative to the 180° 15N pulse to allow inclusion of the g7 decoding gradient during the second τ delay without requiring first order phase correction in the 1H dimension. The open composite 15N pulse is of the 90x-210y-90x type, compensating for both offset and RF inhomogeneity (Freeman et al. 1980), and is applied at time point d (reference) or c (attenuated experiment). The delay T is set to ~1/JNH or 10.75 ms. For deriving the coupling values, using eqs 2 or 3, dephasing during the pulses needs to be taken into account, and a value T+ε is used in eqs 2 and 3, with ε = (4/π)H90−κ, where H90 equals the 1H 90° pulse width and κ equals the total duration of the 15N composite pulse. Other delays: δ = δ′ = ~1/4JNH = 2.71 ms; Δ = 0.75 ms; τ = 1.66 ms. The 13C′ and 13Cα decoupling pulses (only needed for proteins also enriched in 13C) are applied with a RF field strength of , where Δf is the difference in Hz between the centers of the 13C′ and 13Cα chemical shift regions. Gradients: g2 = 0.7 G/cm; g1,3,4,5,6,7 are sine-bell shaped with durations of 1.0, 0.5, 0.5, 1.0, 0.8, and 0.1013 ms, respectively, and strengths of 20.3, 8.4, ± 42, 2.3, 4.9, and 42 G/cm at their mid-points. Phase cycling: φ1 = x, −x; φ2 = 2(y), 2(−y); φ3 = −y; φ4 = 4(x), 4(−x);φ5 = 4(−y), 4(y); φrec = y, 2(−y), y, −y, 2(y), −y. Phase φ5 and the duration of δ′ may be adjusted to reduce anti-TROSY artifacts according to the Clean TROSY method. Given the average relative intensity of the anti-TROSY artifacts, φ5 is generally decreased and δ′ is shortened according to eq 10 of (Schulte-Herbruggen and Sorensen 2000). In practice, anti-TROSY artifacts were vanishingly weak in our integrase spectra, and therefore no such compensation was used. Quadrature in the 15N dimension uses the regular gradient coherence selection method, inverting the phases of φ3, φ5 and the sign of g4 for the second FID collected for each value of t1 (Kay et al. 1992; Pervushin et al. 1998).
Substituting λ = 1JNH + 1DNH (where 1JNH≈−92 Hz), eq. 1 can be rewritten as:
| (2a) |
or
| (2b) |
Alternatively, using the trigonometric identity cos−1(x) = π/2 − sin−1(x) and the fact that the sign of 1JNH is negative this result can be rewritten as:
| (3) |
The above analysis ignores relaxation interference between the 1HN CSA tensor and the 1H-15N dipolar interaction, which causes the two 1H-{15N} components to decay at different rates, R2±Γ, during the T interval, where Γ is the 1HN CSA/15N-1H dipolar cross-correlated relaxation rate. Whereas for the attenuated experiment both components decay by the same factor, R2T, for the reference experiment the two components decay by (R2±Γ/2)T. For (ΓT/2)2 ≪1, to a good approximation this cross correlated relaxation does not significantly impact the buildup of antiphase magnetization at time point b. For example, even when scaling the average Γ= 1.58 s−1 value measured for GB3 at τc = 3.3 ns (Yao et al.) to a protein tumbling at τc = 50 ns, yielding Γ ≈ 24 s−1, this results in a reference spectrum intensity increase of only 0.8% and therefore has a negligible effect on the extracted RDC.
The precision at which a coupling can be determined depends on the experimental uncertainty in the ratio, Q. If equal numbers of scans are recorded for the reference and attenuated spectrum, the error in Q is dominated by the uncertainty in sin(πλT). The uncertainty in Q is found by assuming identical random noise amplitude, N, in both the reference and attenuated spectra. Since Q is the ratio of two independent intensity measurements, the error propagation formula for division applies:
| (4a) |
where IR and IA denote the respective intensities in the reference and attenuated spectra. Once again, using standard error propagation, the uncertainty in λ is then given by:
| (4b) |
For the common situation where Q ≪1, eq 4 simplifies to σλ ≈ 1/[πT(S/N)]. This means that for the recommended T = 10.7 ms, and an observed Q ~ 0, a S/N ratio of 30 in the reference spectrum yields a noise-limited uncertainty in the derived coupling of ca. 1 Hz, more than sufficient for most applications to larger proteins.
In practice, the value for T is adjusted such as to maximize sensitivity of the measured couplings, which occurs for Q ≈ 0, i.e., T = N/|1JNH + 1DNH|. If the 1JNH +1DNH values span a narrow range, a value for N chosen such that T ≈ T2, where T2 is the 1HN transverse relaxation time, will yield the highest precision for the extracted coupling. For application to perdeuterated proteins where alignment strength is typically relatively large (1DNH in the ±25Hz range) and the 1HN T2 is short, the optimum T value is obtained for N=1. With 1DNH values roughly equally distributed about zero, this then requires T ≈ 1/|1JNH| ≈ 10.7 ms.
Accuracy of the method is demonstrated for the perdeuterated, amide-protonated model system GB3, either in isotropic buffer or dissolved in a liquid crystalline Pf1 suspension (11 mg/mL). With a pairwise root-mean-square difference (rmsd) of 0.19 Hz, isotropic 1JNH values agree well with values previously measured with a gradient-enhanced IPAP-HSQC experiment (Yao et al. 2009) (Supporting Information). Similarly, with a Pearson’s correlation coefficient of RP = 0.996, RDCs derived from the difference in 1JNH + 1DNH values in aligned and isotropic samples fit very well to the RDC-refined structure of GB3 (PDB entry 2OED (Ulmer et al. 2003); Supporting Information).
As an application to a system of biological interest, we used ARTSY to measure 1DNH RDC values in a sample of the catalytic core domain of the HIV-1 integrase enzyme. The domain studied comprises residues 50-212, and below is referred to as IN50-212. It includes the following mutations, introduced to improve its solubility and stability: Q53E C56S W131E F185K Q209E. Even with these mutations, this homodimeric protein (36 kDa) has rather unfavorable NMR spectral characteristics and is of limited stability. Its NMR assignment and preliminary characterization was reported recently (Fitzkee et al. 2010), and both chemical shift analysis and 1HN-1HN NOEs measured on the perdeuterated protein indicated that the protein in solution adopts a structure very similar to that observed in the crystalline state (Dyda et al. 1994; Bujacz et al. 1996; Goldgur et al. 1998; Chen et al. 2000). The N-terminal tail, the active site loop, and the loop preceding the final α-helix, for which electron density was missing in many of the X-ray structures, were found to be dynamically disordered as judged by 15N relaxation data (Fitzkee et al. 2010).
ARTSY data for a sample containing 0.4 mM of IN50-212 (0.2 mM dimer) in 4% (w/v) liquid crystalline C12E5 poly-ethylene-glycol/hexanol mixture (2H splitting = 19.6 Hz)(Ruckert and Otting 2000) were recorded on a Bruker Avance 900 MHz spectrometer, equipped with a cryogenic probe. The data were recorded at 298 K in a 20 mM PIPES pH 6.6 buffer, containing 150 mM NaCl and 40 mM MgCl2. The sample was prepared as described previously (Fitzkee 2010). Interleaved reference and attenuated spectra were recorded with acquisition times of 80 ms (t1, 250 complex points), and 120 ms (t2, 1784 complex points) and a recycle delay of 1.5 s, with 64 scans per recorded transient, and a total acquisition time of 27 hr.
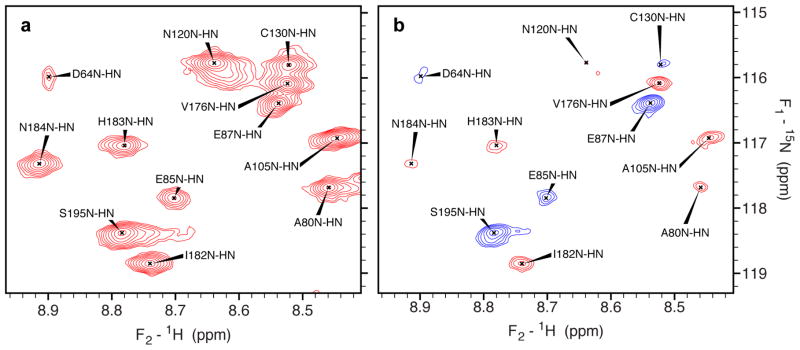
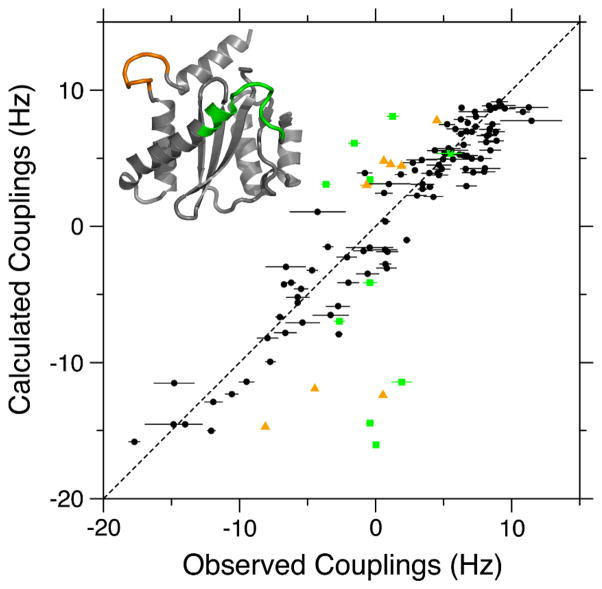
Figure 2 compares a small region of the IN50-212 ARTSY reference spectrum with that of the attenuated spectrum, and the vast majority of previously assigned 1H-15N correlations (Fitzkee et al. 2010) is observed in the reference spectrum. In the attenuated spectrum (Fig. 2B), amides with |1JNH + 1DNH| >93 Hz are opposite in sign relative to those with smaller values. A nearly complete set of RDCs could be extracted from these spectra (Supporting Information). Fitting of these RDCs to the various crystal structures shows fair agreement. For example, chain B of PDB entry 1BIS (Goldgur et al. 1998) exhibits a Q factor of 0.28 (Figure 3), only slightly above the value of 0.2–0.25 expected for a protein solved at 2-Å resolution (Bax 2003). This chain includes coordinates for all of the catalytic loop residues (140–152) as well as for the loop (residues 187–194) immediately preceding the α6 helix. However, as seen in Figure 3, the active site loop fits very poorly to the measured RDCs. The near-zero RDC values observed for most of the active site amide groups are consistent with a high degree of internal dynamics, as also reflected in missing electron density in many other integrase crystal structures (Dyda et al. 1994; Bujacz et al. 1996; Chen et al. 2000) and our previous 15N relaxation measurements.
Figure 2.
Spectral data used for measuring 1H-15N RDCs in IN50-212. Small regions of the reference (a) and attenuated (b) 15N-1H TROSY spectra, recorded at 900 MHz in the presence of 4% (w/v) C12E5 PEG/hexanol (Ruckert and Otting 2000). Peak positions are determined using the reference spectra and then mapped directly on to the attenuated spectra. Positive and negative intensity contours are red and blue, respectively. In the attenuated spectra, negative (positive) peaks correspond to resonances with |J+D| greater than (less than) 93 Hz.
Figure 3.
Best fit correlation between ARTSY-derived 1DNH RDCs for homodimeric IN50-192 and the coordinates of PDB entry 1BIS, chain B (Goldgur et al. 1998). The alignment tensor was best-fitted using the DC program in the NMRPipe software package (Delaglio et al. 1995). Black symbols correspond to the 97 RDCs used in fitting (Q = 0.279). Green squares and orange triangles correspond to the active site loop (residues 140–152) and the loop between helices α5 and α6 (residues 187–194) (see colored regions on the inset structure) and were not included in the RDC fit. These amides were shown to be dynamic in 15N relaxation measurements (Fitzkee et al. 2010). Slightly better fits are obtained using the chains of PDB entry 1BIU (Q ~ 0.26), but its chains lack density for residues 141–148 of the catalytic loop (Goldgur et al. 1998).
ARTSY is particularly well suited for proteins that have poor spectral characteristics, such as the HIV1 integrase catalytic core domain dimer, but the same idea is of course also applicable to less challenging systems too. For smaller proteins, where use of TROSY is not essential, the same ARTSY 1JNH amplitude encoding can be used in the regular gradient-enhanced 1H-15N HSQC experiment (Kay et al. 1992). Similarly, for proteins with substantial resonance overlap in the 2D HSQC or TROSY-HSQC spectra, the ARTSY 1JNH amplitude encoding can be used during the initial 1H→15N INEPT transfer of better resolved 3D experiments, such as HNCO, or HNCO-TROSY, albeit with the concomitant loss associated with carrying out the experiments in a 3D rather than a 2D fashion. Even for the 723-residue protein malate synthase G, an HNCO-TROSY allowed sufficient resolution for measuring more than 95% of the 1HN-15N RDCs using the J-scaling approach (Tugarinov and Kay 2003). Thus, ARTSY should be particularly useful for even more challenging systems, as no resolution is sacrificed to measure the couplings.
One additional point requiring attention is the application of ARTSY to protonated proteins. Although in principle, ARTSY is applicable to protonated proteins, for the TROSY version of the experiment a complicating factor is caused by the buildup of antiphase terms of the type HJxNz between time points a and b in Figure 1, where HJ denotes protons with multi-bond JNH couplings to the 15N considered. These terms transfer into NxHJz at the start of 15N evolution (Supporting Information). Although in regular HSQC experiments, such terms yield vanishing intensity as they remain antiphase with respect to HJ during t1 evolution and therefore do not result in detectable in-phase 1H magnetization during detection, in TROSY-HSQC experiments these terms partially rephase during t1 evolution, giving rise to unresolved anti-phase doublets in the 15N dimension of the spectrum (Supporting Information). Provided that the peak position at which the intensity in the attenuated spectrum is measured is taken from that determined in the reference spectrum (a feature of the NMRPipe (Delaglio et al. 1995) seriesTab peak picking procedure used in our study), the antiphase component does not contribute to the intensity measured in the attenuated spectrum, IA. Additionally, aliphatic protons can be decoupled by using an amide proton selective pulse during the initial INEPT period, and this will largely eliminate the buildup of antiphase terms (Supporting Information). Indeed, ARTSY-derived RDCs for fully protonated GB3 fit very well to the experimentally determined (Yao et al. 2010) GB3 bond vectors (RP = 0.998; Supporting Information). Although, at least in principle, unresolved long range 1HN-15N RDCs could result in similar antiphase contributions to the 15N line shape in ARTSY spectra on perdeuterated proteins, in practice long range 1HN-15N RDCs tend to be very small, and no such antiphase contributions were detected for the IN50-212 sample. As found for protonated GB3, even if such small antiphase contributions were present, to first order they do not impact the IA/IR intensity ratios, used for deriving the coupling values.
Base line correction is one important detail requiring special attention when applying ARTSY to larger proteins that also contain highly disordered residues, giving rise to very intense resonances. It therefore is recommended to record the spectra in such a manner that no frequency dependent linear baseline correction is needed, while scaling the first data point of each FID (particularly in the t1 dimension) by 0.5 (Otting et al. 1986), or by recording the spectra such that a 180° linear phase correction is needed with no scaling of the first data point (Zhu et al. 1993).
In summary, ARTSY is an effective alternative for recording amide 1H-15N RDCs, particularly well suited for larger perdeuterated proteins. The spectral resolution is identical to that of the regular TROSY-HSQC spectrum, which greatly benefits from using the highest available magnetic field strength. Noise in the reference spectrum impacts the size of the coupling, extracted from eq 2, far less than noise in the attenuated spectrum. In principle, therefore, it is favorable to record the attenuated spectrum with more scans than the reference spectrum, and correspondingly scale the ratio Q before applying eq 2b or eq 3. In practice, sensitivity of the spectra recorded for IN50-212 was more than sufficient for accurate measurement of 1DNH RDCs, and the use of equal numbers of scans for both reference and attenuated spectra was adequate.
Supplementary Material
Acknowledgments
We thank Alexander Maltsev for the sample of perdeuterated GB3 and for help in preparing the liquid crystalline solution for IN50-212 measurement, and Lishan Yao for the protonated GB3 mutant. This work was supported in part by the Intramural Research Program of the NIDDK, NIH, and by the Intramural AIDS-Targeted Antiviral Program of the Office of the Director, NIH
References
- Arbogast L, Majumdar A, Tolman JR. HNCO-based measurement of one-bond amide N-15-H-1 couplings with optimized precision. J Biomol NMR. 2010;46:175–189. doi: 10.1007/s10858-009-9391-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bax A. Weak alignment offers new NMR opportunities to study protein structure and dynamics. Protein Science. 2003;12:1–16. doi: 10.1110/ps.0233303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bax A, Grishaev A. Weak alignment NMR: a hawk-eyed view of biomolecular structure. Curr Opin Struct Biol. 2005;15:563–570. doi: 10.1016/j.sbi.2005.08.006. [DOI] [PubMed] [Google Scholar]
- Bax A, Vuister GW, Grzesiek S, Delaglio F, Wang AC, Tschudin R, Zhu G. Measurement of homo- and heteronuclear J couplings from quantitative J correlation. Meth Enzymol. 1994;239:79–125. doi: 10.1016/s0076-6879(94)39004-5. [DOI] [PubMed] [Google Scholar]
- Bhattacharya A, Revington M, Zuiderweg ERP. Measurement and interpretation of N-15-H-1 residual dipolar couplings in larger proteins. J Magn Reson. 2010;203:11–28. doi: 10.1016/j.jmr.2009.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boisbouvier J, Delaglio F, Bax A. Direct observation of dipolar couplings between distant protons in weakly aligned nucleic acids. Proc Natl Acad Sci U S A. 2003;100:11333–11338. doi: 10.1073/pnas.1534664100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bujacz G, Alexandratos J, ZhouLiu Q, ClementMella C, Wlodawer A. The catalytic domain of human immunodeficiency virus integrase: Ordered active site in the F185H mutant. FEBS Lett. 1996;398:175–178. doi: 10.1016/s0014-5793(96)01236-7. [DOI] [PubMed] [Google Scholar]
- Chen JCH, Krucinski J, Miercke LJW, Finer-Moore JS, Tang AH, Leavitt AD, Stroud RM. Crystal structure of the HIV-1 integrase catalytic core and C-terminal domains: A model for viral DNA binding. Proc Natl Acad Sci U S A. 2000;97:8233–8238. doi: 10.1073/pnas.150220297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRpipe - a multidimensional spectral processing system based on Unix pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- Dyda F, Hickman AB, Jenkins TM, Engelman A, Craigie R, Davies DR. Crystal structure of the catalytic domain of HIV-1 integrase - Similarity to other polynucleotidyl transferases. Science. 1994;266:1981–1986. doi: 10.1126/science.7801124. [DOI] [PubMed] [Google Scholar]
- Fitzkee NC, Masse JE, Shen Y, Davies DR, Bax A. Solution Conformation and Dynamics of the HIV-1 Integrase Core Domain. J Biol Chem. 2010;285:18072–18084. doi: 10.1074/jbc.M110.113407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman R, Kempsell SP, Levitt MH. Radiofrequency pulse sequences which compensate their own imperfections. J Magn Reson. 1980;38:453–479. doi: 10.1016/j.jmr.2011.08.032. [DOI] [PubMed] [Google Scholar]
- Goldgur Y, Dyda F, Hickman AB, Jenkins TM, Craigie R, Davies DR. Three new structures of the core domain of HIV-1 integrase: An active site that binds magnesium. Proc Natl Acad Sci U S A. 1998;95:9150–9154. doi: 10.1073/pnas.95.16.9150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay LE, Keifer P, Saarinen T. Pure Absorption Gradient Enhanced Heteronuclear Single Quantum Correlation Spectroscopy with Improved Sensitivity. J Am Chem Soc. 1992;114:10663–10665. [Google Scholar]
- Kontaxis G, Clore GM, Bax A. Evaluation of Cross-Correlation Effects and Measurements of One-Bond Couplings in Proteins with Short Transverse Relaxation Times. J Magn Reson. 2000;143:184–196. doi: 10.1006/jmre.1999.1979. [DOI] [PubMed] [Google Scholar]
- Lerche MH, Meissner A, Poulsen FM, Sorensen OW. Pulse sequences for measurement of one-bond N-15-H-1 coupling constants in the protein backbone. J Magn Reson. 1999;140:259–263. doi: 10.1006/jmre.1999.1820. [DOI] [PubMed] [Google Scholar]
- Mantylahti S, Koskela O, Jiang P, Permi P. MQ-HNCO-TROSY for the measurement of scalar and residual dipolar couplings in larger proteins: application to a 557-residue IgFLNa16–21. J Biomol NMR. 2010;47:183–194. doi: 10.1007/s10858-010-9422-z. [DOI] [PubMed] [Google Scholar]
- Morris GA, Freeman R. Enhancement of nuclear magnetic resonance signals by polarization transfer. J Am Chem Soc. 1979;101:760–762. [Google Scholar]
- Ottiger M, Delaglio F, Bax A. Measurement of J and dipolar couplings from simplified two-dimensional NMR spectra. J Magn Reson. 1998;131:373–8. doi: 10.1006/jmre.1998.1361. [DOI] [PubMed] [Google Scholar]
- Otting G, Widmer H, Wagner G, Wüthrich K. Origin of t1 and t2 ridges in 2D NMR spectra and procedures for suppresion. J Magn Reson. 1986;66:187–193. [Google Scholar]
- Permi P, Rosevear PR, Annila A. A set of HNCO-based experiments for measurement of residual dipolar couplings in N-15, C-13, (H-2)-labeled proteins. J Biomol NMR. 2000;17:43–54. doi: 10.1023/a:1008372624615. [DOI] [PubMed] [Google Scholar]
- Pervushin K, Riek R, Wider G, Wuthrich K. Attenuated T-2 relaxation by mutual cancellation of dipole- dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci USA. 1997;94:12366–12371. doi: 10.1073/pnas.94.23.12366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pervushin KV, Wider G, Wuthrich K. Single transition-to-single transition polarization transfer (ST2-PT) in [N15, H1]-TROSY. J Biomol NMR. 1998;12:345–348. doi: 10.1023/A:1008268930690. [DOI] [PubMed] [Google Scholar]
- Piotto M, Saudek V, Sklenár V. Gradient-tailored excitation for single-quantum NMR spectroscopy of aqueous sloutions. J Biomol NMR. 1992;2:661–665. doi: 10.1007/BF02192855. [DOI] [PubMed] [Google Scholar]
- Prestegard JH, Al-Hashimi HM, Tolman JR. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Q Rev Biophys. 2000;33:371–424. doi: 10.1017/s0033583500003656. [DOI] [PubMed] [Google Scholar]
- Ruckert M, Otting G. Alignment of biological macromolecules in novel nonionic liquid crystalline media for NMR experiments. J Am Chem Soc. 2000;122:7793–7797. [Google Scholar]
- Schulte-Herbruggen T, Sorensen OW. Clean TROSY: Compensation for relaxation-induced artifacts. J Magn Reson. 2000;144:123–128. doi: 10.1006/jmre.2000.2020. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–4. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Grzesiek S, Bax A. Magnetic field dependence of nitrogen-proton J splittings in N- 15-enriched human ubiquitin resulting from relaxation interference and residual dipolar coupling. J Am Chem Soc. 1996;118:6264–6272. [Google Scholar]
- Tolman JR, Flanagan JM, Kennedy MA, Prestegard JH. Nuclear Magnetic Dipole Interactions in Field-Oriented Proteins - Information For Structure Determination in Solution. Proc Natl Acad Sci U S A. 1995;92:9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolman JR, Prestegard JH. A quantitative J-correlation experiment for the accurate measurement of one-bond amide N-15-H-1 couplings in proteins. Journal of Magnetic Resonance Series B. 1996;112:245–252. doi: 10.1006/jmrb.1996.0138. [DOI] [PubMed] [Google Scholar]
- Tolman JR, Ruan K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem Rev. 2006;106:1720–1736. doi: 10.1021/cr040429z. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Kay LE. Quantitative NMR studies of high molecular weight proteins: Application to domain orientation and ligand binding in the 723 residue enzyme malate synthase G. J Mol Biol. 2003;327:1121–1133. doi: 10.1016/s0022-2836(03)00238-9. [DOI] [PubMed] [Google Scholar]
- Ulmer TS, Ramirez BE, Delaglio F, Bax A. Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- Vijayan V, Zweckstetter M. Simultaneous measurement of protein one-bond residual dipolar couplings without increased resonance overlap. J Magn Reson. 2005;174:245–253. doi: 10.1016/j.jmr.2005.02.010. [DOI] [PubMed] [Google Scholar]
- Yang DW, Venters RA, Mueller GA, Choy WY, Kay LE. TROSY-based HNCO pulse sequences for the measurement of (HN)-H- 1-N-15, N-15-(CO)-C-13, (HN)-H-1-(CO)-C-13, (CO)-C-13-C- 13(alpha) and (HN)-H-1-C-13(alpha) dipolar couplings in N-15, C-13, H-2-labeled proteins. J Biomol NMR. 1999;14:333–343. [Google Scholar]
- Yao L, Grishaev A, Cornilescu G, Bax A. Site-specific backbone amide 15N chemical shift anisotropy tensors in a small protein from liquid crystal and cross-correlated relaxation measurements. J Am Chem Soc. 2010;132:4295–4309. doi: 10.1021/ja910186u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao LS, Grishaev A, Cornilescu G, Bax A. The Impact of Hydrogen Bonding on Amide 1H Chemical Shift Anisotropy Studied by Cross-Correlated Relaxation and Liquid Crystal NMR Spectroscopy. J Am Chem Soc. 2010;132:10866–10875. doi: 10.1021/ja103629e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao LS, Ying JF, Bax A. Improved accuracy of N-15-H-1 scalar and residual dipolar couplings from gradient-enhanced IPAP-HSQC experiments on protonated proteins. J Biomol NMR. 2009;43:161–170. doi: 10.1007/s10858-009-9299-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu G, Torchia DA, Bax A. Discrete fourier transformation of NMR signals. The relationship between sampling delay time and spectral baseline. J Magn Reson Ser A. 1993;105:219–222. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.