Desipramine, substrate for CYP2D6 activity: population pharmacokinetic model and design elements of drug–drug interaction trials

Abstract

AIMS

To develop a population pharmacokinetic model to describe the pharmacokinetics of desipramine in healthy subjects, after oral administration of a 50 mg dose. Additional objectives were to develop a semi-mechanistic population pharmacokinetic model for desipramine, which allowed simulation of CYP2D6-mediated inhibition, when using desipramine as a probe substrate, and to evaluate certain study design elements, such as duration of desipramine pharmacokinetic sampling, required sample size and optimal pharmacokinetic sampling schedule for intermediate, extensive and ultrarapid metabolizers of CYP2D6 substrates.

RESULTS

The mean population estimates of the first order absorption rate constant (k_a), apparent clearance (CL/F) and apparent volume of distribution at steady state (V_ss/F) were 0.15 h⁻¹, 111 l h⁻¹ and 2950 l, respectively. Further, using the proposed semi-mechanistic hepatic intrinsic clearance model with Bayesian inference, mean population desipramine hepatic intrinsic clearance was estimated to be 262 l h⁻¹ with between-subject variability of 84%. d-optimal PK sampling times for intermediate metabolizers were calculated to be approximately 0.25, 24, 75 and 200 h. Similar sampling times were found for ultrarapid and extensive metabolizers except that the second d-optimal sample was earlier at 14 and 19 h, respectively, compared with 24 h for intermediate metabolizers. This difference in sampling times between the three genotypes can be attributed to the different intrinsic clearances and elimination rates.

CONCLUSIONS

A two compartment population pharmacokinetic model best described desipramine disposition. The semi-mechanistic population model developed is suitable to describe the pharmacokinetic behaviour of desipramine for the dose routinely used in drug–drug interaction (DDI) studies. Based on this meta-analysis of seven trials, a sample size of 21 subjects in cross-over design is appropriate for assessing CYP2D6 interaction with novel compounds.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Desipramine is extensively metabolized by CYP2D6 to its main metabolite 2-OH-desipramine.

• Alternative metabolic pathways are 10-hydroxylation and further demethylation to didesipramine, but the concentration of these metabolites in plasma upon therapeutic oral doses are very low both in extensive and poor metabolizers of substrates of CYP2D6.

• Desipramine has been used widely as a probe drug for CYP2D6 activity.

THIS STUDY ADDS

• The population pharmacokinetics of desipramine in healthy subjects were characterized.

• The model allows performing simulations of trials which assess CYP2D6 interaction potential of novel compounds.

• Study design elements, such as required sample size based on desipramine within and between-subject variance and optimal sampling schedules for the three subgroups, intermediate, extensive and ultrarapid metabolizers of CYP2D6 are suggested.

Introduction

Imipramine has been highly effective in the treatment of serious depression over the last 50 years and with its active metabolite desipramine, continues to be among the most potent pharmacotherapeutic treatments available for depression. Very early techniques [1–3] for the measurement of desipramine in blood and plasma led to an understanding that steady state plasma concentrations varied considerably in patients given the same dose. Desipramine is nowadays commonly used as a substrate for drug–drug interactions, which makes understanding its variability and pharmacokinetic behaviour relevant and important.

Desipramine is rapidly and completely absorbed when taken orally, with peak concentrations occurring 2 to 6 h post-dose [4]. Distribution is largely determined by the lipophilic nature of desipramine, which distributes widely to various tissues. A high degree of tissue binding results in an apparent volume of distribution (V_d) in the range of 10 to 50 l kg⁻¹[5–7]. Desipramine protein binding ranges from 73% to 92% [8] and its bioavailability is also quite variable and reported to be around 40% [9]. Desipramine is metabolized almost exclusively in the liver and its extraction ratio places it as a moderate extraction ratio drug [9], where desipramine clearance will be affected by alterations in enzyme activity, hepatic blood flow and protein binding.

Desipramine is metabolized by CYP2D6 to its main metabolite 2-OH-desipramine [10, 11]. Alternative metabolic pathways are 10-hydroxylation and further demethylation to didesipramine, but the concentration of these metabolites in plasma upon therapeutic oral doses are very low both in extensive (EM) and poor (PM) metabolizers of substrates of CYP2D6 [12]. Desipramine has been used widely as a probe drug for CYP2D6 activity [13–16]. Clinically, elevated desipramine concentrations due to reduced CYP2D6 activity have been related to increased frequency of adverse drug reactions, and even death, upon chronic administration of therapeutic doses [17, 18].

The discovery of genetic polymorphisms in the oxidative metabolism of sparteine and debrisoquine by CYP2D6 [19, 20] has done much to explain interindividual differences in the metabolism of desipramine. Initially studies described two broad phenotypes in the Caucasian population, namely the extensive and poor metabolizer phenotypes. In Caucasians, 6.5 to 10% of the population is composed of the poor metabolizer phenotype with the remainder being extensive metabolizers [19, 21]. More recently there has been the identification of populations of ultrarapid metabolizers and intermediate metabolizers [22]. In Black, Asian and Arab populations the frequency of poor metabolizers has been reported at 4%, 0.9% and 1%, respectively. Additionally some environmental factors, such as smoking and chronic alcohol use, have been reported to influence desipramine metabolism. Chronic alcohol use appears to result in a three-fold greater intrinsic desipramine clearance compared with healthy subjects [9]. However, both control and detoxified alcoholics who participated in this study were smokers and smoking is reported to increase desipramine metabolism in young compared with older smokers [8]. Desipramine disposition reported by Abernethy et al.[23] appeared to be much less influenced by age with only desipramine elimination half-life increased in an elderly male group. Although a great number of studies has investigated desipramine both in the clinic and as a substrate of CYP2D6, as part of drug–drug interaction (DDI) studies, a population pharmacokinetic evaluation of desipramine in patients or healthy subjects has not been yet reported.

The aims of this analysis were to develop a population pharmacokinetic model to describe the pharmacokinetics of desipramine in healthy subjects determined not to be poor metabolizers of CYP2D6 substrates, after oral administration of a 50 mg dose and to examine the influence of demographic characteristics and other covariates on the pharmacokinetic parameters of desipramine. Excluding poor metabolizers from these initial, usually small sample size studies, increases the chance to detect difference in exposures with and without desipramine, as these differences will be more pronounced in extensive metabolizers due to their higher elimination rate. Additional objectives were to (i) propose a semi-mechanistic population pharmacokinetic model for desipramine, which allows simulation of CYP2D6-mediated inhibition, when using desipramine as a probe substrate and to (ii) evaluate study design elements of DDI studies, such as duration of pharmacokinetic sampling, sample size and optimal pharmacokinetic sampling schedule for intermediate, extensive and ultrarapid metabolizers of CYP2D6 sub-populations.

Methods

Data

Data describing desipramine pharmacokinetics were obtained from seven clinical studies where the desipramine only arm was used, except for one, sponsored by Eli Lilly and Company over a 16 year period, following oral administration of a 50 mg single dose. Table 1 provides a summary of the number of subjects included in the study, their demographic data (Table 1A) and summary of noncompartment pharmacokinetic parameters (Table 1B). All studies were conducted in accordance with the principles for human experimentation as defined in the most recent version of the Declaration of Helsinki available at the time when each particular study was conducted and were approved by the Human Investigational Review Board of each study centre. Informed consent was obtained from each subject after they had been told the potential risks and benefits, as well as the investigational nature of the study.

Table 1A.

Demographic data across studies (statistics are arithmetic mean and %CV)

Study number	Number subjects	Gender	Origin	BMI (kg m–2)	Age (years)	Weight (kg)	Smoking	Alcohol
100	10	6 female	8 Caucasian	25.3 (9.8)	46.7 (22)	69.3 (17)	7 No	5 No
		4 male	2 other				3 Yes	5 Yes
200	16	9 female	14 Caucasian	24.4 (13.4)	41.0 (29.3)	70.8 (17.3)	8 No	7 No
		7 male	2 other				8 Yes	9 Yes
300	22	11 female	20 Caucasian	25.4 (10.8)	44.6 (14.3)	75.6 (16.4)	12 No	13 No
		11 male	2 other				10 Yes	9 Yes
400	16	16 male	13 Caucasian	23.1 (9.6)	32.0 (15.8)	74.2 (11.9)	12 No	Not specified
			3 other				4 Yes
500	18	18 male	17 Caucasian	24.7 (10.8)	34.5 (23.3)	79.9 (14)	18 No	5 No
			1 other					13 Yes
800	6	6 male	5 Caucasian	25.1 (13.3)	42.1 (19.1)	79.7 (17.9)	Not specified	Not specified
			1 other
900	20	20 female	13 Caucasian	28.4 (14.1)	51.4 (21.7)	75.2 (17.3)	18 No	14 No
			7 other				2 Yes	6 Yes

Table 1B.

Comparison of noncompartment pharmacokinetic parameters across studies (statistics are arithmetic mean and %CV unless otherwise stated)

Study number	Cmax (ng ml−1)	AUC(0,∞) (ng ml−1 h)	CL/F (l h−1)	Vz/F (l)	t1/2 (h)
100	21.6 (31)	633 (59)	105 (57)	2528 (41)	20 (10–46)
200	17.9 (38)	623 (71)	110 (48)	3281 (38)	25 (12–54)†
300	18.3 (45)	698 (95)	142 (95)	3340 (46)	23 (8–52)†
400	16.3 (37)	440 (53)	143 (52)	NR§	18 (29)‡
500	12.9 ± 9.3*	353 ± 357*	242 ± 131*	NR§	17 (11–38)†
800	16.8 ± 6.6*	516 ± 266*	118 ± 53.5*	3110 ± 1490*	20 ± 7.2*
900	20.5 (42)‡	768 (99)‡	65 (99)‡	2560 (38)‡	27 (15–159)†

^*Mean ± SD.

^†Geometric mean (range).

^‡Geometric mean (%CV).

^§For some studies, no volume terms were reported (NR).

A total of 108 healthy subjects (62 men, 46 women) with a median age of 41 years (range 21–74 years), a median weight of 76.9 kg (range 47.2–106 kg) and a median height of 173 cm (range 147.3–197 cm) were included in the pooled data analysis.

Extensive pharmacokinetic sampling was scheduled after oral administration of 50 mg of desipramine. In study 100, blood samples were collected before drug administration and at 1, 2, 3, 4, 6, 8, 12, 24, 48, 72, 96 and 120 h after drug administration. In studies 200, 300 and 800 blood samples were collected at pre-dose and 1, 2, 3, 4, 6, 8, 12, 24, 48, 72, 96, 120 and 144 h after drug administration. In studies 400, 500 and 900 blood samples were collected before drug administration and at 1, 2, 3, 4, 6, 8, 12, 24, 48 and 72 h after drug administration. In total, 1110 desipramine concentrations were included in the final dataset file. Desipramine concentrations were measured using an established and validated LC/MS/MS method. The upper limit of quantification was 100 ng ml^–1 and the lower limit of quantification was 0.5 ng ml^–1 for all protocols, except 900 and 800, where the lower limit of quantification was 0.25 ng ml^–1. The trials had intra-assay accuracy, which ranged between −6.4% to 0.75% and −2.2% to 7.3%. The precision ranged between −1.7 to 8.1% CV and 6.6 to 9.9% CV.

Phenotyping for CYP2D6 activity was done by two different methods. In the studies done earlier in time, 400 and 500 extensive metabolizers were selected on the basis of a dextromethorphan : dextrorphan ratio <0.3 (in 8 h urine collection). In more recent protocols genotyping methods were used. Several genotyping methods were used which detected the common alleles known to result in a null phenotype. Those individuals with two null variants were defined as PMs, all others were classified as EMs.

Data analysis

All population PK analyses were performed using nonlinear mixed-effects modeling in NONMEM (version V). The first-order conditional estimation (FOCE) method with interaction was used during modeling. Traditional PK one, two and three compartment models with first order absorption and elimination were fitted to the data. For these nested models the log-likelihood ratio test was performed, as well as choice between alternative models was based on goodness of fit as observed in diagnostic plots and also on changes in the minimum value of the objective function and the precision of the parameter estimates. Noncompartmental pharmacokinetic analyses were performed using WinNonLin Professional Version 4.1 (Pharsight Corporation, Mountain View, CA, USA).

Pharmacokinetic analysis

A two compartment linear pharmacokinetic model with first-order absorption best described the time course of plasma desipramine concentrations. The concentration data for all subjects were analyzed simultaneously using nonlinear mixed effects modelling in NONMEM, ADVAN 4, TRANS 4 [24, 25]. The pharmacokinetic model was parameterized using clearances and distribution volumes. Between-subject variability in the parameters was modelled with an exponential random effects term, and the residual error was modelled as combined additive and proportional. Population mean parameter estimates and between-subject variability together with their associated uncertainties (expressed as relative standard error, defined as the percentage ratio between standard error and mean estimates) were calculated.

A semi-mechanistic model for desipramine was developed, which included intrinsic clearance and allows simulation of the CYP2D6 inhibition potential of a novel compound. This model used the same data from healthy subjects as described above. Additionally a number of assumptions were made. The clearance of desipramine was described by the well-stirred liver model (Equation 1, where CL was the systemic clearance of desipramine, CLint,u was the desipramine unbound intrinsic clearance, f_u was the fraction of desipramine unbound in plasma, Q_h was the hepatic blood flow, R was the desipramine blood to plasma ratio and fu,b is the ratio of f_u and R.). The hepatic blood flow was incorporated as an allometric expression of total bodyweight (Equation 2) [26] with the allometric exponent fixed to a typical value of 0.75. Fraction unbound and blood : plasma ratio were fixed to previously reported values in the literature of 0.2 and 0.96 [9], respectively. The overall bioavailability was assumed to reflect mainly F_H, the fraction that reaches the liver, escapes extraction there and reaches the systemic circulation. With this assumption, bioavailability was expressed as shown below . The assumptions on the pharmacostatistical model were as described in the Appendix.

(Equation 1)

(Equation 2)

Covariate, exploratory analyses and internal model evaluation

Using the two compartment PK model, demographic characteristics such as age, gender, origin, weight, height and body mass index as well as smoking and alcohol behaviour were tested as continuous, except for smoking and alcohol behaviour which were categorical (binary) covariates, on apparent clearance and volume of distribution parameters by graphical exploration followed by a stepwise forward inclusion and backward exclusion procedure. The P value for retaining a covariate in the model was 0.001, corresponding to a decrease in the objective function of >10.8 for one added parameter. Both models underwent internal model evaluation using posterior predictive check with simulation of prediction intervals (Figure 3) and influence of prior assumptions on posterior estimates (see Table 4). Based on individual estimated apparent clearances and volumes of distribution of desipramine, a potential small group of subjects, who appeared to be ultrarapid metabolizers, with individual estimated clearances 10-fold greater than population mean clearance, was identified. In exploring the dataset, the data with and without inclusion of these potential ultrarapid metabolizers were analyzed to look for differences in the population pharmacokinetic parameter estimates between these models.

Figure 3.

Observed desipramine concentration data overlaid onto (A) 95% prediction intervals from population desipramine model with parameters as given in Table 2 and (B) 95% credible intervals from semi-mechanistic hepatic intrinsic clearance of desipramine with parameters as listed in Table 4, column 3 posterior estimated with informative priors. 5th percentile (); 95th percentile (); median (); data (); LLQ (); LLQ:800;900 ()

Table 4.

Bayesian posterior population kinetic parameters (following 10 000 iterations) for desipramine in plasma, assuming the semi-mechanistic model with informative priors (columns 2 and 3) and with non-informative priors (columns 4 and 5)

PK parameter	Priors mean (CV)	Posterior mean (CV)	Priors mean (CV)	Posterior mean (CV)	Posterior mean (CV)
fu	0.2 (30)	0.20 (6)	0.2 (70)	0.2 (12)	0.2 (18)
R	0.96 (30)	0.9 (19)	0.96 (70)	1.9 (17)	0.5 (15)
ka (h−1)	0.12 (30)	0.1 (4)	0.12 (70)	0.1 (8)	0.1 (7)
CLint (l h−1)	538 (30)	262 (20)	538 (70)	571 (16)	151 (20)
V1 (l)	815 (30)	1034 (6)	815 (70)	828 (10)	798 (9)
Q (l h−1)	26 (30)	22 (14)	26 (70)	20 (13)	20 (13)
V2 (l)	499 (30)	707 (18)	499 (70)	764 (18)	660 (12)
BSV (CV%)	_______*	84 (8)	_______*	83 (8)	84 (8)
BSV (CV%)	_______*	59 (11)	_______*	59 (11)	59 (13)
IOV (CV%)	NA	NA	_______*	NA	28 (29)
IOV (CV%)	NA	NA	_______*	NA	38 (42)
σ2	_______†	0.5 (2)	_______†	0.5 (2)	0.5 (2)

BSV between subject variation. NA, IOV not estimated.

^*Non-informative priors gamma(1, 0.01)

^†Non-informative priors gamma(0.1, 0.01); Inter-occasion variability (IOV) estimated by including period 1 as well as period 2 data from protocol 300, where no significant PK interaction was found.

In the semi-mechanistic model in NONMEM (Table 3) fraction of desipramine unbound in plasma and blood : plasma ratio were fixed based on literature reported estimates. This may potentially influence the estimated between and within-subject variability of the remaining pharmacokinetic parameters in the semi-mechanistic desipramine model. To investigate this possibility, Bayesian inference (in WinBUGS [27]) was utilized where both informative and non-informative prior distributions on the pharmacokinetic parameters were assumed. The notation below follows that used by Lunn et al.[28], where the concepts for Bayesian analysis for population PK/PD models are developed. The same nonlinear mixed effects model, as specified in the Appendix, was used for fitting desipramine human data with CLint,u and V₁ having an inter-individual variance component and the remaining PK parameters were fixed effects. At the second stage of the model distributional assumptions were made regarding the individual-specific PK parameter vectors θ_i:

Table 3.

Population kinetic parameters for desipramine in plasma, assuming a two compartment model with first-order absorption and proportional error model (base model with intrinsic clearance, fraction unbound, bioavailability and blood-plasma ratio fixed)

	Parameter estimates		Between-subject variability
Parameter	Value	RSE*	CV (%)	RSE*
fu	0.2	–	–	–
R	0.96	–	–	–
ka (h−1)	0.136	9	NA	NA
CLint (l h−1)	519	7	69	19
V1 (l)	974	12	91	19
Q (l h−1)	30	10	NA	NA
V2 (l)	595	9	NA	NA
Plasma within-subject variability % (proportional error model)	40	6

^*Standard error expressed as percent coefficient of variation; NA not assessed.

p(θ_i|µ, Ω) = MVN_p(Z_i, µ, Ω), i = 1, …, L, where MVN_p(·,·) denotes a p dimensional multivariate normal distribution, Z_i is a p×q covariate-effect design matrix for individual i, µ is a vector of q fixed effects parameters and Ω(p×p) is the inter-individual variance-covariance matrix. The third stage of the hierarchical Bayesian model comprises the prior specification, in which prior distributions are assigned to σ², µ and Ω:

where IG(·,·) and IW(·,·) denote inverse-gamma and inverse-Wishart distributions, respectively. Non-informative priors were assumed for both the residual variances (IG(0.01, 0.01)) and the random effects ( and ) IG(1, 0.01).

Four cases were investigated with different priors, ranging from informative (all CVs 10%) to non-informative priors (all CVs 90%) on all fixed effects PK parameters. A multiplicative error model, by applying log transformation of the data and the prediction, was used. Convergence following 10 000 iterations with 2000 burn-in period for the informative and non-informative priors were checked by visual inspection of the parameter traces as well as by diagnostic checks in CODA [29].

Elements of trial design

Although in routine DDI studies, extensive PK sampling is used it will be of value to understand what are the d-optimal PK sampling times for extensive (including intermediate) and ultrarapid metabolizers. Such a characterization will aid identification of specific blood draws for the three subpopulations in clinical protocols. To this effect, the population optimal design software (PopDes) [30] was used to calculate optimal sampling times for intermediate, extensive and ultrarapid CYP2D6 metabolizers. Based on enzyme abundance information and number of gene copies it was assumed that ultrarapid metabolizers have 10 times higher and intermediate metabolizers have two times lower hepatic intrinsic clearance as compared with extensive metabolizers. The semi-mechanistic desipramine model with parameters as listed in Table 4, column 3 was used. The d-optimal design was constrained between 0.25 h and 200 h due to bioanalytical assay limitations to detect low concentrations at 0.25 h.

The recommended strategy for analyzing comparative data from drug interaction studies is to adapt the confidence interval approach used in large bioequivalence studies [31], where the aim is to show that an interaction is not clinically meaningful by the similarity of exposure (AUC_(0,∞)) and C_max. Confidence limits around mean ratios for within-subject comparisons in crossover studies are constructed from the residual mean-square error (MSE) term in anova, which is converted to a coefficient of variation, CV_W. Sample size estimation for a drug interaction study require knowledge of CV_W. Tables of sample sizes for cross-over designs to attain power of 80% at the 5% nominal level for a given CV_W and expected relative difference in treatment medians or means are published for the multiplicative model with equivalence ranges of 0.8–1.25 [32], where also the minor influence of the between-subject coefficient of variability on sample size estimates is demonstrated.

In population pharmacokinetic analyses, variability of pharmacokinetic parameters is often assumed to be due mainly to differences between individuals. Variations in an individual's pharmacokinetic behaviour are assumed to be small and to manifest themselves within the residual error structure. However, this is not necessarily so, as an individual's pharmacokinetic parameters may appear to vary at random between dosing occasions. The extent of this inter-occasion variability (IOV) may be similar in size to the ‘true’ within-subject variability. Consequently, if IOV is ignored within the population analysis, the values of parameters that explain between-subject variability could be over-estimated. Karlsson & Sheiner [33] conclude that neglecting IOV, when it is actually an important source of pharmacokinetic variability, can lead to biased population parameter estimates. Lunn & Aarons [34] described a fully Bayesian method for the analysis of multi-occasion data. The posterior distribution is derived from a four-stage hierarchical model that accounts for both IOV and between-subject variation of pharmacokinetic parameters. Similar to the definition before but now a four stage model was used, where the second stage is defined by p(λ_ij|θ_i, Ω) = MVN_p(θ_i, Ω), i = 1, …, L, where MVN_p(·,·) denotes a p dimensional multivariate normal distribution, θ_i is a p× 1 vector, representing mean kinetic behavior of the ith individual and Ω(p×p) is the inter-occasion variance-covariance matrix of the pharmacokinetic parameters. Further stage three and four are the previous stage two and three. Ideally for the inter-occasion variability we would have liked to use desipramine observations on several occasions in the same subjects, but these were not available. In the reported database, one of the trials (300) concluded no pharmacokinetic drug–drug interaction. Desipramine pharmacokinetic data were used from both periods of the trial, i.e. desipramine administration on its own and desipramine with potential inhibitor. These data, from trial 300, were combined with data from the remaining trials (desipramine alone) to estimate all PK parameters as discussed before but now with added between-occasion variability on intrinsic clearance and central volume.

Results

A total of one hundred and eight healthy subjects were included in the analyses. Their demographics are described in detail in the Methods section.

Desipramine kinetics

As seen in Figure 1, desipramine was quickly absorbed within 2–6 h following administration, with maximum concentrations reached ranging from 8 to 46 ng ml⁻¹. The mean estimated (in WinNONLIN) apparent clearance was 1.8 l h⁻¹ kg⁻¹ with a range of 0.15 l h⁻¹ kg⁻¹ to 10.9 l h⁻¹ kg⁻¹. After peaking, plasma concentration of desipramine fell initially rapidly and then more slowly with a mean terminal half-life of 20 h.

Figure 1.

Desipramine concentration–time data from all studies

Desipramine population pharmacokinetic model in healthy subjects

A first order absorption linear two-compartment model, with elimination from the central compartment provided the best fit to the plasma data. The corresponding parameter estimates are listed in Table 2. The mean population apparent clearance of desipramine was 111 l h⁻¹ with a standard error, expressed as a percent coefficient of variation (RSE), of 7%. The between-subject variability in apparent clearance was estimated at 73% with RSE of 16%. The initial volume of distribution of desipramine (V₁) was 1900 l, and the steady-state volume of distribution (V_ss = V₁+V₂) 2950 l. Between-subject variability in apparent initial volume of distribution was estimated to be 58% with RSE of 22%. The goodness of fit of the model to the data for desipramine is illustrated in Figure 2. The pharmacokinetic model was assessed in terms of population-weighted residuals (Figure 2, bottom panel). Upon examination of the residual plots (Figure 2) and fits (Figure 3) it appeared that there was under-prediction at later time points, even for individual predicted concentrations. The weighted residuals (Figure 2, middle panel) with time showed an upward trend at later time points, signifying under prediction of observed data, which is also evident in Figure 3. Our attempts to fit a three compartment PK model were unsuccessful. Plotting LOQs for the different studies together with the prediction intervals (Figure 3) it was apparent that these were quite wide and encompass undetectable data. The residual variability was described with a combined error model, including additive and proportional components, which were 0.13 ng ml⁻¹ and 37%, respectively. Prediction intervals, simulating effect of estimated between-subject variability, relevant for any future desipramine trials, were overlaid onto observed data and are plotted on Figure 3A.

Table 2.

Population kinetic parameters for desipramine in plasma, assuming a two compartment model with first-order absorption and combined error model (base model with total clearance, absorption rate constant and volume of distribution)

	Parameter estimates		Between-subject variability
Parameter	Value	RSE*	CV (%)	RSE*
ka (h−1)	0.15	17	NA	NA
CL (l h−1)	111	7	73	16
V1 (l)	1900	16	58	22
Q (l h−1)	58	13	NA	NA
V2 (l)	1050	13	NA	NA
Plasma within-subject variability (ng ml−1) (additive error model)	0.13	43
Plasma within-subject variability (%) (proportional error model)	37	7

^*Standard error expressed as percent coefficient of variation.

Figure 2.

Goodness-of-fit plots of desipramine two-compartment first order absorption pharmacokinetic model. Upper panels: Measured concentrations vs. predictions for the population (left) and for the individuals (right). Middle panels: weighted residuals vs. observed data (left) weighted residuals vs. time (right) Lower panels: weighted residuals vs. population predictions (left) and individual predicted concentrations vs. individual weighted residuals (right)

A number of potential covariates were assessed as to their influence on the objective function of the base model. The continuous covariates included weight, height, age, body mass index (BMI) with either power, exponential or linear functions on apparent clearance and initial volume of distribution. Additionally, categorical covariates, specifically gender, origin (dichotomized to either Caucasians or others), alcohol and smoking behaviour (binary) as linear functions were assessed. A forward covariate search identified BMI and gender as statistically significant (P < 0.01; decrease in objective function of at least 6.635 points) with alcohol consumption covariate just on the border of being included (including it as a covariate caused a decrease in objective function of 6.685 points). However as BMI and gender were highly correlated, a backward covariate search (P > 0.001, decrease in objective function of at least 10.828 points) identified only BMI as a significant covariate on the volume of distribution.

Also identified, based on individual estimated apparent clearances and volumes of distribution were two subjects, who appeared to be potentially ultrarapid metabolizers. Desipramine data were re-analyzed, excluding the small number of potential ultrarapid metabolizers (results not shown). Additionally differences were explored in the population pharmacokinetic parameter estimates based on metabolizer status determined by genotyping or phenotype (results not shown). There were no significant differences found in the population PK estimates by excluding the ultrarapid metabolizers or by stratifying by method for determining metabolizer status.

Desipramine population pharmacokinetic model in healthy subjects with hepatic intrinsic clearance

A first order absorption linear two-compartment model, with elimination from the central compartment, and assumptions as described in the Methods section, provided the best fit to the plasma data. The corresponding parameter estimates are listed in Table 3. The mean population intrinsic clearance of desipramine was 519 l h⁻¹ with RSE of 9%. The between-subject variability in apparent clearance was estimated at 69% with RSE of 19%. The initial volume of distribution of desipramine (V₁) was 974 l, and the steady-state volume (V_ss = V₁+V₂) 1569 l. Between-subject variability in initial volume of distribution was estimated to be 91% with RSE of 19%. The residual variability was described with a proportional error model.

Fraction of desipramine unbound in plasma and blood to plasma ratio were fixed, during the analyses in NONMEM, based on reported literature values. To investigate the influence of fixing these parameters Bayesian inference (in WinBUGS) was performed where both informative and non-informative prior distributions on each of the pharmacokinetic parameters were assumed. The assumed prior distributions together with their posteriors are listed in Table 4, first five columns. Based on the Bayesian analysis with different priors, the between-subject variability of CL_int and V₂ was consistently around 84% and 59%, respectively. These results showed that fixing the uncertain PK parameters had somewhat artificially increased between-subject variability (BSV) of V₂ in the NONMEM runs. Hence by assigning a prior distribution on f_u and R and allowing them to vary during the estimation process more realistic BSVs were calculated.

Elements of trial design

There are three different subgroups within the common screens for the extensive metabolizer population in trials. Different population mean pharmacokinetic profiles were projected for intermediate, extensive and ultrarapid metabolizers (Figure 4). Using d-optimal design as implemented in PopDes, optimal sampling times were obtained for the three subpopulations as listed in Table 5. The design space was constrained between 0.25 and 200 h and exchange algorithm with step size 1 was used to explore the space. All the resulting designs, which minimize the variance-covariance matrix gave low CVSE on the structural PK parameters and moderate variation on between-subject variances (around 40%). Consistent with theory, for any model with proportional error the optimal designs required samples as early as possible after desipramine administration and samples at the end of the constrained space. Additionally PK samples were needed just after the peak concentration as well as two samples to define the biphasic disposition profile of desipramine. The most pronounced difference among the d-optimal designs for the three subpopulations was in the second sample, which was earliest for ultrarapid metabolizers (14 h) and latest for the intermediate population (24 h). Due to the lower clearance for intermediate metabolizers their pharmacokinetic profile appears almost as monophasic and could be represented by a single time point instead of two. These designs are quite theoretical and in practice rich pharmacokinetic sampling would be used. In practical designs samples at the anticipated peak concentrations will be taken to define C_max as this is one of the measures for drug–drug interaction. Nevertheless these theoretical designs can be used as a benchmark for the practical design. These optimal sampling time points can be used to provide a more intensive sampling scheme.

Figure 4.

Mean desipramine concentration–time profiles in extensive, intermediate and ultrarapid metabolizers of CYP2D6. EMs (—); IMs (); UMs (); d-optimal design EMs (); d-optimal design IMs (); d-optimal design UMs ()

Table 5.

d-optimal population design for intermediate, extensive and ultrarapid metabolizers

Design	Optimal sampling times (h)
Intermediate metabolizers	0.25	0.25	24.25	24.25	24.25	73.25	75.25	199.25
Extensive metabolizers	0.25	0.25	19.25	19.25	19.25	58.25	90.25	199.25
Ultrarapid metabolizers	0.25	14.25	14.25	14.25	54.25	54.25	105.25	199.25

	CVSE* (%)
ka	CLint	V1	Q	V2			σ
Intermediate metabolizers	28.5	12.6	20.4	19.9	14.3	43.3	44.8	19.1
Extensive metabolizers	18.2	9.3	16.2	16.8	9.8	38.5	36.9	18.0
Ultrarapid metabolizers	12.0	12.3	12.8	14.8	8.9	42.1	37.9	19.1

^*Coefficient of variation around the standard error. Exchange algorithm with step size 1 was used.

Different population mean exposures (AUC_(0,∞)), using the developed desipramine model, were simulated when the last pharmacokinetic sample was taken on days 9, 6, 4, 3, 2 and 1 (results not shown). It was evident, by examining the absolute value of AUC_(0,∞) and percent reduction of exposure that reducing the last pharmacokinetic sampling time up to 72 h yielded very similar exposure compared with sampling as late as 200 h. This is in agreement with the basic principle to sample for at least to 3.3 times the half-life after dosing as by this time about 90% of the dose is eliminated from the body [35].

Desipramine concentration–time profiles for study 300 where both periods of the trial were used in the estimation are plotted in Figure 5. Using these data together with desipramine alone data from the remaining trials we obtained between-occasion variability of 28% on CL_int (Table 4, last column with non-informative priors (CV 70%) as specified in column 4).

Figure 5.

Desipramine concentration–time profiles for study 300 (A) desipramine only arm (period 1) and (B) desipramine plus potential inhibitor arm (period 2)

Sample sizes between 12 and 20 subjects in exploratory drug–drug interaction trials are commonly used. When determining sample sizes an assumption is made about the within-subject variance. Assuming within-subject variance of 30%, sample size of 17 to 21 subjects covers a very wide range (20% to 100%) of between-patient variance. Based on these analyses of seven trials a sample size of 21 subjects is appropriate for assessing CYP2D6 interaction with novel compounds. Although the between-subject variance is well defined as coming from a large number of trials, the within-subject variance estimate is based on only one trial where desipramine was given on two occasions to the same subjects.

Discussion

Desipramine healthy volunteer data from seven clinical studies were used to derive population pharmacokinetic parameters. A population PK model for desipramine disposition was not available in the literature but the population PK estimates from this meta-analysis compare well with mean estimates from published individual studies. Desipramine was found to have a mean population apparent clearance of 111 l h⁻¹, which corresponds to 1.5 l h⁻¹ kg⁻¹ for a 70 kg volunteer. This is consistent with previous reported mean clearance in adults of 1.8 l h⁻¹ kg⁻¹[5, 6, 8, 23] following oral administration. The population mean estimate for V_ss was 42.1 l kg⁻¹ which is consistent with a reported mean value of 42 l kg⁻¹ by Alexanderson [5]. However, there are some studies reporting values ranging between 20.1 l kg⁻¹ to 30 l kg⁻¹[8]. A reason for the varying apparent volume of distribution between reported studies lies in the study design. Depending on how long blood/plasma draws were taken will have a large effect on the estimated volume of distribution at steady state. The majority of the studies report terminal volume of distribution, which is similar to observing only the first phase of disposition of a two compartment PK model. In the analysis reported here, three studies where blood draws were taken up to 144 h after desipramine administration, one study with a terminal sample at 120 h and the remaining three with 72 h were combined. Inspecting the combined data as shown on Figure 3, it is apparent that by 72 h the first phase of disposition is complete and its volume is 1900 l, which is 27 l kg⁻¹ similar to the majority of the reported values. However, when later sampling is performed, the second distribution phase is identified. In this analysis, a much larger volume of distribution is identified, similar to Alexanderson[5], where PK samples were obtained up to 100 h and a two compartment model was used to characterize desipramine kinetics. Upon examination of the residual plots (Figure 2) and fits (Figure 3) it appears that there is under-prediction at later time points and also underprediction of high observed concentrations. Our attempts to fit a three compartment PK model were unsuccessful. Plotting LOQs for the different studies together with the prediction intervals (Figure 3) it was apparent that these were quite wide and encompassed undetectable data. The assessment here of a number of potential covariates identified BMI as an important covariate. Although there are reports in the literature, that smoking and chronic alcohol use influence desipramine metabolism we did not identify them to be significant covariates in our analysis. This result is not surprising as data came from healthy, young volunteers with height, part of BMI calculation, being the only variable not controlled for in the screening process. Attempting to understand the causes for the relatively high between-subject variability on CL additional exploratory analyses on the dataset were carried out. The desipramine data in the meta-analysis came from studies performed throughout the last 15 years, where CYP2D6 phenotyping and genotyping methods varied in their performance. The gene coding the CYP2D6 enzyme is known to be polymorphic with well defined population subgroups of poor and extensive metabolizers where the latter include ultrarapid, intermediate and extensive metabolizers. In clinical trials where a DDI arm to examine the potential for CYP2D6 inhibition is added, it is common to phenotype or genotype prior to accepting a subject in a study and to exclude if the subject is identified as a poor metabolizer. However this means that both ultrarapid and intermediate metabolizers are commonly subscribed into a trial as belonging to the more general extensive type. In the earlier protocols phenotyping for CYP2D6 activity was done by the urinary dextrophan : dextromethorphan ratio method (studies 400, 500), whereas in more recent protocols genotyping methods were used. It appeared that in the data there were a couple of ultrarapid metabolizers. However as their number was very small excluding them from the dataset did not influence desipramine parameter estimates. The data were collected from trials over almost 15 years. The accuracy of screening methods for identifying an extensive metabolizer subgroup has improved over this time and hence the data were analyzed by splitting into screening by genetic testing or by urine assessment methods. However no difference was found in desipramine PK parameters based on different screening methods.

A semi-mechanistic population pharmacokinetic desipramine model with hepatic intrinsic clearance was proposed. There was no information in the dataset on fraction of drug unbound in plasma and blood : plasma ratio. Therefore literature values for these parameters were used. However fixing them to some reported mean values may have caused inflation in the between subject variability of intrinsic clearance and volume of distribution. It was important to quantify CL_int variance as it is an essential parameter in any model used to simulate CYP2D6-mediated inhibition and such inaccuracy will limit the predictive power of such a simulation model. The overall bioavailability is a composite of drug loss from the gastrointestinal lumen, gut wall and liver before the drug enters the general circulation (F = F_F × F_G × F_H).The dose of desipramine absorbed through the intestinal lumen is assumed to be complete (F_F = 1). As there are no CYP2D6 enzymes in the gut wall there is no loss of desipramine there (F_G = 1). Hence, in this model the overall bioavailability reflects mainly F_H, the fraction that reaches the liver, escapes extraction there and reaches the systemic circulation.

By allowing the uncertain parameters to vary during the estimation in a Bayesian framework BSV estimates were obtained purely reflecting observed variability in the comprehensive dataset. Estimating simultaneously IOV and BSV for desipramine was also investigated. We chose a trial where no interaction was found and used both desipramine periods of this crossover trial to estimate IOV. We also made the assumption that any difference found was solely due to the IOV. However IOV information came from only one of the seven trials and was thus limited. Additionally, the presence of the potential inhibitor could have had some effect on desipramine concentrations. Therefore there is a need for further investigation on the true IOV effect from specifically designed trials. However with the limitations above we found that the overall the extent of IOV was much smaller than BSV. Although the extent of IOV for any pharmacokinetic parameter is of interest and could have clinically significant consequences, the population behaviour of CL was of most interest as variations in this parameter generally have the greatest effect on exposure. The results in Table 4 show that IOV is less than BSV for both CL_int and V₁. Exposure is proportional to the inverse of CL and log AUC has an IOV that is identical to log CL. As CL is the least variable parameter at the interoccasion level, overall exposure to desipramine appears to be less variable than V₁.

Sample sizes between 12 and 20 subjects in exploratory drug–drug interaction trial are commonly used. Such sample sizes correspond to assuming within-subject variance of 30% [32]. If it is supposed that the extent of IOV is similar in size to the ‘true’ within-subject variability, then the within-subject variance is 28%, which combined with a between-subject variance of 80 % will require sample size of 20 subjects. This however needs more investigation as the IOV estimate is based on only one of the studies and needs to be refined when more data with desipramine given on two or more occasions to the same subjects are available.

In summary, a population pharmacokinetic desipramine model was developed based on a relatively large dataset. The model underwent extensive internal validation and a semi-mechanistic model with hepatic intrinsic clearance was proposed. The final semi-mechanistic model developed here may be readily used to simulate CYP2D6-mediated inhibition, when using desipramine as a probe drug. Additionally using the model and the datasets a number of trial design elements were considered.

APPENDIX

Specifically, the pharmacostatistical model is given by , where θ_i is the p-vector (k = 1, …, p) of parameters, θ_i = g(θ, b_i) where g() is a known function, θ is a vector of fixed effects and b_i is a vector of random effects for subject i. Assuming no covariates g(θ, b_i) is given by g(θ, b_i) = θ+b_i or g(θ, b_i) = θexp(b_i). It is also assumed that b_i∼N(0, Ω), where N is a normal distribution and Ω is a p×p variance-covariance matrix of the between-subject variabilities, with each element ω_k corresponding to the variance of the kth component of b_i, as defined by . The 1 ×n vector of sampling times in individual i is given by ξ_i = [t_il, …, t_in]. The error term is characterized by two parameters: 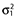(intercept) and (slope) so that .

Competing interests

There are no competing interests to declare.