Electrochemical and homogeneous electron transfers to the Alzheimer amyloid-β copper complex follow a preorganization mechanism

Abstract

Deciphering the electron transfer reactivity characteristics of amyloid β-peptide copper complexes is an important task in connection with the role they are assumed to play in Alzheimer’s disease. A systematic analysis of this question with the example of the amyloid β-peptide copper complex by means of its electrochemical current–potential responses and of its homogenous reactions with electrogenerated fast electron exchanging osmium complexes revealed a quite peculiar mechanism: The reaction proceeds through a small fraction of the complex molecules in which the peptide complex is “preorganized” so as the distances and angles in the coordination sphere to vary minimally upon electron transfer, thus involving a remarkably small reorganization energy (0.3 eV). This preorganization mechanism and its consequences on the reactivity should be taken into account for reactions involving dioxygen and hydrogen peroxide that are considered to be important in Alzheimer’s disease through the production of harmful reactive oxygen species.

Alzheimer’s disease is characterized by both the deposition of amyloid plaques constituted mainly by aggregated amyloid-β peptide (Aβ) in the brain of victims and by marked oxidative damage including glycation, oxidation of protein, DNA and RNA, and peroxidation of lipids (1–3). These oxidative stress processes derive from the redox chemistry of copper ions coordinated to the Aβ peptide (4, 5). The 39 or 42 residue polypeptide consists of a largely hydrophilic N-terminal domain (1–28), containing the metal binding site, and a C-terminal hydrophobic domain (29–40/42). This peptide can bind one equivalent of Cu^II ions with high affinity (6, 7). Most of the Cu^II coordination studies have been performed on the truncated Aβ16 (DAEFRHDSG YEVHHQK) peptide (see structure in SI Appendix) that was shown to be a valuable model of Cu^II binding sites and affinity (6, 8–10). At physiological pH, two Cu^II(Aβ) complexes coexist (7, 10, 11); the predominant form at physiological pH is pure near pH 6.7, whereas the minor form is pure near pH 8.9 (12, 13). The former complex exhibits a distorted square planar geometry with a 3N1O equatorial coordination mode where the -NH₂ terminus, two imidazole rings of His6 and His13 or His14, and an oxygen atom, the attribution of which is still debated, are the ligands deduced from pulsed-EPR studies on ¹³C and ¹⁵N-labeled peptides (13–16). Structure of the Cu^I(Aβ) β complex was recently elucidated by X-ray absorption spectroscopy studies (8, 17), and the Cu^I is coordinated by the two imidazoles rings from the His diad (His13-His14) in an almost linear geometry. These structural characterizations of Cu(Aβ) complexes performed in frozen solution have been completed by NMR studies at ambient temperature that evidence dynamic binding processes in which rapid exchange between equivalent ligands at a given coordination position are observed (12, 18). Generation of harmful reactive oxygen species by the Cu^I(Aβ) complexes requires the reduction of Cu^II to Cu^I by biological reducing agents like ascorbate followed by O₂ or H₂O₂ activation. One piece of the puzzle thus involves the electron transfer reactivity of amyloid-β peptide Cu^I/II complexes. By electron transfer reactivity we do not intend only its thermodynamic aspects, i.e., characteristic standard potentials, but also, and above all, the kinetic aspects that are required to establishing the reaction mechanism. Our study concerns the Aβ16 copper complexes, the truncated Aβ16 peptide being considered as a valid model of Cu coordination and reactivity. We examined both the electrochemical and the homogeneous electron transfer reactivity of these complexes.

Results and Discussion

1. Total Complexation of Copper Ions by the Aβ16 Peptide.

1.1. Variations of the cyclic voltammetric response upon addition of Aβ16.

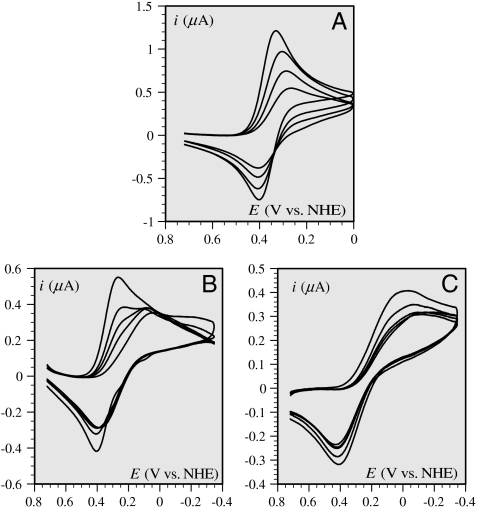
Divergent reports of the electrochemistry of Aβ copper complexes have recently appeared (18–20). In the present study, we noticed that the cyclic voltamogramm of 0.2 mM Cu(Aβ) complex is strongly dependent of the peptide over copper ratio (Fig. 1).

Fig. 1.

Cyclic voltammetric responses, at a glassy carbon electrode, of a 0.2-mM solution of Cu^II in a 25-mM pipes buffer of pH = 6.7 in the presence of 0.2 M KCl as a function of successive addition of the Aβ16 peptide of (from top to bottom) 0, 0.1, 0.2, 0.3 (A), 0.3, 0.4, 0.5, 0.6, 0.8 (B), and 1, 2, 3, 4, 5 (C) equivalents. Scan rate: 0.02 V/s. The background current has been subtracted in all cases. Temperature: 20 °C.

Indeed, when the ratio of peptide over copper is one or even two, as generally the case in the above-mentioned studies with similar or higher concentrations or with excess copper, a small-to-substantial amount of copper ions remains uncomplexed and its electrochemical response strongly interferes with the one of the Cu(Aβ) complex. The resulting electrochemical response is then a superposition of the signals of the free and complexed copper ions, as clearly visible in the series of cyclic voltammetric current–potential curves in Fig. 1, which shows the effect of successive additions of the peptide to a Cu^II solution. It appears that a steady electrochemical response is obtained for a threefold excess of peptide over copper ions. Further additions of the peptide do not change the current–potential curve. These observations show unambiguously that, at these concentrations of peptide, the electrochemical reaction does no longer go through the intermediacy of free copper ions but involves directly Aβ16 copper complexes.

The ensuing experiments were therefore carried out with a fivefold excess of peptide so as to safely represent the intrinsic properties of the amyloid β-peptide copper complexes with no interference of the response of free copper ions in the solution. The choice of the pH value, 6.7, at which the experiments were carried out, was dictated by the previously mentioned observation that a single form of the Cu^II(Aβ) complex exists at pH = 6.7.

1.2. Cyclic voltammetry of the Cu(Aβ) complex.

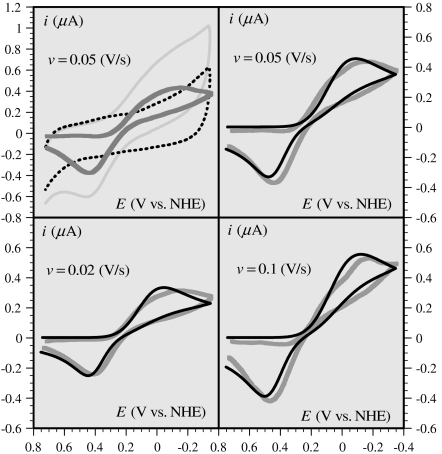
A typical set of cyclic voltammograms of the Cu^II(Aβ) complex obtained under these conditions is shown in Fig. 2. The subtraction of the relatively large background current, recorded in the absence of Cu, to obtain the corrected response is illustrated in the top-left diagram of Fig. 2. A better faradaic-to-background current ratio is expected to be obtained upon increasing the copper concentration. However, a parallel increase of the peptide should be provided in order to maintain its fivefold excess, which is precluded by ensuing precipitation and solubility problems. This is also the reason that scan rates above 0.1 V/s could not be reliably used because the background current increases more rapidly with scan rate than does the copper complex faradaic response. Because of these various constraints, the conditions in which the curves shown in Fig. 2 were recorded represent the best compromise for a meaningful analysis of the electrochemical kinetics of these copper complexes. An estimation of the degree of reproducibility of the cyclic voltammetric responses after subtraction of the current obtained with the peptide alone is given in SI Appendix. Reproducibility is excellent for the two lower scan rates and a little less at 0.1 V/s. The elusive appearance of a splitting of the cathodic wave is not considered as significant in view of uncertainties in the subtraction of large background currents.

Fig. 2.

Gray curves: cyclic voltammetric responses (corrected from the background current), at a glassy carbon electrode, of a 0.2-mM solution of Cu^II in a 25-mM pipes buffer of pH = 6.7 in the presence of 0.2 M KCl after addition of 1 mM Aβ16 peptide, as a function of the scan rate (v). Black curve: simulated current-potential curve according to the preorganization mechanism (third mechanism in Scheme 1); for details and parameter values, see Section 2.6. (Top Left) Diagram illustrates the way in which the background signal (dotted line) has been subtracted from the raw cyclic voltammogram (light gray curve) to obtain the corrected response (gray curve). Temperature: 20 °C.

2. Kinetics and Mechanisms of the Electrochemistry of the Cu^II/I(Aβ) Couple.

2.1. The various possible mechanisms.

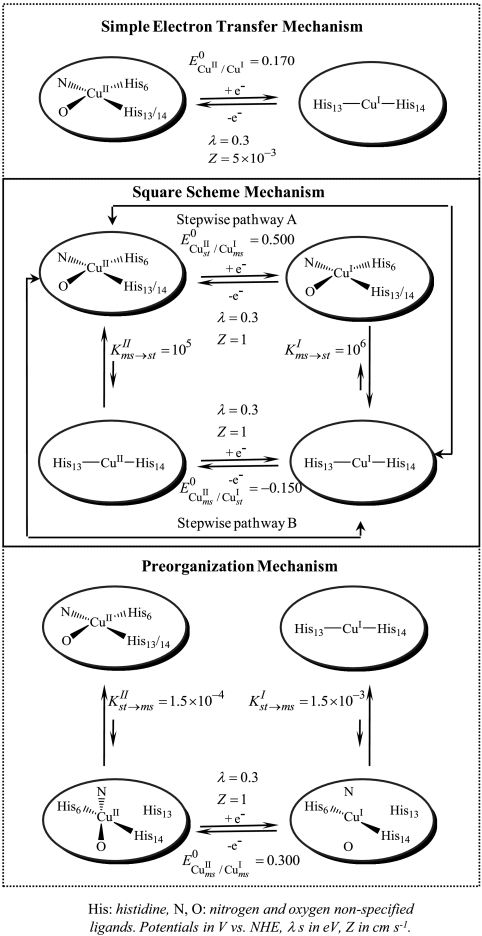
Several mechanisms may be envisaged as depicted in Scheme 1. For the moment, we discuss the qualitative aspects, ignoring the figures appearing in Scheme 1, which will be used later on for the discrimination among the three mechanisms.

Scheme 1.

Reactions schemes

The simplest mechanism one can think of is a plain electron transfer reaction. Electron transfer is accompanied by considerable reshuffling of the coordination sphere from a four-coordination distorted square planar Cu^II arrangement to an unusual two-coordination linear Cu^I configuration. Although such two-coordination Cu^I have been previously described (21–24), they are far less common than four- or three-coordination structures (25, 26). Internal reorganization upon electron transfer is thus expected to be even larger in the first case than in the second. As discussed quantitatively in the next section, this large intramolecular reorganization makes the simple electron transfer mechanism unlikely.

An alternative mechanism is the square scheme mechanism in Scheme 1. It involves classical stepwise pathways as already considered for copper complexes (26–29). Two stepwise pathways may be envisaged. Along pathway A, the reduction of the stable Cu^II complex produces a metastable “Cu^II-like” Cu^I complex, which relaxes to the stable form of the Cu^I complex (an “EC” mechanism according to the electrochemical terminology) (30). Along pathway B, the stable Cu^II complex is first converted into a metastable “Cu^I-like” Cu^II complex, which is then reduced to the stable form of the Cu^I complex (a “CE” mechanism according to the electrochemical terminology) (30).

As discussed in details in the following, the preceding mechanisms failed to match the experimental data, leading us to propose a preorganization mechanism (last mechanism in Scheme 1) in which small fractions of the Cu^II(Aβ) and Cu^I(Aβ) complexes adopt similar structures, resulting in a very small electron transfer reorganization energy. These Cu^II and Cu^I preorganized metastable states are in continuous and rapidly established equilibrium with the corresponding Cu^II and Cu^I predominant (stable) forms. It follows that electron transfer goes entirely through this fast pathway with negligible contribution of direct electron transfer between the ground state complexes, which would require a considerably larger reorganization of the coordination sphere. This mechanism does not follow a square scheme but rather a three-step scheme, similar to the middle pathway invoked in the stepladder scheme of Fig 16 in ref. 26, a “CEC” mechanism according to the electrochemical jargon. We will show, thanks to the continuous spectrum of driving forces offered by the electrochemical approach of the problem, that this preorganization electron transfer (POET) mechanism appears not only as a possible pathway but as the actual mechanism.

2.2. Electrochemical rate law and strategies for mechanism discrimination.

Two characteristics of the cyclic voltammetric responses are worth noticing. One is the fact that electron transfer is extremely slow. The separation between the cathodic and anodic peaks is indeed 600 mV at, e.g., a scan rate of 0.05 V/s. The other is the large thickness of the reduction wave. This indicates that the transfer coefficient (or symmetry factor), α, which measures the rate at which the activation energy of the reaction varies with the driving force, is unusually small, ranging between 0.2 and 0.3, as derivable from the difference between the half-peak and peak potentials (E_p and E_p/2, respectively):

One may also have to take into account the variation of α with potential along current–potential curve. Taking into account these observations points to the necessity of applying to the kinetics of the electrochemical reaction the full Marcus–Hush–Levich (MHL) quadratic model (31–35) rather than a linearized version, amounting to the old Butler–Volmer empirical law, in which the transfer would be constant and close to 0.5 as often done with standard cyclic voltammetric responses (31).

The electrochemical rate law to be applied is therefore

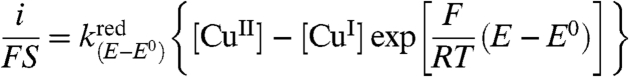[1]

with

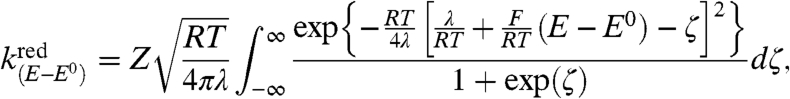[2]

where i is the current flowing through the electrode, counting the cathodic current as positive, S, the electrode surface area, E, the electrode potential, and E⁰ the standard potential of the redox couple. [Cu^II] and [Cu^I] are the concentrations at the electrode surface, of the two redox forms of the Aβ copper complex, respectively. 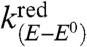and 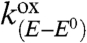are the potential-dependent rate constants for the reduction of Cu^II and oxidation of Cu^I, respectively.

Two key parameters of the electrochemical kinetics are thus introduced, namely, the reorganization energy, λ, accompanying electron transfer and Z, the preexponential factor, defined as the limiting value of the rate constant reached asymptotically at infinite driving force. Eq. 2 takes into account the multiplicity of the electronic states of electrons in the electrode, preventing the existence of an inverted region at large driving forces, in contrast with homogenous reactions.

A way of demonstrating the occurrence of CE and EC mechanisms is to follow the effect of raising the scan rate as shown since the early days of the application of cyclic voltammetry to mechanism analysis [(30), and references therein], requiring that the characteristic rate constants, k, be not too large and that sufficiently high scan rates, v, can be used, so as to maintain the parameter (RT/F)(k/v) close to unity. Such a strategy is obviously precluded in the present case. It was replaced by a strategy based on the shape of the cyclic voltammetric responses. We note, in passing, that combining experiments that start from the reduction of Cu^II with those that start from the oxidation of Cu^I does not bring about more information than cyclic scan experiments involving either one or the other redox state. The information contained in the forward and reverse scan peak potentials concern standard potential and standard rate constants. The latter corresponds to the self-exchange rate constants in homogeneous experiments. The information contained in the portion of voltammograms in between their foot and their peak corresponds to a systematic variation of the driving force of the reaction. They are obviously much easier to obtain in electrochemical conditions where the variation of the electrode potential offers a continuous spectrum of driving forces than in homogeneous experiments that would require investigating a huge number of partner reactants to obtain a similar result. The principle of the mechanism discrimination detailed in the following sections was thus to simulate, using Eqs. 1 and 2 for the electron transfer step, the cyclic voltammetric responses according to each mechanism so as to reproduce the cathodic-to-anodic peak separation in each case and to examine whether or not the whole curve, representing the effect of the variation in driving force, fit the experimental data. The sensitivity of the curve shape, which reflects the transfer coefficient (symmetry factor), to mechanism derives from the quadratic character of the rate law and of its enhancement by low values of the reorganization energy (Eq. 2). Summaries of previous application of this strategy to a great number of examples in the case of dissociative and proton coupled electron transfer are available (36, 37).

2.3. Preliminary measurements.

In order to evaluate quantitatively the various possible reaction mechanisms, we need an estimate of the preexponential factor, Z, and of the reorganization energy, λ, for a simple electron transfer to any of the complexes where the copper species stands inside the Aβ ligand. For this, we start from an estimation of these parameters for a simple complex like the Cu^II aquo-chloro-complex from which the Aβ complex was generated (first voltammogram in Fig. 1A). The variations of the standard rate constant with temperature and the ensuing Arrhenius (see SI Appendix for details), allow the determination of the reorganization energy, λ = 1.4 eV, and of Z^free Cu = 7330 cm s^-1.

It is also interesting to note that the diffusion coefficient, D_free Cu, obtained from the peak current, i_p, of the reversible Nernstian wave of the free copper complex (Fig. 1A):

(31) (v: scan rate) is D_free Cu = 5 × 10^-6 cm² s^-1. It follows from application of the Stokes–Einstein relationship (38),

[R_freeCu: spherical equivalent radius of the free Cu complex, η: viscosity, here, in water at 20 °C, η = 10^-3 Kg m^-1 s^-1 (39)], that .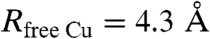

2.4. Quantitative evaluation of the simple electron transfer mechanism.

Although we know that the coordination sphere of the Cu(Aβ) complex strongly reorganizes upon electron transfer, we do not have a definite figure for the reorganization energy, λ. It may, however, be estimated that it is at least equal to the value 1.4 eV just found for the “free” aquo-chloro complex. Simulation according to this mechanism with this value of λ, with E⁰ = 0.17 V vs. NHE (normal hydrogen electrode), D_{Cu(A β)} = 2 × 10^-6 cm² s^-1 [in agreement with a literature value obtained in slightly different conditions (40)] allows a good matching of the peak potentials for Z^Cu(Aβ) = 18 cm s^-1 (Fig. 3A). The predicted shape of the wave is, however, in complete disagreement with experiment (full thin line in Fig. 3A) as foreseen from the approximate estimation of the transfer coefficient (section 2.2). Does this situation change if we go to much smaller values of λ? Even with an unrealistically small value of 0.3 eV, the matching of experimental data (dotted thin line in Fig. 3A) obtained for Z^Cu(Aβ) = 5 × 10^-3 cm s^-1, although somewhat better, is still far from satisfactory. An additional argument against this possibility derives from the low value of Z^Cu(Aβ). Z is indeed predicted to vary with distance according to ref. 41:

taking 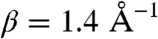(42) into account with the fact that the structure of the peptide is of the random coil type (11) leads to 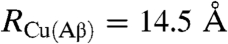. The resulting predicted distance from the reacting center is thus clearly larger than the radius of the complex, 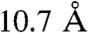, derived from application of the Stokes–Einstein relationship based on D_Cu(Aβ) = 2 × 10^-6 cm² s^-1.

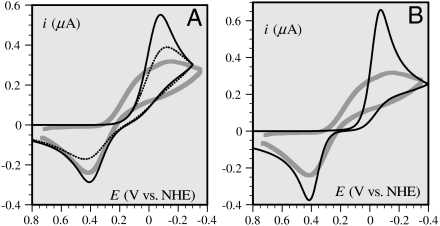
Fig. 3.

Thick gray curves: cyclic voltammetric responses (corrected from the background current), at a glassy carbon electrode, of a 0.2-mM solution of Cu^II in a pipes buffer of pH = 6.7 in the presence of 0.2 M KCl after addition of 1 mM Aβ16 peptide. Scan rate: 0.02 V/s. (A) Thin curves: simulated current-potential curve according to a simple electron transfer mechanism (first mechanism in Scheme 1, section 2.4) obeying the MHL law with E⁰ = 0.17 V vs. NHE and D_Cu(Aβ) = 2 × 10^-6 cm² s^-1. Solid curve: λ = 1.4 eV, Z = 18 cm s^-1, dotted curve: λ = 0.3 eV, Z = 5 × 10^-3 cm s^-1; (B) thin curve simulation according to the square scheme mechanism (Scheme 1, section 2.5).

It may thus be concluded that these various elements rule out the simple electron transfer mechanism.

2.5. Quantitative evaluation of the square scheme mechanism.

Fig. 3B shows an attempt to simulate the cyclic voltammetric responses according to this mechanism. The best fit in terms of peak separation is obtained for the parameter values listed in Scheme 1, with D_Cu(Aβ) = 2 × 10^-6 cm² s^-1 and with a preexponential factor value of Z^Cu(Aβ) = 1 cm s^-1 for the two electron transfer steps. Z^Cu(Aβ) was obtained from the following attenuation relationship (41):

where 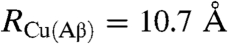as derived from the Stokes–Einstein relationship (assuming that the redox center sits at the center of the equivalent sphere), again with .

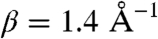Taking for λ a value as small as 0.3 eV takes into account that each electron transfer step involves a minimal structural change. Even smaller values, 0.2, 0.1 eV, have been tested (with Z = 0.3 and 0.1 cm s^-1), leading to no improvement of the fit.

It thus appears that the best fit in terms of peak potential separation reproduces (Fig. 3B) very poorly the shape and height of the cyclic voltammograms, thus ruling out the classical square scheme mechanism.

2.6. Quantitative evaluation of the preorganization mechanism.

Satisfactory simulation of the cyclic voltammetric responses recorded at 0.02, 0.05, and 0.1 V/s was obtained (Fig. 2) with a diffusion coefficient D_Cu(Aβ) = 2 × 10^-6 cm² s^-1, with a preexponential factor value of Z^Cu(Aβ) = 1 cm s^-1, with λ = 0.3 eV, and with the values of the preorganized/ground state equilibrium constants shown in Scheme 1. The standard potential of the preorganized redox couple is 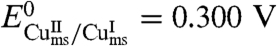vs. NHE, corresponding to 0.241 V vs. NHE for the overall standard potential.

The good agreement between the theoretical predictions and the experimental data (see Fig. 2 and also the successful reproducibility tests described in SI Appendix) establishes the validity of the POET mechanism.

Tests done with slightly different values (± 20%) showed that the values of the equilibrium constants and λ are accurate once the value of Z is considered as correct. In the determination of the latter parameter, some uncertainty may derive from localizing the copper atom at the center of a sphere representing the complex.

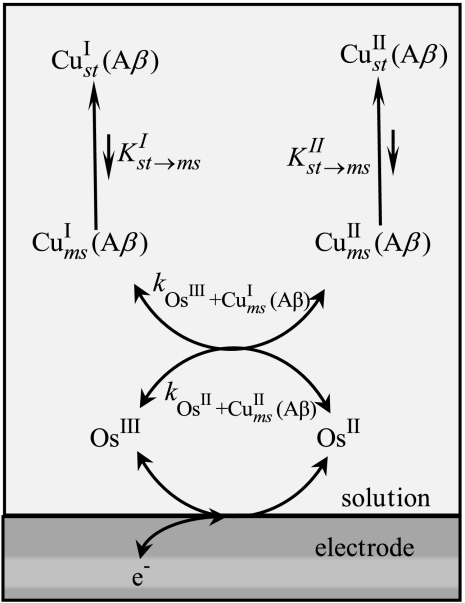
3. Kinetics and Mechanisms of the Homogeneous Electron Transfer Chemistry of the Cu^II/I(Aβ) Couple.

One may wonder if the kinetics and its mechanistic implications depicted so far are not related to some unidentified peculiarity of the electrochemical situation. If this is not the case, the same mechanism should consistently apply to electron transfer reactions from or to a homogeneous reagent. Two examples are given in Fig. 4, which shows the cyclic voltammetric catalytic responses (43, 44) resulting from the homogeneous reaction of Cu(Aβ) complex with the [Os(bpy)₂(py)Cl]^2+/+ and [Os(dmbpy)₂Cl₂]^+/0 complexes (py: pyridine, bpy: 2,2′ bispyridine, dmbpy: 4,4′-dimethyl-2,2′-bipyridine). In the first case, the thermodynamics is in favor of the reaction of the Os^III complex with the Cu^I complex, and vice versa in the second case. Simulation of these catalytic responses using the parameter values listed in Table 1 leads to a satisfactory fitting of the experimental data (Fig. 4) with the two osmium mediators. The rate constants are predicted to obey the following quadratic law (45):

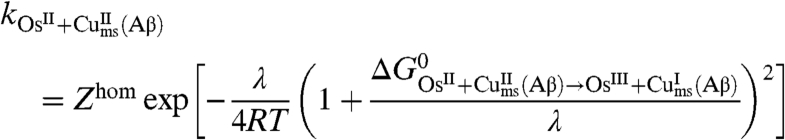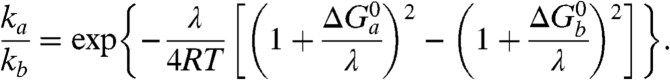Scheme 2 summarizes this electrochemical sensing of the homogeneous electron transfer reactions. Taking as values of the reorganization energies 0.3 eV for both the Cu and Os complexes, and thus λ = 0.3 eV, one predicts that k_a/k_b = 1.9 × 10^-3 in good agreement with the experimental value, k_a/k_b = 2.3 × 10^-3, thus validating in the homogeneous case the preorganization mechanism uncovered by the direct electrochemical approach.

Fig. 4.

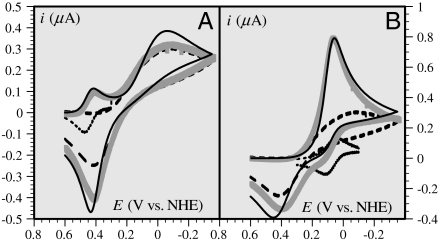
Catalytic cyclic voltammetric responses, at a glassy carbon electrode, of a 0.2-mM solution of Cu^II in a pH = 6.7 pipes buffer containing 0.2 M KCl in the presence of 1-mM solution of Aβ16 and of 0.02 mM [Os^III(bpy)₂(py)Cl](PF₆)₂ (A) and [Os^III(dmbpy)₂Cl₂](PF₆) (B). Dotted line: Os mediator alone; dashed line: Cu(Aβ) alone; thick gray line: mediator and Cu(Aβ) together; solid black line: simulation of redox catalytic response (see text). Scan rate: 0.02 V/s.

Table 1.

Simulation parameters for Fig. 4 and Scheme 2

	CuII/I(Aβ)	[Os(bpy)2(py)Cl]2+/+	[Os(dmbpy)2Cl2]+/0
Standard potentials (V vs. NHE)	0.300	0.445	0.090
Diffusion coefficients (cm2 s-1)	2 × 10-6	4.5 × 10-6	4.5 × 10-6
Driving forces (eV)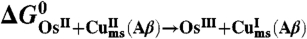
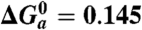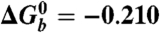Rate constants (M-1 s-1)	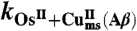	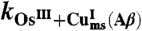ka = 7.0 × 105k-a = 2 × 108	kb = 3 × 108k-b = 7 × 104

Scheme 2.

Indirect electrochemistry of the Cu^II/I(Aβ) couple by means of an Os^III/II couple

Concluding Remarks

In summary, the most important finding of this study is that the homogeneous as well as the electrochemical electron transfer reactivity of the Aβ copper complexes involve a rather peculiar “POET” mechanism: The reaction proceeds through a small fraction (of the order of 1/1,000) of the complex molecules in which, starting either from the Cu^II state or from the Cu^I state, the peptide complex is preorganized so as the distances and angles in the coordination sphere to vary minimally upon electron transfer, thus involving a remarkably small reorganization energy of 0.3 eV. A remarkable feature of the POET mechanism is the fact that the preorganized states are formed continuously by a rapid change of the peptide complex conformation. It is this rapid equilibration that allows the observation of the typical variation of the oxidation rate constant with potential represented in Fig. 2. We may note, in passing, the power of the direct electrochemical approach that, through a technique such as cyclic voltammetry, offers a continuous variation of the reaction driving force, which parallels the variations of the electrode potential. The same technique applied indirectly also allowed the kinetic characterization of homogeneous electron transfer reactions by generation at the electrode surface of the active electron transfer reagent.

There is some similarity between the POET mechanism and mechanisms involving “entatic states,” as introduced to relate the rapidity of electron transfer in the blue copper proteins and other metalloenzymes to the constraint (the Greek “entasis” means tension) exerted by the protein matrix so as to make the coordination sphere of the two oxidation states adopt a similar geometry, thereby minimizing the reorganization energy (46–49). Several artificial systems possessing similar entatic characteristics have been proposed (25, 28, 50–53). These entatic structures are the result of strong constraints exerted on the coordination sphere. The common feature between these mechanisms is the small reorganization energy. With the POET mechanism, however, the oxidized and reduced complexes are not forced to adopt entatic structures. Only a small amount of the oxidized and reduced complexes adopt these favorable, entatic-like structures, being in fast equilibrium with the dominant forms of these complexes.

As regards homogeneous electron transfers, the POET mechanism, with its quadratic electron transfer law, and its consequences on the reactivity should be taken into account for reactions involving dioxygen and hydrogen peroxide as well.

Material and Methods

Information on the origin and structure of the Aβ16 peptide can be found in SI Appendix as well as concerning the origin of all chemicals used. The electrochemical kinetics was obtained from cyclic voltammetric experiments on a glassy carbon electrode as detailed in SI Appendix. Numerical simulations were carried out with the Digielch package (54).