Storage of nuclear magnetization as long-lived singlet order in low magnetic field

Abstract

Hyperpolarized nuclear states provide NMR signals enhanced by many orders of magnitude, with numerous potential applications to analytical NMR, in vivo NMR, and NMR imaging. However, the lifetime of hyperpolarized magnetization is normally limited by the relaxation time constant T₁, which lies in the range of milliseconds to minutes, apart from in exceptional cases. In many cases, the lifetime of the hyperpolarized state may be enhanced by converting the magnetization into nuclear singlet order, where it is protected against many common relaxation mechanisms. However, all current methods for converting magnetization into singlet order require the use of a high-field, high-homogeneity NMR magnet, which is incompatible with most hyperpolarization procedures. We demonstrate a new method for converting magnetization into singlet order and back again. The new technique is suitable for magnetically inequivalent spin-pair systems in weak and inhomogeneous magnetic fields, and is compatible with known hyperpolarization technology. The method involves audio-frequency pulsed irradiation at the low-field nuclear Larmor frequency, employing coupling-synchronized trains of 180° pulses to induce singlet–triplet transitions. The echo trains are used as building blocks for a pulse sequence called M2S that transforms longitudinal magnetization into long-lived singlet order. The time-reverse of the pulse sequence, called S2M, converts singlet order back into longitudinal magnetization. The method is demonstrated on a solution of ¹⁵N-labeled nitrous oxide. The magnetization is stored in low magnetic field for over 30 min, even though the T₁ is less than 3 min under the same conditions.

The NMR of long-lived-spin states is an emerging technique with potential applications to the transport of hyperpolarized spin order and to the investigation of molecular geometry and dynamics (1–15). The long lifetime of long-lived singlet states (in some cases, almost 30 min; ref. 16) suggests many attractive potential applications to in vivo NMR and NMR imaging using hyperpolarized materials.

However, several difficulties must be overcome before long-lived singlet states may be applied in the context of hyperpolarized NMR. One problem is that the established methods for generating nuclear hyperpolarization, such as optical pumping (17, 18) and dissolution dynamic nuclear polarization (DNP) (19, 20), generate hyperpolarized magnetization, not hyperpolarized singlet order. The hyperpolarized magnetization must therefore be converted into singlet order in order to take advantage of its long lifetime. The problem is that, until now, all currently available methods for performing magnetization-to-singlet conversion (1–4, 11, 12) require frequency-selective manipulations that are selective for individual chemical sites. Such methods require chemical-shift resolution of the coupled spins and are difficult to combine with known hyperpolarized methods.

For example, in the dissolution-DNP method (19) the sample is incorporated together with paramagnetic agents in a low-temperature glass which is illuminated with microwaves near the electron resonance frequency. The hyperpolarized solid material is rapidly dissolved by injection of a warm solvent and ejected out of the magnet. Generation of a hyperpolarized singlet state would require either (i) site-selective manipulation of the nuclear spin system in the solid state before dissolution, or (ii) in situ dissolution of the solid material in the polarizer magnet and application of a frequency-selective pulse sequence to the hyperpolarized solution before ejection. Method (i) is seriously hindered by the limited spectral resolution in the solid state, due to chemical-shift anisotropies and dipole–dipole couplings, whereas (ii) would require the incorporation of a high-homogeneity, warm sample chamber inside the polarizer magnet, which is hard to combine with the low-temperature specifications of the polarization chamber, without introducing a second magnet center. Although such difficulties might be overcome, a considerable engineering effort would be required.

So far, combinations of hyperpolarization with singlet states have therefore involved conventional hyperpolarization of ¹³C magnetization, followed by conversion to singlet order at a later stage (13) or the participation of chemical reactions (10).

In this communication, we demonstrate a technique that allows conversion of magnetization into singlet order, and the reverse, entirely outside the NMR magnet. The method operates well even when the magnetic field is much too low to resolve the chemical-shift difference, and even when the magnetic field is inhomogeneous. This pulse sequence employs trains of 180° pulses spaced by intervals of 1/(2J), where J is the scalar coupling constant, in the case of coupled spin pairs. As discussed below, these J-synchronized spin-echo trains induce singlet–triplet transitions by allowing the effect of a very small chemical-shift difference to accumulate over a long period of time, while compensating for magnetic field inhomogeneity. The J-synchronized spin-echo trains are incorporated into two pulse sequences, called M2S and S2M, which transform magnetization into singlet order, and back again.

Results

This technique was demonstrated on 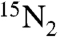-labeled nitrous oxide (N₂O) dissolved in deuterated methyl sulfoxide. This system was chosen on the grounds of familiarity in our group and because its slow conventional relaxation (16) facilitates the sample transport. Nevertheless, the method should be applicable to any molecular system containing inequivalent pairs of spins 1/2. Extensions to multiple-spin systems are also feasible (5, 8, 9).

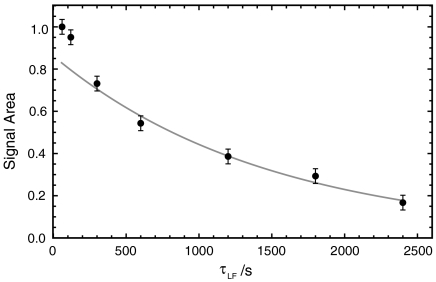
Fig. 1 shows experimental results for the decay of the ¹⁵N magnetization in ¹⁵N–N₂O. The decay is measured outside the NMR magnet, using the technique described below, which involves the temporary storage of magnetization as low-field singlet order by the application of audio-frequency pulse trains. The observed decay is biexponential, for reasons discussed below. The decay beyond ∼500 s has a time constant of 25 ± 3 min, which is an order of magnitude longer than the conventional relaxation times T₁, which are 198 and 114 s for the terminal and central positions, respectively.

Fig. 1.

Decay of ¹⁵N NMR signals for 0.3 M ¹⁵N–N₂O in DMSO-d₆, as a function of the low-field storage interval τ_LF. Circles are experimental data acquired with the pulse sequence in Fig. 2; the solid line is the best fit to an exponential decay, excluding the first few points which are perturbed by the equilibration of the triplet populations (see text). The decay time constant is estimated to be 25 ± 3 min.

The very slow decay of the NMR signal, with a time constant much longer than T₁, proves that magnetization is indeed stored as long-lived singlet order in low magnetic field.

Discussion

The operation of the M2S and S2M sequences will be explained in full elsewhere. The following discussion sketches the basic principles.

Pulse Sequences.

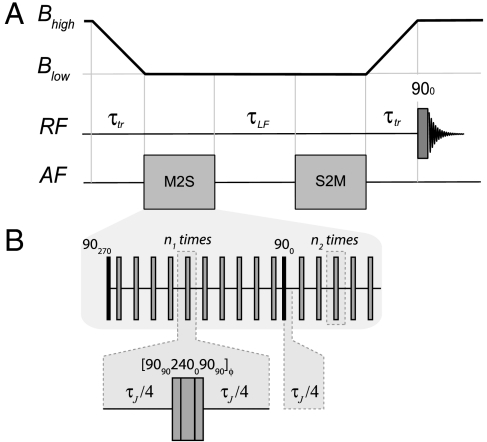
Fig. 2 shows the experimental procedure for demonstrating the storage of nuclear spin magnetization as low-field singlet order. The sample acquires Zeeman magnetization by thermal equilibration in high field. The magnetized sample is transported into the low-field region, and the magnetization is converted into singlet order by the audio-frequency pulse sequence denoted M2S and described in more detail below. The singlet order is left in low magnetic field for an interval τ_LF before the singlet order is converted back into magnetization by a sequence S2M. The sample is transported back into the magnet and a resonant 90° pulse is applied. The amplitude of the high-field NMR signal is proportional to the longitudinal magnetization before the pulse. The decay of singlet order in low field is tracked by repeating the experiment with different values of the low-field waiting interval τ_LF.

Fig. 2.

(A) Pulse sequence for demonstrating the storage of longitudinal magnetization as singlet order in low magnetic field. The top trace shows the trajectory of magnetic fields as the sample is transported from the high-field magnet (B_high) into the low-field region B_low. The transport intervals are denoted τ_tr. A 90° radio-frequency pulse (RF) is applied in high field to estimate the final longitudinal magnetization. Transverse audio-frequency (AF) fields are applied at the nuclear Larmor frequency in the low-field region to convert magnetization into singlet order (M2S) and back again (S2M). The low-field storage interval is denoted τ_LF. (B) Detailed view of the M2S pulse sequence. The pulse sequence contains two 90° pulses with phases 270° and 0, and two spin-echo trains, each generated by repeating a unit consisting of the composite 180° pulse [90₉₀240₀90₉₀]_ϕ bracketed by two intervals of duration τ_J/4, where τ_J = J^-1. The numbers of repetitions are n₁ and n₂ in the first and second parts of the pulse sequence, respectively. The overall phases ϕ of the composite pulses run through the four-step cycle {0,0,180°,180°,…}. An additional τ_J/4 interval is inserted immediately after the second 90° pulse, before the second echo train starts. The pulse sequence S2M is the same as M2S, but in reverse chronological order.

The audio-frequency pulse sequence M2S is sketched in Fig. 2B. Its components are as follows (flip angles and phases are specified in degrees, with phases specified by subscripts): (i) a 90₂₇₀ pulse; (ii) n₁ repetitions of the spin-echo element (τ_J/4 - R_ϕ - τ_J/4), where the intervals are defined using τ_J = J^-1 and R_ϕ denotes a composite 180° pulse. In the current experiments, composite pulses of the form R_ϕ = [90₉₀240₀90₉₀]_ϕ were used, where the overall phase ϕ steps through an error-compensated four-step phase cycle ϕ = {0,0,180,180,0,0,…} as the echo train proceeds (21, 22); (iii) a 90₀ pulse; (iv) a single interval of duration τ_J/4; n₂ repetitions of the spin-echo element (τ_J/4 - R_ϕ - τ_J/4). The echo numbers are given by and 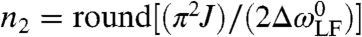, with round[x] defined as the nearest integer to x. Here 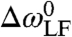is the difference in chemical-shift frequencies in the low magnetic field, defined by

where Δδ is the difference in chemical shifts, B_low is the strength of the low magnetic field, and γ is the magnetogyric ratio of the nuclei.

The pulse sequence S2M is given by M2S in reverse chronological order.

Spin System.

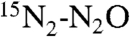contains two ¹⁵N nuclei, which have spin quantum number I = 1/2. The two ¹⁵N sites are chemically inequivalent, with a chemical-shift difference of 82.3 ppm. In the low magnetic field of 2.200 mT, there is a 0.8 Hz difference in the Larmor frequencies of the two sites. This frequency difference is much smaller than the ¹⁵N-¹⁵N J-coupling, which is about 8 Hz. The spin system of the two ¹⁵N nuclei therefore corresponds to a very strongly coupled AB system. The low-field ¹⁵N NMR spectrum is a single peak, with no resolution of the two different chemical sites. To make matters worse, the inhomogeneity of the magnetic field, which is not optimized in any way, corresponds to a ¹⁵N linewidth of around ± 140 Hz, i.e., over two orders of magnitude greater than the chemical-shift frequency difference. In these circumstances, the established methods for converting magnetization into singlet order, which require site-selective spin manipulations, do not work.

Energy Eigenstates.

To a good approximation, the energy eigenstates of the 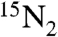system in low magnetic field are as follows:

These are exact eigenstates in the absence of a chemical-shift difference between the spins. The difference in the Hamiltonian eigenvalues for states |0〉 and |2〉 is given by 2πJ.

The chemical-shift difference frequency generates a small off-diagonal element between the singlet state and the central triplet state, as may be seen through the following identity:

This off-diagonal element is much smaller than the difference in the corresponding eigenvalues. According to time-independent perturbation theory, the off-diagonal term may be ignored, to a good approximation.

J-Synchronized Spin-Echo Trains.

The dictates of time-independent perturbation theory may be defeated by introducing a resonant time dependence. In the current case, carefully timed spin-echo trains are used to induce singlet–triplet transitions.

The sign of the chemical-shift difference interaction is effectively inverted by a 180° pulse, while the J-coupling interaction, which is a scalar, is unchanged. If the 180° pulses are repeated at the correct frequency, the modulated chemical-shift difference resonates with the J-coupling interaction. Under these circumstances, the quenching effect of the J coupling is removed, and the effect of the small chemical-shift difference accumulates. A more detailed analysis, given elsewhere, shows that a J-synchronized spin-echo train consisting of n echo repetitions (where n is even) may be represented as a propagator of the following form:

where 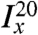is a single-transition operator for the transition between the central triplet state and the singlet state (23, 24). The J-synchronized spin-echo sequences may therefore be used to induce a rotation in the singlet–triplet subspace, in a similar way to extremely low-frequency (ELF) field modulations (25). However, J-synchronized spin-echo trains provide a more robust manipulation of the spin system than ELF field modulations.

In the M2S and S2M pulse sequences, the echo sequences with n₁ repetitions induce an approximate rotation by 180° in the singlet–triplet subspace, whereas the sequences with n₂ repetitions induce an approximate rotation by 90° in the singlet-triplet subspace, i.e.,

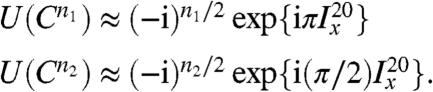The complex phase factors in the equations above are included for the sake of rigor but have no practical consequence.

Magnetization-to-Singlet Conversion.

The sequence of events during the sequence M2S, in the absence of relaxation, is as follows:

1. Longitudinal magnetization is established by thermal equilibration in high field, followed by transport into low field:

   
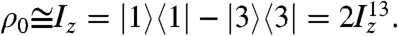
2. The longitudinal magnetization is converted into transverse magnetization by the first 90° pulse. The state after the pulse corresponds to single-quantum coherences between the outer triplet states and the inner triplet state:

   
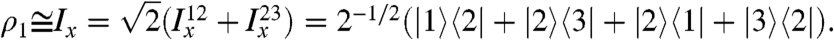
3. The first J-synchronized spin-echo sequence induces a π rotation in the {|0〉,|2〉} subspace. This rotation exchanges the central triplet state with the singlet state, leading to the following result:

   

   At this point, the density operator contains coherences between the outer pair of triplet levels and the singlet state.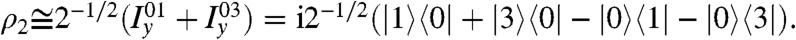
4. The 90₀ pulse acts within the triplet manifold and induces the following transformations:

   

   The density operator after the second 90° pulse is therefore given by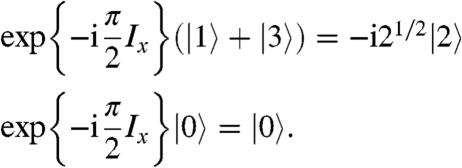

   

   This density operator now contains coherences between the central triplet state and the singlet state.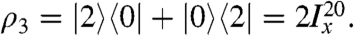
5. Because there is a difference in energy of 2πJ between the central triplet state and the singlet state, a delay of τ_J/4, where τ_J = J^-1, induces a phase rotation of the singlet-triplet coherence by π/2. The density operator after the inserted delay is therefore given by

   
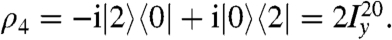
6. The second J-synchronized spin-echo sequence induces an approximate π/2 rotation about the x axis in the {|0〉,|2〉} subspace, rotating the coherence into a population difference between the singlet state and the central triplet state:

   

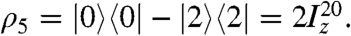
The overall conversion of longitudinal magnetization I_z into a singlet–triplet population difference 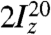is accomplished without chemical-shift resolution of the coupled sites.

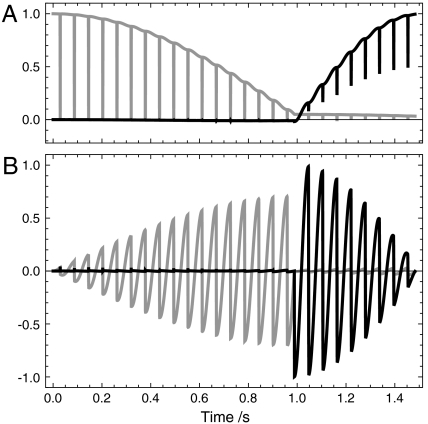
Fig. 3 shows a numerical simulation displaying the trajectories of the most important spin operator components during the M2S pulse sequence.

Fig. 3.

Numerical simulations of the spin operator trajectories during the M2S pulse sequence, neglecting relaxation. All plotted trajectories correspond to quantities Re{Tr(Q^†U(t)ρ(0)U(t)^†)} where U(t) is the pulse sequence propagator, ρ₀ is the initial spin density operator, Tr denotes the trace of the operator matrix representation, and Q is the operator of interest. All trajectories are calculated using Mathematica (Wolfram, Inc.) for numerical integration of the Liouville von-Neumann equation. (A) Trajectories for Q = I_x/2 (gray) and 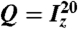(black). This plot shows the transformation of transverse magnetization (generated by the first 90° pulse) into a singlet–triplet population difference. (B) Trajectories for 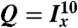(gray) and 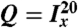(black). This shows the buildup of coherence between the singlet state and the outer triplet states, and its conversion into coherence between the singlet state and the inner triplet state by the second 90° pulse. The spikes in the trajectories indicate rapid excursions of the density operator during the composite pulses. All simulation parameters correspond to the actual experiment.

Low-Field Decay.

Suppose now that the prepared state 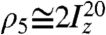is left in low magnetic field for a long interval τ_LF. The density operator may be written as follows:

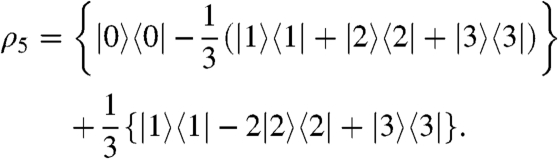The first term represents a differential between the singlet population and the mean of the triplet populations. This state decays slowly, with the singlet relaxation time constant, T_S. The second term, on the other hand, represents nonuniform triplet populations. This term decays relatively fast. The experimental results shown in Fig. 1 display a distinct biexponential decay with an initial decay time constant given by 67 ± 22 s. This time constant is about one-half of T₁, which is consistent with the second-rank nature of the second term in the equation above.

Retrieval of Magnetization.

After a time long compared to T₁, but short compared to T_S, the density operator is given by

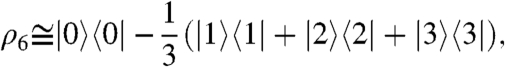which may be expressed as the sum of two orthogonal terms:

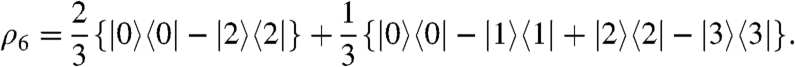The first of these terms corresponds to the operator , which is converted into the operator (2/3)I_z by the S2M sequence, which is the reverse of the M2S sequence. The S2M–M2S combination therefore has a maximum theoretical efficiency of 2/3 = 66.7% for the storage of longitudinal magnetization as long-lived singlet order.

In summary, the audio-frequency pulse sequence in Fig. 2B executes the following transformations of the spin density operator in a low magnetic field:

In practice, some additional loss of spin order occurs due to relaxation during the conversion sequences, pulse imperfections, and magnetic field inhomogeneity.

Conclusions.

We have shown that it is possible to store nuclear magnetization as long-lived singlet order, using manipulations that are performed entirely outside a high-field NMR magnet. The ability to transform magnetization into singlet order, and back again, under conditions of low magnetic field and poor field homogeneity, opens up unique possibilities for combining hyperpolarization techniques with long-lived nuclear singlet states. For example, hyperpolarized nuclear magnetization may be generated by dissolution DNP (19) and converted into singlet order by an M2S sequence applied outside the polarizer magnet, before the hyperpolarized material is introduced into the subject. The long lifetime of the singlet order should allow more time for transport, diffusion, or metabolic processing of the hyperpolarized agent, before conversion of the singlet order back into magnetization and extraction of the spatial or metabolic information by NMR spectroscopy or magnetic resonance imaging.

Although hyperpolarized may have applications to in vivo NMR and NMR imaging, we are also exploring the application of this method to molecular systems of more immediate applicability, such as ¹³C-labeled pyruvate (20).

The technique is also compatible with hyperpolarization methods other than DNP, such as parahydrogen-induced polarization (26, 27).

The pulse sequence also has applications in high-field NMR, where it allows magnetization-to-singlet conversion in systems with very small chemical-shift differences, as will be described elsewhere.

Materials and Methods

Equipment.

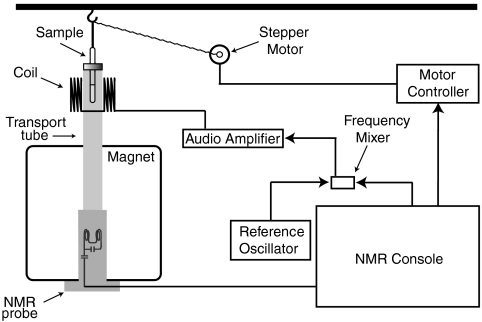
The equipment used is sketched in Fig. 4. This set up is based on a modified 300 MHz NMR system with an 89 mm bore 7.04 T magnet. The 10-mm outer-diameter NMR sample tube is suspended by a string which passes over a hook in the ceiling. The sample is pulled up and down by winding the string around an axle driven by a stepper motor, which is interfaced to the NMR console through transistor–transistor logic lines. The transport from the sweet spot of the magnet to the top of the tube takes 10 s. The return trip takes the same amount of time. The sample is guided in and out of the magnet by an aluminum tube. The aluminum is replaced by plastic at its top end in order to allow penetration of audio-frequency magnetic fields.

Fig. 4.

Equipment used to demonstrate the conversion of longitudinal magnetization into long-lived singlet spin order, and back again, using audio-frequency pulses at the low-field nuclear resonance frequency.

At its highest point, the sample is about 145 cm directly above the magnetic sweet spot in the axial direction. The field at this point, as measured by a Hall device and by precise ¹⁵N Larmor-frequency measurements, is 2.200 mT. No low-field compensation or shimming coils were used. The magnetic field inhomogeneities along the z axis and across the sample were estimated to be ± 33 μT (with respect to the sample center point) by measuring the low-field ¹⁵N line shape of a sodium ¹⁵N-nitrate solution, using an indirect field-cycling procedure.

The Larmor frequency of ¹⁵N in the low-field region is 9.5 kHz. The Larmor-frequency excitation pulses are initially generated at a frequency of 30 MHz in the NMR console and mixed down to 9.5 kHz by using a separate reference oscillator, a radiofrequency mixer, and a low-pass filter. This procedure allows full amplitude and phase agility, using the conventional spectrometer software. The audio-frequency signal is amplified by a 500 W stereo audio amplifier (Behringer A500), used in mono bridge mode.

The audio-frequency pulse sequence is applied to the sample using a transverse Helmholtz coil. The coil consists of two solenoids, each with 20 turns of copper wire (outer diameter 0.56 mm). Each solenoid has a diameter of 15 cm, a length of 1 cm, and the distance between the solenoid centers is 8.6 cm. The peak field generated by the coil is 420 μT, corresponding to a ¹⁵N nutation frequency of 910 Hz.

Sample.

The sample tube contained 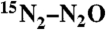(Cambridge Isotopes), dissolved in DMSO-d₆ in a concentration of about 0.3 M under a pressure of ∼3 bar and degassed to reduce paramagnetic relaxation caused by molecular oxygen. The ¹⁵N–¹⁵N J coupling is 8.21 Hz and the chemical-shift difference between the two ¹⁵N sites is 82.3 ppm. The flame-sealed glass sample tube had an outer diameter of 10 mm and the liquid region was about 2.5-cm long.

Pulse Sequence Parameters.

The experiments used the following pulse sequence parameters: τ_tr = 10 s; τ_J = 123.4 ms; n₁ = 18; n₂ = 9. The duration of a 90° audio-frequency pulse was 275 μs. The 90° pulse duration in high magnetic field was 25 μs.